1 Introduction
The combinatorial optimization problems included in the NP-complete class are of great scientific and technological interest given their everyday applicability.They cover different areas of knowledge including Mathematics, Computer Science, Operational Research, Genetics, Engineering and Electronics. They involve optimization from the classic problems of telecommunication network design, route programming, frequency assignment, machine planning or production organization to the most current engineering and software re-engineering [11].
Traveling Salesman Problem (TSP), is a classic problem of class NP-Complete and has as objective given the complete graph Kn with edge weights cuv, find a shortest Hamiltonian tour in Kn [13]. Due to their intractability, a large number of approximate methods have been designed to solve them, which find good solutions in reasonable times.
One of these methods is the Metaheuristic of Optimization by Ant Colonies. Since its inception, ACO algorithms have proven effective in solving combinatorial optimization problems, but collective intelligence, which is the main weapon of these, makes the quality of the solutions found directly proportional to the number of agents (Ants), that are interacting in the colony. This coupled with the existence of many problems characterized by the large size of their real instances, makes the execution of the ACO algorithms very costly for the time it takes to reach a sufficiently good, or perhaps optimal solution.
Obtaining information and interacting with a run-time algorithm, with its parameters, components and/or strategies is a powerful variant to improve its efficiency.
Moreover, in ACO metaheuristics algorithms, characterized by a set of parameters that influence, to a great extent, the search, its levels of intensification and exploration. From the above, we derive the problem of ignorance of adequate mechanisms to interact with real-time optimization algorithms that improve their efficiency.
To solve the problem we proposed: design a model of integration of visualization techniques to the ACO optimization algorithms, which would allow the user to guide the search of the solutions through their interaction with the visualization of the algorithm in real time and in this way improve their quality; and implement a software tool according to the model to solve TSP problems with the algorithm System of Ant Colony and user interaction [3].
The topic of the user-driven search is very young, the literature on the subject covers some studies: Fast and Robust Hand Tracking Using Detection-Guided Optimization [15], RNA-guided human genome engineering via Cas9 [10], Superior solution guided particle swarm optimization combined with local search techniques [18], Guided Policy Search [9].
2 Related Work
2.1 Metaheuristic Optimization by Ant Colonies
The metaheuristic of Optimization by Ant Colonies has its source of inspiration in the behavior of the real ants that minimize the route between its colony and any source of supply, and is based fundamentally in the indirect communication that takes place between the same ones the traces of a substance called pheromone, which they leave behind [1].
The structure of a generic algorithm for ACO metaheuristics is as follows [5]:
Procedure ACOMetaheuristic
Schedule Activities
1. ConstructAntsSolutions
2. UpdatePheromones
3. DaemonActions
End-Procedure
End-ScheduleActivities
— ConstructAntsSolutions: manages a colony of ants that concurrently and asynchronously visit adjacent states of the considered problem by moving through neighbor nodes of the problems construction graph. They move by applying a stochastic local decision policy that makes use of pheromone trails and heuristic information. In this way, ants incrementally build solutions to the optimization problem. Once an ant has built a solution, or while the solution is being built, the ant evaluates the (partial), solution that will be used by the UpdatePheromones procedure to decide how much pheromone to deposit [5].
— UpdatePheromones: is the process by which the pheromone trails are modified. The trails value can either increase, as ants deposit pheromone on the components or connections they use, or decrease, due to pheromone evaporation. From a practical point of view, the deposit of new pheromone increases the probability that those components/connections that were either used by many ants or that were used by at least one ant and which produced a very good solution will be used again by future ants. Differently, pheromone evaporation implements a useful form of forgetting: it avoids a too rapid convergence of the algorithm toward a suboptimal region, therefore favoring the exploration of new areas of the search space [5].
— DaemonActions: procedure is used to implement centralized actions which cannot be performed by single ants. Examples of daemon actions are the activation of a local optimization procedure, or the collection of global information that can be used to decide whether it is useful or not to deposit additional pheromone to bias the search process from a nonlocal perspective. As a practical example, the daemon can observe the path found by each ant in the colony and select one or a few ants (e.g., those that built the best solutions in the algorithm iteration), which are then allowed to deposit additional pheromone on the components/connections they used [5].
Several algorithms of ACO metaheuristics have been proposed, among those most cited in the literature: An Ant System (AS) [7], Ant Colony System (ACS) [6] and Max-Min Ant or Max-Min Ant System (MMAS) [16].
2.2 Integration Model of Visualization Techniques
Among the goodness of the visualization we can mention that it allows to describe the behavior of the algorithms at each moment of its execution, the state of each variable, the search space, in order to give a more direct treatment to the algorithm and to be able to search for desired behaviors or to locate regions of interest, and interact with the information provided in order to find solutions that are closer to the best and faster. All this based on the ability of the human brain to easily analyze visual images with a lot of information [2, 8, 17].
Visualization also contributes to the balance between intensification and diversification, as the user can guide the search as appropriate. We refer to intensification as the way to direct the most exhaustive search process in a given neighborhood and to diversification as the ability to appropriately visit various distant neighborhoods.
This balance is of fundamental importance since in most of the optimization problems the intensification and diversification strategies are opposed, in other words, a metaheuristic the more time it takes to intensify the search in a given region, the less time it can devote to diversify it in regions still unexplored, and vice versa [11].
For example, with the modification in the execution time of the algorithm of the amount of pheromone in the arcs that have higher values, it is possible to increase the exploration.
2.3 Visualizations and Interactions that can be Implemented
An interactive system provides the possibility for the user to have external control over the information being displayed and allows him to modify the algorithm whose behavior is being observed or the values of the data or parameters being processed. The information with which the ACO algorithms work can be visualized and thus a set of interactions can be implemented. Here are some alternatives:
— Display at each moment of the execution of the algorithm the route of each of the ants. It allows us to observe the trajectory that the ants follow to construct their solution and the accumulated cost in each moment, to analyze preferences of the ants for following certain trajectories, which is proportional to the high amount of pheromone in the arches that compose it.
— Show the best / worst trajectories of ants from time to time.
— Clone or delete one or more ants. This interaction is associated with the two previous views. When cloning an ant, usually one with a good trajectory, the chances of obtaining a better solution in the end are increased and by eliminating the ants that follow a bad trajectory would save time by exploring bad solutions.
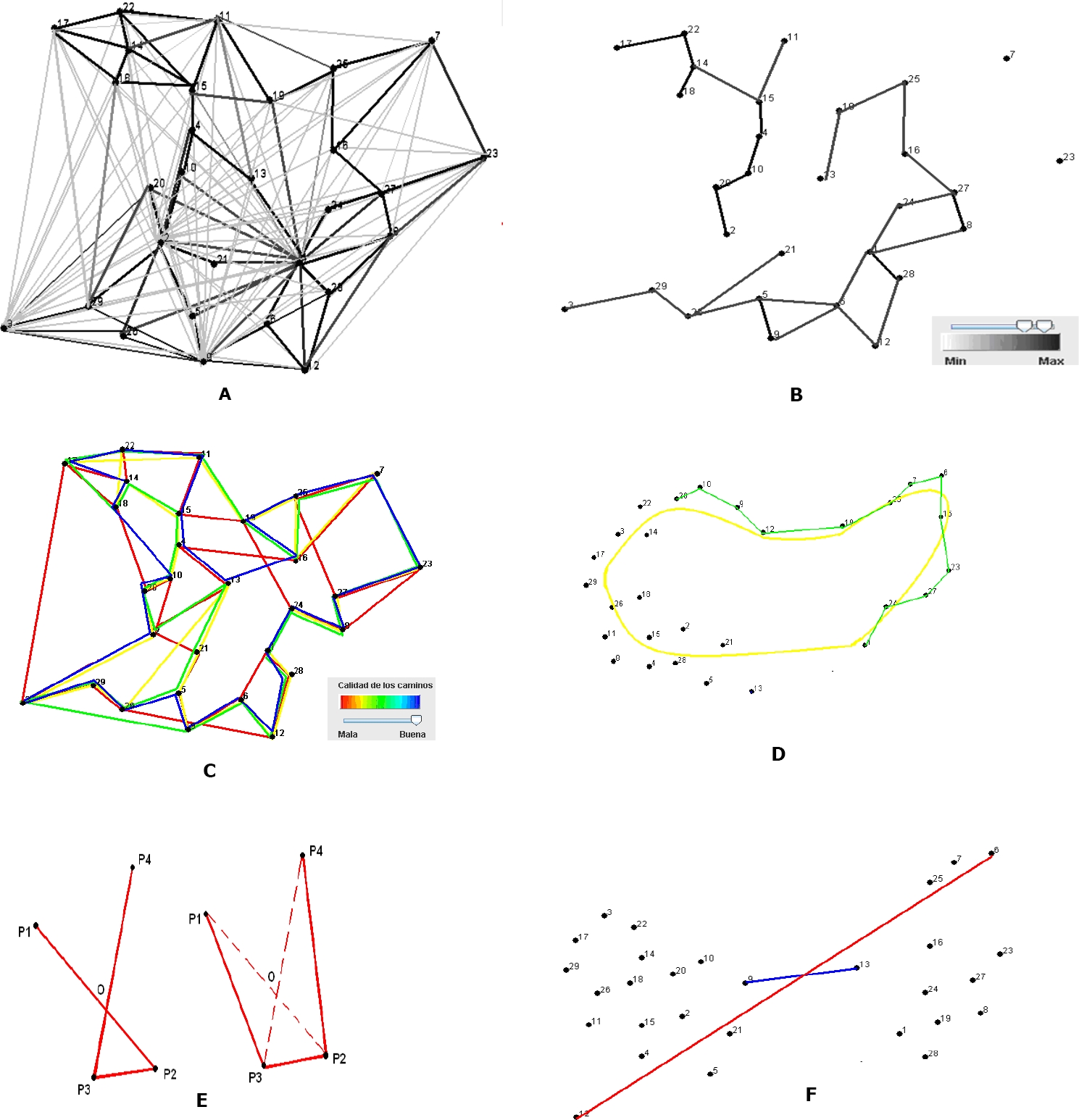
— Display and interact with the pheromone matrix by adding or deleting a value to the pheromone imprint in certain arcs. Adding pheromone to the arc joining the nodes i and j means raising the probability that an ant being at the node I is decided by the option to go to node j, likewise when removing pheromone in an arc restricts to a greater extent the choice to opt for that arc. This possibility is of vital importance, since the construction of the solutions of the ants and in general the solution of the problem to be optimized depends directly on the matrix of pheromone traces and in this way the construction of the solutions can be guided by the user. Figure 1A, shows an example of a pheromone matrix display, where the arcs are drawn in shades of gray and represent the pheromone trace in them. The greater the clarity of the bow, the less pheromone and vice versa.
— Filter the graph where the pheromone levels are shown showing only the arcs whose pheromone fingerprint is in a certain range (See Figure 1B).
This interaction is important since it shows more clearly the arcs whose levels of pheromone are in a selected range. In another case all arcs (n2 - n), would be shown, which would make it difficult to analyze them.
— Set an initial node or a region from where to get the initial node with which the ants begin building their solution.
— Set an initial node or a region from where to get the initial node with which the ants begin building their solution.
— Provide information about nodes and arcs. It includes the number of the node that identifies it in the path and the weight of the arcs, it is very useful when the data is displayed in a certain scale. This information can be displayed from the beginning and statically or dynamically, for example by moving or clicking the mouse over the node or arc.
— Show in more detail a selected region. It is very advantageous if the number of nodes in the graph is large and you want to better observe the behavior of ants in a certain region or modify parameters that are not easy Visual access.
— Visualize the solutions and filter according to their quality. It allows us to compare the finished solutions with the ones that ants are building. One way of representing the solutions can be seen in Figure 1C. This provides a lot of visual information, because the solutions found are displayed in different colors, where values closer to red would be the worst solutions, while the best would be close to blue.
— Vary the run speed of the algorithm. It makes it possible to look more closely at the data or how the trajectories of the ants vary.
— Stop the algorithm. In this way the parameters involved in the algorithm can be analyzed without being modified during the time that the analysis is consumed.
— Change the number of ants at any point in the execution of the algorithm. Each running ant means an attempt to find a good solution, but in turn implies a greater consumption of computational resources. Both indicators should be balanced appropriately depending on the available conditions.
— Vary the execution time of the algorithm.
— Modify algorithm parameters, e.g. initial pheromone and evaporation constant. The researcher is free to experiment by modifying these values for their specific problems in order to find the most appropriate ones, which provides a convenient flexibility to the algorithm.
— Fix a global path to which the solution of the problem must approach while optimizing the objective function. There are two fundamental reasons for this interaction: one is that we intuitively identify what can be a good route, and whether total or partial; and the second, the possibility of having certain risks in specific areas, which would condition to some extent the chosen path. In Figure 1D, the path in yellow would be the one that the user would set, whereas the trajectory of the ant (drawn in green) should approach that path.
— Draw a part of the path. P1-P2-P3-P4 draws a non-convex polygon that can be replaced by the path P1-P3-P2-P3-P4. P4 with the same nodes that minimizes the cost.
— Fix or delete an arc of the path. It can be assumed in certain cases that a specific arc must belong to the solution (Figure 1F, arc in blue) and fix it by means of the interaction. This implies that the moment one of the vertex of the arc appears in the solution, automatically the other vertex of the arc will be next.
— Show numerical results of the algorithm state. The execution of the algorithm at each moment is producing numerical values that can be visualized.
2.4 Model Schema
The integration of visualization techniques in algorithms presupposes the visualization, during the execution of the algorithm, of the information that is handled. This information is presented to the user so that he can interact with it and can modify it at his convenience. Figure 2, exemplifies an integration model of visualization techniques in ACO metaheuristics algorithms.
The operation of this model is as follows. The algorithm begins with the initialization of parameters that could be: quantity of ants, initial pheromone, evaporation constant, visibility scaling factor, among others. The nodes that make up the graph of the problem are displayed, for example their number, with this visualization the user can interact (represented in the figure by a rectangle with circular corners), selecting the initial node in which the ants must begin to construct their solution or a region from which to obtain said initial node. After the creation of the ants, these begin their activity in parallel and asynchronous.
For each one of them, the construction of its solution is visualized in real time drawing the arcs between the states in which they are moving. From the visualization of the trajectories (to visualize also the ants with better and worse trajectories), can be cloned or eliminated ants. When an ant is cloned, the new ant receives the path traversed by the cloned ant. From the visualization of the trajectories the interactions that have to do directly with the decision to choose the next node that will be part of the route, are given off, among them: to fix a global route to which the solution of the problem must be approached at the same time as optimize the objective function, draw a part of the path, set or exclude an arc of the path.
When the ants deposit pheromone, the same for algorithms with online update step by step, that for those who update the pheromone a posteriori, the visualization of the matrix of pheromones (resource represented in the figure by a circle), must also be updated so that the user can interact in real time with this visualization and modify the matrix. The pheromone graph can be shown with arcs in different colors, illustrating the amount of pheromone in each arc.
The user can at any time filter this graph to choose the arcs that have a certain amount of pheromone. After each iteration of the algorithm can be visualized, also with different colors, the solutions found according to a pre-established scale. The user can also filter the display that is presented, according to the quality of the solutions. In addition, the numerical results of the algorithm can be displayed and the parameters of the algorithm can be varied at any time in the run.
2.5 Visualization Tool
To validate the proposed integration model, we developed a software prototype: ACOVis version 1.0, which solves TSP problems with the ACS algorithm. This tool allows the user guide the search to find a good solution to the problem by interacting with the visualization of the algorithm. The implementation was done in Java language, using the Java2D library for visual representations and multi-thread programming to simulate the parallel and asynchronous behavior of the ants [4].
Figure 3, shows how the main view of the application was conformed. In general, this view has: a menu with several options, four panels, some buttons: two that allow you to exchange the left and right panels, one to change the displayed ant, another to activate the window that shows the best and worst paths in the moment that is executed and the others with movement functions of the major panel, three input fields to set the parameters: number of ants, run time and number of iterations and several slider. The larger left panel is mainly to visualize the path of the ants, the upper right shows the graph of pheromone traces, the lower right displays the solutions found in some of the iterations of the algorithm and the panel below shows the numerical results of the algorithm.
2.6 Experimental Results
An experimental study was carried out to compare the behavior of the pure ACS algorithm and the ACS algorithm with user interaction through the graphical interface created. We work with a set of instances representative of TSP [12], namely: eil51, berlin52, st70, kroA100, a280, rat783 and pr1002. The algorithm was applied to each of them with and without user interaction using the same parameters:
proposed by Gambardella and Dorigo [6], and 10 ants. There were 10 executions for the first five instances and 5 executions for the remaining ones, in both tests.
In the case of user-guided executions, the main interaction that was applied was the modification of the pheromone matrix, before and after the beginning of the algorithm, increasing or decreasing a value to the pheromone trace in the arcs estimated convenient (arcs that visually the user estimates that increasing the degree of pheromone can obtain better solutions), also in some iterations ants with good or bad behaviors respectively were cloned or eliminated.
The results were obtained in a workstation that among its features has a Core i5-3470 processor, with 8 gigabyte of DDR3 RAM and graphics adapter Intel HD Graphics 2500. The dataset and the best solution registered at TSPLIB1. TSPLIB is a library of sample instances for the TSP (and related problems), from various sources and of various types [14]. Table 1, summarizes the results obtained in the study.
Table 1 Experimental results
| Name | # Nodes | ACS | ACS user-guided | Best Solution | ||
|---|---|---|---|---|---|---|
| Cost | Iterations | Cost | Iterations | |||
| eil51 | 51 | 443.6 | 500 | 426.9 | 300 | 426 |
| berlin52 | 52 | 7585.4 | 500 | 7542 | 300 | 7542 |
| st70 | 70 | 705.3 | 500 | 675 | 300 | 675 |
| kroA100 | 100 | 24024.5 | 500 | 21321.5 | 300 | 21282 |
| a280 | 280 | 2885.9 | 500 | 2599.3 | 300 | 2579 |
| rat783 | 783 | 10005.6 | 1000 | 8901.4 | 300 | 8806 |
| pr1002 | 1002 | 301957.2 | 1000 | 279066.3 | 300 | 259045 |
To compare the mean values of the costs obtained in the executed runs of the pure ACS algorithm and the ACS algorithm guided by the user, for the seven instances of the TSP analyzed, we used the nonparametric test of the Wilcoxon signed ranges. This test yielded an asymptotic significance value of 0.018 (< 0.05), so that there are significant differences between the solutions obtained by both tests.
Therefore, user interaction with the optimization algorithm may lead to better results. On the other hand, considering that the number of iterations for each run of the user-guided ACS algorithm (300 iterations), was intentionally lower than for pure ACS runs (500 or 1000 according to the TSP instance), it is evident that only through interaction with the user can better solutions be obtained, but better solutions can be obtained in a shorter time.
We consider it fair to recognize that the measure of how beneficial the guided search by the user can be depends on several factors, among them: familiarization of the user with the problem, size of the problem and distribution of the nodes in the plane.
3 Conclusion and Future Work
During the present investigation, the metaheuristics of Optimization with Ant Colonies were described, identifying the types of interactions that the user could perform with the visualization of the ACO algorithms and the contributions of these to the solution of the optimization problems. In addition, a model of integration of visualization techniques was proposed to the algorithms for optimization of ACO metaheuristics, implementing a software tool to interact with the visualization of the ACS algorithm in the TSP solution.
An experimental study with the implemented tool showed that when the user interacts with the optimization algorithm at runtime it can achieve better quality solutions and in acceptable time periods, always depending on the knowledge, intuition and insight of the specialist operating the tool. User-guided search for solving optimization problems offers considerable advantages, so it is recommended that you continue your study.











 text new page (beta)
text new page (beta)