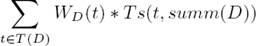1 Introduction
Automatic text summarization is the holy grail for people battling information overload, which becomes more and more acute over time. Hence it has attracted many researchers from diverse fields since the 1950s. However, it has remained a serious challenge, especially in the case of single news articles. The single document summarization competition at Document Understanding Conferences (DUC) was abandoned after only two years, 2001-2002, since many automatic summarizers could not outperform a baseline summary consisting of the first 100 words of a news article. Those that did outperform the baseline could not do so in a statistically significant way [35].
Summarization can be extractive or abstractive [29]: in extractive summarization sentences are chosen from the article(s) given as input, whereas in abstractive summarization sentences may be generated or a new representation of the article(s) may be output. Extractive summarization is popular, so we explore whether there are inherent limits on the performance of such systems.1 We then generalize existing models for summarization and define compressibility of a document. We explore this concept for documents from three genres and then unify new and existing heuristics for summarization in a single framework. Our contributions:
We show the limitations of single and multi-document extractive summarization when the comparison is with respect to gold-standard human-constructed abstractive summaries on DUC data (Section 3).
Specifically, we show that when the documents themselves from the DUC 2001-2002 datasets are compared using ROUGE [26] to model abstractive summaries written by human experts, the average Rouge-1 (unigram) recall is around 90%. On ROUGE evaluations, no extractive summarizer can do better than just returning the document itself (in practice it will do much worse because of the size constraint on summaries).
For multi-document summarization, we show limits in two ways: (i) we concatenate the documents in each set and examine how this “superdocument” performs as a summary with respect to the manual abstractive summaries, and (ii) we study how each document measures up against the manual summaries and then average the performance of all the documents in each set.
Inspired by this view of documents as summaries, we introduce and explore a generalized model of summarization (Section 4) that unifies the three different dimensions: abstractive versus extractive, single versus multi-document and syntactic versus semantic.
We prove that constructing certain extractive summaries is isomorphic to the min cover problem for sets, which shows that not only is the optimal summary problem NP-complete but it has a greedy heuristic that gives a multiplicative logarithmic approximation.
Based on our model, we can define the compressibility of a document. We study this notion for different genres of articles including: news articles, scientific articles and short stories.
We present new and existing heuristics for single-document summarization, which represent different time and compressibility trade-offs. We compare them against existing summarizers proven on DUC datasets.
Although many metrics have been proposed (more in Section 2), we use ROUGE because of its popularity, ease of use and correlation with human evaluations.
2 Related Work
Most of the summarization literature focuses on single-document and multi-document summarization algorithms and frameworks rather than limits on the performance of summarization systems. As pointed out by [11], competitive summarization systems are typically extractive, selecting representative sentences, concatenating them and often compressing them to squeeze in more sentences within the constraint. The summarization literature is vast, so we refer the reader to the recent survey [15], which is fairly comprehensive for summarization research until 2015. Here, we give a sampling of the literature and focus more on recent research and/or evaluation work.
Single-document extractive summarization. For single-document summarization, [30] explicitly model extraction and compression, but their results showed a wide variation on a subset of 140 documents from the DUC 2002 dataset, and [36] focused on topic coherence with a graphical structure with separate importance, coherence and topic coverage functions. In [36], the authors present results for single-document summarization on a subset of PLOS Medicine articles and DUC 2002 dataset without mentioning the number of articles used. An algorithm combining syntactic and semantic features was presented by [3], and graph-based summarization methods in [44, 13, 34, 24]. Several systems were compared against a newly-devised supervised method on a dataset from Yahoo in [32].
Multi-document extractive summarization. For multi-document summarization, extraction and redundancy/compression of sentences have been modeled by integer linear programming and approximation algorithms [45, 31, 18, 5, 1, 25, 6, 48]. Supervised and semi-supervised learning based extractive summarization was studied in [46]. Of course, single-document summarization can be considered as a special case, but no experimental results are presented for this important special case in the papers cited in this paragraph.
Abstractive summarization. Abstractive summarization systems include [7, 16, 8, 27, 39, 9]. Techniques range from graph-based approaches to recent trends in neural network based methods[15].
Frameworks. Frameworks for single-document summarization were presented in [14, 31, 42], and some multi-document summarization frameworks are in [20, 49].
Metrics and Evaluation. Of course, ROUGE is not the only metric for evaluating summaries. Human evaluators were used at NIST for scoring summaries on seven different metrics such as linguistic quality, content coverage, overall coherence, etc. There is also the Pyramid approach [37], BE [43], and information-theoretic measures/N-gram graphs [17, 40, 28], for example. Our choice of ROUGE is based on its popularity, ease of use, and correlation with human assessment [26]. Our choice of ROUGE configurations includes the ones that were found to be best according to the paper [19].
3 Limits on Extractive Summarization
In all instances the ROUGE evaluations include the best schemes as shown by [19], which are usually Rouge-2 (bigram) and Rouge-3 (trigram) with stemming and stopword elimination. We also include the results without stopword elimination. The only modification was if the original parameters limited the size of the generated summary; we removed that option.
3.1 Single-document Summarization
To study limits on extractive summarization, we will pretend that the document is itself a summary that needs to be evaluated against the human (abstractive) summaries created by NIST experts. Of course, the “precision” of such a summary will be very low, so we focus on recall (and F-score by letting the document get all its recall from the same size as the human summary (100 words)).
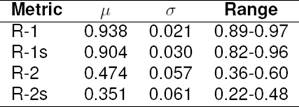
Table 2 shows that, for the DUC 20022 dataset, when the document themselves are considered as summaries and evaluated against a set of 100-word human abstractive summaries, the average Rouge-1 (unigram) [26] score is approximately 91 %. Tables 1 through 4 and Figures 3 and 4 use the following abbreviations: (i) R-n means ROUGE metric using n-gram matching, and (ii) lowercase s denotes the use of stopword removal option.
This means that on the average about 9% of the words in the human abstractive summaries do not appear in the documents. Since extractive automatic summarizers extract all the sentences from the documents given to them for summarization, clearly no extractive summarizer can have Rouge-1 recall score higher than the documents themselves on any dataset, and, in general, the recall score will be lower since the summaries are limited to 100 words whereas the documents themselves can be arbitrarily long.
Thus, we establish a limit on the Rouge recall scores for extractive summarizers on the DUC datasets. The DUC 2002 dataset has 533 unique documents and most include two 100-word human abstractive summaries. We note that if extractive summaries are also exactly 100 words each, then the precision can also be no higher than recall score. In addition, the F1-score is upper bounded by the highest possible recall score. Therefore in the single document summarization, no extractive summarizer can have an average F1-score better than about 91%.
When considered in this light, the best current extractive single-document summarizers achieve about 54% of this limit on DUC datasets, e.g., see [3, 24].
3.2 ROUGE insights
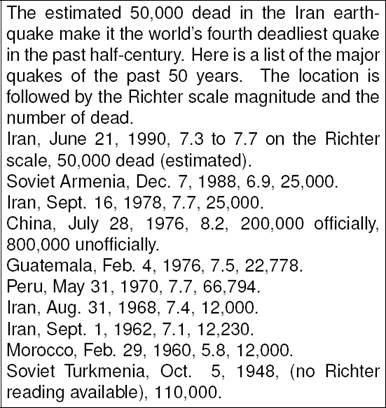
In Table 2, comparing R-1 and R-1s, we can see an increase in the lower range of recall values with stopword removal. This occurred with Document #250 (Figures 1–2). Upon deeper analysis of ROUGE, we found that it does not remove numbers under stopword removal option. Document #250 had a table with several numbers. In addition ROUGE treats numbers with the comma character (and also decimals such as 7.3) as two different numbers (e.g. 50,000 become 50 and 000).
This boosted the recall because after stopword removal, the summaries significantly decreased in unigram count, whereas the overlapping unigrams between document and summary did not drop as much. Another discovery is that documents with long descriptive explanations end up with lower recall values with stopword removal. Tabel 1 shows a steep drop on the lower range values from R-1 to R-1s. When looking at the lower scoring documents, the documents usually had explanations about events, whereas the summary skipped these explanations.
3.3 Multi-document Extractive Summarization
For multi-document summarization, there are at least two different scenarios in which to explore limits on extractive summarization. The first is where documents belonging to the same topic are concatenated together into one super-document and then it is treated as a summary. In the second, we compare each document as a summary with respect to the model summaries and then average the results for documents belonging to the same topic.
For multi-document summarization, experiments were done on data from DUC datasets for 2004 and 2005. The data was grouped into document clusters. Each cluster held documents that were about a single topic. For the 2004 competition (DUC 2004), we focused on the English document clusters. There were a total of 50 document clusters and each document cluster had an average of 10 documents. DUC 2005 also had 50 documents clusters, however, there were a minimum of 25 documents for each set.
Please note that since the scores for R-3 and R-4 were quite low (best being 0.23) these scores are not reported here.
3.3.1 Super-document Approach
Now we consider the overlap between the documents of a cluster with the human summaries of those clusters. So for this limit on recall, we create super-documents. Each super-document is the concatenation of all the documents for a given document set. These super-documents are then evaluated with ROUGE against the model human summaries. Any extractive summary is limited to only these words, so the recall of a perfect extractive system can only reach this limit. The results can be seen in Table 3 and Table 4.
3.3.2 Averaging Results of Individual Documents
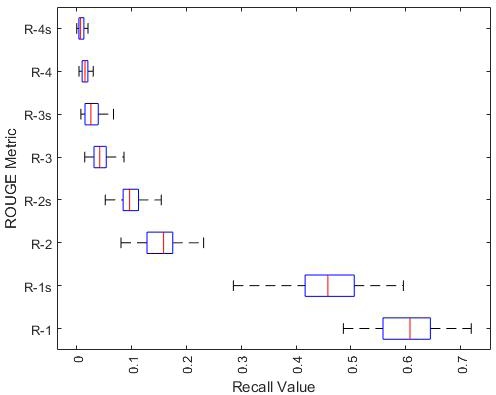
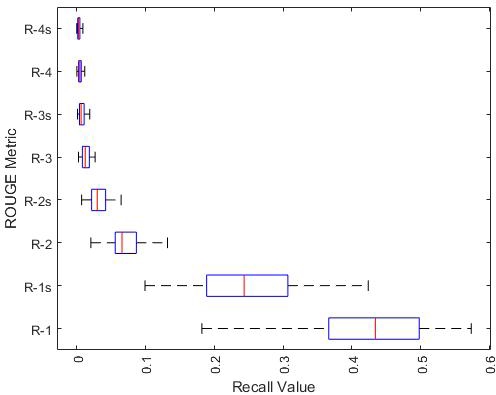
Here we show a different perspective on the upper limit of extractive systems. We treat each document as a summary to compare against the human summaries. Since all the documents are articles related to a specific topic, these documents can be viewed as a standalone perspective. For this experiment we obtained the ROUGE recall of each document and then averaged them for each cluster. The distribution of the averages are presented in Figure 3 and Figure 4. Here the best distribution average is only about 60% and 42% for DUC 2004 and DUC 2005, respectively. The best system did approximated 38% in DUC 2004 and 46% in DUC 2005
4 A General Model for Summarization
Now we introduce our model and study its implications. Consider the process of human summarization. The starting point is a document, which contains a sequence of sentences that in turn are sequences of words. However, when a human is given a document to summarize, the human does not choose full sentences to extract from the document like extractive summarizers. Rather, the human first tries to understand the document, i.e., builds an abstract mental representation of it, and then writes a summary of the document based on this.
Therefore, we formulate a model for semantic summarization in the abstract world of thought units,3 which can be specialized to syntactic summarization by using sequences of words (or phrases) in place of thought units. In any theory there are some undefinable objects, so are thought units for us, which should be understood as indivisible or “atomic” thoughts. We hypothesize that a document is a collection of thought units, some of which are more important than others, with a mapping of sentences to thought units. The natural mapping is that of implication or inclusion, but this could be partial implication, not necessarily full implication. That is, the mapping could associate a degree to represent that the sentence only includes the thought unit partially (e.g. allusion). A summary must be constructed from sentences, not necessarily in the document, that cover as many of the important thought units as possible, i.e., maximize the importance score of the thought units selected, within a given size constraint C. We now define it formally for single and multi-document summarization. Our model can naturally represent abstractive versus extractive dimension of summarization.
Let S denote an infinite set of sentences, T an infinite set of thought units, and I : S × T → R be a mapping that associates a non-negative real number for each sentence s and thought unit t that measures the degree to which the thought unit is implied by the sentence s. Given a document D, which is a finite sequence of sentences from S, let S(D) ⊂ S be the finite set of sentences in D and T(D) ⊂ T be the finite set of thought units of D. Once thoughts are assembled into sentences in a document with its sequencing (a train of thought) and title(s), this imposes a certain ordering4 of importance on these thought units, which is denoted by a scoring function WD : T → R. Note that the scoring function need not always respect the ordering of the thought units in the document, e.g., in a story the author needs to spend some sentences in the introduction building up the characters, and the ordering may be adjusted for thoughts that are repeated or emphasized in the document. The size of a document is denoted by |D|, which could be, for example, the total number of words or sentences in the document. A size constraint, C, for the summary, is a function of |D|, e.g., a percentage of |D|, or a fixed number of words or sentences in which case it is a constant function. A summary of D, denoted by summ(D) ⊂ S, is a finite sequence of sentences that attempts to represent the thought units of D as best as possible within the constraint C. The size of a summary, |summ(D)| is measured using the same procedure for measuring |D|. With these notations, for each thought unit t ∈ T (D), we define the score assigned to summ(D) for expressing thought unit t as Ts(t, summ(D)) = max{I(s, t) | s ∈ summ(D)}. Formally, the summarization problem is then, select summ(D) to maximize Utility(summ(D)):
subject to the constraint |summ(D)| ≤ C.
The Utility of the summary is the sum, over all thought units, of the importance of that thought unit in the document multiplied by the highest degree to which it is expressed by a sentence in the summary. Note that our model: (i) does not reward redundancy, because it just takes the maximum degree to which a thought unit is expressed in the summary and then multiplies by its importance, and (ii) can represent some aspects of summary coherence as well, by imposing the constraint that the sequencing of thought units in the summary be consistent with the ordering of thought units in the document.
For the multi-document case, we are given a Corpus = {D1, D2, . . . Dn}, each Di has its own sequencing of sentences and thought units, which could conflict with other documents. One must resolve the conflicts somehow when constructing a single summary of the corpus. Thus, for multi-document summarization, we hypothesize that WCorpus is an importance hierarchy that is maximally consistent with the WDi’s, by which we mean that if two thought units are assigned the same relative importance by every document in the collection that includes them, then the same relative order is imposed by WCorpus as well, otherwise WCorpus chooses a relative order that is best represented by the collection and this could be based on a majority of the documents or in other ways. Note that the importance score of a thought unit in WCorpus will not necessarily be equal to the importance score of this thought unit in any of the documents that contain it. There could be several reasons for this, e.g., it may be adjusted up to reflect the emphasis when several documents agree on its importance. With these adjustments, our previous definition extends to multi-document summarization as well, but we replace summ(D) by summ(Corpus), WD by WCorpus, and T(D) by T(Corpus). In the multi-document case, the summary coherence can be defined as the constraint that the sequencing of thought units in a summary be maximally consistent with the sequencing of thought units in the documents and in conflicting cases makes the same choices as implied by WCorpus.
The function W is a crucial ingredient that allows us to capture the sequencing chosen by the author(s) of the document(s), without W we would get the bag of thought units or words models popular in previous work. We note that W does need to respect the sequencing in the sense that it is not required to be a decreasing (or even non-increasing) function with sequence position. This flexibility is needed since W must fit the document structure.
As defined our model covers abstractive summarization directly since it is based on sentences that are not restricted to those within D. For extractive summarization, we need to impose the additional constraint summ(D) ⊆ S(D) for single-document, and summ(D) ⊆ S(Corpus), where S(Corpus) = ∪iS(Di), for multi-document summarization. Some other important special cases of our model as as follows:
Restricting I(S, T ) to a boolean-valued function. This gives rise to the “membership” model and avoids partial membership.
Restricting WD(t) to a constant function. This would give rise to a “bag of thought units” model and it would treat all thought units the same.
Further, if “thought units” are limited to be all words, or all words minus stopwords, or key phrases of the document, and under extractive constraint, we get previous models of [14, 31, 42]. This also means that the optimization problem of our model is NP-hard at least and NP-complete when WD(t) is a constant function and I(S, T) is boolean-valued.
Theorem 1. The optimization problem of the model is at least NP-hard. It is NP-complete when I(S, T) is boolean-valued, WD(t) is a constant function and thought units are: words, or all words minus stopwords or key phrases of the document, with sentence size and summary size constraint being measured in these same syntactic units. We call these NP-complete cases extractive coverage summarization collectively.
Proof. The proof of NP-hardness is by a polynomial-time reduction from the set cover problem, which is known to be NP-hard. Given a universe U, and a family of S of subsets of U, a cover is a subfamily C of S whose union is U. In the set cover problem the input is a pair (U, S) and a number k, the question is whether there is a cover of size at most k. We reduce set cover to summarization as follows. For each member u of U, we select a thought unit t from T a nd a clause c that expresses t. For each set S in the family, we construct a sentence s that consists of the clauses corresponding to the members of S(I is boolean-valued). We assemble all the sentences into a document. The capacity constraint C = k and represents the number of sentences that we can select for the summary. It is easy to see that a cover corresponds to a summary that maximizes the Utility and satisfies the capacity constraint and vice versa.
Of course, the document constructed above could be somewhat repetitive, but even “real” single documents do have some redundancy. Coherence of clauses appearing in the same sentence can be ensured by choosing them to be facts about a person’s life for example. We call the NP-complete cases of the theorem, extractive coverage summarization collectively. For this case, it is easy to design a greedy strategy that gives a logarithmic approximation ratio [21] and an optimal dynamic programming one that is exponential in the worst case.
Based on this generalized model, we can define:
Definition 1. The extractive compressibility of a document D is |D|−|d|, where |d| is the size of a smallest collection of sentences from the document that cover its thought units. If the thought units are words, we call it the word extractive compressibility.
Definition 2. The abstractive compressibility of a document D is |D|−|d|, where |d| is the size of a smallest collection of arbitrary sentences that cover its thought units. If the thought units are words, we call it the word abstractive compressibility.
Definition 3. The normalized compressibility of a document D is defined as κ/|D|, where κ is the compressibility of the document, and the incompressibility is the difference of 1 and normalized compressibility.
Similarly, we can define corresponding compressibility notions for key phrases, words minus stopwords, and thought units.
We investigate compressibility of three different genres: news articles, scientific papers and short studies. For this purpose, 25 news articles, 25 scientific papers, and 25 short stories were collected.
The 25 news articles were randomly selected from several sources and covered disasters, disaster recovery, prevention, and critical infrastructures. Five scientific papers, on each of the following five topics: cancer research, nanotechnology, physics, NLP and security, were chosen at random. Five short stories each by Cather, Crane, Chekhov, Kate Chopin, and O’Henry were randomly selected.
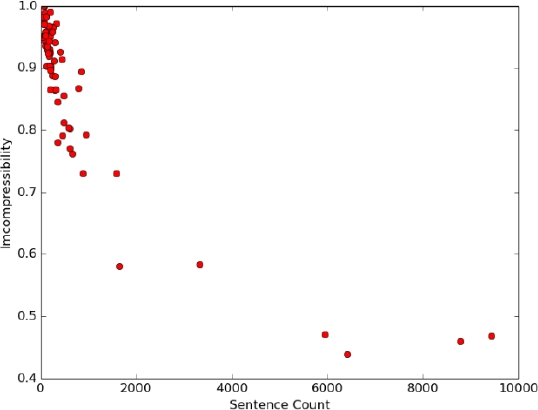
In addition to these, we looked at several longer texts [38, 22, 23, 4, 10, 2, 41, 12]. Experiments showed that large sentence counts lead to decrease incompressibility. Figure 5 shows a direct relationship between document size and incompressibility.
5 Summarization Framework and Experiments
5.1 Algorithms for Single-document Summarization
We have implemented several heuristics in a tool called DocSumm written in Python. Many of our heuristics revolve around the TF/IDF ranking, which has been shown to do well in tasks involving summarization. TF/IDF ranks the importance of words across a corpus. This ranking system was compared to other popular keyword identification algorithms and was found to be quite competitive in summarization evaluation results [33]. To apply to the domain of single-document summarization, we define a corpus as the document itself. The documents referred to in inverse document frequency are the individual sentences and the terms remain the same, words. The value of a sentence is then the sum of the TF/IDF scores of the words in the sentence.
5.1.1 DocSumm Greedy Heuristics
DocSumm, includes both greedy and dynamic programming based algorithms. The greedy algorithms use the chosen scoring metric to evaluate every sentence of a document (Algorithm 1). There are different scoring functions that can be used to score a sentence of a document.
— size: This option looks only at the length of a sentence.
— tfidf: This option computes “inverse document frequency” based on the idea that a sentence is a “document” and the whole document is considered the “corpus”. However, the term frequency value is determined based on the whole document [47].
— stfidf: This option is similar to tfidf, however, the term frequency value is based on a per sentence rather than per document level.
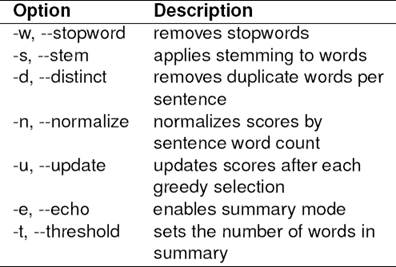
The greedy algorithm simply selects the highest scoring sentence, until either a given threshold of words is met or every word is covered in the document. Besides the choices for the scoring metrics, there are several other options (normalization of weights, stemming, etc.) that can be toggled for evaluation. Table 5 gives a brief description of those options.
One of the options that will be seen in the results is the −d option. It influences the score, by allowing the frequency of a word to be capped at 1. This proves to be a good boost to the size score, and it is reported in results as size + d.
5.1.2 Dynamic Programming
DocSumm includes two dynamic programming algorithms. Neither provides an optimal solution, i.e., the absolute minimum number of sentences necessary to cover all words of the document. An optimal solution can be viewed as an upper bound on the maximum compression achievable of a document for extractive summary. However, this is an NP-hard problem, so computing the optimal answer would be intractable.
The first algorithm attempts to make the problem more tractable, by exploring a smaller subset of the solution space. Rather then look at every possible subset s, it only searches those that are possible from differences of existing sentences, i.e. family S. It creates possible subfamilies in a heuristic manner, starting with the smallest sentence. The algorithm then uses dynamic programming to build subfamilies in a bottom up fashion. The solutions are analyzed until a subfamily C ⊂ S that covers the universe of words, U.
The second algorithm implements a version of the algorithm presented in [31]. McDonald frames the problem of document summarization as the maximization of a scoring function that is based on relevance and redundancy. In essence, selected sentences are scored higher for relevance and scored lower for redundancy. If the sentences of a document are considered on a inclusion/exclusion basis, then the problem of document summarization can be reduced to the 0-1 Knapsack problem if the overlap of sentences is ignored (each sentence has a score or value, e.g., the words it covers from the document, and each sentence has a size, and there is a capacity constraint on the size of the summary). However, McDonald’s algorithm is approximate, because the inclusion/exclusion of the algorithm influences the score of other sentences. A couple of greedy algorithms and a dynamic programming algorithm of DocSumm appeared in [42], the rest are new to our knowledge, e.g., the tf-idf versions and the update versions of the greedy algorithms in which sentence scores are updated after each greedy selection to reflect the words that were chosen.
5.2 Results
Our results include experiments on running time comparisons of DocSumm’s algorithms. In addition we compare the Rouge performance measures of DocSumm on the DUC 2001 and DUC 2002 datasets.
5.2.1 Run times
The dataset for running times is created by sampling sentences from the book of Genesis. We created documents of increasing lengths, where length is measured in verses. The verse count ranged from 4 to 320. However, for documents greater than 20 sentences, the top-down dynamic algorithm runs out of memory. So there are no results on the top-down exhaustive algorithm. Table 6 shows slight increases in time as the document size increase. For both tfidf and bottom-up there is a significant increase in running time.
5.2.2 Summarization
We now compare the heuristics for single-document summarization on DUC 2001 and DUC 2002 datasets. For the 305 unique documents of the DUC 2001 dataset we compared the summaries of DocSumm algorithms. The results were in line with the analysis of the three domains.
For each algorithm, we truncated the solution set as soon as a threshold of 100 words was covered. The ROUGE scores of the algorithms were in line with the compressibility performances. The size algorithms performed similarly and the best was the bottom-up algorithm with ROUGE F1 scores of 0.396, 0.147 and 0.223 for ROUGE-1, ROUGE-2 and ROUGE-LCS, respectively. The tfidf algorithm performance was not significantly different.
5.2.3 Comparison
On the 533 unique articles in the DUC 2002 dataset, we now compare our greedy and dynamic solutions against the following classes of systems: (i) two top of the line single-document summarizers, SynSem [3], and the best extractive summarizer from [24], which we call KKV, (ii) top five (out of 13) systems, S28, S19, S29, S21, S23, from DUC 2002 competition, (iii) TextRank, (iv) MEAD, (v) McDonald Algorithm and (vi) the DUC 2002 Baseline summaries consisting of the first 100 words of news articles. The Baseline did very well in the DUC 2002 competition - only two out of 13 systems, S28 and S19, managed to get a higher F1 score than the Baseline. For this comparison, all manual abstracts and system summaries are truncated to exactly 100 words whenever they exceed this limit.
Note that the results for SynSem are from [3], who also used only the 533 unique articles in the DUC 2002 dataset. Unfortunately, the authors did not report the Rouge bigram (ROUGE-2) and Rouge LCS (ROUGE-L) F1 scores in [3]. KKV’s results are from [24], who did not remove the 33 duplicate articles in the DUC 2002 dataset, and who do not clarify whether they are reporting recall or F1-scores (but we suspect they are recall scores), which is why we flagged those entries in Table 7 with an asterisk (i.e. *). Hence their results are not comparable to ours. In addition KKV did not report ROUGE-LCS scores.
Our experiments are inline with the results of TF/IDF in [33]. They show that the TF/IDF version ranks a close second to bottom-up on the Rouge-2 and Rouge-LCS metrics, and is better than three of our algorithms on the Rouge-1 metric. Thus, it is a pretty consistent performer. We observe that for Rouge unigram (ROUGE-1) F1-scores the bottom-up algorithm performs the best amongst the algorithms of DocSumm. However, it still falls behind the Baseline. When we consider Rouge bigram (ROUGE-2) F1-scores all heuristics of DocSumm outperform the rest of the field. The margin of out-performance is even more pronounced in ROUGE-LCS F1-scores.
6 Conclusions and Future Work
We have shown limits on the recall (and F-score) of automatic extractive summarization on DUC datasets under ROUGE evaluations. Our limits show that the current state-of-the-art systems evaluated on DUC data [3, 24] and S28 from Duc 2002 competition are achieving about 54% of this limit for recall and about 51% for F1-score 5 for single-document summarization and the best systems for multi-document summarization are achieving about a third of their limit. This is encouraging news, especially for single-document summarization, but at the same time there is much work remaining to be done. We also explored compressibility, a generalized model, and new and existing heuristics for single-document summarization.
To our knowledge, compressibility, the way we have defined and studied it, is a new concept and we plan to investigate it further in future work. We believe that compressibility could prove to be a useful measure to study the performance of automatic summarization systems and also perhaps for authorship detection if, for instance, some authors are shown to be consistently compressible.











 text new page (beta)
text new page (beta)