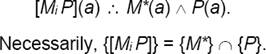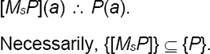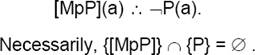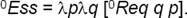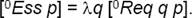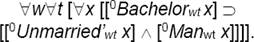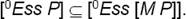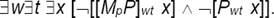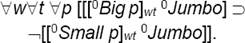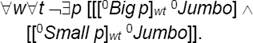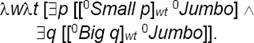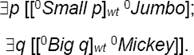1 Introduction
I introduce a logic of property modifiers modelled as a mapping from properties to properties, such that the result of the application of a modifier to a property is another property.1 I agree with Montague that the result of modification does not depend on the state of the world, nor on time.2 For instance, if one applies the modifier Skillful to the property Surgeon, they obtain the property of being a skillful surgeon. On the other hand, a property is (modelled as) a mapping from a logical space of possible worlds to a mapping from times to sets of individuals. A set of individuals is in turn a characteristic function from individuals to truth-values. So, for an individual to instantiate a property, whether modified or not, is to be an element of its extension at a given world and time. The novel contribution of this paper is a new definition of subsective and privative modifiers in terms of intensional essentialism.
Kamp’s seminal [9] seeks to draw a line between those adjectives whose meaning is a property and those adjectives whose meaning is a function that maps properties to properties. He (ibid., pp. 147ff) suggests that most adjectives have a property as their meaning. Yet he admits that it would seem that some adjectives must occur in attributive position and are incapable of occurring in predicative position. Their meaning is a property-to-property function:
The same can be said to be true […] of adjectives such as fake, skillful, or good. Where precisely we should draw the boundaries of the class of adjectives to which the second theory [property-to-property function] applies I do not know. For example, does skillful belong to this class? Surely we must always ask ‘skillful what?’ before we can answer the question whether a certain thing or person is indeed skillful […].
(9, pp. 153-4)
I agree with Kamp’s linguistic observations. Kamp is concerned with a demarcation among adjectives. We can hypothesize that his demarcation is in effect a demarcation between those adjectives that represent properties and those that represent property modifiers. Furthermore, some adjectives can represent both, that is, they can occur both in attributive position and in predicative position. For instance, if a is a round peg then a is round; not ‘round what’ but ‘round simpliciter’.
As a starting point, here is a standard taxonomy of the three kinds of modifiers, with rigorous definition coming afterwards. Let {…} be an operation forming sets from properties,3 M standing for a modifier, M* for a property corresponding to a modifier.4
Intersective. “If a is a round peg, then a is round and a is a peg”:
Necessarily, i.e., in all worlds and times, the set of round pegs equals to the intersection of the sets of round objects and pegs.
Intersectivity is the least interesting form of modification, since antecedent and consequent, or premise and conclusion, are equivalent. Still, even in the case of the apparently logically trivial intersectives we cannot transfer Mi from the premise to the conclusion. The reason is that a modifier cannot also occur as a predicate; these are objects of different types. Hence M* instead of just M.
Subsective. “If a is a skillful surgeon, then a is a surgeon.” :
Necessarily, i.e., in all worlds and times, the set of skillful surgeons is a subset of the set of surgeons.5
The major difference between subsective and intersective modification is that subsectivity bans this sort of argument: [MsP](a), Q(a) ∴ [MsQ](a). Tilman may be a skillful surgeon, and he may be a painter too, but this does not make him a skillful painter. Or, Jumbo may be a small elephant, as well as a mammal, but this does not make Jumbo a small mammal. Jumbo is small as an elephant rather than as a mammal. Scalar adjectives like ‘small’, ‘big’ or ‘skillful’ represent subsective modifiers. On the other hand, to each intersective modifier Mi there is a unique ‘absolute’ property M* such that if a is an [Mi P] then a is M* not only as a P but absolutely.6
Privative. “If a is a forged banknote, then a is not a banknote”:
Necessarily, i.e., in all worlds and times, the intersection of the set of forged banknotes and banknotes is empty.
Partee, in [11], attempts to reduce privative modifiers to subsective modifiers so that “the [linguistic] data become much more orderly” (ibid.). In her case guns would divide into fake guns and real guns, and fur into fake fur and real fur. Her argument is that only this reduction can do justice to the meaningfulness of asking the following sort of question: “Is this gun real or fake?” At first blush, however, it would seem the question pre-empts the answer: if some individual is correctly identified as a gun, then surely it is a real gun, something being a gun if, and only if, it is a real gun. However, if we go along with the example, we think the argument is easily rebutted by putting scare quotes around ‘gun’ so that the question becomes, “Is this ‘gun’ fake or real?” The scare quotes indicate that ‘gun’ is something ‘gun-like’, including toy guns, which are not guns. If the answer is that the gun-like object is a fake gun (hence not a gun), the scare quotes stay on. If the answer is that it is a real gun (i.e., a gun), the scare quotes are lifted. Similarly with “Is this ‘fur’ fake or real?” A more direct way of phrasing the question would be, “Is this fur?”, which does not preempt the answer and which does not presuppose that there be two kinds of fur, fake and real. For an intuitive test, ask yourself what the sum is of a fake €10 bill and a €10 bill.
If Forged is privative, then a forged banknote is not a banknote that is forged, such that there would be two kinds of banknotes: those that are genuine and those that are forged. The sum of four genuine banknotes and one forged banknote is four banknotes and not five (though five pieces of paper).7 This is also to say that Genuine is an idle modifier: anything is a genuine F iff it is an F. This is not to say that the same material object may not be genuine in one respect and fail to be genuine in another. For instance, an artefact being passed off as a paper banknote may fail to be a banknote (being a forged banknote), while being indeed made of paper (rather than polymer, say), thereby being a paper artefact. (“The ‘banknote’ is fake, the paper is real”).
Modifiers are intersective, subsective and privative with respect to a property P. One and the same modifier can be intersective with respect to a property P and privative with respect to another property Q. For instance, a stone bridge is stony and is a bridge, but a stone lion is not a lion. We leave aside the question whether there are modifiers privative with respect to any property. Most probably, yes, modifiers like faked, forged, false appear to be privative with respect to any property. Yet this issue is irrelevant to the main goal of this paper, which is to define the rule of pseudo-detachment (PD) and prove its validity for any kind of modifiers. The applicability of (PD) presupposes the validity of existential generalisation over properties and of substituting identical properties, something I am not going to doubt.
My background theory is Transparent Intensional Logic (TIL) with its procedural semantics that assigns abstract procedures to terms of natural language as their context-invariant meanings. These procedures are rigorously defined as TIL constructions that produce lower-order objects as their products or in well-defined cases fail to produce an object by being improper.
The rest of the paper is organised as follows. Section 2 introduces the fundamentals of TIL necessary to deal with property modifiers, which is the issue I deal with in Section 3. Here in Section 3.1 the difference between non-subsective and subsective modifiers is defined in a novel way, and the main result presented, which is formulation of the rule of pseudo-detachment defined in Section 3.2. Concluding remarks can be found in Section 4.
2 Basic Notion of TIL
Definition 1 (construction)
(i) Variables x, y, … are constructions that construct objects (elements of their respective ranges) dependently on a valuation v; they v-construct.
(ii) Where X is an object whatsoever (even a construction), 0X is the construction Trivialization that constructs X without any change of X.
(iii) Let X, Y1,…,Yn be arbitrary constructions. Then Composition [X Y1…Yn] is the following construction. For any v, the Composition [X Y1…Yn] is v-improper if at least one of the constructions X Y1…Yn is v-improper, or if X does not v-construct a function that is defined at the n-tuple of objects v-constructed by Y1…Yn. If X does v-construct such a function, then [X Y1…Yn] v-constructs the value of this function at the n-tuple.
(iv) (λ-) Closure [λx1…xm Y] is the following construction. Let x1, x2, …, xm be pair-wise distinct variables and Y a construction. Then [λx1…xm Y] v-constructs the function f that takes any members B1, …, Bm of the respective ranges of the variables x1, …, xm into the object (if any) that is v(B1/x1,…,Bm/xm)-constructed by Y, where v(B1/x1,…,Bm/xm) is like v except for assigning B1 to x1, …, Bm to xm.
(v) Where X is an object whatsoever, 1X is the construction Single Execution that v-constructs what X v-constructs. Thus, if X is a v-improper construction or not a construction as all, 1X is v-improper.
(vi) Where X is an object whatsoever, 2X is the construction Double Execution. If X is not itself a construction, or if X does not v-construct a construction, or if X v-constructs a v-improper construction, then 2X is v-improper. Otherwise 2X v-constructs what is v-constructed by the construction v-constructed by X.
(vii) Nothing is a construction, unless it so follows from (i) through (vi).
With constructions of constructions, constructions of functions, functions, and functional values in our stratified ontology, we need to keep track of the traffic between multiple logical strata. The ramified type hierarchy does just that. The type of first-order objects includes all non-procedural objects. Therefore, it includes not only the standard objects of individuals, truth-values, sets, mappings, etc., but also functions defined on possible worlds (i.e., the intensions typical of possible-world semantics). The type of second-order objects includes constructions of first-order objects and functions with such constructions in their domain or range. The type of third-order objects includes constructions of first- and/or second-order objects and functions with such constructions in their domain or range. And so on, ad infinitum.
Definition 2 (ramified hierarchy of types). Let B be a base, where a base is a collection of pair-wise disjoint, non-empty sets. Then:
T1 (types of order 1):
(i) Every member of B is an elementary type of order 1 over B.
(ii) Let α, β1, ..., βm (m > 0) be types of order 1 over B. Then the collection (α β1, ..., βm) of all m-ary partial mappings from β1 × ... × βm into α is a functional type of order 1 over B.
(iii) Nothing is a type of order 1 over B unless it so follows from (i) and (ii).
Cn (constructions of order n):
(iv) Let x be a variable ranging over a type of order n. Then x is a construction of order n over B.
(v) Let X be a member of a type of order n. Then 0X, 1X, 2X are constructions of order n over B.
(vi) Let X, X1, ..., Xm (m > 0) be constructions of order n over B. Then [X X1…Xm] is a construction of order n over B.
(vii) Let x1, ..., xm, X (m > 0) be constructions of order n over B. Then [λx1…xm X] is a construction of order n over B.
(viii) Nothing is a construction of order n over B unless it so follows from Cn (i)-(iv).
Tn+1 (types of order n+1) Let *n be the collection of all constructions of order n over B. Then
(i) *n and every type of order n are types of order n+1.
(ii) If m > 0 and α, β1, ..., βm are types of order n+1 over B, then (α β1 ... βm) (see T1 ii)) is a type of order n+1 over B.
(iii) Nothing is a type of order n+1 over B unless it so follows from (i) and (ii).
For the purposes of natural-language analysis, we are assuming the following base of ground types:
ο: the set of truth-values {T, F};
ι: the set of individuals (the universe of discourse);
τ: the set of real numbers (doubling as discrete times);
ω: the set of logically possible worlds (the logical space).
We model sets and relations by their characteristic functions. Thus, for instance, (οι) is the type of a set of individuals, while (οιι) is the type of a relation-in-extension between individuals. Empirical expressions denote empirical conditions that may or may not be satisfied at the particular world/time pair of evaluation. We model these empirical conditions as possible-world-semantic (PWS-) intensions. PWS-intensions are entities of type (βω): mappings from possible worlds to an arbitrary type β. The type β is frequently the type of the chronology of α-objects, i.e., a mapping of type (ατ). Thus α-intensions are frequently functions of type ((ατ)ω), abbreviated as ‘ατω’. Extensional entities are entities of a type α where α ≠ (βω) for any type β. Where w ranges over ω and t over τ, the following logical form essentially characterizes the logical syntax of empirical language: λwλt […w….t…].
Examples of frequently used PWS intensions are: propositions of type οτω, properties of individuals of type (οι)τω, binary relations-in-intension between individuals of type (οιι)τω, individual offices (or roles) of type ιτω.
As mentioned above, we define property modifiers as mappings from α-properties to α-properties, for any type α. In this paper we deal mostly with modifiers of individual properties of type ((οι)τω(οι)τω), or sometimes (ππ) for short.
Logical objects like truth-functions and quantifiers are extensional: ∧ (conjunction), ∨ (disjunction) and ⊃ (implication) are of type (οοο), and ¬ (negation) of type (οο). Quantifiers ∀α, ∃α are type-theoretically polymorphic total functions of type (ο(οα)), for an arbitrary type α, defined as follows. The universal quantifier ∀α is a function that associates a class A of α-elements with T if A contains all elements of the type α, otherwise with F. The existential quantifier ∃α is a function that associates a class A of α-elements with T if A is a non-empty class, otherwise with F.
Below all type indications will be provided outside the formulae in order not to clutter the notation. Moreover, the outermost brackets of the Closure will be omitted whenever no confusion arises. Furthermore, ‘X/α’ means that an object X is (a member) of type α. ‘X →v α’ means that X is typed to v-construct an object of type α, if any. We write ‘X → α’ if a valuation v does not matter. Throughout, it holds that the variables w →v ω and t →v τ. If C → ατω then the frequently used Composition [[C w] t], which is the intensional descent (a.k.a. extensionalization) of the α-intension v-constructed by C, will be encoded as ‘Cwt’. For instance, if Student/(οι)τω is the property of being a student, the procedure of extensionalizing this property to obtain its population in a given world w and time t is the Composition:
for short.
Whenever no confusion arises, we use traditional infix notation without Trivialisation for truth-functions and the identity relation, to make the terms denoting constructions easier to read. Thus, for instance, instead of:
we usually write:
3 Property Modifiers and Essences of Properties
3.1 Privative vs. Subsective Modifiers
The fundamental distinction among modifiers is typically considered to be one between the subsectives and the non-subsectives. The former group consists of the pure subsectives (that are governed by the rule of right subsectivity, which amounts to eliminating the modifier and predicating the surviving property) and the intersectives (that are governed by the rule of right subsectivity and a rule of left subsectivity).8 The latter group consists of the modals and the privatives. Since I am not dealing with modal modifiers here, I now want to define the distinction between subsectives and privatives. At the outset this distinction between modifiers subsective (Ms) and privative (Mp) with respect to a property P has been characterized by the rules of right subsectivity as follows:
Now we have the technical machinery at our disposal to define these modifiers in a rigorous way. To this end, I apply the logic of intensions based on the notions of requisite and essence of a property, which amounts to intensional essentialism.9 The idea is this. Every property we countenance has a host of other properties necessarily associated with it. For instance, the property of being a bachelor is associated with the properties of being a man, being unmarried, and many others. Necessarily, if a happens to be a bachelor then a is a man and a is unmarried. We call these adjacent properties requisites of a given property.
The requisite relations Req are a family of relations-in-extension between two intensions, so they are of the polymorphous type (οατωβτω), where possibly α = β. Infinitely many combinations of Req are possible, but for our purpose we will need the following one: Req /(ο(οι)τω(οι)τω); a property of individuals is a requisite of another such property.
TIL embraces partial functions.10 Partiality gives rise to the following complication. The requisite relation obtains analytically necessarily, i.e., for all worlds w and times t, and so the values of intensions at particular 〈w, t〉-pairs are irrelevant. But the values of properties are isomorphic to characteristic functions, and these functions are amenable to truth-value gaps.
For instance, the property of having stopped smoking comes with a bulk of requisites like, e.g., the property of being a former smoker. If a never smoked, then the proposition that a stopped smoking comes with a truth-value gap, because it can be neither true nor false.
Thus, the predication of such a property P of a may also fail, causing [0Pwt 0a] to be v-improper. There is a straightforward remedy, however, namely the propositional property of being true at a given 〈w, t〉: True/(οοτω)τω. Given a proposition v-constructed by X, [0Truewt X] v-constructs the truth-value T if the proposition presented by X is true at 〈w, t〉; otherwise (i.e., if the proposition v-constructed by X is false or else undefined at 〈w, t〉) the truth-value F. Thus, we define:
Definition 3 (requisite relation between ι-properties). Let P, Q be constructions of individual properties; P, Q/*n → (οι)τω; x → ι. Then:
Gloss definiendum as, “Q is a requisite of P”, and definiens as, “Necessarily, i.e. at every 〈w, t〉, if it is true that whatever x instantiates P at 〈w, t〉 then it is also true that this x instantiates Q at 〈w, t〉.”11
Example. Let the property of being a person be a requisite of the property of being a student. Then the hyperproposition that all students are persons is an analytic truth. It constructs the proposition TRUE, which is the necessary proposition, which takes value T at all world-time pairs. Wherever and whenever somebody happens to be a student they are also a person. Formally:
Next, I am going to define the essence of a property. Our essentialism is based on the idea that since no purely contingent property can be essential of any individual, essences are borne by intensions rather than by individuals exemplifying intensions.12 That a property P has an essence means that a relation-in-extension obtains a priori between the property P and a set Ess of the requisites of P, that is, other properties such that, necessarily, whenever an individual instantiates P at some 〈w, t〉 then the same individual also instantiates any of the properties belonging to Ess at the same 〈w, t〉. Hence, our essentialism is based on the requisite relation, couching essentialism in terms of a priori interplay between properties, regardless of who or what exemplifies a given property. Intensional essentialism is technically an algebra of individually necessary and jointly sufficient conditions for having a certain property (or other sort of intension). The 〈w, t〉-relative extensions of a given property are irrelevant, as I said.
Definition 4 (essence of a property). Let p, q → (οι)τω be constructions of individual properties, and let Ess/((ο(οι)τω)(οι)τω) be a function assigning to a given property p the set of its requisites defined as follows.
Then the essence of a property p is the set of its requisites:
Each property has (possibly infinitely) many requisites. The question is, how do we know which are the requisites of a given property? The answer requires an analytic definition of the given property, which amounts to the specification of its essence.13 For instance, consider the property of being a bachelor. If we define this property as the property of being an unmarried man, then the property of being an unmarried man is a requisite of the property of being a bachelor. From this definition, it follows that, for instance, the sentence “bachelors are unmarried men” comes out analytically true:
And since the modifier Unmarried is intersective, it also follows that necessarily, each bachelor is unmarried and is a man:
Note, however, that Unmarried’/(οι)τω and Unmarried/((οι)τω(οι)τω) are entities of different types. The former is a property of individuals uniquely assigned to the latter, which is an intersective modifier.
With these definitions in place, we can go on to compare two kinds of subsectives against privatives.14 Since these modifiers change the essence of the root property, we need to compare the essences, that is sets of properties, of the root and modified property. To this end, we apply the set-theoretical relations of being a subset and a proper subset between sets of properties, and the intersection operation on sets of properties, defined as follows.
Let π = (οι)τω, for short, ⊆, ⊂/(ο(οπ)(οπ)), and let a, b →v (οπ); p →v π. Then:
Furthermore, the intersection function ∩/((οπ)(οπ)(οπ)) is defined on sets of properties in the usual way:
In what follows I will use classical (infix) set-theoretical notation for any sets A, B; hence instead of ‘[0⊆ A B]’ I will write ‘[A ⊆ B]’, and instead of ‘[0∩ A B]’ I will write ‘[A ∩ B]’.
Definition 5 (subsective vs. privative modifiers). Let the types be: P → (οι)τω, M → ((οι)τω(οι)τω), p → (οι)τω, x → ι. Then
Example. The modifier Stony/((οι)τω(οι)τω) is subsective with respect to the property of being a bridge, Bridge/(οι)τω, but privative with respect to the property of being a lion, Lion/(οι)τω. Of course, a stony bridge is a bridge, but the essence of the property [0Stony 0Bridge] is enriched by the property of being stony. This property is a requisite of the property of being a stony bridge, but it is not a requisite of the property of being a bridge, because bridges can be instead made of wood, iron, etc.:
But a stony lion is not a lion. The modifier Stony, the same modifier that just modified Bridge, deprives the essence of the property of being a lion, Lion/(οι)τω, of many requisites, for instance, of the property of being an animal, having a bloodstream, a heartbeat, etc. Thus, among the requisites of the property [0Stony 0Lion] there are properties like not being a living thing, not having a bloodstream, etc., which are contradictory (not just contrary) to some of the requisites of the property Lion. On the other hand, the property [0Stony 0Lion] shares many requisites with the property of being a lion, like the outline of the body, having four legs, etc., and has an additional requisite of being made of stone. We have:
A modifier M is non-trivially subsective with respect to a property P iff the modified property [M P] has all the requisites of the property P and at least one another requisite that is not a requisite of P. In other words, the essence of the property P is a proper subset of the essence of the property [M P]. For instance, a skillful surgeon is a surgeon because the property of being a skillful surgeon must have all the requisites of the property of being a surgeon, and the additional property of being skillful as a surgeon, i.e., with respect to the property of being a surgeon.
A modifier M is trivially subsective with respect to P iff the modified property [M P] has exactly the same requisites as the property P. In other words, the essence of the property [M P] is identical to the essence of the property P. These modifiers are trivial in that the modification has no effect on the modified property and so might just as well not have taken place.
For instance, there is no semantic or logical (but perhaps rhetorical) difference between the property of being a leather and the property of being a genuine leather. Trivial modifiers such as genuine, real, actual are pure subsectives. As mentioned above, genuine leather things are not located in the intersection of leather things and objects that are genuine, for there is no such property as being genuine, pure and simple.15
A modifier M is privative with respect to a property P iff the modified property [M P] lacks at least one, but not all, of the requisites of the property P. However, in this case we cannot say that the essence of the property [M P] is a proper subset of the essence of the property P, because the modified property [M P] has at least one other requisite that does not belong to the essence of P, because it contradicts to some of the requisites of P. Hence, M is privative with respect to a property P iff the essence of the property [M P] has a non-empty intersection with the essence of the property P, and this intersection is a proper subset of both the essences of P and of [M P]. For instance, a well-forged banknote has almost the same requisites as does a banknote, but it has also another requisite, namely the property of being forged with respect to the property of being a banknote.
As a result, if Mp is privative with respect to the property P, then the modified property [MpP] and the property P are contrary rather than contradictory properties:
It is not possible for x to co-instantiate [MpP] and P, and possibly x instantiates neither [MpP], nor P.
The left-hand conjunct:
is the clause that [MpP] and P are mutually exclusive. This is because among the requisites of the properties P and [MpP] there is at least one pair of mutually contradictory properties. The second conjunct:
is the contrariety clause that the negation of one of the conjuncts [[MpP]wt x], [Pwt x] does not entail the truth of the other one. This is because only some but not all the requisites of [MpP] contradict some of the requisites of P, and the intersection of the essences of P and [MpP] is non-empty. Since we are talking about non-trivial properties, it is possible that an individual x has none of the properties [MpP] and P.
3.2 The Rule of Pseudo-Detachment
The issue I am going to deal with now is left subsectivity.16 We have seen that the principle of left subsectivity is trivially (by definition) valid for intersective modifiers. If Jumbo is a yellow elephant, then Jumbo is yellow. Yet how about the other modifiers? If Jumbo is a small elephant, is Jumbo small? If you factor out small from small elephant, the conclusion says that Jumbo is small, period. Yet this would seem a strange thing to say, for something appears to be missing: Jumbo is a small what? Nothing or nobody can be said to be small — or forged, skilful, temporary, larger than, the best, good, notorious, or whatnot, without any sort of qualification. A complement providing some sort of qualification to provide an answer to the question, ‘a … what?’ is required. I am going to introduce now the rule of pseudo-detachment that is valid for all kinds of modifiers including subsective and privative ones. The idea is simple. From a is an MP we infer that a is an M-with respect to something.
For instance, if the customs officers seize a forged banknote and a forged passport, they may want to lump together all the forged things they have seized that day, abstracting from the particular nature of the forged objects. This lumping together is feasible only if it is logically possible to, as it were, abstract forged from a being a forged A and b being a forged B to form the new predications that a is forged (something) and that b is forged (something – possibly else), which are subsequently telescoped into a conjunction.
Gamut claims that if Jumbo is a small elephant, then it does not follow that Jumbo is small [3, §6.3.11]. I am going to show that the conclusion does follow. The rule of pseudo-detachment (PD) validates a certain inference schema, which on first approximation is formalized as follows:
where ‘a’ names an appropriate subject of predication while ‘M’ is an adjective and ‘P’ a noun phrase compatible with a.
The reason why we need the rule of pseudo-detachment is that M as it occurs in MP is a modifier and, therefore, cannot be transferred to the conclusion to figure as a property. So, no actual detachment of M from MP is possible, and Gamut is insofar right. But (PD) makes it possible to replace the modifier M by the property M* compatible with a to obtain the conclusion that a is an M*. (PD) introduces a new property M* ‘from the outside’ rather than by obtaining M ‘from the inside’, by extracting a component from a compound already introduced. The temporary rule above is incomplete as it stands; here is the full pseudo-detachment rule, SI being substitution of identical properties (Leibniz’s Law).
To put the rule on more solid grounds of TIL, let π = (οι)τω for short, M → (ππ) be a modifier, P → π an individual property, [MP] → π the property resulting from applying M to P, and let [MP]wt →v (οι) be the result of extensionalizing the property [MP] with respect to a world w and time t to obtain a population of the property at the world and time of evaluation, i.e. a set in the form of a characteristic function, applicable to an individual a → ι. Further, let =/(οππ) be the identity relation between properties, and let p →v π range over properties, x →v ι over individuals. Then the proof of the rule is this:
Any valuation of the free occurrences of the variables w, t that makes the first premise true will also make the second, third and fourth steps true. The fifth premise is introduced as valid by definition. Hence, any valuation of w, t that makes the first premise true will, together with step five, make the conclusion true.
Additional type: ∃/(ο(οπ)).
Here is an instance of the rule.
(1’) a is a forged banknote,
(2’) forged* is the property of being a forged something,
(3’) a is forged*.
The schema extends to all (appropriately typed) objects. For instance, let the inference be, “Geocaching is an exciting hobby; therefore, geocaching is exciting”. Then a is of type π, P → (οπ)τω, M → ((οπ)τω(οπ)τω), and M* → (οπ)τω.
Now it is easy to show why this argument must be valid:
Types: Number_of/(τ(οι)); Banknote, Passport, Forged*/(οι)τω; Have/(οιι)τω; Forged/((οι)τω (οι)τω).
There are three conceivable objections to the validity of (PD) that I am going to deal with now.
First objection. If Jumbo is a small elephant and if Jumbo is a big mammal, then Jumbo is not a small mammal; hence Jumbo is small and Jumbo is not small. Contradiction!
The contradiction is only apparent, however. To show that there is no contradiction, we apply (PD):
Types: Small, Big/(ππ); Mammal, Elephant/π; Jumbo/ι; p, q → π.
To obtain a contradiction, we would need an additional premise; namely, that, necessarily, any individual that is big (i.e., a big something) is not small (the same something). Symbolically:
Applying this fact to Jumbo, we have:
This construction is equivalent to:
But the only conclusion we can draw from the above premises is that Jumbo is a small something and a big something else:
Hence, no contradiction.
The conclusion ought to strike us as being trivial. If we grant, as we should, that nobody and nothing is absolutely small or absolutely large, then everybody is made small by something and made large by something else. And if we grant, as we should, that nobody is absolutely good or absolutely bad, then everybody has something they do well and something they do poorly. That is, everybody is both good and bad, which here just means being good at something and being bad at something else, without generating paradox (Good, Bad/(ππ)):
But nobody can be good at something and bad at the same thing simultaneously:
Second objection. The use of pseudo-detachment, together with an innocuous-sounding premise, makes the following argument valid:
Yet it is not so. Well, it is necessarily true that if x is a small something and y is a big object of the same kind, then y is a bigger object of that kind than x:
Additional type: Bigger/(οπιι)τω: the relation of being bigger with respect to a property which obtains between individuals and the property.17 This cannot be used to generate a contradiction from the above premises, because p ≠ q:
Geach, in [4], launches an argument similar to the one we just dismantled to argue against a rule of inference that is in effect identical to (PD). He claims that that rule would license an invalid argument. And indeed, the following argument is invalid:
a is a big flea, so a is a flea and a is big; b is a small elephant, so b is an elephant and b is small; so a is a big animal and b is a small animal. (Ibid., p. 33.)
But pseudo-detachment licenses no such argument. Geach’s illegitimate move is to steal the property being an animal into the conclusion, thereby making a and b commensurate. Yes, both fleas and elephants are animals, but a’s being big and b’s being small follow from a’s being a flea and b’s being an elephant, so pseudo-detachment only licenses the following two inferences, p ≠ q:
And a big p may well be smaller than a small q, depending on the values assigned to p, q.
Third objection. If we do not hesitate to use ‘small’ not only as a modifier but also as a predicate, then it would seem we could not possibly block the following fallacy:
But we can and must block it, for this argument is obviously not valid. The premises do not guarantee that the property p with respect to which Jumbo is small is identical to the property Elephant. As was already pointed out, one cannot start out with a premise that says that Jumbo is small (is a small something) and conclude that Jumbo is a small B.
4 Conclusion
In this paper, I applied TIL as a logic of intensions to deal with property modifiers and properties in terms of intensional essentialism. Employing the essences of properties, I defined the distinction between non-subsective (that is privative) and subsective modifiers. While the former ones deprive the root property of some but not all of its requisites, the latter enrich the essence of the root property. The main result is the rule of pseudo-detachment together with the proof of its validity for any kind of modifiers. The next step is to examine iterated modifiers. While obviously, the iteration of subsective modifiers goes smoothly due to right subsectivity, iterated privatives are much more complicated. For instance, while a nice, skilful surgeon is a skilful surgeon and is a surgeon as well, a demolished damaged house is not a house, while a repaired damaged house is a house. On the other hand, a demolished damaged house is not a demolished damaged bridge. The definitions provided in this paper make it possible to examine iteration of modifiers within these ideas. The issue of iterated privation has been dealt with by Jespersen & Carrara whom later the author of this paper joined. For the results see [7].











 text new page (beta)
text new page (beta)