1. Introducción

Un marco de referencia ampliamente aceptado en el área del razonamiento en sistemas inteligentes es el enfoque de sistemas basados en bases de conocimiento. La idea general de estos sistemas es mantener el conocimiento en algún lenguaje de representación con una connotación bien definida. En este caso, las sentencias se almacenan en una base de conocimiento (KB - por sus siglas en inglés) provista de un mecanismo de razonamiento [⁹].

Un reto fundamental de estos sistemas es la automatización del razonamiento deductivo a partir de la KB. El razonamiento deductivo proposicional es generalmente resumido como sigue: dada una KB K, que contiene el conocimiento acerca de un dominio (“el mundo”), y una sentencia φ que representa la consulta que captura la situación actual, ambas expresadas en lógica proposicional, el objetivo es decidir si K implica φ (en símbolos: K ⊨ φ), lo que se conoce como el problema de implicación proposicional.

La implicación proposicional es una tarea relevante en problemas como: estimar el grado de creencia, revisión y actualización de creencias, al trabajar con explicaciones abductivas, y en muchos otros procedimientos en aplicaciones de la Inteligencia Artificial (AI, por sus siglas en inglés), por ejemplo, al trabajar en planeación, diseño de sistemas multiagentes, diagnóstico lógico, razonamiento aproximado, entre otras aplicaciones [⁷, ¹³]. En general, el problema de la implicación lógica es un reto difícil en el área de razonamiento automático, y resulta ser un problema Co-NP difícil, incluso en el caso proposicional [¹⁷].

La revisión de creencias consiste en incorporar nuevas creencias a una base de conocimiento (KB) ya establecida, cambiando lo menos posible las creencias originales y manteniendo la consistencia de la KB. La función básica de la revisión de creencias es ofrecer un método de cómo cambiar una base de conocimiento cuando nos enfrentamos con nueva información φ. La nueva información puede entrar en conflicto con la que teníamos antes, y en ese caso, si queremos mantener consistencia, se deberán eliminar algunos elementos previos de la KB.

Es deseable que los cambios en la base original de conocimiento no se efectúen de cualquier manera, sino de forma racional. En la revisión de creencias se trata por tanto, de una teoría normativa que nos indica en cada caso, cuál es la manera óptima de proceder.

En cierto sentido, la revisión de creencias propone una teoría formal, cuyos efectos podemos interpretar de diferente manera. Las creencias pueden aludir a entidades mentales de un agente, a elementos de una base de conocimiento del mundo real, o tal vez, a elementos de un problema en la teoría de la decisión. Esta característica proporciona su versatilidad a la teoría de revisión de creencias [⁵].

Al proceso de revisión de creencias lo donotare-mos con el operador (◦) que actúa sobre una KB K y sobre una nueva evidencia φ, para formar una nueva KB K′ = K ◦ φ. Cuando K ⊨ φ entonces K′ = K ◦ φ = K. Cuando K ⊭ φ, la idea de la revisión de creencias es formar una nueva KB K′ a partir de la previa K, que permita inferir la nueva evidencia φ y al mismo tiempo, minimice la pérdida de información de K [⁹], [¹²].

Aunque la inferencia proposicional es un problema Co-NP-completo en su versión general [²²], existen también algunos casos que se pueden resolver de manera eficiente [¹⁷]. Consideraremos una KB 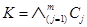y 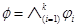, donde cada C_j ∈ K y cada ϕ_i ∈ φ son cláusulas expresadas bajo un mismo conjunto de n variables Booleanas. Este artículo muestra que el uso de patrones falsificantes de las cláusulas, ayuda a determinar si una FC se infiere de otra FC, y por tanto, a construir un algoritmo para la revisión de creencias entre formas normales conjuntivas.

Es común el uso de FC’s en el proceso de razonamiento automático, ya que el procedimiento de resolución ha abierto un área de relevancia práctica para revisar consistencia entre FC’s. Aunque es bien conocido que la inferencia basada en el principio de resolución tiene limitaciones intrínsecas [³]. Al tener un método efectivo de revisión de creencias entre FC’s, su extensión para considerar otras formas normales no es difícil, dado que cualquier fórmula Booleana se puede expresar en forma conjuntiva.

2. Preliminares

Sea X = {x₁, . . . , x_n} un conjunto de n variables Booleanas. Una literal denotada como lit es, o una variable x_i o una variable negada ¬x_i. Como es usual, para cada x ∈ X, x⁰ = ¬x y x¹ = x. Sean ⊥ and > dos constantes representando los valores lógicos falso y verdadero, respectivamente.

Una cláusula es una disyunción de diferentes literales. Para k ∈ N, una k-cláusula es una cláusula que consiste exactamente de k literales, y una (≤ k)-cláusula es una cláusula con a lo más k literales. Una frase es una conjunción de literales. Una k-frase es una frase con exactamente k literales. Una variable x ∈ X aparece en una cláusula (frase) C si x o ¬x es un elemento de C.

Una forma normal conjuntiva (F C) es una conjunción de cláusulas (que también llamaremos forma conjuntiva), y una k-F C es una F C que contiene sólo k-cláusulas.

Una forma normal disyuntiva (F D) es una disyunción de frases, y una k-F D es una F D que contiene sólo k-frases. Una FC F con n variables representa una función Booleana n-aria F :{0, 1}ⁿ → {0, 1}. Por el contrario, cualquier función Booleana F tiene infinitamente muchas representaciones equivalentes, entre estas, algunas en FC y también otras en FD.

Denotamos con Y a cualquiera de los elementos lógicos básicos que estamos utilizando, como: una literal, una cláusula, una frase, una FD o una FC, y v(Y ) denota el conjunto de variables involucradas en el objeto Y . Por ejemplo, v(¬x₁ ∨ x₂) = {x₁, x₂}. Mientras lit(Y ) denota el conjunto de literales involucradas en el objeto Y . Por ejemplo, si X = v(Y ) entonces lit(Y ) = X ∪ ¬X = {x₁, ¬x₁, . . . , x_n, ¬x_n}. También usamos ¬Y como el operador de negación sobre el objeto Y . Denotaremos a {1, 2, 3, . . .,n} por [[1, n]], y a la cardinalidad de un conjunto A por |A|.

Una asignación s para una fórmula F es un mapeo Booleano s : v(F ) → {1, 0}. Una asignación s puede también ser considerada como un conjunto de literales no complementarias: l ∈ s sí y sólo si s asigna l a cierto y ¬l a falso. s es una asignación parcial para la fórmula F cuando s ha determinado un valor lógico sólo para las variables de un subconjunto propio de F , a saber s : Y → {1, 0} y Y ⊂ v(F ). Si s tiene valores lógicos determinados para todas las variables en F entonces s es una asignación total de F .

Si F₁ ⊂ F es una FC que consiste de algunas cláusulas en F , y v(F₁) ⊂ v(F ), una asignación sobre v(F₁) es una asignación parcial sobre v(F ). Considerando n = |v(F )| y de igual forma n₁ = |v(F₁)|, cualquier asignación sobre v(F₁) tiene 2ⁿ⁻ⁿ¹ extensiones sobre v(F ).

Considerando una cláusula C y una asignación s como conjuntos de literales, C es satisfecha por s si s ∩ C ≠ ∅, de otra manera s contradice (o falsifica) a C. Una FC F es satisfecha por una asignación s si cada cláusula en F es satisfecha por s; F es contradicha por s si alguna cláusula en F es falsificada por s. Un modelo de F es una asignación sobre v(F ) satisfaciendo F .

Una frase f es satisfecha por una asignación s si f ⊆ s, de otra manera s falsifica a f. Una FD F es satisfecha por s si alguna frase en F es satisfecha por s. F es contradicha por s si todas las frases en F son falsificadas por s.

Dada una fórmula F , sea S(F ) el conjunto de todas las posibles asignaciones definidas sobre v(F ). Si n = |v(F )| entonces |S(F )| = 2ⁿ. s ⊨ F denota que la asignación s es un modelo de F (s satisface a F ). s ⊭ F denota que s es una asignación falsificante de F . Denotamos por SAT (F ) al conjunto de asignaciones en S(F ) que son modelos de F . F als(F ) denota el conjunto de asignaciones de S(F ) que falsifican a F .

Dadas dos fórmulas Booleanas F y G definidas sobre un mismo conjunto de variables, esto es v(F ) = v(G), decimos que F es consecuencia lógica de G, denotado como G ⊨ F , si para toda asignación s que satisface a G se cumple que s también satisface a F . Y diremos que F y G son logicamente equivalentes, denotado como G ≡ F , si ambas fórmulas tienen el mismo conjunto de modelos, esto es, una asignación s satisface a G si y sólo si s satisface a F . En términos de los conjuntos de modelos, podemos denotar que: G ⊨ F si y sólo si SAT (G) ⊆ SAT (F ), y que G ≡ F si y sólo si SAT (F ) = SAT (G).

#SAT (F ) denota el número de asignaciones de S(F ) que satisfacen a la fórmula F . Mientras que #F als(F ) representa al número de asignaciones de S(F ) que no satisfacen a F .

Para cualquier fórmula proposicional F , se cumple que: S(F ) = SAT (F ) ∪ F als(F ). El problema SAT consiste en decidir, para una fórmula de entrada F , si F es satisfactible, esto es, si F tiene un modelo o no. Una base de conocimiento KB es un conjunto K de fórmulas. Dada una KB K y una fórmula proposicional φ, decimos que K implica φ, y escribimos K ⊨ φ, si φ es satisfecha por todo modelo de K, es decir, SAT (K) ⊆ SAT (φ).

3. Inferencia entre formas conjuntivas

Un problema fundamental en el razonamiento deductivo es el problema de la implicación lógica: dada una KB K y una fórmula φ, debemos decidir si K ⊨ φ. En este trabajo analizaremos la complejidad computacional del caso del problema de implicación entre formas conjuntivas: FC ⊨ FC.

Sea una base de conocimiento K que se encuentra en forma conjuntiva, 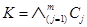y sea una consulta expresada también en FC 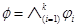, donde cada C_j ∈ K y cada ϕ_i ∈ φ son cláusulas expresadas bajo un mismo conjunto de n variables Booleanas.

Dadas dos FC’s F₁ y F₂, decidir si F₁ ⊨ F₂ es lógicamente equivalente a probar que ¬F₂ ⊨ ¬F₁, que resulta en revisar la inferencia entre formas disyuntivas, ya que si F es una FC entonces ¬(F ) es una FD, debido a que negar una FC F se realiza en tiempo lineal sobre el tamaño de F , a través de una generalización de las reglas de De Morgan.

Por otro lado, revisar la inferencia entre formas disyuntivas se reduce a revisar si una FD G es una tautología, lo que es un problema clásico en la clase de complejidad Co-NP completo [²²]. La reducción proviene de considerar que la existencia de un procedimiento que determina si G₁ ⊨ G₂, con G₁ y G₂ formas disyuntivas, permite a su vez, determinar la tautologicidad de cualquier forma disyuntiva G, ya que basta con hacer G₁ ≡ > que es una tautología, y entonces G₁ ⊨ G se cumplirá sólo si G es a su vez una tautología.

Como K y φ están en FC, las cadenas falsificantes de sus cláusulas F als(K) y F als(φ) se pueden calcular eficientemente [⁹]. Usar las cadenas falsificantes es la base para revisar si K ⊨ φ, lo que en términos de sus asignaciones equivale a revisar si SAT (K) ⊆ SAT (φ), o bien que: F als(φ) ⊆ F als(K). El resultado de aplicar el operador de revisión de creencias sobre la KB K y la nueva evidencia φ es denotado como K′ = K ◦ φ. Cuando K ⊨ φ entonces K′ = K ◦ φ = K.

Si K ⊭ φ entonces F als(φ) ⊄F als(K), lo que implica que existe un conjunto de asignaciones S tal que S ⊆ F als(φ) y S ⊈ F als(K). Si K ⊭ φ, entonces S = (F als(φ) - F als(K) ) ≠ ∅. En este caso, nuestro método de revisión de creencias trabaja construyendo tal conjunto S, lo que permite construir una nueva FC F s, tal que S = F als(F s) y K′ = K ∧ F s, cumple que: K′ ⊨ φ.

El método que proponemos obtiene S = (F als(φ)−F als(K)) como un conjunto de cadenas falsificantes, lo que nos lleva a construir de forma directa una FC F s, donde S = F als(F s) y tal que K′= K ∧ F s es una nueva FC con menos información que K (dado que K′ tiene más cláusulas que K), de hecho, se cumple que si S ≠ ∅ entonces F als(K) ⊂ F als(K′), y por tanto, SAT (K′) ⊂ SAT (K).

3.1. Construcción de conjuntos independientes de cláusulas

Dada una forma conjuntiva 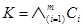, con n = |v(K)|, para cualquier cláusula C_i ∈ K, hay exactamente 2⁽ⁿ⁻|^Ci|⁾ asignaciones de S(K) falsificando C_i. Debido a que todas las falsificaciones de C_i tiene valores fijos en las posiciones de las variables v(C_i) y tales valores falsifican cada literal de C_i. Por tanto, hay n - | C_i | variables a las que se les puede asignar cualquier valor de verdad. Esto significa que hay 2⁽ⁿ⁻|^Ci|⁾ asignaciones falsificantes para C_i.

Sea A_i un conjunto de cadenas tales que la longitud de cada cadena es n. El valor en la j-ésima posición de la cadena A_i, 1≤j≤n representa el valor de verdad de x_j que falsifica C_i. Es decir, si x_j ∈ C_i entonces el j-ésimo elemento de cualquier cadena en A_i es 0. De otra manera si ¬x_j ∈ C_i entonces el j-ésimo elemento es 1.

Usaremos el símbolo * para representar los elementos que pueden tomar cualquier valor de verdad en las cadenas A_i. Por ejemplo, si K = {C₁, .., C_m} es una 2-FC, n = |v(K)|, C₁ = {x₁, x₂} y C₂ = {x₂, ¬x₃} entonces se representa A₁ como 00**· · · * y A₂ como *01*· · · *. Este abuso de notación nos permitirá dar una representación concisa y clara en el resto del documento, considerando a las cadenas A_i como patrones que representan las falsificaciones de la cláusula C_i. A tales cadenas las llamaremos cadenas falsificantes de una cláusula.

Definición 1 [¹¹] Dadas dos cláusulas C_i y C_j, si ellas tienen al menos una literal complementaria, se les llamará cláusulas independientes. En otro caso, se dice que ambas son cláusulas dependientes.

Definición 2 Sea K = {C₁, C₂, . . . , C_m} una FC. K es llamada independiente si para cualquier par de cláusulas C_i, C_j ∈ K, i ≠ j, se cumple la propiedad de independencia.

Definición 3 Dadas dos cadenas falsificantes A y B, ambas de la misma longitud, si hay una i tal que A[i] = x y B[i] = 1 − x, x ∈ {0, 1}, se dice que tienen la propiedad de independencia. En otro caso, decimos que ambas cadenas son dependientes.

Sea C una cláusula cualquiera, para cualquier variable x se cumple que:

(1)

Además, esta reducción conserva el número de asignaciones falsificantes, ya que para cualquier par de cláusulas independientes C_i, C_j se cumple que F als(C_i)∩F als(C_j) = ∅ y entonces #F als(C) = 2⁽ⁿ⁻|^c|⁾ = 2⁽ⁿ⁻⁽|^c|⁺¹⁾⁾+2⁽ⁿ⁻⁽|^c|⁺¹⁾⁾ = #F als((C ∨ ¬x) ∧ (C ∨ x)), porque (C ∨ ¬x) y (C ∨ x) son cláusulas independientes.

La conjunción de un par de cláusulas dependientes C₁ y C₂ puede expresarse mediante una conjunción de cláusulas independientes. Supongamos que hay literales en C₁ que no están en C₂, sea L = {x₁, x₂, . . . , x_p} tales literales. Esto es, L = lit(C₁) − lit(C₂). Existe una reducción para transformar C₂ (o C₁) como cláusula independiente con C₁ (o C₂) llamada reducción de independencia, y que trabaja de la siguiente manera.

Por (1) se puede escribir:

C₁ ∧ C₂ = C₁ ∧ (C₂ ∨ ¬x₁) ∧ (C₂ ∨ x₁). Ahora C₁ y (C₂ ∨ ¬x₁) son independientes. Aplicando (1) a (C₂ ∨ x₁) : C₁ ∧ C₂ = C₁ ∧ (C₂ ∨ ¬x₁) ∧ (C₂ ∨ x₁ ∨ ¬x₂) ∧ (C₂ ∨ x₁ ∨ x₂). Las primeras tres cláusulas son independientes. Repitiendo la reducción de independencia hasta x_p, se tiene que C₁ ∧ C₂ puede expresarse como:

C₁ ∧ (C₂ ∨ ¬x₁) ∧ (C₂ ∨ x₁ ∨ ¬x₂) ∧ . . . ∧ (C₂ ∨ x₁ ∨ x₂ ∨ . . . ∨ ¬x_p) ∧ (C₂ ∨ x₁ ∨ x₂ ∨ . . . ∨ x_p).

La última cláusula contiene todas las literales de C₁, así que puede eliminarse porque es subsumida por la cláusula C₁, obteniéndose que:

(2)

Las cláusulas del lado derecho de la ecuación (2) son independientes por construcción.

El operador central para revisar inferencia entre FC’s es un operador de independiencia que trabaja sobre dos cláusulas ϕ y C, y que construye un conjunto de cláusulas independientes equivalentes a ϕ ∧ C. Sea L = {x₁, x₂, . . . , x_p} = lit(C) − lit(ϕ) se define el operador de independencia entre ϕ y C como sigue:

La complejidad en tiempo para ejecutar Ind(ϕ, C), que denotaremos como T_Ind(|ϕ|, |C|), depende directamente del tiempo para ejecutar operaciones básicas entre conjuntos de literales. Por ejemplo, la operación lit(C) − lit(ϕ) podría realizarse como: para cada x ∈ lit(C) revisar si x ∈ lit(ϕ) o si ¬x ∈ lit(ϕ), lo que requiere de a lo más |C| * |ϕ)| ≤ n² operaciones de comparación. Si los conjuntos lit(C) y lit(ϕ) se representan mediante arreglos de n posiciones (fijando una posición para cada una de las n posibles variables), entonces lit(C) − lit(ϕ) se realizará en a lo más O(n) operaciones lógicas entre las posiciones de ambos arreglos.

Por otro lado, cuando L = lit(C) − lit(ϕ) ≠ ∅, se realiza un ciclo de |L| ≤ (n − 1) iteracciones, y en cada iteracción i se agrega una disyunción y una negación para formar (ϕ ∨ x₁ ∨ . . . ∨ ¬x_i), y a través de una conjunción se adiciona esta cláusula a la FC que se esta construyendo. Esto nos lleva a un proceso, en el peor caso, de orden O(n) para construir Ind(ϕ, C).

Veamos como este operador de independencia Ind(ϕ_i, C_j) entre cláusulas ϕ_i ∈ φ y C_j ∈ K es la base para realizar la revisión de creencias entre K y φ.

4. Revisión de Creencias entre formas conjuntivas

Nuestro método de Revisión de Creencias se basa en las siguientes dos propiedades:

1. Si ∀ s ∈ F als(φ) se cumple que s ∈ F als(K), entonces K ⊨ φ.

2. Si ∃ s ∈ F als(φ), y s ∉ F als(K), entonces K ⊭ φ.

El primer caso considera que todas las asignaciones de F als(φ) están en el conjunto F als(K), lo que demostraría que K ⊨ φ. Y en este caso K′ = K, ya que no se necesita cambiar la KB K.

En el segundo caso, se detectarán los conjuntos de asignaciones S tal que ∃ϕ ∈ φ, S ⊆ F als(ϕ) y S ⊈ F als(K). Para construir estos conjuntos S se inicia con la cadena A₁ que representa a F als(ϕ₁) y se aplica el operador Ind con cada una de las cadenas B_j que representan F als(C_j), j = 1, . . . , m.

La operación Ind(ϕ_i, C_j) forma una cadena que representa el conjunto de asignaciones falsificantes: F als(ϕ_i) − F als(C_j). Esto es, Ind(ϕ_i, C_j) determina las asignaciones que están en F als(ϕ_i) pero que no están contenidas en F als(C_j). Si se aplica la operación Ind sobre todo C_j ∈ K, obtendremos como resultado el conjunto S ⊆ F als(ϕ_i) ∧ S ⊄ F als(K).

El conjunto S permite construir una FC F s_i, F s_i = (D₁ ∧ D₂ ∧ . . . D_t), donde S = F als(F s_i). Al agregar las nuevas cláusulas de F s_i a K, obtenemos una nueva KB K′_i = K ∧ F s_i, que cumple que: K′_i ⊨ ϕ_i, y además, K′_i sigue siendo una FC. Presentamos algorítmicamente este proceso.

Ind(ϕ_i, K) consiste de dos ciclos, uno externo sobre C_j ∈ K, de orden O(|K|). Este ciclo (el F or) recorre las columnas de una tabla donde se irán colocando los resultados de Ind(ϕ_i, C_j).

El cuerpo del ciclo interno consiste esencialmente de realizar el operador Ind(ϕ_i, C_j) que es de orden O(n), y de realizar ajustes a la FC F s_i que inicia con la cláusula ϕ_i y que involucra no más de O(n) operaciones.

El número de filas de la tabla se va ajustando de forma dinámica, dependiendo del resultado de Ind(ϕ_i, C_j). En el peor caso, este ciclo sobre el número de filas puede llevarnos a un crecimiento exponencial sobre el número de cláusulas que contiene una F s_i, como se mostrará en la sección de análisis de complejidad de nuestro método.

Cuando el proceso Ind(ϕ_i, K) itera sobre toda ϕ_i ∈ φ, se forman las cláusulas F s_i tal que F als(∪₍F s_i)) = F als(φ) − F als(K). Al adicionar a K el conjunto de cláusulas ∪₍F s_i), se forma una nueva KB K′ tal que K′ ⊨ φ, puesto que F als(φ) ⊆ F als(K′), y por tanto, SAT (K′) ⊆ SAT (φ).

Ejemplo 1. En todos los ejemplos a presentar, supondremos un ordenamiento alfanumérico sobre el conjunto de variables que se utilizan. Sea K = (¬p∨q∨s)∧(¬q∨¬r∨s)∧(¬q∨r∨¬s)∧(¬p∨¬q∨r) y φ = (¬p ∨ ¬r) ∧ (¬q ∨ r) ∧ (p ∨ q ∨ ¬r ∨ ¬s) ∧ (¬t). Probar que K ⊨ φ, es equivalente a revisar que: F als(φ) = {1*1**, *10**, 0011*, ****1} ⊆ F als(K) = {10*0*, *110*, *101*, 110**}. En cada celda de las columnas 2 en adelante de la Tabla 1, se va mostrando el resultado de Ind(ϕ_i, C_j).

Tabla 1 Construyendo Ind(φ, K) 

Dadas 2 cláusulas C_i, C_j que difieren en el signo de sólo una variable, la reducción por literal complementaria genera una sóla cláusula de C_i ∧ C_j, de hecho, la reducción se basa en la aplicación de la ecuación (1).

Por ejemplo, sea C_i = (x ∨ q), y C_j = (¬x ∨ q), entonces C_i ∧ C_j = (q). En términos de las cadenas falsificantes de las cláusulas, denotaremos tal reducción como: V arcom(A_i, A_j). En el caso de nuestro ejemplo, se tiene que: V arcom(1111*, 1011*) = 1 * 11*.

Es relevante aplicar la operación de reducción por literales complementarias sobre las cadenas en S, para así minimizar el número total de cláusulas.

Aplicando la reducción V arcom y eliminando cláusulas subsumidas al resultado del ejemplo 1, se tiene que: S = {1*11*, 0100*, 0011*, 00**1, *1111, 10*11}. Escribiendo S como una FC, F s = (¬p ∨ ¬r ∨ ¬s) ∧(p ∨ ¬q ∨ r ∨ s) ∧ (p ∨ q ∨ ¬r ∨ ¬s) ∧ (p ∨ q ∨ ¬t) ∧ (¬q ∨ ¬r ∨ ¬s ∨ ¬t) ∧ (¬p ∨ q ∨ ¬s ∨ ¬t). Y así, la nueva KB K′ = K ∧ F s es una FC que cumple: K′ ⊨ φ.

4.1. Propiedades del método de Revisión de Creencias

El conjunto de cláusulas construido mediante Ind(ϕ_i, K) se agrega a la KB original K, y así, cada ϕ_i ∈ φ se infiere de K ∧ Ind(ϕ_i, K). Esto se demuestra en el siguiente teorema sobre la corrección de nuestro método.

Teorema 1 Dadas dos cláusulas ϕ_i y C_j se cumple que (C_j ∧ Ind(ϕ_i, C_j) ) ⊨ ϕ_i.

Demostración.

Si ϕ_i y C_j son cláusulas independientes, entonces ϕ_i = Ind(ϕ_i, C_j) y por tanto (C_j ∧ Ind(ϕ_i, C_j)) = (C_j ∧ ϕ_i). Así (C_j ∧ ϕ_i) ⊨ ϕ_i, por la propiedad proposicional: (p ∧ q) ⊃ q y por la reflexividad de la inferencia lógica: ϕ_i ⊨ ϕ_i.

Si ϕ_i y C_j no son independientes, pero Ind(ϕ_i, C_j) = ∅, esto implica que F als(ϕ_i) ⊆ F als(C_j) y por tal C_j ⊨ ϕ_i. Como C_j = (C_j ∧ Ind(ϕ_i, C_j)), entonces (C_j ∧ Ind(ϕ_i, C_j)) ⊨ ϕ_i.

Cuando ϕ_i y C_j no son independientes, e Ind(ϕ_i, C_j) ≠ ∅, se cumple que (C_j ∧ Ind(ϕ_i, C_j)) ≡ (C_j ∧ ϕ_i) por (2), cumpliéndose que: (C_j ∧ ϕ_i) ⊨ ϕ_i, por la propiedad proposicional: (p ∧ q) ⊃ q, y por la reflexividad: ϕ_i ⊨ ϕ_i.

Así, para cualquiera de los tres posibles resultados de Ind(ϕ_i, C_j), se cumple: (C_j ∧Ind(ϕ_i, C_j)) ⊨ ϕ_i.

El conjunto de cláusulas construido mediante Ind(ϕ_i, C_j) contiene exactamente las cláusulas necesarias que permitirán inferir cada ϕ_i ∈ φ a partir de C_j ∧ Ind(ϕ_i, C_j). Al iterar Ind(ϕ_i, C_j) sobre todo C_j ∈ K, se obtiene un conjunto de cláusulas con las que se asegura cumplir (K ∧ Ind(ϕ_i, K)) ⊨ ϕ_i. El teorema anterior demuestra así la corrección de nuestro método.

Mostremos ahora que el conjunto de cláusulas en Ind(ϕ_i, C_j) representa el conjunto mínimo de cláusulas que permiten cubrir el espacio: F als(ϕ_i) − F als(C_j), que es el espacio mínimo necesario de asignaciones para que F als(ϕ_i) ⊆ F als(C_j)∪F als(Ind(ϕ_i, C_j)), y por tanto, para que se cumpla (C_j ∧ Ind(ϕ_i, C_j)) ⊨ ϕ_i.

Teorema 2 F als(Ind(ϕ_i, C_j)) = F als(ϕ_i) − F als(C_j).

Demostración.

Si Ind(ϕ_i, C_j) = ∅, se cumple que Ind(ϕ_i, C_j) es el número mínimo de cláusulas que permiten inferir (C_j ∧ Ind(ϕ_i, C_j)) ⊨ ϕ_i, ya que de hecho, C_j ⊨ ϕ_i.

Supongamos ahora que Ind(ϕ_i, C_j) ≠ ∅. Veamos que ∀s ∈ F als(Ind(ϕ_i, C_j)) se cumple que s ∈ F als(ϕ_i), y s ∉ F als(C_j). Sea s ∈ F als(Ind(ϕ_i, C_j)), entonces s falsifica a ϕ_i, ya que cada cláusula en Ind(ϕ_i, C_j) tiene la forma (ϕ_i ∨ R), con R una disyunción de literales. Si s falsifica a (ϕ_i ∨ R) entonces s falsifica tanto a (ϕ_i) como a (R), por tanto s ∈ F als(ϕ_i). Además, s ∉ F als(C_j), ya que C_j es independiente con cada una de las cláusulas de Ind(ϕ_i, C_j) (por construcción del operador de independencia), y por tal, s ∉F als(C_j).

El teorema anterior demuestra que el operador de independencia Ind(ϕ_i, C_j) construye un conjunto de cláusulas que cubren de forma exacta el espacio de asignaciones que hacen falta para que F als(ϕ_i) ⊆ F als(C_j) ∪ F als(Ind(ϕ_i, C_j)). Aún más, el conjunto F als(Ind(ϕ_i, C_j)) es el conjunto mínimo de asignaciones para cubrir el espacio F als(ϕ_i) − F als(C_j), ya que F als(C_j) y F als(Ind(ϕ_i, C_j)) son ajenos (por construcción del operador de independencia), y por tanto F als(C_j) ∩ F als(Ind(ϕ_i, C_j)) = ∅.

Corolario 1 F als(Ind(ϕ_i, K)) ⊆ F als(ϕ_i).

Demostración.

Por el teorema (2), se tiene que F als(Ind(ϕ_i, C_j)) = F als(ϕ) − F als(C_j), al iterar sobre cada C_j de K se cumple que F als(Ind(ϕ_i, K)) = F als(ϕ_i) − F als(K). Y por propiedades entre conjuntos, se cumple que F als(Ind(ϕ_i, K)) ⊆ F als(ϕ).

Al iterar Ind(ϕ_i, C_j) sobre todo C_j ∈ K, se obtiene un conjunto mínimo de cláusulas: F s_i que asegura que: (K ∧ F s_i) ⊨ ϕ_i.

Al extender K con las cláusulas obtenidas en Ind(ϕ_i, K) se va formando K′. Así K′ extiende al conjunto de cláusulas de K, y por tanto, extiende también el espacio inicial de falsificaciones de K, agregando las asignaciones que falsifican a Ind(ϕ_i, K). De hecho, estos dos conjuntos de falsificaciones son excluyentes por construcción de Ind(ϕ_i, K), y por tanto, F als(K)∩F als(Ind(ϕ_i, K)) = ∅. En otras palabras, el conjunto de modelos de K′ es ahora un subconjunto de los modelos de K, SAT (K′) ⊆ SAT (K).

Sin embargo, al iterar el operador Ind(ϕ_i, K), sobre cada ϕ_i ∈ φ, i = 1, . . . , k, se tiene que los k conjuntos de cláusulas F s_i formados por Ind(φ, K) podrían no tener un número mínimo de cláusulas. La reducción V arcom permite reducir el número de cláusulas en Ind(φ, K).

Así, después de obtener el conjunto de cláusulas Ind(φ, K), se reduce su cardinalidad, eliminando cláusulas subsumidas y aplicando la reducción V arcom entre cláusulas de dos diferentes conjuntos Ind(ϕ_i1, K) e Ind(ϕ_i2, K).

Este último proceso de reducción de cláusulas a través de literales complementarias y de eliminación de cláusulas subsumidas, se ejecuta en tiempo polinomial (de hecho en tiempo cuadrático) sobre la longitud inicial de |Ind(φ, K)|, ya que consistiría en ir tomando una cláusula C ∈ Ind(φ, K), y revisar si es subcláusula (como subconjunto de literales) o si hay una literal complementaria con alguna otra cláusula en Ind(φ, K) − C. Además, el resultado de la reducción mantiene la forma de una FC.

Un proceso similar a V arcom se aplicó en el cálculo de los implicantes primos de una fórmula, presentada por Quine y McCluskey [²⁴]. En esta propuesta, los autores buscan los implicantes primos esenciales que sean necesarios y suficientes para generar la función Booleana de entrada.

Sin embargo, cuando la heurística de éste método recibe una fórmula con un gran número de variables, conduce a resultados no mínimos, por lo que se tiene que recurrir al método de Petrick con el fín de poder caracterizar la expresión mínima de la función Booleana [²³].

Ejemplo 2.

Sea K = (¬p∨q∨r∨s) ∧ (¬p∨¬q) ∧ (¬p∨¬r) y φ = (¬p∨¬s∨¬t) ∧ (q∨¬r∨¬s∨¬t) ∧ (¬p∨q∨r∨¬s∨t) ∧ (¬p), probar que K ⊨ φ, es equivalente a revisar si F als(φ) = {1**11, *0111, 10010, 1****} ⊆ F als(K) = {1000*, 11***, 1*1**}. En cada celda de la Tabla 2, se va calculando Ind(ϕ_i, C_j).

Tabla 2 Aplicación del operador Ind(φ, K) 

Como se puede observar en la Tabla 2, al aplicar el operador Ind(φ, K) se genera un número de cadenas mayor a las que aparecen en la Tabla 3, debido a que en la Tabla 3, antes de aplicar el operador de independencia, se ordenan las cláusulas C_i ∈ K, de acuerdo al tamaño |lit(C_j) − lit(ϕ_i)| de menor a mayor, dado que el número de literales de C_j diferentes con ϕ_i determinará el número de cláusulas independientes a generarse, además de descartar con anticipación cadenas que serán subsumidas.

Tabla 3 Cálculo de Ind con las C_i ∈ K ordenadas H_H 

Por tanto, antes de aplicar el operador Ind(ϕ_i, K) es conveniente ordenar las cláusulas en K de acuerdo al valor de cada ϕ_i que se esté considerando, tal y como se muestra en la Tabla 3. Con lo que se obtiene una estrategia de reducción sobre el número de cláusulas independientes a generar. Al aplicar el proceso de reducción de cláusulas vía literales complementarias, se tiene como resultado para el caso del ejemplo 2, que S = {1001*, 00111}, cuya FC es F s = (¬p ∨ q ∨ r ∨ ¬s) ∧ (p ∨ q ∨ ¬r ∨ ¬s ∨ ¬t). Así, K′ = K ∧ F s = (¬p ∨ q ∨ r ∨ s) ∧ (¬p ∨ ¬q) ∧ (¬p ∨ ¬r) ∧ (¬p ∨ q ∨ r ∨ ¬s) ∧ (p ∨ q ∨ ¬r ∨ ¬s ∨ ¬t).

5. Postulados KM

Katsuno y Mendelzon (KM) unificaron los diferentes enfoques semánticos que un operador de revisión de creencias debería cumplir [¹⁶]. Presentamos aquí el análisis de estos postulados sobre nuestra propuesta de operador de revisión de creencias K′ = K ◦ φ = K ∧ Ind(φ, K).

Consideremos ahora los postulados KM.

El teorema 1, muestra que nuestro operador de revisión de creencias cumple el postulado R1. Si K ∧φ es satisfactible y K ⊨ φ, entonces cada ϕ_i ∈ φ se infiere de K y por tanto, Ind(ϕ_i, K) = ϕ_i, i = 1, . . . , k. Así, K ◦ φ = K ∧ Ind(φ, K) = K ∧ φ, cumpliéndose el postulado R2.

Analicemos el cumplimiento del postulado R3. Este se cumple si K ◦ φ es satisfactible (por R2). Pero si F als(K) ∪ F als(Ind(φ, K)) cubriera a todo el espacio de asignaciones: 2ⁿ, entonces sólo en este caso se redefine K ◦ φ. Por ejemplo, si K = (p∨q)∧(p∨¬q) y φ = (¬p), como φ es independiente con cada cláusula de K, se tendría que K◦φ = (¬p) ∧ (p∨q) ∧ (p∨¬q), que claramente es una fórmula insatisfactible.

Bajo estas circunstancias de comprobación de que (K ∧ Ind(φ, K)) es insatisfactible, se redefine K ◦ φ para que cumpla R3. Se redefine K ◦ φ = ((K ∧ Ind(φ, K))-C_j), seleccionando la cláusula C_j ∈ K con la menor información (note que |SAT (C_j)| es mínimo sobre la cardinalidad del conjunto de modelos de cada C_j ∈ K, si |C_j| es máximo en K), y de esta forma se mantendría la satisfactibilidad del resultado de la revisión de creencias.

Los postulados R4 y R5 se cumplen debido a que nuestro operador de revisión es cerrado sobre las formas conjuntivas. Por ejemplo, si consideramos dos diferentes KB; K1 ≡ K2, y dos subfórmulas φ1 ≡ φ2, se cumple que F als(K1) = F als(K2) y F als(φ1) = F als(φ2). Al trabajar nuestro método sobre los conjuntos F als(Ind(φ, K)) y al ser tanto K, φ y Ind(φ, K) FC’s, se cumple de forma directa el postulado R4.

Veamos que se cumple R5 (K ◦ φ) ∧ γ ⊨ K ◦ (φ ∧ γ). Consideremos: K ◦ (φ ∧ γ) = K ∧ Ind(φ ∧ γ, K) por definición del operador (◦), K ◦ (φ ∧ γ) = K ∧ Ind(φ, K) ∧ Ind(γ, K) por definición del operador Ind y puesto que tanto φ como γ son FC’s. Entonces, K ◦ (φ ∧ γ) = K ∧ S ∧ Ind(γ, K) con S = Ind(φ, K). Por otro lado, F als(K ◦ (φ ∧ γ)) = F als(K ∧ S ∧ Ind(γ, K)) = F als(K ∧ S) ∪ F als(Ind(γ, K)) = F als(K◦φ)∪F als(Ind(γ, K)) ⊆ F als(K ◦ φ) ∪ F als(γ), por el Corolario 1. Así, F als(K ◦ (φ ∧ γ)) ⊆ F als(K ◦ φ) ∪ F als(γ) = F als((K ◦ φ) ∧ γ) cumpliéndose R5.

(R6) Si (K ◦ φ) ∧ γ es satisfactible, entonces K ◦ (φ ∧ γ) ⊨ (K ◦ φ) ∧ γ. Sea F als((K ◦ φ) ∧ γ) = F als(K ∧ Ind(φ, K) ∧ γ), pero (γ) sólo sería igual a Ind(γ, K) sí y solo si γ fuera independiente con cada cláusula de K, y entonces sólo en ese caso se tiene que F als(K ∧ Ind(φ, K) ∧ γ) = F als(K ∧ Ind(φ, K) ∧ Ind(γ, K)) = F als(K ◦ (φ ∧ γ) y así se cumpliría el postulado R6.

6. Análisis de complejidad en tiempo

La función que mide el tiempo de nuestro operador de revisión de creencias K ◦ φ, que denotaremos como: T₀(|φ|, |K|), depende principalmente del tiempo de ejecución del operador de independencia: Ind(φ, K). Y como Ind(φ, K) se obtiene del cálculo iterativo de Ind(ϕ_i, K), ∀ϕ_i ∈ φ, entonces el tiempo de construcción para Ind(φ, K) depende del tiempo máximo que requiere algún Ind(ϕ_i, K), ϕ_i ∈ φ.

Como se presentó en la sección del diseño del algoritmo 1, la complejidad en tiempo del proceso Ind(ϕ_i, K) es de orden O(|K| · n · f(|ϕ_i|, |K|)), donde f(|ϕ_i|, |K|) es una función entera, que dada una cláusula ϕ_i y una FC K, determina el número de cláusulas que regresará el proceso Ind(ϕ_i, K). Analicemos ahora, el número máximo posible de cláusulas que se pueden generar a través del proceso Ind(ϕ_i, K).

En algunos casos, Ind(ϕ_i, K) puede generar conjuntos nulos (cuando ∃ C_j ∈ K, tal que C_j ⊨ ϕ_i), pero en los peores casos, la complejidad en tiempo del cálculo de Ind(ϕ_i, K), dependerá de la longitud de los conjuntos: S_ij = {x₁, x₂, . . . , x_p} = lit(C_j) - lit(ϕ_i), j = 1, . . . , m.

Como se hizo notar en el ejemplo 2, fija una ϕ_i ∈ φ, es conveniente ordenar las cláusulas C_j ∈ K de acuerdo a la cardinalidad de los S_ij, j = 1, . . . , m de menor a mayor, y eliminando de este ordenamiento las cláusulas que sean independientes con ϕ_i. Una vez ordenadas las cláusulas en K en función a la longitud de S_ij, se va aplicando el operador Ind(ϕ_i, C_j), j = 1, . . . , m, determinándose así, la sucesión:

S_i0 = v(ϕ_i)

S_i1 = v(C₁) - v(ϕ_i)

S_i2 = v(C₂) - (v(C₁) ∪ v(ϕ_i))

. . .

S_im = v(C_m) - (v(C_m−1) ∪ . . . ∪ v(C₁) ∪ v(ϕ_i)).

El número de cláusulas que se generan por Ind(ϕ_i, C₁) sería |S_i1|, y para Ind(ϕ_i, C₂) se podría tener en el peor caso, hasta |S_i2| nuevas cláusulas por cada una de las cláusulas generadas en Ind(ϕ_i, C₁), y así sucesivamente. Para Ind(ϕ_i, C_m), habría a lo más |S_im| posibles cláusulas que se pueden generar por cada una de las anteriores cláusulas en Ind(ϕ_i, C_m−1).

Esto nos genera un proceso multiplicativo sobre el número de cláusulas en Ind(ϕ_i, K), dado por: 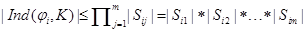y bajo la restricción 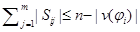, ya que cada conjunto S_ik cubre el espacio de asignaciones formado por las variables que no ha sido cubierto por las variables de las C_j, j = 1,. . ., k−1 y las variables de ϕ_i, y en todo este proceso no puede cubrirse más de n − v(ϕ_i) variables.

De hecho, si algún S_ij = ∅, entonces el conjunto de cláusulas en Ind(ϕ_i, K) es también vacío, indicando que el K actual no cambiará al considerar tal ϕ_i y entonces Q_mj=1| S_ij ⊨ 0.

Cuando no hay cláusulas independientes con ϕ_i, ni ningún S_ij = ∅ para j = 1, . . . , m, entonces la complejidad en tiempo para calcular Ind(ϕ_i, K) es acotado por su número de cláusulas, en otras palabras, se tiene que |Ind(ϕ_i, K)| ≤ |S_i1| * |S_i2| * . . . * |S_im| * P oly(n). Donde P oly(n) resume un tiempo polinomial sobre el número de variables que se genera de aplicar el operador Ind(ϕ_i, C_j) y por aplicar el ordenamiento inicial sobre las cláusulas de K.

Es claro que el valor |Ind(ϕ_i, K)| no puede ser mayor al número de asignaciones que están en F als(ϕ_i) − F als(K), ya que de hecho, se está cubriendo este espacio de asignaciones vía cláusulas independientes. Esto significa que |S_i1| * |S_i2| * . . . * |S_im| ≤ 2⁽ⁿ⁻|^ϕi|⁾.

Podemos inferir entonces que la complejidad en tiempo T₀(|φ|, |K|) para nuestro operador de revisión de creencias, en el peor de los casos, esta acotado superiormente por Max{|S_i1| * |S_i2| * . . . * |S_im| : ∀ϕ_i ∈ φ}, suprimiendo factores polinomiales sobre n (el número de variables) y sobre el tamaño de la KB K. A su vez, este valor máximo está acotado superiormente por 2^(n−min{|^ϕi|^:ϕi∈φ}). Cumpliéndose entonces que: T₀(|φ|, |K|) ≤ Max{|S_i1| * |S_i2| * . . . * |S_im| : ∀ϕ_i∈φ} ∈ O(2^(n−min{|^ϕi|^:ϕi∈φ})). Y por tanto, la complejidad en tiempo de nuestra prouesta es de O(|K| · n · 2^(n−min{|^ϕi|^:ϕi∈φ})).

7. Conclusiones

Un problema fundamental del razonamiento automático en el cálculo proposicional y de los sistemas inteligentes en general, es el problema de revisión de creencias.

En este trabajo se presenta un método novedoso para construir K′ = K ◦ φ, a partir de considerar que K y φ son FC’s. Como K y φ son FC’s, el proceso de revisión entre K y φ se va reduciendo a realizar la revisión entre cada ϕ_i de φ y cada C_j de K, simplificando el problema total de revisión en resolver los |K| * |φ| subproblemas de revisión entre dos cláusulas.

Se construyó un operador lógico llamado Ind(ϕ_i, C_j), que encuentra las cláusulas que cubren el espacio de asignaciones faltantes para que se cumpla que: F als(ϕ_i) ⊆ F als(C_j) ∪ F als(Ind(ϕ_i, C_j)), al iterar este proceso sobre todo ϕ_i ∈ φ, y cuidando reducir clásulas complementarias, encontramos un proceso efectivo para la revisión de creencias entre formas conjuntivas.

Se demuestra la corrección de nuestra propuesta de revisión de creencias, la verificación de cumplimiento de los postulados KM, así como el análisis de la complejidad en tiempo de los procesos involucrados en nuestro método.