1. Introducción
Se ha encontrado que la geometría fractal es la más apropiada para describir muchos patrones naturales [1, 2]. Un fractal, matemáticamente hablando, se define cómo un objeto geométrico invariante de escala cuya autosimilitud es exacta [3], como por ejemplo el triángulo de Koch (Fig. 1) [4]. En la práctica, las estructuras fractales tienen auto-similitud estadística [5]. Otra característica de un conjunto fractal es que la dimensión que lo caracteriza, Df, es fraccionaria, si se entiende como dimensión el número mínimo de coordenadas necesarias para describir cualquier punto del conjunto [5, 6].

Fig. 1 Proceso de generación del copo de Koch. Este objeto geométrico es una curva cerrada continua pero no diferenciable en ningún punto [4]
Se define usualmente la dimensión de caja como [5]:
donde N(ε) es el número de celdas de tamaño ε necesarias para cubrir el conjunto. Una forma de calcular la dimensión fractal Df es mediante la representación de N(ε) vs ε en gráficas log-log. Si se obtiene una relación lineal con un coeficiente de correlación alto entonces Df se identifica como la pendiente de la recta [7].
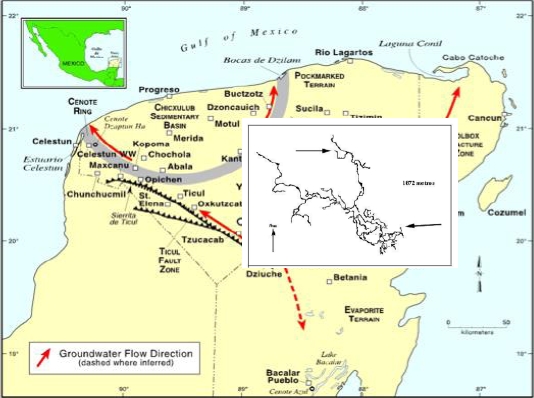
Distintos procesos geológicos como la erosión, la sedimentación y la disolución química son responsables de la formación de estructuras naturales complejas [8]. Los sistemas subacuáticos de cuevas que existen en Quintana Roo, Estado ubicado al noreste de la península de Yucatán, México, ver Fig. 2, son los de mayor extensión en el mundo [9, 10].
Desde hace más de 30 años se han explorado los grandes sistemas de cuevas sumergidas de esta región, entre uno de ellos se encuentra el sistema de Ox Bel Ha, la cueva subacuática.
La geometría de 13 cuevas subacúaticas de esta región fue analizada utilizando como base teórica la Ec. (1), encontrándose que muestran un comportamiento fractal (y por lo tanto una invarianza de escala) a lo largo de hasta cuatro ordenes de magnitud para los sistemas más desarrollados (Fig. 3 y Tabla 1), [13].

Fig. 3 Ajuste en escala log-log de dimension fractal (Eq. 1) para la Cueva “Del Mar” (Mapa interior [11]). El coeficiente de correlación r2=0.99 nos indica un comportamiento fractal del Sistema mapeada más grande del mundo con 269.8 km de conductos [11]
Tabla 1 Dimensión fractal de 13 sistemas de cuevas
| Cueva | Longitud [m] | Df |
|---|---|---|
| Cubera | 180 | 1.06 |
| Venado | 121 | 1.05 |
| Gran Cenote | 700 | 1.06 |
| Pequeño cenote | 660 | 1.19 |
| El Punto | 607 | 1.2 |
| Cascabel | 547 | 1.22 |
| Las Palmas | 160 | 1.26 |
| Minotauro | 596 | 1.23 |
| Del Mar | 1872 | 1.31 |
| Actun Koh | 628 | 1.31 |
| Xel.Ha | 900 | 1.33 |
| Sac Actun | 1100 | 1.31 |
| Ox Bel Ha | 2500 | 1.38 |
La litología de la Península de Yucatán consiste en pura roca carbonatada formada por depósitos marinos hace millones de años [14]. El proceso mediado por la disolución que se lleva a cabo en las rocas carbonatadas se le conoce como karstificación [15]. El objetivo de este trabajo es utilizar un modelo genérico de crecimiento conocido por formar estructuras fractales, llamado modelo de Agregación Limitada por Difusión, ALD, (o DLA, Diffusion Limited Aggregation) [16, 17, 18].
Por lo tanto, utlizaremos el modelo ALD para simular el crecimiento de los sistemas subacuáticos descritos en parráfos anteriores Es necesario para ello implementar algunas modificaciones que describan mejor este tipo de sistemas, por ejemplo la heterogeneidad de las estructuras rocosas que pueden inducir un crecimiento confinado por zonas de baja permeabilidad o fracturas. La presencia de una dirección preferencial favorecida por el desnivel y la influencia fuerza de gravedad es otro aspecto que será tomado en cuenta.
2. Zona de estudio: Karst y cuevas
Un paisaje superficial o subterráneo que exhibe irregularidades en su superficie causadas por disolución es conocido como paisaje kárstico. Estos paisajes son usualmente formados sobre caliza y en un menor grado sobre roca dolomita [15]. En las áreas kársticas normalmente se pueden encontrar cuevas como resultado de un largo proceso de disolución. La reacción química que ocurre sobre la roca caliza (carbonato de calcio, CaCO3) al estar en contacto con el exterior (dióxido de carbono CO2 y agua H2O), produce su disolución, al formar calcio y anhídrido carbónico:
Este proceso disuelve la roca formando con el paso de millones de años grandes sistemas de cuevas subterráneas [19]. El efecto de la disolución de la roca carbonatada depende del contenido de carbonato de calcio y de la acidez del agua en cada sitio específico [20].
Otra de las condiciones que influyen sobre la formación del karst es la hidrodinámica, es decir la existencia de una energía potencial o un gradiente hidráulico entre el área de carga (regiones donde se concentra el agua, p.e. sumideros o dolinas) y de descarga del agua (ya sea el mar o un río); así como también la existencia de discontinuidades que garantizen el flujo, p.e. fracturas preexistentes en el medio [21].
Por tanto, al ser la karstificación un proceso que se da en las discontinuidades de las rocas ya existentes, se tienen zonas de alta permeabilidad (fracturas) y zonas impermeables o de permeabilidad reducida (bloques) [20, 21]. La relación entre el flujo de agua y la estructura de los huecos genera una red de drenaje principal en la que el agua tiende a concentrarse en un reducido número de gruesos conductos que por lo general se comunican con el área de descarga. El término fractura se usa de manera general para describir distintos tipos de aberturas continuas cuya longitud suele exceder el ancho de las mismas. Las fracturas pueden considerarse como elementos discretos cuyo ancho puede variar de centímetros hasta metros [22].
2.1. Hidrogeología: Península de Yucatán
La península de Yucatán es una plataforma que consiste de roca carbonatada y evaporitas en varias centenas de sus metros superiores con muy poco relieve y una alta permeabilidad [23].
La fracturación de la superficie y la karstificación del subsuelo, favorecen la rápida infiltración de la lluvia; teniendo como resultado el desarrollo de sistemas kársticos interconectados a través de fracturas y abiertos al exterior por el colapso de alguna de estas conocidos como cenotes [22].Por la geología que presenta esta península se puede dividir en tres regiones principales: El Este, la Zona Central y el Noroeste. De estas tres zonas las menos estudiadas son la Zona Central y la región Este. En la parte Noroeste se encuentra la huella del cráter Chicxulub [10, 12]. Los sistemas de cuevas que se encuentran en la zona Este son el objeto de análisis de este trabajo. La Península ha tenido un desarrollo geológico complejo y se caracteriza por ser bastante plana con excepción de algunas elevaciones máximas de 275 m.s.n.m. [24].
En el caso de la península de Yucatán el agua subterránea se mueve de las zonas de mayor precipitación (ubicadas al sur) hacia la costa, donde se realiza la descarga natural del acuífero al mar (Fig. 2) [21]. Los principales ejes estructurales de la Península de Yucatán presentan una orientación ONO-ESE y NNE-SSO, asociados con la Sierrita de Ticul y el Sistema Bacalar-Río Hondo, respectivamente [21]. Otros rasgos estructurales de suma importancia son las fracturas que se encuentran en la parte NNE de la península conocida como la “zona de fracturas de Holbox” (Fig. 4). Estas fracturas son lineamientos de cientos de kilómetros de extensión observadas por Weidie [25] y posteriormente por Escolero et al. [26] mediante imagenes de radar. Se observa que la orientación de las cavernas en esta zona es NNW-SSE, casi perpendicular a la costa.
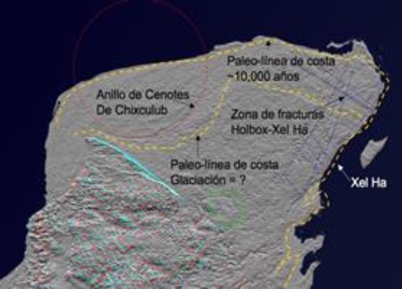
Fig. 4 Imagen en radar de la Península de Yucatán donde se observan las fracturas y discontinuidades de su estructura [21]
Su formación multifacética ocurrió cuando el nivel del mar se encontraba más abajo que el actual.
Estos sistemas de cuevas tienen dimensiones que van desde cinco metros hasta cincuenta metros de ancho, y de dos hasta diez metros de alto [26]. En el último kilómetro antes de llegar a la costa los conductos tienden a ser paralelos a ésta influenciados por el sistema de fracturas de la zona. El flujo está dirigido hacia la parte alta de las caletas que tienen una forma característica de “Y” donde a través de fracturas con orientación N-S descargan a canales principales que conducen el agua dulce al mar, como se ve en las caletas de Yal-Ku y Xel-Ha [21] (Figura 5). Se encuentran dos áreas a lo largo de la costa en donde la concentración de los sistemas de cuevas es mayor; Puerto Aventuras/Xpu Ha y Tulum. En el área entre Puerto Aventuras y Xpu Ha se encuentran cinco sistemas con más de 40 km de desarrollo. El área alrededor de Tulum tiene la mayor concentración de cuevas con 13 sistemas mayores [21, 13].

Fig. 5 Mapa en el que se muestra con flechas a dirección del flujo del agua subterránea. Las estructuras en linea rojo son los mapas de algunos de los sistemas de cavernas de la zona de Xel Ha [20]
3. Formas de crecimiento y modelo ALD
3.1. Fractales generados de manera estocástica: caminantes aleatorios
Los fenómenos aleatorios juegan un papel importante en el desarrollo de estructuras naturales. Muchos sistemas muestran propiedades fractales mejor descritas dentro del concepto de los fractales aleatorios [27]. Un fenómeno que ha jugado un papel importante en el desarrollo de los fractales aleatorios es el movimiento Browniano. Robert Brown [28] fue el primero en describir físicamente el movimiento de partículas de polen que se difunden en agua, utilizando un microscopio.
El movimiento de una partícula difundiéndose en agua, por ejemplo, se encuentra sujeto a constantes cambios, impredecibles tanto en magnitud como en dirección. De este modo la partícula browniana realiza movimientos fluctuantes debido a las colisiones prácticamente aleatorias entre los componentes del sistema fluido en equilibrio termodinámico. En este contexto se considera la caminata aleatoria como un modelo discreto que describe un movimiento Browniano [5]. La trayectoria recorrida por una partícula Browniana resulta ser estadísticamente auto-similar y su descripción probabilística se hace mediante la ecuación de difusión [29].
Muchos fractales estocásticos en la naturaleza se generan por fenómenos de crecimiento que involucran fenómenos difusivos. Un modelo de crecimiento que se puede aplicar a la descripción de una amplia gama de fenómenos tales como disolución química, agregación de nanopartículas, ruptura dieléctrica, dedos viscosos, procesos fluviales, crecimiento de cristales [p.e. 30] etc, es el modelo ALD (o DLA). En este modelo los agregados que se forman son controlados por la difusión de las partículas que se adhieren a ellos y para las cuales se aplica procesos de caminantes aleatorios [5]. El concepto de ALD fue introducido por Witten y Sander [15, 16] y describe el crecimiento de un sistema en el que los efectos azarosos, como la difusión, dominan sobre efectos estabilizadores (como de minimización de energía interfacial).
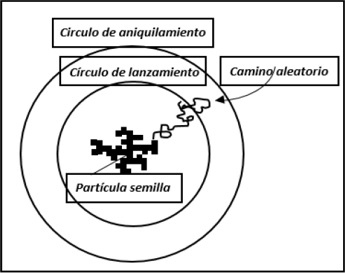
El modelo genera estructuras fractales de manera emergente [18]. Se coloca una partícula semilla fija en el centro de una red bi-dimensional regular, por ejemplo, y alrededor de la semilla se coloca un círculo de lanzamiento de diámetro bastante grande como lo ejemplifica la Figura 6 [5]. El algoritmo del modelo ALD se describe en [15, 16, 5] de la siguiente forma. Se elige una posición al azar sobre el círculo y se inicia ahí la trayectoria de una partícula que sigue una caminata aleatoria sobre la red. Cuando la partícula difusiva choca por primera vez con la partícula semilla, se adhiere a esta de manera irreversible. Luego se repite el proceso con otra partícula que parte desde una nueva posición aleatoria elegida en el círculo de lanzamiento. La partícula se adhiere de manera irreversible cuando choca con el agregado formado por la semilla y las partículas previamente unidas. Si una partícula difusiva cruza el círculo de aniquilamiento (de radio mayor al de lanzamiento) sin haber podido alcanzar el agregado, se considera como perdida y se remueve del sistema.
Después de iterar muchas veces este algoritmo, se puede observar en la Fig. 7a una extensa estructura ramificada [5]. Las partículas se van pegando con mayor probabilidad en las puntas del cúmulo que en las partes hundidas. La dimensión fractal que se obtiene numéricamente para las estructuras generadas con el modelo de ALD es Df=1.6 en dos dimensiones espaciales y Df=2.5 en tres dimensiones [16].

(reproducido con permiso de [32] Copyright (1984) by the American Physical Society)
Fig. 7 A) Resultado del crecimiento de un agregado de DLA después de repetir muchas veces el algoritmo [5]. B) Patrones de descargas electrícas, los cuales son muy similares a los generados por DLA
Los patrones generados por el proceso de DLA se han observado en diferentes sistemas donde el crecimiento se encuentra controlado por una ecuación de Laplace [31]. Por ejemplo, los patrones que se encuentran en las descargas eléctricas (con Df≈1.7) son similares a los generados con DLA (Fig. 7b) [32, 33].
3.2. Fractales formados por disolución química
Se han observado patrones altamente ramificados que se producen por el flujo de un fluido reactivo a través de un medio soluble poroso [34]. A estos patrones se les conoce como patrones de disolución y se pueden obtener experimentalmente inyectando agua a través de yeso puro resultando una estructura fractal [35]. La reacción química entre el agua y el yeso ocurre instantáneamente y la cinética en conjunto queda limitado por la separación de los productos de disolución, por la difusión molecular y por convección cuando el fluido está en movimiento [18, 34]. En dos dimensiones los patrones de disolución son muy similares a los patrones asociados con DLA, descargas eléctricas, dedos viscosos, o polimerización limitada por diffusion [34, 36].
En la naturaleza se observan este tipo de disoluciones químicas por la acción de un fluido en movimiento como en el caso de la formación de cuevas. Se encontró que el flujo de inyección tiene un efecto importante sobre los patones formados, es decir, si el flujo disminuye, el número de ramificaciones decrece (Fig. 8) [18]. El ensanchamiento de las ramas con el tiempo se puede explicar por el efecto cumulativo de la erosión [37].

(reproducido con permiso de [18] Copyright (1987) by the American Physical Society)
Fig. 8 Patrones bi-dimensionales formados por disolución química. a) la velocidad de flujo del agua de 48 cm3/h. b) velocidad de 4 cm3/h. c) 2 cm3/h. Cuando la velocidad del flujo disminuye las ramas se ensanchan
3.3. Extensiones del modelo ALD
Para describir el crecimiento de las redes de drenaje como los sistemas kársticos se proponen tres modificaciones al modelo de DLA, dos de ellas inspiradas en modelos propuestos bajo contextos muy diferentes.
3.3.1. Dedos viscosos
Cuando dos fluidos inmiscibles están confinados entre dos placas rectangulares paralelas de ancho finito, al ser empujado uno dentro del otro en dirección longitudinal, la interfase que separa los dos fluidos toma formas fractales con diferentes valores de dimensión, que dependen principalmente del ancho de las placas [36]. Entre mayor es la separación de las placas Df tiende al valor del DLA isotrópico en dos dimensiones, mientras que para anchos pequeños se encuentran Df~1 [37].
En el laboratorio se utiliza típicamente una celda de Hele-Shaw rectangular que contiene un fluido viscoso (como una solución polimérica), al cual se le inyecta un fluido de menor viscosidad (como agua o aire) por el lado más angosto [37]. Se observa que dependiendo del ancho de la celda y de la velocidad con que sea inyectado el fluido menos viscoso se formarán patrones de naturaleza fractal con una Df que los caracteriza, desde 1 hasta el límite máximo de 1.6 [18, 37].
El algoritmo numérico que se utiliza para reproducir el crecimiento de estos dedos viscosos difiere del DLA clásico ya que ocurre en una red rectangular (0<x<X, 0≤y≤Y) en donde se fija una partícula semilla en una orilla del rectángulo (0, y=2). Las dos paredes laterales son absorbentes (en la posición y=0 y y=Y).
Desde la orilla opuesta a la partícula semilla (en x=X) se tira una partícula que sale de una posición aleatoria sobre el eje y la cual seguirá una caminata aleatoria [36]. De la misma forma que en el modelo original DLA, si en su trayectoria la partícula difusiva toca a la partícula semilla, se pegará haciendo crecer el agregado.
Si la partícula difusiva toca una de las paredes laterales será absorbida y se generará una nueva partícula para repetir el proceso. Iterando este algoritmo un gran número de pasos, se reproducen patrones observados en experimentos de dedos viscosos con fluidos no newtonianos en donde también se observa un cambio en la dimensión fractal dependiendo de la distancia entre las paredes absorbentes [5, 36].
3.3.2. Efectos de una dirección preferencial sobre los agregados de ALD
Paul Meakin [38] estudió una variante del modelo ALD imponiendo la restricción de que la trayectoria de las partículas difusivas tienen un sesgo hacia una dirección determinada, con el objetivo de analizar si la difusión sigue controlando la formación del cúmulo en presencia de una dirección preferencial de movimiento. En este caso la simulación utiliza una red bi-dimensional cuadrada de celdas regulares que al inicio tendrá una celda ocupada por la partícula semilla. Se establece un parámetro que define la probabilidad de tendencia, p.
Las partículas que se adherirán sucesivamente realizan caminatas aleatorias tales que, a cada paso, con probabilidad p el paso se da en la dirección preferencial. Con la probabilidad complementaria 1-p, se selecciona al azar una de las cuatro celdas vecinas, con igual probabilidad, para escogerla como siguiente posición de la partícula [39]. Si la probabilidad de tendencia es uno, la partícula seguirá una trayectoria lineal en esta misma dirección y si la probabilidad de tendencia es cero, la partícula seguirá una caminata aleatoria no sesgada. La dimensión fractal que se obtiene en este modelo va de Df =1.6 hasta Df=2 dependiendo de la escala de observación [40]. Más precisamente, para todo valor del parámetro p>0 se observa que en ventanas pequeñas de observación este modelo tiene una estructura espacial idéntica a los agregados de DLA, mientras que si se crece la ventana de observación la dimensión del cúmulo tiende a dos [38].
4. Resultados: Modelo aplicado al crecimiento de los sistemas kársticos
Para modelar el crecimiento de las cuevas subacuáticas hemos aplicado algunas modificaciones al modelo clásico DLA:
Se toma la idea del modelo propuesto por Nittman et al. [36] para dedos viscosos: en nuestro caso la existencia de fallas y fracturas de alta permeabilidad en la zona de estudio confina el crecimiento de las cuevas. Por lo tanto se modela este confinamiento mediante paredes absorbentes laterales que simulan las condiciones que se observan en la Península de Yucatán.
De acuerdo con el ciclo hidrológico, el agua subterránea se encuentra sometida a la fuerza de gravedad, lo que implica que fluirá preferencialmente de las zonas altas (montañas por lo general) a las zonas bajas del continente (el mar). Por lo que la idea propuesta por Meakin [38] se utiliza para imponer una dirección preferencial de crecimiento simulando los efectos de la fuerza de gravedad sobre la formación de los sistemas kársticos.
Por último, al ser el acuífero de Yucatán heterogéneo, se tiene que las propiedades de la litología cambian de un lugar a otro presentando zonas de baja permeabilidad. Esta heterogeneidad se simula mediante la inclusión de regiones cuadradas que representarán zonas de menor conductividad hidráulica, las cuales estarán ubicadas en el medio entre las paredes absorbentes. Estas regiones se modelaran como absorbentes para las caminatas.
Con estas tres modificaciones el algoritmo de nuestro modelo numérico opera de la siguiente manera. Se toma un espacio bi-dimensional de coordenadas XY cuyas dos paredes paralelas horizontales son absorbentes. Se fija una partícula semilla entre las paredes en la posición (4L/3, l/2), donde L será la longitud de la pared y l la distancia de separación entre las paredes (Fig. 7). Dentro del area se introducen los bloques absorbentes, los cuales pueden ser de diferentes tamaños y cada uno con una posición determinada (al azar en general) en el plano XY.
Desde el lado opuesto a la semilla se lanzan partículas una a una desde una posición aleatoria sobre el eje Y en X=0. De esta manera cada partícula avanza siguiendo una caminata aleatoria en vecindades de Moore (no se permiten movimientos diagonales) con cuatro libertades de movimiento: adelante, abajo, atrás y arriba. Si la partícula lanzada toca a la semilla o al agregado ésta se unirá al cúmulo. Si toca a alguna de las paredes o bloques absorbentes, ésta desaparece generándose una nueva partícula en la zona de lanzamiento para que comience otra caminata aleatoria.
Por lo tanto en este modelo se permiten variar siete parámetros o propiedades del medio: 1) el número de partículas que formarán parte del agregado; 2) la probabilidad p de sesgo direcciónal que se quiere aplicar a la partícula lanzada; 3) la longitud L; 4) la separación l de las paredes; 5) el número de bloques; 6) tamaño de bloques; y 7) la posición de estos. Cabe mencionar que la dirección preferencial está dirigida de X=0 hacia X=L (flecha verde en Fig. 9).El primer experimento consistió en analizar la dimension fractal de los agregados cuando modificamos la probabilidad de tendencia sobre las partículas lanzadas.
El análisis de la dimensión fractal de las estructuras se realizó mediante el programa Fractal Analysis [41]. El tamaño de la caja (L=500 celdas x l=300 celdas) y el número de partículas agregadas (igual a 9000) se mantuvo constante. En la Figura 9 se muestra el cambio de la estructura dependiendo del valor de p. Cuando p=0 se obtiene un agregado típico del modelo DLA clásico, Df=1.6. Conforme se incrementa p la estructura se vuelve mas lineal y su Df disminuye hasta alcanzar un valor Df=1 cuando p=1.
La segunda parte de la simulación consistió en colocar zonas de baja permeabilidad y modificar la probabilidad de tendencia. De esta manera se observa que las estructuras muestran una similitud mayor a las cavidades de Yucatán en lo que a su dimension fractal se refiere. Algunos ejemplos se pueden observar en la Figura 11, donde se muestra que la configuración de los bloques absorbentes determinan en gran medida la geometría y la estructura del agregado.Este resultado es destacable ya que nos ofrece información sobre la influencia directa de la heterogeneidad y la anisotropía del medio en la configuración actual de las cuevas. El modelo DLA clásico genera estructuras cuya dimensión fractal Df=1.6 el cual es mayor que el que se encuentra en las 18 cuevas analizadas 1≤ Df≤1.4 (Tabla 1).
Cabe mencionar que la escala proporcionada por los mapas abarca máximo cuatro ordenes de magnitud en los sistemas más desarrollados (de metros a km), sin embargo, es probable que el comportamiento fractal a escalas menores (p.e. cm, mm, etc) se mantenga. Las estructuras que se obtienen en la simulación muestran una Df que varía entre 1.3 y 1.5, cuando p=0.1. Estos valores dependen en gran medida de cómo se encuentran ubicados los bloques absorbentes dentro del espacio donde se forma el agregado. Cuando las inhomogeneidades son de tamaños pequeños y en densidad alta, las estructuras crecen de manera más lineal.
Cuando no se introducen estas regiones de baja permeabilidad (i.e. se considera un medio homogéneo) y p=0.1 se encuentra que Df es mayor, con valor de 1.54 (Fig. 10). Por lo tanto, el incluir en el modelo bloques absorbentes nos permite generar estructuras más parecidas a las reales, con una Df similar.
El considerar una dirección de preferencia para el crecimiento de los agregados pretende simular que el agua subterránea se encuentra sometida a la fuerza de gravedad la cual fluye de las áreas de mayor a menor altitud. Siendo en el caso específico de la zona de estudio la dirección del flujo de oeste a este siguiendo el desnivel del terreno y la estructura de las fallas [27, 42].
5. Conclusiones
La geometría fractal es apropiada para describir distintas estructuras que se observan en la naturaleza [1, 5]. Se observa que las cuevas analizadas en este trabajo muestran un comportamiento fractal auto-similar que se refleja en su dimensión fraccionaria (Fig. 3). En la Tabla 1 se observa que en general los sistemas con mayor tamaño de desarrollo (kilómetros) son más ramificados que las cuevas que tan solo alcanzan decenas de metros de pasajes de disolución. Esta característica suele influir el cálculo de Df, el cual es en general mayor para los sistemas que alcanzan kilómetros de desarrollo (Tabla 1). Cabe mencionar que la escala mínima de resolución que se considera en el análisis de la geometría de las cuevas son de algunos metros debido a que los mapas se dibujan a partir de la escala humana (espeleobuzos). El modelo de este trabajo se inspira en parte en trabajos previos sobre el análisis experimental de los dedos viscosos [36, 37], que se desarrollan en sistemas confinados. En nuestro caso particular las paredes laterales del espacio rectangular que confina el crecimiento del agregado simula las fracturas de la zona de estudio.
Una modificación plausible podría tener en cuenta que el espacio que confina el crecimiento es más complejo que un simple rectángulo. Se ha observado que la distribución de las fracturas es fractal [2], por lo tanto si el espacio tiene una geometría fractal las estructuras crecerían siguiendo esta misma forma naturalmente. En este sentido Nieto-Smaniego et al., [43] sugieren que el desarrollo mismo de las cuevas y cavernas de Yucatán a grande escala podría estar afectado por una distribución fractal de las fracturas.
La dirección preferencial en el movimiento difusivo intenta simular la fuerza de gravedad a la que esta sometida el flujo de agua, y por lo tanto la corriente principal de disolución. Además es destacable que la dimensión fractal de los agregados disminuye cuando se insertan zonas de baja permeabilidad dentro del area de crecimiento. Estos “bloques” crean un sistema inhomogéneo que modela las regiones en la que no hay formación de sistemas kársticos ya sea por la presencia de fracturas o por que la composición de la roca no permite fácilmente su disolución.
Al colocar estas condiciones se logra disminuir Df en comparación al valor del modelo DLA clásico (Df≈1.6), acercándose a los valores que muestran las cuevas analizadas. Sin embargo, en la mayoría de las simulaciones realizadas no se obtienen estructuras tan compactas como en los sistemas reales sino formas más ramificadas. El modelo de ALD parte de la idea de generar estructuras por difusión, donde el crecimiento ocurre sobretodo por las puntas [33,5]. Si bien el proceso principal que da lugar al crecimiento de los sistemas kársticos es la disolución, en el cual las fases sólido (caliza) y líquido (agua) al estar en contacto se diluyen creando una difusión molecular de los componentes, también puede existir un proceso de advección que se da cuando el fluido está en movimiento [19]. En en los modelos de tipo ALD no se considera la advección, por lo que puede ser una interacción a considerar en futuros trabajos.
Estos resultados abren la puerta a experimentos numéricos para poder investigar las propiedades del modelo en todo el espacio de sus parámetros. Por ejemplo reducir el ancho de las paredes podría producir estructuras más lineales; o bien incrementar el valor de la tendencia p; o variar la forma o tamaño de los bloques absorbentes que intentan simular un medio heterogéneo. Por lo tanto, en conclusión nuestro modelo intenta aproximarse al proceso complejo que da lugar a la emergencia de los sistemas kársticos. Mostramos que condiciones iniciales sencillas pueden evolucionar en complejidad a lo largo del tiempo, hasta formar estructuras similares a las observadas en cuevas.











 text new page (beta)
text new page (beta)