1 Introduction

Similarity measures have numerous applications in computational linguistics, ecology, medicine, biology, social sciences, etc. They play important role in pattern recognition, machine learning, classification and statistics ^{1,5-7,10,12-14,16,18,19} . Dozens of similarity (or dissimilarity) measures for binary data have been proposed and the problem of their comparison and selection for specific application is studied in many works ^{2-10,15,17-20}. In different papers, such measures are referred to as association coefficients, similarity coefficients, resemblance measures etc. Different approaches for comparing similarity measures are based on: similarity of the properties of these measures, similarity of formulas, possibility of transformation of one measure into another one, ordering of the measures, distance between them etc. ^{2,3,6-12,18-20}.

To the best of our knowledge, there are not works on 3D visualization of the binary similarity measures. Such visualization can be useful for comparing the shapes of similarity measures and selecting measure more suitable for specific applications. The paper proposes the methods of 3D visualization of the most popular similarity measures used for binary data and 2 x 2 tables. Such visualization of similarity measures gives the direct, visual, method of comparison of these measures and can help to understand the similarity and the difference between them.

Several authors have proposed different parametric families of similarity and dissimilarity measures ^3,9,19,20. Based on the visualization of the two known parametric families of similarity measures the paper proposes the new parametric family of the similarity measures generalizing these two families and giving possibility to construct similarity measures occupying intermediate position between them.

The paper has the following structure. Section 2 considers some basic definition related with the similarity measures for binary data and describes the most popular similarity measures. Section 3 proposes the methods of 3D visualization of similarity measures for binary data and visualize the most popular measures. Section 4 proposes the new parametric family of similarity measures. The last section contains discussion and conclusion.

2 Basic Definitions

Consider objects described by n binary attributes, descriptors or properties. The object x is coded by the vector x=(x1,…,xn) of n attribute values such that xk=1 if the object possesses the property k and xk=0 otherwise. Such data are called also presence/absence data ^8,11. For any two objects x=(x1,…,xn) and y=(y1,…,yn) the following four numbers are calculated:

The numbers a and d also referred to as the numbers of positive and negative matches, correspondingly ^9,17.

Note that the following is fulfilled for these four number:

where n is the number of binary attributes. These four numbers are represented in Table 1 also known as 2(2 contingency table (¹).

Table 1 2 x 2 contingency table 

Below there are presented some popular similarity measures defined for such tables ^4,5,10.

Jaccard (1908):

Dice (1945), Czekanowski (1913), Sorensen (1948):

Sokal & Sneath (1963):

Sokal & Michener (1958) or “simple matching”:

Rogers & Tanimoto (1960):

Sokal & Sneath (1963):

Rassel & Rao (1940):

Faith (1983):

3 Visualization of Similarity Measures

Let us consider parametric families of similarity measures that include the known similarity measures as particular cases ^9,20. The similarity measures (2)-(4) can be generalized as follows:

where 𝜃 is some positive real number. The similarity measures (5)-(7) can be considered as the particular cases of the following parametric family of functions:

For us it will be more convenient to use the following notation of these parametric families of similarity measures:

where t is some positive real number. The similarity measures (2)-(4) are obtained from (12) for the parameter values t= 1, 0.5, 2, correspondingly. The similarity measures (5)-(7) are obtained from (13) for the parameter values t= 1, 2, 0.5, correspondingly. Taking into account that from (1) it follows

the formulas (12) and (13) can be given in such form:

S(a)x,y

The parametric families of the similarity measures (15) and (16) have been considered in ²⁰ in the following forms:

where A=an,  D=dn. Further we will use the formulas (15) and (16) for the considered parametric families of similarity measures that will be referred to as (a)-family and (a+d)-family of similarity measures, correspondingly.

We propose to use the relationship (14) for representation of other similarity measures. The similarity measures (8) and (9) do not belong to the considered families of measures, but, using the relation (1), they also can be written as the functions of a and d:

As it is clear from the formulas (15), (16), (19), (20) for fixed numbers n and t one can build all of these formulas in 3D space as the functions of 2 variables a and d. (The formula (19) will depend really only from a). From (1) and (14) we obtain:

This condition defines restrictions on the domain of the considered functions. In all figures below we use the value n = 100 and build the graphics of all functions for values a and d changing from 0 to 100 with the step 1, with the domain restriction (21).

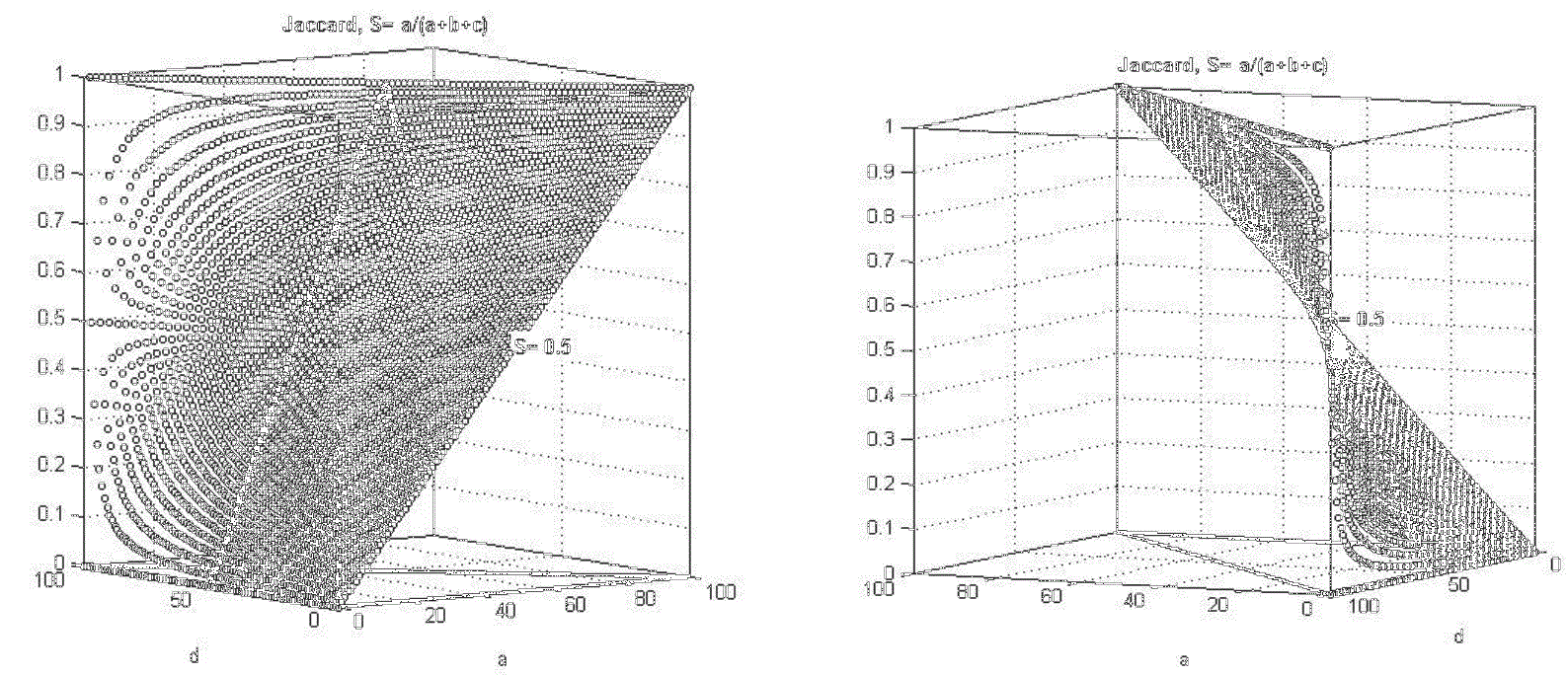
Figures 1 (a) and 1(b) show in two different projections Jaccard similarity measure obtained from the parametric formulas (12) and (15) for parameter value t=1 as follows:

Fig. 1(a) Jaccard similarity measure (view 1) Fig. 1(b). Jaccard similarity measure (view 2) 

The domain (21) is presented on the plane S=0 by triangle with bold sides. Two black lines show the profiles of the surface of the similarity measure: 1) for value a=50 and all values of d; 2) for value d=50 and all values of a. The value S = 0.5 depicts the value of the measure S for a = 50 and d= 0. When d = 0 we obtain in (22) S=a/n that corresponds on Figure 1 (a) to the line increasing from 0 to 1 when d=0 and a is increasing from 0 to 100. Figure 1 (b) is obtained from Figure 1 (a) by rotation of the axis to show the profile of the surface for small values of a and large values of d. This situation corresponds to large number of negative matches d and hence to small values of nominator and denominator in (2). The similar comments can be done for the figures of other similarity measures shown later.

Figures 2 (a) and 2(b) show two projections of Rogers & Tanimoto similarity measure. From (6), (13) and (16) we obtain for t=2:

Fig. 2(a) Rogers & Tanimoto similarity measure (view 1) Fig. 2(b). Rogers & Tanimoto similarity measure (view 2) 

Figure 3 shows the surfaces of the following similarity measures belonging to the parametric (a)-family of measures (from the left to the right): 1) Dice-Czekanowski-Sorensen, 2) Jaccard, 3) Sokal-Sneath-I.

Fig. 3 (a)-family of similarity measures in 2 views 

Figure 4 shows the surfaces of the following similarity measures belonging to the parametric (a+d)-family of measures (from the left to the right): 1) Sokal-Sneath-II, 2) Sokal & Michener, 3) Rogers and Tanimoto.

Fig. 4 (a+d)-family of similarity measures in 2 views 

For all of these similarity measures the formulas like (22) and (23) can be easily obtained from their original definitions by replacement b+c by n-a-d, see (1) and (14).

Figure 5 depicts the surfaces of Rassel & Rao and Faith measures in the same projection as the similarity measures shown on Figures 1 (a) and 2(a). Rassel & Rao and Faith measures do not belong nor to (a)-family nor to (a+d)-family of similarity measures and one can see that they have the shapes quite different from the shapes of similarity measures from these families shown on Figure 3 and 4.

Fig. 5 Russel & Rao (on the le^ side) and Faith (on the right side) similarity measures 

The main problem with these two measures that they do not satisfy the reflexivity property S(x,x)= 1 that requires that reflexive similarity measure should have the value 1 on the border of the domain where a+d= n and b= c= 0. One can see that the similarity measures both from (a)-family and from (a+d)-family are reflexive.

4 New Parametric Family of Similarity Measures

As one can see from Figures 3 and 4 the shapes of the similarity measures from (a)-family and (a+d)-family are sufficiently different. The similarity measures S(x,y) from (a)-family are based on the positive matches of binary attributes in x and y. The similarity measures from (a+d)-family are based both on positive and on negative matches. Discussions pro and contra of these two types of similarities measures can be found for example in ^5,10,17,19. We propose the new parametric family of binary similarity measures formally generalizing both these families and giving the possibility to build the similarity measures intermediate between these two families. Below are the two equivalent forms of the new parametric family of measures called (a+pd)-family:

where t is the positive real number and p is the number from the interval [0,1]. When p = 0 we obtain the (a)-family of similarity measures and when p = 1 we obtain the (a+d) family of similarity measures. Changing parameter p between 0 and 1 one can move similarity measure from (a)-family to (a+d) family. Generally, the parameters p and t can be tuned in some procedure of selection of suitable similarity measure for specific application. The selected value of the parameter p can reflect the trade-off or relative importance of positive and negative matches in the constructed similarity measure.

Figures 6, 7, 8 show the shapes of binary similarity measures from (a+pd)-family when parameter p is changed from 0 (on the left sides) to 1 (on the right sides) such that on the left sides we have similarity measures from (a)-family and on the right sides the measures from (a+d)-family. The parameter t has the values 1, 0.5 and 2 on Figures 6, 7 and 8, respectively. On Figure 6. the similaty measures are changed from Jaccard (on the left side) to Sokal & Michener (on the right side). On Figure 7. the similaty measures are changed from Dice & Czekanowski & Sorensen (on the left side) and Sokal & Sneath - II (on the right side). On Figure 8. The similaty measures are changed from Sokal & Sneath - I (on the left side) and Rogers & Tanimoto (on the right side).

Fig. 6 (a+pd)-family of similarity measures: Jaccard (on the left side) and Sokal & Michener (on the right side) 

Fig. 7 (a+pd)-family of similarity measures: Dice & Czekanowski & Sorensen (on the left side) and Sokal & Sneath - II (on the right side) 

Fig. 8 (a+pd)-family of similarity measures: Sokal & Sneath - I (on the left side) and Rogers ا، Tanimoto (on the right side) 

5 Discussion and Conclusion

The paper proposes the methods of visualization of the popular similarity measures for binary data and contingency 2 x 2 tables. Such visualization helps to understand the relationships between these measures and can explain why these similarity measures joined in clusters of similar measures obtained in different works where the clustering of these measures is applied ^6,12. The new parametric family of the similarity measures is proposed. This family generalizes the two known parametric families of similarity measures and gives the possibility to construct similarity measures intermediate between these two families. Such intermediate position can reflect the trade-off or relative importance of positive and negative matches in the construction of similarity measures from the new parametric class of similarity measures. The proposed methodology of visualization of binary similarity measures can be extended on other binary similarity and association measures considered in literature.