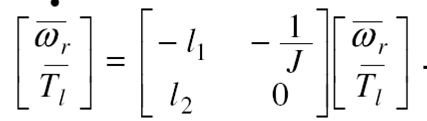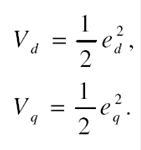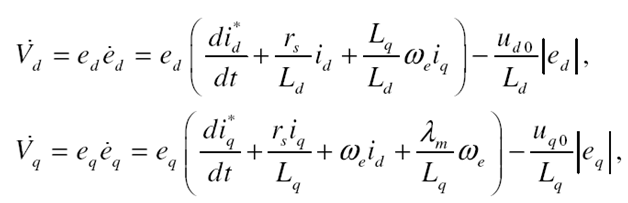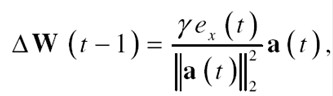1. Introducción
Los nuevos desarrollos tecnológicos en materiales magnéticos, semiconductores de potencia, electrónica digital y teoria de control han permitido que los motores de corriente alterna (CA), sean capaces de hacer frente a los desafios de alta eficiencia y requerimientos de alto desempeno que demanda el sector industrial. En este sentido, los motores síncronos de imanes permanentes (MSIP) son una alternativa y serios competidores de las máquinas de inducción debido a que presentan alta eficiencia, alto factor de potencia, excelente robustez, alta relación torque/inercia y mantenimiento económico 1.
En la actualidad los MSIP se emplean en una amplia gama de aplicaciones industriales que van desde pequenos servomotores para máquinas herramientas, motores eléctricos de vehículos híbridos y propulsores en barcos y submarinos 2. Estas aplicaciones demandan una respuesta rápida y precisa ante disturbios y perturbaciones. Para cumplir con estas exigencias se requieren complejos esquemas de control que permitan un desempeno dinámico seguro y confiable ante diferentes condiciones operativas 1,3.
El control vectorial es un método eficiente para motores síncronos en aplicaciones de velocidad variable en amplios rangos de operación. Normalmente se usa en máquinas de CA para convertirlas en cuanto a su rendimiento, en máquinas de corriente directa (CD) con excitación separada, esto permite características de control altamente deseables 1.
El principio del control para el MSIP está basado en la orientación de campo, dónde las corrientes en dq juegan un papel determinante para su desempeno. Para asegurar el control vectorial del MSIP, se define que la corriente en eje directo, id, sea igual a cero, con lo que se obtiene el torque máximo del motor 4,5. El esquema convencional proporcional-integral (PI) es el regulador más utilizado para controlar las corrientes dq del MSIP. La implementación del control de campo orientado requiere controladores de corriente con respuesta rápida y alta precisión, con el fin de proporcionar servo accionamientos de eficiencia óptima 5.
Convencionalmente los controladores PI se emplean en lazos de control por su simplicidad y amplia aceptación, sin embargo, se sabe que presentan algunas limitaciones, como su dependencia en el modelo completo y la exactitud de los parámetros. Por lo tanto, para hacer frente a las no linealidades y sensibilidad de parámetros se deben incorporar en la estructura del controlador mecanismos de adaptabilidad, llevando a un escenario de diseno complejo. En la literatura se han propuesto diversos mecanismos de adaptación como control adaptativo, modos deslizantes, controlador de estructura variable, controlador PI auto-sintonizado, controlador predictivo, entre otros. Sin embargo, el mayor problema que presentan estos controladores es su alta dependencia de los modelos matemáticos y su dificultad para representar un sistema práctico 2,4.
Por otro lado, el diseno de controladores inteligentes no requiere de un modelo matemático exacto, debido a su capacidad para resolver problemas no lineales a través del aprendizaje, por ejemplo las redes neuronales artificiales son muy útiles en esta área 4,6. Otra herramienta de control es la lógica difusa, que se puede entender como una clase de inteligencia artificial, dónde el conocimiento y experiencia de un experto se pueden convertir en reglas de control lingüísticas reproduciendo la toma de decisiones de una persona 2,7.
En este trabajo se presenta un análisis comparativo de la respuesta de un motor síncrono de imanes permanentes con cuatro controladores diferentes: Controlador PI convencional, esquema de control por modos deslizantes, redes neuronales y un regulador difuso. Los controladores se establecen sobre la técnica de control vectorial con desacoplo de las corrientes id e iq. La aplicabilidad se presenta mediante estudios de simulación del MSIP considerando diferentes condiciones operativas y diversas perturbaciones.
2. Modelo dinámico del MSIP
El modelo matemático que describe el comportamiento dinámico del MSIP en un marco de referencia estacionario dq se puede definir
como:
donde vd y vq son los voltajes aplicados en el estator en un marco de referencia dq, respectivamente; id e iq son las corrientes en dq; rs es la resistencia en el estator; Ld y Lq son las inductancias propias del estator en dq; ωe es la velocidad angular eléctrica del rotor; Te es el par electromagnético del motor, np es el número de pares de polos y λm es el flujo magnético constante producido por el imán permanente en el rotor.
La ecuación dinámica de la velocidad y la posición del rotor son:
y se tiene que
donde ωΓ es la velocidad mecánica del rotor, J es el momento de inercia del rotor, Br es la posición del rotor y T es el par de carga aplicado al motor. En este trabajo se considera un MSIP de polos no salientes con los imanes montados en la superfície del rotor 8, por lo cual las inductancias en eje d y eje q, son iguales, en consecuencia el par electromagnético se calcula mediante
Para diseñar el regulador de velocidad se emplean tres lazos de control con retroalimentación negativa, esto permite obtener la velocidad deseada del rotor y mejorar el desempeno del motor en estado estable y transitorio. El sistema de regulación incluye un lazo para la velocidad del rotor, un lazo de control de corriente en eje d y otro en eje q.
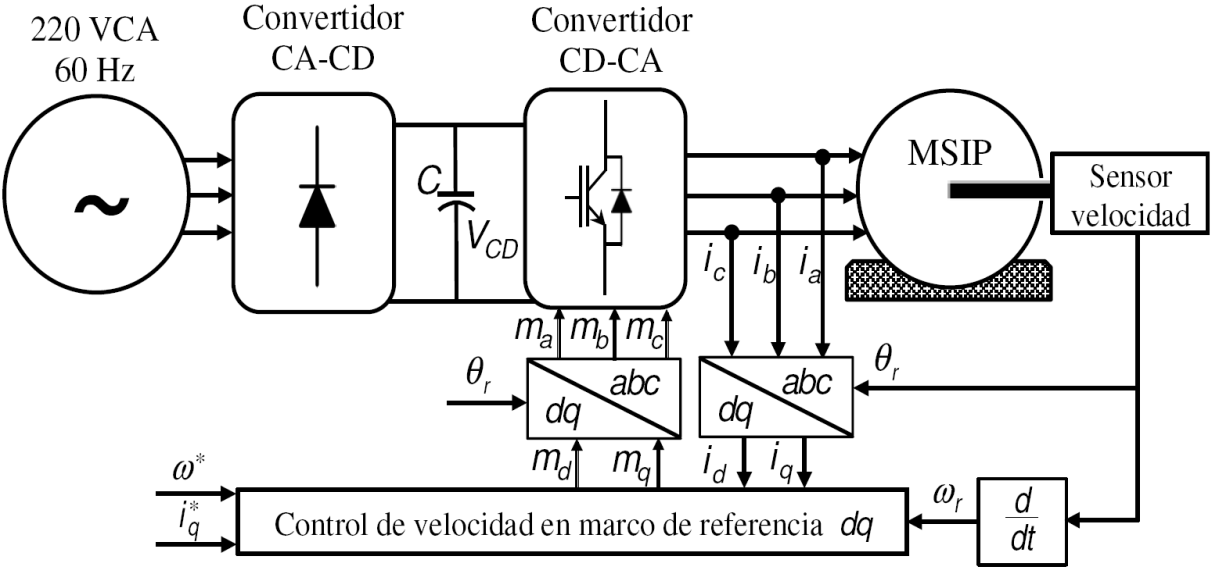
El diagrama de bloques del sistema de control para regular la velocidad del rotor utilizando la técnica de control vectorial se muestra en la Fig. 1. El sistema de control consiste en una fuente rectificadora de voltaje CA-CD, un MSIP, una fuente inversora de voltaje CD-CA, un control automático de corriente, un sensor de posición que determina la velocidad del rotor y un regulador de velocidad. El ángulo eléctrico se calcula multiplicando el ángulo mecánico del rotor por el número de polos.
3. Esquema de control del MSIP
En la Fig. 1 se pueden observar que las entradas al sistema de control de velocidad son la velocidad de referencia, ω*, la corriente deseada en eje directo, id*, y la velocidad del rotor, ωτ. La corriente deseada iq * se determina a partir del par electromecánico, que es proporcional a la corriente en eje q.
3.1. Diseño del esquema de control del MSIP (control campo orientado)
El modelo del MSIP, (1), (2) y (4), es un sistema dinâmico con dos entradas de control, vd y vq. Si se puede hacer que la componente de la corriente en eje directo sea igual a cero, se obtiene un comportamiento similar al de un motor de corriente directa con excitación de flujo constante 9. Las ecuaciones indican que el MSlP es un sistema no lineal debido al acoplamiento que existe entre las diferentes variables de estado (corrientes y velocidad del rotor). También, se puede observar que los parámetros dependen de las condiciones de operación, principalmente del par de carga y temperatura de operación. La principal meta del controlador es regular la velocidad angular del rotor para que siga una trayectoria deseada ante diferentes perturbaciones paramétricas y variaciones del par de carga. Por lo tanto, la principal señal de error se puede definir como,
donde ω* es la velocidad deseada para el rotor. En (1) se tienen dos variables de control independientes, vd y vq, si la señal de control vq regula la velocidad del motor, se tiene un grado libertad disponible, Vd, y se puede tomar ventaja de ello. Una ventaja es evitar la desmagnetización de los imanes permanentes, lo cual se logra haciendo que la corriente en eje directo sea igual a cero 9,12.
Si se cumple esta condición, la corriente del estator es igual a la corriente en eje q, entonces el par electromagnético del MSIP es proporcional a iq. Otra ventaja es que los enlaces de flujo constantes tienen una relación lineal con la corriente en el estator, con lo cual se pude fácilmente estimar su valor. Definiendo el error de seguimiento de la corriente en eje d como
donde id* es la señal de referencia para la corriente en eje d. En teoría el controlador propuesto obliga a la corriente id a tener un valor igual a cero en un tiempo finito y, que el par eléctrico sea proporcional a la corriente iq . Por lo tanto, se define el error para la corriente en eje q,
donde iq* es la señal de referencia para la corriente en eje q. El sistema de control propuesto se basa en un esquema sinusoidal por ancho de pulso (SPWM), donde las señales de modulación en el marco de referencia dq son md y mq, Fig. 1. La señal de modulación se transforma al sistema abc utilizando la transformada de Park y la posición del rotor θr, para compararla con la señal portadora de alta frecuencia.
3.2. Cálculo de la corriente deseada, iq*
La corriente deseada en eje q se determina sustituyendo (2) y (4) en la derivada de (5), con la dinámica deseada del error. Despejando iq, se obtiene la corriente deseada, iq*, para el controlador de corriente en eje de cuadratura,
donde c es la velocidad de convergencia del error de la velocidad. Se puede observar que el valor de la corriente deseada está en función de la derivada de la velocidad de referencia, el par de carga y la velocidad del rotor, por lo que es necesario medirlos o estimarlos
3.3. Estimación del par de carga, Tl*
En la práctica el par de carga es desconocido, por lo cual es necesario disenar un estimador para conocer su valor y calcular la corriente deseada, iq*. Las ecuaciones que describen al estimador no lineal son 13:
donde
Combinando las ecuaciones del estimador (9) y (10) y la ecuación dinâmica de la velocidad del rotor, se puede obtener un conjunto de ecuaciones que describen el seguimiento dinámico del error del estimador.
El conjunto de ecuaciones diferenciales (11) representa um sistema lineal autónomo, asintóticamente estable con la elección adecuada de los parámetros l 1 y l 214:
4. Sintonización de controladores
El esquema de regulación para el motor síncrono de imanes permanentes se ha definido en la sección tres, sin embargo, su correcta operación requiere de estratégias de control robustas o adaptativas que garanticen un desempeno seguro y confiable, además, debe responder rápida y adecuadamente ante diversos escenarios a los que se pueda enfrentar.
En este trabajo se proponen tres formas de sintonización y aplicación del esquema de control orientado de campo, comparando el desempeno con un controlador lineal PI.
4.1. Diseno del controlador convencional PI para el MSIP
Para regular la velocidad del rotor del MSIP y mejorar su desempeno dinâmico primero se diseña un esquema de control convencional PI, Fig. 2. Considerando (1) se definen las siguientes señales de control como en 15,
sustituyendo (12) en (1), se obtienen el siguiente sistema dinámico de primer orden:
Para regular la velocidad del rotor de un MSIP utilizando dos controladores convencionales PI se pueden establecer dos sistemas de control a lazo cerrado uno para regular idy otro para iq. En la Fig. 2 se muestra que el controlador para id, permite calcular u d.

Fig. 2 Diagrama de bloques para regular la velocidad de un MSIP utilizando dos compensadores convencionales PI
De forma similar, el controlador de iq determina uq. La magnitud de la corriente iq* la determina el lazo de control del par electromagnético que está en función de la velocidad de referencia. Asumiendo que la función de transferencia a lazo cerrado entre Vd(s) y Ed(s), son de primer grado y semejantes, los parámetros del controlador PI se determinan como kp=Ld/t y kl=kp(rs/Ld).
El coeficiente τ es el retardo de tiempo de la respuesta del controlador. Las señales de control que entregan los controladores de corriente se transforman al marco de referencia abc, para compararlos con una señal triangular. Los pulsos que genera la comparación de las dos señales se envían a los dispositivos semiconductores de potencia de la fuente inversora de voltaje que alimenta al motor síncrono de imanes permanentes.
4.2. Control robusto por modos deslizantes
Utilizando (1), (5), (6) y (8) se diseña la ley de conmutación del controlador no lineal por modos deslizantes 16,
donde ud0 y uq0 son los valores máximos de las señales de control, respectivamente. El diagrama de bloques para regular la velocidad del MSIP utilizando la técnica de modos deslizantes se muestra en la Fig. 3.

Fig. 3 Diagrama de bloques para regular la velocidad del MSIP utilizando la técnica de modos deslizantes
La condición de existencia de modos deslizantes es equivalente a la condición de estabilidad, por lo tanto, se seleccionan dos funciones de Lyapunov definidas positivas de la siguiente forma:
Derivando respecto al tiempo sobre la trayectoria de (6) y (7), respectivamente, y sustituyendo se obtiene
donde |ei |=ei sign ei para i=d, q. Las derivadas de la funciones de Lyapunov son negativas si,
Por lo tanto, ed, eq y eω son igual a cero después de un intervalo de tiempo finito.
4.3. Control adaptativo mediante redes neuronales B-spline
Para el diseño del neurocontrolador se emplea una red neuronal de entrenamiento instantâneo B-spline (BSNN) debido a que presentan mejores características comparadas con otras redes neuronales (RN) inteligentes, por ejemplo: la RN de retropropagación (RNBP) y la RN de función base radial (RNRBF). En este caso la BSNN se compone por tres capas, que son: 1) un espacio l-dimensional de entradas normalizado; 2) un conjunto de funciones base p; y 3) la función de salida de la red.
Uno de los elementos medulares a definir en la estructura de las BSNN son las funciones base, que pueden incorporar conocimiento previo de la planta por parte del disenador. Las funciones base B-Spline se obtienen utilizando una relación recurrente 17,18, las cuales son numéricamente estables, computacionalmente eficientes, y pueden tratar con cualquier distribución estratégica de puntos de control.
La función de salida de la red neuronal adaptativa (RNA) es una combinación lineal de las salidas de las funciones base y en general es continua. Los coeficientes lineales son los pesos ajustables, wi, y debido a que la salida es linealmente dependiente del conjunto de pesos, el entrenamiento es simplemente un problema de optimización lineal 19. puede escribir 20,
donde a es un vector p-dimensional que contiene las salidas de las funciones base, y w es el vector correspondiente de pesos. Para disminuir el tiempo y esfuerzo computacional, en este caso se utilizan solamente dos factores de peso para cada RN.
En este trabajo el esquema de control del MSIP utiliza un algoritmo de control que se basa en una RNA que se encarga de determinar el valor de la salida teniendo como entradas: salidas pasadas y entradas actuales. Con base a esos valores se determina el valor óptimo de la entrada de control de tal forma que el error tienda a cero.
La regla de aprendizaje que se utiliza es de gradiente descendente, en vez de los algoritmos recursivos de mínimos cuadrados que son más complicados Para la actualización de los pesos ΔW(t-l) se utiliza una regla de aprendizaje instantáneo de la forma 20
donde γ es la relación de aprendizaje, a es el vector que contiene las salidas de las funciones base, w es el vector de pesos y ex= m(t)-
4.4 Control adaptativo mediante lógica difusa
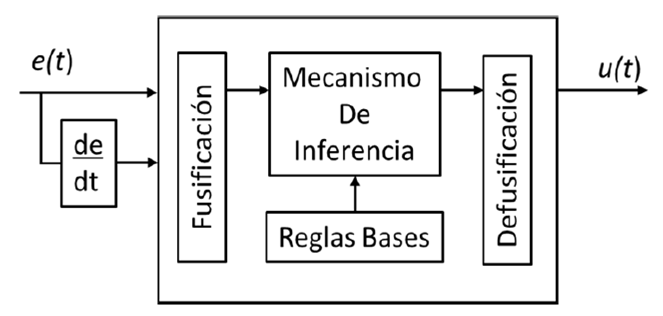
Un sistema difuso emula la acción de un experto humano, está compuesto por cuatro etapas básicas que se muestran en el esquema de la Fig. 4.
El mecanismo de inferencia es el núcleo de un controlador difuso, es dónde se generan las acciones de control en función del conjunto de reglas base usando los conectores lingüísticos SIENTONCES. Entonces, en este trabajo para el diseno del controlador difuso se emplea un esquema de tipo Mamdani con 5 funciones de membresía para el error e(t) y su derivada de(t)/dt.
Existen diversas formas para llevar a cabo la etapa de fusificación, como es el caso de 21 donde se emplea una técnica de razonamiento inductivo difuso, con funciones de membresía Gaussianas usando únicamente valores entre 0.5 y 1 para los grados de pertenencia.
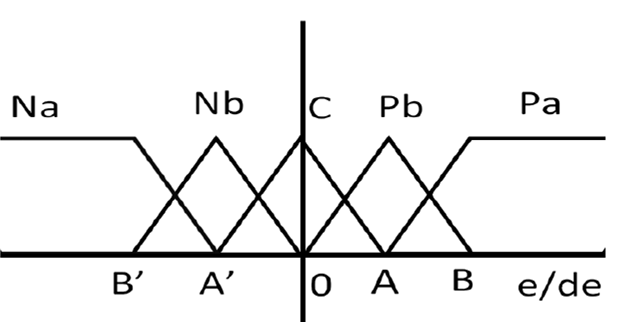
En este trabajo se definen conjuntos difusos de otro tipo: trapezoidal y triangular, lo que permite usar todo el rango posible en el grado de pertenencia, Fig. 5 22. Se obtienen grupos: {Negativo alto, Negativo bajo, Cero, Positivo bajo, Positivo alto}. Entonces, las funciones de membresía son:
donde el grado de pertenencia para los grupos trapezoidales y triangulares se obtiene com
En la etapa de defusificación, la acción de control descrita en forma lingüística, se transforma en un valor preciso defiendo un nuevo valor para la salida de control s, el cual se obtiene por medio del centroide sobre la función de membresía y se representa por:
donde μB j(δ j ) es el grado de membresía.
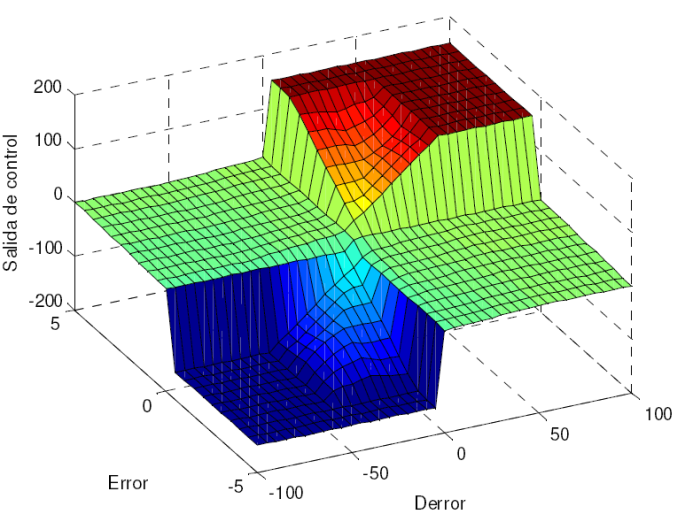
En las Fig. 6 y 7 se muestran las superficies de control para la corriente iq y para la corriente id, respectivamente. Se usan los valores de 0.07 y 3 en A y B para desarrollar la fusificación del error en la corriente iq, en el caso de su derivada es 1 y 80.
De la misma forma para la fusificación del error de la corriente í- se utiliza 0.1 y 4, finalmente, para su derivada es de 1 y 50.
5 Resultados y análisis
En esta sección se presentan los resultados de las simulaciones que se realizaron para verificar y comparar el desempeno de los diferentes esquemas de control de velocidad del rotor del MSIP. Estos resultados se utilizan para examinar la respuesta dinámica del control adaptativo (PI NN) que se compara con tres esquemas de control diferentes: controlador PI (PI FIX), controlador por modos deslizantes (SM) y controlador difuso (FUZZY).
La implementación de los cuatro controladores se realiza en Matlab/Simulink, Fig. 1. Los parámetros del MSIP se asumen conocidos, Tabla 2. En los 4 esquemas de control se emplea el mismo observador propuesto del par de carga y del controlador de corriente, se emplean los siguientes valores para las ganancias: l1 ;=880, l 2=-6.776 y c =500. Las magnitudes de la velocidad deseada del rotor y el par de carga aplicado al motor se indican en la Tabla 3, el tiempo es en segundos. El escenario de simulación propuesto demanda grandes variaciones de velocidad y perturbaciones externas que representan condiciones reales de trabajo para el MSIPLas Fig. 8-11 resumen los resultados obtenidos mediante simulación del control de velocidad del rotor del MSIP trifásico, que tiene una potencia nominal de 1kW y una velocidad de 3000 rpm.
Tabla 2 Parámetros del MSIP
| Parametro | Símbolo | Valor de unidades |
|---|---|---|
| Coeficiente de inercia | J | 3.5e-5 Nm |
| Voltaje nominal | v | 120 V |
| Inductancia del estator | rs | 2.6Ω |
| Inductancia del estator en eje d | Ld | 6.73 mH |
| Inductancia del estator en eje q | Lq | 6.73mH |
| Inductancia de dispersión del estator | Lls | 0.1 Lq |
| Flujo magnético del imán permanente | λm | 0.319 Wb |
| Pares de polos | P | 2 |
Tabla 3 Condiciones operativas a las que se somete el MSIP
| Par de carga T l (Nm) | Velocidad del rotor ωr(rmp) |
|---|---|
| 0 si t ≤ 0.10 | 0 si t ≤ 0.05 |
| 0.8 si 0.10 < t ≤ 0.19 | 150 si 0.05 < t ≤ 0.15 |
| 1.5 si 0.19 < t ≤ 0.29 | 220 si 0.15 < t ≤ 0.25 |
| 0.9 si 0.29 < t ≤ 0.38 | 60 si 0.25 < t ≤0.35 |
| 1.3 si 0.38 < t ≤ 0.45 | -120 si 0.35 < t ≤ 0.50 |
| 0 si t > 0.45 | 0 si t >0.50 |
La Fig. 8 muestra el desempeno dinámico de la velocidad del rotor empleando diferentes esquemas de control. Se observa como el controlador adaptativo exhibe un mejor desempeno respecto a los otros controladores, en particular cuando se presentan modificaciones radicales en los valores de la velocidad deseada y par de carga.
La Fig. 9 presenta la comparación de los errores de velocidad obtenidos, donde se puede observar que el rango de error de velocidad para el esquema adaptativo es del 0.96% de la velocidad nominal, mientras que para el control PI el error para esta variable alcanza el 1.25%, 1.74% para el control por MD y 1.97% para el FUZZY. La implementación de los cuatro controladores se realiza en Matlab/Simulink, Fig. 1.
Los parámetros del MSIP se asumen conocidos, Tabla 2. En los 4 esquemas de control se emplea el mismo observador propuesto del par de carga y del controlador de corriente, se emplean los siguientes valores para las ganancias: l 1=880, l 2=-6.776 y c=500.
Las magnitudes de la velocidad deseada del rotor y el par de carga aplicado al motor se indican en la Tabla 3, el tiempo es en segundos. El escenario de simulación propuesto demanda grandes variaciones de velocidad y perturbaciones externas que representan condiciones reales de trabajo para el MSIP.
La comparación de las corrientes del estator del motor en dq se muestra en la Fig. 10. En la Fig. 10.b se observa que en estado estacionario los esquemas de control demandan la misma amplitud de corriente, iq, pero en la respuesta transitoria el controlador por modos deslizantes presenta menores sobreimpulsos.
En la Fig. 11 se aprecia que id =0, excepto en el controlador por modos deslizantes y difuso. Se puede observar que la respuesta de i- que entrega el controlador por modos deslizantes oscila en un intervalo acotado entre 0.25 y -0.2 A. La Fig. 10 indica que en algunos periodos de la simulación el controlador convencional PI requiere menor amplitud de corriente para alcanzar satisfactoriamente la velocidad deseada del rotor. Sin embargo, de acuerdo a los resultados mostrados, el controlador adaptativo basado en redes neuronales B-spline exhibe el mejor desempeno tanto en respuesta transitoria como en estado estacionario, por lo que se presenta como una solución más atractiva para el problema de regulación de velocidad del rotor para un motor síncrono de imanes permanentes sujeto a altas demandas.
En la Fig. 12 se muestra la evolución de las ganancias kp y k1 de los dos controladores PI que entrega la BSNN. Para las ganancias del controlador adaptativo que regula i q; al inicio de la simulación su magnitud cambia radicalmente de la condición inicial, hasta alcanzar un valor cercano a 1.5 y 0.71. Posteriormente, la red neuronal sigue aprendiendo y modificando las ganancias en función a los cambios de velocidad de referencia y del par de carga.
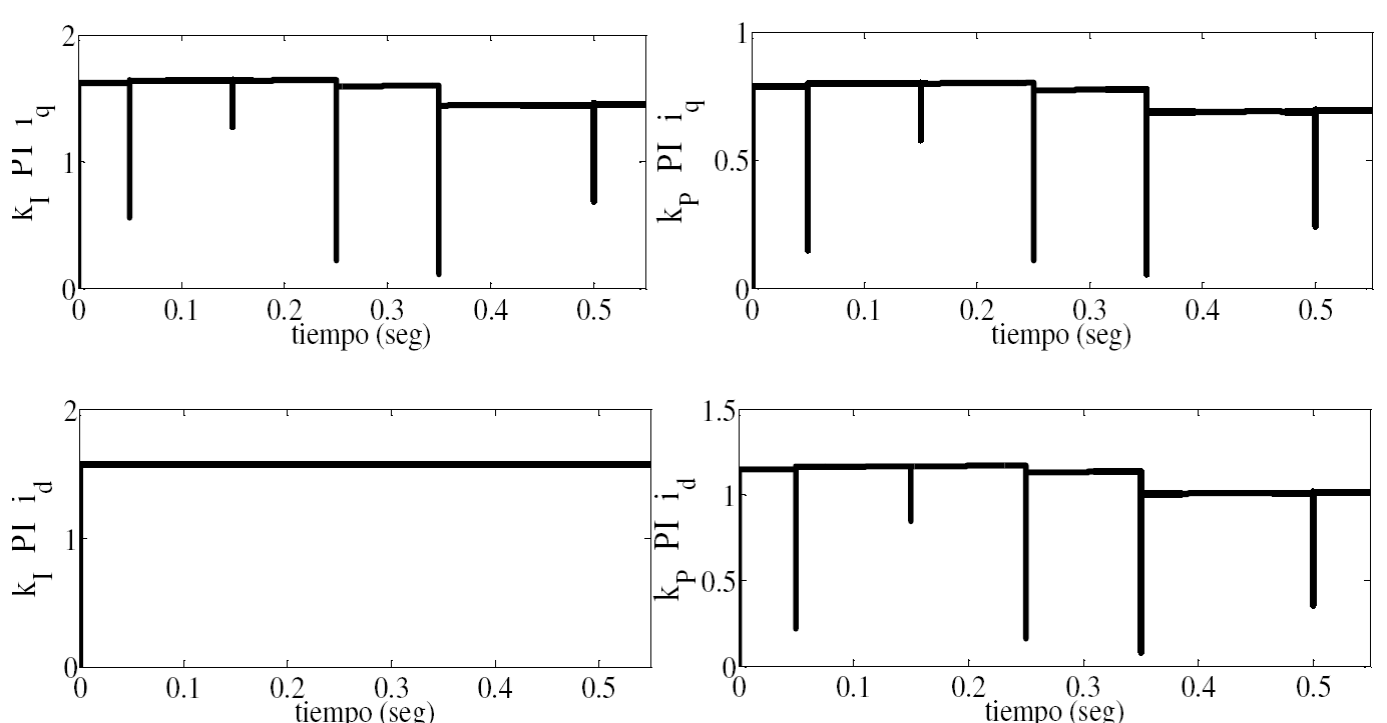
Fig. 12 Evolución de las ganancias kp y ki de los dos controladores PI que entrega el neurocontrolador
Es evidente que el neurocontrolador tiene la capacidad de aprender y adaptarse en línea, por lo cual puede utilizarse en aplicaciones como en robots manipuladores, máquinas de bordar, control de altitud y velocidad de una aeronave donde, la adaptación de los parámetros se requiere en momentos críticos y el reajuste o calibración manual de las ganancias del controlador es imposible.
6. Conclusiones
En este trabajo se realiza el estudio comparativo de cuatro diferentes estrategias de control basadas en reguladores convencionales, inteligencia artificial, esquemas adaptativos y de estructura variable para regular la velocidad de un MSIP. Las estrategias de control se implementan en Matlab/Simulink para conocer su respuesta transitoria y desempeno en estado estable cuando se presentan disturbios en el par de carga y diferentes requerimientos de la velocidad deseada.
Los resultados de las simulaciones muestran que todos los controladores funcionan relativamente bien, pero el controlador adaptativo basado en redes neuronales artificiales presenta una excelente respuesta dinámica comparada con los otros esquemas de control. El análisis indica que los parámetros del neurocontrolador se actualizan en línea de acuerdo a la ley de aprendizaje para obtener robustez y seguimiento preciso de la trayectoria deseada.











 text new page (beta)
text new page (beta)