Introducción
La ecuación base para el estudio mecanicista de los procesos de transferencia de agua, en la zona no saturada del suelo, se establece combinando el principio general de conservación de la masa y la ley de Darcy-Buckingham. La aplicación de la ecuación de transferencia requiere representar las propiedades hidráulicas del suelo, con el contenido volumétrico de agua (θ) expresado como función del potencial de presión (ѱ; curva de retención de humedad) y la conductividad hidráulica (K), como función de θ o ѱ (curva de conductividad hidráulica). En la literatura existen modelos analíticos para describir las propiedades hidráulicas del suelo, los cuales varían conceptualmente y en sofisticación. Al respecto, Assouline y Or (2013) realizaron su revisión. Ese conjunto de modelos abarca funciones de pedotransferencia (Sobieraj et al. 2001, Wösten et al. 2001, Tóth et al., 2015) y modelos mecanicistas basados en las leyes de Poiseuille y Laplace (Brooks y Corey 1964; van Genuchten 1980; Braddock et al., 2001). El primer grupo de modelos se establece sin considerar explícitamente las bases físicas del movimiento del agua en el suelo, y el segundo grupo permite representar detalladamente los mecanismos fundamentales del proceso a partir de leyes físicas.
Modelos mecanicistas para las propiedades hidráulicas están disponibles en programas de cómputo que simulan el flujo del agua en suelos parcialmente saturados (Diersch, 2014). También se ha estudiado la capacidad descriptiva de grupos de modelos para las propiedades hidráulicas (Too et al., 2014)). Sin embargo, la justificación de los modelos en el contexto de la teoría de la infiltración se ha considerado limitadamente, ya que la mayoría de los análisis evalúa sólo su flexibilidad para describir datos experimentales de campo o laboratorio.
Fuentes et al. (1992) analizaron los modelos mecanicistas reportados en la literatura para algunas propiedades hidráulicas del suelo. Los autores demostraron que solo los modelos de Fujita (1952)) y Parlange et al. (1982) y la curva de retención de van Genuchten (1980), sujeta a la restricción de Burdine (1953) y combinada con la curva de conductividad de Brooks y Corey (1964) satisfacen las propiedades integrales de la infiltración. Aunque la conductividad hidráulica a saturación (Ks) sea conocida, la aplicación de esos modelos requiere la estimación de dos parámetros de forma y uno de escala, simultáneamente con series experimentales de retención de humedad y conductividad hidráulica para determinarlos.
Fuentes et al. (2001) estudiaron la conductividad hidráulica con base en las leyes de Poiseuille y Darcy y en el contexto de la geometría fractal, representando el espacio poroso del suelo como un sistema de capilares. Ellos obtuvieron un modelo conceptual que les permitió establecer, a partir del peso dado a los radios de los capilares en la resistencia al flujo del agua en el suelo, las relaciones fractales integrales denominadas poro neutro, poro geométrico y poro grande. El primer modelo correspondió a la relación integral para la conductividad de Burdine (1953) con un factor de corrección, el segundo a la relación de Mualem (1976) también con un factor de corrección y el tercero fue un modelo nuevo, establecido por los autores de ese estudio. Ellos consideraron restricciones particulares entre los parámetros de forma de la curva de retención de van Genucthen (1980) y derivaron las expresiones respectivas. Esas relaciones, particulares entre m y n, permitieron explicitar que las correcciones de los modelos analíticos para la conductividad derivadas por Van Genucthen (1980) dependen de la dimensión fractal del suelo. Los modelos fractales de Fuentes et al. (2001) para la conductividad hidráulica satisfacen las propiedades integrales de la infiltración y con Ks conocida se deben determinar solo dos parámetros, uno es de forma y otro de escala, y se requiere solo la curva experimental de retención de humedad para estimarlos.
El objetivo de este estudio fue evaluar la capacidad descriptiva de los modelos fractales de Fuentes et al. (2001) denominados poro neutro, poro geométrico y poro grande, con información experimental de la base de datos UNSODA (Leij et al., 1996; Nemes et al., 2001). La evaluación consistió en calibrar los parámetros del modelo de retención de van Genuchten (1980) sujeto a sus restricciones, aplicar el modelo analítico para la conductividad hidráulica y comparar sus predicciones con los datos experimentales. La hipótesis fue que con la calibración de los dos parámetros que intervienen en los modelos fractales de retención de humedad pueden aplicarse las relaciones para conductividad hidráulica relativa del suelo, prediciendo con precisión la evolución de esta variable.
Materiales y métodos
La Ecuación que describe los procesos de transferencia de agua en suelos parcialmente saturados es:
donde H=ѱ-z es el potencial hidráulico [L]; ѱ es el potencial de presión del agua en el suelo [L]; z es la coordenada vertical [L] positiva en sentido descendente; θ es el contenido volumétrico de agua [L3L-3] que es función del potencial de presión, relación conocida como curva de retención de humedad, K es la curva de conductividad hidráulica del suelo [LT-1] que es función de la presión o del contenido volumétrico de agua, θ (ѱ) y K(θ) son también conocidas como las propiedades hidráulicas del suelo, S es el volumen de agua que extraen las raíces de las plantas por unidad de volumen de suelo en la unidad de tiempo [L3L-3T-1];
Para considerar formalmente la relación existente entre la geometría del medio poroso y las propiedades hidráulicas del suelo, se deben tomar en cuenta dos leyes fundamentales:
1) Ley de Poiseuille, la cual relaciona modelos mecanicistas tradicionales la velocidad media del agua (v) en un capilar cilíndrico de radio (r) con el gradiente de la energía
donde ρw es la densidad del agua [ML-3]; µ es la viscosidad dinámica [ML-1T-1]; y g es la aceleración de la gravedad [LT-2].
2) Ley de Laplace, la cual relaciona el potencial de presión con el radio de curvatura rc del menisco de agua en un poro de radio r:
donde σ es la tensión superficial en la interfaz agua-aire [MT-2]. Los radios de curvatura y poro se relacionan a través del ángulo de contacto a que se tiene entre el menisco del agua y las partículas del suelo: r=rc cos a.
Los modelos de Fuentes et al. (2001) se establecieron representando al suelo como un objeto fractal y considerando las Ecuaciones (2) y (3). Las representaciones analíticas obtenidas al introducir la curva de retención de van Genuchten (1980) en los modelos fractales generales de conductividad hidráulica K(Se) son:
Modelo del poro geométrico:
Modelo del poro neutro:
Modelo del poro grande:
donde m y n son parámetros de forma; ѱd parámetro de escala de la presión [L]; Se(ѱ)=[(θ(ѱ)- θr)/(θs- θr)] es la saturación efectiva; θs es el contenido volumétrico de agua a saturación [L3L-3]; θr es el contenido volumétrico residual [L3L-3]; Ks es la conductividad hidráulica a saturación [LT-1]; 0≤Kr≤1 es la conductividad hidráulica relativa; s es la dimensión cociente 0≤s=D/E≤1, donde D es la dimensión fractal del objeto (suelo) y E es la dimensión del espacio de Euclides. En el estudio se estableció que la dimensión cociente del suelo es una función implícita de su porosidad volumétrica:
La Ecuación (7) se resolvió con el método numérico de Newton-Raphson (Burden et al., 2015) y para acelerar la convergencia del proceso de cálculo del valor de la dimensión cociente s, se usó como estimador inicial
La evidencia experimental para calibrar y validar los modelos (4)-(6) se tomó de la base de datos UNSODA versión 2.0, presentada por Nemes et al. (2001) quienes mejoraron la versión original desarrollada por Leij et al. (1996). La versión 2.0 tiene información experimental de 790 suelos, abarcando las doce clases texturales definidas por el Departamento de Agricultura de los Estados Unidos (USDA, por sus siglas en inglés), con 184 arenas, 64 franco arenosos, 133 arenas francas, 52 franco-arcilloso-arenosos, 3 limos, 142 franco limosos, 36 franco arcillosos, 70 francos, 33 franco-arcilloso-limosos, 3 arcillas arenosas, 21 arcillas limosas y 39 arcillas.
De la información experimental en la base UNSODA se seleccionaron 208 suelos (Cuadro 1). Los suelos seleccionados presentaron información experimental de granulometría, retención de humedad θ(ѱ), conductividad hidráulica K(θ), porosidad volumétrica (ϕ), contenido volumétrico a saturación (θs) y conductividad hidráulica a saturación (Ks). Otro criterio en la selección fue considerar solo suelos con datos experimentales de retención de humedad y conductividad hidráulica estimados a partir del análisis de procesos similares del flujo del agua en el suelo (pruebas de drenaje de suelos inicialmente húmedos o totalmente saturados), para que fueran compatibles ambas series experimentales y minimizar el efecto de la histéresis capilar que se acentúa en la curva de retención de humedad.
Cuadro 1 Suelos seleccionados de la base UNSODA.
| Textura | Código del suelo |
| Arena (75) | 1014 1041 1042 1043 1050 1052 1053 1054 1060 1061 1063 1070 1071 1072 1073 1074 1075 1140 1141 1142 1240 1241 1460 1461 1462 1463 1464 1465 1466 1467 2100 2120 2121 2122 2123 2124 2125 2126 2210 2211 2212 2213 2217 2220 2221 2310 2540 2550 3070 3080 4000 4001 4021 4051 4052 4060 4061 4132 4140 4141 4142 4150 4151 4152 4440 4441 4443 4444 4445 4480 4490 4650 4651 4660 4661 |
| Franco limoso (40) | 1280 1281 1282 1490 2491 2492 2493 3240 3242 3250 3252 3253 3260 3261 3262 3263 3264 4030 4031 4032 4033 4040 4041 4042 4043 4070 4071 4080 4082 4090 4091 4092 4180 4181 4182 4183 4570 4671 4672 4673 |
| Franco arenoso (31) | 1091 1120 1121 1130 1131 1161 1380 1381 1390 1391 1392 2111 2130 2131 2132 2532 2541 2551 3050 4100 4110 4111 4112 4160 4161 4162 4170 4171 4172 4470 4500 |
| Arena franca (26) | 1010 1011 1012 1013 1015 1051 1062 1090 1143 1160 2101 2102 2103 2104 2105 2110 4010 4011 4020 4050 4062 4130 4580 4581 4582 4583 |
| Arcilla (10) | 1162 1163 1181 1182 3281 3282 4120 4121 4680 4681 |
| Franco arcilloso arenoso (10) | 1092 1132 1164 1165 1166 1184 1382 2542 2552 4460 |
| Franco (8) | 1260 1261 2530 2531 4101 4102 4780 4790 |
| Franco arcilloso limoso (7) | 1362 1371 2021 2022 3241 3251 4450 |
| ranco arcilloso (1) | 1180 |
Resultados y discusión
Los parámetros m y ѱd se determinaron para cada modelo de retención de humedad θ(ѱ)=(θs- θr) Se+θr, a partir de análisis de regresión no lineal con las funciones de retención (4)-(6) y la información experimental correspondiente. En estos análisis se consideraron las restricciones entre los parámetros m y n especificadas y se asumió θr=0 (Haverkamp et al., 2002). En las Figuras 1a-1c se presentan los resultados de la calibración realizada para el suelo de textura arenosa denominado Grenoble (código 4444), que es un suelo cuyos datos experimentales se obtuvieron bajo condiciones controladas en laboratorio y tiene amplio uso en la literatura (Fuentes et al., 1992; Berlotti y Mayergoys, 2006). El mayor ajuste de datos se obtiene con el modelo del poro grande (6), lo que se comprueba con el coeficiente de determinación (r2) que se calcula con
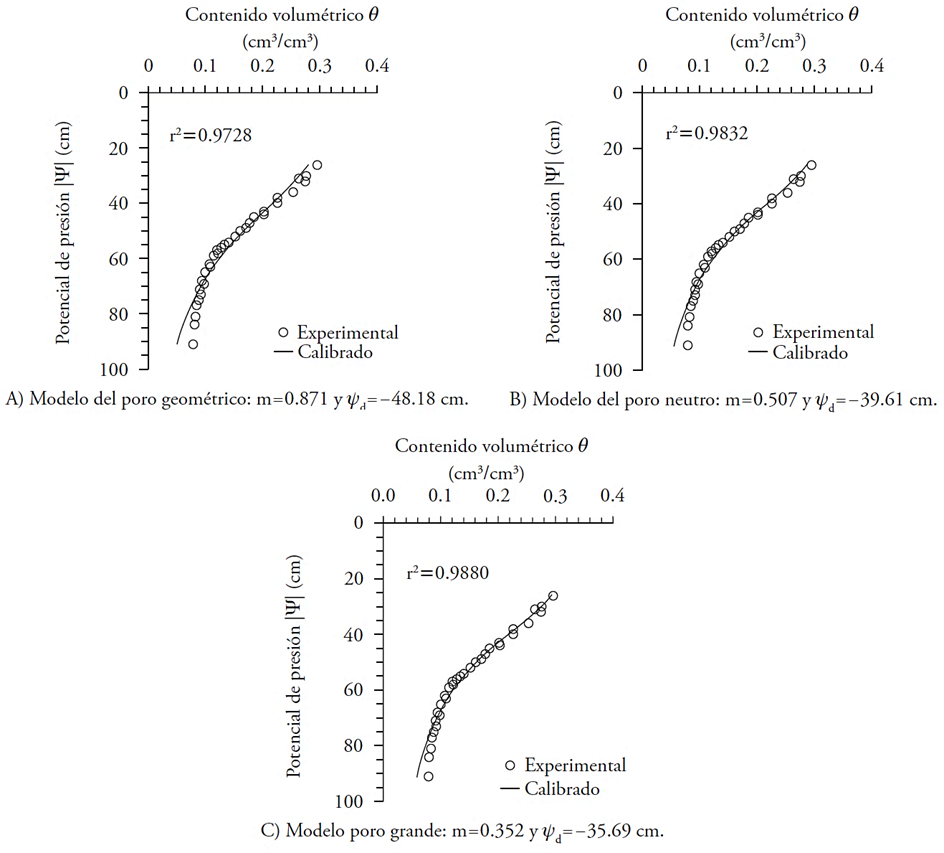
Figura 1 Ajuste de los datos experimentales de retención de humedad del suelo 4444 con φ=0.370 cm3/cm3, s=0.667, θs=0.312 cm3/cm3 y θr =0 cm3/cm3.
Cuadro 2 Resultados de los análisis de regresión no lineal a los datos experimentales de retención de humedad de los primeros suelos analizados.
| ID | ϕ | θs | s | Poro geométrico Ecuación (4) | Poro neutro Ecuación (5) | Poro grande Ecuación (6) | |||
| cm3/cm3 | cm3/cm3 |
ѱd cm |
m (-) |
ѱd cm |
m (-) |
ѱd cm |
m (-) |
||
| 1010 | 0.390 | 0.384 | 0.670 | -23.10 | 0.325 | -17.56 | 0.167 | -17.18 | 0.148 |
| 1011 | 0.433 | 0.411 | 0.680 | -25.38 | 0.406 | -19.38 | 0.212 | -18.91 | 0.184 |
| 1012 | 0.474 | 0.381 | 0.688 | -22.03 | 0.369 | -17.37 | 0.196 | -17.04 | 0.171 |
| 1013 | 0.442 | 0.376 | 0.682 | -24.19 | 0.463 | -18.56 | 0.243 | -18.04 | 0.206 |
| 1014 | 0.446 | 0.361 | 0.682 | -29.16 | 0.521 | -21.99 | 0.273 | -21.09 | 0.226 |
| 1015 | 0.346 | 0.262 | 0.662 | -14.15 | 0.134 | -11.71 | 0.067 | -11.66 | 0.064 |
| 1041 | 0.429 | 0.330 | 0.679 | -39.01 | 0.564 | -28.40 | 0.290 | -26.95 | 0.236 |
| 1042 | 0.395 | 0.340 | 0.672 | -41.50 | 0.663 | -30.45 | 0.346 | -28.44 | 0.271 |
| 1043 | 0.390 | 0.320 | 0.671 | -48.36 | 0.783 | -36.74 | 0.424 | -33.70 | 0.314 |
| 1050 | 0.396 | 0.384 | 0.672 | -13.49 | 0.383 | -10.98 | 0.204 | -10.77 | 0.178 |
| 1051 | 0.400 | 0.389 | 0.673 | -8.80 | 0.353 | -7.25 | 0.188 | -7.19 | 0.166 |
| 1052 | 0.415 | 0.365 | 0.676 | -8.08 | 0.379 | -6.88 | 0.207 | -6.87 | 0.182 |
| 1053 | 0.419 | 0.366 | 0.677 | -9.67 | 0.512 | -8.13 | 0.289 | -8.02 | 0.242 |
| 1054 | 0.419 | 0.367 | 0.677 | -12.19 | 0.682 | -9.79 | 0.390 | -9.30 | 0.303 |
| 1060 | 0.415 | 0.361 | 0.676 | -16.62 | 0.410 | -13.31 | 0.219 | -13.07 | 0.189 |
Los modelos fractales de conductividad hidráulica (4)-(6) se aplicaron con los parámetros de la calibración, se comparó su predicción con los datos experimentales y se determinó el r2 por clase textural. La conductividad relativa (Kr) se usó en lugar de la conductividad hidráulica (K) porque la primera varía entre 0 y 1 en cualquier tipo de suelo, lo que simplifica el análisis. En el caso de la validación del suelo 4444, la predicción mejor se obtuvo con el modelo del poro geométrico, aunque esta se aproximó al resultado del modelo del poro grande (Figuras 2a-2c). La validación por clase textural de los 208 suelos del Cuadro 1 mostró que las predicciones de los modelos de conductividad relativa del poro geométrico, poro neutro y poro grande fueron estables y las diferencias entre ellos fueron mínimas (Cuadro 3). Los tres modelos fractales exhibieron capacidad predictiva adecuada en la mayoría de las clases texturales, aunque los valores de porosidad volumétrica (ϕ) y contenido volumétrico de agua a saturación (θs) (Cuadro 2) reportados en UNSODA son diferentes. Esto impacta en la predicción de los modelos evaluados porque sus parámetros m y n son dependientes del parámetro s, que es función de ϕ (Ecuación 7).
Cuadro 3 Coeficiente de determinación r2 por clase textural (Kr_experimental vs Kr_modelo)
| Textura | Modelos de conductividad hidráulica relativa | ||
| Poro geométrico (4) | Poro neutro (5) | Poro grande (6) | |
| Arena (75) | 0.8641 | 0.8629 | 0.8626 |
| Franco limoso (40) | 0.7946 | 0.7893 | 0.8008 |
| Franco arenoso (31) | 0.7482 | 0.7503 | 0.7529 |
| Arena franca (26) | 0.8697 | 0.8708 | 0.8710 |
| Arcilla (10) | 0.8850 | 0.8863 | 0.8858 |
| Franco arcilloso arenoso (10) | 0.7470 | 0.7621 | 0.7629 |
| Franco (8) | 0.8604 | 0.8495 | 0.8613 |
| Franco arcilloso limoso (7) | 0.7998 | 0.7829 | 0.8010 |
| Franco arcilloso (1) | 0.9953 | 0.9952 | 0.9953 |
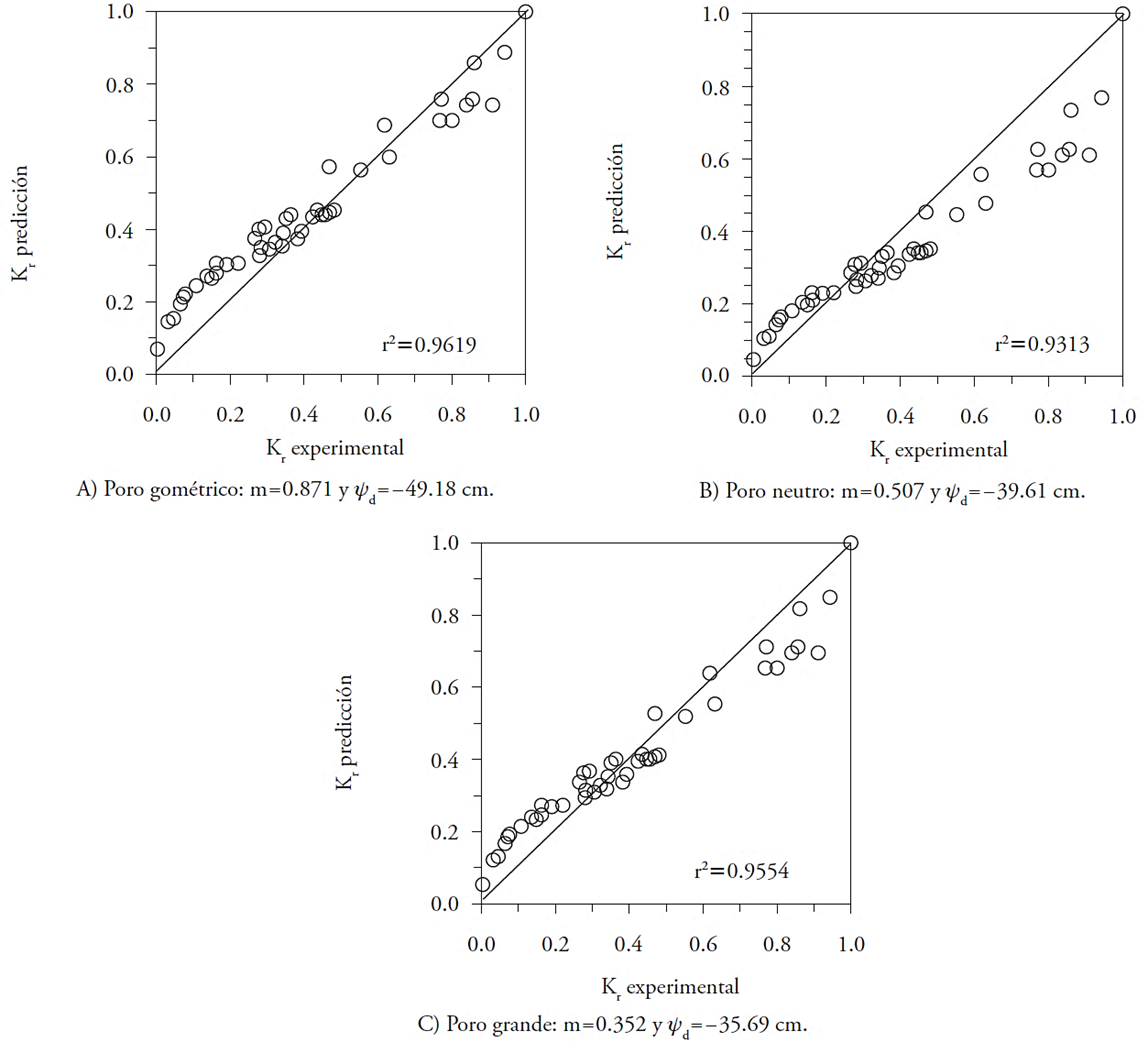
Figura 2 Validación de los modelos de conductividad fractal (4)-(6) considerando los datos experimentales de conductividad hidráulica relativa (Kr=K(θ)/Ks) del suelo Grenoble 4444: Ks=368.9 cm/d y s=0.667.
El procedimiento de calibración y validación, descrito en este estudio, se aplicó para contrastar los niveles de predicción de los modelos fractales, considerando el modelo clásico de retención de humedad de van Genuchten (1980) sujeto a la restricción de Burdine (1953) combinado con el modelo de conductividad hidráulica de Brooks y Corey (1964). Este conjunto de funciones satisface las propiedades integrales de la infiltración (Fuentes et al., 1992) y lo usan analistas y modeladores del flujo de agua en la zona vadosa del suelo:
donde η es un parámetro de forma que debe calibrarse considerando los datos experimentales de conductividad hidráulica. Así, este exponente constituyó un parámetro adicional por determinar, respecto de los tres modelos fractales. Para eliminar η del proceso de calibración y hacer compatible la comparación de resultados, se retoma el análisis desarrollado por Fuentes et al. (2001) quienes establecieron que el exponente está relacionado con los parámetros de forma de la curva de retención de van Genuchten (1980) como sigue:
La Ecuación de retención de humedad (8) se aplicó para ajustar los datos experimentales de contenido volumétrico de humedad de los suelos (Cuadro 1) y calcular los valores de m y ѱd; la Ecuación (9) se usó para estimar η y con la ecuación de conductividad hidráulica relativa, de Brooks y Corey (8), se determinó por clase textural la correspondencia lineal entre datos modelados y datos experimentales (Cuadro 4). Los modelos fractales (Cuadro 3) mejoraron la descripción en ocho de las nueve clases texturales. Sólo en la textura franco-limosa los modelos clásicos (8) presentaron r2 mayor, pero con diferencia pequeña respecto del modelo del poro grande (0.8021 contra 0.8008).
Cuadro 4 Coeficiente de determinación r2 por clase textural (Kr_experimental respecto a Kr_modelo).
| Textura | Ecuaciones (8) y (9) |
| Arena (75) | 0.8425 |
| Franco limoso (40) | 0.8021 |
| Franco arenoso (31) | 0.7498 |
| Arena franca (26) | 0.8697 |
| Arcilla (10) | 0.8538 |
| Franco arcilloso arenoso (10) | 0.7760 |
| Franco (8) | 0.8381 |
| Franco arcilloso limoso (7) | 0.7592 |
| Franco arcilloso (1) | 0.9953 |
Conclusiones
Las funciones analíticas de las curvas de retención de humedad de los modelos fractales poro geométrico, poro neutro y poro grande, con dos parámetros para calibrar, ajustan los datos experimentales de los suelos y se ajustan similarmente al modelo de retención clásico de van Genuchten (1980), sujeto a la restricción de Mualem (1976). Los modelos fractales para la conductividad hidráulica relativa describen satisfactoriamente el comportamiento de esta variable hidráulica en una gama de texturas de suelo e incluso presentan mejor nivel de predicción que el modelo clásico de Brooks y Corey (1964). Los tres modelos fractales son confiables y pueden considerarse en simulaciones del flujo de agua en la zona no saturada del suelo. El modelo del poro grande proporciona las predicciones mayores de la conductividad hidráulica relativa.











 texto em
texto em 


