Introducción
La planeación y dimensionamiento hidrológico de las obras hidráulicas se basa en las crecientes de diseño, que son predicciones asociadas a cierta probabilidad de no excedencia; con esto se brinda seguridad al diseño hidrológico. Este es el caso de los diques de protección, encauzamientos y rectificaciones, puentes y drenaje pluvial urbano. En los embalses de aprovechamiento o control también son necesarias las crecientes de diseño, durante sus etapas de construcción y de operación (Jakob, 2013).
La estimación hidrológica de las crecientes de diseño tiene dos enfoques, el determinístico y el probabilístico. El primero establece una tormenta de diseño que se transforma con modelación matemática del proceso lluvia-escurrimiento en el hidrograma. En el segundo enfoque se ajusta un modelo probabilístico al registro de gastos máximos anuales y se realizan las inferencias buscadas. En ambos enfoques, el análisis hidrológico de frecuencias (AHF) es necesario para obtener predicciones de intensidades de lluvia, precipitación máxima diaria y gasto máximo anual (Katz, 2013).
El AHF utiliza una función de distribución de probabilidades (FDP) para representar a la muestra disponible de datos máximos anuales. El procedimiento engloba cinco etapas (Rao y Hamed, 2000; Meylan et al., 2012): 1) recopilación de los datos y verificación de su calidad estadística, 2) selección de una FDP, 3) aplicación de uno o varios métodos de estimación de sus parámetros de ajuste, 4) cuantificación objetiva del ajuste logrado con cada FDP y técnica de estimación de parámetros y, 5) selección de resultados.
El AHF se basa en el supuesto de estacionariedad, de un clima y una cuenca que no cambian con el tiempo en el sentido estadístico. Por esto se acepta que los registros disponibles de datos hidrológicos máximos anuales sean independientes y estén idénticamente distribuidos, condición denominada “iid”. El impacto del cambio climático global se ha verificado y en muchas cuencas del planeta han ocurrido cambios físicos originados por la construcción de embalses y la urbanización. Estas dos condiciones físicas han generado modificaciones del ciclo hidrológico, con incrementos en la frecuencia e intensidad de los eventos extremos de precipitación por el clima y reducción o aumento del escurrimiento en las cuencas. Esos cambios en periodos cortos han producido tendencias, saltos y variabilidad diferente en los registros de datos hidrológicos máximos, transformándolos en no estacionarios (Jakob, 2013; Katz, 2013; Kim et al., 2015; Álvarez-Olguín y Escalante-Sandoval, 2016).
Los enfoques del AHF de registros no estacionarios los describieron Khaliq et al. (2006). Uno de esos enfoques, quizás el más simple, consiste en una extensión de la teoría de valores extremos y por ello aplica la FDP clásica de estos procedimientos; la distribución General de Valores Extremos (GVE) con tres parámetros (u, a, k), permite el ajuste gradual al introducir el tiempo t como una covariable en sus parámetros de ubicación u y escala a y conserva constante el de forma k (Park et al., 2011; Jakob, 2013; Katz, 2013). Los AHF con esta FDP no estacionaria permiten estimar crecientes de diseño al término de la vida útil de la obra hidráulica, en 2050 o 2100 (Mudersbach y Jensen, 2010a, b; Franks et al., 2015). El Adlouni et al. (2007) y Aissaoui-Fqayeh et al. (2009) establecieron una nomenclatura para esas FDP no estacionarias y definieron la función GVE estacionaria como GVE0, con su parámetro de ubicación variable linealmente con el tiempo (u = α1 + α2·t) GVE1 y GVE2 cuando la variación es cuadrática (u = α1 + α2·t + α3·t2). En el modelo GVE11 los parámetros de ubicación y de escala varían linealmente con el tiempo.
El objetivo de este estudio fue exponer el método de los momentos L móviles para estimar los parámetros de ajuste de FDP no estacionaria GVE11, que fue propuesto por Cunderlik y Burn (2003) y aplicado por Mudersbach y Jensen (2010a, b). Por medio del error estándar de ajuste se aceptó o rechazó la distribución GVE11 para modelar probabilísticamente series anuales amplias de datos hidrológicos extremos que presentan tendencia y variabilidad no constante. Dos aplicaciones numéricas se describen con datos procedentes de la literatura especializada; los resultados destacan la simplicidad y utilidad del método de los momentos L móviles para el ajuste de FDP no estacionaria GVE11, en registros del tipo citado.
Materiales y Métodos
Momentos L poblacionales y de la muestra
La teoría y aplicación de los momentos L, como sistema alternativo para describir las formas de las FDP, las expuso Hosking (1990). Los momentos L son combinaciones lineales de los momentos de probabilidad pesada (MPP), desarrollados por Greenwood et al. (1979), y se definen, para una variable aleatoria x con FDP acumulada F(x) y función de cuantiles x(F) como:
La expresión del momento: βr = M1,r,0 es:
La definición ordinaria de momentos es:
Al compararla con la ecuación anterior se deduce que la definición convencional de momentos involucra potencias sucesivas de la función de cuantiles x(F) y que los MPP implican potencias sucesivas de F, y por ello pueden considerarse como integrales de x(F) ponderadas por polinomios Fr , de ahí su nombre. Los MPP mejoran notablemente las propiedades del muestreo porque los valores extremos o dispersos no los influyen (Asquith, 2011). Los primeros tres momentos L poblacionales corresponden a (Hosking, 1990; Hosking y Wallis, 1997):
En una muestra de tamaño n, con sus elementos en orden ascendente (x1 ≤ x2 ≤ …≤ xn) los estimadores insesgados de βr son (Stedinger et al., 1993; Hosking y Wallis, 1997):
Los estimadores muestrales de λr serán lr y las ecuaciones 4 a 6 los definen.
Ajuste con momentos L de la distribución GVE0
La distribución GVE ahora es el modelo probabilístico básico de los AHF de datos máximos y mínimos, como gastos, lluvias, niveles, temperaturas y vientos. Hosking y Wallis (1997) y El Adlouni et al. (2008) destacaron que la aceptación de la función GVE se debe a que cuando su parámetro de forma es negativo (k < 0) tiene su cola derecha más gruesa o densa que las otras FDP, que por lo común se utilizan en los AHF; además, tiene límite superior cuando k > 0 y define a la distribución Gumbel de dos parámetros, cuando k = 0. Por lo anterior, su intervalo de aplicación en x es: u + a/k ≤ x < ∞ si k < 0; - ∞ < x < ∞ si k = 0 y - ∞ < x ≤ u + a/k si k > 0.
La solución inversa x(F) de la distribución GVE0 es la siguiente, con ella se estiman las predicciones que se asocian a una cierta probabilidad de no excedencia (F) y las ecuaciones que permiten estimar sus tres parámetros de ajuste (u, a, k) correspondientes a la ubicación, escala y forma, con el método de momentos L son:
donde:
Para estimar la función Gamma se utilizó la fórmula de Stirling (Davis, 1972):
Verificación de la no estacionariedad del registro
Una serie cronológica de datos hidrológicos máximos es estacionaria si está libre de tendencias, saltos o periodicidad. Lo anterior implica que los parámetros estadísticos de esa serie, como la media y la varianza, son básicamente constantes a través del tiempo; de otra manera, la serie no será estacionaria (Cunderlik y Burn, 2003; Khaliq et al., 2003). Mudersbach y Jensen (2010 a) indicaron que el estudio de los momentos de orden mayor, como la asimetría, es innecesario porque es poco probable que esa propiedad varíe con el tiempo, pero en un registro no estacionario los parámetros de ubicación y escala de una FDP seguramente cambiarán en el tiempo.
Campos-Aranda (2015) estimó la tendencia lineal con varios métodos y verificó si es estadísticamente diferente de cero. El cambio en la varianza se probó con una versión simplificada del procedimiento sugerido por Al Saji et al. (2015). Este consistente en restar a cada dato la tendencia lineal estimada y elevarlas al cuadrado, para observar si son relativamente constantes o presentan épocas con variabilidad alta y baja. Lo anterior permitió concluir que el registro no es estacionario en la varianza.
Ajuste con momentos L móviles de la distribución GVE11
La distribución GVE no estacionaria, con sus parámetros de ubicación (u) y escala (a) variables en el tiempo (t), está indicada en registros amplios de datos máximos anuales con tendencia y variabilidad no constante (Cunderlik y Burn, 2003). La variación lineal o exponencial de u y a se recomienda por su ajuste sencillo y la facilidad que brinda a la extrapolación, esto es (Mudersbach y Jensen, 2010 a, b):
En el método de los momentos L móviles se emplea una ventana corrediza en el tiempo (sliding time window), con longitud en años n que se desliza año con año a través del registro de datos máximos de tamaño nt . La anchura de la ventana (n) se seleccionará de manera que en esa amplitud del registro pueda considerarse estacionario y entonces el número de ventanas (nv) por procesar será:
Para cada tramo del registro de las nv ventanas móviles se calculan sus parámetros de ubicación y escala con base en las ecuaciones 11 a 15. Las dos series cronológicas que se obtengan serán funciones no paramétricas que no podrán extrapolarse al futuro y que se caracterizarán por sus valores promedio: um , am y km. Al ajustar a la serie cronológica de u los modelos definidos por las ecuaciones 16 y 18 y la serie de a, los de las ecuaciones 17 y 19, se definen descripciones paramétricas de los parámetros móviles, cuya calidad de ajuste se mide con el error estándar medio, expresado como:
En las expresiones anteriores, los valores estimados
En las expresiones anteriores “ln” es el logaritmo natural y “exp” la función exponencial, es decir, el número e elevado al valor del paréntesis. Cambiando en las ecuaciones 24 a 27, ui por ai y um por am se estiman los coeficientes β y δ de las ecuaciones 17 y 19.
Para las predicciones de cierto periodo de retorno de diseño (Tr) en años, estimadas en un cierto tiempo futuro, comúnmente los años 2025, 2050 y 2100, se aplica la ecuación 10, con km y los valores siguientes de la probabilidad de no excedencia (F) y del tiempo final (Tf), en los parámetros de ubicación y escala (ecuaciones 16 a 19), por lo que habrá predicciones con la extrapolación lineal y con la exponencial:
donde AFP y AFR son los años finales de la predicción (2025, 2050 ó 2100) y del registro.
Error estándar de ajuste
A mediados de la década de los años setenta se estableció al error estándar de ajuste (EEA) como indicador estadístico cuantitativo de la calidad del ajuste logrado entre los datos y las predicciones con la FDP que se prueba, ya que evalúa la desviación estándar de esas diferencias. En el presente estudio la FDP que se prueba es la distribución no estacionaria GVE11 y su expresión es la siguiente (Kite, 1977; Pandey y Nguyen, 1999):
donde nt y np son el número de
datos del registro y de parámetros de ajuste, en el caso estacionario tres
(u, a, k) y en el no
estacionario cinco (α0, α1, β0, β1,
k
m , o bien, γ0, γ1,
δ0, δ1,
km );
Xi son los datos máximos
ordenados de menor a mayor y
donde m es el número de orden del dato, con 1 para el menor y nt para el mayor. La evaluación del EEA permite seleccionar entre el modelo lineal y el exponencial para realizar la extrapolación de las predicciones de diseño.
Ajuste de las distribuciones no estacionarias LOG11 y PAG11
FDP Logística Generalizada (LOG) y Pareto Generalizada (PAG) son modelos que se utilizan en los AHF (Stedinger et al., 1993; Kim et al., 2015), que se pueden ajustar en sus versiones no estacionarias, con el método de los momentos L móviles, al cambiar las ecuaciones 11 a 14, para estimar sus parámetros de ubicación y escala y después realizar sus predicciones con la ecuación 10, que les corresponda. Las fórmulas para las distribuciones estacionarias LOG0 y PAG0 las documentó Campos-Aranda (2016). El método de los momentos L móviles puede aplicarse usando los momentos L de orden mayor (Wang, 1997; Campos-Aranda, 2016) y obteniendo el mejor ajuste en los tramos de registro, que definen las ventanas deslizables.
Registros de valores máximos anuales por procesar
Dos registros de la literatura especializada se seleccionaron para ilustrar la aplicación de la distribución no estacionaria GVE11 ajustada con método de los momentos L móviles (Mudersbach y Jensen, 2010 a, b). Los datos son aproximados a los que se presentan en las gráficas originales (Cuadro 1).
Cuadro 1 Datos máximos anuales de gasto (Q, m3· s-1) y precipitación máxima diaria (PMD, milímetros) en las estaciones indicadas.
| No. | Estación hidrométrica del río Aberjona, EUA | Estación pluviométrica Manjimup, Australia | ||||||
| Año | Q | Año | Q | Año | PMD | Año | PMD | |
| 1 | 1940 | 9.1 | 1978 | 18.7 | 1930 | 35.7 | 1968 | 34.7 |
| 2 | 1941 | 5.9 | 1979 | 39.6 | 1931 | 49.0 | 1969 | 24.8 |
| 3 | 1942 | 7.4 | 1980 | 7.1 | 1932 | 37.8 | 1970 | 33.6 |
| 4 | 1943 | 6.8 | 1981 | 9.3 | 1933 | 47.1 | 1971 | 24.8 |
| 5 | 1944 | 5.0 | 1982 | 24.4 | 1934 | 84.0 | 1972 | 29.9 |
| 6 | 1945 | 6.2 | 1983 | 12.7 | 1935 | 44.9 | 1973 | 28.3 |
| 7 | 1946 | 9.1 | 1984 | 22.9 | 1936 | 54.1 | 1974 | 34.8 |
| 8 | 1947 | 9.1 | 1985 | 8.5 | 1937 | 45.9 | 1975 | 36.1 |
| 9 | 1948 | 10.2 | 1986 | 14.7 | 1938 | 64.8 | 1976 | 34.1 |
| 10 | 1949 | 3.4 | 1987 | 24.6 | 1939 | 35.1 | 1977 | 34.9 |
| 11 | 1950 | 7.1 | 1988 | 8.8 | 1940 | 52.3 | 1978 | 35.0 |
| 12 | 1951 | 6.8 | 1989 | 8.8 | 1941 | 63.9 | 1979 | 30.0 |
| 13 | 1952 | 6.2 | 1990 | 19.8 | 1942 | 42.5 | 1980 | 35.0 |
| 14 | 1953 | 7.1 | 1991 | 13.9 | 1943 | 31.4 | 1981 | 28.1 |
| 15 | 1954 | 13.9 | 1992 | 6.8 | 1944 | 54.6 | 1982 | 28.0 |
| 16 | 1955 | 19.5 | 1993 | 13.9 | 1945 | 97.5 | 1983 | 51.5 |
| 17 | 1956 | 10.8 | 1994 | 15.0 | 1946 | 49.6 | 1984 | 32.1 |
| 18 | 1957 | 4.8 | 1995 | 5.9 | 1947 | 95.9 | 1985 | 37.0 |
| 19 | 1958 | 11.0 | 1996 | 9.1 | 1948 | 50.0 | 1986 | 24.1 |
| 20 | 1959 | 4.8 | 1997 | 34.0 | 1949 | 42.9 | 1987 | 32.0 |
| 21 | 1960 | 5.4 | 1998 | 31.1 | 1950 | 51.8 | 1988 | 63.7 |
| 22 | 1961 | 6.8 | 1999 | 13.3 | 1951 | 35.6 | 1989 | 33.3 |
| 23 | 1962 | 10.8 | 2000 | 11.0 | 1952 | 37.2 | 1990 | 46.3 |
| 24 | 1963 | 22.4 | 2001 | 45.3 | 1953 | 57.0 | 1991 | 51.8 |
| 25 | 1964 | 6.5 | 2002 | 6.8 | 1954 | 53.9 | 1992 | 37.9 |
| 26 | 1965 | 8.8 | 2003 | 8.8 | 1955 | 54.8 | 1993 | 41.2 |
| 27 | 1966 | 2.8 | 2004 | 28.3 | 1956 | 43.5 | 1994 | 34.1 |
| 28 | 1967 | 10.8 | 2005 | 6.5 | 1957 | 47.0 | 1995 | 35.0 |
| 29 | 1968 | 18.4 | 2006 | 36.8 | 1958 | 36.7 | 1996 | 35.0 |
| 30 | 1969 | 13.0 | 2007 | 15.3 | 1959 | 29.2 | 1997 | 43.4 |
| 31 | 1970 | 21.2 | 2008 | 8.2 | 1960 | 34.3 | 1998 | 36.0 |
| 32 | 1971 | 4.0 | - | - | 1961 | 48.2 | 1999 | 51.4 |
| 33 | 1972 | 15.6 | - | - | 1962 | 50.7 | 2000 | 30.0 |
| 34 | 1973 | 8.5 | - | - | 1963 | 37.6 | 2001 | 34.1 |
| 35 | 1974 | 7.4 | - | - | 1964 | 42.7 | 2002 | 37.0 |
| 36 | 1975 | 6.5 | - | - | 1965 | 31.9 | 2003 | 36.0 |
| 37 | 1976 | 13.0 | - | - | 1966 | 38.8 | 2004 | 27.3 |
| 38 | 1977 | 10.2 | - | - | 1967 | 29.4 | - | - |
El primer registro, tomado de Vogel et al. (2011), incluyó 69 datos de gasto máximo anual (1940 a 2008), en una estación hidrométrica del Río Aberjona, cerca de la ciudad de Boston, Massachusetts, EUA, y cuya cuenca de drenaje ha estado impactada por el desarrollo urbano. Esta serie tuvo comportamiento con tendencia lineal ascendente y variabilidad creciente al final del registro (Figura 1).
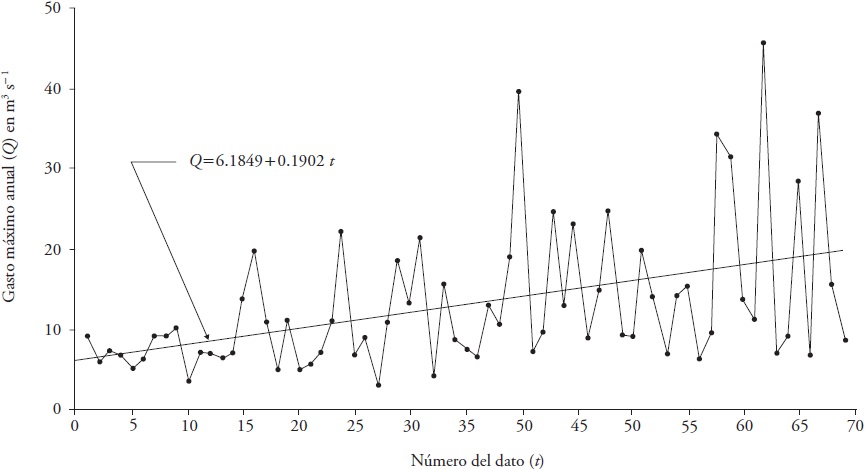
Figura 1 Tendencia lineal (ascendente) de la serie cronológica de gastos máximos anuales (Q) en la estación hidrométrica del Río Aberjona, EUA.
El segundo registro, tomado de Katz (2013), es ejemplo de la reducción drástica de la precipitación máxima diaria (PMD) de invierno (mayo a octubre) que registró la estación Manjimup del extremo suroeste de Australia. El registro incluyó 75 valores anuales (1930 a 2004), con tendencia descendente y variabilidad mayor en el inicio del registro (Figura 2).
Resultados y Discusión
Predicciones de Q en una estación del río Aberjona, EUA
Los datos (Cuadro 1) tuvieron tendencia lineal ascendente y significativa, con estadística de la distribución Student de 3.850 y valor crítico de 1.996 (p ≤ 0.05). El diagrama de diferencias al cuadrado, entre cada dato y la tendencia lineal calculada, mostró que la variabilidad fue mayor hacia el final del registro (Figura 3).
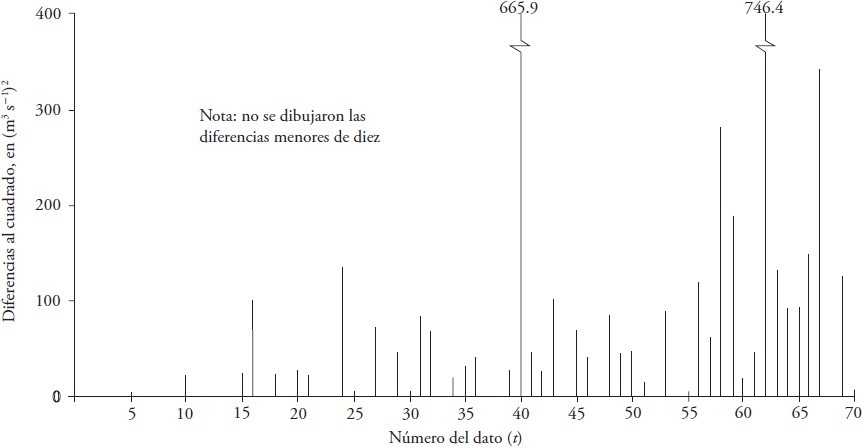
Figura 3 Diferencias (gasto máximo anual menos la tendencia lineal ascendente) al cuadrado del registro de la estación hidrométrica del Río Aberjona, EUA.
El modelo lineal con el tiempo t de los parámetros de ajuste u y a, conduce a errores estándar de ajuste (EEA) menores en comparación con los del modelo exponencial (Cuadro 2). Con anchura de ventana móvil de 20 datos se obtuvo el EEA menor, por lo que, esos resultados se adoptaron para obtener las predicciones para el futuro (Figura 4).
Cuadro 2 Ajuste no estacionario con momentos L móviles de la distribución GVE11 con tamaño de la ventana de 10, 15, 20 y 25 datos de gasto máximo anual del río Aberjona, EUA.
| Ajuste no estacionario (GVE11) con ancho de ventana móvil (n) de 10 datos | |||||
| nv = 59 | u m = 9.166 | a m = 5.005 | k m = -0.109 | ||
| Modelo lineal con t | Modelo exponencial con t | ||||
| α0 = 4.380 | α1 = 0.120 | ECM = 1.104 | γ0 = 5.226 | γ1 = 0.01325 | ECM = 1.116 |
| β0 = 0.957 | β1 = 0.101 | ECM = 1.344 | δ0 = 1.962 | δ1 = 0.02112 | ECM = 1.322 |
| EEA = 2.876 m-3·s | EEA = 3.103 m-3·s | ||||
| Ajuste no estacionario (GVE11) con ancho de ventana móvil (n) de 15 datos | |||||
| nv = 54 | u m = 8.990 | a m = 4.760 | k m = -0.175 | ||
| Modelo lineal con t | Modelo exponencial con t | ||||
| α0 = 4.209 | α1 = 0.112 | ECM = 0.620 | γ0 = 5.083 | γ1 = 0.01290 | ECM = 0.683 |
| β0 = 1.305 | β1 = 0.081 | ECM = 0.658 | δ0 = 2.001 | δ1 = 0.01915 | ECM = 0.740 |
| EEA = 2.330 m-3·s | EEA = 2.873 m-3·s | ||||
| Ajuste no estacionario (GVE11) con ancho de ventana móvil (n) de 20 datos | |||||
| nv = 49 | u m = 9.039 | a m = 4.745 | k m = -0.181 | ||
| Modelo lineal con t | Modelo exponencial con t | ||||
| α0 = 3.548 | α1 = 0.122 | ECM = 0.504 | γ0 = 4.720 | γ1 = 0.01398 | ECM = 0.584 |
| β0 = 1.298 | β1 = 0.077 | ECM = 0.581 | δ0 = 1.995 | δ1 = 0.01835 | ECM = 0.672 |
| EEA = 2.136 m-3·s | EEA = 2.473 m-3·s | ||||
| Ajuste no estacionario (GVE11) con ancho de ventana móvil (n) de 25 datos | |||||
| nv = 44 | u m = 9.093 | a m = 4.824 | k m = -0.176 | ||
| Modelo lineal con t | Modelo exponencial con t | ||||
| α0 = 2.892 | α1 = 0.131 | ECM = 0.394 | γ0 = 4.435 | γ1 = 0.01473 | ECM = 0.448 |
| β0 = 1.078 | β1 = 0.079 | ECM = 0.486 | δ0 = 1.984 | δ1 = 0.01804 | ECM = 0.551 |
| EEA = 2.171 m-3·s | EEA = 2.241 m-3·s | ||||
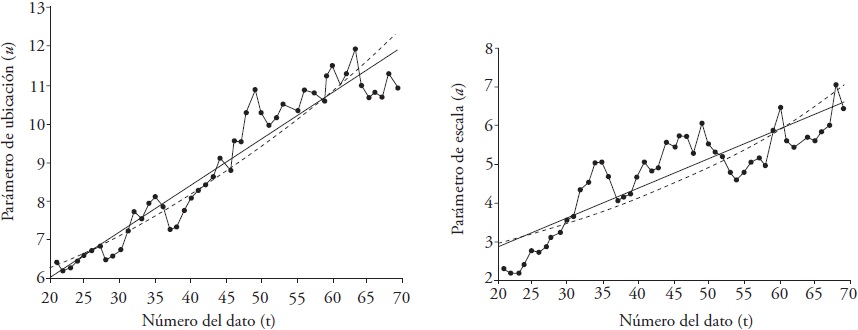
Figura 4 Tendencia lineal (recta) y exponencial (curva) de los parámetros de ubicación (u) y escala (a) estimados con momentos L con 20 datos en el ancho de la ventana móvil de los gastos máximos anuales del Río Aberjona, EUA.
Con las ecuaciones 11 a 15 se obtuvieron los parámetros de ajuste del modelo estacionario (GVE0): u = 8.407, a = 4.481 y k = -0.3034, con un EEA = 1.556 m3· s-1, y con la ecuación 10 las predicciones (Cuadro 3). La distribución no estacionaria GVE11 aportó predicciones mayores, en todos los periodos de retorno e incluso al término del registro histórico (Cuadro 3). En los periodos de retorno extremos (500 y 1000 años) y hacia el año 2100 las predicciones del modelo no estacionario fueron el doble de las del modelo estacionario que no tomó en cuenta la tendencia ascendente, ni la variabilidad mayor hacia el final del registro.
Cuadro 3 Predicciones de gasto máximo anual (m3· s-1) obtenidas con las distribuciones GVE0 y GVE11 con parámetros u y a variando linealmente y ancho de la ventana móvil de 20 datos, en el río Aberjona, EUA.
| Distribuciones GVE0 y GVE11 |
Periodos de retorno en años | |||||||
| 2 | 5 | 10 | 25 | 50 | 100 | 500 | 1000 | |
| Estacionario | 10.1 | 16.9 | 22.9 | 32.6 | 41.9 | 53.3 | 90.9 | 113.7 |
| En el año 2008 | 14.5 | 23.3 | 30.2 | 40.5 | 49.3 | 59.2 | 87.4 | 102.4 |
| En el año 2025 | 17.0 | 27.6 | 35.9 | 48.2 | 58.7 | 70.6 | 104.5 | 122.3 |
| En el año 2050 | 20.8 | 34.0 | 44.3 | 59.5 | 72.6 | 87.3 | 129.5 | 151.7 |
| En el año 2100 | 28.4 | 46.7 | 61.0 | 82.2 | 100.4 | 120.9 | 179.5 | 210.4| |
Predicciones de PMD en la estación Manjimup de Australia
Los datos de precipitación máxima diaria (PMD) anual (Cuadro 1) tienen tendencia lineal descendente (Figura 2) y significativa, con estadística de la distribución Student de -4.085 y valor crítico de 1.993 con p ≤ 0.05. En el diagrama de diferencias al cuadrado, entre cada dato y la tendencia lineal, la variabilidad fue notablemente mayor al inicio del registro (Figura 5).
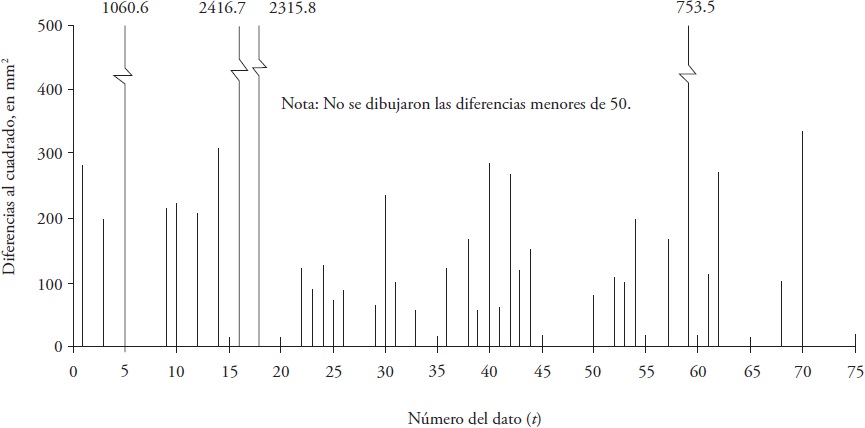
Figura 5 Diferencias (precipitación máxima diaria anual menos la tendencia lineal ascendente) al cuadrado del registro de la estación pluviométrica Manjimup, Australia.
El modelo exponencial con el tiempo t de los parámetros de ajuste u y a, conduce a errores estándar de ajuste (EEA) menores comparados con los del modelo lineal (Cuadro 4). Conforme crece el tamaño de la ventana móvil se obtienen menores EEA, por lo cual se adoptan los del valor máximo probado de n = 30 (Figura 6).
Cuadro 4 Ajuste no estacionario con momentos L móviles de la distribución GVE11 con tamaño de la ventana de 15, 20, 25 y 30 datos de PMD anual de la estación Manjimup, Australia.
| Ajuste no estacionario (GVE11) con ancho de ventana móvil (n) de 15 datos | |||||
| nv = 60 | u m = 36.930 | a m = 8.050 | k m = -0.009 | ||
| Modelo lineal con t | Modelo exponencial con t | ||||
| α0 = 48.982 | α1 = -0.265 | ECM = 3.410 | γ0 = 49.3973 | γ1 = -0.00690 | ECM = 3.253 |
| β0 = 14.124 | β1 = -0.134 | ECM = 1.670 | δ0 = 15.684 | δ1 = -0.01606 | ECM = 1.536 |
| EEA = 12.804 mm | EEA = 12.176 mm | ||||
| Ajuste no estacionario (GVE11) con ancho de ventana móvil (n) de 20 datos | |||||
| nv = 55 | u m = 36.292 | a m = 7.828 | k m = -0.072 | ||
| Modelo lineal con t | Modelo exponencial con t | ||||
| α0 = 49.933 | α1 = -0.284 | ECM = 2.949 | γ0 = 51.545 | γ1 = -0.00753 | ECM = 2.773 |
| β0 = 14.137 | β1 = -0.131 | ECM = 1.378 | δ0 = 16.183 | δ1 = -0.01620 | ECM = 1.255 |
| EEA = 12.472 mm | EEA = 11.898 mm | ||||
| Ajuste no estacionario (GVE11) con ancho de ventana móvil (n) de 25 datos | |||||
| nv = 50 | u m = 35.733 | a m = 7.647 | k m = -0.105 | ||
| Modelo lineal con t | Modelo exponencial con t | ||||
| α0 = 50.660 | α1 = -0.296 | ECM = 2.528 | γ0 = 52.906 | γ1 = -0.00795 | ECM = 2.351 |
| β0 = 14.867 | β1 = -0.143 | ECM = 1.023 | δ0 = 18.459 | δ1 = -0.01835 | ECM = 0.923 |
| EEA = 12.427 mm | EEA = 11.826 mm | ||||
| Ajuste no estacionario (GVE11) con ancho de ventana móvil (n) de 30 datos | |||||
| nv = 45 | u m = 35.275 | a m = 7.666 | k m = -0.120 | ||
| Modelo lineal con t | Modelo exponencial con t | ||||
| α0 = 50.327 | α1 = -0.284 | ECM = 1.904 | γ0 = 52.923 | γ1 = -0.00778 | ECM = 1.761 |
| β0 = 15.864 | β1 = -0.155 | ECM = 0.800 | δ0 = 21.281 | δ1 = -0.02000 | ECM = 0.731 |
| EEA = 11.777 mm | EEA = 11.199 mm | ||||
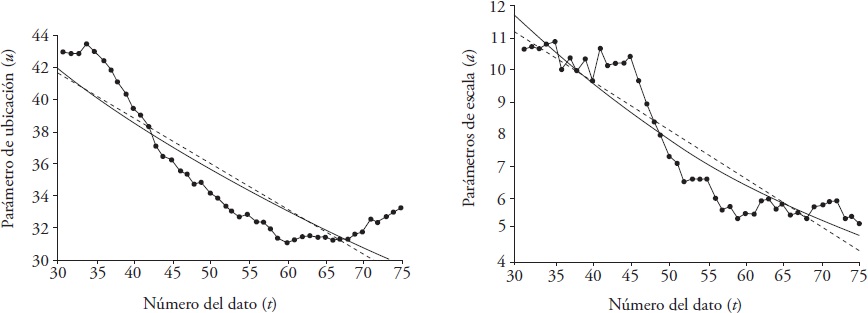
Figura 6 Tendencia lineal (recta) y exponencial (curva) de los parámetros de ubicación (u) y escala (a) estimados con momentos L con 30 datos en el ancho de la ventana móvil en la PMD anual de la estación Manjimup, Australia.
Con base en las ecuaciones 11 a 15 se obtuvieron los parámetros de ajuste del modelo GVE0 estacionario: u = 35.488, a = 8.431 y k = -0.1846, con un EEA =2.881 mm. Las predicciones respectivas, obtenidas con la ecuación 10, mostraron que la distribución no estacionaria GVE11 aportó predicciones menores, desde el final del registro histórico y en todos los periodos de retorno analizados (Cuadro 5). En los periodos de retorno extremos analizados (500 y 1000 años) y hacia el año 2100 las predicciones de PMD tendieron a estabilizarse alrededor de los 21 mm.
Cuadro 5 Predicciones de PMD obtenidas con las distribuciones GVE estacionaria y no estacionaria (GVE11) con parámetros variando exponencialmente y ancho de la ventana móvil (n) de 30 datos, en la estación Manjimup, Australia.
| Distribuciones GVE0 y GVE11 |
Periodos de retorno en años | |||||||
| 2 | 5 | 10 | 25 | 50 | 100 | 500 | 1000 | |
| Estacionario | 38.7 | 50.1 | 59.0 | 72.2 | 83.7 | 96.6 | 133.6 | 153.3 |
| En el año 2004 | 31.3 | 37.3 | 41.8 | 48.0 | 53.1 | 58.7 | 73.3 | 80.6 |
| En el año 2025 | 26.3 | 30.2 | 33.1 | 37.3 | 40.6 | 44.2 | 53.9 | 58.6 |
| En el año 2050 | 21.4 | 23.8 | 25.5 | 28.0 | 30.1 | 32.3 | 38.1 | 41.0 |
| En el año 2100 | 14.3 | 15.1 | 15.8 | 16.7 | 17.5 | 18.3 | 20.4 | 21.5 |
Aplicabilidad del método de los momentos L móviles
La representación lineal de ambos parámetros y sensiblemente mejor del parámetro de ubicación (u) es aceptable para el río Aberjona, EUA (Figura 4). En la estación Manjimup, Australia (Figura 6) la representación del parámetro de escala (a) puede ser aceptable, pero la relativa al de ubicación u no.
La calidad estadística mayor del ajuste con el método de los momentos L móviles se destaca numéricamente por la similitud que muestran los errores estándar de ajuste (EEA) de los modelos estacionario (GVE0) y no estacionario (GVE11). En el caso del río Aberjona, EUA, los EEA de la GVE estacionaria y no estacionaria fueron 1.556 y 2.136 m3·s-1; es decir, con orden de magnitud similar. En cambio, en la estación Manjimup, Australia, los EEA de ambos modelos (2.881 y 11.199 mm) fueron diferentes y bastante mayor el de la distribución GVE11, por lo cual, no es aceptable al grupo de datos de PMD.
Conclusiones
El método de los momentos L móviles (MLM) propuesto por Cunderlik y Burn (2003) y aplicado Mudersbach y Jensen (2010 a, b), para el ajuste de la distribución GVE11, con parámetros de ubicación y escala variables, lineales o exponenciales con la covariable tiempo, es un procedimiento práctico, recomendado para el análisis hidrológico de frecuencias de datos máximos anuales que presentan tendencia y variabilidad cambiante través de su registro, que debe ser amplio.
El uso de diferentes tamaños de la ventana móvil se sugiere en el procedimiento operativo del método de los MLM, para ajustar de acuerdo a cada uno la distribución GVE11, seleccionando la más conveniente al registro procesado a través del menor error estándar de ajuste.
La conveniencia estadística o bondad de ajuste del método de los MLM al registro no estacionario procesado, se juzga mediante la representatividad lineal o exponencial de las series cronológicas de los parámetros de ubicación, escala calculados y similitud numérica que tenga el error estándar de ajuste de las distribuciones GVE0 y GVE11.
Con dos aplicaciones numéricas se demuestra la sencillez del método de los MLM y con base en las predicciones, se destaca su importancia y utilidad, en los análisis probabilísticos de registros amplios de datos hidrológicos extremos que exhiben tendencia y variabilidad no constante.











 texto en
texto en 



