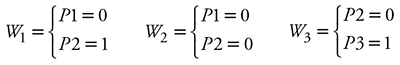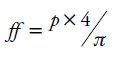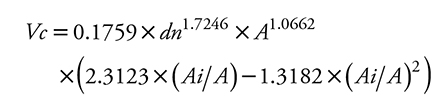Services on Demand
Journal
Article
Indicators
Related links
Share
Agrociencia
On-line version ISSN 2521-9766Print version ISSN 1405-3195
Agrociencia vol.51 n.5 Texcoco Jul./Aug. 2017
Natural Renewable Resources
Eucalyptus urophylla merchantable volume estimation with total volume and ratio models
1Postgrado en Ciencias Forestales, Colegio de Postgraduados. 56230. Carretera México-Texcoco, km. 36.5. Montecillo, Texcoco, Estado de México.
2Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias (INIFAP). 74060. Campo experimental San Martinito, Tlahuapan, Puebla, México. (tamarit.juan@inifap.gob.mx).
3Woods Hole Research Center. Gilman Ordway Campus. 149 Woods Hole Road. Falmouth, MA 02540. apeduzzi@whrc.org
The functional relationships between diameter at breast height (dn) and height (A) with the total volume (Vt) of a tree is essential for the technical management and exploitation of commercial forest plantations (PFC), along with the rate of different commercial heights (Ai) or minimum diameters (di) along the bole with the merchantable volume (Vc). Based on the hypothesis that with such mathematically-expressed relationships it is possible to accurately estimate Vt and Vc, the objective was to propose a tool to quantify the Vt and Vc in Eucalyptus urophylla PFCs from seed and clones in southeastern Mexico, by means of volume-ratio functions (r). Six Vt models -fitted and corrected for heteroscedasticity taking variance into consideration- and ten ratio models -correcting autocorrelation with an autoregressive structure- were evaluated using dasometric information from 175 clone trees measured in 2007 (P1), 93 in 2014 (P2), and 459 in 2007 (P3); the third group was grown from seeds. The Schumacher-Hall model -which includes dichotomous variables- showed that populations are statistically different. The best Vt models were: Schumacher-Hall for P1 and P3, and Spurr for P2. The best r models -which consider the diameter at different heights- were: Burkhart for P1 and P2, and Cao for P3. When bole height models are used, Zepeda’s was the most appropriate for the three populations. With these Vt and r models, each population’s Vc was determined at any given di or Ai, which accounted for more than 94 % of the variability. The slenderness ratio was 114, 122, and 118 cm cm-1 and the form factor was 0.45, 0.34, and 0.34 for P1, P2 and P3, respectively.
Key words: stem profile; taper; forest plantations; product distribution; Eucalyptus urophylla
Para el manejo técnico y aprovechamiento de plantaciones forestales comerciales (PFC), es fundamental el conocimiento de las relaciones funcionales entre el diámetro normal (dn) y la altura (A) con el volumen total (Vt) de un árbol, además de la proporción de distintas alturas comerciales (Ai) o diámetros mínimos (di) a lo largo del fuste con el volumen comercial (Vc). Con la hipótesis de que con tales relaciones expresadas matemáticamente es posible realizar estimaciones precisas de Vt y Vc, el objetivo fue proponer una herramienta para cuantificar el Vt y Vc en PFC de Eucalyptus urophylla procedentes de semilla y clones en el sureste mexicano a través de funciones de razón volumétrica (r). Con información dasométrica de 175 árboles de clones medidos en 2007 (P1), 93 en 2014 (P2) y 459 provenientes de semilla y medidos en 2007 (P3), se evaluaron seis modelos de Vt, ajustados y corregidos por heterocedasticidad ponderando la varianza, y diez de razón corrigiendo la autocorrelación con una estructura autoregresiva. El modelo de Schumacher-Hall con inclusión de variables dicotómicas demostró que las poblaciones son diferentes estadísticamente. Los mejores modelos de Vt fueron el de Schumacher-Hall para P1 y P3 y el de Spurr para P2; en los de r que consideran el diámetro a distintas alturas, el modelo de Burkhart fue el mejor para P1 y P2 y el de Cao para P3. Para los modelos que utilizan la altura en el fuste, el de Zepeda fue el adecuado para las tres poblaciones. Con estos modelos de Vt y r, por población se determinó el Vc a cualquier di o Ai establecidos, que explicaron más de 94 % de la variabilidad. El índice de esbeltez fue 114, 122 y 118 cm cm-1 y el factor de forma fue 0.45, 0.34 y 0.34 para P1, P2 y P3.
Palabras clave: Perfil fustal; ahusamiento; plantaciones forestales; distribución de productos; Eucalyptus urophylla
Introduction
Commercial forest plantations (PFC) are an option to achieve the reduction of the pressure over natural forests in Mexico (CONAFOR-COLPOS, 2012). In the last decade, PFC establishment has increased significantly (CONAFOR, 2014) and it has supplied timber to the industry (Rodríguez-Juárez et al., 2014). The Eucalyptus genus is one of the most frequently used sources of germplasm in PFC (Juárez-Palacios et al., 2013, CONAFOR, 2014) and it’s ranked in second place among the species established in Mexico between 2000 and 2014, with a surface of 32 452 ha (18.31 %) (CONAFOR, 2015).
Eucalyptus urophylla is the most frequently used species in tropical climates (CONAFOR, 2012) and it is planted worldwide due to its rapid growth (Rosa et al., 2011), its wide altitudinal range (0 to 1200 m), and its minimum edaphic establishment requirements (Nieto and Rodríguez, 2003). In addition, it can adapt to places with mean annual precipitation between 2000 and 3000 mm and mean annual temperature between 24 and 28 °C (Vieira and Bucsan, 1980).
The timber volume of the plantations is an indicator of the stand productive potential (Moret et al., 1998) and it can be divided in total volume (Vt) and merchantable volume (Vc) (Chauchard and Sbrancia, 2005). According to Prodan et al. (1997), there are three Vc estimation methodologies for individual trees: 1) to implement Vt functions with the restriction of a limit diameter or height, in which the portion of the remaining tree is omitted in the prediction (Gilabert and Paci, 2010), for example the free bole volume equations (Vtfl); 2) to adjust functions that describe the tree profile and, afterwards, to estimate the Vc at a defined diameter or a given height (Chauchard and Sbrancia, 2005), based on a taper function; 3) to implement the proportional ratio between a predetermined volume and the Vt for different tree types (Pece, 1994), using volume-ratio functions (frv).
The frv concept was introduced by Honner (1967), and developed by Burkhart (1977), Alder (1980), Cao et al. (1980), Van Deusen et al. (1981), and Parresol et al. (1987) provided some complementary variants. Their efficiency was discussed by Prodan et al. (1997) who pointed out that using this type of function enables the accurate calculation of the volume at any dimension of diameter or height defined in a simpler way, than fitting or using a taper model. In addition, Gilabert and Paci (2010) compared the results of this type of systems in two species, in Chile, with those of a taper function and pointed out the precision of the results and the simplicity to obtain them.
These percentage functions are a system of equations made up of a Vt equation and a volume ratio equation (r), which operate together in order to estimate the volume by product type per tree (Vc) (Chauchard and Sbrancia, 2005; Gilabert and Paci, 2010); r matches the volume ratio up to a utilization percentage or a non-merchantable diameter (Vi) and the Vt of the bole (Vi/Vt) (Trincado et al., 1997; Barrio et al., 2007; Barrios et al., 2014).
The models that include a frv are conceptually and mathematically simple, generate consistent results, can be used to estimate Vc in different diameter and height ranges without implementing complex numerical integration methods, and can be coupled with any type of Vt function (Chauchard and Sbrancia, 2005). In addition, based on independent variables, using a ratio function (r), the minimum diameter (di) or merchantable height (Ai) can be estimated by product type (Chauchard and Sbrancia, 2005).
The increasing demand for high-quality timber products and the changing standards of the sawmill industry have replaced the concept of total timber volume (Vt), as an indicator of PFC performance, with the concepts of product volume (Vp) or merchantable volume (Vc), which are important for the planning, management, and estimation of this type of forest masses. Therefore, based on the hypothesis that it is possible to carry out precise estimates of Vt and Vc, by means of the mathematical representation of the functional relations between the variables of a tree, the objective of this study was to propose a tool made up of a total volume model and a volume ratio model, in order to quantify total and merchantable volumes in commercial plantations in southeastern Mexico; these plantations use seed and two clonal sources of E. urophylla.
Materials and Methods
Study Area
The E. urophylla PFCs evaluated are located in the municipality of Huimanguillo, Tabasco, Mexico. The climate is hot and humid (Am): the mean annual temperature is 26 °C and the mean annual precipitation is 2500 mm. The soils belong to the Phaeozem group and the terrain is made up of low hills (INEGI, 2005).
Description of the sample and estimation of the total volume
The sample was taken from 727 E. urophylla trees, out of which: 175 belonged to clones measured in 2007 (P1), 93 to clones measured in 2014 (P2), and 459 to trees grown from seeds measured in 2007 (P3). The clones’ age (P1 and P2) fluctuated from one to seven years, while trees grown from seeds (P3) ranged from two to eleven years.
The sample trees were chosen according to: their morphological condition (to cover the greatest possible phenotypic variability within the plantations); the variability between their dn and A dimensions; and their age distribution. In each tree, the diameter at breast height (dn) and total height (A) were measured, and then they were felled and cut at different sections (di and Ai) along the bole, in order to measure their diameter and height; measures were taken 1 m distance from each other, starting with the diameter and height of the tree stump (dt and ht, respectively). The Newton and the cone formulas were used to find out the volume of each log (Vtroza) and each tip (Vpunta), respectively. The total volume (Vt) was calculated using Bailey’s overlapping bolts method (1995).
Interpopulation comparison of trees
In order to determine differences between clones’ populations (P1 and P2) with regard to trees grown from seeds (P3), the following hypotheses were tested on the dn and A variables. The analysis was performed contrasting P1 vs. P2, P1 vs. P3, and P2 vs. P3.
Null hypothesis (Ho): populations are the same.
Alternative hypothesis (Ha): populations are different.
In order to verify if trees of the three populations have differences in Vt -and on the assumption that two trees can have the same volume without necessarily presenting the same dn and A dimensions-, the Vt of the two types of clones and plantations grown from seed was fitted. In addition, to quantify the effect of each type of tree (either clone or grown from seeds), an indicator variable was inserted into the Schumacher-Hall (Draper and Smith, 1966) volume model (Table 1). Analyzes were carried out with SAS 9.2. (Institute Inc. Statistical Analysis System, 2008).
The indicator variables (Wn) were programmed in the Schumacher-Hall volume model (1), according to the contrast performed for each population.
The model is expressed as follows:
where a0, a1, and a2 are the regression parameters, whereas a 0c and a1c are the addition parameters for the different populations.
Estimation of slenderness ratio and form factor
The slenderness ratio (IE) was calculated to verify the trees’ degree of mechanical stability against winds or hurricanes, dividing the A average by the dn average, as reported by Arias (2004 and 2005) and Nájera and Hernández (2008). In order to verify if these are statistically different from each other, a one-factor ANOVA was carried out for the average IE between the populations at a p=0.05 level.
The form factor (ff) was calculated with the slope (p) of the bole volume and the combined variable (dn2 A), and, then, the factor was calculated with regard to a theoretical cylinder, using the following formula:
The adjusted total volume models are those of Da Cunhaa y Guimaraes (2009), Corral-Rivas and Návar-Cháidez (2009), Tschieder et al. (2011), and Casnati et al. (2014). Meanwhile, the standard type or double-entry types (Prodan et al., 1997) only differ in the form and number of parameters to be estimated (Table 1).
The best model was selected on the basis of the highest value of the determination coefficient, adjusted by the number of parameters (R2aj) and the lower values in the sum of squares error (SCE) and the root mean square error (RCME), as well as the best graphic distribution of residuals. With a model that complied with the above-described conditions, and, in order to avoid increasing the variance as the diameter increases (heteroscedasticity), weighted regression was used (Cailliez, 1980; Tschieder et al., 2011), with the following weight variables: 1/dn, 1/dn2, 1/dnA y 1/d 2 A. The bole volume estimates for the three populations were made with the corrected models.
Volumetric ratio models
The volumetric ratio (r) was calculated as the volume (at different heights and diameters) and the total volume (Vi/Vt) quotient. With this purpose, volume ratio models using dn, di, A, and Ai as independent variables were successfully utilized in other studies (Pece, 1994; Chauchard and Sbrancia, 2005; Barrio et al., 2007; Gilabert and Paci, 2010; Barrios et al., 2014) (Table 2).
Table 2 Volume ratio models used in E. urophylla PFC.
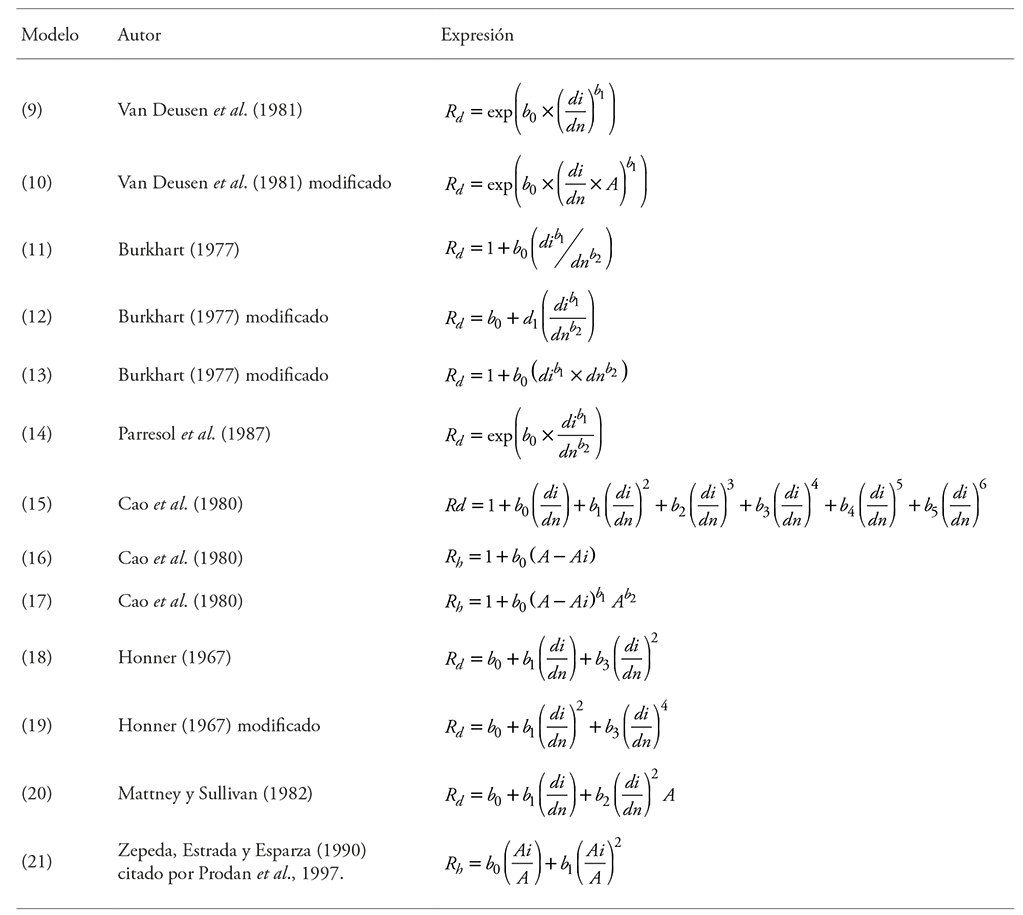
Rd is the volume ratio that uses the following as independent variables: the diameter at breast height (dn) and the diameter at different heights (di); Rh, which includes in the model the total height (A) and height at different sections along the bole (Ai); b0, b1, b2, b3, b5, and b 6 are the parameters to be estimated.
To fit these models, 1958, 2113 and 6060 pairs of di-Ai data were used for the P1, P2 and P3 populations, respectively. As a first step, the volume ratio models were adjusted without including the error term with the purpose of verifying the residuals trends and the value of the Durbin-Watson (DW) autocorrelation statistic, as Barrios et al. (2014) indicate.
In order to fit this type of models, the volume is calculated at different heights and diameters to obtain a volumetric ratio. Therefore, the longitudinal structure of the information used is inevitable; its measures are different along the bole and they have a close correlation, because they belong to the same tree. As a result of this, a continuous-time autoregressive (CAR) model was used to correct the error structure (Zimmerman and Nuñez-Antón, 2001), and the model is expressed as follows:
Where Yij is the vector of the dependent variable. Xij is the matrix of independent variables. B is the vector of the parameters to be estimated. eij is the j-th residual of i tree. Ik =1 for j>k and I k =0 for j≤k. ρk is the autoregressive parameter of the k order to be estimated. hij -h ij-k is the distance that separates the j-th measurement height from the j-th-k measurement height in each tree (hij >h ij-k). εij is the random error (Barrios et al., 2014). The number of lags applied in the CAR(X) model was established at the moment that the DW statistic was evaluated, which should have been close to 2 as mentioned by Verbeek (2004).
Model adjustment and evaluation criteria
The statistical fit of Vt and r models was carried out using the MODEL procedure in SAS 9.2 and the full information maximum likelihood (FIML) technique (Institute Inc. Statistical Analysis System, 2008).
The evaluation and selection of the best model was performed with the highest value of R2aj and the lowest values in the SCE and RCME, along with the tests of independence (DW) and normality of the frequency of the residuals (Da Cunha and Guimaraes, 2009). The homogeneity of variance was subject to a graphical evaluation (Tschieder et al., 2011), while the predictive capacity of the best models was evaluated estimating the absolute bias (Ē) and the aggregate deviation (DA %) for each population.
Determination of merchantable volume (Vc)
In order to estimate the merchantable volume at any point along the bole, a scale system consisting of the best Vt and r model was formed for each of the populations. With the tree’s Vt and applying the volumetric ratio model, the merchantable volume is the result of multiplying the two equations results (Chauchard and Sbrancia, 2005). The evaluation of the estimation accuracy was carried out with a linear trend chart of predicted against observed values (Pece, 1994).
Results and Discussion
Interpopulation comparison of Vt, dn and A in trees
The fitting of the Schumacher-Hall model was acceptable (Table 3) and the values of the parameters in the W n indicator variable were significant (p≤0.05), which confirms that the three populations have different dn and A averages, as well as different Vt averages, and that their growth rates are different. This difference between the 2007 and 2014 clones is the result of the reproduction selection of the latter, because it was made on the basis of their larger dn or A dimensions, without taking into account the Vt or the form factor.
Table 3 Estimated parameters and goodness of fit statistics of the Schumacher-Hall Vt model with indicator variables in the three populations of E. urophylla, in Huimanguillo, Tabasco, Mexico.
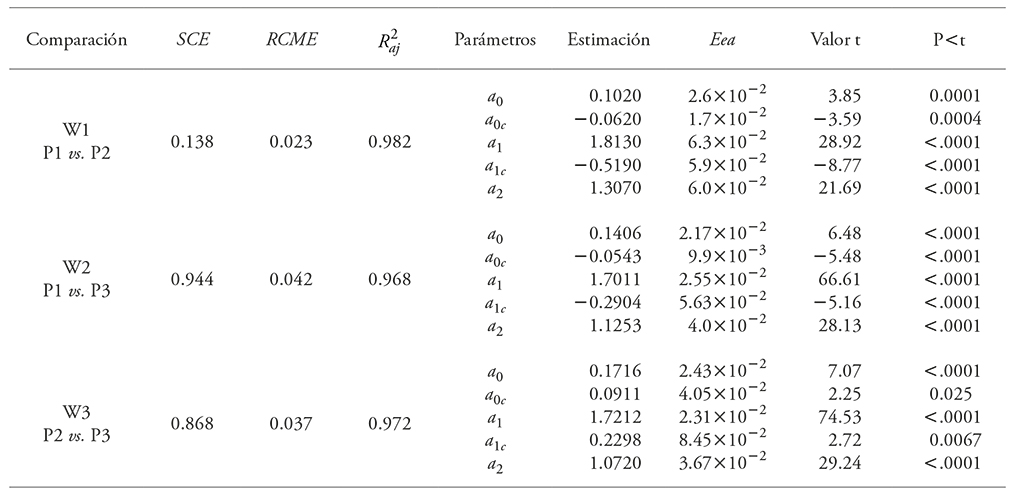
SCE: Squared sum of errors; RCME: Root mean square error; R2aj: Adjusted coefficient of determination; Eea: Approximate standard error; an: Parameters to be estimated.
Estimation of slenderness index, form factor, and total volume
Once it was identified that the three populations should be analyzed separately, IE was calculated. The mean values by population were 114, 122, and 118 cm cm-1, for P1, P2 and P3, respectively. The lower average IE value suggests that the clones measured in 2007 were selected for their growth in diameter, rather than for their growth in height, because it is more practical and simple to take only the diameter at breast height as a production indicator. In the ANOVA test, the minimum significant IE difference was 4.77; in addition, the means of the slenderness ratio between the populations were statistically different (P1=122.571, P2=112.168, and P3=93.804), because the error probability value was low (Pr>F=<0.0001).
These indexes are similar to those for fast-growing tropical species such as E. Nitens (IE=124) (Díaz et al., 2012), Hieronyma alchorneoides (IE=111), and Terminalia amazonia (IE=106) (Arias, 2005). However, because IE is higher than the 1:1 growth ratio between dn and A, the trees are assumed to be thin and strong thinning intensities must be applied with care (Arias, 2005; Díaz et al., 2012), due to the PFC’s susceptibility to the mechanical damages caused by winds (Wilson and Oliver, 2000).
With regard to ff, the shape of trees in the P2 and P3 populations was the same (conical type with a value of 0.34), while it was different in the P1 population (ff=0.45), which indicates that the shape of trees is more similar to a paraboloid.
As a result of the fit statistics of the best Vt models -determined by the higher R2aj values, the lower SCE and RCME values and the significance of the parameter value (p<t)-, the Schumacher-Hall model was best fitted to P1 and P3 data, and the Spurr model for P2 (Table 4).
Table 4 Estimated parameters and goodness of fit statistics of the Vt models for the three populations of E. urophylla, in Huimanguillo, Tabasco, Mexico.
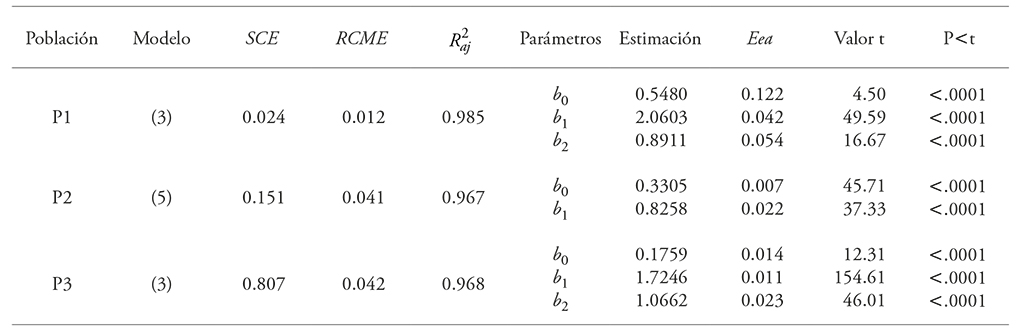
SCE: sum of squared errors; RCME: Root mean square error; R2aj: Adjusted coefficient of determination; Eea: Approximate standard error; bn: Parameters to be estimated.
In the three fittings, all the resulting parameters were significant (95 % confidence), and the Shapiro-Wilk normality test showed values higher than W=0.92 and a level of Pr<W=0.0001, whereas the residual plots showed a tendency towards a straight line in the form of a Gaussian bell curve, which indicates that the data are normal. However, in the variance homogeneity test, very marked trends were observed; therefore, heteroscedasticity problems were assumed, and the weighted variable with best corrective results was 1/dn2A, with which a homogenous distribution of residuals was obtained (Figure 1). The estimation of the parameters and the goodness of fit indicators of the bole volume equations for the P1, P2, and P3 populations are shown in Table 5.

Figure 1 Distribution of Vt residuals with respect to the diameter at breast height (dn) of the best fitted models, corrected by heteroscedasticity, for the P1, P2, and P3 plantations of E. urophylla, in Huimanguillo, Tabasco, Mexico.
Table 5 Estimated parameters and goodness of fit statistics of the Schumacher-Hall (P1 and P3) and Spurr (P2) models, corrected for heteroscedasticity, for the three populations of E. urophylla, in Huimanguillo, Tabasco, Mexico.
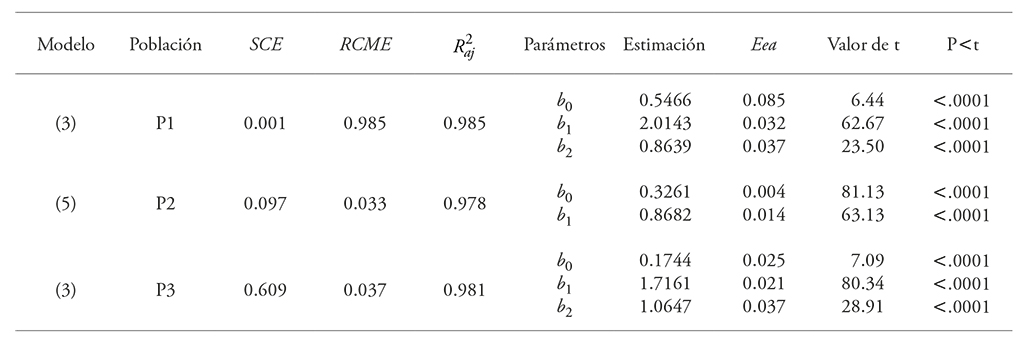
SCE: sum of squared errors; RCME: Root mean square error; R2aj: Adjusted coefficient of determination; Eea: Approximate standard error; bn: Parameters to be estimated.
In the estimates made with the corrected models, as well as their projections, the average IE was considered when calculating the height of each population. As it is observed, the selection of the vegetative material to produce the clones measured in 2014 was carried out taking the samples of highest dn and A, without considering the Vt, because the line that corresponds to this population is the lowest of the three and makes reference to the more slender trees (conical form) and have less volume than the 2007 clones and the trees grown from seeds (Figure 2).
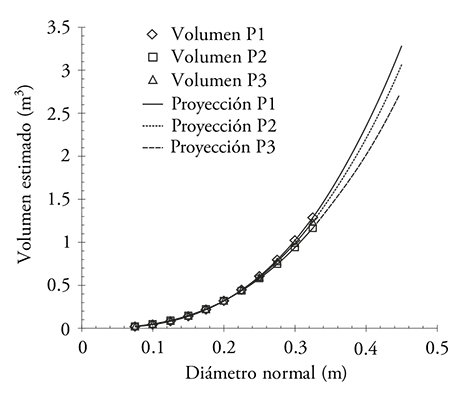
Figure 2 Estimation and projection of Vt with the Schumacher-Hall model for P1 and P3 and Spurr model for P2 of E. urophylla populations, in Huimanguillo, Tabasco, Mexico.
Taking as reference the 2007 clone plantations -which have more Vt than the rest-, it was observed that, up to the 0.30 diameter range -which on average is the maximum in the three populations-, the 2014 plantations have 3.60 % less Vt than those grown in 2007, and 1.47 % less than trees grown from seeds (Figure 2). Projections outside the sample up to 45 cm diameter indicate that the differences increase to 11.35 % and 4.72 % in the P2 and P3 populations, respectively, with regard to P1’s projected Vt.
Volumetric ratio models
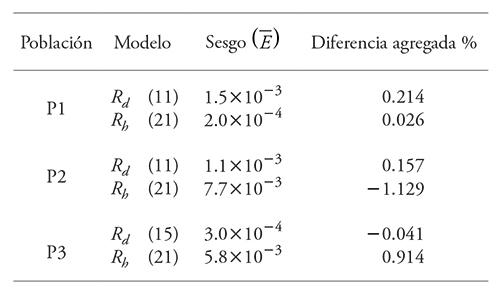
When the first fitting was made, the values of the parameters and the statistics obtained were relevant, but the residuals showed a trend towards heteroscedasticity, and the value of DW for P1 varied from 0.59 to 1.03, for P2 from 0.13 to 0.82, and for P3 from 0.44 to 1.09, which shows that the data are correlated. Therefore -after a graphical analysis of the autocorrelation function (ACF) was carried out in the three populations-, a auto-regressive structure of first, second, and third order was used to correct the autocorrelation of the errors (CAR (X)) and the one that had best results was selected (Table 5).
After the autocorrelation was corrected for the Rd model (11) of P2, we decided that this was the best one, based on Fuentes et al. proposal (2001a and 2001b) about the absence of correlation for values in this statistic that are higher and equal to 1 and the greater precision that this model generated with regard to the rest. The DW values demonstrate an autoregressive type CAR(1) serial correlation, due to the existence of logs with bole diameters at a given height, related to a similar or equal diameter to a different Ac (Pérez, 1996; 1998), and that -when another delay was applied to the errors and the DW value was improved- we observed that quality was lost in the fit, because no significant parameters were evident (i.e., R2aj lower or biased estimations with regard to the observed data).
In the three populations analyzed, one Rd -type and one Rh -type volume ratio models were selected in order to use either of these two variants to estimate Vc. This selection was based on the highest R2aj values, and the lowest SCE and RCME values, as reported by Trincado et al. (1997) and Barrio et al. (2007). The fit of best models had satisfactory results and all the parameter values were different than zero (p≤0.05) (Table 6).
Table 6 Estimated parameters and goodness of fit statistics of the volume ratio models that best fit each population in E. urophylla PFC, in Huimanguillo, Tabasco, Mexico.
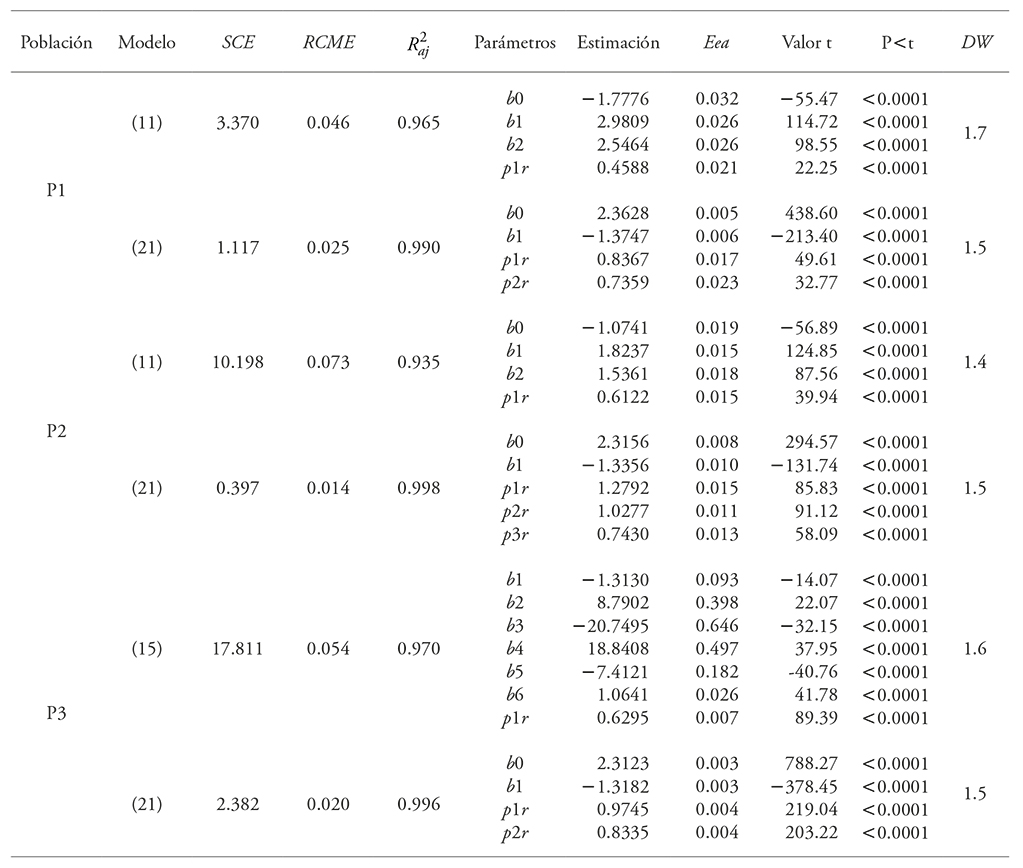
SCE: Sum of squared errors; RCME: Root mean square error; R2aj: Adjusted coefficient of determination; Eea: Approximate standard error; bn: Parameters to be estimated; p1r, p2r and p3r indicate the order and number of delays applied in the CAR (X) type model applied.
When the residuals’ distribution was verified (Figure 3) for the Rd models in the P1 and P3 populations, the results matched those mentioned by Barrios et al. (2014) for E. grandis, which has an homoscedastic distribution (a and c). However, there is a slight presence of heteroscedasticity in P2; but it does not affect the estimations made with this model, because when the volume ratio was calculated with better distribution models, the absolute error was lower in the selected model (b). In no case, the R h models show a trend (d, e, and f), which matches what Pece (1994) described when he used this type of model for E. pellita.

Figure 3 Residuals of the best volumetric ratio models for trees of the three E. urophylla populations evaluated in Huimanguillo, Tabasco, Mexico.
When the absolute bias (Ē) and the aggregate deviation (DA %) for each population were estimated -and with the purpose of verifying the precision of the estimations with the Rd y Rh models- we observed that their values were low for the three populations, and in no situation did DA without exceed 1.29 % (Table 7).
Estimation of the merchantable volume of trees
The fitted models allow us to find the volumetric accumulation ratio, as the total height is reached, starting from the tree stump height, as well as the relation between the total volume and the volume of a limited diameter or height. The expressions used to obtain the Vc of individual trees in each population consist of a Vt and r model; when multiplied, they will result in the Vc of any diameter or height of defined exploitation. The resulting equations are the following:
Vc equations for the P1 population.
Vc equations for the P2 population.
Vc equations for the P3 population.
When the Vc predictions obtained with the volume ratio method are subject to a graphic comparison with the accumulated volume, the result is close to a straight line (Figure 4); and, when a linear regression is applied to these data the use of the R d -type models shows -by the value of R2- that the sample estimation is higher than 94 %, while the use of Rh -type models has 96 % results. When the accuracy and absolute bias are verified, taking as reference the R 2 value and the difference in its approximation to the unit, the difference for the Rd models is 3.0, 5.4 and 5.5 % in the P1, P2 and P3 populations, respectively; while it is 1.1, 3.1, and 2.6 % in Rh models (Figure 4). The trend observed and the values of the fittings between the predicted and the observed values match those indicated in the studies carried out by Pece (1994) in Eucalyptus pellita, by Chauchard and Sbrancia, (2005) in P. radiata, and by Barrios et al. (2014) in E. grandis.
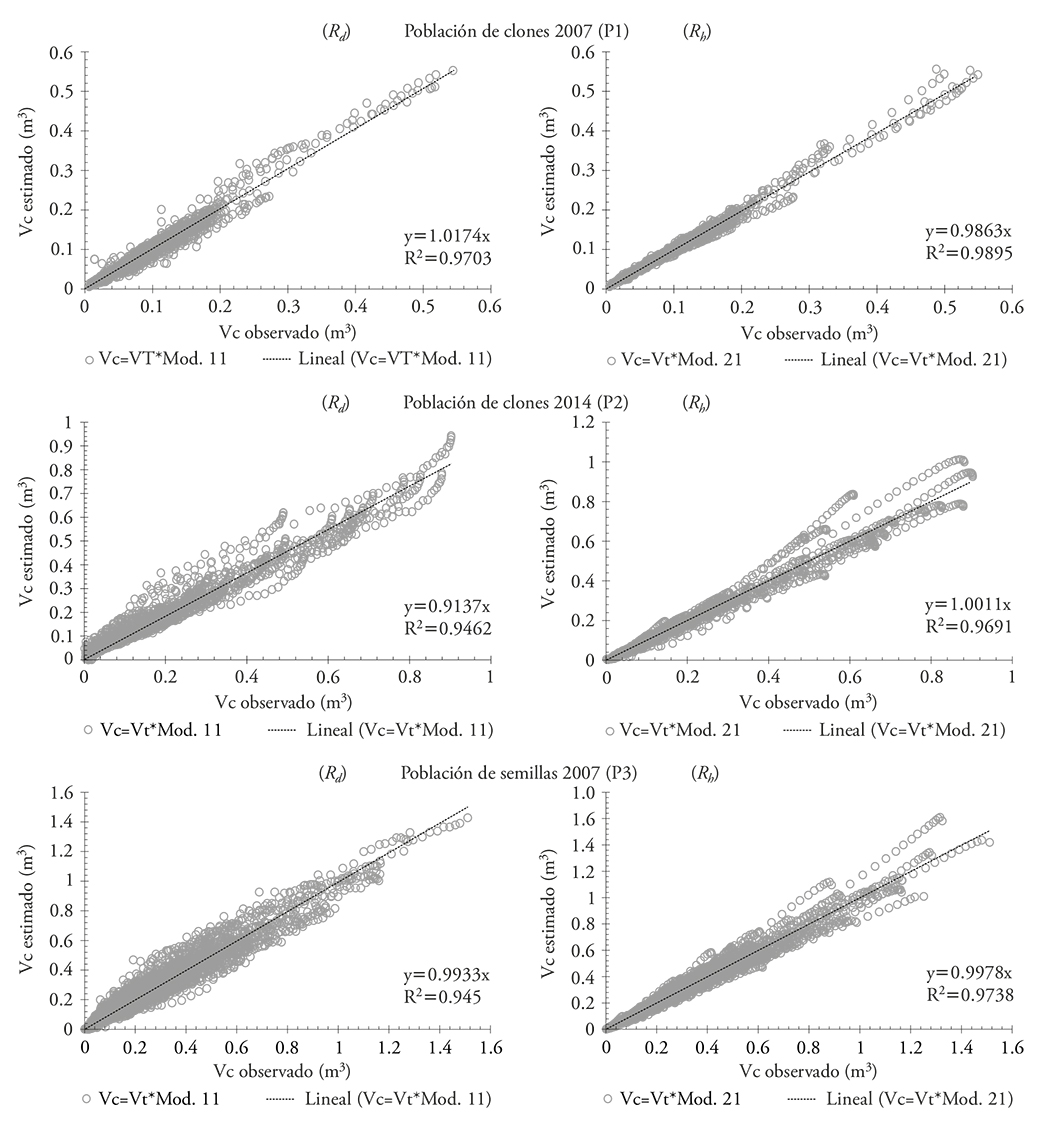
Figure 4 Estimated merchantable volume (Vc) vs. the predicted Vc for P1, P2, and P3 populations, using the models selected.
In order to estimate a merchantable diameter at a given commercial height for P1 and P2 populations, we solve for di from equation (11) and R d is replaced by Rh (equation 30), according to the procedure set forth by Trincado et al. (1997), using the parameters estimated for each model and replacing them in the resulting equation. If the inverse calculation was necessary (i.e., to estimate Ac for a specific diameter in the three populations), Ai would be solved from equation (21), and Rh would be replaced by Rd (equation 31).
For P3, in model 15 of Rd, di at any height is calculated by a numerical approximation with the Excel tool SOLVER, because when this variable is solved from the equation, the roots can be mathematically reduced until they disappear.
The models selected show consistency in the total and merchantable volume determination, their values do not crossover, and they enable a direct estimation of the bole diameter at an established height, or the bole height at a limit diameter. As a whole, these models are highly trustworthy and allow to carry out estimations of product distribution, to create tables of merchantable volumes for any useful diameter or height established by the sawmill industry or to calculate the economic valuation of plantations. Stock and operational harvest data are required to validate the models generated.
Conclusions
The functional relations between the tree’s dn and A variables are reliable in the estimation of total and merchantable volume. In addition, the adjustment of their mathematical expressions suggests that -if the owners or investors intend to maximize the volume to be obtained in Eucalyptus urophylla clone plantations- the selection of trees for clonal reproduction purposes should consider an analysis of the tree’s total volume (rather than the diameter at breast height and total height). Likewise, we observed statistically significant changes in the populations in a relatively short period (7 years); the reliability of the models used to estimate the potential timber harvest and the value of the forestry investment also underwent changes. Therefore, in this type of fast-growing plantations, these models must be updated at the same rate that the vegetative material used and the applied cultural practices are replaced
Literatura Citada
Alder, D., 1980. Estimación del volumen forestal y predicción del rendimiento con referencia especial a los trópicos. Vol. 22/2. Predicción del Rendimiento. Ed. FAO, Montes, 189 p. [ Links ]
Arias, D. 2004. Estudio de las relaciones altura-diámetro para seis especies maderables utilizadas en programas de reforestación en la zona sur de Costa Rica. Rev. For. Kurú 1: 1-11. [ Links ]
Arias, D . 2005. Morfometría del árbol en plantaciones forestales tropicales. Rev. For. Kurú 2: 2-11. [ Links ]
Barrio, M., H. Sixto, I. Cañellas, y F. González. 2007. Sistema de cubicación con clasificación de productos para plantaciones de Populus×euramericana (Dode) Guinier cv. ‘I-214’ en la meseta norte y centro de España. Inv. Agraria: Sistemas Recursos For. 16: 65-75. [ Links ]
Barrios, A., A. M. López, y V. Nieto. 2014. Predicción de volúmenes comerciales de Eucalyptus grandis a través de modelos de volumen total y de razón. Colombia For. 17: 137-149. [ Links ]
Bailey, R. L. 1995. Upper-stem volumes from stem-analysis data: An overlapping bolt method. Can. J. For. Res. 25: 170-173. [ Links ]
Burkhart, H. E. 1977. Cubic-foot volume of loblolly pine to any merchantable top limit. Southern J. App. For. 1: 7-9. [ Links ]
Cailliez, F. 1980. Estimación del volumen forestal y predicción del rendimiento con referencia especial a los trópicos: estimación del volumen. Vol. 22/1. Estudio FAO: Montes, Roma, Italia. 92 p. [ Links ]
Cao, Q., H. Burkhart, and T. Max. 1980. Evaluation of two methods for cubic volume prediction of loblolly pine to any merchantable limit. For. Sci. 26: 71-80. [ Links ]
Casnati, C., G. Mason E., R. Woollons, and F. Resquin. 2014. Volume and taper equations for P. tadea (L.) and E. grandis (Hill ex. Maiden). Agrociencia 18: 47-60. [ Links ]
Chauchard, L., y R. Sbrancia. 2005. Funciones de razón para la estimación de los volúmenes maderables de Pino radiata en el País Vasco. Inv. Agraria: Sistemas Recursos For . 14: 185-194. [ Links ]
CONAFOR (Comisión Nacional Forestal). 2012. Logros y perspectivas del desarrollo forestal en México 2007-2012. http://www.conafor.gob.mx/biblioteca/documentos/LOGROS_Y_PERSPECTIVAS_DEL_DESARROLLO_FORESTAL_EN_MEXICO.PDF (Consulta: diciembre, 2015). [ Links ]
CONAFOR (Comisión Nacional Forestal). 2014. México cuenta con 270 mil hectáreas de Plantaciones Forestales Comerciales. Boletín 77. http://www.conafor.gob.mx:8080/documentos/docs/7/5752M%C3%A9xico%20cuenta%20con%20270%20mil%20hect%C3%A1reas%20de%20%20Plantaciones%20Forestales%20Comerciales.pdf . (Consulta: diciembre 2015). [ Links ]
CONAFOR (Comisión Nacional Forestal). 2015. Principales especies maderables establecidas en PFC por año (2000 - 2014) y Principales especies maderables establecidas en PFC por Entidad Federativa (2000 - 2014). http://www.conafor.gob.mx/web/temas-forestales/plantaciones-forestales / (Consulta: diciembre 2015). [ Links ]
CONAFOR-COLPOS (Comisión Nacional Forestal-Colegio de Posgraduados). 2012. Situación Actual y Perspectivas de las Plantaciones Forestales Comerciales en México. http://www.conafor.gob.mx/web/temas-forestales/plantaciones-forestales/ (Consulta: enero 2017). [ Links ]
Corral-Rivas, S., y J. de J. Návar-Cháidez. 2009. Comparación de técnicas de estimación de volumen fustal total para cinco especies de pino de Durango, México. Rev. Chapingo Serie Ciencias For. Ambiente 15: 5-13. [ Links ]
Da Cunha, T., y C. A. Guimaraes F. 2009. Modelo de regresión para estimar el volumen total con corteza de árboles de Pinus tadea L. en el sur de Brasil. Rev. For. Kurú : 2-15. [ Links ]
Díaz B., S. M. Espinosa. L. Valenzuela, J. Cancino, y J. P. Lasserre. 2012. Efecto del raleo en el crecimiento y algunas propiedades de la madera de Eucalyptus nitens en una plantación de 15 años. Madera, Ciencia Tecnol. 14: 373-388. [ Links ]
Draper, N., R., and H. Smith. 1966. Applied Regression Analysis. John Wiley & Sons, New York. USA. 407 p. [ Links ]
Fuentes E., D., J. J. Troncoso, y C. A. Bonilla. 2001a. Operaciones forestales y concentración de sedimentos en cauces naturales I: Formulación de un modelo matemático. Bosque 22: 15-24. [ Links ]
Fuentes E., D., J. J. Troncoso, y C. A. Bonilla. 2001b. Operaciones forestales y concentración de sedimentos en cauces naturales II: Análisis de sensibilidad y comparación con otros modelos. Bosque 22: 25-27. [ Links ]
Gilabert, H., and C. Paci. 2010. An assessment of volume-ratio functions for Eucalyptus globulus and E. nitens in Chile. Ciencia Inv. Agraria 37: 5-15. [ Links ]
Honner, T. G. 1967. Standard volume tables and merchantable conversion factors for the commercial tree species of central and eastern Canada. Information Report FMR-X-5. Forest Management Research and Service Institute. 162 p. [ Links ]
INEGI (Instituto Nacional de Estadística y Geografía). 2005. Marco Geoestadístico Municipal 2005, v. 3.1. http://www3.inegi.org.mx/contenidos/app/mexicocifras/datos_geograficos/27/27008.pdf (Consulta: diciembre 2015). [ Links ]
Institute Inc. Statistical Analysis System. 2008. SAS/STAT 9.2 User’s Guide Second Edition. SAS Institute Inc. Raleigh, NC USA. (Consulta: diciembre, 2015). [ Links ]
Juárez-Palacios, J. C., J. A. Honorato-Salazar, L. Vázquez-Silva, y J. F. C. Parraguirre-Lezama. 2013. Patogenicidad de Crysoporthe cubensis en clones de Eucalyptus grandis y E. urophylla en el sureste de México. Madera y Bosques 19: 17-36. [ Links ]
Matney, T. G., and D. Sullivan A. 1982. Variable top volume and height predictors for slash pine trees. For. Sci . 22: 283-289 [ Links ]
Moret, A. Y., M. Jerez, y A. Mora. 1998. Determinación de ecuaciones de volumen para plantaciones de teca (Tectona grandis L.) en la unidad experimental de la reserva forestal Caparo, estado de Barinas-Venezuela. Rev. For. Venez. 42: 41-50 [ Links ]
Nájera, L., J. A., y E. Hernández H. 2008. Relaciones morfométricas de un boque coetáneo de la región del Salto, Durango. Ra-Ximhai 4: 69.81. [ Links ]
Nieto, V. M., y J. Rodríguez. 2003. Eucalyptus urophylla Dehnh. In: Vozzo, J.A. Manual de Semillas JA Árbol Tropical. Parte II. Especies descripciones. Washington, DC: USDA Forest Service. 473 p. [ Links ]
Parresol, B. R., J. E. Hotvedt, and Q. V. Cao. 1987. A volume and taper prediction system for bald cypress. Can. J. Forest Res. 17: 250-259. [ Links ]
Pece, R., M. 1994. Tabla de volumen comercial para Eucalyptus pellita utilizando el método de la razón volumétrica. Quebracho 2: 54-63. [ Links ]
Pérez, C. 1996. Econometría y Análisis Estadístico Multivariable con Statgraphics. Técnicas Avanzadas. Ed. Rama. Madrid, España, 745 p. [ Links ]
Pérez, C. 1998. Métodos Estadísticos con Statgraphics para Windows. Técnicas Básicas. Ed. Rama. Madrid, España, 705 p. [ Links ]
Prodan, M., R. Peters, F. Cox, y P. Real. 1997. Mensura Forestal. Serie Investigación y Educación de Desarrollo Sostenible. Instituto Interamericano de Cooperación para la Agricultura (IICA)/BMZ/GTZ. San José, Costa Rica. 561 p. [ Links ]
Trincado, G., K.Von Gadow, y V. Sandoval. 1997. Estimación de volumen comercial en latifoliadas. Bosque 18: 39-44. [ Links ]
Tschieder E. F., E. Fassola H., y M. García C. 2011. Ecuaciones de volumen total para Populus deltoides de plantaciones del Bajo Delta del Paraná. Rev. Inv. Agropec. 37: 172-179. [ Links ]
Rodríguez-Juárez M., I., A. Velázquez-Martínez, A. Gómez-Guerrero, A. Aldrete, y M. Domínguez-Domínguez. 2014. Fertilización con boro en plantaciones de Eucalyptus urophylla S. T. Blake en Tabasco. Rev. Chapingo : Serie Ciencias For. 20: 204-213. [ Links ]
Rosa, F.G., C. Morel P., R. Montanari., J.Motta S., G.Machado S., y E.Casarin Z. 2011. Variabilidade espacial de propriedades dendrométricas do eucalipto e de atributos físicos de um Latossolo Vermelho. Bragantia, Campinas 70: 439-446. [ Links ]
Van Deusen, P., A. Sullivan, and T. Matney. 1981. A prediction system for cubic foot volume of loblolly pine applicable through much of its range. Southern J. Appl. For. 5: 186-189. [ Links ]
Verbeek, M. 2004. A Guide to Modern Econometrics. Second edition. West Sussex: John Wiley & Sons. 429 p. [ Links ]
Vieira, F. S. y Bucsan, B. 1980. Ocurrencia natural de Eucalyptus urophylla en Indonesia. Silvicultura 3: 359-361. [ Links ]
Wilson, J. S., and C. Oliver. 2000. Stability and density management in Douglas-fir plantations. Can. J. Forrest Res. 30: 910-920. [ Links ]
Zimmerman, D., L., and V. Núñez-Antón. 2001. Parametric modelling of growth curve data: An overview (with discussion). Test 10: 1-73. [ Links ]
Received: February 2016; Accepted: February 2017











 text in
text in