Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Agrociencia
On-line version ISSN 2521-9766Print version ISSN 1405-3195
Agrociencia vol.50 n.1 Texcoco Jan./Feb. 2016
Water-Soils-Climate
Fitting of the GEV, GLO and GPA distributions with trimmed L moments (1, 1) in 21 annual flood records of the hydrological region no. 10 (Sinaloa), Mexico
1Facultad de Ingeniería de la Universidad Autónoma de San Luis Potosí. Genaro Codina Número 240. 78280 San Luis Potosí, San Luis Potosí. México. (campos_aranda@hotmail.com)
The hydrological dimensioning and security of all water use or control works depend on the flood design. The reliable estimation of those hydrologic magnitudes is related to the availability of the most accurate possible maximum annual discharge data and their representation, in a probability distribution function (PDF). The method of L moments, which are linear combinations of the order statistics, is one of the most accurate fitting procedures that allow to estimate the parameters of an PDF. Robust versions have been proposed for L moments, since they give no weight to the extreme values of the sample; such is the case of the trimmed L moments (1,1), which do not take into account the lowest nor the highest data. This study presents both fitting methods for the PDFs general extreme value (GEV), generalized logistic (GLO) and generalized Pareto (GPA), which are probability models with worldwide acceptance in the frequency analysis of hydrological extreme data. Using the standard error of fit (SEF) the contrast was performed for the application of the mentioned PDFs, to 21 records of annual floods available in the Hydrological Region No. 10 (Sinaloa, Mexico). The results indicated that the PDFs led to the lowest SEFs in three, seven, and eleven of the records processed. The method of adjustment by trimmed L moments (1,1) achieved a lower SEF in ten of the records processe. Therefore, its systematic use is recommended in the frequency analyses of extreme hydrological data.
Key words: L moments; trimmed L moments (1,1); GEV; GLO; and GPA distributions; Fitting Standard Error; diagnosis graphs
El dimensionamiento y seguridad hidrológica de todas las obras hidráulicas de aprovechamiento o control depende de las crecientes de diseño. La estimación confiable de esas magnitudes hidrológicas está asociada con la disponibilidad de datos de gastos máximos anuales y su representación, lo más exacta posible, en una función de distribución de probabilidades (FDP). El método de los momentos L, que son combinaciones lineales de los estadísticos de orden, es uno de los procedimientos de ajuste más exactos que permite la estimación de los parámetros de una FDP. Versiones robustas se han propuesto de los momentos L, al dar peso nulo a los valores extremos de la muestra; es el caso de los momentos L depurados (1,1) que no toman en cuenta el dato menor ni el mayor. En este estudio, se exponen ambos métodos de ajuste para las FDP general de valores extremos (GVE), logística generalizada (LOG) y Pareto generalizada (PAG), que son modelos probabilísticos con aceptación mundial en el análisis de frecuencia de datos hidrológicos extremos. Mediante el error estándar de ajuste (EEA) se realizó el contraste de la aplicación de las FDP citadas, a los 21 registros de crecientes anuales disponibles en la Región Hidrológica No. 10 (Sinaloa, México). Los resultados indicaron que las FDP condujeron a los EEA menores en tres, siete y once de los registros procesados. El método de ajuste por momentos L depurados (1,1) logró un EEA menor en diez de los registros procesados. Por lo tanto, se recomienda su aplicación sistemática en los análisis de frecuencia de datos hidrológicos extremos.
Palabras clave: momentos L; momentos L depurados (1,1); distribuciones GVE; LOG y PAG; error estándar de ajuste; gráficos de diagnóstico
Introduction
The infrastructure for water use and control, such as reservoirs, protection dikes, embankments and rectifications, bridges, and rainwater drainage, require in their stages of planning, design, operation and revision of the most accurate possible estimations of the flood designs. Based on these hydrological estimations, all these hydraulic works re dimensioned, and their security depends on them. The flood designs are predictions that relate to a reduced robability of exceedance. The most reliable method to obtain them is to represent the available data of maximum annual discharge or annual series of maximums with a probability function distribution (PDF), and from this, carry out the desired predictions (Deka and Borah, 2011; Ahmad et al., 2013). This procedure is known as the flood frequency analysis (FFA) and it consists of the following five stages (Campos-Aranda, 2014): 1) compilation of information and verifying its statistical quality, 2) selecting an PDF, 3) choosing a method for estimating its fitting parameters, 4) objective quantification of the fitting achieved with each PDF and estimation technique, and 5) selecting results.
The FFA helps carry out predictions whose yearly recurrence average intervals generally exceed severalfold the amplitude of the record available, and they are therefore extrapolations that involve errors. In order to minimize these errors, two different approaches are suggested. The first one consists of using increasingly flexible PDFs, which is why the two fitting parameter models were changed for those with three parameters, and even the four parameter Kappa and Wakeby or mixed functions with five fitting parameters were used. The second approach seeks the improved use of the available data, giving more importance to its higher values. Statistically, there is work with two new types of data series, known as partial duration series, and censored or truncated samples (Moisello, 2007).
The initial application of the partial duration series began in mid-20th century, and corresponds to the use of all the data higher than a threshold value, whereas the use of the censored series began in the 1980s. Since the 1990s, the technique for fitting a PDF using L moments, which are linear combinations of the order statistics of the data, has become a standard procedure due to its ease and to the consistency of its results. Besides, the trimmed L moments (1,1) were proposed, which give no value to the lowest and highest values in the series, which is why they are more robust, since they are more sensitive to scattered or extreme values (Shabri et al. 2011; Ahmad et al. 2013).
The aim of this study was to expose the theory of the L moments as a base to describe in detail the trimmed L moments (1,1). The equations that estimate the three fitting parameters were mentioned, with the methods of L moments and trimmed L moments (1,1), in the three PDFs: the general extreme value (GEV), generalized logistics (GLO), and generalized Pareto (GPA). Next, these three PDFs were fitted, using both methods, to the 21 available records of annual floods in Hydrological Region No. 10 (Sinaloa; Mexico), and based on the fitting standard error, the results were analyzed and the conclusions were drawn.
Materials and Methods
Population L Moments
Statistical moments are used to characterize a series of observed data or a PDF. The L moments and trimmed L moments were established as alternative procedures to conventional moments, since they have lower sampling variance and are more robust when there are disperse values. Like conventional moments, those of order one to four characterize the location, scale, asymmetry, and kurtosis (Hosking, 1990; Elamir and Seheult, 2003).
According to Karvanen (2006), the concept of L moments was created at the end of the 1960’s, with various isolated results on linear combinations of the order statistics, which culminated with the work by Greenwood et al. (1979). Hosking (1990) unified the theory of L moments and provided guides for their practical use, which have extended to the areas of hydrology, meteorology, and other disciplines of engineering.
moments are related to the expected values of the order statistics. Let X a random variable and Xj:n its order statistic, another random variable distributed as its j-th smallest element from a random sample with size n, extracted from the PDF of X. Also, let Q(u) the so-called quantile function, i.e., the reverse solution of the PDF equation, is then a function that is increased in the interval of uϵ[0,1]. The first four population L moments are (Hosking, 1990; Hosking y Wallis, 1997; Karvanen, 2006):
its general expression is:
where the second parenthesis is a quotient of factorials that defines the number of possible combinations of the m terms, taking q in each arrangement; its general expression is (Asquith, 2011):
By conventions 0! = 1 and the Gamma factorial function is Г(m+1)=m! The values expected of the order statistics of Equation 5 are estimated using the following expression (Hosking and Wallis, 1997; Kottegoda and Rosso, 2008; Asquith, 2011):
The above equation establishes the relation between the probability weighted moments by Greenwood et al. (1979) and the L moments. The quotients of L moments of asymmetry for r=3 and kurtosis for r=4 are:
Trimmed population L moments (1,1)
These moments, designated as “TL” for “Trimmed,” which means depurated, cut, or truncated, give no weight to extreme observations and are therefore robust generalizations of the L moments. Its population expressions are (Elamir and Seheult, 2003; Hosking, 2007):
its general expression is:
Trimmed L moments (1,1) of the sample
In a sample or series of data sized n, ordered progressively in such a way that X1:n≤X2:n≤...≤Xn:n, the estimation is not biased for l r (t) , because s=t, it will be (Elamir and Seheult, 2003; Hosking, 2007):
where l r (t) is a symmetrically pondered linear combination of a trimmed or truncated sample sized (n-2t) of values ordered X t+1:n , ..., X n-t:n . The quotients of trimmed L moments (1,1) of the sample shall be: t 3 (1,1) and t 4 (1,1), evaluated with Equation 8.
Fittings with the L moments of the distributions GEV, GLO, and GPA
Hosking and Wallis (1997) point out in their Table 5.1 that these three PDFs, when their shape parameters are negative (k<0), have ticker or more dense right tails than all other PDFs commonly used in the FFA. Due to this, they have gained acceptance in the frequency analysis of hydrological extreme data (El Adlouni et al. 2008). Such PDFs, when k=0, define functions with two fitting parameters known as Gumbel, logistic, and exponential. These PDFs also coincide in having a top limit when k>0.
Below are the formula F(x), and quantile function x(F) used for distributions GEV, GLO, and GPA, to estimate the predictions that relate to a certain probability of non-exceedance (F) and the equations that help estimate its three fitting parameters (k, a, u) for form, scale, and location, using the method of L moments.
GEV distribution (Stedinger et al., 1993): interval of x: u+a/k≤x<¥ si k<0; -¥<x<¥ si k=0; -¥<x≤u+a/k si k>0.
where y is the reduced variable:
where:
To evaluate the Gamma function, the Stirling formula (Davis, 1965) was used:
GLO distribution (Rao and Hamed, 2000): interval of x, identical to that of GVE.
where y equals Equations 16 and 17.
GPA distribution (Hosking and Wallis, 1997): interval of x:u≤x<∞ si k≤0;u≤x≤u+a/k si k>0
where y equals Equations 16 and 17.
Using the L moments and quotients displayed by Campos- Aranda (2014), the three fitting parameters of distributions GEV, GLO, and GPA were estimated using Equations 20 to 24, 28 to 30, and 34 to 36, respectively.
Fitting with trimmed L moments (1,1) of the distributions GEV, GLO, and GPA
For the GEV distribution, Deka and Borah (2011) developed an equation of t3 (1,1) based on the parameter of shape (k), whose reverse empirical expression is:
which is valid when -0.70≤k≤0.50 and has a determination coefficient close to one and a standard error of estimation of 0.00261. Equations 38 to 45 come from Deka and Borah (2011), Shabri et al. (2011), and Ahmad et al. (2013).
For the GLO distribution, we have:
and for GPA distribution:
Diagram of quotients for trimmed L moments (1,1)
Hosking and Wallis (1997) displayed the graphic and numeric relation (Equation 46) between the quotient of asymmetry L moments (t3) and that for kurtosis (t4) in five PDFs, which constitutes the diagram for L moment quotients. This graph can be used to select the best PDF, according to the values of the quotients for asymmetry and kurtosis L moments (t 3 and t 4) of the local sample, or to its regional pondered estimation. To obtain the diagram of quotients of trimmed L moments (1,1), a relation must be found between t3 (1,1) and t4 (1,1) for each PDF. Shabri et al. (2011) and Deka and Borah (2011) obtained such theoretical relations and represented them with fourth-degree polynomials for the distributions GVE and GPA, and second-degree polynomials for the GLO; the coefficients of Equation 46 of each polynomial are in Table 1.
Table 1 Coefficients of the polynomials of approximation of t4 (1,1) based on t3 (1,1) in the distributions GEV, GLO, and GPA according to Shabri et al. (2011).
| Coeficiente | GVE | LOG | PAG |
|---|---|---|---|
| a0 | 0.0576 | 0.0833 | - |
| a1 | 0.0943 | - | 0.1610 |
| a2 | 0.9183 | 0.9450 | 0.9904 |
| a3 | -0.0745 | - | -0.1295 |
| a4 | 0.0373 | - | 0.0184 |
Based on Equation 46 and its coefficients (Table 1), a diagram was created for trimmed L moments (1,1) for the distributions GEV, GLO, and GPA (Figure 1).
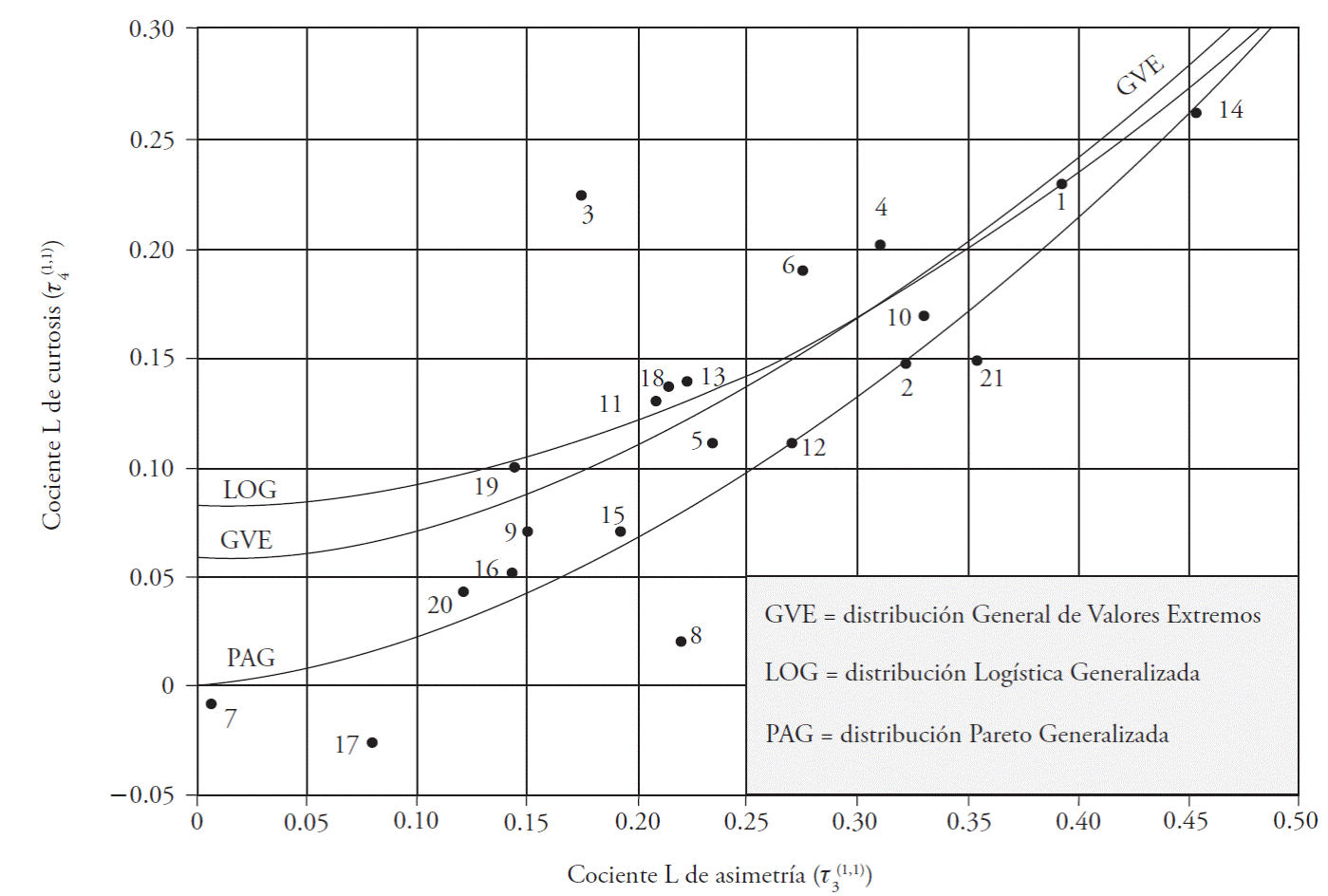
Figure 1 Diagram of quotients of trimmed L moments (1,1) of the GEV, GLO, and GPA distributions according to Shabri et al. (2013), and localization of flood records of the Hydrological Region No. 10, Sinaloa, México.
Standard Error of Fit
In the mid-1960’s, the standard error of fit (SEF) was established as a quantitative statistical indicator, since it evaluates the standard deviation of the differences between the values observed and estimates with the PDF tested. Its expression is as follows (Kite, 1977):
where n and np are the number of data in the samples and fitting parameter, in this case, 3; x
i
are the data arranged from lowest to greatest, and
In which m is the number of the order of data, with 1 for lowest, and n for the greatest.
Qualitative indicators of the fitting
The diagnostic diagrams for probability and for quantities have become popular (Coles, 2001; Wilks, 2011); the first uses in the horizontal axis the empirical probability estimated using Equation 48, and in the vertical axis, the probability that defines the PDF adjusted for all data available, ordered by magnitude (x 1≤x 2≤...≤x n ), which is estimated with Equations 15, 25, and 31 for distributions GEV, GLO, and GPA. The graph for quantities indicates, on the horizontal axis, the value of the data observed x 1≤x 2≤...≤x n , and on the vertical, the value estimated using the reverse solution of the PDF using Equations 18, 26, and 32 for functions GEV, GLO, and GPA, and the empirical probability, estimated using Equation 48. In sum, the coordinates for x and y of each diagram are (Coles, 2001):
Records processed of annual floods
Among the records for maximum annual discharge (m3·s-1) in the hydrometric stations of the Hydrological Region No. 10 (Sinaloa; Mexico), 21 have no runoff regime affected by reservoirs, drastic physical changes or both in their basins, and they display data of over twenty years in the BANDAS system (IMTA, 2002). The records in the hydrometric stations Huites and Guamuchil reach up to the year in which the construction of the respective reservoir affected its runoff. The data from the San Francisco station come from the Hydrological Bulletin No. 36 (SRH, 1975). Campos-Aranda (2014) verified the statistical quality of the records cited and presents the L quotients and moments, and displays a map with the location of the 21 hydrometric stations and their respective basins.
The shortest record have 19 years old and the longest, 56, with an average value of 33 years (Table 2). The fitted L moments (1,1) estimated using Equation 14 and the quotients of the moments calculated with Equation 8 are shown in Table 2.
Table 2 General characteristics, trimmed L moments and quotients (1,1) in 21 processed records from annual floods of Hydrological Region No. 10, Sinaloa, Mexico.
| No. | Estación hidrométrica | Área de cuenca (km 2 ) | Años de Registro (n) | L 1 (1,1) | L 2 (1,1) | L 3 (1,1) | L 4 (1,1) | T 3 (1,1) | T 4 (1,1) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Huites | 26 057 | 1942-1992 (51) | 2578.9710 | 643.4111 | 252.0877 | 148.1874 | 0.39180 | 0.23032 |
| 2 | San Francisco | 17 531 | 1941-1973 (33) | 1417.6250 | 334.2696 | 107.8858 | 49.8560 | 0.32275 | 0.14915 |
| 3 | Santa Cruz | 8919 | 1944-2002 (52) | 825.6472 | 191.9839 | 33.6176 | 43.3249 | 0.17511 | 0.22567 |
| 4 | Jaina | 8179 | 1942-1998 (56) | 789.5898 | 188.1527 | 58.7587 | 38.1695 | 0.31229 | 0.20286 |
| 5 | Palo Dulce | 6439 | 1958-1986 (21) | 818.7865 | 145.9885 | 34.1639 | 16.8504 | 0.23402 | 0.11542 |
| 6 | Ixpalino | 6166 | 1953-1999 (45) | 986.9792 | 186.6518 | 51.6721 | 35.2875 | 0.27684 | 0.18906 |
| 7 | La Huerta | 6149 | 1970-1999 (28) | 927.6062 | 197.2018 | 1.4513 | -1.7109 | 0.00736 | -0.00868 |
| 8 | Chinipas | 5098 | 1965-2002 (24) | 790.5296 | 159.9196 | 35.3124 | 3.2871 | 0.22081 | 0.02055 |
| 9 | Tamazula | 2241 | 1963-1999 (32) | 531.4827 | 76.7720 | 11.5965 | 5.4135 | 0.15105 | 0.07051 |
| 10 | Naranjo | 2064 | 1939-1984 (45) | 497.4072 | 157.6427 | 51.9003 | 26.6872 | 0.32923 | 0.16929 |
| 11 | Acatitán | 1884 | 1955-2002 (43) | 664.8182 | 195.9668 | 40.7487 | 25.5050 | 0.20794 | 0.13015 |
| 12 | Guamuchil | 1645 | 1940-1971 (32) | 577.3327 | 128.4394 | 34.5535 | 14.3540 | 0.26903 | 0.11176 |
| 13 | Choix | 1403 | 1956-2002 (38) | 290.3594 | 55.7844 | 12.2758 | 7.7038 | 0.22006 | 0.13810 |
| 14 | Badiraguat | 1018 | 1974-1999 (26) | 746.8054 | 239.1029 | 108.2557 | 62.7376 | 0.45276 | 0.26239 |
| 15 | El Quelite | 835 | 1961-2001 (33) | 408.9254 | 109.0321 | 20.8927 | 7.7677 | 0.19162 | 0.07124 |
| 16 | Zopilote | 666 | 1939-2001 (56) | 319.5128 | 89.7444 | 12.7530 | 4.5793 | 0.14210 | 0.05103 |
| 17 | Chico Ruiz | 391 | 1977-2002 (19) | 196.6518 | 52.4802 | 4.1569 | -1.4225 | 0.07921 | -0.02711 |
| 18 | El Bledal | 371 | 1938-1994 (56) | 241.8649 | 54.0593 | 11.5716 | 7.4244 | 0.21405 | 0.13734 |
| 19 | Pericos | 270 | 1961-1992 (30) | 229.4434 | 44.2758 | 6.3602 | 4.4083 | 0.14365 | 0.09956 |
| 20 | La Tina | 254 | 1960-1983 (24) | 75.5672 | 21.1883 | 2.5428 | 0.9513 | 0.12001 | 0.04490 |
| 21 | Bamícori | 223 | 1951-1983 (33) | 153.8719 | 45.9496 | 16.1642 | 6.8401 | 0.35178 | 0.14886 |
†quotients of trimmed L moments (1,1) from the sample.
¶Trimmed L moments (1,1) from the sample.
Results and Discussion
Selection of the most convenient PDF
Each record of floods was taken into the diagram of quotients of trimmed L moments (1,1) to obtain the most convenient PDF according to its L quotients for asymmetry and kurtosis (Table 2). Eleven records came close to the GPA function, seven to GLO, and three could be represented with the GEV distribution (Figure 1) (Table 3).
Table 3 Standard errors of fit (m3·s-1) obtained using the L moment and trimmed L moment (1,1) methods in 21 annual flood records of Hydrological Region No. 10, Sinaloa, Mexico.
| No. | Estación Hidrométrica | FDP según DCM ¶ | Error Estándar de Ajuste (EEA) † | |||||
|---|---|---|---|---|---|---|---|---|
| GVE | LOG | PAG | ||||||
| moL § | moLD § | moL | moLD | moL | moLD | |||
| 1 | Huites | LOG | 979 | 1101 | 1061 | 1099 | (834) | 875 |
| 2 | San Francisco | PAG | 377 | 232 | 419 | 249 | 302 | (200) |
| 3 | Santa Cruz | LOG | (406) | 599 | 421 | 564 | 409 | 691 |
| 4 | Jaina | GVE | 360 | 285 | 382 | (270) | 346 | 382 |
| 5 | Palo Dulce | GVE | 895 | 1063 | 922 | 1056 | (866) | 1095 |
| 6 | Ixpalino | LOG | 346 | 349 | 367 | (332) | 334 | 432 |
| 7 | La Huerta | PAG | 96 | 111 | 124 | 148 | (53) | 63 |
| 8 | Chinipas | PAG | 139 | 98 | 154 | [98] | 126 | 117 |
| 9 | Tamazula | GVE | (145) | 189 | 150 | 179 | 147 | 216 |
| 10 | Naranjo | PAG | 156 | 185 | 173 | 193 | (127) | 132 |
| 11 | Acatitán | LOG | 227 | 219 | 239 | (196) | 231 | 293 |
| 12 | Guamuchil | PAG | 235 | 210 | 247 | (202) | 225 | 245 |
| 13 | Choix | LOG | 105 | 126 | 110 | 120 | (101) | 149 |
| 14 | Badiraguato | PAG | 1077 | (791) | 1130 | 860 | 1037 | 872 |
| 15 | El Quelite | PAG | 87 | 71 | 98 | (69) | 74 | 93 |
| 16 | Zopilote | PAG | 48 | 62 | 61 | 81 | 25 | [25] |
| 17 | Chico Ruiz | PAG | 28 | 30 | 34 | 36 | (16) | 17 |
| 18 | El Bledal | LOG | 64 | 72 | 67 | (63) | 68 | 100 |
| 19 | Pericos | LOG | 29 | 26 | 33 | 26 | (24) | 33 |
| 20 | La Tina | PAG | 90 | 116 | 92 | 114 | (87) | 122 |
| 21 | Bamícori | PAG | 52 | 77 | 57 | 77 | (43) | 64 |
| Número de mínimos | 2 | 1 | 0 | 7 | 9 | 2 | ||
† In circular or rectangular parenthesis the minimum value of each station.
¶ Diagram of quotients of moments.
§ moL: fittings by L moments and moLD: fitting by trimmed L moments (1,1).
Standard error of fit
Using the reverse solutions of PDF (Equations 18, 26, and 32) the
With the trimmed L moments and quotients (1,1) (Table 2) and Equations 37 to 45, the three fitting parameters were obtained for functions GEV, GLO, and GPA. Afterwards, using their reverse solutions (Equations 18, 26, and 32) the values of
The lowest SEF of the six calculated was identified (Table 3, in circular parentheses) and equal values occurred in the records for Chinipas and Zopilote, selecting the adjustment that provided the largest predictions (Table 3, in rectangular parentheses). The minimum SEFs defined by distributions GEV, GLO, and GPA coincided with PDFs in eleven records (Figure 1): San Francisco, Ixpalino, La Huerta, Tamazula, Naranjo, Acatitán, Zopilote, Chico Ruiz, El Bledal, La Tina, and Bamícori.
The fitting of distributions GEV, GLO, and GPA, based on the trimmed L moments (1,1) (Table 3, last line) is an option that can systematically take down the SEF of the method of L moments, since this took place in ten records. The fitting using this method of the GLO function stands out, showing the lowest SEFs in seven records. The GPA distribution also stood out, which led to the highest fittings in eleven of the 21 records processed, nine of them with the method of L moments.
The final result must not guide to the exclusive application of such PDF, since the records for Santa Cruz, Palo Dulce, Tamazula, Choix, Badiraguato, and La Tina, with the other functions, gave minimum SEFs, nearly equal, and in several records, such as Ixpalino, Chinipas, Guamuchil, El Quelite, and Pericos, similar SEFs were obtained. Due to this, we recommend the application of under precepts to the distributions GEV and GLO.
Predictions obtained with the best fit
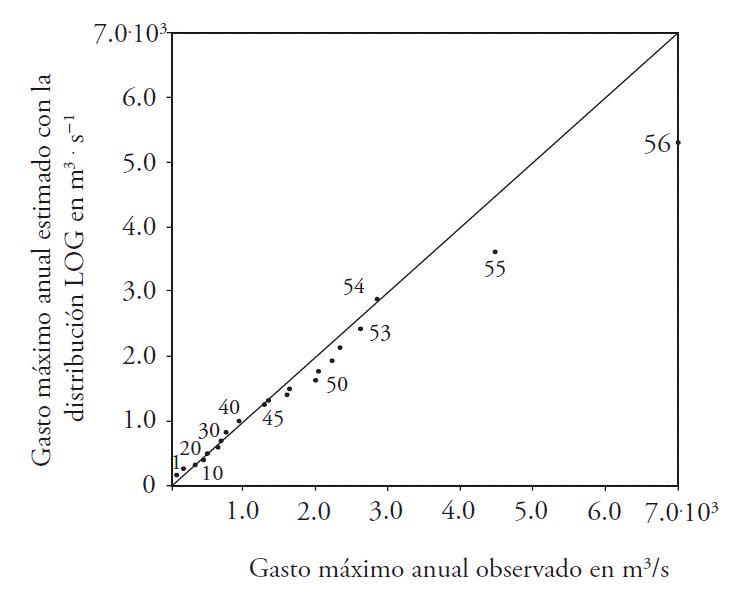
The predictions with each of the best adjustments in the records processed (third column in Table 4) were obtained according to the moLD results (Table 3). For the record of the Jaina hydrometric station, the method of L moments produced SEF of around 360 m3·s-1 with distributions GEV, GLO, and GPA; on the other hand, using the procedure of the trimmed L moments (1,1) this was reduced to 270 m3·s-1 with the function GLO. For this fitting in the respective diagnostic diagrams, the fitting reached was verified (Figures 2 and 3).
Table 4 Predictions (m3·s-1) obtained with the best fittings in 21 annual floods records of Hydrological Region No. 10, Sinaloa, Mexico.
| No. | Estación hidrométrica | FDP y MA † | Periodos de retorno en años | |||||
|---|---|---|---|---|---|---|---|---|
| 10 | 25 | 50 | 100 | 500 | 1000 | |||
| 1 | Huites | PAG-moL | 6710 | 10 581 | 14 355 | 19 056 | 34 919 | 44 673 |
| 2 | San Francisco | PAG-moLD | 3619 | 5771 | 7926 | 10 673 | 20 327 | 26 486 |
| 3 | Santa Cruz | GVE-moL | 2104 | 3258 | 4410 | 5883 | 11 118 | 14 497 |
| 4 | Jaina | LOG-moLD | 1990 | 3365 | 4967 | 7317 | 17 985 | 26 512 |
| 5 | Palo Dulce | PAG-moL | 1984 | 3386 | 4988 | 7282 | 17 183 | 24 745 |
| 6 | Ixpalino | LOG-moLD | 2141 | 3340 | 4665 | 6523 | 14 340 | 20 125 |
| 7 | La Huerta | PAG-moL | 1764 | 1935 | 2002 | 2041 | 2079 | 2085 |
| 8 | Chinipas | LOG-moLD | 1725 | 2553 | 3396 | 4495 | 8563 | 11 288 |
| 9 | Tamazula | GVE-moL | 1009 | 1390 | 1745 | 2173 | 3543 | 4349 |
| 10 | Naranjo | PAG-moL | 1449 | 2183 | 2815 | 3522 | 5506 | 6534 |
| 11 | Acatitán | LOG-moLD | 1793 | 2758 | 3720 | 4955 | 9396 | 12 297 |
| 12 | Guamuchil | LOG-moLD | 1365 | 2167 | 3042 | 4258 | 9262 | 12 944 |
| 13 | Choix | PAG-moL | 683 | 998 | 1275 | 1592 | 2514 | 3009 |
| 14 | Badiraguato | GVE-moLD | 2691 | 5510 | 9584 | 16776 | 62319 | 109 957 |
| 15 | El Quelite | LOG-moLD | 1025 | 1528 | 2017 | 2632 | 4765 | 6114 |
| 16 | Zopilote | PAG-moLD | 787 | 976 | 1087 | 1175 | 1319 | 1361 |
| 17 | Chico Ruiz | PAG-moL | 429 | 490 | 518 | 537 | 558 | 562 |
| 18 | El Bledal | LOG-moLD | 555 | 828 | 1102 | 1458 | 2752 | 3608 |
| 19 | Pericos | PAG-moL | 480 | 599 | 676 | 742 | 865 | 906 |
| 20 | La Tina | PAG-moL | 239 | 392 | 539 | 722 | 1335 | 1709 |
| 21 | Bamícori | PAG-moL | 418 | 610 | 769 | 942 | 1403 | 1630 |
† method of fitting: moL, by L and moments and moLD, by L moments and moLD, by trimmed L moments (1,1).
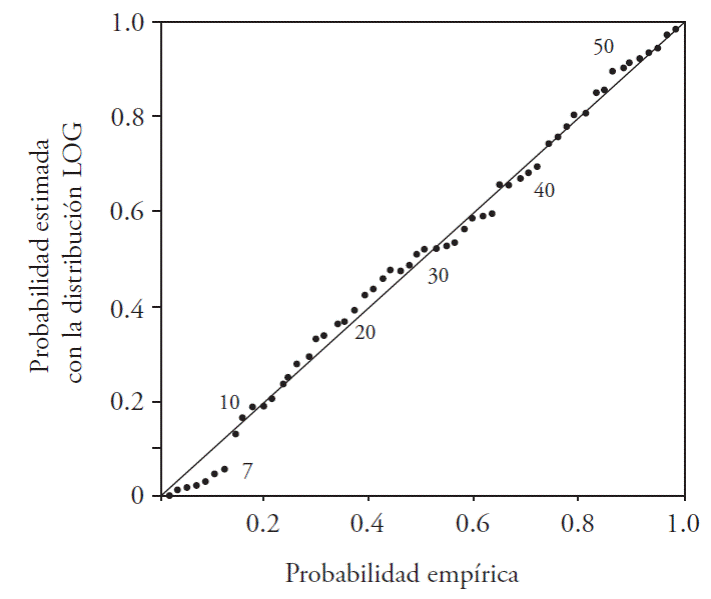
Figure 2 Diagram of probability for the record of annual floods in the Jaina hydrometric station, with a fit ting distribution GLO (SEF=270 m3·s-1).
Conclusions
The motivation to represent the maximum annual discharge data with an PDF consisted in permitting to carry out reliable predictions or estimations of the design floods, which depends on the accuracy of the fitting achieved. Therefore, SEF is the basic selection element.
The results of the contrast of the distributions GEV, GLO, and GPA, in 21 annual flood records of Hydrological Region No. 10 (Sinaloa, Mexico), along with the methods of fitting L moments and trimmed L moments (1,1), highlight the convenience of systematically applying the distribution GPA, since it led to the lower SEFs in eleven of the series processed. With the function GLO the lowest SEFs are obtained in seven records and with the GEV distribution in three.
The use of the method of trimmed L moments (1,1) to achieve better fittings of the three distributions applied, helps suggest its systematic application in the analyses of frequency of floods, since it reduces the SEF in half of the records processed. The fitting of the distribution GLO with this procedure stood out, since it also obtains lower SEFs in seven records.
Literatura Citada
Ahmad, U. N., A. Shabri and Z. A. Zakaria. 2013. An analysis of annual maximum streamflows in Terengganu, Malaysia using TL-moments approach. Theor. Appl. Climatol. 111: 649-663. [ Links ]
Asquith, W. H. 2011. Order Statistics. In: Distributional Analysis with L-moment Statistics using the R Environment for Statistical Computing. Author edition (ISBN-13: 9781463508418). Texas, U.S.A. pp: 47-59. [ Links ]
Benson, M. A. 1962. Plotting positions and economics of engineering planning. J. Hydraulics Div. 88: 57-71. [ Links ]
Campos-Aranda, D. F. 2014. Análisis regional de frecuencia de crecientes en la Región Hidrológica No. 10 (Sinaloa), México. 2: contraste de predicciones locales y regionales. Agrociencia 48: 255-270. [ Links ]
Coles, S. 2001. Model diagnostics. In: An introduction to Statistical Modeling of Extreme Values. Springer-Verlag London Limited. London, England. pp: 36-44. [ Links ]
Davis, P. J. 1965. Gamma function and related functions. In: Abramowitz M. and I. Stegun (ed). Handbook of Mathematical Functions. Dover Publications. New York, U.S.A. pp: 253-296. [ Links ]
Deka, S. and M. Borah. 2011. Statistical analysis of flood peak data of North Brahmaputra region of India based on the methods of TL-moment. Theor. Appl. Climatol. 104: 111-122. [ Links ]
El Adlouni, S., B. Bobée and T. B. M. J. Ouarda. 2008. On the tails of extreme event distributions in hydrology. J. Hydrol. 355: 16-33. [ Links ]
Elamir, E. A. H. and A. H. Seheult. 2003. Trimmed L-moments. Computational Stat. & Data Analysis 43: 299-314. [ Links ]
Greenwood, J. A., J. M. Landwehr, N. C. Matalas and J. R. Wallis. 1979. Probability weighted moments: Definition and relation to parameters of several distributions expressible in inverse form. W. Res. Research 15: 1049-1054. [ Links ]
Hosking, J. R. M. 1990. L-moments: analysis and estimation of distributions using linear combinations of order statistics. J. R. Stat. Soc. B. 52: 105-124. [ Links ]
Hosking, J. R. M. 2007. Some theory and practical uses of trimmed L-moments. J. Stat. Plann. Inference 137: 3024-3039. [ Links ]
Hosking, J. R. M. and J. R. Wallis. 1997. Regional Frequency Analysis. An Approach Based on L-moments. Cambridge University Press. Cambridge, England. 224 p. [ Links ]
IMTA (Instituto Mexicano de Tecnología del Agua). 2002. Banco Nacional de Datos de Aguas Superficiales (BANDAS). 8 CD’s. Comisión Nacional del Agua-Secretaría de Medio Ambiente y Recursos Naturales-IMTA. Jiutepec, Morelos. [ Links ]
Karvanen, J. 2006. Estimation of quantile mixtures via L-moments and trimmed L-moments. Comp. Stat. Data Anal. 51: 947-959. [ Links ]
Kite, G. W. 1997. Comparison of frequency distributions. In: Frequency and Risk Analyses in Hydrology. Water Resources Publications. Fort Collins, Colorado, U.S.A. pp: 156-168. [ Links ]
Kottegoda, N. T. and R. Rosso. 2008. Random variables and their properties. In: Applied Statistics for Civil and Environmental Engineers. Blackwell Publishing. Chichester, United Kingdom. pp: 83-164. [ Links ]
Moisello, U. 2007. On the use of partial probability weighted moments in the analysis of hydrological extremes. Hydrol. Proc. 21: 1265-1279. [ Links ]
Rao, A. R. and K. H. Hamed. 2000. The Logistic Distribution. In: Flood Frequency Analysis. CRC Press. Boca Raton, Florida, U.S.A. pp. 291-321. [ Links ]
SRH (Secretaría de Recursos Hidráulicos). 1975. Boletín Hidrológico No. 36. Tomos I y VI. Región Hidrológica No. 10 (Sinaloa). Dirección de Hidrología. México, D. F. [ Links ]
Shabri, A. B., Z. M. Daud and N. M. Ariff. 2011. Regional analysis of annual maximum rainfall using TL-moments method. Theor. Appl. Climatol. 104: 561-570. [ Links ]
Stedinger, J. R., R. M. Vogel and E. Foufoula-Georgiou. 1993. Frequency analysis of extreme events. In: Maidment, D. R. (ed). Handbook of Hydrology. McGraw-Hill, Inc. New York, U.S.A. pp: 18.1-18.66. [ Links ]
Wilks, D. S. 2011. Qualitative assessments of the goodness fit. In: Statistical Methods in the Atmospheric Sciences. Academic Press (Elsevier). San Diego, U.S.A. Third edition. pp: 112-116. [ Links ]
Received: May 01, 2015; Accepted: December 01, 2015











 text in
text in