Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Agrociencia
On-line version ISSN 2521-9766Print version ISSN 1405-3195
Agrociencia vol.49 n.3 Texcoco Apr./May. 2015
Recursos naturales renovables
Partición de la biomasa aérea en tres especies arbóreas tropicales
Aboveground biomass allocation in three tropical tree species
Martín Aquino-Ramírez1, Alejandro Velázquez-Martínez1*, Juan F. Castellanos-Bolaños2, Héctor De los Santos-Posadas1, Jorge D. Etchevers-Barra3
1 Postgrado en Ciencias Forestales. *Autor responsable. (alejvela@colpos.mx).
2 INIFAP-CIRPAS-Campo Experimental Valles Centrales de Oaxaca. Melchor Ocampo No. 7. 68200. Santo Domingo Barrio Bajo, Villa de Etla, Oaxaca.
3 Postgrado Edafología, Campus Montecillo, Colegio de Postgraduados. Carretera México-Texcoco km 36.5. 56230. Montecillo, Texcoco, Estado de México.
Recibido: junio, 2014.
Aprobado: marzo, 2015.
Resumen
El conocimiento de los almacenes de carbono en bosques es fundamental para generar inventarios de este elemento cercanos a la realidad. Para ello es necesario tener estimaciones de la biomasa de los árboles. Las ecuaciones alométricas permiten estimar la biomasa y su distribución en ecosistemas forestales. El objetivo del presente estudio fue desarrollar ecuaciones para estimar la biomasa aérea total y de los componentes estructurales, en árboles de la región fisiográfica de la Sierra Madre del Sur en el municipio de Pluma Hidalgo, Oaxaca, México. Las especies seleccionadas por su abundancia relativa fueron Cupania dentata DC., Alchornea latifolia Sw. e Inga punctata Willd. Las especies se agruparon mediante una prueba de adicionalidad en un modelo de regresión, constituyendo dos grupos. En los modelos ajustados para la estimación de la biomasa aérea total; las variables predictoras fueron el diámetro normal y la altura total del árbol. Además se incluyeron variables indicadoras para definir el efecto del grupo dentro del modelo. Los modelos se ajustaron por medio de regresión lineal y no lineal, y los valores del coeficiente de determinación ajustado fueron altos (R2Adj > 0.98). Esto mostró diferencias en la cantidad de biomasa aérea total entre grupos, situación atribuida a la densidad específica de la madera y a la morfología de los árboles. La biomasa en los componentes estructurales del árbol (tocón, fuste, corteza, ramas, y hojas) se estimó con un sistema de ecuaciones con factores de partición mediante regresión SUR (Seemingly Unrelated Regressions) para ajustar los parámetros de la regresión. En las tres especies, la mayor acumulación de biomasa se concentró principalmente en las ramas, seguida por el fuste, la corteza, el tocón y las hojas.
Palabras clave: Árboles tropicales, variable indicadora, ecuaciones alométricas, Cupania dentata, Alchornea latifolia, Inga punctata.
Abstract
Knowledge of forest carbon stores is fundamental to generating inventories that approximate real C stores. For these inventories, it necessary to have estimations of tree biomass. Allometric equations are tools for estimating biomass and its distribution in forest ecosystems. The objective of this study was to develop equations to estimate total above-ground biomass and the biomass of structural components of trees in the physiographic region of the Sierra Madre del Sur, in the municipality of Pluma Hidalgo, Oaxaca, Mexico. The species selected for their relative abundance were Cupania dentata DC., Alchornea latifolia Sw. and Inga punctata Willd. These species were grouped using an additionality test; a regression model was used resulting in two groups. In the models fit for estimation of total above-ground biomass, the predicting variables were diameter at breast height and total tree height. Indicator variables were also included to define the effect of the group within the model. Models were fit by linear and non-linear regression, which resulted in high values of the adjusted coefficient of determination (R2Adj > 0.98). This showed differences in the quantity of total aerial biomass between groups, a situation that was attributed to the specific density of the wood and to tree morphology. Biomass in the structural components of the tree (stump, stem, bark, branches and leaves) was estimated with a system of equations based on partition factors using SUR (Seemingly Unrelated Regressions) to fit the regression parameters. In the three species, the greatest accumulation of biomass was concentrated mainly in the branches, followed by the stem, bark, stump and leaves.
Key words: Tropical trees, indicator variable, allometric equations, Cupania dentata, Alchornea latifolia, Inga punctata.
Introducción
En la mayoría de los bosques neotropicales de México se desconocen los reservorios y el potencial de almacenamiento de biomasa. Así, es indispensable realizar estimaciones exactas y precisas para entender la función de esos bosques en el ciclo global de carbono. La estimación de la biomasa y su integración en los componentes estructurales del árbol, es muy importante en los estudios de productividad, ciclo de nutrientes, flujos de energía, almacenes y captura de carbono (Pompa-García y Yerena-Yamallel, 2014), disturbios naturales, antropógenicos (Parresol, 1999; Bi et al., 2004; Návar, 2009), en el monitoreo de la salud del bosque y el manejo forestal sustentable (Brandeis et al., 2006).
Gran parte de la incertidumbre en las estimaciones de la cantidad y la variación espacial de la biomasa en los bosques se debe a la falta de ecuaciones alométricas (Djomo et al., 2010). Por tanto, el desarrollo de ecuaciones específicas para especies o grupos de especies para condiciones locales o del sitio (Basuki et al., 2009) es importante para mejorar la precisión en la estimación no destructiva de la biomasa en la vegetación arbórea (Kuyah et al., 2012). Las relaciones alométricas con frecuencia incorporan variables dasométricas, como el diámetro normal y la altura total del árbol, como variables predictoras (Rutishauser et al., 2013), porque presentan una correlación alta con la biomasa y son fáciles de medir directamente en campo.
Los estudios para generar ecuaciones de las especies nativas del trópico mexicano son escasos (Acosta et al., 2002; Douterlungne et al., 2013), aunque muchas de estas especies se usan en programas de plantaciones forestales comerciales y de restauración, y en sistemas agroforestales. En estudios para generar ecuaciones alométricas y estimar biomasa en el bosque tropical seco en la península de Yucatán (Cairns et al., 2003) y en Sinaloa (Návar, 2009), en el bosque tropical húmedo en Oaxaca (Acosta et al., 2002) y en Chiapas (Douterlungne et al., 2013), y en plantaciones comerciales de hule (Rojo et al., 2005; Monroy y Navar, 2004) se ajustaron modelos lineales y no lineales. Las variables predictoras fueron diámetro normal, altura total, diámetro de la base, área basal y gravedad especifica de la madera.
En nuestro estudio se consideraron tres especies del bosque tropical subperennifolio y se usan como sombra de plantaciones de café (Pennington y Sarukhán, 2005). Además, Cupania dentata DC., Alchornea latifolia Sw. e Inga punctata Willd. son especies localmente consideradas como multipropósito (Ventura-Aquino et al., 2008), y destaca el uso como leña, construcción, ornamental, restauración, medicinal y comestible (Pennington y Sarukhán, 2005; Luna-José y Rendón-Aguilar, 2008). Por tanto, estas especies no comerciales son un potencial de almacenamiento de carbono en los sistemas agroforestales de café y en la vegetación natural de la región, que deben ser cuantificadas.
Los objetivos de este estudio fueron: 1) desarrollar modelos alométricos para estimar la cantidad de biomasa aérea total en C. dentata, A. latifolia e I. punctata, especies arbóreas nativas de la Sierra Sur de Oaxaca, usando variables indicadoras; y 2) desarrollar un sistema para identificar la distribución de la biomasa en los distintos componentes del árbol. La hipótesis fue que las características de morfología del árbol y la densidad de la madera en la acumulación de biomasa, son similares en las tres especies y se pueden estimar con un mismo modelo.
Materiales y Métodos
Área de estudio
El estudio se realizó en la finca La Cabaña, municipio de Pluma Hidalgo, Oaxaca, en una superficie aproximada de 300 ha, ubicadas entre 15° 56' 13" N, 96° 24' 09" O y 15° 55' 12" N, 96° 23' 51.83" O, con una altitud de 700 a 1200 m. El clima es semicálido húmedo con abundantes lluvias en verano (ACm), temperatura de 18 a 26 °C y precipitación de 1500 a 3500 mm (INEGI, 2005). La zona está en la región fisiográfica de la Sierra Sur de Oaxaca con una geomorfología de sierra baja compleja; las rocas son metamórfica gneis del Jurásico, con un tipo de suelo Phaeozem (INEGI, 2009). En la zona de estudio las especies arbóreas son: A. latifolia Sw., I. punctata Willd., C. dentata DC., Ficus sp., Clethra sp., Inga paterno Harms, Pterocarpus acapulcensis Rose, Homalium trichostemon S.F. Blake, Saurauia serrata DC, Cecropia obtusifolia Bertol., Diphysa robinioides Benth., Lonchocarpus guatemalensis Benth., Abutilon purpusii Standl., Calycophyllum candidissimum (Vahl) DC., Cupania glabra Sw. y Bursera simaruba (L.) Sarg., las cuales tienen abundancia relativa mayor en la vegetación natural (Acosta, 1997). Para este estudio se seleccionaron las tres primeras especies para desarrollar ecuaciones alométricas, por ser las más abundantes y con mayor uso por los productores agroforestales de café de la región.
Muestreo destructivo de árboles
Para el estudio se derribaron 48 árboles: 17 C. dentata, 17 A. latifolia y 14 I. punctata. La metodología para estimar la biomasa aérea fue similar a la propuesta por Hitchcock y McDonnell (1979). Los árboles se cortaron a ras de suelo y separados en cinco componentes estructurales: tocón, fuste, corteza de fuste, ramas y hojas. Antes del derribo se midió el diámetro normal (Dn) con cinta diamétrica a una altura de 1.30 m sobre el nivel del suelo. A esta altura perpendicularmente, se tomó una muestra de madera (viruta) con un taladro Pressler (Haglöf Sweden) (5 mm diámetro) para determinar la densidad específica de la madera (ρ). Después del derribo se midió la altura total del árbol (H) con cinta métrica.
El fuste fue seccionado en trozas de 1 m de longitud para obtener el peso verde. Cada componente del árbol se pesó in situ por separado para obtener su peso verde con una báscula digital (TECNOCOR modelo IPEN) de 100 kg, con una precisión de ±0.5 kg. El peso seco de cada componente se obtuvo mediante la relación peso seco: peso fresco, para lo cual se obtuvieron submuestras de madera en secciones transversales (rodajas) de fuste aproximado de 4 a 6 cm de grosor. Las primeras dos rodajas se obtuvieron a una altura de 0.30 y 1.30 m sobre el nivel suelo y después, en la parte superior de cada troza donde el diámetro fue mayor, separando la corteza de cada una de ellas. Además, se dividió la copa en dos secciones de manera horizontal (alta y baja) y se recolectaron al azar dos muestras en cada una de ellas y cuatro muestras de 0.5 kg de hojas de la misma forma. Todas las submuestras se pesaron de inmediato para evitar pérdidas de humedad, se colocaron en bolsas de papel con sus respectivas etiquetas, se transportaron y se pusieron 96 h en una estufa de secado de madera (Nyle modelo L500) a 70 °C o hasta lograr un peso constante. El peso verde y el peso seco de las submuestras pequeñas se obtuvieron en una báscula electrónica (TECNOCOR modelo COR-30) con una precisión de ±5 g. La relación peso seco: peso fresco promedio se usó para obtener la biomasa (peso seco) en el tocón, las ramas y las hojas; para el fuste y la corteza, dicha relación se obtuvo de cada submuestra de las trozas.
La biomasa total aérea (Bt) de cada árbol (kg) fue la suma de la biomasa de cada componente:

Determinación de la densidad específica de la madera
La densidad específica de la madera (ρ) en las virutas se obtuvo por la relación del peso seco con el volumen verde (g cm-3), y el volumen verde por el método de desplazamiento de agua. El peso seco se obtuvo colocando las muestras en una estufa de secado por 48 h o hasta a alcanzar un peso constante, a 75 °C. Los valores medios de la densidad específica de la madera en las tres especies se compararon con la prueba de Tukey HSD (p≤0.05).
Comparación de grupos de especies
La biomasa total de las tres especies se analizó de manera conjunta para conocer la posibilidad de agruparlas como una sola especie o grupos de especies, y determinar su contribución relativa en una sola ecuación. Para ello se desarrolló una prueba de adicionalidad simple con un análisis de regresión lineal incorporando variables indicadoras (dummy) (Draper y Smith, 1981; Montgomery y Peck, 1982). El modelo fue:

A éste se incorporó el factor especie como una variable indicadora de la siguiente forma:

donde Bt es la biomasa área total del árbol (kg), Dn es el diámetro normal (cm), H es la altura total (m), Z1 y Z2 son las variables indicadoras, α0, β0 son los parámetros de regresión, α1, α2, β1, β2 los parámetros de regresión debidos a la adicionalidad, y ε el error aleatorio. Cupania dentata se consideró como la especie base en el modelo por presentar el mayor número de observaciones del total de los árboles derribados. Para agrupar a las especies como un solo grupo o grupos de especies, se consideró la homogeneidad de interceptos y de pendientes  .
.
Ajuste de los modelos de regresión
Una vez agrupadas las especies se ajustaron los modelos alométricos con procedimientos de regresión. Tres modelos (Cuadro 1) que expresan la Bt como una función del diámetro normal y la altura del árbol fueron seleccionados para estimar la biomasa aérea total (Brown et al., 1997; Parresol, 1999, 2001):

Los tres modelos incluyen a las variables indicadoras que definen el efecto del grupo de especies. Para comparar estos modelos y seleccionar el mejor, se consideró el coeficiente de determinación ajustado  , que expresa la variabilidad explicada por el modelo tomando en cuenta el número de parámetros, la raíz de los cuadrados medios del error (RMSE), que define la precisión de las estimaciones, el coeficiente de variación en porcentaje (CV) que explica la variabilidad relativa respecto a la respuesta media, así como el error relativo promedio porcentual
, que expresa la variabilidad explicada por el modelo tomando en cuenta el número de parámetros, la raíz de los cuadrados medios del error (RMSE), que define la precisión de las estimaciones, el coeficiente de variación en porcentaje (CV) que explica la variabilidad relativa respecto a la respuesta media, así como el error relativo promedio porcentual 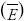 y el sesgo promedio
y el sesgo promedio  , que permiten evaluar a posteriori el comportamiento del modelo (Chave et al., 2005; Basuki et al., 2009). Estos estadísticos se calcularon así:
, que permiten evaluar a posteriori el comportamiento del modelo (Chave et al., 2005; Basuki et al., 2009). Estos estadísticos se calcularon así:

donde  es la biomasa total del árbol observado, predicho y medio respectivamente; n es el número de observaciones; y p es el número de parámetros del modelo.
es la biomasa total del árbol observado, predicho y medio respectivamente; n es el número de observaciones; y p es el número de parámetros del modelo.
Partición de la biomasa individual del árbol
La distribución de la biomasa en los componentes estructurales del árbol se ajustó como una función directa de la Bt y un factor de partición (F ) expresado como:

El cual permitió derivar el siguiente sistema de ecuaciones, con las siguientes funciones:

La propiedad de aditividad se cumple en el sistema de ecuaciones descrito, ya que la suma de las predicciones de biomasa en cada componente estructural es igual a la predicción de la biomasa aérea total del árbol (Parresol, 1999, 2001; Carvalho y Parresol, 2003; Brandeis et al., 2006).
Ajuste de los modelos de regresión
Los parámetros de regresión en los modelos de partición de biomasa fueron estimados con el método SUR (Seemingly Unrelated Regressions), por suponer una correlación entre las ecuaciones individuales de los componentes. Así se reduce la varianza en el sistema y por tanto hay un mejor ajuste que aumente la sensibilidad de las pruebas de hipótesis. La aditividad en el sistema se garantizó al definir restricciones para el modelo con el desarrollo de contrastes de los coeficientes de regresión (Parresol, 1999). El procedimiento MODEL de SAS/ETS® (SAS Institute Inc., 2004) se usó para ajustar los modelos.
Resultados y Discusión
Biomasa aérea y densidad específica
El Dn de los árboles derribados tuvo un intervalo de 3.3 a 54.7 cm, H de 6.9 a 27.2 m y biomasa promedio por árbol de 260.2, 190.2 y 144.7 kg para A. latifolia, C. dentata e I. punctata (Cuadro 2). Las ramas fue el componente estructural con un gran aumento en la proporción de biomasa al aumentar el Dn. La densidad específica de la madera en A. latifolia, C. dentata e I. punctata presentó valores promedio de 0.30±0.04, 0.46±0.04 y 0.48±0.05 g cm-3. La primera especie tuvo densidad baja (0.201-0.40 g cm-3) según la clasificación de la densidad específica, y la tabla FITECMA (Sotomayor, 2008); las otras dos especies tuvieron densidad media (0.401-0.60 g cm-3).
Otros estudios reportan resultados similares de la densidad específica de la madera de A. latifolia con otras metodologías (Fuentes, 1998; Tamarit y Fuentes, 2003) y para C. dentata (Tamarit y López, 2007). Sin embargo, el valor promedio de I. punctata fue inferior a 0.63±0.10 g cm-3 al reportado por Segura et al. (2006). Esta diferencia puede deberse a las prácticas de manejo en el sistema agroforestal de café con esta especie en la zona de estudio, similares a las de San Ramón, Nicaragua (Segura et al., 2006).
De acuerdo con la prueba de Tukey HSD, no hubo diferencia significativa (p=0.25) en la densidad específica promedio de C. dentata e I. punctata, pero A. latifolia fue estadísticamente diferente (p≤0.0001) a las anteriores (Figura 1).

Grupos de especies
Los resultados obtenidos en la prueba de adicionalidad (Cuadro 3) indican que las especies C. dentata e I. punctata pueden agruparse como una sola especie (Grupo 1), es decir, no hubo diferencias significativas entre interceptos (α0= α2, p=0.658), ni entre pendientes (β0= β2, p=0.724), por lo cual el efecto de la variable indicadora Z no fue significativo. Al contrario, en la misma prueba hubo diferencias estadísticas entre C. dentata y A. latifolia, ya que la adicionalidad en los parámetros de la pendiente fue significativa (β0≠ β1, p≤0.0001), aunque no hubo diferencias entre interceptos (α0= α1, p=0.302); por tanto, la especie A. latifolia conformó por si sola al Grupo 2. De la misma manera, los resultados de la comparación de la densidad específica de la madera entre especies, indicaron esta misma tendencia de agrupamiento. El valor positivo y negativo de los parámetros de adicionalidad β1 y β2 (Cuadro 3), correspondiente al efecto de las especies, indicaron mayor biomasa aérea por árbol en C. dentata e I. punctata que para A. latifolia, dado el mismo diámetro y altura; estas diferencias fueron estadísticamente significativas.
El uso de variables indicadoras en un modelo lineal tiene la ventaja de realizar pruebas de hipótesis directamente con el método de la suma extra de cuadrados (Montgomery et al., 2005) y comparar los parámetros de los modelos de estimación de biomasa debidos al efecto de la especie. Lo anterior permitiría agrupar especies con características morfológicas similares simplificando la complejidad de los modelos.
Modelos de biomasa
Los modelos ajustados para la estimación de la Bt en los dos grupos (Cuadro 4) presentaron valores altos en el coeficiente de determinación ajustado  . Por esta razón, la variación explicada por el modelo es mayor al incluir, además del Dn, la H o una combinación (Dn2H); es decir, la precisión en la estimación de la biomasa mejora significativamente. Resultados similares fueron obtenidos al estimar biomasa en árboles tropicales (Nogueira et al., 2008; Feldpausch et al., 2012).
. Por esta razón, la variación explicada por el modelo es mayor al incluir, además del Dn, la H o una combinación (Dn2H); es decir, la precisión en la estimación de la biomasa mejora significativamente. Resultados similares fueron obtenidos al estimar biomasa en árboles tropicales (Nogueira et al., 2008; Feldpausch et al., 2012).
Los dos grupos de especies tuvieron diferencias estadísticas, por lo que los modelos generales (Cuadro 1) tendieron a reducirse y el efecto de la variable indicadora Z fue significativo (Cuadro 5). De acuerdo con los valores menores de RMSE, CV,  y comportamiento mejor, se seleccionó el modelo 3 de la forma Schumacher y Hall (Figura 2), aunque el
y comportamiento mejor, se seleccionó el modelo 3 de la forma Schumacher y Hall (Figura 2), aunque el  fue ligeramente mayor que en el modelo 1; y los estadísticos de ajuste de los modelos 1 y 2 pueden considerarse satisfactorios. Los coeficientes de regresión en los modelos fueron altamente significativos, excepto α0 el del modelo 1 (Cuadro 5).
fue ligeramente mayor que en el modelo 1; y los estadísticos de ajuste de los modelos 1 y 2 pueden considerarse satisfactorios. Los coeficientes de regresión en los modelos fueron altamente significativos, excepto α0 el del modelo 1 (Cuadro 5).

El modelo seleccionado con variables indicadoras fue equivalente a tener dos modelos específicos para cada grupo (Figura 2), los cuales fueron estadísticamente diferentes. Las diferencias en los pesos secos se atribuyen al efecto de la densidad de la madera (Kuyah et al., 2012; Fayolle et al., 2013) y a la arquitectura del árbol (Basuki et al., 2009). El ajuste de un modelo con variables indicadoras da mayor robustez al modelo que el ajuste individual. Además, el desarrollo de ecuaciones específicas para especies locales es importante para mejorar la precisión en la estimación de biomasa, porque las condiciones ambientales o estructurales influyen en la alometría del árbol, diámetro: altura, en la misma manera que la variación originada por la localización geográfica (Feldpausch et al., 2011; Fayolle et al., 2013).
En los tres modelos, los valores mayores de error relativo corresponderon a los árboles menores a 20 cm de diámetro. Parte de esta variación en la biomasa puede deberse a que en estas categorías diamétricas los árboles crecen bajo una competencia fuerte por la luz con los árboles vecinos (Návar, 2009).
Partición de biomasa
El sistema de ecuaciones de partición de biomasa en cada especie cumple la propiedad de aditividad; así se logra una consistencia lógica entre las funciones de biomasa de los componentes (Bi et al., 2004; Brandeis et al., 2006). Por tanto, la suma de las predicciones de los componentes estructurales (tocón, fuste, corteza, ramas y hojas) es igual a la predicción total del árbol (Parresol, 1999, 2001; Carvalho y Parresol, 2003; Brandeis, 2006), porque la Bt es multiplicada por un factor de partición.
En todas las ecuaciones de partición de biomasa (Cuadro 6) se incorporó el efecto de las variables indicadoras. Por tanto, es necesario sumar o restar el efecto de dichas variables sobre los parámetros de regresión para conocer la predicción de biomasa en algún componente estructural específico del árbol (Figura 3). Los valores del coeficiente de determinación ajustado en cada modelo fueron altos  , excepto para la corteza
, excepto para la corteza 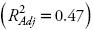 .
.
La distribución de biomasa entre los componentes fue notablemente variable debido al tamaño del árbol. Cupania dentata tuvo en promedio la mayor cantidad de biomasa en las ramas (51.64 %) y el fuste (40.69 %), le siguió la corteza (5.59 %), el tocón (4.12 %) y hojas (2.68 %). En A. latifolia las ramas y el fuste tuvieron más biomasa (44.07 % y 38.53 %), les siguió la corteza (8.17 %), las hojas (6.51 %) y el tocón (2.70 %). En I. punctata también las ramas y el fuste presentaron la cantidad mayor de biomasa (55.73 y 33.65 %), y les siguieron el tocón, las hojas y la corteza (3.77, 3.53 y 3.29 %).
La variación de la partición de biomasa (Figura 4) se puede atribuir a la competencia por luz entre los árboles; ramas pequeñas y menor cantidad de hojas se presentan en las especies con una posición dominante, y en árboles que crecen en espacios abiertos se registra la cantidad mayor de biomasa en ramas y hojas (Návar, 2009). Las ecuaciones propuestas para la biomasa total y su partición en este estudio, se deben usar dentro del intervalo de los datos obtenidos para su construcción.

Conclusiones
La ecuación alométrica generada para estimar la Bt en las tres especies tropicales estudiadas incluye variables indicadoras, de uso práctico y de aplicabilidad fácil en la zona de estudio, ya que sus variables predictoras son sólo el diámetro normal y la altura total. El sistema de ecuaciones de partición de biomasa propuesto permite garantizar estimaciones precisas porque cumple con la propiedad de aditividad.
La diferencia estadística en la biomasa aérea entre grupos de especies se atribuye a la densidad específica de la madera y a la morfología del árbol. La densidad específica de la madera puede ser considerada en los métodos no destructivos para estimar la Bt.
En C. dentata, A. latifolia e I. punctata las ramas son el componente estructural del árbol que acumula más biomasa, seguidas por el fuste, la corteza, el tocón y las hojas.
Agradecimientos
Este estudio fue financiando por la Fundación Produce Oaxaca A.C. a través del proyecto "Almacenamiento de carbono y conservación de la biodiversidad vegetal en el área de Pluma Hidalgo-Loxicha, Oaxaca". Agradecimientos especiales a todas las personas de la finca La Cabaña por los esfuerzos dedicados, así como a los revisores que hicieron posible la elaboración de este trabajo.
Literatura Citada
Acosta C., S. 1997. Afinidades fitogeográficas del bosque mesófilo de montaña de la zona de Pluma Hidalgo, Oaxaca, México. Polibotánica 6: 25-39. [ Links ]
Acosta M., M., J. J. Vargas H., A. Velázquez M. y J. D. Etchevers B. 2002. Estimación de la biomasa aérea mediante el uso de relaciones alométricas en seis especies arbóreas en Oaxaca, México. Agrociencia 36: 725-736. [ Links ]
Basuki T., M., P. E. van Laake, A. K. Skidmore, and Y. A. Hussin. 2009. Allometric equations for estimating the above-ground biomass in tropical lowland Dipterocarp forests. For. Ecol. Manage. 257: 1684-1694. [ Links ]
Bi, H., J. Turner, and M. J. Lambert. 2004. Additive biomass equations for native eucalypt forest trees of temperate Australia. Trees 18: 467-479. [ Links ]
Brandeis, T. J., M. Delaney, B. R. Parresol, and L. Royer. 2006. Development of equations for predicting Puerto Rican subtropical dry forest biomass and volume. For. Ecol. Manage. 233: 133-142. [ Links ]
Brown, S. 1997. Estimating biomass and biomass change of tropical forests: A primer. FAO. For. Pap. 134. Rome 55 p. [ Links ]
Cairns, M. A., I. Olmsted, J. Granados, and J. Argaez. 2003. Composition and aboveground tree biomass of a dry semi-evergreen forest on Mexico's Yucatan Peninsula. For. Ecol. Manage. 186: 125-132. [ Links ]
Carvalho, J. P., and B. R. Parresol. 2003. Additivity in tree biomass components of Pyrenean oak (Quercus pyrenaica Willd.). For. Ecol. Manage. 179: 269-276. [ Links ]
Chave, J., C. Andalo, S. Brown, M. A. Cairns, J. Q. Chambers, D. Eamus, H. Fölster, F. Fromard, N. Higuchi, T. Kira, J. P. Lescure, B. W. Nelson, H. Ogawa, H. Puig, B. Riéra, and T. Yamakura. 2005. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 145: 87-99. [ Links ]
Djomo, A. N., A. Ibrahima, J. Saborowski, and G. Gravenhorst. 2010. Allometric equations for biomass estimations in Cameroon and pan moist tropical equations including biomass data from Africa. For. Ecol. Manage. 260: 1873-1885. [ Links ]
Douterlungne, D., A. M. Herrera G., B. G. Ferguson, I. Siddique, y L. Soto P. 2013. Ecuaciones alométricas para estimar biomasa y carbono de cuatro especies leñosas neotropicales con potencial para la restauración. Agrociencia 47: 385-397. [ Links ]
Draper, N. R., and H. Smith. 1981. Applied Regression Analisys. 2da. ed. John Wiley & Sons. New York. 709 p. [ Links ]
Fayolle, A., J. L. Doucet, J. F. Gillet, N. Bourland, and P. Lejeune. 2013. Tree allometry in Central Africa: Testing the validity of pantropical multi-species allometric equations for estimating biomass and carbon stocks. For. Ecol. Manage. 305: 29-37. [ Links ]
Feldpausch, T. R., J. Lloyd, S. L. Lewis, R. J. W. Brienen, M. Gloor, A. Monteagudo-Mendoza, G. Lopez-Gonzalez, L. Banin, K. Abu Salim, K. Affum-Baffoe, M. Alexiades, S. Almeida, I. Amaral, A. Andrade, L. E. O. C. Aragão, A. Araujo-Murakami, E. J. M. M. Arets, L. Arroyo, G. A. Aymard, T. R. Baker, O. S. Bánki, N. J. Berry, N. Cardozo, J. Chave, J. A. Comiskey, E. Alvarez, A. de Oliveira, A. Di-Fiore, G. Djagbletey, T. F. Domingues, T. L. Erwin, P. M. Fearnside, M. B. França, M. A. Freitas, N. Higuchi, E. Honorio, Y. Iida, E. Jiménez, A. R. Kassim, T. J. Killeen, F. Laurance, J. C. Lovett, Y. Malhi, B. S. Marimon, B. H. Marimon-Junior, E. Lenza, A. R. Marshall, C. Mendoza, D. J. Metcalfe, E. T. A. Mitchard, D. A. Neill, B. W. Nelson, R. Nilus, E. M. Nogueira, A. Parada, K. S. H. Peh, A. Pena-Cruz, M. C. Peñuela, N. C. A. Pitman, A. Prieto, C. A. Quesada, F. Ramírez, H. Ramírez-Angulo, J. M. Reitsma, A. Rudas, G. Saiz, R. P. Salomão, M. Schwarz, N. Silva, J. E. Silva-Espejo, M. Silveira, B. Sonké, J. Stropp, H. E. Taedoumg, S. Tan, H. ter-Steege, J. Terborgh, M. Torello-Raventos, G. M. F. van der Heijden, R. Vásquez, E. Vilanova, V.A. Vos, L. White, S. Willcock, H. Woell, and O. L. Phillips. 2012. Tree height integrated into pantropical forest biomass estimates. Biogeosci. Discuss. 9: 2567-2622. [ Links ]
Feldpausch, T. R., L. Banin, O. L. Phillips, T. R. Baker, S. L. Lewis, C. A. Quesada, K. Affum-Baffoe, E. Arets, N. J. Berry, and M. Bird. 2011. Height-diameter allometry of tropical forest trees. Biogeosciences 8: 1081-1106. [ Links ]
Fuentes S., M. 1998. Propiedades tecnológicas de las maderas mexicanas, de importancia en la construcción. Revista Chapingo Serie Ciencias Forestales y del Ambiente 4: 221-229. [ Links ]
Hitchcock, H. C., and J. P. McDonnell. 1979. Biomass measurement: a synthesis of the literature. In: Proceedings of the Forest Inventory Workshop, SAF-IUFRO. Ft. Collins, Colorado. pp: 596-614. [ Links ]
INEGI. 2005. Conjunto de datos vectoriales del uso del suelo y vegetación, Serie III (continuo nacional), escala 1:250 000. Instituto Nacional de Estadística, Geografía e Informática, Aguascalientes, México. [ Links ]
INEGI. 2009. Prontuario de información geográfica municipal de los Estados Unidos Mexicanos. http://www3.inegi.org.mx/sistemas/mexicocifras/datosgeograficos/20/20071.pdf. (Consulta: septiembre 2013). [ Links ]
Kuyah, S., J. Dietz, C. Muthuri, R. Jamnadass, P. Mwangi, R. Coe, and H. Neufeldt. 2012. Allometric equations for estimating biomass in agricultural landscapes: I. Aboveground biomass. Agric. Ecosyst. Environ. 158: 216-224. [ Links ]
Luna-José, A. D. L., y B. Rendón-Aguilar. 2008. Recursos vegetales útiles en diez comunidades de la Sierra Madre del Sur, Oaxaca, México. Polibotánica 26: 193-242. [ Links ]
Monroy, R. C., y J. J. Návar C. 2004. Ecuaciones de aditividad para estimar componentes de biomasa de Hevea brasiliensis Mull. Arg., en Veracruz, México. Madera y Bosques 10: 29-43. [ Links ]
Montgomery D., C., and E. A. Peck. 1982. Introduction to Linear Regression Analysis. Wiley. New York. 504 p. [ Links ]
Montgomery, D. C., E. A. Peck, y G. G. Vining. 2005. Introducción al Análisis de Regresión Lineal. Tercera edición. Ed. Continental. México. 742 p. [ Links ]
Návar, J. 2009. Allometric equations for tree species and carbon stocks for forests of northwestern Mexico. For. Ecol. Manage. 257: 427-434. [ Links ]
Nogueira, E. M., P. M. Fearnside, B. W. Nelson, R. I. Barbosa and E. W. H. Keizer. 2008. Estimates of forest biomass in the Brazilian Amazon: New allometric equations and adjustments to biomass from wood-volume inventories. For. Ecol. Manage. 256: 1853-1867. [ Links ]
Parresol, B. 1999. Assessing tree and stand biomass: a review with examples and critical comparisons. For. Sci. 45: 573-593. [ Links ]
Parresol, B. R. 2001. Additivity of nonlinear biomass equations. Can. J. For. Res. 31: 865-878. [ Links ]
Pennington, T. D., y K. Sarukhán. 2005. Manual para la Identificación de Campo de los Principales Árboles Tropicales de México. Tercera ed. Inst. Nal. Invest. Forest. SAG. México. 523 p. [ Links ]
Pompa-García, M., y J. I. Yerena-Yamallel. 2014. Concentración de carbono en Pinus cembroides Zucc: fuente potencial de mitigación del calentamiento global. Revista Chapingo Serie Ciencias Forestales y del Ambiente 20: 169-175. [ Links ]
Rojo M., G. E., J. Jasso M., J. J. Vargas H., D. J. Palma L. y A. Velázquez M. 2005. Biomasa aérea en plantaciones comerciales de hule (Hevea brasiliensis Mull. Arg.) en el estado de Oaxaca, México. Agrociencia 39: 449-456. [ Links ]
Rutishauser, E., F. Noor'an, Y. Laumonier, J. Halperin, Rufi'ie, K. Hergoualc'h, and L.Verchot. 2013. Generic allometric models including height best estimate forest biomass and carbon stocks in Indonesia. For. Ecol. Manage. 307: 219-225. [ Links ]
SAS Institute Inc. 2004. SAS/ETS® 9.1 User's Guide. Cary, NC. 2416 p. [ Links ]
Segura, M., M. Kanninen, and D. Suárez. 2006. Allometric models for estimating aboveground biomass of shade trees and coffee bushes grown together. Agrofor. Syst. 68: 143-150. [ Links ]
Sotomayor C., J. R. 2008. Segunda edición. Tabla Fitecma de clasificación de características mecánicas de maderas mexicanas. FITECMA. UMSNH. Formato: 30x60 cm. [ Links ]
Tamarit U., J. C., y M. Fuentes S. 2003. Parámetros de humedad de 63 maderas latifoliadas mexicanas en función de su densidad básica. Revista Chapingo Serie Ciencias Forestales y del Ambiente 9:155-164. [ Links ]
Tamarit U., J. C., y J. L. López T. 2007. Xilotecnología de los principales árboles tropicales de México. Libro técnico No. 3. INIFAP-CIR Golfo Centro, Campo Experimental San Martinito, Tlahuapan, Puebla, México. [ Links ]
Ventura-Aquino, Y., B. Rendón, S. Rebollar and G. Hernández. 2008. Use and conservation of forest resources in the municipality of San Agustín Loxicha, Sierra Madre del Sur, Oaxaca, México. Agrofor. Syst. 73: 167-180. [ Links ]














