Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Agrociencia
versión On-line ISSN 2521-9766versión impresa ISSN 1405-3195
Agrociencia vol.42 no.3 Texcoco abr./may. 2008
Matemáticas aplicadas, estadística y computación
Aplicación de dos pruebas estadísticas de bondad de ajuste en muestras complejas: un caso práctico en el campo forestal
Application of two statistical goodness –of–fit tests in complex samples: a practical case in forest field
María A. Quintero–Méndez y Mariano J. Durán–Núñez
Universidad de Los Andes. Falcultad de Ciencias Forestales y Ambientales. Escuela de Ingeniería Forestal. Mérida, Venezuela (mariaq@ula.ve) (mjdurann.ureach.com)
Recibido: Julio, 2007.
Aprobado: Febrero, 2008.
Resumen
En esta investigación se comparan dos pruebas de bondad de ajuste en términos de su error tipo I: ji–cuadrada de Pearson y Rao–Scott con corrección de segundo orden, aplicadas a datos recolectados mediante técnicas de muestreo que no cumplen los supuestos de independencia e igual probabilidad de inclusión de las observaciones, llamadas muestras complejas. Ambas pruebas se usaron para ajustar categorías diamétricas en una plantación de gmelina (Gmelina arborea), aplicando muestreo sistemático con parcelas de área fija y parcelas de área variable (Muestreo de Bitterlich o Parcelas de Radio Variable), mediante técnicas de simulación. La prueba de Rao–Scott con corrección de segundo orden registra un error tipo I más bajo y cercano al valor nominal α que la prueba ji–cuadrada de Pearson, debido a que toma en cuenta los efectos del diseño muestral y corrige la violación de los supuestos. Los resultados obtenidos en esta investigación muestran la inconveniencia de usar la prueba de bondad de ajuste ji–cuadrada de Pearson en datos obtenidos mediante muestreos con parcelas fijas y parcelas de área variable, ampliamente usados en el campo forestal. Por tanto, es necesario usar pruebas estadísticas que consideren la complejidad del diseño muestral, a fin de obtener inferencias válidas.
Palabras clave: Gmelina arborea, error tipo I, parcelas de área fija, parcelas de área variable.
Abstract
In this research two goodness–of–fit tests are compared in terms of their type I error: Pearson's Chi–square test and Rao–Scott test with correction of second order, applied to data collected using sampling methods that do not fulfill the assumptions of independence and equal probability of inclusion of observations, methods called complex surveys. Both tests were utilized to fit diametric categories in a gmelina plantation (Gmelina arborea), applying systematic sampling with fixed area plots and with variable area plots (Bitterlich Sampling or variable radius plot), and employing simulation techniques. The Rao–Scott test with correction of second order registered a lower Type I error, close to the nominal α, when compared to the Pearson Chi–square test, due to the fact that the former takes into account the effects of the sample design and corrects the violation of the assumptions. The results obtained in this research show that the use of Pearson's Chi–square goodness–of–fit test is inappropriate in data obtained applying fixed area and variable area plots, widely used in forestry inventories. Therefore, it is important to use statistical tests that take into account sampling design complexity, in order to achieve valid inferences.
Key words: Gmelina arborea, type I error, fixed area plots, variable area plots.
INTRODUCCIÓN
Muchos de los análisis estadísticos que se aplican a los datos de una muestra requieren que las observaciones sean independientes y que tengan iguales probabilidades de selección (Skinner et al., 1989). Estos supuestos sólo se satisfacen cuando se emplea un muestreo aleatorio simple con reemplazo, y se cumplen aproximadamente en una muestra aleatoria simple sin reemplazo, para una fracción de muestreo pequeña (Sarndal et al., 2003).
En la práctica, muchas veces los diseños muestrales usados no satisfacen los supuestos del muestreo aleatorio simple; algunas observaciones pueden tener diferentes probabilidades de selección o, por razones logísticas, los individuos de una muestra forman conglomerados, causando que las unidades muestrales no sean independientes. Al conjunto de observaciones realizadas usando una técnica de muestreo con estas características, se le denomina muestra compleja (Carlson, 1998).
Usualmente los análisis estadísticos de una muestra compleja se hacen como si las observaciones cumplieran con los supuestos del muestreo aleatorio simple (Lee et al., 1989). Es bastante común emplear paquetes estadísticos estándar y no considerar la complejidad del diseño muestral. Pero, ¿se puede ignorar la violación de los supuestos de independencia e igual probabilidad de selección de las observaciones sin afectar la validez de los métodos estadísticos usados?
La prueba ji–cuadrada de Pearson es una de las más usadas para estudiar la bondad de ajuste, por lo que es importante determinar si la violación de los supuestos que ocurre en el muestreo con parcelas de área fija y de área variable, diseños muestrales complejos usados en el campo forestal, afecta su validez estadística. Se ha analizado el comportamiento de la prueba cuando se usa muestreo estratificado y muestreo por conglomerados (Holt et al., 1980; Rao y Scott, 1981; Thomas y Rao, 1987); sin embargo, no se ha estudiado su comportamiento cuando se aplica a datos obtenidos mediante técnicas de muestreo forestal.
Se han propuesto métodos alternativos para probar bondad de ajuste considerando la complejidad del diseño muestral: Fay (1985), Rao y Scott (1979, 1981, 1984), Rai et al. (2001). Una prueba de bondad de ajuste con estas características es la de Rao–Scott con corrección de segundo orden; usa un estadístico de prueba que corrige la violación de los supuestos del muestreo aleatorio simple e incorpora el efecto del diseño muestral.
En este trabajo se estudia el comportamiento de las pruebas de bondad de ajuste ji–cuadrada de Pearson y Rao–Scott con corrección de segundo orden en términos del error tipo I, para ajustar categorías dia–métricas de gmelina (Gmelina arborea) en muestreos con parcelas fijas y parcelas variables. Se intenta demostrar, mediante un ejemplo que utiliza datos reales de una plantación, que una prueba estadística de bondad de ajuste que considere información sobre el diseño muestral permite realizar inferencias más confiables que la prueba clásica ji–cuadrada de Pearson.
MATERIALES Y MÉTODOS
Muestreo con parcelas de área fija
Este método de muestreo se basa en el establecimiento de parcelas con dimensiones y forma fija (rectangular, circular, o cuadrada). Un árbol o cualquier otro individuo u objeto que se desea estudiar es incluido en la muestra si se encuentra dentro de los límites de las parcelas establecidas (Schreuder et al., 1993).
En el muestreo con parcelas de área fija, la probabilidad de que un árbol u sea incluido en la muestra (pu) está dada por:

donde, au es el área definida por el conjunto de puntos donde se puede localizar una parcela, tal que el árbol u sea incluido en la muestra; esta área se denomina área de inclusión. A representa el área del bosque, plantación o sitio a muestrear.
Para parcelas muestrales de forma circular es fácil verificar que el área de inclusión de un árbol es un círculo concéntrico a él, con el mismo radio de la parcela muestral (Schreuder et al., 1993). De esta forma au= a y es constante para todos los árboles, por ende todos los individuos tienen igual probabilidad de ser incluidos en la muestra, cumpliéndose uno de los supuestos del muestreo aleatorio simple.
Sin embargo, en el muestreo con parcelas de área fija no se cumple el supuesto de independencia de las observaciones, ya que una vez elegido el punto donde se aplica el muestreo, los árboles de cada parcela forman conglomerados y existe una correlación espacial entre ellos.
Muestreo con parcelas de área variable
El muestreo con parcelas de área variable, también llamado muestreo con parcelas de radio variable o método de Bitterlich, es una técnica que permite seleccionar árboles de una parcela con una probabilidad proporcional al área de la sección transversal o área basal o, lo que es igual, proporcional al cuadrado del diámetro del árbol (De Vries, 1986).
Si A representa el área del sitio del cual se extraerá la muestra y a es el ángulo de barrido utilizado en el muestreo, la probabilidad (pu) de que un árbol u de diámetro du sea muestreado desde un punto localizado aleatoriamente es:
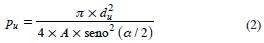
Para una demostración matemática de esta ecuación y obtener detalles de esta técnica de muestreo consultar De Vries (1986) y Schreuder et al. (1993).
De acuerdo con la ecuación 2, la probabilidad de seleccionar un árbol es proporcional al cuadrado de su diámetro. De esta manera, en el muestreo con parcelas de área variable no se satisface el supuesto de igual probabilidad de selección para todas las unidades muestrales, ya que los árboles con mayor diámetro tienen una probabilidad más alta de ser seleccionados. También influye la distancia del árbol al punto de muestreo.
Esta técnica de muestreo tampoco satisface el supuesto de independencia de las observaciones, ya que los árboles seleccionados en un punto muestral forman conglomerados.
Pruebas de bondad de ajuste ji–cuadrada de Pearson y Rao–Scott de segundo orden
Para aplicar la prueba de bondad de ajuste ji–cuadrada de Pearson las observaciones son clasificadas en k categorías o clases, y se supone que son independientes e idénticamente distribuidas. La hipótesis nula es Ho: pi = pio para i = 1, 2,...,k; donde pies la proporción de individuos que pertenecen a la categoría i, pio es la proporción teórica de la categoría i, y k es el número de categorías.
El estadístico de prueba es:
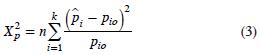
donde  se obtiene dividiendo el número de individuos de la categoría i observados entre el total de individuos
se obtiene dividiendo el número de individuos de la categoría i observados entre el total de individuos 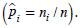
Si las observaciones son independientes y cada individuo tiene la misma probabilidad de ser seleccionado en la muestra, el estadístico Xp2 sigue asintóticamente una distribución ji–cuadrada con k–1 grados de libertad.
Cuando se utiliza un diseño muestral complejo, el estadístico Xp2 no se distribuye X2(k–1)pero tiene una distribución simétrica, y un múltiplo de Xp2 podría seguir aproximadamente una distribución x2 (Lohr, 2000).
Rao y Scott (1981) determinaron que el estadístico Xp2 se distribuye asintóticamente como una suma ponderada δ1W1 + δ2W2+......+ δk_1Wk_1 de variables aleatorias ji–cuadradas Wj , cada una con un grado de libertad. Los pesos δj son los valores propios de la matriz de los efectos del diseño generalizados; esta matriz se define como D = Po–1 V, donde Po = diag (po) – pop'o, poes el vector de proporciones teóricas y V/n es la matriz de covarianzas del vector de proporciones estimadas  . Si se utiliza un muestro aleatorio simple, los valores propios d: de la matriz de los efectos del diseño generalizados son iguales a uno. Así, la suma ponderada
. Si se utiliza un muestro aleatorio simple, los valores propios d: de la matriz de los efectos del diseño generalizados son iguales a uno. Así, la suma ponderada  se reduce a una suma de k–1 variables aleatorias ji–cuadradas independientes con un grado de libertad, cuya distribución es X2(k–1). Si el diseño muestral es más complejo, los efectos del diseño generalizados δj no son iguales a 1; por tanto, la distribución asintótica de la variable aleatoria
se reduce a una suma de k–1 variables aleatorias ji–cuadradas independientes con un grado de libertad, cuya distribución es X2(k–1). Si el diseño muestral es más complejo, los efectos del diseño generalizados δj no son iguales a 1; por tanto, la distribución asintótica de la variable aleatoria  no es (k–1)(Lehtonen y Pahkinen, 2004).
no es (k–1)(Lehtonen y Pahkinen, 2004).
Basados en este hecho, Rao y Scott (1981) proponen dos correcciones al estadístico ji–cuadrado de Pearson. La corrección de primer orden ajusta la esperanza, y la de segundo orden la esperanza y la varianza asintótica. En este estudio se emplea la corrección de segundo orden, también llamada corrección de Satterthwaite. La prueba de Rao–Scott con corrección de segundo orden usa el estadístico:
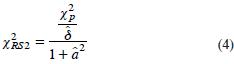
donde, Xp2 es el estadístico ji–cuadrado de Pearson;  es un estimador de la media
es un estimador de la media  de los valores propios δj de la matriz de los efectos del diseño generalizados; â es un estimador del coeficiente de variación de los valores propios δj .
de los valores propios δj de la matriz de los efectos del diseño generalizados; â es un estimador del coeficiente de variación de los valores propios δj .
Si el diseño muestral tiene probabilidades de inclusión desiguales, se calcula el estadístico Xp2 utilizando estimadores de proporciones δj ponderados por las probabilidades de inclusión:
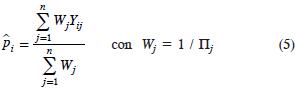
donde,  es la probabilidad de que el individuo j sea seleccionado en la muestra (probabilidad de inclusión del individuo j), y Yij es una variable indicadora con valor 1 si el individuo j pertenece a la categoría i y 0 en otro caso.
es la probabilidad de que el individuo j sea seleccionado en la muestra (probabilidad de inclusión del individuo j), y Yij es una variable indicadora con valor 1 si el individuo j pertenece a la categoría i y 0 en otro caso.
Las ecuaciones para calcular  y â2 son:
y â2 son:
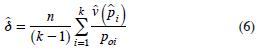
siendo  la varianza del estimador de la proporción de la categoría i,
la varianza del estimador de la proporción de la categoría i,
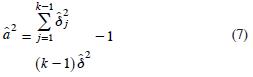
 se calcula de la siguiente manera:
se calcula de la siguiente manera:
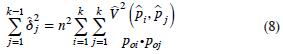
donde, 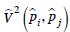 es el elemento i, j de la matriz de covarianza de los estimadores de proporciones; poi y poj corresponden a las proporciones teóricas para las categorías i y j. Los valores de
es el elemento i, j de la matriz de covarianza de los estimadores de proporciones; poi y poj corresponden a las proporciones teóricas para las categorías i y j. Los valores de 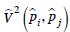 se pueden estimar utilizando una técnica de re–muestreo como la técnica de replicación balanceada, bootstrap o Jackknife. En esta investigación se utilizó la técnica de Jackknife.
se pueden estimar utilizando una técnica de re–muestreo como la técnica de replicación balanceada, bootstrap o Jackknife. En esta investigación se utilizó la técnica de Jackknife.
El estadístico  se distribuye aproximadamente como una ji–cuadrada con
se distribuye aproximadamente como una ji–cuadrada con  grados de libertad. En la mayoría de los casos los grados de libertad son un número decimal, por lo que se redondean al entero inferior más próximo. Los fundamentos teóricos de esta prueba pueden verse en Rao y Scott (1979, 1981, 1984), Sarndal et al. (2003) y Lehtonen y Pahkinen (2004).
grados de libertad. En la mayoría de los casos los grados de libertad son un número decimal, por lo que se redondean al entero inferior más próximo. Los fundamentos teóricos de esta prueba pueden verse en Rao y Scott (1979, 1981, 1984), Sarndal et al. (2003) y Lehtonen y Pahkinen (2004).
Recolección de datos
En este trabajo se utilizaron datos de una plantación de gmelina ubicada en la finca El Hierro, Estado Portuguesa, propiedad de la empresa SMURFIT Cartón de Venezuela. En la plantación se hizo un censo de un área de 4.8 ha, con 4841 árboles. Cada árbol se ubicó en un eje cartesiano (x,y), y se midió el diámetro a la altura de pecho (DAP). Se establecieron tres variables categóricas del diámetro usando 5, 10 y 15 categorías, usadas en las pruebas de bondad de ajuste. Así, por ejemplo, para establecer una variable con 5 categorías diamétricas se dividió el rango de valores de DAP en 5 intervalos, y a cada árbol se le asignó un número del 1 al 5 dependiendo del intervalo donde se ubica su DAP. De manera similar se procedió en el caso de 10 y 15 categorías.
Obtención de muestras y aplicación de las pruebas de bondad de ajuste mediante simulación
Se construyeron dos programas de computación que permiten simular la obtención de muestras usando parcelas de área fija y parcelas de área variable. Con los datos de una muestra, estos programas aplican a la variable categoría diamétrica las pruebas de bondad de ajuste ji–cuadrada de Pearson y Rao–Scott con corrección de segundo orden. Para implementar los programas se utilizó el lenguaje GAUSS, versión 3.1.4.
Los programas de simulación requieren como entrada una base de datos con la información de la población de árboles de donde se extraerá la muestra, la cual debe incluir la ubicación de cada árbol expresada como coordenadas cartesianas (x,y), el DAP y la categoría diamétrica. También es necesario indicar las dimensiones del área a muestrear, el número de puntos de muestreo, el radio de las parcelas muestrales (para el muestreo con parcelas de área fija) y el ángulo de barrido (para el muestreo con parcelas de área variable).
Para simular el muestreo con parcelas de área fija se trabajó con parcelas circulares de radio igual a 10 m, y los puntos iniciales de muestreo se seleccionaron con un diseño sistemático. Se hicieron pruebas con 5 y 8 puntos, correspondientes a una intensidad de muestreo de 3 y 5 %. En la simulación del muestreo de parcelas de área variable se tomaron los mismos puntos iniciales utilizados en la simulación del muestreo con parcelas de área fija, para posteriormente realizar comparaciones entre los dos tipos de muestreo.
Los programas aplican el método Mirage para corregir el llamado efecto de borde en los límites del área a muestrear, y el sesgo que producen. El efecto de borde supone que un árbol ubicado cerca de los límites de la parcela puede tener una probabilidad de ser incluido en la muestra diferente a la de un árbol similar situado en el centro de la parcela (Schreuder et al., 1993).
Medición del desempeño de la pruebas de bondad de ajuste
Para medir el desempeño de las dos pruebas de bondad de ajuste consideradas, se estima el error tipo I el cual, si difiere significativamente del nivel nominal (teórico) establecido, se considera que la prueba no es robusta y, por tanto, no puede garantizarse la validez de los resultados obtenidos. Uno de los criterios de robustez más usados es el de Bradley (1978), el cual establece que una prueba es robusta si las tasas empíricas de error tipo I están en el intervalo [0.5α, 1.5α]; así, para α=0.05 este criterio de robustez requiere que el error tipo I estimado esté entre 0.025 y 0.075, en otro caso, la prueba no puede considerarse robusta.
Estimación del error tipo I
El error tipo I se estimó mediante técnicas de simulación o método Monte Carlo. Para ello, el programa se ejecutó r veces, lo que implica que se obtienen r muestras y que a cada una de ellas se le aplican las pruebas para determinar si las proporciones de cada categoría diamétrica en la muestra (pi) son iguales a las proporciones de cada categoría diamétrica en la población (pio), entendiéndose por tal el conjunto de todos los árboles en la plantación.
Al finalizar las r corridas, el programa estima el error tipo I de las dos pruebas estadísticas, con la ecuación:

donde,  es el error tipo I estimado; X el número de veces que se rechazó Ho siendo verdadera; r es el número de replicaciones. En todas las simulaciones se utilizaron 5000 replicaciones.
es el error tipo I estimado; X el número de veces que se rechazó Ho siendo verdadera; r es el número de replicaciones. En todas las simulaciones se utilizaron 5000 replicaciones.
Una vez calculado el valor de  para las pruebas de bondad de ajuste, se compara con el nominal establecido (0.05).
para las pruebas de bondad de ajuste, se compara con el nominal establecido (0.05).
Comparación de las pruebas de bondad de ajuste
Se usó la Prueba de Mc Nemar (Conover, 1980) para comparar el error tipo I de las pruebas y establecer si hay diferencias significativas entre ambas.
RESULTADOS Y DISCUSIÓN
Los valores del error tipo I estimado  de las pruebas aplicadas en categorías diamétricas de gmelina, se muestran en los Cuadros 1 y 2. Se presentan los resultados obtenidos para los dos tipos de mues–treo utilizados y diferentes condiciones experimentales, así como los valores del estadístico de Mc Nemar obtenidos al comparar las dos pruebas de bondad de ajuste.
de las pruebas aplicadas en categorías diamétricas de gmelina, se muestran en los Cuadros 1 y 2. Se presentan los resultados obtenidos para los dos tipos de mues–treo utilizados y diferentes condiciones experimentales, así como los valores del estadístico de Mc Nemar obtenidos al comparar las dos pruebas de bondad de ajuste.
En todas las situaciones simuladas la prueba ji–cuadrada de Pearson tiene un error tipo I más alto que la de Rao–Scott con corrección de segundo orden. Los valores del estadístico de McNemar son menores a –2.33, indicando diferencias altamente significativas entre los resultados de la prueba de bondad de ajuste ji–cuadrada de Pearson y los de la prueba de Rao–Scott con corrección de segundo orden.
En el Cuadro 1 se muestra que cuando se usan parcelas de área fija la prueba ji–cuadrada de Pearson registra valores de  que oscilan entre 0.0836 y 0.1470, alejándose del valor nominal (α =0.05). En el muestreo con parcelas de área variable (Cuadro 2), la prueba ji–cuadrada de Pearson presenta valores muy altos de
que oscilan entre 0.0836 y 0.1470, alejándose del valor nominal (α =0.05). En el muestreo con parcelas de área variable (Cuadro 2), la prueba ji–cuadrada de Pearson presenta valores muy altos de  (0.7750 a 0.9920), un error tipo I inaceptable para una prueba de hipótesis. Estos valores tan altos para el error tipo I estimado se deben fundamentalmente a las características propias del muestreo con parcelas de área variable, ya que este método favorece la selección de árboles con diámetros mayores a la altura de pecho, y uno de sus objetivos es estimar el área basal total y el volumen total, donde los árboles de las categorías diamétricas superiores hacen el mayor aporte para estimar estos parámetros. Así, al analizar los resultados de las simulaciones se observó que las categorías diamétricas inferiores no estaban representadas en las muestras, o el número de árboles incluidos de esas categorías era pequeño, ocasionando que las proporciones de las categorías diamétricas en una muestra (pi) fueran muy diferentes de las proporciones registradas en la población (pio). Por tanto, en la mayoría de los casos se rechazó una hipótesis nula verdadera y el error tipo I estimado fue muy alto. En ésto radica básicamente la diferencia con el muestreo de parcelas de área fija, donde se incluyen todos los árboles ubicados dentro del perímetro de la parcela, de modo que los árboles de cierta clase diamétrica se muestrean en forma proporcional a la frecuencia en el bosque de esa clase particular de árboles.
(0.7750 a 0.9920), un error tipo I inaceptable para una prueba de hipótesis. Estos valores tan altos para el error tipo I estimado se deben fundamentalmente a las características propias del muestreo con parcelas de área variable, ya que este método favorece la selección de árboles con diámetros mayores a la altura de pecho, y uno de sus objetivos es estimar el área basal total y el volumen total, donde los árboles de las categorías diamétricas superiores hacen el mayor aporte para estimar estos parámetros. Así, al analizar los resultados de las simulaciones se observó que las categorías diamétricas inferiores no estaban representadas en las muestras, o el número de árboles incluidos de esas categorías era pequeño, ocasionando que las proporciones de las categorías diamétricas en una muestra (pi) fueran muy diferentes de las proporciones registradas en la población (pio). Por tanto, en la mayoría de los casos se rechazó una hipótesis nula verdadera y el error tipo I estimado fue muy alto. En ésto radica básicamente la diferencia con el muestreo de parcelas de área fija, donde se incluyen todos los árboles ubicados dentro del perímetro de la parcela, de modo que los árboles de cierta clase diamétrica se muestrean en forma proporcional a la frecuencia en el bosque de esa clase particular de árboles.
La prueba ji–cuadrada de Pearson presenta una distorsión del error tipo I estimado con respecto al valor nominal (α=0.05) mucho mayor en el muestreo con parcelas de área variable que en el de parcelas de área fija. Además, en el muestreo con parcelas de área fija se viola sólo el supuesto de independencia de las observaciones, mientras que en el de parcelas de área variable se violan los supuestos de independencia e igual distribución de las observaciones.
En los Cuadros 1 y 2 las pruebas ji–cuadrada de Pearson y Rao–Scott con corrección de segundo orden muestran variaciones en su desempeño en relación con el tamaño de muestra. En ambas pruebas el error tipo I estimado disminuye cuando aumenta la cantidad de puntos muestrales, para un número fijo de categorías diamétricas. Éste es el comportamiento esperado, puesto que en muestras de tamaño mayor las categorías diamétricas están mejor representadas, por lo que se rechaza en menor proporción la hipótesis nula.
Si se mantiene constante el número de puntos muestrales, se observa que en el muestreo con parcelas de área fija (Cuadro 1) el valor de  crece cuando aumenta el número de categorías diamétricas. En el muestreo con parcelas de tamaño variable (Cuadro 2), el error tipo I estimado es menor para un número mayor de categorías.
crece cuando aumenta el número de categorías diamétricas. En el muestreo con parcelas de tamaño variable (Cuadro 2), el error tipo I estimado es menor para un número mayor de categorías.
La prueba de Rao–Scott con corrección de segundo orden, en parcelas fijas y en parcelas variables, presenta valores del error tipo I estimado menores y más cercanos a 0.05 que la prueba ji–cuadrada de Pearson. Los resultados de la prueba de Rao–Scott con las correcciones, basadas en la esperanza y la varianza asintótica además de la inclusión de los efectos del diseño muestral, disminuyen considerablemente el error tipo I.
Rao y Scott (1981) también encontraron diferencias importantes entre las dos pruebas de bondad de ajuste al estudiar el efecto de la estratificación y de los conglomerados sobre la distribución asintótica del estadístico ji–cuadrado de Pearson. Igualmente, Thomas y Rao (1987) reportaron niveles de significancia altos para la prueba ji–cuadrada de Pearson con el muestreo por conglomerados, y resultados bastante buenos para la prueba de Rao–Scott. Sin embargo, en ninguno de estos trabajos la prueba de bondad de ajuste ji–cuadrada de Pearson mostró un error tipo I tan alto como al muestrear por parcelas variable. El desempeño de la prueba de Rao–Scott en términos del error tipo I reportado en los trabajos mencionados es mejor que el registrado en las simulaciones realizadas en este trabajo, ya que en la mayoría de los experimentos los autores obtuvieron niveles de significancia iguales al valor teórico, mientras que en el presente estudio el error tipo I estimado siempre fue mayor al nivel nominal o teórico. No obstante, sólo en 3 (20%) de los casos simulados el error tipo I de la prueba de Rao–Scott supera el límite superior del intervalo de Bradley. Por tanto, puede decirse que en la mayoría de las situaciones esta prueba de bondad de ajuste se mostró robusta. Las discrepancias entre los valores de  obtenidos para la prueba de Rao–Scott con corrección de segundo orden y los reportados en otras investigaciones son consecuencia de las diferencias entre las condiciones experimentales, las características de la población y los diseños muestrales aplicados.
obtenidos para la prueba de Rao–Scott con corrección de segundo orden y los reportados en otras investigaciones son consecuencia de las diferencias entre las condiciones experimentales, las características de la población y los diseños muestrales aplicados.
CONCLUSIONES
Los resultados obtenidos en esta investigación indican que la validez de la prueba de bondad de ajuste ji–cuadrada de Pearson es influenciada por la violación de los supuestos de independencia e igual distribución de las observaciones que ocurre en el muestreo con parcelas de área variable. Lo mismo sucede cuando se utiliza el muestreo con parcelas de área fija. La violación del supuesto de independencia hace que la prueba ji–cuadrada de Pearson tenga un error tipo I diferente del valor nominal establecido. La magnitud de la distorsión del error tipo I de estas pruebas varía de un muestreo a otro, siendo mayor cuando se usan parcelas de tamaño variable.
Los niveles de significación altos para la prueba de bondad de ajuste ji–cuadrada de Pearson cuando se aplican en muestras obtenidas con parcelas fijas y parcelas variables puede conducir a conclusiones erróneas acerca de la población en estudio, razón por la cual no se recomienda su uso. Es conveniente aplicar una prueba de bondad de ajuste que corrija las violaciones de los supuestos de independencia e igual probabilidad de inclusión para todos los individuos. Una de estas pruebas es la de Rao–Scott con corrección de segundo orden, que en esta investigación registró valores del error tipo I menores que la prueba ji–cuadrada de Pearson y en muchos casos bastante cercanos al valor nominal.
Los resultados de este trabajo muestran la importancia de considerar la complejidad del diseño muestral utilizado cuando se analizan datos de una muestra compleja.
LITERATURA CITADA
Bradley, J. V. 1978. Robustness? The Br. J. Mathematical & Statistical Psychology 31: 144–152. [ Links ]
Carlson, B. L. 1998. Software for statistical analysis of sample survey data. In: Armitage P., and T. Colton (eds). Encyclopedia of Biostatistics. John Wiley and Sons. New York. pp: 4160– 4167. [ Links ]
Conover, W. J. 1980. Practical Nonparametric Statistics. 2nd. ed. John Wiley & Son. New York. 493 p. [ Links ]
De Vries, P. 1986. Sampling Theory for Forest Inventory. Springer– Verlag. Nueva York. 399 p. [ Links ]
Fay, R. E. 1985. A jacknifed Chi–squared test for complex samples. JASA 80: 148–157. [ Links ]
Fellegi, I. 1980. Aproximate tests of independence and goodness of fit based on stratified multistage samples. JASA. 75: 261– 268. [ Links ]
Holt, D., A. J. Scott, and P. D. Ewings. 1980. Chi–squared tests with survey data. JRSS, A. 143: 303–320. [ Links ]
Lee, E. S., R. N. Forthofer, and R. J. Lorimer. 1989. Analyzing Complex Survey Data. Sage University Paper series on Quantitative Applications in the Social Sciences 07–071. Sage Publications. Beverly Hills, USA. 79 p. [ Links ]
Lehtonen, R., and E. Pahkinen. 2004. Practical Method for Design and Analysis of Complex Surveys. Second Edition. John Wiley & Sons. New York. 320 p. [ Links ]
Lohr, S. 2000. Muestreo: Diseño y Análisis. Internacional Thomson Editores. Buenos Aires, Argentina. 420 p. [ Links ]
Nathan, G. 1975. Test of independence in contingency tables from stratified proporcional samples. Sankhya C 37: 77–87. [ Links ]
Rai, A., A. K. Srivastava, and H.C. Gupta. 2001. Small sample comparison of modified chi–square test statistics for survey data. Biometrical J. 43: 483–495. [ Links ]
Rao, J. N .K, and A. J. Scott. 1979. Chi–Squared tests for analysis of categorical data from complex surveys. Proceedings of The American Statistical Association, Section on Survey Research Methods.pp: 58–66. [ Links ]
Rao, J. N .K, and A. J. Scott. 1981. The analysis of categorical data from complex sample surveys: Chi–squared tests for goodness of fit and independence in two–way tables. JASA 76: 221–230. [ Links ]
Rao, J. N .K, and A. J. Scott. 1984. On Chi–squared tests for Multi–way contingency tables with cell proportions estimated from survey data. The Annals of Statistics 12: 46–60. [ Links ]
Sarndal, C. E., B. Swensson, and J. Wretman. 2003. Model Assisted Survey Sampling. Springer– Verlag. New York. 694 p. [ Links ]
Schreuder, H., T. Gregoire, and G. Wood. 1993. Sampling Methods for Multiresource Forest Inventory. John Wiley and Sons. New York. 446 p. [ Links ]
Skinner, C. J., P. Holt, and T. M. K. Smith. 1989. Analysis of Complex Surveys. John Wiley & Sons. Chicester. 328 p. [ Links ]
Thomas, D. R., and J. N. K. Rao.1987. Small–simple comparisons of level and power for simple goodness–of–fit statistics under cluster sampling. JASA 82: 630–636. [ Links ]














