INTRODUCCIÓN
Los movimientos del terreno en forma de flujos de derrubios, avalanchas, desplomes, vuelcos y caídas de bloques rocosos son algunos de los mayores peligros geológicos que afectan a las vías de comunicación y estructuras civiles asentadas en regiones montañosas (Evans y Hungr, 1993; Dorren, 2003; Baillifard et al., 2003; Corominas et al., 2003; Crosta et al., 2015, entre otros). En particular, la caída de rocas supone la liberación y el desprendimiento de un bloque o fragmentos de roca, desde la superficie de los escarpes rocosos, en lugares que no se distribuyen al azar, sino sujetos a evidencias geológicas, geomorfológicas y ambientales. Generalmente se inician por un pequeño deslizamiento, corrimiento, o vuelco, continuando con un rápido movimiento que implica el desplazamiento de un bloque rocoso o de una avalancha de rocas (Evans y Hungr, 1993), que se desprende del macizo, a favor de una o varias discontinuidades (diaclasas, fracturas, fallas, contactos, foliaciones, etc.) nuevas o preexistentes (Lambert et al., 2012; Crosta et al., 2015) que forman la cicatriz de desprendimiento. Seguidamente, el movimiento de la roca puede limitarse desde un desplome hasta tener una trayectoria compuesta de múltiples caídas libres, rebotes, rodaduras y deslizamientos (Varnes, 1978; Hutchinson, 1988). Una vez que se ha disipado suficiente energía, a través de los impactos y la fricción de los clastos entre sí y con el terreno, el flujo rocoso generalmente se detiene cerca del borde del talud, donde la pendiente se atenúa de forma importante, aunque en muchos casos los bloques pueden llegar mucho más allá de este límite (Evans y Hungr, 1993).
Las factores condicionantes, por los que el terreno rocoso se vuelve inestable, se encuentran fundamentalmente relacionados con sus características geológicas (litología, estratigrafía, tectónica, etc.), geomorfológicas e hidrológicas (Selby, 1993; Dorren, 2003). La ocurrencia, o frecuencia del fenómeno en el tiempo, se encuentra normalmente asociada a los denominados factores desencadenantes o detonantes que inician el movimiento de la masa rocosa y que, ordinariamente, son de origen meteorológico (precipitaciones: Wieczorek y Jäger, 1996; Chau et al., 2003; térmicos: Matsuoka y Sakai, 1999; Davies et al., 2001) o sísmico, de magnitud superior a 4.5 grados en la escala de Richter (Keefer, 1984; Harp y Wilson, 1995). En numerosas ocasiones, éstos no son reconocibles, y no se encuentra una relación de causalidad entre un evento y su origen, incluso cuando se encuentran monitoreados (Crosta et al., 2015).
Para valorar el riesgo de las caídas y movimiento de bloques en zonas de montaña, es necesaria la delimitación del área expuesta a éstos, o área de afectación (Dorren et al., 2011), que suele quedar por debajo de las áreas fuente situadas en los riscos y paredes rocosas. Sin embargo, a pesar de los numerosos estudios que analizan la dependencia de este fenómeno con la variabilidad de los factores condicionantes y desencadenantes en zonas montañosas (Baillifard et al., 2003; Marquínez et al., 2003; Stoffel, 2006; Piacentini y Soldati, 2008), resulta muy complicado modelizar y simular el movimiento de bloques debido al gran número de incertidumbres ligadas a la distribución espacial y temporal de ambos factores (Menéndez-Duarte y Marquínez, 2002; Wang et al., 2013). En esta misma línea, son abundantes las publicaciones sobre el desarrollo y aplicación de diferentes modelos de simulación del movimiento de uno o varios bloques, desprendidos desde un área fuente, por métodos heurísticos, empíricos o cinemáticos (Jones et al., 2000; Guzzetti et al., 2002; Dorren, 2003; Jaboyedoff y Labiouse, 2003; Stoffel et al., 2006; Lan et al., 2007; Topal et al., 2007; Metzger et al., 2009, entre otros) para el cálculo de la peligrosidad sobre el área afectada por futuros o posibles desprendimientos en zonas de montaña. Actualmente se han desarrollado códigos de cálculo que incorporan sobre un sistema de información geográfica (SIG) la información para resolver numérica y estocásticamente las ecuaciones del movimiento de los bloques sobre amplias zonas cartografiadas a escala 1:25,000 (Dorren y Seijmonsbergen, 2003; Guzzetti et al., 2003; Jaboyedoff et al., 2005; Copons et al., 2009; Shirzadi et al., 2012). Como elemento común en estos trabajos, la selección del modelo se hace de acuerdo no solo a la extensión de la zona de estudio y a la escala cartográfica, sino al propósito de los resultados y a la disponibilidad de modelos digitales del terreno (MDT) o catálogos de eventos in situ. Independientemente de lo sofisticado que sea el modelo, debido a la incertidumbre de la información y a la sensibilidad de las trayectorias con las características locales del terreno (Wyllie, 2014), los resultados obtenidos con éste deben ser cotejados con los ocurridos en el pasado. Además, cuanto mayor sea la extensión del área de estudio, mayor será la información necesaria y su incertidumbre (Wang et al., 2013). En ese caso, los modelos empíricos (Toppe, 1987; Evans y Hungr, 1993) precisan una información menos exhaustiva (en cuanto a la precisión y exactitud en todo el área de estudio) para el cálculo de las simulaciones que la requerida en los modelos cinemáticos (Dorren, 2003), por lo que resultan adecuados en las fases preliminares de los estudios de detalle (Corominas et al., 2013) en los que se evalúa el riesgo para establecer y dimensionar medidas de mitigación y contención.
Los primeros modelos empíricos fueron utilizados por Toppe (1987) y Evans y Hungr (1993), ambos basados en Heim (1932), que propuso el principio del Fahrböschung, o ángulo entre la horizontal y una línea trazada desde la cresta del área fuente hasta el punto en el que se detiene un bloque. Este ángulo se estima como la tasa entre la altura desde la que se desprende el bloque en el área fuente y la distancia recorrida, en proyección horizontal, hasta que se detiene. Geométricamente, esta razón es la tangente del ángulo de inclinación entre la horizontal y una línea que une la fuente con el punto de detención de los bloques. También se le conoce a este índice de movilidad como ángulo de desplazamiento (Cruden y Varnes, 1996), de alcance (Corominas, 1996), o de distancia recorrida (Hunter y Fell, 2003), entre otros.
Alternativamente, Evans y Hungr (1993) proponen otro modelo empírico basado en el ángulo de sombra (Lied, 1977), entre la horizontal y una línea trazada desde el punto más alto del piedemonte hasta el bloque desprendido más alejado. Lied (1977) supone en su modelo que una gran parte de la energía cinética con la que llega el bloque al pie del risco, tras su caída libre, se pierde durante los primeros impactos con la parte alta del talud. Entonces, la distancia recorrida, a partir de aquí, depende de la energía cinética de traslación y rotación que queda por perder en su trayectoria sobre el talud. Esta hipótesis puede considerarse válida siempre que el desprendimiento sea de fragmentos individuales, sin interacción entre ellos y menores de 105 m3, cuando parten desde un punto alejado del talud.
Paralelamente a la evolución de los diferentes modelos de simulación, se ha investigado el reconocimiento y la distribución de las áreas fuente de bloques rocosos, ya que las simulaciones no son de calidad si se desconocen las características geológicas y geomorfológicas del punto desde el que los bloques se desprenden, por ser su condición inicial. Su localización se encuentra fuertemente ligada tanto al afloramiento de las discontinuidades, como a las características del relieve que inducen la inestabilidad. El hecho de que en muchas ocasiones las áreas de desprendimiento se encuentren inaccesibles, motiva el diseño de técnicas de identificación basadas en el análisis remoto (Matasci et al., 2011; Ferrero et al., 2011) o en el análisis de los MDT: morfométrico del MDE, vegetación, suelos, geomorfológico, etc. (Loye et al., 2009; Fernández-Hernández et al., 2012; Zieher et al., 2012) para evidenciar los factores condicionantes más relevantes.
El fenómeno de caída de bloques rocosos en la Comunidad de Madrid (España) se encuentra muy localizado. En especial, ocurren esporádicamente en algunas zonas montañosas de la mitad oriental de la sierra de Guadarrama (Sistema Central Español, SCE) y próximos a vías de comunicación y núcleos de población (Ayala-Carcedo, 1988). La relativa baja frecuencia de este tipo de peligros geológicos les ha restado importancia. Sin embargo, existen evidencias y registros de grandes bloques desprendidos (unos 12 m3), algunos de ellos formando parte de áreas edificadas. El riesgo que puede provocar la caída de un bloque de varias toneladas se hace más evidente si se tiene en cuenta el atractivo turístico, natural y deportivo que tienen algunas zonas de la sierra de Guadarrama como parque nacional. La sierra de La Cabrera, es una de estas zonas en la que, además, se encuentra una población que lleva el mismo nombre, ubicada al pie de la vertiente sur. A pesar de la existencia de desprendimientos (el más reciente ocurrido el 02/02/2013 desde el Pico de la Miel), la sierra de La Cabrera ha sido objeto de escasos estudios para valorar su peligrosidad (Ayala-Carcedo et al., 2003), por lo que se hace pertinente un estudio preliminar como el presentado en este trabajo.
El propósito de este trabajo es establecer una estimación de las distancias alcanzadas por caídas de bloques en la zona de La Cabrera, utilizando un método de simulación empírico, verificar los resultados obtenidos con desprendimientos pasados y discutir la importancia de los mismos en el marco del riesgo para la población. Con este método se obtiene una estimación preliminar calibrada para las áreas potencialmente en peligro frente a una posible caída de bloques. Esta estimación es necesaria para valorar estimaciones de la peligrosidad y riesgo por este tipo de movimientos del terreno en escenarios de montaña como el de La Cabrera (Corominas et al., 2003; Ghazipour et al., 2008, entre otros).
ÁREA DE ESTUDIO: LA CABRERA
El Macizo, también conocido como sierra de La Cabrera, forma parte de la sierra de Guadarrama, alineación montañosa perteneciente a la mitad este del Sistema Central Español (SCE). Este macizo se localiza en las coordenadas 40°52'30.9"N - 3°37'15.0"O, a una distancia de 60 km al NNE de Madrid (Figura 1a), entre las localidades de Valdemanco y El Berrueco (Figura 1b). Tiene una longitud de aproximadamente 5 km, una superficie de 125 km2 con forma semielíptica irregular, orientada ENE a OSO, y un rango de alturas que se encuentra entre los 1,150 m y los 1,564 m (pico de Cancho Gordo). Este macizo se prolonga en dirección ENE hacia oriente de forma muy continua, hasta una importante apertura en el macizo, situada entre las poblaciones de La Cabrera y El Berrueco (Figura 1b), debida a una serie de fallas de rumbo N-S. El sector central del Macizo de La Cabrera es, por su extensión, el más importante y también el más relevante, ya que los desprendimientos más importantes se producen en la vertiente sur donde además se encuentra la población de La Cabrera (2,600 hab. en 2014 y 115 hab./km2), con el mismo nombre que la sierra.
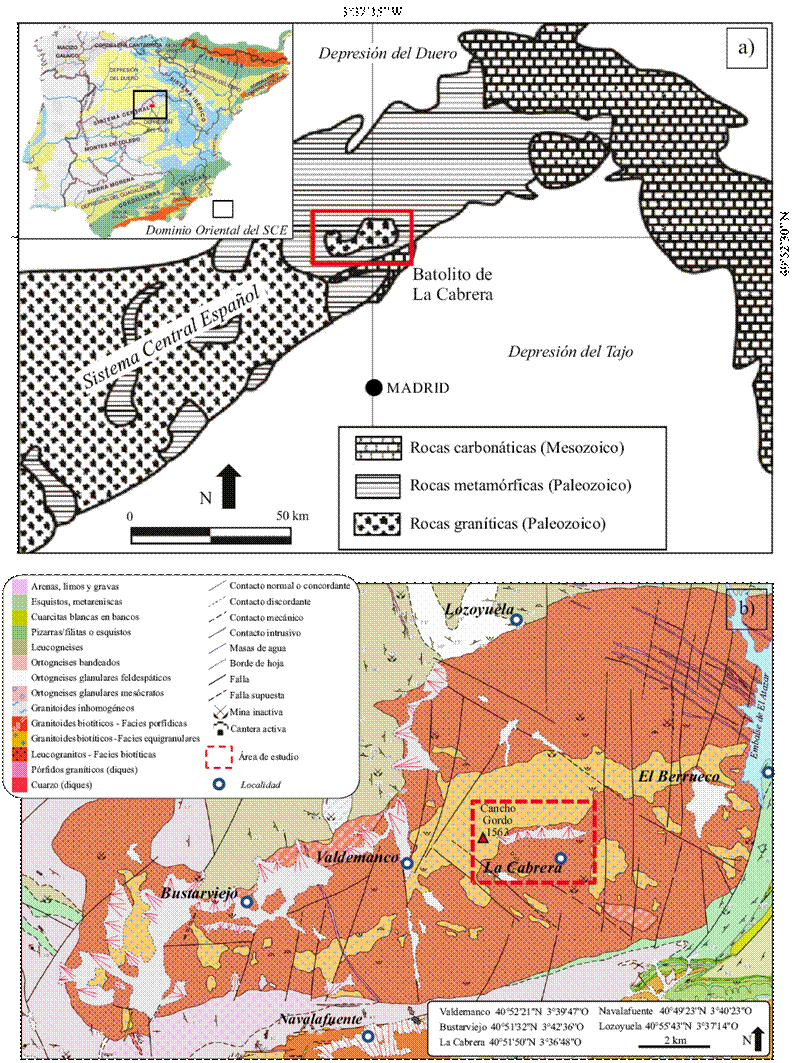
Figura 1 a) Localización geográfica-geológica del batolito de La Cabrera en la Península Ibérica (recuadro superior izquierdo en la que se diferencian las unidades morfoestructurales) y en el marco del Sistema Central Español. b) Mapa geológico local de la sierra de La Cabrera (extracto de las hojas 484 y 509 de la 2a serie Magna 1:50,000); el recuadro en trazo discontinuo ubica la zona de estudio sobre la que se realizó este trabajo.
Marco geológico regional y local
La sierra de La Cabrera se enmarca geológicamente (Figura 1a) en el borde sur del sector oriental del SCE (Bellido et al., 1981). Es el plutón más oriental de la sierra de Guadarrama. En su génesis, se trata de un batolito surgido como cuerpo intrusivo Varisco tardío, a favor de un régimen distensivo post-orogénico (Orogenia Hercínica, hace 380 m.a.) de edad Carbonífera, alóctono, que se emplazó a lo largo de un periodo entre 40 y 50 m.a. y que intruye (Figura 1b) en las formaciones paleozoicas suprayacentes: ortogneises y metasedimentos (Lozano y Jimenez, 2011) con posterioridad a las principales fases de deformación de la orogenia Hercínica. Esta intrusión se descompone en dos cuerpos principales (Figura 1b). En la parte baja de la "rampa" se encuentran adamellitas (o monzogranitos) y granitos biotíticos de grano medio a grueso más meteorizados. En la vertiente sur, más abundantes son los leucogranitos de grano fino y medio, también biotíticos (Bellido, 1979; Bellido et al. 1991).
La intensa tectónica que afecta al intrusivo se manifiesta según dos direcciones de fracturación NNE y ONO que marcan las orientaciones de las principales familias de fallas a escala regional (discontinuidades y diques en la Figura 1b), además del conjunto de diaclasas asociadas, diques de cuarzo y pórfidos, y el diaclasado semicurvo de alivio de carga (Ubanell, 1994; González-Laguna, 2005; de Vicente, 2009; Lozano y Jimenez, 2011). Ayala-Carcedo et al. (2002) identifican localmente los rumbos de estas dos familias principales de fallas como N25°O y N65°E. Estas direcciones, que poseen un desarrollo cuasi vertical bastante penetrativo y un espaciamiento de métrico a decamétrico, son las que determinan la compartimentación general del macizo, en forma de bloques delimitados por los diedros que forman ambas familias. Frecuentemente, estos bloques son descalzados por una familia subhorizontal de diaclasas que, a menudo, aflora buzando en el mismo sentido que la ladera (Sanz y Arenillas, 1981).
Factores geomorfológicos condicionantes
El rasgo más llamativo del relieve regional de La Cabrera es la notable disimetría que existe entre las laderas norte y sur (Figura 3a). El tallado de esta sierra es un ejemplo de inselberg o monte-isla, derivado de una erosión diferencial en el macizo oriental del Guadarrama (Sanz, 1988; Pedraza-Gilsanz, 1989). En este monte-isla la vertiente septentrional presenta una pendiente relativamente suave, y la meridional está caracterizada por un pronunciado y casi continuo escarpe de paredes rocosas muy verticalizadas. Las pendientes de la vertiente norte están tendidas en torno a los 15° y las de la ladera sur alcanzan los 75° (Sanz y Arenillas, 1981).
La fragmentación debida a la Orogenia Alpina (entre 35 y 17 m.a.), condiciona la morfología de los paisajes serranos y sus alrededores, marcando unas formas de relieve en los granitos a diferentes escalas, que son el resultado de la acción de distintos procesos de tipo estructural y climático. El diaclasado y la fracturación, como patrones de debilidad estructural impresos en la roca, se abren con la meteorización, marcando la morfología del paisaje con torrenteras orientadas NNE que compartimentan la sierra. A menor escala, la acción continuada de los mecanismos erosivos, principalmente debidos al hielo, lluvia y variaciones térmicas, sobre la vertiente sur, más alterable, ha dado lugar a un gran número de formas típicas de los paisajes graníticos más abruptos. En esta sierra es posible encontrar, en las zonas de cumbrera, domos campaniformes (afloramientos del granito que se va erosionando con forma de cúpula, p.ej., el Pico de la Miel), berrocales (estructuras graníticas que surgen cuando un domo es erosionado; esta erosión provoca grietas que dividen un bloque en varios, que aparecen apilados ordenadamente), cimas escarpadas, agujas, crestas, galayares, cornisas (p.ej., Agujas de las Pedrizas, la Peña del Águila), pedrizas, pináculos (tors), piedras caballeras (testigos esféricos) y formas redondeadas en las zonas de menor altura como lanchares o llambrías (superficies rocosas curvas e inclinadas que se forman a partir de diaclasas curvas), alternando con pendientes rocosas de material disgregado que forman laderas de transición hacias las zonas elevadas (Figura 2).
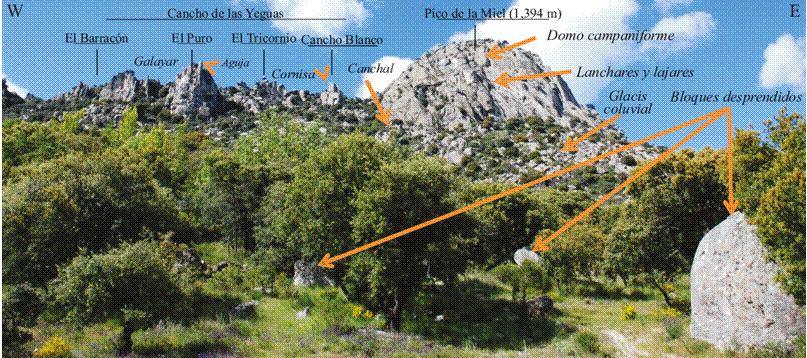
Figura 2 Panorámica orientada de acuerdo al eje E-O sobre la ladera sur del sector oriental de la sierra de La Cabrera (tomada desde La Encerrada, ubicada con un aspa  en la Figura 3a) en la que se destacan los rasgos geomorfológicos más notables del relieve en los granitos de la vertiente sur de la sierra.
en la Figura 3a) en la que se destacan los rasgos geomorfológicos más notables del relieve en los granitos de la vertiente sur de la sierra.
El patrón de debilidades estructurales que controla el paisaje de la sierra no se distribuye por igual. Hacia el sur, son frecuentes las diaclasas sensiblemente rectilíneas, verticales o subverticales y de variada orientación, que han dado lugar a la continua crestería de galayares y canchos (peñascos grandes) en los que culmina el escarpe meridional. Tales litoclasas son las que han guiado la evolución de la vertiente. Cuando la fracturación vertical es menos frecuente, como ocurre en el Pico de la Miel, la descompresión no ha podido canalizarse en su totalidad a través de estas litoclasas y el granito se ha fracturado frágilmente según nuevas disyunciones subparalelas a las superficie del terreno, acomodándose en mayor medida a las formas curvas características de estos peñascos, generando lanchares o domos. Cuando se presentan verticales y horizontales, sin predominio aparente de ninguna, aparecen los berrocales, formados por canchos y bolos, de aristas redondeadas, que pueden llegar a caer si se desestabilizan.
Al pie de las agujas y promontorios graníticos de la vertiente sur se encuentran mantos de derrubios que recubren parcialmente la ladera, que acaba formando un glacis o piedemonte coluvial, principalmente en sus partes medias y bajas. Las agrupaciones de los bloques y cantos angulosos desprendidos forman algunos canchales que, sin solución de continuidad, se extienden como conos de deyección al pie de la sierra. La localización del ápice y desarrollo de estos canchales parece estar controlada estructuralmente puesto que las rupturas de pendiente que definen el cantil-talud, que suelen ir asociadas a fallas u otros accidentes estructurales, en el caso de La Cabrera se orientan NNO. Los clastos, muy heterométricos, proceden del desmantelamiento de las áreas más altas y escarpadas, expuestas directamente a los fenómenos meteorológicos.
Las características geológico-estructurales y geomorfológicas así como la falta de una cobertura vegetal protectora en las partes más altas, confirman que la fracturación de la roca es uno de los factores condicionantes más relevantes para que surja un área fuente (Jaboyedoff et al., 1999; Jaboyedoff, 2002; Dussauge-Peisser et al., 2002). La localización de áreas fuentes parece no depender de las variaciones en el tipo de material, ya que la distribución litológica de los materiales es muy homogénea. Los bloques desprendidos que rodean al pie de la sierra meridional son testimonio del ataque violento de los agentes meteoríticos mencionados que desgajan los duros granitos del monteisla al debilitar los planos de discontinuidad presentes en el macizo.
MATERIALES Y MÉTODOS
Tras las consideraciones anteriores, cabe plantear que, en la sierra de La Cabrera, no hay inestabilidades si no hay discontinuidades que las condicionen. Así pues, la detección y caracterización de las discontinuidades, como planos de deslizamiento o desprendimiento, con posibles alteraciones de la roca, desplazamientos, arcillas, recristalizaciones o la circulación de agua, son necesarias para la localización de las zonas potencialmente inestables, como paso previo, ya que afectan al grado de estabilidad de la masa rocosa (Rouiller et al., 1998; Jaboyedoff et al., 2004).
Para delimitar las áreas fuente, zonas de desprendimiento de fragmentos o bloques rocosos, se han inventariado los planos de debilidad medidos en campo. Los datos estructurales han sido agrupados en familias según criterios geológicos y estadísticos. A continuación se analizan cinemáticamente las laderas de mayor desnivel y pendiente para evaluar si tienen una orientación desfavorable con respecto a cada familia de discontinuidades, considerando la probabilidad y densidad de afloramiento de éstas.
Trabajo de campo
Los datos que componen el inventario han sido recogidos en seis estaciones de medidas estructurales (señalados con un asterisco * en la Figura 3a) repartidas sobre el sendero PR-13 que discurre paralelo al eje E-O de la Sierra, por la vertiente norte, muy próximo a la línea de crestas desde donde se tiene constancia, por eventos pasados, que hay desprendimiento de bloques y fragmentos de roca. Se han tomado un total de 107 datos de planos de discontinuidad, espacio entre éstos y existencia de agua y arcillas. Para cada estación se ha representado la rosa de direcciones de los rumbos de las discontinuidades medidas (Figura 3b), en la que se distinguen tres modas direccionales en los rumbos: 0°, 60° y 120° (Tabla 1). La agrupación de los datos, de acuerdo al sector sobre el que se encuentra la estación de medida (oriental: 1, 2, 3, y 4; occidental: 5 y 6), permite identificar (Figura 3c) que mientras el rumbo 0° está presente en ambos sectores, el 120° prevalece en el más oriental, y el 60° en el más occidental.
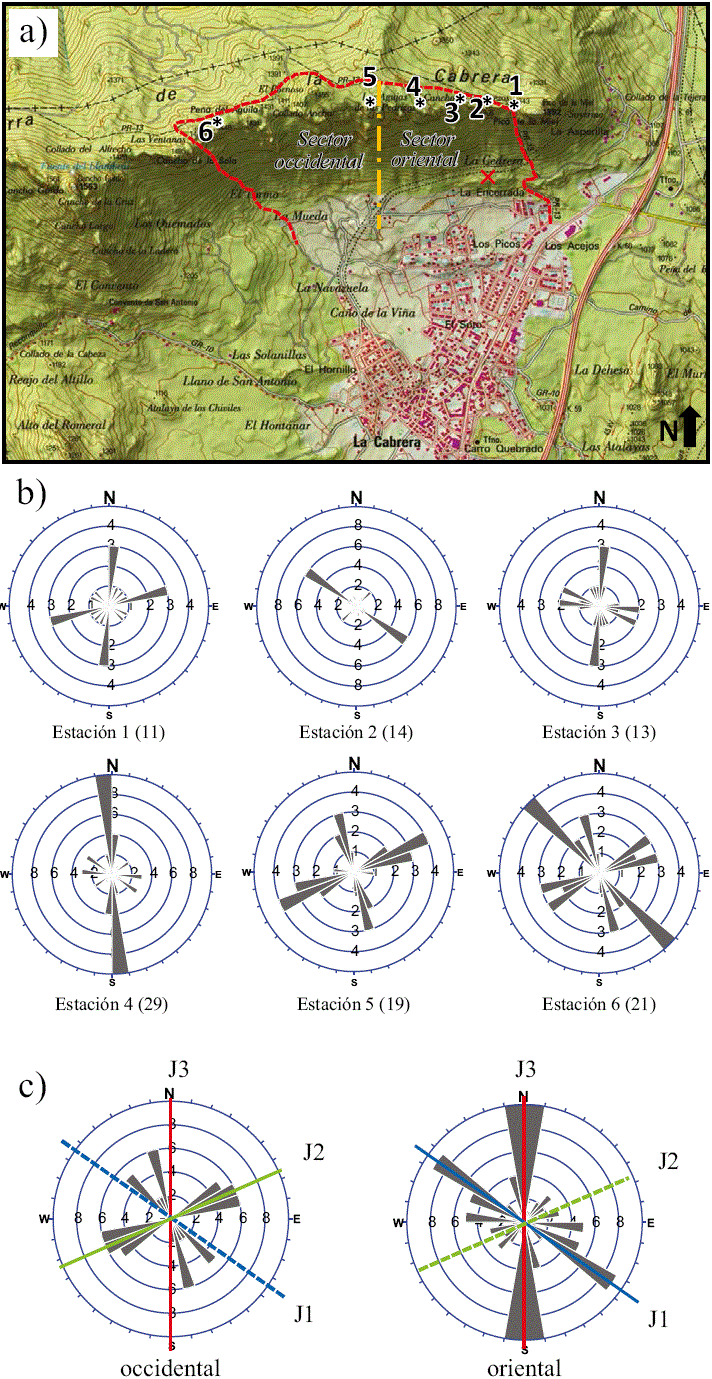
Figura 3 a) Topografía (extraída de la hoja 484-4, serie 1:25,000 del Instituto Geográfico Nacional) de la zona de estudio en la que se han ubicado las estaciones de muestreo (asteriscos * de 1 a 6). La línea discontinua representa el itinerario seguido sobre el sendero PR-13. b) Rosas de direcciones (rumbos) de la base de datos tomada en cada estación referenciada según su número (Figura 3a); número de datos en cada estación entre paréntesis. c) Rosas de direcciones para el sector oriental y el occidental (sectores separados en la Figura 3a por la línea -• -•) sobre las que se han marcado las direcciones encontradas más relevantes.
Tabla 1 Direcciones más frecuentes de las discontinuidades tomadas en las estaciones (*) de medida que se encuentran marcadas en la Figura 3a y encontradas en las rosas de direcciones de las Figuras 3b y 3c.

En la representación estereográfica de las medidas de dirección de buzamiento y buzamiento ha sido posible reconocer que los polos de los datos se agregan en torno a cuatro máximos de densidad (zonas más oscuras en la Figura 4a). Considerando la proximidad del polo (buzamiento, dirección de buzamiento) a los máximos de densidad de polos (Figura 4b), a las modas direccionales (Tabla 1) y las características genético-tectónicas regionales, las discontinuidades han sido agrupadas (Tabla 2) en cuatro familias estructurales denominadas J1: 80°, 212°; J2: 83°, 155°; J3: 83°, 83°; J4: 13°, 358° y J4*: 13°, 178° (familia: buzamiento, dirección de buzamiento). La variación de cada familia alrededor del polo medio no supera los 10°, tal y como indica el límite de confianza de 99.74 % para una función de densidad esférica de Fisher de parámetro K.
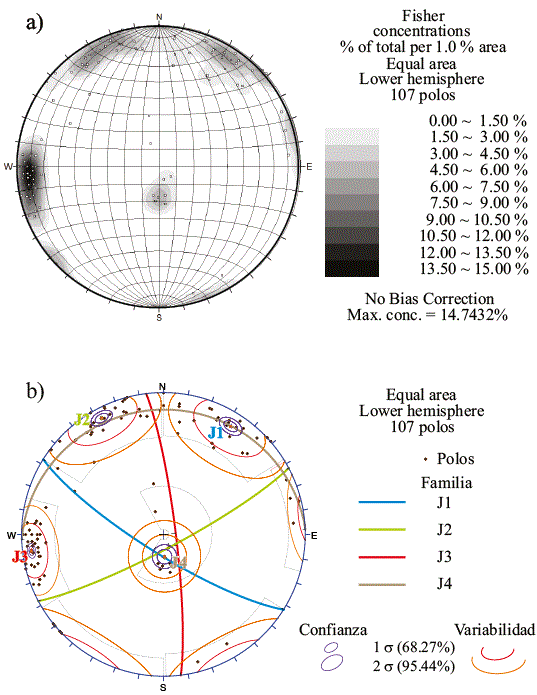
Figura 4 a) Representación estereográfica de áreas iguales de los polos medidos en campo y su densidad. b) Sectores utilizados para definir las familias J1, J2, J3 y J4 con sus respectivos círculos mayores y límites de confianza (azul) a 68.27 % y 95.44 %, y variabilidad (marrón) a una y dos desviaciones estándar.
Comparativamente, las familias J1 y J3 concuerdan con las direcciones tectónicas regionales ONO y NNE, respectivamente, identificadas en Lozano y Jimenez (2011); las familias J2 y J3 han sido identificadas en Ayala-Carcedo et al. (2002) como N25°O y N65°E, condicionantes de las inestabilidades.
En campo también se han reconocido conjunciones de discontinuidades (J1, J3) y (J2, J3) formando diedros de caras semiverticales que suelen estar descalzados por discontinuidades cuasi horizontales (Figura 5). Éstos se encuentran frecuentemente ubicados en zonas abruptas y escarpadas del acantilado rocoso, pero distribuidos desigualmente por sectores. Particularmente, en el sector oriental, predomina la conjunción J1 y J3 (Figura 5a); en cambio, hacia el oeste, es la J3 junto con la J2 (Figura 5b). Las discontinuidades cuasi horizontales pueden asociarse con la familia J4, cuyo polo medio orienta su buzamiento en contra de la ladera, tal y como ha sido identificado sobre el sector occidental, donde descalzaba los bloques y permitía su desprendimiento por gravedad (Figura 5c). Sin embargo, sobre el tercio más oriental de La Cabrera se ha observado (sin datos, por ser zonas inaccesibles) que la J4 buza a favor de la pendiente, encontrándose como base de lanchares y algunos deslizamientos planares, por lo que se ha incluido ésta como la familia J4* (Tabla 2).

Figura 5 Conjunciones de las discontinuidades encontradas en el terreno formando diedros. En a) diedros (J1, J3) descalzados por J4* a favor de la pendiente en el sector oriental del macizo; en b) paralelepípedos delimitados por (J2, J3) en el sector occidental; en c) descalce de los bloques por J4 a contrapendiente y deslizamiento por J4* a favor de pendiente.
Tabla 2 Familias Jen las que se han agrupado las discontinuidades.
| Familia | Promedio | K de Fisher | Límite de confianza al 99.74% | Lozano y Jimenez (2011) | Ayala-Carcedo et al. (2002) | ||
|---|---|---|---|---|---|---|---|
| Rumbo (°) | Dir. de buzamiento (°) | Buzamiento (°) | |||||
| J1 | N120°E | N210°E | 80° | 24.7 | 7.6° | ONO | - |
| J2 | N60°E | N155°E | 83° | 27.9 | 6.9° | - | N65°E |
| J3 | N0°E | N83°E | 83° | 54.6 | 4.4° | NNE | N25°E |
| J4 | - | N358°E | 13° | 47.9 | 9.6° | - | - |
| J4* | - | N178°E | - | - | - | - | - |
Los espacios registrados para las diferentes familias J1, J2, y J3 se encuentran alrededor de los 0.45 m, siendo el más probable de 0.25 m, aunque en algunas ocasiones ha sido posible encontrar espacios muy superiores a un metro (Figuras 5a y 5b). La familia J4 es la que presenta un espacio mayor con distancias entre discontinuidades superiores a un metro, frecuentemente hay 3 m de distancia entre una y otra, lo que origina bloques con una morfología prismática y propensos a que se desprendan inicialmente de la pared por vuelco y/o deslizamiento (bloque de la derecha en la Figura 5b). Estas dimensiones pueden dar lugar a unos bloques que, en la situación más desfavorable, pueden tener una decena de metros cúbicos.
Modelo digital de elevaciones MDE y modelo de pendientes MDP
La pendiente de la ladera es un factor que condiciona la inestabilidad de los bloques (Varnes, 1984). La mayoría de los estudios de peligrosidad utilizan este ángulo, como una variable independiente, a través de un factor de seguridad que cuantifica su tendencia a desestabilizarse (Cruden y Varnes, 1996). Tras el trabajo de campo se reconocieron muchas cicatrices de desprendimiento y posibles áreas fuente en la parte alta de los acantilados rocosos, en paredes muy inclinadas (> 40°), en zonas muy aéreas y expuestas. Esto confirma que los factores condicionantes morfológicos ligados al relieve son el desnivel local y la pendiente.
La localización de estas zonas altas escarpadas en la zona de estudio se ha hecho mediante un análisis morfométrico de los desniveles y las pendientes sobre el MDE. El MDE utilizado en este trabajo (Figura 6a), que procede del Centro Nacional de Información Cartográfica (Instituto Geográfico Nacional), ha sido calculado con 5 m de píxel mediante interpolación de modelos digitales del terreno procedentes del Plan Nacional de Ortofotografía Aérea (PNOA), de la cartografía 1:25000 y datos LIDAR. El tamaño tomado para el MDE, de 5 m de píxel, es lo suficientemente pequeño para permitir reproducir las fuertes pendientes de las rampas, caras rocosas y pequeños barrancos o torrenteras (Felicisimo, 1994) de la vertiente meridional de La Cabrera.
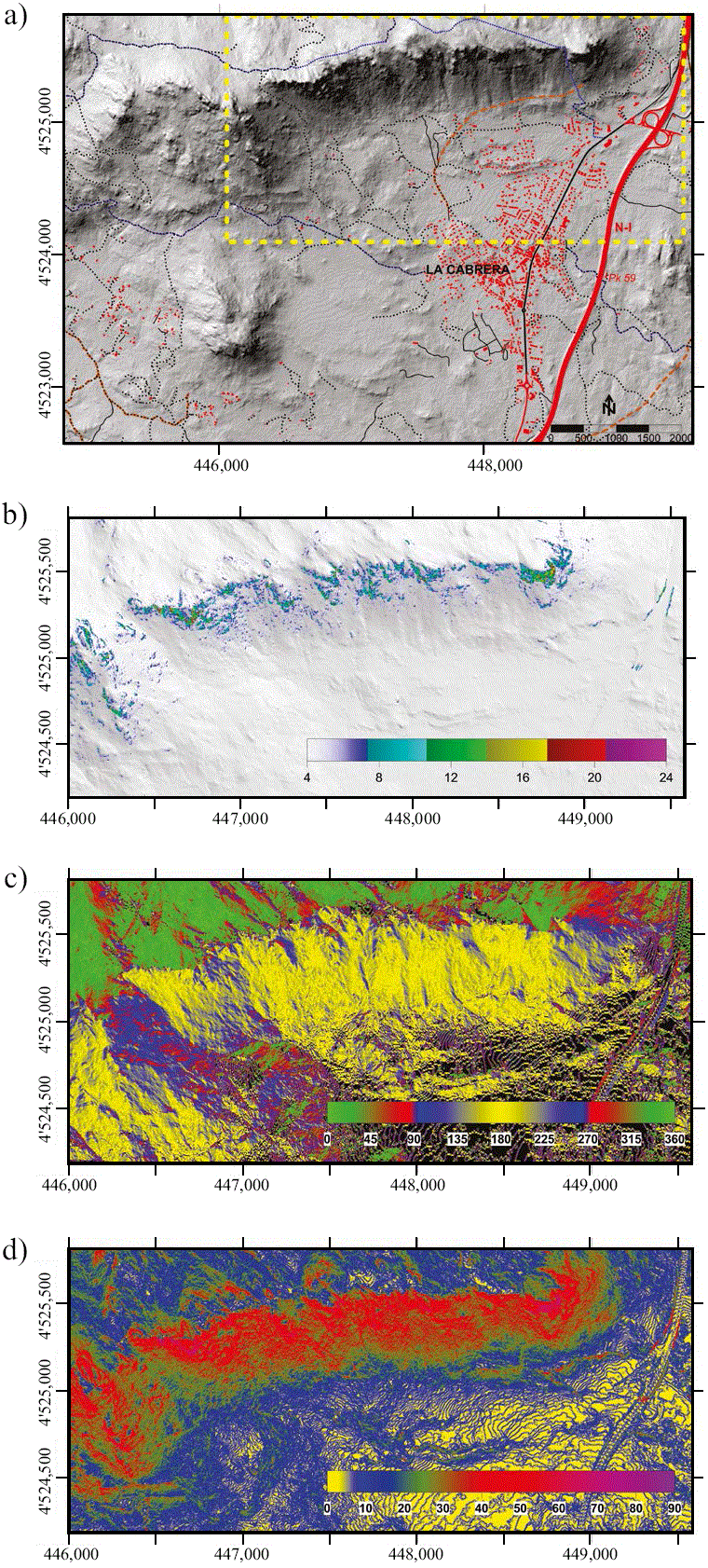
Figura 6 a) Modelo digital de elevaciones (MDE 5×5 m/píxel) procedente de la hoja 1:2500, 484-4 La Cabrera (Figura 3a). La zona de estudio sobre la que se va a analizar la distribución de desprendimientos de bloques queda enmarcada por el recuadro con línea discontinua. Para dicha zona se han calculado: b) modelo digital de máximas diferencias altimétricas (escala en m), c) modelo digital de pendientes según su ángulo y d) modelo digital de aspectos según su orientación respecto al N.
El desnivel o altura del acantilado ha sido estimada en cada punto (píxel) del MDE calculando las máximas diferencias hipsométricas entre éste y los puntos adyacentes en un entorno de 5 m. La distribución de desniveles así obtenida (Figura 6b) muestra que hay zonas donde las paredes pueden llegar a salvar diferencias de 24 m en la vertical. En estas zonas es donde, de acuerdo a Varnes (1984), Jaboyedoff et al. (1999), Jaboyedoff et al. (2003), Guzzetti et al., (2003), Ferrero et al. (2011), entre otros, pueden encontrarse las zonas fuente, cuya susceptibilidad al desprendimiento sea mayor cuanto mayor sea su desnivel local.
El modelo digital de pendientes (MDP) ha sido calculado como la tasa de máximo cambio que se produce en la altura al pasar de un punto a otro suficientemente próximos (Felicisimo, 1994). Se ha obtenido el MDP (Figura 6c) en cada punto del MDE, a partir de las alturas en los cuatro píxeles más próximos a éste, como el gradiente hipsométrico del terreno, transformado a grados de inclinación respecto a la horizontal.
La delimitación de las áreas fuente sobre el MDP utiliza la definición de un umbral en la inclinación del terreno (Toppe, 1987; Van Dijke y Van Westen, 1990), valor característico del área a partir del cual el material que lo forma tiende a desestabilizarse. En macizos rocosos cristalinos este umbral resulta estar relacionado con el ángulo de fricción interno a escala de macizo (Loye et al., 2009; Fernández-Hernández et al., 2012; entre otros). Según Loye et al. (2008) la distribución de frecuencias de las pendientes permite obtener el ángulo de fricción interno asociado a cada unidad morfológica del macizo, el cual puede considerarse como umbral crítico por encima del cual la pendiente puede ser inestable.
Para destacar las zonas más propensas al desprendimiento de rocas, el área de interés ha sido subdividida en unidades, de acuerdo a las características geomorfológicas de sus pendientes (Strahler, 1950) y su distribución estadística de frecuencias. Esta distribución ha sido planteada como el histograma del gradiente hipsométrico transformado en grados. En este histograma, la frecuencia relativa, en cada clase angular de pendientes, ha sido ponderada por el inverso del coseno de la pendiente para reducir el efecto de sesgo debido a que el área planimétrica en zonas de elevada pendiente es menor que su superficie real en el terreno.
Ya que el histograma de pendientes del MDP recoge conjuntamente el de todas las unidades morfológicas presentes en la zona, el resultado es la composición de unos con otros, obteniéndose un histograma multimodal (línea de rombos ♦ en la Figura 7a). En éste no es posible una detección directa, sobre sus máximos (aproximadamente 3°, 10°, 15° y 30°), de un único valor de la pendiente crítica para las zonas de mayor pendiente, ya que son ángulos inferiores al encontrado en el terreno como umbral de los desprendimientos (> 40°). Para identificar un ángulo crítico en cada unidad, el histograma de frecuencias ha sido desagregado en funciones gausianas de probabilidad mediante una formulación óptima basada en el método de maximización de la esperanza o EM (Expectation Maximization en Dempster et al. 1977). El método de optimización EM aplicado a una mezcla de distribuciones gausianas (McLachlan y Krishnan, 1997) ha permitido obtener la media, la varianza y el peso relativo de la distribución de los ángulos de pendientes para cada unidad morfológica o distribución gausiana de la unidad morfológica o GDMU (Gaussian Distribution of a Morphological Unit en Loye et al. 2009). Las distribuciones gausianas resultantes de la desagregación (distribuciones en trazo continuo en la Figura 7a) poseen valores medios o máximos en 2.6°, 8.6°, 24.7° y 42.2° (señalados en la Figura 7a), que caracterizan el ángulo de fricción promedio del terreno en cada una de las unidades morfológicas (Loye et al., 2009). Así, ha sido posible identificar cuatro unidades morfológicas en la zona de La Cabrera, con un ángulo de fricción promedio asociado según la media de las GDMU obtenidas: los llanos y rampas leves (2.6°), los pies de ladera y relieves suaves asociados a depósitos (8.6°), las faldas de sierra (24.7°) y crestas o acantilados semiverticales (42.2°). En estos últimos se evidencia la existencia de una unidad morfológica asociada a los mayores desniveles en la zona, donde se encuentran los riscos, escarpes, farallones y agujas, subelementos desde los que se desprenden los bloques. Esta unidad morfológica posee un ángulo de fricción de unos 43° que es coherente con la pendiente umbral observada en el terreno (> 40°) y con los valores indicados por otros autores (e.g. > 45° Jaboyedoff y Labiouse, 2004; > 37° Frattini et al., 2008). Su distribución geográfica (Figura 7b), se ha obtenido limitando la representación a valores de pendiente mayores de 40°. En la leyenda inferior de la Figura 7a se indica la subdivisión de las crestas en subelementos morfológicos.
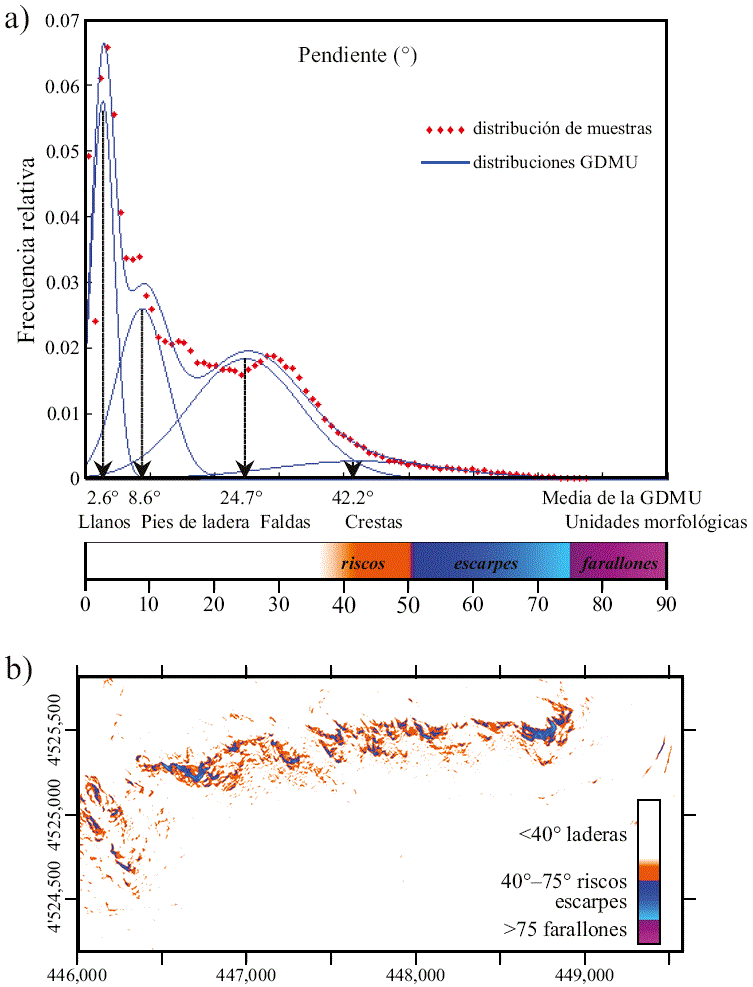
Figura 7 Análisis morfométrico de descomposición del modelo digital de pendientes. a) Distribución de frecuencias de pendientes medidas (puntos) y su descomposición EM-GDMUs calculada (curvas de trazo continuo) y acumulada (envolvente trazo continuo). b) Distribución de las zonas propensas a sufrir inestabilidad teniendo en cuenta el criterio de pendiente superior al valor de 40°.
Identificación de zonas estructuralmente inestables
Además de la influencia morfológica del relieve sobre la inestabilidad, existe una influencia estructural ligada a la orientación relativa de las discontinuidades respecto al relieve. En particular, cuando éstas poseen una dirección de buzamiento semejante a la orientación local (aspecto) de la ladera (Figura 6d) y su pendiente es mayor que el ángulo de fricción φ en la discontinuidad, es frecuente que se produzcan deslizamientos planos de rocas. Considerando el par dirección de buzamiento y buzamiento (αl, βl ) para la cara de la ladera y (αd, βd ) para el plano de la discontinuidad, las condiciones estructurales para que un bloque se desestabilice (Wyllie y Mah, 2007) son:
El buzamiento de la discontinuidad debe ser menor que el de la ladera: βd < βl ,
La dirección de buzamiento de la discontinuidad debe estar a 20° de la dirección de buzamiento de la ladera: αl 20° < αd < αl + 20°,
El buzamiento de la discontinuidad debe ser mayor que la fricción: βd > φ,
Las pendientes del terreno en la unidad morfológica anteriormente reconocida como propensa a liberar bloques poseen 90° > βl > 40°. Entonces, según la Tabla 2, solo las familias J4 y J4* (βd = 13° < βl ) verifican la condición a), y de ambas, solo J4* es la única capaz de producir deslizamientos planos, ya que según su dirección de buzamiento (αd = 178°) J4* se orienta a favor de la ladera (αl ~ 180°). Por el contrario, la J4 solo sería capaz de producir descalces o viseras por descuelgue de los bloques al buzar en sentido contrario (αd = 358°) a la ladera. En la Figura 8a se representan las zonas pertenecientes a la unidad morfológica de crestas y acantilados donde se verifican las tres condiciones para J4*, por lo que pueden concebirse como áreas fuente. Esta distribución ha sido obtenida sobre un SIG a partir del modelo digital de aspectos (Figura 6d) sobre el que se han realizado las operaciones lógicas condicionales que establecen las tres situaciones estructurales anteriores.
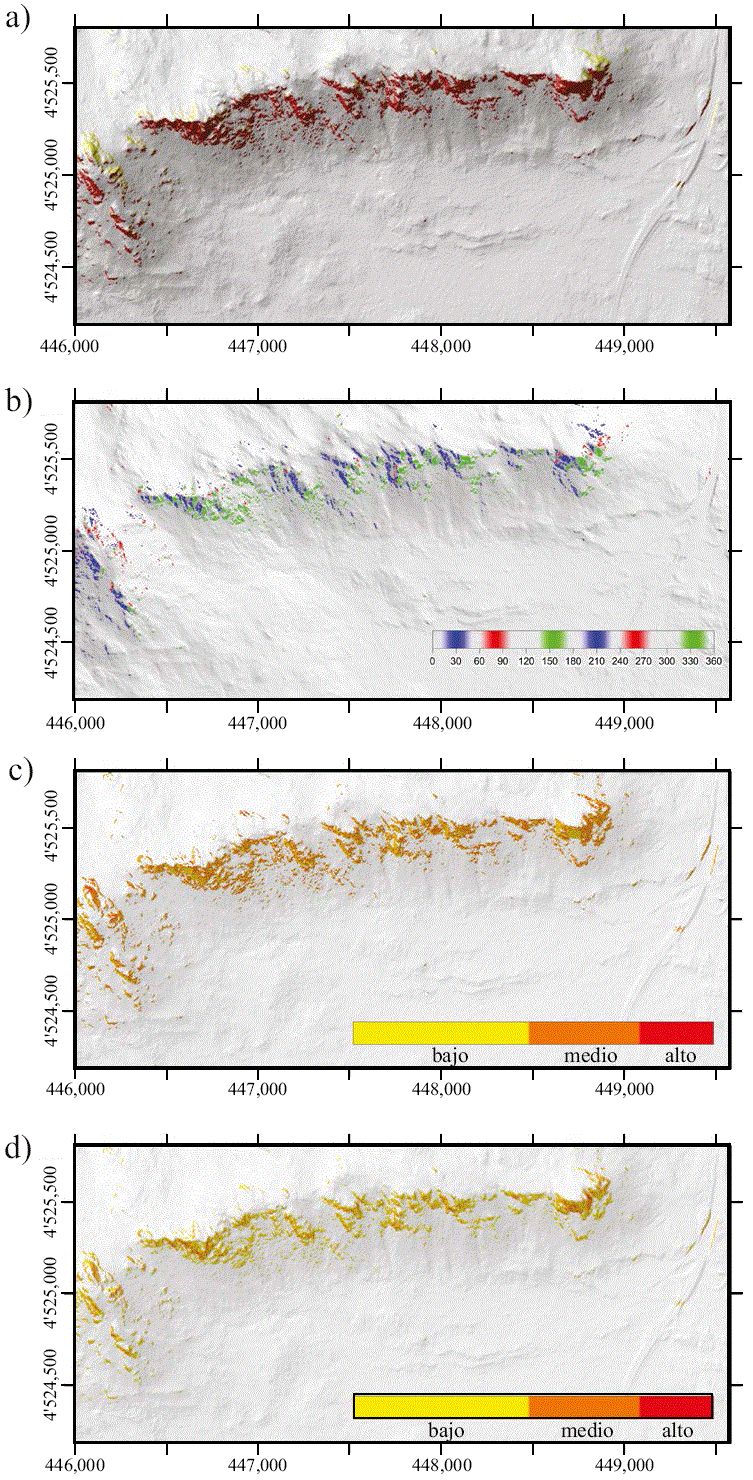
Figura 8 Resultados del análisis del condicionamiento estructural en superficie. Distribución de los puntos en los que: a) es probable una inestabilidad por deslizamiento plano sobre la familia J4* (178°, 13°); b) ) la orientación del relieve βl [βd-20°, βd+20°], siendo βd la dirección de alguna de las familias de discontinuidades geológicas sub-verticales (J1, J2, J3), en las zonas del área de estudio donde la pendiente es superior a los 40°. Distribución en las zonas por sectores, con pendiente > 40°, de los valores relativos de: c) número medio de discontinuidades para cada familia que, por píxel del MDE, afloran en superficie; d) número de cuñas de geometría coherente con la orientación del relieve, para los diedros observados sobre el terreno (J1/J3, J1/J4, J2/J3, J2/J4 y J3/J4).
Un estudio detallado del modelo digital de aspectos permite identificar las zonas donde las familias J1, J2 y J3 verifican solo la condición b). En estas zonas (Figura 8b) las discontinuidades de cada familia limitan lateralmente la extensión del bloque o bien por su cara externa (por la orientación del relieve) o bien por su cara interna (si es que el bloque fue liberado y es lo que muestra ahora la superficie topográfica). Además, en caso de encontrarse una discontinuidad J4, ésta produciría un descalce en los bloques por su base, aumentando la posibilidad de desprendimiento por desplome.
La persistencia con la que afloran las discontinuidades también influye en la inestabilidad ya que modifica el grado de tectonización del macizo (Rouiller et al., 1998; Jaboyedoff y Labiouse, 2004, entre otros). Para conocer cómo se distribuye, para cada familia, la persistencia de afloramiento sobre el terreno se ha usado el método Matterock (CREALP, 2003). Con éste es posible estimar el número promedio de discontinuidades de una familia que afloran sobre un dominio estructural homogéneo, comparando las características estructurales con la superficie topográfica (Jaboyedoff, 2003). Si se conoce la orientación media, el espaciado medio y una longitud media de la traza de una discontinuidad, es posible determinar el número de discontinuidades por unidad de área en la superficie. Así mismo, con este método, teniendo en cuenta la frecuencia de afloramiento conjunto de dos familias de discontinuidades y su orientación relativa, es posible localizar y valorar los lugares sobre el MDE en los que una pareja de familias se conjugan para producir diedros. De esta manera puede estimarse la probabilidad de encontrar, al menos, una discontinuidad en la superficie.
Así, para cada familia estructural (J1, J2, J3 y J4) y para las parejas de las que se ha observado forman diedros (J1/J3, J1/J4, J2/J3, J2/J4 y J3/J4), se han obtenido la distribución del número medio de discontinuidades y de diedros que afloran en superficie, para todos los puntos del MDE cuya 90° > βl > 40°. Para obtener una distribución que recoja el comportamiento de la persistencia conjunta de todos los patrones estructurales, tanto los que se evaluaron individualmente como los que forman diedros, y dado que hay notables diferencias de persistencia entre las familias, los valores absolutos obtenidos para cada familia se relativizaron, de forma que fue posible integrar el resultado en un solo mapa (Figuras 8c y 8d).
Como el comportamiento de la susceptibilidad al desprendimiento está relacionado al factor condicionante de la fracturación, se establecieron tres niveles arbitrarios para valorar su influencia, de acuerdo a los valores relativos de la distribución de la persistencia: baja, hasta el 50 %, media, hasta el 75 % y alta, hasta el 100 %.
Síntesis y verificación de zonas de desprendimiento
El conocimiento del relieve físico, de sus formas particulares y de su morfometría, es necesario para asegurar una identificación objetiva de las posibles zonas de desprendimiento de bloques; más allá de las que, por ser inaccesibles, pudieran localizarse sobre el terreno. La combinación de los resultados obtenidos en los epígrafes anteriores ha permitido elaborar un mapa integral de posibles áreas fuente sobre el Macizo de La Cabrera (Figura 9a) con alta susceptibilidad al desprendimiento. El mapa recoge la distribución de los puntos del área de estudio (Figura 6a) que tienen una diferencia altimétrica superior a los 10 m (Figura 6c), una pendiente superior a la crítica de 40° (Figura 7b) y, verifican al menos, una de las siguientes condiciones:
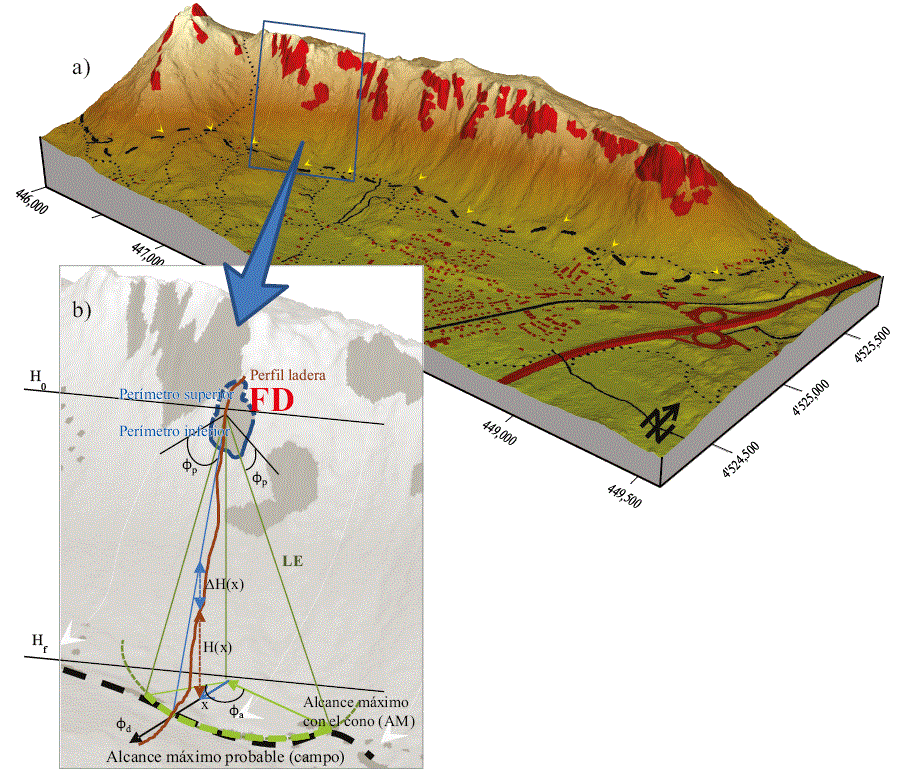
Figura 9 Representación en tres dimensiones de la síntesis de zonas susceptibles a ser área fuente y línea de máximo alcance probable. Esquema del modelo geométrico de fricción del cono con las variables implicadas en el cálculo.
Inestabilidad probable por la orientación de J4* (Figura 8a).
a)Una orientación paralela a alguna de las familias J1, J2 o J3 (Figura 8b).
Elevada persistencia relativa de afloramiento de familia coherente con la orientación del relieve (Figura 8c).
Elevado número relativo de cuñas (diedros entre pares de familias) coherentes con la orientación del relieve (Figura 8d).
MODELIZACIÓN DEL ALCANCE DE BLOQUES
En el macizo de La Cabrera, los desprendimientos se caracterizan por la rotura de bloques aislados con volúmenes inferiores o iguales a los 100 m3, cuyas trayectorias son independientes; es decir, si se libera más de un bloque en un mismo evento, éste no interactúa con el resto, por lo que se podría usar el modelo del ángulo de sombra. Por otra parte, las áreas fuente (Figura 9a) se encuentran en la parte más alta de la falda serrana (Figura 6b), como continuación inmediata de las mismas sobre la pared rocosa, y con un fuerte cambio de pendiente media (aproximadamente el doble). Por ello, el modelo recomendado a utilizar sería el de ángulo de alcance máximo. Sin embargo, ya que la diferencia de cota entre la cabecera del talud y la cresta de las áreas fuentes es del orden de 20 m (Figura 6c) como máximo, y la distancia horizontal que se ha registrado en los bloques más alejados es de unos 500 m, la diferencia entre el ángulo de máximo alcance (Heim, 1932) y de sombra (Lied, 1977), es prácticamente despreciable para todas las áreas. Así ambos métodos, en el caso de La Cabrera, son equivalentes, y pueden ser reunidos en un solo ángulo φp , ligado al coeficiente de fricción cinemática del terreno (Scheidegger, 1973), teniendo en cuenta que la línea de energía, que une el punto de desprendimiento con el de parada, representa el promedio de pérdidas energéticas del bloque o fragmento por impacto, fricción, deslizamiento o rodadura a lo largo de su trayectoria. Por las características estructurales y morfométricas de cada área, además de su localización geográfica, el φp puede variar de un área a otra, a lo largo del eje de la sierra.
Para realizar las simulaciones del alcance de un bloque emitido desde cualquiera de las áreas fuente, en este trabajo se ha utilizado un modelo empírico que utiliza una relación estadística entre los parámetros topográficos de la inestabilidad o del talud y la distancia recorrida (Corominas, 1996). La extensión a tres dimensiones del modelo empírico se denomina método del cono (Jaboyedoff y Labiouse, 2001, 2004 y 2011). Los modelos empíricos se basan en simplificar la trayectoria del principio de conservación de la energía, lo que conlleva un error cuyo margen es admisible en estudios preliminares a media escala. En tres dimensiones la línea de energía es la generatriz de un cono cuyo vértice está en un punto del área fuente (Figura 9b), y su directriz es la intersección de la superficie del cono con la superficie topográfica. La pendiente φp de la generatriz (LE) que se encuentra a una cota H0 , uniendo la cabecera del área fuente del desprendimiento (FD), con el punto más lejano de la avalancha, a una cota Hf , es:
Tan φp= (H0-Hf)/AM,
a partir de la línea perimetral de alcances máximos (AM) de una avalancha desde FD, o directriz del cono.
La energía perdida por la caída de la masa rocosa a lo largo de su trayectoria se aproxima con la debida a la fricción, en promedio, cuasilinealmente con un coeficiente de fricción μ. Suponiendo un bloque de una masa puntual, la energía cinética de rotación es despreciable en comparación con el resto de energías implicadas. El balance de la energía mecánica entre el instante inicial y un punto de la trayectoria a una distancia x, recorrida en la horizontal, establece que la energía potencial inicial se ha transformado en energía cinética, energía de fricción disipada hasta el punto x y energía potencial restante hasta que se detenga:
De acuerdo con la geometría del triángulo FD-AM-LE (Figura 9b), en el que la distancia recorrida es x = AM, en cuyo punto se detiene v(AM) = 0, tras superar el desnivel H(AM) = H f , el coeficiente de fricción cinemática es:
μ = (H0-Hf)/AM = Tan φp
es decir, el bloque se detiene en el lugar donde la línea LE trazada desde el área FD y con una pendiente φp con la que intersecta en la superficie del terreno ladera abajo.
Por otro lado, a partir de (1), la velocidad instantánea del bloque:
y teniendo en cuenta que:
La velocidad v(x) es independiente de la masa del bloque y depende de la distancia que hay entre la superficie topográfica y la línea de energía ∆H(x):
Una vez calculada el área potencialmente afectada por un posible bloque desprendido desde FD y las velocidades en cada punto interior de cono, que dista x de FD y al que le corresponde un ∆H(x), para evaluar la energía cinética del bloque, se corrige v(x) con un factor f < 1, de acuerdo a:
f2= 1-(Erot/Ekt) = Etr/Ekt
que considera cuánta energía es por pura transformación de la energía cinética total. El factor f, incorpora la pérdida energética debida a los sucesivos rebotes que tiene en su trayectoria (Pasquier et al., 2010) y que afecta a la velocidad:
Y a la energía cinética debida al desplazamiento, a una distancia
El modelo empírico del cono en tercera dimensión, de acuerdo a la formulación descrita, y que ha sido utilizado en este trabajo, se encuentra implementado en Conefall (Jaboyedoff y Labiouse, 2011), un programa informático que resuelve las áreas de afectación o áreas potenciales de propagación de un bloque que se desprende de un área fuente sobre un MDE. Para cada área fuente, se proporcionan tres argumentos (Figura 9b): el ángulo de alcance máximo φp , el ángulo de apertura φa del cono y la dirección en la que salen desprendidos los bloques φd , con los que se definen las dimensiones del cono.
Elección de los ángulos de φ p sombra, dispersión φ a y orientación φ d
La localización de los bloques desprendidos en eventos pasados y la delimitación de sus áreas fuente es un paso crítico previo a la simulación con los modelos empíricos. La distancia máxima a la que llegan los bloques y el desnivel salvado en su caída desde FD en la pared rocosa controlan φp . El término mínimo φp define el ángulo más pequeño que pueda encontrarse en la zona local de estudio que usualmente corresponde con el bloque más alejado. Esta inclinación varía según las condiciones del terreno y el alcance (Guzzetti et al., 2003; Jaboyedoff et al., 2003; Frattini et al., 2008), aunque estudios posteriores han demostrado que se encuentra relacionada con el volumen de roca movilizado (Corominas, 1996; Jaboyedoff y Pedrazzini, 2008). Por ello, si se pretende capturar su variabilidad local, su elección debe hacerse particularmente para cada área fuente. Comparando los valores aportados por varios autores, el ángulo mínimo se suele encontrar entre los 17° y 32° (Lied, 1977; Evans y Hungr, 1993; Domaas, 1994; Wieczorek et al., 1999; Dorren, 2003; Copons et al., 2009), según las condiciones del terreno y la dimensión del desprendimiento.
Para asignar un valor de φp en cada área fuente de La Cabrera, se ha situado el vértice de un cono sobre su centro y la directriz sobre el límite perimetral de los alcances máximos probables AM. El ángulo de su generatriz (recta FD-AM) con la horizontal se ha tomado como estimación de φp preliminar propia del área fuente.
Las trayectorias de los bloques rocosos se encuentran fuertemente influenciadas por las condiciones geométricas y mecánicas del terreno por lo que su representación en tercera dimensión es mucho más compleja que en dos dimensiones, entre otras razones, porque aparece una dispersión lateral condicionada por la rugosidad del terreno y su representación digital o MDE (Crosta y Agliardi, 2004). La dispersión puede estar condicionada si la trayectoria se canaliza en una torrentera y en cuya salida da lugar a un cono o abanico de depósitos. Sin embargo, a pesar de que algunas torrenteras surcan la vertiente sur de La Cabrera, no se han encontrado evidencias de conos de material desprendido sino más bien bloques dispersos por todo el piedemonte. Por ello, la geometría del cono de propagación ha sido limitada lateralmente con un ángulo que representa la dispersión lateral que se estima pueda producir un área fuente. Este ángulo configura geométricamente un sector de cono (un cono cuya base es un sector circular) cuya apertura se asigna mediante el valor φa (Figura 9b).
El tercer parámetro, que determina la geometría no axi-simétrica del sector de cono, es su orientación φd . Cuando un bloque se desprende lo hace en una dirección respecto al Norte. Esta dirección está determinada generalmente por el aspecto de la cara rocosa en FD y condiciona desde el instante inicial el desarrollo de la trayectoria. Geométricamente, para orientar el sector de cono, se ha tomado φd como el ángulo formado entre el Norte y la orientación del punto medio del arco circular que modela el máximo alcance, respecto al eje del cono, desde la fuente FD (Figura 9b).
Para la elección de los ángulos se ha asignado inicialmente sobre cada área φ0 p y φ0 a , mientras que φd se fija según el aspecto del MDE (Figura 6d) en el punto de desprendimiento. El valor inicial de φ0 a =15° en todas las áreas fuente, lo que a 500 m son unos 65 m de dispersión a cada lado de la dirección marcada por Nφ0 a E desde un área de desprendimiento. Por otro lado, φ0 p se calcula tomando n bloques en el talud, que proceden supuestamente de la misma FD (a cota Hf ), cada uno a distancia di , y cota Hi , valores que se obtienen sobre la ortofoto calibrada de la zona y de su ubicación con un aparato de posición geográfica (GPS) durante el trabajo de campo. Se propone tomar el promedio:
A continuación, individualmente para cada área de desprendimiento, se han realizado simulaciones del modelo empírico del cono para la calibración de (φp, φa, φd ,) contra la línea perimetral de alcances máximos (modificada de Ayala-Carcedo et al., 2002), representada en la Figura 10a. Esta línea ha sido trazada mediante la localización con GPS de los bloques caídos en la zona de estudio. Los valores obtenidos para φd ∈ [25°, 32°], varían de este a oeste levemente, en el rango admisible referido bibliográficamente y sin un patrón reconocible (Figura 10a) a lo largo del eje de la sierra. Concretamente, para esta zona, Ayala-Carcedo et al. (2003) proponen un valor promedio único de 28° sobre toda la cumbrera del macizo.
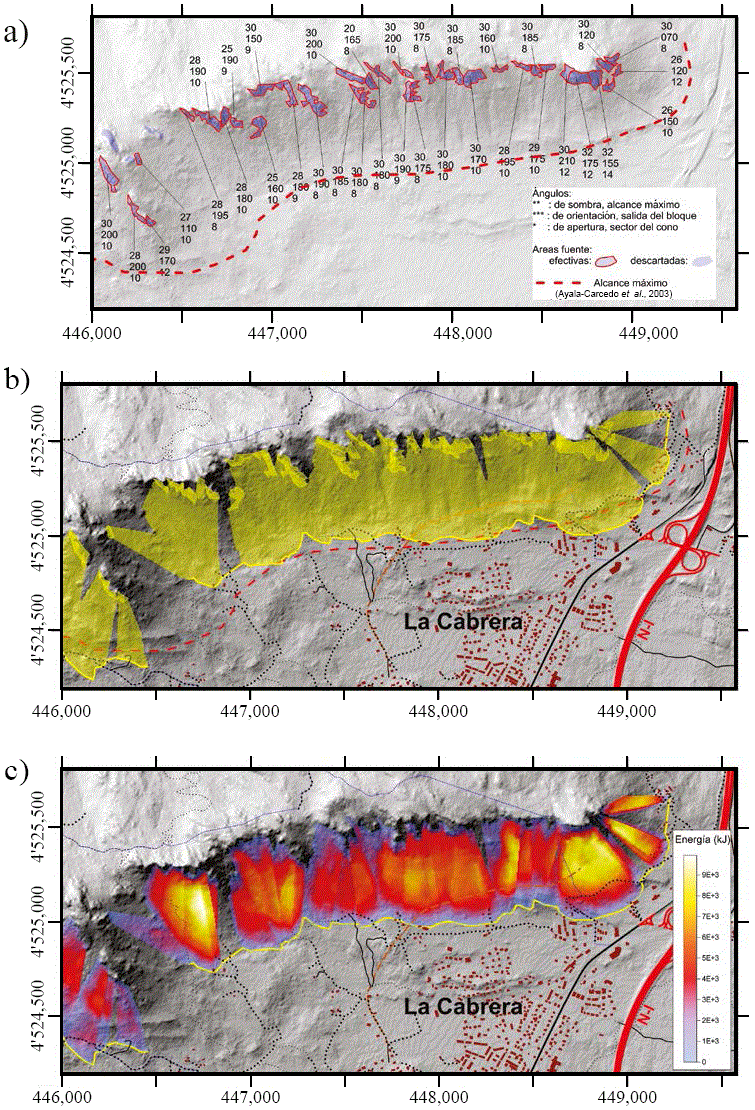
Figura 10 a) Datos de entrada al modelo: argumentos (φp, φd, φa ) calibrados para cada área fuente efectiva utilizada en el cálculo de los alcances con el modelo empírico. La línea discontinua representa el alcance máximo utilizado en la calibración. b) Resultados del modelo: representación conjunta para todos los conos de la distribución del área de afectación (sombreado en amarillo) y los máximos alcances; c) representación conjunta de las máximas energías (en kJ) de caída de un bloque resultado del solape de las simuladas sobre cada área fuente.
Los valores de φa ∈ [16°, 24°] han sido calibrados de acuerdo a la longitud del arco que abarca el cono a fin de que, en el área afectada, la dispersión de la trayectoria desde cada fuente, tenga como ancho un tramo de AM suficientemente largo, tratando que el solapamiento entre los conos sea verosímil. En algunos casos, un φa mayor produce una dispersión lateral del cono que se traduce en una acumulación aparente de bloques en los bordes, y si éste se reduce, los resultados muestran unos bordes rectos, que corresponden con el borde geométrico del cono sin afectar por el relieve.
RESULTADOS
Tras la calibración geométrica del modelo empírico en la que se han asignado la terna de argumentos a cada área fuente, se ha tomado un bloque del mayor tamaño observado de 4×3×1 m3 y 30,000 kg, según los espaciamientos entre discontinuidades y el tamaño de bloques en el piedemeonte (granito de densidad media 2,700 kg/m3), para obtener la estimación de la distribución de velocidades y energías del bloque en la situación más desfavorable. El factor de pérdida energética f tomado es 0.6 en las ecuaciones (5) y (6), excepto en la zona del Pico de la Miel que, por ser donde se encuentran las mayores alturas de escarpe (Figura 6c) y dar lugar a trayectorias más aéreas, se ha tomado un valor de 0.8. Esto implica que las energías rotacionales representan alrededor del 30% al 50% de la energía cinética total del bloque, según donde se produzca el desprendimiento.
El pronóstico de la línea de máximos alcances ha sido calculada como la línea envolvente perimetral de los máximos alcances de todos los conos simulados con Conefall usando los parámetros (φp, φa, φd) calibrados en cada área individual (Figura 10a). Los alcances obtenidos (Figura 10b) se encuentran marcadamente condicionados por la morfología del relieve en la zona más baja del piedemonte, es decir, en la intersección de cada cono trazado desde cada área fuente con la superficie del terreno.
La distribución de energías sobre toda el área se determina, inicialmente, por separado desde cada área, evaluando las velocidades (ecuación 5) y energías (ecuación 6) en el cono de afectación. A continuación, se componen los conos de cada área fuente para extraer la máxima energía que haya en cada punto del terreno entre todos los conos que se solapan en éste (Figura 10b) como el escenario más desfavorable. La velocidad máxima obtenida en el área de estudio es 25.7 m∙s-1 al pie de las crestas de mayor pendiente y mayores diferencias altimétricas. Particularmente, las mayores energías se producen bajo el Pico de la Miel y el Cancho de la Bola, siendo en este último bajo el que se localizan los mayores valores de energía, 9,950 kJ para un bloque de 30 tm. Por la orientación de sus áreas fuente, los bloques de mayor energía, se desprenden en dirección SSO, lo que marcaría su trayectoria en un primer tramo y se modificaría después para tomar dirección SSE por la morfología y dirección del gradiente regional, llegando a alcanzar moderadamente algunas zonas urbanizadas.
DISCUSIÓN Y CONCLUSIONES
El problema de análisis preliminar de la susceptibilidad a la caída de bloques desde las áreas fuente que se han delimitado sobre la sierra de La Cabrera, ha sido resuelto mediante un método empírico basado en el ángulo de máximo alcance que se encuentra implementado en el programa Conefall. La simplificación lineal realizada sobre las pérdidas energéticas por fricción (impacto elástico, rodadura y deslizamiento) de un bloque de masa puntual, descarta la necesidad de utilizar las características geomecánicas y de un MDE muy detallado, así como obtener información costosa, heterogénea y de difícil certidumbre en terrenos tan irregulares como los montañosos. Por ello, resulta ser un método que se adapta muy bien a extensas regiones con este tipo de peligros geológicos, sobre las que no es posible recoger todos los datos del terreno que harían falta para un modelo físico (cinemático y dinámico) de las trayectorias. El modelo empírico puede ser representado geométricamente en tres dimensiones como un cono de fricción vertical, cuyo vértice se sitúa sobre el área de desprendimiento, y su traza es la línea de máximos alcances en la superficie de terreno. La región que queda dentro de la proyección del cono sobre el terreno recoge los puntos que pueden ser alcanzados por la trayectoria de un bloque.
Sin embargo, el método empírico, al estar basado en el máximo alcance, debe de ser aplicado cuidadosamente. No todos los bloques rocosos desprendidos pueden tener la misma línea de energía, luego el ángulo de alcance puede variar para cada área potencialmente inestable. Por ello, las áreas fuente deben ser apropiadamente ubicadas y medidas en cuanto a su localización, geometría, dimensión de los bloques que liberan, incluso la orientación del desprendimiento. Es decir, para cada área fuente debe describirse su geomorfología detallada y, de ser posible, estudiarse particularmente sobre el terreno. Por ello ha sido necesario definir el conjunto de áreas fuente de bloques de acuerdo a los factores condicionantes más relevantes en la zona, considerando su geología, tectónica, y geomorfología, y las características morfométricas del MDE.
Los datos geológicos estructurales, recogidos en las zonas de las cumbreras, han definido cuatro familias de discontinuidades como principales condicionantes estructurales del desprendimiento de los bloques, cuyos rumbos son para la J1: 120°; J2: 60° y J3: 0°, muy verticales (buzamiento ~83°), y las familias prácticamente horizontales (buzamiento ~13°) de direcciones de buzamiento J4: 358° y J4*: 178°. Las conjunciones (J1/J3) y (J2/J3), según el sector del macizo, forman diedros que limitan lateral y verticalmente las caras de los bloques que pueden desprenderse, que son descalzados, en su parte inferior, por la familia J4 (sector occidental) o J4* (sector oriental). El espaciado entre las familias que delimitan un bloque da lugar a que éstos puedan llegar a tener hasta 30000 kg de peso. Las zonas de desprendimiento que delimita la familia subhorizontal J4 están establecidas porque aflora muy frecuentemente sobre las paredes rocosas de la vertiente sur, tal y como se observó sobre el terreno. Normalmente, aparecen en conjunción con las familias J1, J2 y J3, formando diedros y triedros, y delimitando inferior y superiormente la dimensión del bloque; así, cuando está buzando en el mismo sentido que la ladera (sector oriental) da origen a los lanchares, si lo hace en sentido contrario (sector occidental) genera desplomes y viseras. Las caras que se orientan hacia el oeste están condicionadas por J1 y las orientadas hacia el este están controladas por J2. El condicionamiento de J3 es muy escaso, reflejado en muy pocos puntos ya que, como se registró durante las mediciones en el campo, prácticamente solo delimita lateralmente las dimensiones del bloque en las direcciones N-S.
El otro factor considerado como condicionante de la susceptibilidad al desprendimiento es la morfometría del terreno, del que para un MDE de 5 m se ha calculado: variación altimétrica, gradiente, aspecto y orientación relativa a las familias de discontinuidades encontradas a lo largo del eje E-O de la vertiente sur de sierra de La Cabrera. Las zonas con mayor variación altimétrica forman una unidad morfológica que ha sido extraída mediante una técnica numérica de descomposición óptima de la esperanza (EM-GDMU) de poblaciones sobre del modelo digital de pendientes. Estas zonas, de pendientes superiores a los 40°, corresponden con las crestas donde se producen la mayoría de los desprendimientos de bloques. La orientación relativa del relieve con respecto a las discontinuidades presentes determina la posible inestabilidad estructural, únicamente debida a J4* por sus características, o la orientación de la cara de desprendimiento de un bloque.
Evaluadas las condiciones geológicas estructurales (por familias y sus conjunciones) y morfométricas conjuntamente sobre la unidad morfológica de mayores pendientes (> 40°) se han ubicado 35 zonas de mayor susceptibilidad a la inestabilidad. A cada una de éstas se le ha asignado inicialmente una terna de ángulos (φp, φa, φd ) que caracterizan la geometría del modelo empírico del cono: el alcance, la orientación y la dispersión. Estos tres valores han sido calibrados para cada área individual, mediante sucesivas simulaciones del modelo, hasta reproducir con verosimilitud el alcance y la dispersión observada en el terreno. Los ángulos φp obtenidos tras la calibración se encuentran dentro de los límites publicados por otros autores (25°-32°), alrededor del valor promedio de 28° que Ayala-Carcedo et al. (2003) sugieren.
Con los resultados obtenidos del modelo empírico utilizado ha sido posible estimar la localización de la línea de máximos alcances, así como la distribución de las velocidades y energías de un bloque que se desprenda desde las áreas fuente. A diferencia de los resultados publicados por Ayala-Carcedo et al. (2002 y 2003), la distribución de los alcances próximos a la localidad de La Cabrera ha sido delimitada con mayor detalle que utilizando una única zona de emisión distribuida sobre toda la cumbrera. Esto ha sido logrado gracias a la utilización de un conjunto de fuentes caracterizadas individualmente y de un modelo empírico que incorpora la información geométrica local del movimiento de bloques. En general, para cada área de desprendimiento, el cono de afectación que se obtiene posee una extensión lateral de su zona de propagación ligeramente mayor que la que puedan tener los bloques en el terreno, lo cual es una solución conservadora frente a la seguridad, pero más detallada. Para limitar lateralmente el cono, se ha calibrado un arco de apertura entre 8°-16° alrededor de la dirección de desprendimiento, ajustando localmente el efecto de canalización de las trayectorias y el solape por fuentes próximas. Las velocidades y energías han sido evaluadas para un bloque rocoso de 30,000 kg, con un volumen de 12 m3, acorde con las observaciones in situ. La máxima velocidad de traslación obtenida en la zona de estudio ha sido de 25.7 m∙s-1, que es comparable con los 21.9 a 41.4 m∙s-1 obtenidos con el programa ROTOMAP (Geo&Soft) en la misma zona (Ayala-Carcedo et al., 2003). La energía cinética máxima total se ha estimado en 9,950 kJ, en la caída de un bloque de 30,000 kg.
En suma, los resultados de este estudio regional preliminar en alcances, velocidades y energías son, con mucho mayor detalle en su distribución en el terreno, comparables con estudios previos de la zona y con las observaciones del terreno. Por ello, no puede desestimarse la posibilidad de que algunos de los alcances probables por ejemplo, desde el Pico de la Miel, en la ladera de Las Ventanas, entre el collado del Alfredo y el Cancho de la Bola, pudieran llegar a afectar a la zona urbana o a sus viales. El transformar los efectos obtenidos con este método en términos de susceptibilidad a una cartografía de zonificación (Jaboyedoff et al., 2005) no es posible de forma directa ya que serían precisas otras herramientas de simulación de caída de bloques de tipo dinámico para las que se requiere un estudio del terreno más detallado, y que este trabajo no pretende abordar.











 text new page (beta)
text new page (beta)


