Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Sociedad Química de México
Print version ISSN 0583-7693
Rev. Soc. Quím. Méx vol.44 n.1 Ciudad de México Jan./Mar. 2000
Investigación
Traveling Through the Square Mechanism of the Quinone Reduction Pathways. Influence of the Proton Donor Addition on the Reaction Intermediaries in a Non-Aqueous Solvent
Martha Aguilar-Martínez,1*(a) Norma Macías-Ruvalcaba2 and Ignacio González3
1 Instituto de Química.
2 Facultad de Química, Departamento de Fisicoquímica de la Universidad Nacional Autónoma de México, Ciudad Universitaria, 04510 México, D.F. Tel: (52)56-22-45-07, Fax: (52)56-16-22-03. e-mail: marthaa@servidor.unam.mx
3 Departamento de Química de la Universidad Autónoma Metropolitana-Iztapalapa. Apartado Postal 55-534.
Recibido el 14 de enero del 2000.
Aceptadoel 29 de marzo del 2000.
Abstract
In this work cyclic voltammetry was applied to describe mechanistic changes in the reduction of the electromechanical system consisting of a quinone, the 2-phenylamine-1,4-naphtalenedione (PAN), and increasing quantities of phenol, a weakacid reagent. The quinone system was allowed to proceed deliberately along the different characteristic reduction pathways. It was observed step by step the merging of the two waves, corresponding to one-electron charge transfer observed in aprotic media, into a single, two-electron charge transfer wave in the presence of phenol. Applying the Nernst equation for the different redox pairs involved, it was provided a semiquantitative explanation of the potential dependence on the phenolic additive concentration along with the basic properties of the intermediaries Q2−/QH− and Q·−/QH·.
Keywords: Organic electrochemistry, quinone reduction mechanisms, reactive intermediates, redox reactions.
Resumen
En este trabajo se aplicó la voltametría cíclica para describir los cambios mecanísticos en la reducción del sistema electroquímico de una quinona, la 2-fenilamino1,4-naftalendiona y cantidades crecientes de fenol, un ácido débil. Esto permitió al sistema quinona proceder deliberadamente a través de las diferentes trayectorias de reducción características. Se observó de una manera gradual la fusión de las dos ondas de transferencia de un electrón, observadas en medio aprótico, en una onda única, correspondiente a la transferencia de carga de dos electrones en presencia de fenol. Se da una explicación semi-cuantitativa de la influencia de la concentración de fenol sobre el potencial, así como de las propiedades básicas de los intermediarios Q2−/QH− and Q·−/QH·.
Palabras clave: Electroquímica orgánica, mecanismo de reducción de quinonas, intermediarios reactivos, reacciones redox.
Dedicated to the memory of Dr. Raúl Cetina Rosado
Introduction
The majority of inorganic electrochemical reductions involve a simple addition of electrons, while organic reductions require addition of protons, as well, since neutral molecules are involved. This requirement for proton addition results in complex mechanisms in voltammetry of organic compounds and lead us to describe many reactions as irreversible. In solvents with low proton availability, electron addition can take place with little or no complication by protonation. In such cases, it is possible to observe the changes in behavior brought about when acid addition or a change in solvent increases the rate of protonation. Square diagrams are used in organic electrochemistry to describe the different mechanisms resulting from changes in media acidity where electron and proton transfers are exchanged. There are simple square mechanisms, such as the bielectronic reduction of quinones [1] where nine species are involved, or much more complex mechanisms in which six electrons are transferred, as in the reduction of a nitro group [2]. Scheme 1 shows the general redox diagram for the quinone/hydroquinone system, where electron and proton transfers are represented in the horizontal and vertical lines, respectively. In protic solvents, it is impossible to monitor the variety of intermediates present at different acidity levels due to the high proton availability (this is especially true for radical anions and dianions). Thus, reductions are global processes resulting in the transfer of two protons and two electrons for quinones. The redox potential of the quinone/hydroquinone system has been described as a function of pH in aqueous solution, where only the global redox pair Q/QH2 was studied with no further details on the proton transfer mechanism [3].

In aprotic solvents, the electroreduction of quinone compounds has generally been studied in the presence of uncontrolled amounts of a proton donor [4, 5]. In such cases, the transformation leads directly, in a global pathway of two electrons and two protons from quinone to hydroquinone. In these conditions the detection of different possible pathways followed by the reactive intermediates described in scheme 1 is eluded.
Quione reduction mechamism can present a variety of changes when different amount of acid reagents are added (i.e., water, phenol, benzoic acid) [6-7]. Successive interactions between acid reagent and the different species (Q, Q·−, Q2−) allows to obtain different trajectories described by the square diagram (scheme 1). The nature of this interaction could be as hydrogen-bonding or direct protonation, these depends of the relative acidity of the acidic reagent and the relative basicity of the quinone and the different intermediates [8].
For a better comprehension of the mechanism that follows the quinone reduction system in the presence of an acid reagent, it is neccessary to find experimental conditions to control the stability of the various intermediaries to be able to study some of the suggested trajectories on the square diagram.
In order to establish the proton donor influence on the different reduction pathways, we performed a voltammetric study of the reduction of a quinone without acidic protons in its structure (2-phenylamine-1,4-naphthalenedione, PAN, figure 1) with increasing amounts of phenol. Phenol added in small amounts allows its successive interaction with each one of the intermediates involved in the dielectronic reduction of the quinone. Applying the Nernst relations associated with the electromechanical transformations on the quinone, brought about by different acid reagent amounts added, we assembled a semi-quantitative explanation for the presence or absence of voltammetric peaks and their relationships to phenol concentration. This study could provide to the chemists more information concerning the comprehension and control of organic molecule transformations.

2. Experimental
PAN was synthetized in our laboratory as described by Mohammed [9]. Cyclic voltammetric measurements were carried out on a Bioanalytical Systems Inc 100B/W Electrochemical Workstation instrument. A three-electrode cell was used for all electrochemical experiments. A platinum wire was used as auxiliary electrode. And a BAS platinum disk electrode (3 × 10−4 cm2) was used as working electrode. Prior to each experiment, the working electrode was cleaned by polishing with alumina 0.05 µ (Buehler, Ltd.) and rinsed thoroughly with distilled water and acetone. As a reference electrode a saturated calomel electrode (SCE) was used, separated from the bulk solution by a bridge filled with acetonitrile and supporting electrolyte. This reference is commonly used in organic electrochemistry despite of the important liquid-union potential [18]. Solutions in the bridge were changed periodically to avoid aqueous contamination entering the cell via SCE. In order to establish a reference system that took into account the experimental characteristics of our system, the redox potentials reported here refer to the ferrocene/ ferricinium couple (Fc/Fc+), as recommended by IUPAC [12]. The potential of the Fc/Fc+ couple was 399 mV vs SCE, determined from the corresponding voltammogram under the chemical conditions of the voltammetric study.
The ohmic drop was automatically compensated throughout the study and proved to be insignificant. Acetonitrile was used as solvent and Et4NBF4 was chose as the supporting electrolyte, as it does not formchelates with the semiquinone radical anion [10]. The electrolytic solutionwas bubbled with N2 (previously saturated with dry acetonitrile) for 50 minutes before dissolving PAN. The inert atmosphere was found to be particularly important throughout the experiments since dissolved oxygen within the solution could be reduced at potential values near those of PAN, and could also oxidize the radical anion generated in the first reduction step, as occurs with other quinones [11]. Cyclic voltammograms for PAN were run at 100 mV/s at 25°C. A 0.5 M phenol stock solution in acetonitrile was prepared and 5 µl increments were added to a 1 mM PAN solution in the electrolytic media to achieve phenol concentrations from 0.5to 6.5 mM.
3. Results and Discussion
3.1 Electromechanical Reduction of PAN in aprotic media
Cyclic voltrammogram of 1 mM PAN in 0.1 M Et4NBF4 /CH3CN (Fig. 2a) shows the typical behavior of quinones in these media [13]. Under our experimental conditions, PAN is reduced by means of an electrochemical-electrochemical mechanism (EE), giving rise to two, one-electron charge transfers signlas I and II (equations 1 and 2). No signals resulting from oxidation or reduction of intermediate species brought about by chemical reactions coupled to the charge transfer process are detected [14].


Equations (1) and (2) correspond to the first horizontal of the square diagram in scheme 1. Since the hydroquinone anion Q2− is an extremely unstable chemical species (highly basic species) that immediately undergoes interaction with the acidic reagent [15], the reversibility observed of the second wave for PAN (ΔEp = Epa − Epc = 69 mV, ipa/ipc = 0.9) shows that the electrolytic system was totally free of any traces of humidity and that the hydrogen bonded to the amine group of PAN has non acidic properties. These values of ΔEp and ipa/ipc for the second wave have been reported for other types of quinones [8].
The potentials used for the discussion in this wokr correspond to the cathodic potential peak (Epc) obtained from the corresponding voltammograms at 100 mV/s. Peak potential, in cyclic voltammetry, can be associated to the equilibrium potential (E) of the redox couples formed at the interfase. The experimental conditions are described at the literature [16-20] where this assumption is valid.
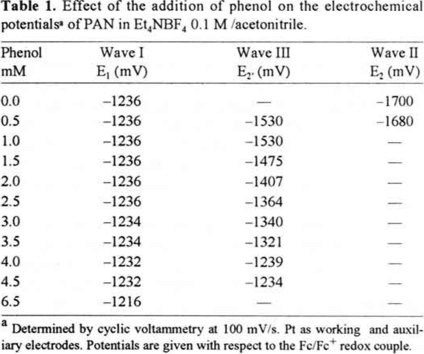
Both redox pairs involved in the reduction process are presented in a potential scale (scheme 2), since the potential E2 (Q·−/Q2−) is more negative than E1 (Q/Q·−), the resulting cyclic voltammogram produced two pairs of well-defined oxidation/reduction peaks (Fig. 2a). The potential values obtained in this work are reported in the table 1.

3.2 Electromechanical reduction of PAN in 0.5 mM phenol
The cyclic voltammogram whown in figure 2b was registered at a phenol concentration of 0.5 mM. Under these conditions, the potential of the first wave remained unchanged; however, a third reduction wave (IIIc) appeared between the first and the second reduction waves. These results suggest that one of the species formed in the interface throughout the reduction process is having an interaction with phenol. According to scheme 1, species that could be present at the interface during the reduction process are: Q, Q·− and Q2− in the absence of an acid reagent. As the basicity of the species increases in the order Q < Q·− < Q2−, it is likely that the Q2− anion is the base to undergo interaction first when phenol is added. The interaction between Q, Q·−, Qw− and phenol could be a simple hydrogen-bonding or a direct protonation. The identification of this kind of interaction requires of a deep study. In this work, in order to make a schematic discussion of voltammetric behavior, we are initially considering a direct protonation. Despite of this assumption, the relationship between potential shifts and the phenol concentration, could be described in the same manner if hydrogen-bonding could be present, acidity constants may be changed by hydrogen-bonding constants [8]. In certain cases we considered this situation.
Protonation of Q2− give rise to a new wave (IIIc) at a less negative potential than E2. Accordingly, electrochemical reduction of PAN likely proceeds via the following mechanism, shown in equations (1), (3) and (2). Wave I corresponds to reaction (1), wave III corresponds to reaction (3) (pathway E2 → K3, scheme 1), while wave II corresponds to reaction (2).

Where DH corresponds to phenol and D− corresponds to phenolate ion. In order to explain how in the presence of the proton donor the potential for the Q·−/QH− (Es′) pair is less negative than that corresponding to the Q·−/Q2− (E2) pair, the redox potential of both systems were calculated using the Nernst equation (equations 4-9).
From reaction (2), equation (4) is obtained:

The reaction constant for the QH− species (reaction 5) in presence of DH is given by equation (6):

Where KDH corresponds to acidity constant of phenol:
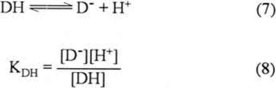
And K3 corresponds of acidity constant of QH− (see scheme 1).
Equation (4) can be rewritten as:

The Q·−/QH− potential (reaction 3) is:

In the equilibrium, EQ·−/Q2− = EQ·−/QH−

Equations (4) and (11) show that the redox potential for Q·−/QH− is less negative than that corresponding to the Q·−/Q2− couple since the potential of the Q·−/QH− pair depends not only on the pK3 (QH−) but also on the D−/DH ratio in solution. This ratio is relatedto the acidity level whichis determined by the D−/DH equilibrium.

By placing the three redox systems involved in the process on a potential scale (scheme 3), the Q·−/QH− potential (E2′) is observed to the left of the Q·−/Q2− potential (E2). The potential values are shown in table 1. As E2′ is less negative than E2, the favored reduction path would be that with the least negative potential value, for this case, the reduction that yields the QH− species through reactions (1) and (3). This would explain the presence of the third reduction wave (III) observed in the voltammogram in figure 2b. It is possible to see that wave II is still present, however its current decreased compared to the one obtained in the absence of phenol (figure 2a). This indicates that the amount of acid reagent added to the system was insufficient to protonate all of the Q2− product of the reduction of Q·− (reaction 2).

3.3 Electromechanical reduction of PAN from 1.0 to 2.5 mM phenol.
Figure 3b-c shows that as phenol concentration increased, the potential for the first electron transfer (wave I) remained unchanged, wave II disappeared and wave III moved toward less negative potentials (table 1). This indicates acidity sufficient to protonate all Q2−.

The potential for wave III becomes less negative, according to equation (11), in which the potential for the Q·−/QH− pair is shown to depend on the phenol concentration in the system. As phenol concentration increases, the ratio of [D−]/[DH] and the paH+, decrease. From the equation (11), as log [D−]/[DH] decreases, the Q·−/QH− potential becomes less negative. A potential scale can be used to show the variation of the Q·−/QH− potentialvalue as a function of phenol addition. As phenol concentration increases in the electrolytic solution, the potential for the Q·−/QH−electron transfer (wave III) becomes closer to the potential value of the first electron transfer (Q/Q·−) (scheme 4).

When the acidity level was controlled only by the phenol addition (simple protonation), it expects a variation of 60 mV of the potential of peak III with a variation of one order of magnitude of phenol concentration. From potential data reported in table 1, the potential of cathodic peak III varies 327 mV when the phenol concentration varies in one order of hydrogen-bonding between Q2− and phenol. This hydrogen-bonding allows an interaction of several molecules of phenol with Q2−. From the obtained results, it can be proposed an interaction of five molecules of phenol with one molecule of Q2− [8]. This interaction can be represented in the same type of reactions proposed by the direct protonation (see reactions 1-3), the direct protonation reaction constant for QH− species in presence of DH (reaction 5) must be replaced by hydrogen-bonding reaction [8]. As the equations used to describe the hydrogen-bonding are similar to those of hydrogen-protonation we consider an hydrogen-protonation to continue the semi-quantitative discussion of the reduction pathway modification with phenol addition, in order to a better comprehension of the potential displacements.
3.4 Electromechanical reduction of PAN in 3.0 to 4.5 mM phenol
Table 1 and Fig., 4b (c, d)-e establish that for phenol concentrations greater than 3.0 mM, the first reduction wave begins to moving to less negative potentials. This could occur as a result of achieving sufficient phenol concentration to partially protonate Q·− (reaction 13′), causing E1′ (reaction 14, pathway E1 → K2, scheme 1) (peak Ic′) to become less negative than E1. Therefore, part of the quinone was reduced to QH· in the first reduction wave (reaction 14) and the rest was reduced to yield Q·− (reaction 1), which at a potential E2′ is reduced to QH− (reaction 3). We will demonstrate latter that QH· is reduced at a potential equal to or less negative than E1′, resulting in a disproportionation reaction (reaction 15) [5], this reaction provokes a great modification in the associated current in the first reduction peak, this effect will be discussed in the following section.


Figures 4b (c, d)-e show that the reactions (1) and (14) take place in a single reduction wave (wave 1), suggesting that the potentials for both redox pairs Q/Q·− (E1) and Q/QH· (E1′) must be very close to one another (scheme 5). The potential for wave I, where both reductions occur, is therefore, at an intermediate potential value between E1 and E1′.

Just as Q2− protonation results in an increase in the potential value from E2 to E2′, the protonation of Q·− also results in an increase in the potential value from E1 to E1′. The following equations (16 to 21) describe the redox potential for the Q/QH· pair.
Equation (16) shows that the Q/Q·− potential (reaction 1) is the following:

From the reaction of QH· with D− (reaction 17), the QH− conditional acidity constant is obtained (equation 18):

Hence, equation (16) can be described as follows:

From the Q/QH· redox couple, reaction (14), equation (20) is obtained:

In equilibrium conditions, EQ/Q·− = EQ/QH·.
Therefore, the following equation is demonstrated:

As shown in equation 21, the potential for the Q/QH· pair becomes less negative than that corresponding to the Q/Q·− couple, which depends on the QH· acidity constant (K2) and the ratio of [D−]/[DH] in the system.
3.5 Electrochemical reduction of PAN in 6.5 mM phenol
Figure 5 compares two cyclic voltammograms for PAN: a) without phenol and b) in the presence of 6.5 mM phenol. Figure 5b shows that in the presence of 6.5 mM phenol, the two reduction waves merge into a single wave. The peak for PAN reduction in the presence of phenol (peak Ic′) is approximately twice the height of the Ic peak, indicating that the reduction of PAN takes place through a two-electron process.

The potential scale shown in scheme 6 provides a more detailed explanation of the outline of the cyclic voltammogram in figure 5b. Since 6.5 mM phenol is sufficient to completely protonate Q·− at the E1′ potential, reduction of Q to QH· must occur (pathway E1 → K2). As previously reported [21], electromechanical reduction of QH· takes place at a less negative potential (E4)(scheme 1) than reduction of Q. Therefore, these reactions can be represented in a potential scale in scheme 6, as follows:

According to this potential scale, QH· reduction proceeds by two different mechanisms, as described below:

From reaction (3), the equilibrium potential was described by equation (11).

From the reaction of QH· with D− (reaction 17), the QH− conditioned acidity constant is obtained (equation 18):


Hence, equation (11) can be described as follows:

From the QH·/QH− redox couple (reaction 23), equilibria (25) is obtained:

At equilibrium, equation (24) equals equation (25), so:

Considering that the pK3 (QH−) > pK2 (QH·) (according to the strength of the bases Q2− and Q·− mentioned earlier), equation (26) allows us to establish that the potential for the QH·/QH− pair is less negative than the potential for the Q·−/Q2− pair. Although we are unable to place it in the potential scale for comparison with E1′, the factor that QH· is more easily reduced than Q, suggests that E4 is less negative than E1′. Assuming that the potential for the redox pair QH·/QH− (E4) is less negative than the potential for Q/QH· (E1′) (scheme 6), only one reduction wave will be present with a cathodic current due to the simultaneous reduction of both species, Q and QH·.
Since QH· is more easily reduced that Q, the electron addition reaction of QH· can also take place in solution by means of a disproportionation reaction (14). The presence of this reaction could compete with the ECE mechanism. As mentioned, when QH· appears at the interface, it is immediately transformed into QH− (reaction 23) due to the electrode potential conditions (E1′) where QH· is formed. This accounts for the increase in the current of reduction of wave 1 (Fig. 5) and also for the different potentials at which QH· and Q·− are reduced. The reduction peak Ic′ and its corresponding oxidation peak Ia′ with an E1/2 = (Epa + Epc)/2 = −1174 mV, and ΔEp = Epa− Epc = 85 mV, (figure 5b) are thus related to the global reaction (22). The reduction reaction from Q to QH− can take place via either mechanism, depending on the velocity of the protonation reaction of Q·− (reaction 13′).
The variation of the cathodic peak potentials with the addition of phenol, have allowed to describe schematically the modification of the reduction pathways of this quinone. However, a more detailed study to the mechanism must be taken into account the variation of the cathodic peak current with the phenol concentration.
4. Conclusions
Applying cyclic voltammetry to stude PAN in acetonitrile, it was demonstrated that small changes in phenol concentrations produced detectable alterations in the reduction pathway followed by the quinone system. Due to the presence of hydrogen-bonding it is possible to detect the variation of peak III potential with the addition of phenol. We were able to explain displacements and the absence or presence of the different voltammetric waves based on assumptions for basicity of the different intermediates in the reduction of PAN and calculations of potential relationships for the redox pairs using the Nernst equation. Figure 6 illustrates the different reduction pathways than PAN can undergo within the 0.5 to 6.5 mM phenol concentration range evaluated. According to these data, in the absence of phenol, the electromechanical reduction takes place through two, one-electron charge transfers, from Q to Q·− and then from Q·− to Q2−. As the equations used to describe the hydrogen-bonding are similar as those of hydrogen-protonation, we have considered an hydrogen-protonation continue the semi-quantitative discussion of the reduction pathway modificationwith phenol addition, in order to a better comprehension of the potential displacements.

Between 0.5 mM to 3.0 mM phenol, reduction of PAN proceeds initially with transformation of Q to Q·−. At these concentrations, the quantity of phenol is insufficient to protonate Q·−, while succeeding to protonate Q2−. Thus, the second electron transfer corresponds to the Q·− transformation to QH−.
Between 3.5 and 4.5 mM phenol, the quantity of phenol allows partial interaction of the Q·− product of the first one-electron transfer. Therefore, the PAN reduction takes place in a one-electron step to form Q·− or QH·, species wich can undergo a second one-electron transfer to form QH−. The difference of the potentials for both one-electron transfer processes becomes less as the phenol concentration increases.
When phenol concentration reaches 6.5 mM, the phenol added allows total protonation of Q·−, giving rise to QH·, which undergoes a reaction of disproportionation. The PAN reduction thereby proceeds through a two-electron charge transfer in a single step, to form QH−.
This study is important because it contributes to chemists to have a better comprehension about the organic molecules reductions showing them the possibilities to guide the mechanism not only by controling the potential variation, but by modifying the proton donor concentrations in the system.
Acknowledgment is made to Consejo Nacional de Ciencia y Tecnología (CONACyT) for the financial support given via grant No. 28016E. One of us (NMR) thanks to CONACyT and DGEP for award of a doctoral fellowship.
References
1. Chambers, J. Q. "Electrochemistry of Quinones", In The Chemistry of the Quinonoid Compounds; Ed. S. Patai, John-Wiley & Sons, New York, 1974, Part 2, Chapter 14. [ Links ]
2. Fry, A. J. In Chemistry of Amino, Nitroso and Nitro Compounds and Their Derivatives; Ed. S. Patai; John-Wiley & Sons, Chichester, U.K, 1982, Chapter 8. [ Links ]
3. Walczak, M. M.; Dryer, D. A.; Jacobson, D. D.; Foss, M. G.; Flynn, N. T. J. Chem. Educ. 1997, 74, 1195-1197. [ Links ]
4. Given, P. H.; Peover, M. E. J. Chem. Soc. 1960, 385-393. [ Links ]
5. Eggins, B. R.; Chambers, J. Q. J. Electrochem. Soc. 1970, 117, 186-192. [ Links ]
6. Wawzonek, S.;Berkey, R.; Blaha, E.W., Runner, M.E. J. Electrochem. Soc. 1956, 103, 456-459. [ Links ]
7. Given, P.H.; Peover, M. E. J. Chem. Soc. 1960, 385-393. [ Links ]
8. Gupta, N.; Linschitz, H. J. Am. Chem. Soc. 1997, 119, 6384-6391. [ Links ]
9. Mohammed, R. A.; Ayad, M. A.; Chaaban, A. I. Acta Pharm. Jugoslav 1976, 26, 287. [ Links ]
10. Rüssel, C.; Jaeniche, W. J. Electroanal. Chem. 1986, 199, 139-151. [ Links ]
11. Wilson, I.; Wardman, P.; Tai-Shun, L.; Sartorelli, A. C. J. Med. Chem. 1986, 29, 1381-1384. [ Links ]
12. Gritzner, G.; Küta, J. J. Pure Appl. Chem. 1984, 4, 462-466. [ Links ]
13. Mann, C. K.; Barnes, K.K. "Carbonyl Compounds" in Electrochemical Reactions in Nonaqueous Systems, Marcel Dekker, New York, 1970, Chapter 6. [ Links ]
14. Aguilar-Martínez, M., Cuevas, G., Jiménez-Estrada, M., González, I., Lotina-Hennsen, B., Macías-Ruvalcaba, N. A. J. Org. Chem. 1999, 64, 3684-3694. [ Links ]
15. Jensen, B. S.; Parker, V. D. J. Am. Chem. Soc. 1975, 97, 5211-5217. [ Links ]
16. Bard, A. J.; Faulkner, L. R. Electrochemical Methods. Fundamentals and Applications; John Wiley & Sons: New York. 1980; Chapter 6. [ Links ]
17. Heinze, J. Angew. Ing. Ed. Eng., 1984, 23, 831-847. [ Links ]
18. Kissinger, P. T., Heineman, W. R. J. Chem. Educ. 1983, 60, 702-706. [ Links ]
19. Evans, D.H.; O'Connell, K.M.; Petersen, R. A.; Kelly, M. J. J. Chem. Educ. 1983, 60, 290-292. [ Links ]
20. Evans, D. H., Accounts of Chemical Research, 1977, 10, 313-319. [ Links ]
21. Ortiz, J.L.; Delgado, J.; Baeza, A.; González, I., Sanabria, R.; Miranda, R. J. Electroanal. Chem. 1996, 411, 103-107. [ Links ]
Nota
(a) Permanent address: Universidad Nacional Autónoma de México. Facultad de Química. Departamento de Fisicoquímica, Ciudad Universitaria, 04510 México, D.F. (México).














