Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Problemas del desarrollo
Print version ISSN 0301-7036
Prob. Des vol.50 n.198 Ciudad de México Jul./Sep. 2019 Epub Nov 16, 2019
https://doi.org/10.22201/iiec.20078951e.2019.198.67469
Articles
Economic costs of hurricane Alex in Nuevo León, Mexico
a The College of Mexico, Mexico Email addresses: dmtinoco@colmex.mx, albamendez@uadec.edu.mx
b Autonomous University of Coahuila, Mexico. Email addresses:amercado@colmex.mx.
The periodic heavy flooding which Mexico experiences impacts negatively on its economic development. Adaptation and risk-management measures are predominantly based on cost evaluation, which therefore needs to be comprehensive. This paper evaluates the total economic cost of Hurricane Alex in the state of Nuevo León in 2010, which was the most devastating natural phenomenon recorded during the last 50 years. Therefore, for the first time in Mexico, a methodology was applied which factors in both direct costs (material damage) and indirect costs (productivity losses) in the affected region’s economy (MIP). This methodology was based on the input-output model. The results suggest that total costs were $20.5 billion MXN, of which 29% (6 billion) were indirect costs.
Keywords: natural disasters; indirect costs; risk management; tropical cyclones; inputoutput model
México es afectado periódicamente por fuertes inundaciones que inhiben su desarrollo económico. Medidas de adaptación y gestión de riesgos se basan sobre todo en la evaluación de costos, por lo que ésta debe ser comprehensiva. Este artículo evalúa los costos económicos totales ocasionados por el huracán Alex en el estado de Nuevo León en el año de 2010, fenómeno natural que fue catalogado como el más devastador de los últimos 50 años. Así, se aplicó por vez primera, para un caso en el país, una metodología que considera, además de los costos directos (daños materiales), los costos indirectos (afectaciones a la producción) en los sectores económicos de la región afectada, basada en el modelo insumo producto (MIP). Los resultados estiman MXN$20.5 mil millones en costos totales, de los cuales 29% (6 mil millones) corresponden a costos indirectos.
Palabras clave: desastres naturales; costos indirectos; gestión de riesgos; ciclones tropicales; modelo insumo producto
Clasificación JEL: O13; O54; O56; P28
1. Introduction
During the past few years, the intensity and frequency of hydrometeorological natural disasters have increased as a consequence of climate change1 . Among these natural disasters, those that affect Mexico most are tropical cyclones and consequent extreme flooding2 . The hydrographic characteristics and geographic distribution of large urban agglomerations increases the country’s vulnerability in the face of these natural phenomena.
In recent years calculations have been disseminated regarding Mexico’s vulnerability to hydrometeorological events. For example, it has been calculated that the extent of the territory which is at risk measures 162,000 km2, which is the equivalent of 8.2% of the national territory (Arreguín-Cortés et al., 2016). It has also been observed that between 2000 and 2016, natural disasters had an economic impact of $424.9296 billion MXN (CENAPRED, 2014). According to the National Meteorological Service, one of the years with the worst devastation in the country was 2010, with nine tropical cyclones being registered on national territory; some of these grew to be categorized as hurricanes, and in doing so surpassed the degree of devastation seen with Karl and Matthew, which also affected the state of Veracruz. Ultimately, Alex was the most catastrophic, which caused damage in the states of Tamaulipas, Nuevo León and Coahuila, at the estimated amount of $25.0149 billion MXN3.
Alex was considered one of the most powerful hurricanes of the past 50 years (CENAPRED, 2014); the state of Nuevo León was most damaged by Alex4. The region’s geography (the state and in particular its capital, Monterrey) presents conditions which foster flooding, landslides and droughts (Torres et al., 2010). The Santa Catarina river, which runs through the city of Monterrey, is the main cause of flooding, provoked by the presence of hurricanes in the Gulf of Mexico, which affect the region’s society and economy in an important way.
The case of hurricane Alex was chosen given the devastation it incurred, due to the amount of rain that fell during a short period of time5 . Accordingly, the purpose of this work is to calculate the total economic costs caused by this natural phenomenon in the Mexican Republic.
However, traditional evaluations of the record of losses caused by natural disasters only take direct damage to physical infrastructure into account (Veen, 2004; Cole, 2003; Steenge and Bockarjova, 2007); that is, the monetary quantification of the physical destruction caused by the natural phenomenon. On the other hand, there is evidence of the chain effect caused by direct damage, which are referred to as indirect costs and which include all of the costs associated to restrictions in production as a consequence of physical destruction. It is estimated that these costs represent a considerable part of the total economic costs of a disaster (Cochrane, 1997; Hallegatte and Przyluski, 2010; Veen, 2004). Calculation of indirect costs is fundamental in achieving efficient management of the risks due to flooding. To do this, it is necessary to evaluate the loss of labor productivity and industrial capital, with the objective of calculating the effects which permeate the rest of the economy during the rebuilding process. Upon considering the foregoing factors, vulnerability could be diminished and the resilience of regions affected by natural disasters could be increased (Okuyama, 2009; Rose, 2004; Veen and Logtmeijer, 2003).
The objective of this work is to calculate the total economic impact caused by hurricane Alex in the state of Nuevo León. This impact includes direct and indirect effects to the economy. The methodology employed here allowed for a calculation of direct costs caused by damage to industrial capital, residential capital and infrastructure. Additionally, it presents a calculation of indirect damages associated with productivity restrictions caused by the damages to infrastructure and industrial capital. It also calculates the costs associated with labor restrictions and changes in behavior of demand in households.
One advantage of the methodology that was used for the calculation of damages is that it took as a base the input-output model (IO), that allows for a measurement of chain effects (or indirect ones) which result from sectorial and regional interrelationships. In general, the methodological proposal presented here will contribute to a more effective preparation and adaption for future natural events in these regions.
Section 2 offers a summary of the principal methodologies for economic evaluation of damages caused by natural disasters, and examines in particular various application of the IO methodology to this issue. The third section explicates a model which was used for the calculation of damages caused by flooding; the data are described in section 4. Results are presented in section 5, and finally, conclusions are offered in section 6.
2. Precedents to economic evaluation methods
Methodologies
Within the economics literature an intense debate exists regarding which methodology should be used in the analysis of natural disasters. The conversation is derived from the influence that assumptions, data and referenced theories have on the results (Okuyama, 2007; Greenberg et al., 2007). Among the most widely applied methodologies are econometric models, the IO model and the applied general equilibrium model (AGE). All of the alternatives seek to rectify the weaknesses that have emerged when natural disasters are subjected to analysis.
On one hand, the statistical rigorousness of econometric models allows for making predictions about the impact of natural disasters. Still, the application of this type of analysis requires historical information about natural disasters in the regional environment, a fact which complicates the implementation of these sorts of tools, given the scarcity of data during the time period and for the region. Another related problem concerning the data is that it does not distinguish between direct and indirect losses generated by natural events. Consequently, the lack of adequate data for the analysis limits the applicability of econometric models (Cochrane, 2004; Greenberg et al., 2007; Hallegatte and Przyluski, 2010; Li et al., 2013; Okuyama, 2007 and 2009).
On the other hand, the circular flow of the economy in equilibrium is the basis for IO models, which are made up of inter-industrial transaction tables for the whole economy. This information is then organized in matrices. When learning about transactions between economic agents, it is possible to evaluate the indirect effects through the value chain. One advantage of using this methodology is that it requires less calibration of parameters as compared to other methodologies; another advantage is that IO matrices can be regionalized. The foregoing allows for regional analyses, and for the calculation of indirect losses from natural disasters. Nonetheless, disadvantages in the application of this methodology include the fact that they constitute a static model based on a function of production for fixed proportions and fixed prices, and that it does not consider input substitution or imports (Cole, 2003; Greenberg et al., 2007; Okuyama, 2007 and 2009; Rose, 2004).
As opposed to the limitations of IO models, EGA models seek to reduce the rigidity related to supply restrictions, price changes, nonlinearity and the substitution of input and imports. The disadvantage is that they increase considerably the number of parameters with an exogenous calibration. In the analysis of natural disasters, the problem is that EGA models assume that the economy is in equilibrium at all times, which is in fact impossible to sustain in the case of a negative natural phenomenon (Cole, 2003; Greenberg et al., 2007; Okuyama, 2007 and 2009; Rose, 2004).
Applications of the IO model
The decision to study the impact of hurricane Alex with the IO model is based on its capacity to undertake a regional analysis (the state of Nuevo León), to calculate the indirect effects and to measure damages in a scenario of economic disequilibrium provoked by a weather event.
Before explaining the IO model as applied to this case study, some studies that adopt this model and apply it to the topic of natural disasters will be reviewed. Natural disasters provoke economic disequilibria in the IO model that Steenge and Bockarjova (2007) incorporate using an accounting matrix of the event’s damages (AMED). The main diagonal of an AMED shows the damaged proportion of each sector’s productive capacity. As such, disequilibria and possible bottlenecks after a negative natural phenomenon are accounted for using the AMED, in addition to recuperation.
Another adaptation of the model consists of including an analysis of goods and services substitution by way of imports (Bockarjova et al., 2004; Steege and Bockjarjova, 2007). A further contribution of the IO model was developed by Hallegatte (2008), who added a temporal dimension, with the goal of studying the recuperation process. This model is called the regional adaptive input-output model (RAIOM). For the analysis of the recuperation process, this model considers bottlenecks in production that are caused by natural disasters, and the adaptive behavior of consumers and producers before the event. However, a weakness of this model is the fact that it excludes restrictions in productive labor capacity from the analysis, and likewise with losses of residential capital (Li et al., 2013).
Li et al. (2013) seek to make up for the limitations of the RAIOM by taking into account restrictions in production caused by damages from a natural disaster, including those caused to the labor force. Another element of Li et al.’s (2013) model is the incorporation of damage to residential capital. The RAIOM covers desirable characteristics for the analysis of natural disasters, given that it includes the analysis of damages to capital and industry work, and it incorporates economic disequilibria that result from the event, as well as bottlenecks in the economic supply of the affected economy.
Recently, Mendoza-Tinoco et al. (2017) developed the so-called “flood footprint,” which is an analytical framework for the evaluation of damages, both of the flooded region and of those economic systems which are interconnected on a broader scale. The methodology builds on what is developed by Li et al. (2013).
The present article applies Mendoza-Tinoco et al.’s (2017)methodology (refer to the article for a more detailed explication of the model), and in addition it broadens the methodology so as to include a capital matrix, which provides consistency to the transition from a stock variable (industrial capital) and a flow variable (production), during the process of recovery. Finally, changes in final demand are explained by modeling the adaptive behavior of consumers.
3. Empirical strategy
Below, the most relevant equations of the methodology are presented, and the incorporation of the capital matrix concept is developed.
The methodology gathers the fundamentals of the IO model6 . The IO tables offer information regarding inter-industrial transactions of the whole economy in a matrix arrangement, which can be represented using a system of linear equations:
Where x is a vector-column with dimension n x 1 (n is the number of sectors), that represents the total production of each sector7 . Ax represents the intermediate demand vector, while every element of matrix A ([a ij ]) is the technical coefficient that indicates the quantity of product i which is necessary to produce a unit of product j. Finally, f stands for the final demand vector of each industry.
In order to consider other principal productive factors, the basic equation developed by Steenge and Bockarjova (2007) is utilized (see equation 2), which includes all intermediate goods transactions and the requirements for labor in each sector. At this point the economy is considered to be in equilibrium, with full usage of the productive factors:
After a negative shock to the economy, like that caused by a natural disaster, market forces become unbalanced, which produces a gap between the reduced supply -caused by the disruptions of the productive capacity of the industry and of labor-; and changes in demand -caused by changes in behavior and the demand for reconstruction goods-. As such, the total production capacity of the economy, after considering the restrictions to industrial capital and the workforce, is proportional to the least of them:
Where
Accordingly, the final total demand for each period during recovery sees as necessary the inputs of said industry, plus the final demand that includes the capital goods necessary for reconstruction (see equation 4)8.
Where o
t
(j) t represents the intermediate input
requirements of industry i for the rest of the sectors. And
For the process of economic recovery, the capital matrix concept is incorporated into the methodology, allowing for a methodological transformation consistent between capital investment and productive capacity.
Recovery processes after a disaster
An economy may be considered recovered once the labor capacities and industrial production are in equilibrium and the value of the total demand and production regain their level previous to the disaster. The method of using the remaining resources, to reach conditions before the disaster, is modeled following the rationing diagram.
The first step is to determine the production capacity available in each period following the disaster. In the context of Leontief production functions, productive capacity is determined by the minimum of each productive, capital and labor factor, as is demonstrated below:
Second, the level of restricted production capacity is compared to the total demand, to determine the allocation strategy of the remaining resources, and for reconstruction planning. The rules for this process constitute what is called the rationing diagram, which is described below.
Rationing diagram
The recovery process requires the allocation of remaining resources in
order to meet the society’s necessities during the aftermath of the
disaster. In the present work, a diagram of proportional prioritization
rationing was used which assigns first the remaining production between
the inter-industrial demand
When calculating the productive possibilities for the following period, real production is
compared first to inter-industrial demand. Defining
The first scenario arises if
This process happens for each industry; subsequently, one should consider
the fact that the industries that produce less also have less demand,
and in this way, affect and reduce production of other industries.
Iterations of this process continue until the production capacity can
satisfy the adjusted intermediate demand and a portion of the remaining
production is available to satisfy a part of the final demand and for
reconstruction, and accordingly increase the productive capacity of the
following period. This situation leads to a partial equilibrium, where
This process continues until the total available production at each
momento
The second scenario is produced when
It should be mentioned that the first scenario only happens when the shock to the economy is of such a magnitude that some of the businesses are not capable of satisfying even intermediate demand, after which the second scenario arises. In the case of the economy having the capacity to satisfy intermediate demand following the disaster, only the second scenario will be modeled.
In both cases, the remaining production after having satisfied intermediate demand is allocated proportionally to recovery demand and to other categories of final demand. Additionally, it is assumed that part of the unsatisfied final demand is covered by imports, some of which contribute to the recovery process when they are allocated to reconstruction demand.
Capital matrix
This section describes the incorporation of the capital matrix to the analytical framework of economic impact evaluation, in order to achieve a methodological transformation consisting of investment of capital to productive capacity. A capital matrix is generally used in the IO analysis to simulate economic growth through the accumulation of capital. Albert Steenge (Triple E Consulting, 2014) proposes using a capital matrix when analyzing the economic impact of natural disasters, and he considers investment in recovery an exogenous variable which allows for recovery planning.
The capital matrix is adapted within the analytical framework that has been presented, where investment in reconstruction is allocated according to the proportion of reconstruction demand, as relating to the other types of final demand. As was mentioned with the rationing diagram, it is assumed that non-damaged production is allocated to different categories of final demand once it satisfies intermediate demand.
A capital matrix K is a square matrix in which each element [ k (i, j) ] denotes the amount of capital goods produced by sector i to increase the production capacity of sector j in the unit. That is to say, the elements in column j represent the “formula” of the machinery, the equipment and other capital goods which are necessary for sector j to increase its productivity in one unit, while maintaining input and technology levels constant (Miller and Blair, 2009).
It bears remembering that the recovery process requires restoring and replacing damaged capital and residential stock. Throughout this process, the production capacity increases across local production and imports allocated to reconstruction investments. Note that residential capital reconstruction happens through the consumption of final products in the reconstruction sectors.
Inversion of capital for reconstruction,
It is worth mentioning that in this case the investment in recovering
industrial capital implies both technical requirements for capital, by
industry, broken down in capital matrix
K, in addition to the productive capacity amount that is
added to the following period (
Likewise, the participation of imports that invest in recovering capital
can be expressed, in order to calculate its contribution to the increase
in production capacity during the process of reconstruction. Once the
amount of imports designated for investment in capital is determined, as
in equation (7), the
productive capacity restored via imports can be obtained easily
It should be remembered that the sum
Multiplication by the inverse of the capital matrix provides industrial
productive capacity, which is added for the following period,
Accordingly, for the following period, the possibilities of industrial capacity production is given by the following expression:
This allows for the reformulation of the function for the vector
A new iteration of this process begins again and continues until the total demand and total production is found to be in equilibrium and at the same level as before the disaster.
Total economic impact
Lastly, the total economic impact of event (tec), is the sum of
direct costs (va dir) and indirect costs (va
ind) generated during each period of the recovery
process, as expressed in equation
(11). Costs are measured in terms of value added, which in the
case of direct damages, is equal to the cost of replacement, at market
price. This makes up the total recovery demand
4. Data
The data necessary to undertake the analysis using the proposed methodology can be described in two general groups. On one hand, it is necessary to collect information on the socioeconomic variables of the region that received the hurricane’s impact. The other set of necessary information regards damages incurred by the hurricane. A monthly time scale is utilized in the temporal analysis, and a sector disaggregation of 19 economic sectors (see sector disaggregation in column 1 of table A1 in the Appendix). Below is a detailed account of this.
It should be noted that all of the data are for the year 2010, and in the case of monetary values, they are deflated to 2007 prices10.
Economic data
The economic variables that need corresponding data are the following: capital stock, household stock, final demand, employment and the level of inter-industrial commerce. The information is required at a regional level (for the state of Nuevo León), and when not available at that scale, statistical techniques are used as a way to regionalize the data.
Capital stock, employment and final demand (or GDP) are available at a regional level. The first two variables were obtained from the Economic Census of 2014, by the National Institute of Statistics and Geography [Spanish INEGI]; the GDP was obtained from the Bank of Economic Information (BEI), while household stock was obtained at the national level from the 2010 Population and Household Census by INEGI. Lastly, the interindustrial transactions that were used are found in the national input-output matrix (IOM) for 2008. As part of the methodology, Flegg´s coefficient technique for increased localizations was used to regionalize the technical coefficient matrix, starting from the regional employment in relation to the national employment. The distribution of final regional demand for household costs, governmental costs, capital formation, and exports and imports, follows the same distribution as the national.
Information on damages
The model requires information on damages to industrial capital, residential capital and infrastructure. Additionally, information is needed regarding impacts to the workforce´s productive capacity, as well as changes to final demand.
Statistics for damages to physical capital were obtained from the Characteristics and socioeconomic impact of main disasters that occurred in the Mexican republic during 2010 report (CENAPRED, 2014), which also gives an account of the damages to social sectors (households, health, education and hydraulic infrastructure) of $7.275 billion MXN; economic infrastructure (highways, electricity production, navy and urban)of $13.356 billion MXN; productive sectors (agriculture, livestock and aquaculture, commerce and services) of $706 million, and the environment. For the industrial sectors, a distribution of damages based on the size of each industry within the regional economy was performed. This distribution can be consulted in column 5 of table A1 of the Appendix, in which event’s damage vector is designated.
As concerning impacts to the productivity of the workforce and household consumption, the novel character of this methodology establishes the need for data that is sometimes not available, as was the case for the effects of hurricane Alex. To resolve this situation, an analysis of various cases was performed based on the values of other variables. In the case of impacts to the workforce, the reported proportion of population affected was considered with respect to the total regional population, a proportion which was applied directly to the PEA proportion in Nuevo León. It is also assumed that this population suffered delays of one hour for transportation to their jobs during the first month, which then decreased linearly for six months until reaching zero. This parameter adds uncertainty which can be overcome by undertaking a sensibility analysis, which determines the stability of the model and tests the solidity of the scenario’s data.
Meanwhile, the changes in final demand for households follow psychological patterns, as has been observed following a disaster, when the population decreases consumption of nonbasic goods, showing prevention behavior. In this regard, it was assumed that such a decrease applies only to the affected population; an estimate of a 20% decrease in non-basic goods is given, with a linear recuperation of five months. A sensibility analysis was performed with respect to this parameter as well.
The cases under consideration are: a) impacts to industrial capital without impacts to the workforce or final demand; b) impacts on industrial capital with impacts on the workforce (disequilibria in productive factors); c) impact to industrial capital and final demand; and d) impact to industrial capital, the workforce, and final demand. In these cases, impacts on residential capital are also considered.
5. Results
Below are presented the most relevant results of the analysis. The first part shows the total costs (direct and indirect) caused by damages to industrial capital, residential capital and infrastructure. The second part demonstrates the results of cases for probable impact values to productive capacity of labor, and to household consumption. A sensibility analysis proves the stability of the model.
Total economic costs to the state of Nuevo León
The entity’s GDP in 2010 was $855 billion MXN (in 2009 prices), which represents approximately 0.73% of the national GDP for that year. Additionally, around 1,234,000 employees were registered in the region, which makes up about 0.6% of the total workforce in Mexico.
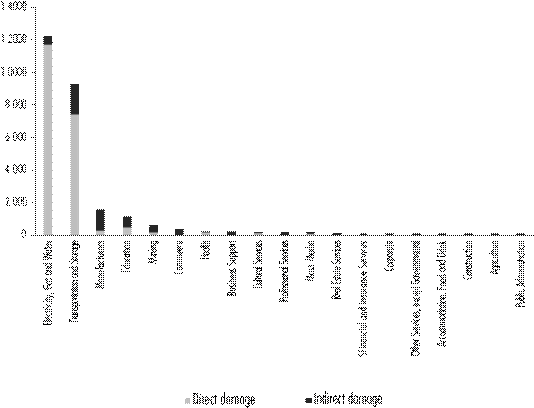
According to the present analysis, Nuevo León’s economy took around 20 months to recover after the natural phenomenon’s occurrence. Within the proposed methodological framework, recovery is reached with the economy reaches equilibrium again, and when the production level is the same as before the disaster. The quantification of the total economic loss rises to $27.423 billion MXN, which would amount to 3.2% of the state’s GDP for that year.
Figure 1 shows the composition of damages by category. Direct economic losses (which are made up of damages to industrial capital, the city’s infrastructure and to homes) represent 2.3% of the regional annual GDP ($21.500 billion MXN), of which 95% correspond to industrial and infrastructure damages. Indirect economic loss -which is the sum of all production flows that are not performed as a consequence of disruptions to productivity- represents an additional loss, equivalent to 1% of the state’s GDP ($5.922 billion MXN). This means that indirect damages were 28% higher than direct costs.
Economic recovery
This section describes the trajectories of economic variables which are involved in the recovery process, such as recovery of the productive capacity of industry, the participation of imports in recovery, and the dynamics of final demand that include demand for reconstruction.
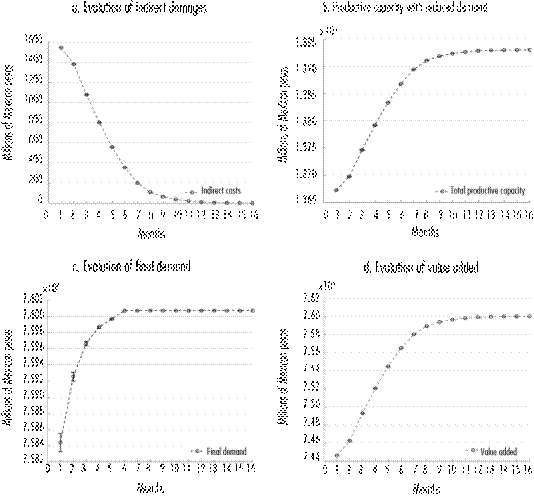
Figure 2a shows the indirect damaged accumulated during the recovery process, and is calculated as the distance between the final demand satisfied by the available production during a period and at a level preceding the disaster. It can be seen that the initial decrease of the productive capacity is 2% compared to the value added in Nuevo León. This figure also shows the rapid initial recovery, especially during the first five months, a period when the economy recovered approximately 95% of the damaged productive capacity. However, the shape of the recovery curve is influenced by the rationing diagram chosen for the model, within which inter-industrial demand and recovery demand are prioritized above the rest of the final demand. The results indicate that for period (month) 15, the production level was basically the same as before the disaster; yet, disequilibria in the markets do exist, and accordingly the process continues until period 20.
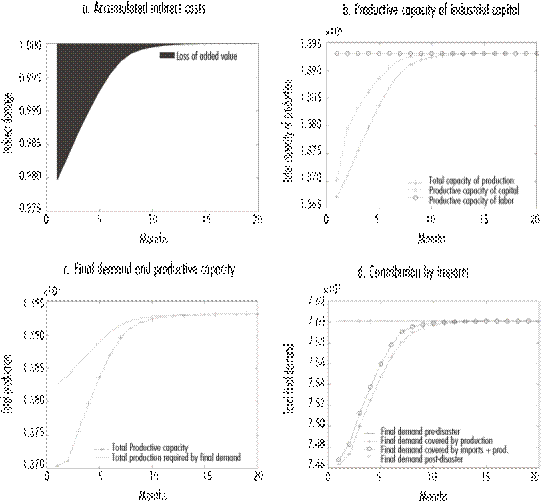
Source: prepared by the authors based on the model’s results.
Figure 2 Dynamics of economic variable during the recovery process
Figure 2b then shows the dynamics of recovery of the productive capacity of capital, and its interaction with total productive capacity. Delays in production in following the recovery pace of industrial capital is due to secondary effects caused by disequilibria across production chains in each industry. Figure 2c illustrates the disequilibria between supply and demand. Finally, figure 2d demonstrates the contribution of imports to the recovery process.
Sectoral analysis
One of the advantages of the methodology being used here is that, given that it is circumscribed in the IO analysis, a sectoral analysis of the results is possible, which allows for a look at how the effects of the shock to the economy are distributed across production chains. This element of the methodology becomes useful for planning in flood risk management, in addition to adjustment policy.
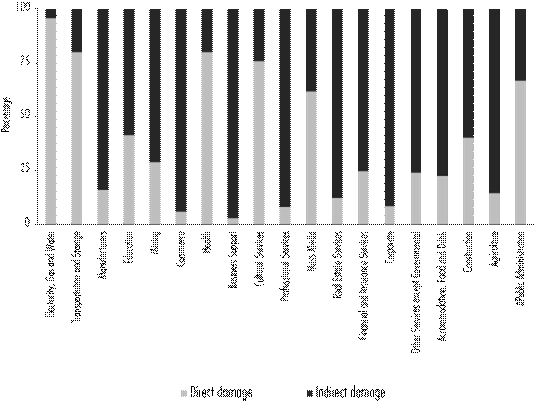
Figure 3 presents the distribution of economic impact in the 19 productive sectors, divided into direct and indirect damages. The damages, in particular direct ones, are concentrated in sectors related to infrastructure, i.e. that of Electricity, Gas and Water, and the Transportation sector. These two sectors concentrate 81% of the event’s total damage, which for direct damages represents 93%, though only 39% as regards indirect damages.
Source: prepared by the author based on the results of the model.
Figure 3 Sectorial distribution of economic impact
Additionally, it can be observed that the remaining sectors were affected primarily by indirect damages, despite not having been reached directly by the effects of the hurricane.
Direct losses in the sector with highest damage, that of Electricity, Gas and Water, represent 57% of the total direct economic losses; while the sector with the next highest direct damages (Transportation and Storage) make up 36% of the rubric.
Regarding the sectors with highest indirect damage, that of Transportation and Storage sees the highest concentration, with 31% of total indirect damages. Following it is the manufacturing industry sector, whose indirect losses are 22% of the total.
It is worth noting that the Transportation and Storage sector and that of Education are found to be among the three most affected sectors in each category, even though the proportion of indirect damages is much higher for Education (58%) than for Transportation and Storage (20%).
Figure 4 allows for a more detailed analysis of the distribution of direct and indirect damages by sector, independently of their amounts. This makes it possible to know which of the sectors were found to be proportionally more affected in an indirect way. It is especially the Service sectors, which are at the end of the production chain, that turn out to be the most indirectly affected-such as the Commerce, Business Support and Professional Services sectors. The proportion of indirect damages in primary sectors such as Agriculture and secondary, such as Manufacturing, is notable. The foregoing can be explained as a result of high levels of damage to energy and transportation infrastructure.
Case and sensibility analyses
Here, the effect of impacts to workers and possible changes to households’ final demand are analyzed. To do this, hypothetical values were used, based on possible scenarios and in line with information from reports on damages caused by hurricane Alex in Nuevo León. Nonetheless, information on these variables is scarce, especially in the form that the model requires, such that various scenarios were considered for its implementation.
In the case of impact to the workforce, the proportion of people affected with respect to the total population was taken and applied to the total working population for impacts that caused delays in transportation of up to two hours during the first month. A linear recuperation was modeled for five months.
For the case of changes to household consumption, the total portion of the affected population was taken into account. A 20 % decrease in their consumption of non-basic products during the first month. A linear recuperation was modeled over five months.
The parameters under consideration are conservative and based on reported data. Nonetheless, a sensibility analysis was performed for the parameters in order to prove the model’s stability and the solidity of the results. The sensibility analysis considered the variation of the parameters to be +/- 10% with respect to the initial values.
From figure 5a to 5b the values of different variables across the recovery process are shown. The error bars calculate the standard deviation for each point across time. The sensibility analysis applies for the case in which the workforce is affected, but not the final demand. In that case, the average value of indirect costs is $6.086 billion MXN, with a standard deviation of +/- $80 (+/- 1.3%) million MXN, which represents an additional 3% than when not considering the decrease in productivity because of impacts to the workforce.
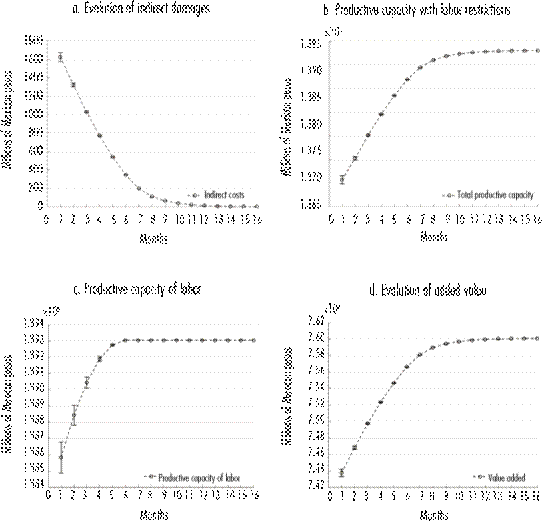
Source: Prepared by the authors based on results from the model.
Figure 5 Analysis of damages due to impacts to the workforce
Figure 6 shows, on the other hand, the effect of changes to final demand, but without variation of the workforce and with respect to indirect damage variables (see figure 5a), for total production, given the changes in behavior of final consumers (see figure 5b), the evolution of final demand (see figure 5c), and the evolution of value added under this scenario (see figure 5d). The results show average indirect damages of a total of $6.172 billion MXN, with a standard deviation of +/- $15 million (+/- 0.3%) MXN, and an increase of 4% as compared to the base scenario.
Source: prepared by the authors based on the results of the model.
Figure 6 Analysis of damages by impacts to final demand
Finally, a global sensibility analysis was performed. That is, varying all of the parameters at the same time (for workforce and household final demand). The results show average indirect damages of a total of $6.636 billion MXN, with a standard deviation of $96 million (+/- 1.5%) MXN, which represents 7% compared to the base scenario. A summary of the results can be seen in table 1, where the damage increase index (DII) indicates how much indirect economic cost was implied by each damage monetary unit to the productive (or industrial) capital.
Table 1 Summary of damages under different scenarios
| Scenario | Residential damages | Direct industrial damages | Indirect damages | Total damages | DII (%) |
| 1.Direct damages to capital | $962.65 | $20 538.21 | $5 922.31 | $27 423.17 | |
| 3.51% | 74.89% | 21.60% | 100.00% | 28.84 | |
| 2.Direct in industrial and labor damages | $962.65 | $20 538.21 | $6 086.48 | $27 587.34 | |
| 3.49% | 74.45% | 22.06% | 100.00% | 29.63 | |
| 3.Direct industrial damages and reduced house hold demand | $962.65 | $20 538.21 | $6 172.15 | $27 673.01 | |
| 3.48% | 74.22% | 22.30% | 100.00% | 30.05 | |
| 4.Direct industrial and labor damages and reduced house hold demand | $962.65 | $20 538.21 | $6 336.27 | $27 837.13 | |
| 3.46% | 73.78% | 22.76% | 100.00% | 30.85 |
Source: prepared by the authors base don the results of model.
6. Conclusions
The present article analyzed the total costs of damages caused by hurricane Alex in the state of Nuevo León in 2010. To do so, a methodology was implemented to evaluate such damages, considering in particular the disequilibrium in the productive capacity caused by damages to industrial capital and infrastructure. The analysis demonstrates that, for each $1 MXN of real estate, equipment and infrastructure destruction, losses in production were generated of almost $0.29 MXN, due to inter-sectoral connections in the industry that are disrupted after the disaster.
Additionally, a sensibility analysis was performed, to measure the probable effects of impacts to the productive capacity of the workforce and of changes to consumption patterns. The average values suggest an impact to the workforce equivalent to 4.14% plus 0.8% to indirect damages. A reduction in consumption of non-basic goods by 20% by the affected population represents an additional 0.4% to indirect damages. Finally, an analysis that considers variation in all parameters allows for a calculation of indirect damage close to 31% of that occasioned by damages to industry.
This analysis shows the relevance of indirect damages to total costs caused by a natural disaster and demonstrates which sectors were most indirectly affected, given the physical destruction. Evidence was provided that there are industrial sectors which are economically vulnerable to natural disasters in an indirect way, including when they are not directly impacted by the natural phenomenon.
Research based on this methodology seeks to improve the efficiency of adjustment policies, to consider minimizing indirect costs. Additionally, it allows for an evaluation of public policies for recovery, with an analysis of different scenarios of resource allocation for reconstruction.
The pioneering character of this study of natural disasters in Mexico faces some challenges. The main challenge was the lack of data for direct damages and their degree of aggregation. Future studies anticipate development and implementation of damage functions that allow for a more rapid and precise evaluation of total economic costs. In addition, the analysis of all affected regions at a national level may be considered to the same effect, which would make better national adjustment policies possible.
REFERENCES
Arreguín-Cortés, F. I., López-Pérez, M. y Marengo Mogollón, H. (2016), “Las inundaciones en un marco de incertidumbre climática”, Tecnología y Ciencias del Agua, vol. 7, núm. 5, México, septiembre-octubre. [ Links ]
Bočkarjova, M., Steenge, A. y van der Veen, A. (2004), “On direct estimation of initial damage in the case of a major catastrophe: derivation of the basic equation”, Disaster Prevention and Management, 13(4). DOI <https://doi. org/10.1108/09653560410556555>27 [ Links ]
CENAPRED (2014), “Características e impacto socioeconómico de los principales desastres ocurridos en la República Mexicana en el año 2010”, en N. García Arróliga, R. Marín Cambrains, K. Méndez Estrada y R. Reyes Rodríguez (eds.), Impacto socioeconómico de los desastres naturales, México, Dirección de Análisis y Gestión de Riesgos, Centro Nacional de Prevención de Desastres. [ Links ]
Cochrane, H. (1997), “Economic impact of a midwest earthquake”, NCEER Bulletin, vol. 11, núm. 1, Buffalo, New York, January. [ Links ]
______ (2004) “Economic loss: myth and measurment”, en M. Shinozuka, A. Rose y R. T. Eguchi (eds.), Engineering and socioeconomic impacts of earthquakes: an analysis of electricity lifeline disruptions in the New Madrid Area, Multidisciplinary Centre for Earthquake Engineering Research, Buffalo, New York, USA. [ Links ]
Cole, S. (2003), “Protection, risk, and disaster in economic network”, en A. van der Veen, A. L. V. Arellano y J. P. Nordvik, (eds.), Search of a common methodology for damage estimation, Workshop Proceedings, Netherlands, Office for Official Publications of the European Communities, Joint nedies and University of Twente. [ Links ]
Greenberg, M. R., Lahr, M. y Mantell, N. (2007), “Understanding the eco nomic costs and benefits of catastrophes and their aftermath: a review and suggestions for the U.S. Federal Government”, Risk Analysis, vol. 27, núm. 1, marzo. [ Links ]
Hallegatte, S. (2008), “An adaptive regional input-output model and its application to the assessment of the economic cost of Katrina”, Risk Analysis, vol. 28, núm. 3, junio. [ Links ]
Hallegatte, S. y Przyluski, V. (2010), “The economics of natural disasters. Concepts and methods”, Policy Research Working Paper, núm. 5507. Recuperado de <https://openknowledge.worldbank.org/handle/10986/3991> [ Links ]
IPCC (2012), “Managing the risks of extreme events and disasters to advance climate change adaptation. A special report of working groups I and II of the intergovernmental panel on Climate Change”, en C. B. Field, V. Barrios, T. F. Stocker, D. Qin, D. J. Dokken, K. L. Ebi, M. D. Mastrandrea, K. J. Mach, G. K. Plattner, S. K. Allen, M. Tignor y P. M. Midgley (eds.), Cambridge, United Kingdown and New York, USA, Cambridge University Press. [ Links ]
Li, J., Crawford-Brown, D., Syddall, M. y Guan, D. (2013), “Modeling imbalanced economic recovery following a natural disaster using input-output Analysis”, Risk Analysis, vol. 33, núm. 10, octubre. [ Links ]
Mendoza-Tinoco, D., Guan, D., Zeng, Z., Xia, Y. y Serrano, A. (2017), “Flood footprint of the 2007 floods in the UK: the case of the Yorkshire and the humber region”, Journal of Cleaner Production, 168. DOI <https:// doi.org/10.1016/j.jclepro.2017.09.016> [ Links ]
Miller, R. E. y Blair, P. D. (2009), Input output analysis: foundations and extensions (2 ed.), USA, Prentice-Hall. [ Links ]
Okuyama, Y. (2007), “Economic modeling for disaster impact analysis: past, present, and future”, Economic Systems Research, 19(2). DOI <https://doi. org/10.1080/09535310701328435> [ Links ]
______ (2009), “Critical review of methodologies on disaster impact estimation”, Background Paper to the Joint World Bank‐UN Assessment on the Economics of Disaster Risk Reduction. Recuperado de <https://www.gfdrr. org/sites/gfdrr/files/Okuyama_Critical_Review.pdf> [ Links ]
Rose, A. Z. (2004), “Economic principles, issues, and research priorities in hazard loss estimation”, en Y. Okuyama, y S. E. Chang (eds.), Modelling spatial and economic impacts of disasters, Berlin, Heidelberg New York, Springer-Verlag. [ Links ]
Steenge, A. E. y Bočkarjova, M. (2007), “Thinking about imbalances in post-catastrophe economies: an input-output based proposition”, Economic Systems Research, 19 (2). DOI <https://doi.org/10.1080/09535310701330 308> [ Links ]
Torres Navarro, I., Valdez Carrasco, I., Arévalo Pérez, B. N., Cruz Hernández, G., Ramírez Vázquez, R. y Ojeda González, J.C. (2010), Huracán Alex en Nuevo León, la memoria. Riesgos, testimonios y acción social, México, Secretaría de Desarrollo Social, Gobierno del Estado de Nuevo León. [ Links ]
Triple E Consulting (2014), “Climate extremes. Defining a pilot approach on estimating the direct and indirect impacts on economic activity”. Recuperado de European Commission. [ Links ]
Veen, A. V. d. (2004), “Disasters and economic damage: macro, meso and micro approaches”, Disaster prevention and management, 13 (4). DOI <https:// doi.org/10.1108/09653560410556483> [ Links ]
Veen, A. V. d. y Logtmeijer, C. (2003), “How vulnerable are we for flooding? a GIS approach”, en A. van der Veen, A. L. V. Arellano y J. P. Nordvik (eds.), Search of a Common Methodology for Damage Estimation, Workshop Proceedings, Netherlands, Office for Official Publications of the European Communities: Joint NEDIES and University of Twente. [ Links ]
1Climate change affects the hydrological cycle and provokes the existence of some dry regions and others with abundant rain, that turns into flooding. In the period from 19852010, flooding across the planet occurred mostly in urban areas. This is combined with poor urban development in cities, and changes in soil usage—problems which impede proper water filtration (Arreguín-Cortés et al., 2016).
2Flooding is caused by overflowing rivers, intense rain that accumulates in some area, failing sewage systems in urban zones, deforestation, urbanization, inadequate dams, tides, tropical cyclones, and other factors (IPCC, 2012).
3The direct total economic impact of natural disasters in 2010 was an estimated $92.1461 billion MXN (CENAPRED, 2014).
4Its direct impact was $21.5008 billion MXN (CENAPRED, 2014, p. 321).
5From the night of June 30, to the morning of July 1, Alex destroyed urban and residential infrastructure, leaving 15,800 families homeless.
6Note that with respect to symbols and formulas: the matrices are represented
by uppercase letters in bold italics (XX), vectors in bold italics (xx) and
scalars with italics (xx). Vectors are column vectors, and line vectors are
obtained by transporting vector (x´x´); a conversion of a diagonal matrix
vector is expressed with an uppercase letter with circumflex
9It is assumed that the productivity of any productive factor does not change during the recovery process, as is the case with Leontief production functions. It is also supposed that the disaster happens just after time t = 0 and that the recovery process starts at t = 1.
Appendix
Table A1 Sectorial disaggregation of the information
| Nuevo León Capital (millions of pesos) | Participation by sector (%) | Damage to capital (cillions of pesos) | Damage vector of the event | |
| STATE TOTAL (NUEVO LEÓN) | 490 027.40 | 20 538.21 | 0.04 | |
| Agriculture, livestock raising and exploitation, Forest use, fishing and hunting | 25.86 | 0.00 | 2.35 | 0.09 |
| Mining | 1 971.05 | 0.00 | 178.87 | 0.09 |
| Electric energy generation, transmisión and distribution pipeline supplies of wáter and gas to final consumer | 121 687.96 | 0.25 | 11 722.01 | 0.10 |
| Construction | 8 677.06 | 0.02 | 12.51 | 0.00 |
| Manufacturing industries | 173 304.41 | 0.35 | 249.89 | 0.00 |
| Trade | 15 236.34 | 0.03. | 21.97 | 0.00 |
| Transportation, mail and storage | 27 041.21 | 0.06 | 7 411.99 | 0.27 |
| Mass media information | 65 048.98 | 0.13 | 93.80 | 0.00 |
| Financial and insurance services | 15 738.77 | 0.03 | 22.69 | 0.00 |
| Real state services and renting of personal property and intangible godos | 12 236.65 | 0.02 | 17.64 | 0.00 |
| Professional, scientific and technical services | 9 225.56 | 0.02 | 13.30 | 0.00 |
| Corporate | 3 123.93 | 0.01 | 4.50 | 0.00 |
| Business support services, waste management and remediation services | 3 993.87 | 0.01 | 5.76 | 0.00 |
| Educational services | 3 603.87 | 0.01 | 469.33 | 0.13 |
| Health services and social assistance | 7 794.29 | 0.02 | 162.15 | 0.02 |
| Cultural entertaiment and sport services, and other recreational services | 4 452.72 | 0.01 | 125.13 | 0.03 |
| Temporary lodging services and food and beverage preparation | 5 005.34 | 0.01 | 7.22 | 0.00 |
| Other services, except governmental activities | 7 748.73 | 0.02 | 11.17 | 0.00 |
| Legislative, governmental judicial, international organizaional and offshore services | 4 110.80 | 0.01 | 5.93 | 0.00 |
Source: prepared by authors
Received: August 29, 2018; Accepted: February 04, 2019











 text in
text in