Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista mexicana de ingeniería biomédica
On-line version ISSN 2395-9126Print version ISSN 0188-9532
Rev. mex. ing. bioméd vol.33 n.2 México Dec. 2012
Artículo de investigación original
Computational Model of the Cochlea using Resonance Analysis
Modelo computacional de la cóclea usando análisis por resonancia
M. Jiménez-Hernández, J.L. Oropeza-Rodríguez, S. Suarez Guerra y R. Barrón-Fernández
Centro de Investigación en Computación, Instituto Politécnico Nacional, México D.F.
Correspondencia:
Mario Jiménez Hernández
Centro de Investigación en Computación,
Instituto Politécnico Nacional,
Laboratorio de Procesamiento Digital de Señales,
Av. Juan de Dios Bátiz, Esq. Miguel Othón de Mendizábal,
Col. Nueva Industrial Vallejo,
Delegación Gustavo A. Madero,
C.P 07738, México D.F. Piso 2, Sección 1.
Correo electrónico: mjimenezh@ipn.mx
Fecha de recepción: 02/Octubre/2012.
Fecha de aceptación: 6/Diciembre/2012.
Abstract
This paper presents the development of a computational model of the cochlea using a new solution by resonance analysis to the models of fluid mechanics in the cochlea and the basilar membrane as a system of forced harmonic oscillators proposed by Lesser and Berkeley. The computational model of resonance analysis is successfully compared with the method of numerical integration developed by Peterson and Bogert, the method of Green function proposed by Allen, the method of finite difference described by Neely and the measurements obtained in the experiments of Békésy, getting the same results with the new solution developed. Its contribution regarding the different solutions already found in the literature is to obtain a frequency-distance function to identify the maximum amplitude of displacement of each section along the basilar membrane for each specific excitation frequency in the hearing system. The model developed presents the advantage over the previous solutions, that the function obtained depends only of the physical characteristics of mass per unit area, damping coefficient and stiffness per unit area along the basilar membrane, and is the first time that the resonance analysis is used to obtain a methodology consistent with the place theory of hearing of Békésy.
Keywords: resonance analysis, basilar membrane, cochlea, inner ear.
Resumen
En este trabajo de investigación se propone una nueva solución a partir del análisis por resonancia del modelo de mecánica de fluidos de la cóclea y su solución del comportamiento de la membrana basilar como un sistema de osciladores armónicos forzados propuesto por Lesser y Berkeley. El modelo computacional del análisis por resonancia se compara en forma satisfactoria con el método de integración numérica desarrollado por Peterson y Bogert, con el método de la función de Green propuesto por Allen, con el método de diferencias finitas propuesto por Neely y con las mediciones experimentales de Békésy, obteniendo los mismos resultados a partir de la nueva solución desarrollada. Su aportación respecto a las diferentes soluciones ya encontradas en la bibliografía, es obtener una relación frecuencia-distancia que permite identificar la distancia a la que ocurre la amplitud máxima de resonancia a lo largo de la membrana basilar para cada frecuencia específica de excitación al sistema auditivo. El modelo desarrollado tiene la ventaja de depender sólo de las características físicas a lo largo de la membrana basilar de: coeficiente de elasticidad, factor de amortiguamiento y masa por unidad de área; siendo la primera vez que se emplea el análisis por resonancia para obtener una metodología concordante en su totalidad con la teoría de los puntos de audición de Békésy.
Palabras clave: análisis por resonancia, membrana basilar, cóclea, oído interno.
INTRODUCTION
In this paper we develop a computational model of the cochlea using a new solution by resonance analysis for the model of fluid mechanics in the cochlea and the basilar membrane as a system of forced harmonic oscillators proposed by Lesser and Berkeley [1], the goal is to obtain a relation for determining the maximum amplitude displacement along the basilar membrane to an input stimulus in the auditory system, which is dependent of the physical characteristics of mass, damping and stiffness along the basilar membrane.
The shape and structure of the cochlea is similar to a snail longitudinal divided into three compartments: the scala vestibuli which is in contact with the oval window, whereby acoustic waves are transmitted from the middle ear to the inner ear, the scala tympani which is communicated with the round window, and the scala media located between the other two scales. The physical modeling of the cochlea as a system of fluid mechanics is necessary because the scala vestibuli and the scala tympani are filled with an incompressible fluid clear and viscous called perilymph, and the scala media is filled with a fluid called endolymph. Structurally the scale media and the scala vestibuli are separated by Reissner's membrane and the scala media is separated from the scala tympani by the basilar membrane [2] [3].
The functioning of the auditory system consist in that the vibrations of sound are transmitted through the middle ear and channeled through the oval window into the scala vestibuli, the resulting waves within the perilymph travel along the scala vestibuli creating waves complementary in the basilar membrane and the scala tympani. The transduction of the acoustic waves into electrical impulses takes place in the organ of Corti, which is placed on top of the basilar membrane. In the organ of Corti are the hair cells, when the waves on the basilar membrane generate a force on the hair cells this cause a change in their potential, which is transmitted through the auditory nerves directly to the brain where the interpretation is performed for different frequencies. Each part of basilar membrane responds to the maximum value of the crest of the wave envelope and therefore it is considered that the mechanism of the cochlea determines the frequency of the input signal from the place where the basilar membrane has a maximum amplitude, this is known as place theory of hearing of Békésy [3] [4].
The first mechanical theory of the cochlea was proposed by Peterson and Bogert in 1950, was based on the hydrodynamic considering the cochlea as a system of two channels that vary in shape similar in cross section and separated by an elastic membrane with constant dynamic variables, for modeling were used the parameters reported in the experimental work of Békésy [5]. In the following years theories about the mechanics of the cochlea were developed, but in 1971 Rhode present physical measurements supported in the physiology of this organ, and the theories that were proposed previously found to be inadequate [6] [7]. Later in 1972, Lesser and Berkley developed a model that matches all the observations previously reported, modeling to the cochlea as a system of fluid mechanics and the basilar membrane as a system of forced harmonic oscillators concatenated [1]. In 1976 Allen uses the Lesser and Berkley model to obtain the parameters of the basilar membrane using the Green’s function, obtaining an approximate set of parameters of their behavior [8]. Later in 1981 Neely proposed a two-dimensional mathematical model of the cochlea, and their numerical solution using finite difference approximations using Laplace’s equation, obtaining up to now the best parameters of the mechanical response of the cochlea [9].
The solution to the model of the basilar membrane as a system of forced harmonic oscillators has been proposed in numerical form from the potential flow modeling using Fourier series by Lesser and Berkeley in 1972 [1]. Later in 1974 Siebert generalizes the solution of Lesser and Berkley considering a mechanical force at the two ends of the basilar membrane [10], a similar solution was found in 1981 by Peskin [11]. The following studies considered the physical structure of the basilar membrane to solve the model, emphasizing studies in 1984 by Rhode [12], in 1985 by Hudspeth [13] and 1996 by Boer [14]. In recent years have been developed solutions considering state space models, in 2007 by Elliott et al. [15] and 2008 by Ku et al. [16]. In this research aims to provide a new solution using resonance analysis, which has the advantage over the solutions mentioned above to determine the distance of the maximum amplitude along the basilar membrane for each excitation frequency of the system.
FLUIDS MECHANICS IN THE COCHLEA
The movement of fluids in the cochlea can be described from the equations of motion for an incompressible and viscous fluid, considering that the cochlea is divided into two rectangular compartments, separated by the basilar membrane and filled with a fluid of similar characteristics to the perilymph and endolymphm [3]. The upper compartment corresponds to the scala vestibuli and the lower compartment corresponds to the scala tympani, for simplicity the scala media is omitted. Figure 1 shows the diagram of the fluid mechanics in the cochlea, showing the boundary conditions of displacement in the basilar membrane.
The fluid in the cochlea is incompressible and present homogeneous characteristics, where the fluid velocity is u =(u1,u2,u3) and the mass of fluid is constant with a pressure P and density ρ. Therefore the volume V of the fluid only can change due to the variation of fluid flow in a cross section for a given time, having an equal on both volumes which depends on the variables mentioned.

Where S is the surface area of the volume V and n =(n1,n2,n3) is the unit outward normal volume. Similarly the fluid in a fixed domain V can change only in response to forces applied to the flow crosses in the domain boundaries. Then for a viscous fluid is considered the conservation of the momentum as follows

Using the divergence theorem for convert surface integrals to volume integrals, thus

Considering that the volume is arbitrary, we obtain

When the movement of fluid have small amplitudes is possible ignore the nonlinear terms in the cochlea, yielding

An important special case is when u = ∇ø for some potential in an irrotational flow, leaving the above equations of the form
THE BASILAR MEMBRANE AS A HARMONIC OSCILLATOR
In their work Lesser y Berkeley proposed that one way to model the physical behavior of the cochlea is to combine the equations 9 and 10 with the equation of a forced harmonic oscillator [1]. If one considers the pressure value as an arbitrary constant in the upper and lower compartments of the basilar membrane, there are two copies of the two equations given above

Each point on the basilar membrane can be modeled as a harmonic oscillator with m(x) mass per unit area, Rm(x) damping coefficient and k(x) stiffness per unit area, which vary along the membrane. In this condition, the movement of each part along the membrane is considered to be independent of the movement of neighboring parts, assuming no lateral coupling [1]. The deflection of the membrane is then a one-dimensional wave equation η(x, t) which is the solution for forced harmonic oscillator equation, is specific by

The vertical displacement of the membrane is small and therefore the force is considered as the difference of pressure between the point y = 0 and the maximum y = η. This simplifies the harmonic oscillator equation can specify the boundary conditions. If we consider that the fluid velocity ∂φ/∂t is the component y and therefore the boundary conditions on the basilar membrane, thus
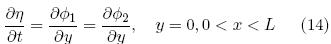
If there is no vertical motion at the top, thus we have

Although there are many ways to excite externally an oscillator forced, is considered that the system is excited by a movement of the stapes in contact with the window oval. Since ∂ø/∂x is the x component of the fluid velocity, the boundary condition at x =0 is

Where F (y, t) is the horizontal displacement of the oval window, whereas there is no horizontal motion at the far end, so that x = L

RESONANCE ANALYSIS OF THE COCHLEA
A new solution to the model of Lesser y Berkeley can be developed using the resonance analysis from the equation of forced oscillator described by equation 13. This solution has the advantage of determining the maximum amplitude of displacement by resonance for each section along the basilar membrane, which depend on the characteristics of their mass per unit area, damping coefficient and stiffness per unit area.
To perform the analysis we considers each section of the membrane as a forced harmonic oscillator isolated, which is excited by an external force Fejωt that representing the driving force on each section of the basilar membrane, this force is produced by vibration transmitted into the cochlea by the oval window. The differential equation describing the resulting motion of the system is as follows

Where F is the magnitude of the driving force and ω its angular frequency. This implies that the driving force Fejωt is periodic and complex, therefore can be considered that the displacement η is also complex, and then the solution of the differential equation is defined by displacement η = Aejωt, where A is the complex amplitude. Substituting the displacement, its first derivative and second derivative and considered η as common factor, we obtain an equation that models the displacement as a function of the other terms

The above equation can be expressed in a simpler form defining complex mechanical impedance as follows

Where the mechanical reactance is defined by the following

The mechanical impedance may also be expressed in polar form Zm(x)= Zm(x)ejΘ(x), then taking an equation in terms of magnitude and one that determines the phase angle.

From equations 22 and 23 we can write the displacement complex in the form.

The equation 24 is simplified to a single exponential term reducing algebraically as follows.

Then we proceed to obtain the real part and complex part using Euler's identity

And therefore the displacement of each membrane section is defined by the real part of the equation 26.
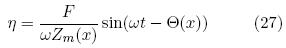
In equation 27 the amplitude is defined by A = F/ωZm(x) and can be expressed algebraically in terms of mass, damping and stiffness, by the following expression

The equation 28 shows that the amplitude for each section of the membrane depends of the frequency ω in the applied force. The amplitude has a maximum when the denominator has its minimum value, this occurs at a specific frequency excitation called resonance frequency, which is defined by the values of mass and stiffness, when the frequency ω of the applied force is equal to k(x)/m(x), we said that the system is resonant in amplitude and we obtain the maximum value of displacement of the basilar membrane.
COMPUTATIONAL MODEL OF THE COCHLEA
Equation 28 can be expressed as a function of frequency and distance, if we consider that ω = 2πƒ, thus we have

From equation 29 we develop a computational model to obtain the distance where occurs the maximum displacement of the basilar membrane to a specific excitation frequency of the system, which depends of the physical characteristics of the basilar membrane. The figure 2 shows the block diagram of the computational model of the cochlea using resonance analysis.
The value of the magnitude of the external excitation force is considered normalized because the magnitude variation does not change the position along of the basilar membrane where the maximum value of displacement is obtained.
EXPERIMENTS AND RESULTS
The computational model of the cochlea by resonance analysis is compared with the results obtained in the works of Peterson and Bogert [5], Allen [8] and Neely [9], using the parameters of mass, damping and stiffness along the basilar membrane for each of the models. For the realization of the experiments are considered the same frequencies of assessment used in the original articles in order to make the comparison with the results obtained from the analysis by resonance. In the proposed methodologies were chosen these frequencies because are in the range of maximum sensitivity within the human audibility threshold. The Table I shows the respective parameters.
The computational model of the cochlea by resonance is first compared with the model of Peterson and Bogert. This is evaluated in the frequency range of 20 Hz to 12000 Hz in increments of 1 Hz and in the range of distances of 0.001 cm to 3.300 cm in increments of 0.001 cm. We obtain for each distance a maximum amplitude value, which depends of the excitation frequency. The table II shows the comparison between the two results.
In Figure 3 we show the graph of resonance analysis for the value of frequency 1000 Hz. Because the model Peterson and Bogert not model the damping, the graph has a closed behavior on the x axis for each frequency value.
The results confirm the similarity between the resonance analysis and the method of numerical integration developed by Peterson and Boger.
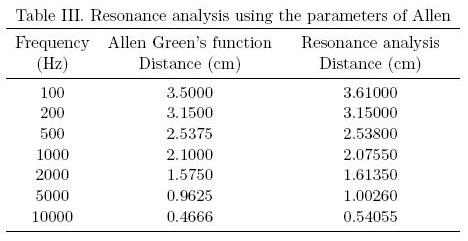
The computational model of the cochlea is also compared with the model of Allen and evaluated with the parameters described in his work considering the value of α =1.5. This is evaluated in the range of excitation frequencies from 20 Hz to 12000 Hz in increments of 1 Hz and in the range of distances of 0.0001 cm to 3.5000 cm in increments of 0.0001 cm. Table III shows the results obtained by both models with the same frequencies.
Figure 4 shows the result of the resonance analysis for the frequency of 1000 Hz, the graphic shows the difference in behavior for a model with damping respect to a model without damping like the model of Peterson and Bogert.
Equality is observed in all results, which means that the same values are obtained using different processes, taking in one case the Green's function and the other resonance analysis.
Next the resonance computational model is compared with the model of Neely, this is evaluated in the frequency range of 20 Hz to 10000 Hz in increments of 1 Hz and in the range of distances of 0.00001 to 3.50000 in increments of 0.00001 cm. The table IV shows the results of both models for the same frequencies.
Figure 5 shows the graph of resonance analysis for the value of frequency 1130 Hz. The behavior is similar to the model of Allen which corresponds to a system with damping.
Similar to previous models there is equality between the results obtained by both processes, either using finite differences or resonance analysis.
The three graphs compare satisfactorily the physical behavior of the basilar membrane using resonance analysis with the values obtained in the three different methodologies show the physical response of the system in the frequency domain.
Finally Table V shows the comparison between the resonance analysis and the results of pathological observations by Békésy.
In the last test we used the parameters of Neely because they are the best approximated to the behavior of the cochlea until today.
CONCLUSION
The studies of the inner ear are based in the hydrodynamics of the cochlea, the mechanical movement of the basilar membrane and the biological processes in the inner ear, however do not provide a relationship between the excitation frequency to the auditory system and the distance along the basilar membrane in which is presents the maximum displacement of amplitude.
This new computational model of the cochlea provides this relationship, is developed from the fluid mechanics in the cochlea and their solution of the behavior of the basilar membrane as a set of harmonic oscillators forced proposed by Lesser and Berkeley, obtaining the relationship frequency-distance using the resonance analysis.
This new solution has the advantage over the previous solutions of determined from the physical characteristics of mass per unit area, damping coefficient and stiffness per unit area along the basilar membrane, the distance of maximum amplitude by resonance for each frequency of excitation.
The results of the computational model by resonance were compared satisfactorily with the obtained analytically by Peterson and Bogert using numerical integration (Table II), the method of the Green function of Allen (Table III), the approximation by finite difference of Neely (Table IV) and the experimental results obtaining by Békésy (Table V), being the new model consistent with place theory of hearing.
The model developed presents the disadvantage that at high frequencies near to the base of the cochlea has a frequency-distance relationship with abrupt increases in the frequency domain, this is not significant because the intervals of more intelligible are below to 4 kHz, for frequencies above of this range the model should be evaluated based on increments in octaves similar to how the auditory system works.
The next stage of our research project is to apply the model of resonance and the frequency-distance function for to determine quantitatively the distances along the cochlea where the electrodes are positioned in cochlear implants.
REFERENCES
1. Lesser MB, Berkeley DA, "Fluid Mechanics of the cochlea. Part 1," J. Fluid Mech., 1972; 51:497-512. [ Links ]
2. Yost WA, Fundamentals of hearing: An introduction, Fifth Edition, Academic Press (USA), 2006. [ Links ]
3. Keener J, Sneyd J, Mathematical Physiology. Springer (USA), 2008. [ Links ]
4. Bekesy V, Experiments in hearing. Mc Graw Hill (USA), 1960. [ Links ]
5. Peterson LC, Bogert BP, "A dynamical Theory of the Cochlea" J. Acoust. Soc. Amer., 1952; 22:175-84. [ Links ]
6. Rhode WS, "Observations of the vibration of the Basilar Membrane in Squirrel Monkeys using the Mössbauer Technique" J. Acoust. Soc. Amer., 1971; 49:1218-1231. [ Links ]
7. Rhode WS, Robles L, "Evidence of Mossbauer experiments for nonlinear vibration in the cochlea" J. Acoust. Soc. Amer., 1974; 55:558-596. [ Links ]
8. Allen JB, Hirano M, "Two-Dimensional cochlear fluid model: New Results" J. Acoust. Soc. Amer., 1971; 61:110-119. [ Links ]
9. Neely ST, "Finite difference solution of a two-dimensional mathematical model of the cochlea" J. Acoust. Soc. Amer., 1981; 69:1386-1396. [ Links ]
10. Siebert WM, "Ranke revisited-a simple short-wave cochlear model" J. Acoust. Soc. Amer., 1974; 56:594-600. [ Links ]
11. Peskin CS, "Lectures on mathematical aspects of physiology" AMS Lectures in Applied Mathematics, 1981; 19:38-69. [ Links ]
12. Rhode WS, "Cochlear Mechanics" Ann. Rev. Physiol., 1984; 46:231-246. [ Links ]
13. Hudspeth AJ, "The cellular basis of hearing: the biophysics of hair cells" Science, 1985; 230:745-752. [ Links ]
14. Boer SE, Ed. by: Dallos P, Fay RR, The cochlea Chapter 5: Mechanics of the cochlea: modeling effects. Springer (USA), 1996. [ Links ]
15. Elliot SJ, Ku EM, Lineton BA, "A state space model for cochlear mechanics" J. Acoust. Soc. Amer., 2007; 122: 2759-2771. [ Links ]
16. Ku EM, Elliot SJ, Lineton BA, "Statistics of instabilities in a state space model of the human cochlea" J. Acoust. Soc. Amer., 2008; 124:1068-1079. [ Links ]