Introducción
La cimentación de una estructura es la parte esencial para transmitir las cargas de columna o pared al terreno subyacente de la estructura. Las cargas que bajan de la estructura a las cimentaciones superficiales descansan directamente sobre el suelo, y en las cimentaciones profundas las cargas que provienen de la estructura descansan sobre una llamada tapa o cabezales de los pilotes o zapatas, y a su vez se trasmiten a los pilotes.
La presión del suelo bajo una zapata se distribuye de acuerdo con el tipo de suelo, la rigidez relativa del suelo y la cimentación y la profundidad de contacto entre la cimentación y el suelo. La Figura 1a muestra el diagrama de distribución de presión para la zapata que descansa sobre suelos arenosos (suelos granulares). La Figura 1b presenta el diagrama de distribución de presión para la zapata que descansa sobre suelos arcillosos (suelos cohesivos). Por lo tanto, se supone, por simplicidad, que la zapata es un cuerpo perfectamente rígido, que el suelo se comporta elásticamente y que las distribuciones del esfuerzo y la deformación son lineales en el suelo debajo de la base de la zapata. Por consiguiente, el diseño propuesto asume que la presión del suelo se distribuye linealmente. La distribución de la presión del suelo es uniforme si el centroide de la zapata coincide con la fuerza resultante de las cargas aplicadas sobre la zapata (Figura 1c) (Luévanos-Rojas, 2014; 2015; Luévanos-Rojas, Barquero-Cabrero, López-Chavarría & Medina-Elizondo, 2017).

Fuente: Luévanos-Rojas (2014).
Figura 1 Diagrama de presión debajo de la zapata: (a) zapata sobre arena; (b) zapata sobre arcilla; (c) presión equivalente.
La Figura 1 muestra los tipos de cimentaciones (ver Parte 1).
Los documentos más importantes sobre el diseño óptimo de cimentaciones que han presentado para algunos investigadores son: Diseño óptimo basado en algoritmos genéticos de cimentaciones de balsas apiladas con pruebas de modelo (Kim, Yoo & Kang, 2002); Diseño óptimo de cimentaciones superficiales rectangulares; Formulación (Chagoyén, Negrín, Cabrera, López & Padrón, 2009); Estudio teórico sobre optimización de longitud de pilotes de grupos de pilotes y balsas apiladas (Leung, Klar & Soga, 2010); Optimización del diseño del grupo de pilotes utilizando un enfoque genético real (Hwang, Lyu & Chung, 2011); Metodología de selección experto basada en el conocimiento para optimizar la construcción de pilotes de concreto (Penteado & de Brito, 2012); Diseño óptimo de cimentaciones superficiales poco profundas con suelos limosos (Hassaan, 2014); Metodologías de diseño óptimo para cimentaciones de pilotes en Londres (Letsios, Lagaros & Papadrakakis, 2014); Aplicación del algoritmo genético en el diseño óptimo de la cimentación de tira (Hui, Zhuoyi & Mingji, 2015); Método de análisis de optimización del diámetro de pilote de cimientos de balsas apiladas basado en la minimización de asentamientos diferenciales (Wang, Yang & Shangguani, 2015); Dimensionamiento óptimo para las zapatas combinadas de esquina (López-Chavarría, Luévanos-Rojas & Medina-Elizondo, 2017); Diseño óptimo para zapatas aisladas rectangulares utilizando la presión real del suelo (Luévanos-Rojas et al., 2017); Diseño óptimo de zapatas basadas en la optimización de MINLP (Jelušič & Žlender, 2018); Experimentación numérica para el diseño óptimo de las zapatas combinadas rectangulares de concreto reforzado (Velázquez-Santillán, Luévanos-Rojas, López-Chavarría, Medina-Elizondo & Sandoval-Rivas, 2018); Diseño robusto y procedimiento de optimización para cimientos de balsas apiladas para soportar aerogeneradores altos en arcilla y arena (Ravichandran, Shrestha & Piratla, 2018).
Los trabajos más relevantes sobre el diseño de cabezales que han estudiado algunos investigadores son: Diseño de cabezales en pilotes profundos por el modelo de punta y liga (Adebar & Zhou, 1996); Cimentaciones de losas sobre pilotes: Diseño y aplicaciones (Poulos, 2001); Un análisis elastostático FEM / BEM de losas cargadas verticalmente y cimientos de losas sobre pilotes (Mendonҫa & Paiva, 2003); Modelo de punta y liga adaptable para el diseño y verificación de cabezales sobre cuatro pilotes (Souza, Kuchma, Park & Bittencourt, 2009); Seis cabezales sobre pilotes de concreto armado: Simulación numérica y diseño por el método de punta y liga (Oliveira, Barros & Giongo, 2014); Minimización de costos de la cubierta de pilotes de concreto reforzado utilizando técnicas de optimización (Regupathi & Sugumar, 2017); Diseño de cabezales rígidos sobre pilotes usando un modelo iterativo de punta y liga (Araújo, 2016); Análisis de confiabilidad de los cabezales rígidos sobre pilotes usando un modelo iterativo de punta y liga (Araújo, 2017).
La presente investigación muestra un modelo optimizado para el diseño óptimo (costo mínimo) para cabezales rectangulares apoyados sobre un grupo de pilotes que soporta una carga axial y dos momentos sobre el eje X y Y debido a una columna. La primera parte de esta investigación presenta un modelo para obtener la superficie mínima en planta (área óptima). Este modelo considera que los cabezales son perfectamente rígidos y los pilotes están articulados en la unión de los cabezales con los pilotes y, por lo tanto, los pilotes transmiten solamente carga vertical. La metodología normalmente utilizada para obtener el diseño de los cabezales considera que todos los pilotes transmiten la misma carga vertical; esto funciona únicamente cuando la columna transmite carga axial y no momentos. Además, cinco ejemplos de cabezales apoyados sobre un grupo formado por dos, tres, cuatro, cinco y seis pilotes se muestran para demostrar la precisión del modelo presentado en este documento.
Metodología
Las secciones críticas para la zapata que sostiene una columna de concreto reforzado de acuerdo con el código de construcción son: 1) Para el momento flexionante ocurre en la cara de la columna (unión de la columna con la zapata); 2) Para el cortante por flexión se presenta a una distancia (d) a partir de la cara de la columna; 3) Para el cortante por punzonamiento se ubica en b o (perímetro de la sección crítica que se ubica a una distancia d/2 de la cara de la columna en ambas direcciones) (American Concrete Institute[ACI], 2014).
La ecuación general para obtener el esfuerzo generado por cada pilote sobre los cabezales o zapatas apoyadas sobre pilotes (cimentación profunda) sujetas a flexión biaxial se muestra en la Parte 1 de este documento:
donde σ p = esfuerzo generado por el pilote sobre el cabezal (presión del pilote); A p = área de contacto del pilote en estudio; A pT = área de contacto de todos los pilotes; x p = distancia en dirección del eje X a partir del eje Y a la ubicación del pilote en estudio; y p = distancia en dirección del eje Y a partir del eje X a la ubicación del pilote en estudio; ∑I yp = suma de momentos de inercia de la superficie de contacto de todos los pilotes alrededor del eje Y general; ∑I xp = suma de momentos de inercia de la superficie de contacto de todos los pilotes alrededor del eje X general; y N p = fuerza axial generada por cada pilote sobre el cabezal.
La ecuación general para obtener la fuerza ejercida por cualquier pilote es (ver Parte 1):
donde i = 1, 2, 3, … n
Formulación del nuevo modelo
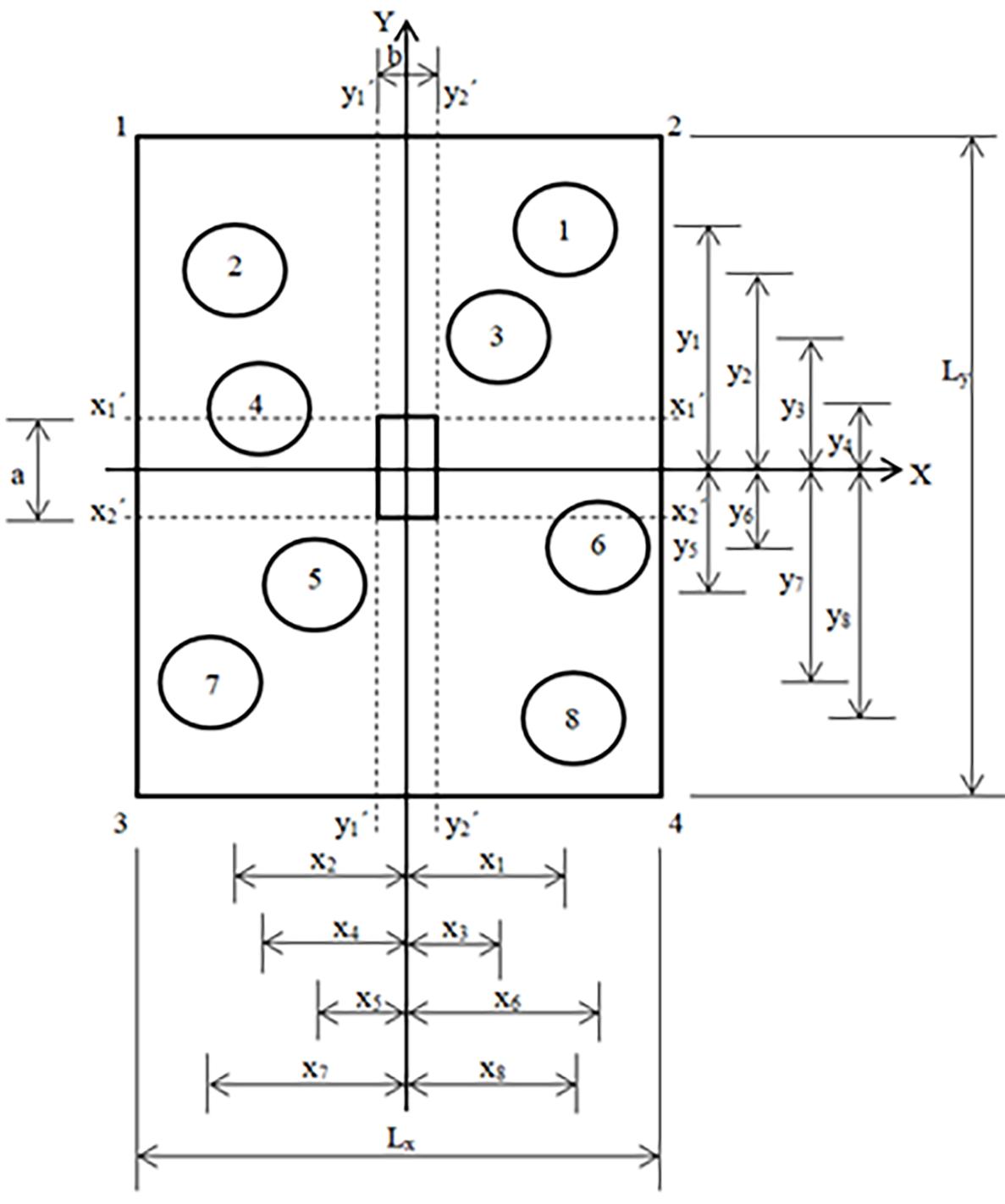
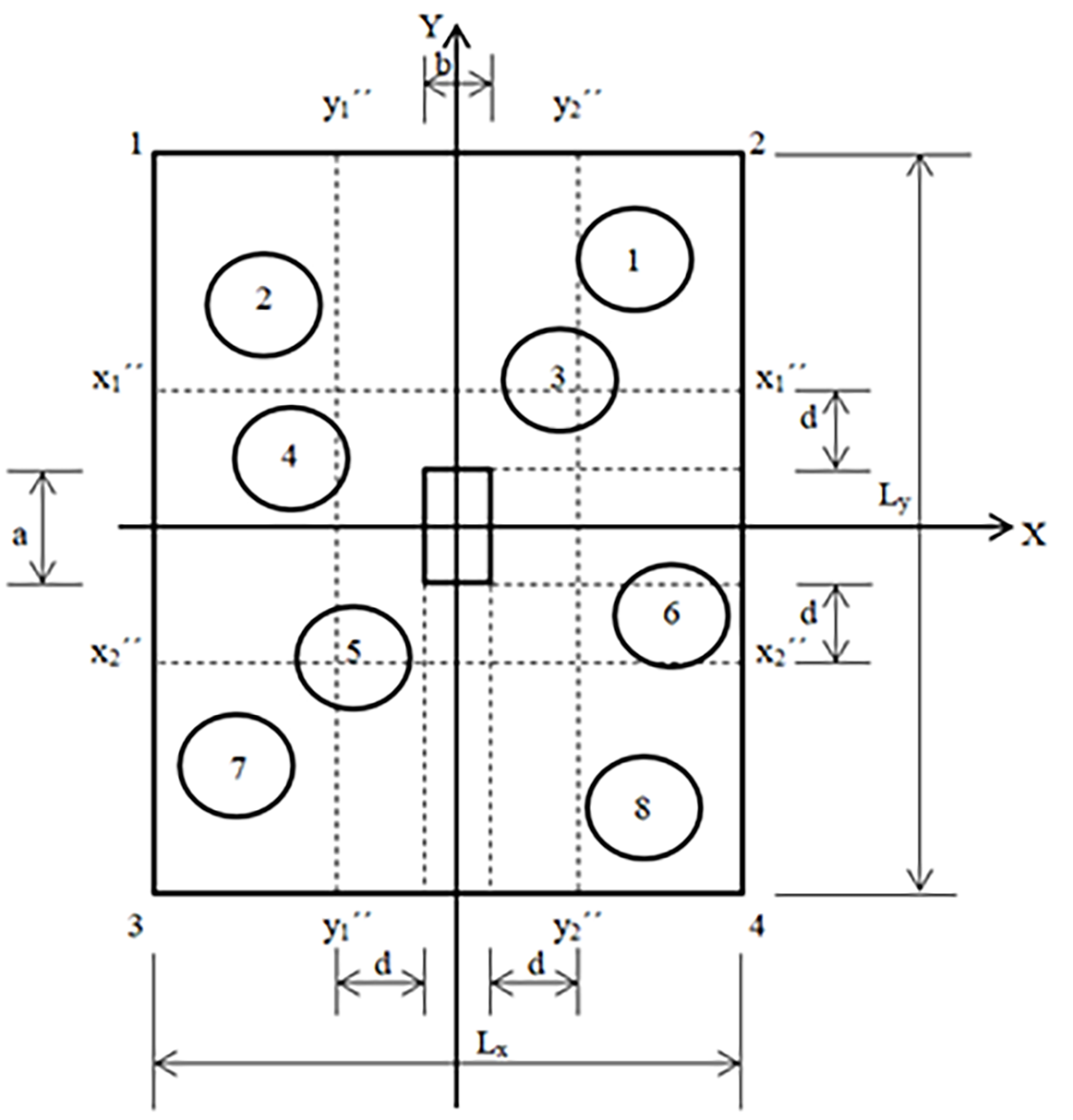
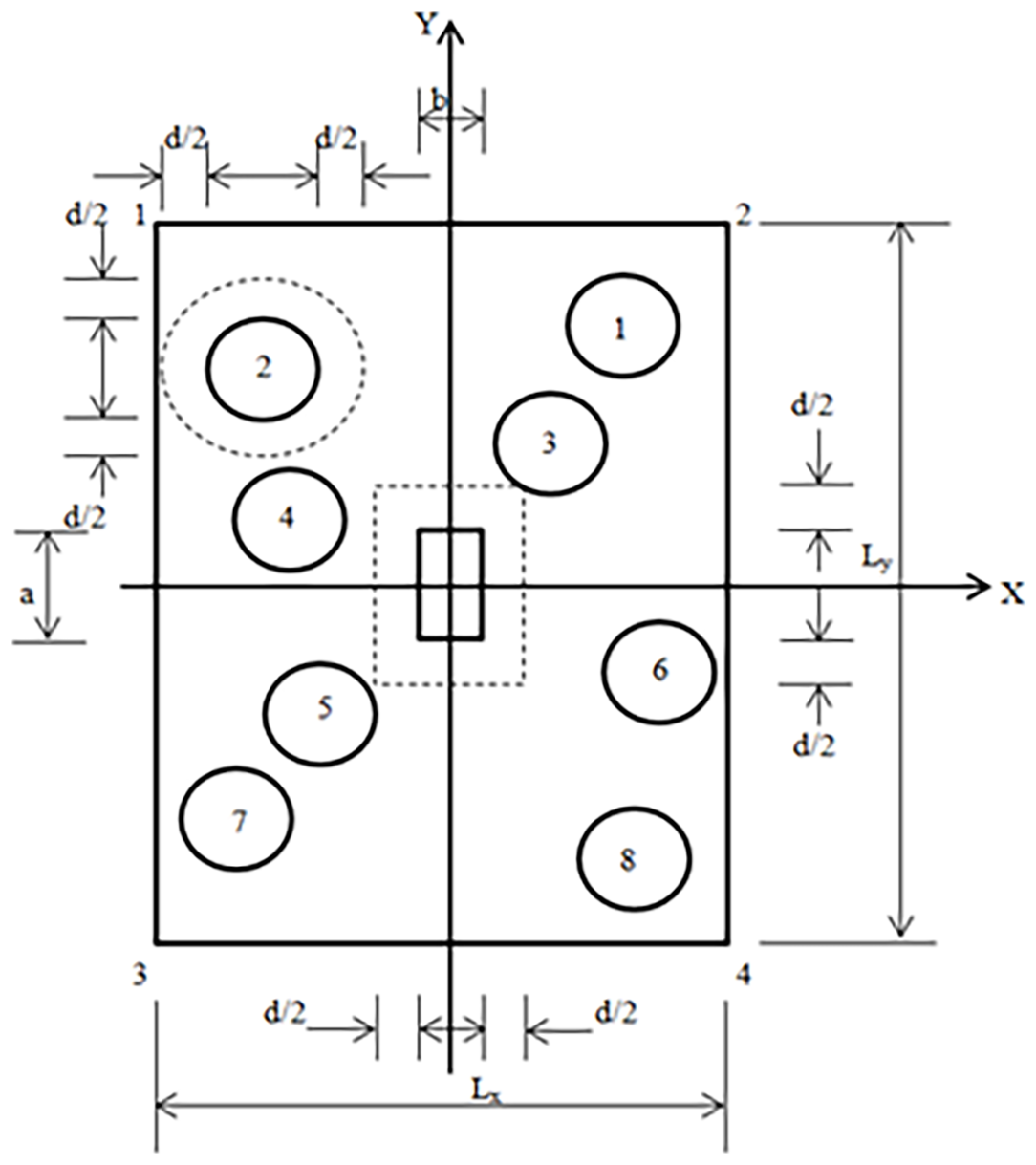
Las Figuras 2, 3 y 4 muestran un cabezal que soporta una columna y que está apoyado sobre varios pilotes de forma desorganizada para mostrar el modelo generalizado.
Para los momentos, las secciones críticas se presentan sobre los ejes x1´-x1´, x2´-x2´, y1´-y1´ y y2´y2´ (Figura 2).
Las ecuaciones generalizadas para los momentos sobre los ejes x1´-x1´ y x2´-x2´ se presentan como sigue:
donde i = 1, 2, 3, … k, l, … n. Los valores de 1 a k son los ubicados sobre los cuadrantes I y II (área delimitada por las esquinas 1, 2 y el eje x1´-x1´); los valores de l a n son los ubicados sobre los cuadrantes III y IV (área delimitada por las esquinas 3, 4 y el eje x2´-x2´).
El momento máximo sobre el eje x´-x´ se considera el momento mayor de los obtenidos por las ecuaciones (3) y (4).
Las ecuaciones generalizadas para los momentos sobre los ejes y1´-y1´ y y2´-y2´ se presentan como sigue:
donde i = 1, 2, 3, … j, m, … n. Los valores de 1 a j son los ubicados sobre los cuadrantes II y III (área delimitada por las esquinas 1, 3 y el eje y1´-y1´); los valores de m a n son los ubicados sobre los cuadrantes I y IV (área delimitada por las esquinas 2, 4 y el eje y2´-y2´).
El momento máximo sobre el eje y´-y´ es considerado el momento mayor de los obtenidos por las ecuaciones (5) y (6).
Para los cortantes por flexión, las secciones críticas se presentan sobre los ejes x1´´-x1´´, x2´´-x2´´, y1´´-y1´´ y y2´´-y2´´ (Figura 3).
Las ecuaciones generalizadas para los cortantes por flexión sobre los ejes x1´´-x1´´ y x2´´-x2´´se presentan como sigue:
donde i = 1, 2, 3, … k, m, … n. Los valores de 1 a k son los ubicados sobre los cuadrantes I y II (área delimitada por las esquinas 1, 2 y el eje x1´´-x1´´); los valores de l a n son los ubicados sobre los cuadrantes III y IV (área delimitada por las esquinas 3, 4 y el eje x2´´-x2´´).
El cortante por flexión máximo sobre el eje x´´-x´´ se considera el valor mayor de los obtenidos por las ecuaciones (7) y (8).
Las ecuaciones generalizadas para los cortantes por flexión sobre los ejes y1´´-y1´´ y y2´´-y2´´se presentan como sigue:
donde i = 1, 2, 3, … j, m, … n. Los valores de 1 a j son los ubicados sobre los cuadrantes II y III (área delimitada por las esquinas 1, 3 y el eje y1´´-y1´´). Los valores de m a n son los ubicados sobre los cuadrantes I y IV (área delimitada por las esquinas 2, 4 y el eje y2´´-y2´´).
El cortante por flexión máximo sobre el eje y´´-y´´ se considera el valor mayor de los obtenidos por las ecuaciones (9) y (10).
Para los cortantes por punzonamiento, las secciones críticas se presentan en dos casos; el primero es la columna sobre el cabezal y el segundo es el pilote (carga mayor) sobre el cabezal (Figura 4).
La ecuación generalizada para el cortante por punzonamiento de la columna sobre el cabezal V Pc se presenta como sigue:
donde N pi es la fuerza axial generada por cada pilote sobre el cabezal que se ubica dentro del área delimitada por el perímetro de la sección critica.
Ahora, la ecuación generalizada para el cortante por punzonamiento del pilote (carga mayor) sobre el cabezal V Pp se presenta como sigue:
donde N p1 es la fuerza axial generada por el pilote que tiene la mayor carga.
La función objetivo para obtener el costo mínimo para diseño del cabezal C mínimo se muestra como sigue:
donde C c es el costo en dólares del concreto por 1 m3 de concreto armado premezclado; A sx es el área de acero de refuerzo en la dirección X; A sy es el área de acero de refuerzo en la dirección Y; d es la profundidad efectiva de la zapata (distancia desde la fibra más alejada en compresión al centroide del acero de refuerzo); r es el recubrimiento de concreto; 𝛼 es la relación del costo de acero de refuerzo y el concreto por 1 m3.
Las funciones de restricciones para obtener el costo mínimo para diseño del cabezal se muestran a continuación:
Para los momentos:
Para los cortantes por flexión:
Para el cortante por punzonamiento de la columna sobre el cabezal:
Para el cortante por punzonamiento del pilote más cargado sobre el cabezal:
Porcentajes de acero de refuerzo:
Acero de refuerzo:
donde Ø f es el factor de reducción de resistencia por flexión y su valor es 0.90; f’ c es la resistencia a la compresión especificada del concreto a los 28 días, f y es la resistencia del límite elástico especificado del acero de refuerzo; Ø v es el factor de reducción de resistencia por cortante y su valor es 0.85; b 0 = [2(a + b + 2d)] es el perímetro de la sección crítica del cortante por punzonamiento de la columna sobre el cabezal; b 0 = [π(D + d)] es el perímetro de la sección crítica del cortante por punzonamiento del pilote sobre el cabezal; ρ x es el porcentaje de acero de refuerzo en la dirección X; ρ y es el porcentaje de acero de refuerzo en la dirección Y; A sxT es el área de acero por temperatura; 𝛼s = 40 para columnas interiores, 30 para columnas de borde y 20 para columnas de esquina; β c es la relación del lado largo entre el lado corto de la columna; β 1 es el factor que relaciona la profundidad del bloque de esfuerzo de compresión rectangular equivalente con la profundidad del eje neutro.
Nota: La segunda parte de las ecuaciones (14) a (27) son propuestas por los reglamentos de construcción (ACI, 2014).
Ejemplos numéricos
En esta sección se muestran cinco ejemplos numéricos para obtener el costo mínimo de diseño de cabezales que soportan a una columna en la parte superior y los cabezales están apoyados sobre pilotes. Los cabezales para los casos A y B se aplican para soportar una carga axial P y momento en una dirección. Y para los casos C, D y E, se aplican para soportar una carga axial P y momentos en dos direcciones (Figura 2 de la parte 1). La información general para todos los casos es: a = 45 cm; b = 30 cm; D = 30 cm; r = 10 cm; f’ c = 21 Mpa; f y = 420 Mpa; Ø f = 0.90; Ø v = 0.85; 𝛼s = 40; β c (columna) = 1.5; β c (pilote) = 1; β 1 = 0.85; 𝛼 = 90. El diámetro de todos los pilotes para todos los ejemplos se considera de 30 cm. La función objetivo del costo mínimo para todos los casos es la misma ecuación. Las soluciones se obtienen por medio del software MAPLE-15.
Caso A
Este caso muestra el diseño de costo mínimo para un cabezal que soporta una columna en la parte superior y está apoyado sobre dos pilotes (Figura 2a de la parte 1). La información para este caso es: P = 800 kN y Mx = 200 kN-m.
Todos los valores correspondientes se sustituyen en la ecuación (17) para encontrar la función objetivo (área mínima), así como en las ecuaciones (18) a (24) para obtener las funciones de restricción (Parte 1).
La solución para el área mínima es: A min = 0.90 m2; L x = 0.60 m; L y = 1.50 m; M x = 200 kN-m; N 1 = 622.22 kN; N 2 = 177.78 kN; P = 800 kN; x 1 = 0 m; y 1 = 0.45 m.
Ahora, por las ecuaciones (3) y (4) los momentos se obtienen: M x1´-x1´ = 139.95 kN-m y M x2´-x2´ = 40.05 kN-m. Por las ecuaciones (7) y (8) los cortantes por flexión se encuentran: V Fx1´-x1´ = 622.22 kN y V Fx2´-x2´ = 177.78 kN. Por la ecuación (11) el cortante por punzonamiento para la columna se obtiene: V Pc = 800 kN. Por la ecuación (12) el cortante por punzonamiento para el pilote se encuentra: V Pp = 622.22 kN.
Enseguida, se sustituyen todos los valores correspondientes en la ecuación (13) para encontrar la función objetivo (costo mínimo), y también en las ecuaciones (14) a (27) para obtener las funciones de restricción. Para este caso, las ecuaciones (16), (17), (20), (21) y (26) se eliminan porque los momentos y cortantes por flexión no existen; la ecuación (28) se agrega (acero por temperatura).
La solución para el costo mínimo es: C min = 2.14Cc; A sx = 42.28 cm2; A sy = 31.32 cm2; d = 1.57 m; ρ y = 0.0033333. Ahora, si se observa la solución, la profundidad efectiva d es mucho mayor que y 1 - a/2 (ubicación de los pilotes a partir de la cara de la columna), entonces los pilotes se ubican dentro de la sección crítica del cortante por flexión. Por lo tanto, los cortantes por flexión no existen y se considera 0.
Ahora, la nueva solución para el costo mínimo es: C min = 0.58Cc; A sx = 8.10 cm2; A sy = 13.54 cm2, d = 0.30 m, ρ y = 0.0075243.
Caso B
Este caso muestra el diseño de costo mínimo para un cabezal que soporta una columna en la parte superior y está apoyado sobre tres pilotes (Figura 2b de la Parte 1). La información para este caso es: P = 800 kN y M x = 200 kN-m.
Todos los valores correspondientes se sustituyen en la ecuación (26) para encontrar la función objetivo (área mínima), al igual que en las ecuaciones (27) a (34) para obtener las funciones de restricción (Parte 1).
La solución para el área mínima es: A min = 1.44 m2; L x = 0.60 m; L y = 2.40 m; M x = 200 kN-m; N 1 = 377.78 kN; N 2 = 266.67 kN; N 3 = 155.56 kN; P = 800 kN; x 1 = 0 m; y 1 = 0.90 m.
Ahora, por las ecuaciones (3) y (4) los momentos se obtienen: M x1´-x1´ = 255.00 kN-m y M x2´-x2´ = 105.00 kN-m. Por las ecuaciones (7) y (8) los cortantes por flexión se encuentran: V Fx1´-x1´ = 377.78 kN y V Fx2´ x2´ = 155.56 kN. Por la ecuación (11) el cortante por punzonamiento para la columna se obtiene: V Pc = 533.33 kN. Por la ecuación (12) el cortante por punzonamiento para el pilote se encuentra: V Pp = 377.78 kN.
Enseguida, se sustituyen todos los valores correspondientes en la ecuación (13) para encontrar la función objetivo (costo mínimo), y en las ecuaciones (14) a (27) para obtener las funciones de restricción. Para este caso, las ecuaciones (16), (17), (20), (21) y (26) se eliminan porque los momentos y cortantes por flexión no existen, y la ecuación (28) se agrega (acero por temperatura).
La solución para el costo mínimo es: C min = 1.42Cc; A sx = 41.08 cm2; A sy = 19.02 cm2; d = 0.95 m; ρ y = 0.0033333. Ahora, si se observa la solución, la profundidad efectiva d es mucho mayor que y 1 - a/2 (ubicación de los pilotes a partir de la cara de la columna), entonces los pilotes se ubican dentro de la sección crítica del cortante por flexión. Por lo tanto, los cortantes por flexión no existen y se considera 0.
Ahora, la nueva solución para el costo mínimo es: C min = 0.78Cc; A sx = 15.05 cm2; A sy = 22.13 cm2; d = 0.35 m; ρ y = 0.0105869.
Caso C
Este caso muestra el diseño de costo mínimo para un cabezal que soporta una columna en la parte superior y está apoyado sobre cuatro pilotes (Figura 2c de la Parte 1). La información para este caso es: P = 1200 kN; M x = 800 kN-m y M y = 400 kN-m.
Todos los valores correspondientes se sustituyen en la ecuación (36) para encontrar la función objetivo (área mínima), así como en las ecuaciones (37) a (45) para obtener las funciones de restricción (Parte 1).
La solución para el área mínima es: A min = 6.29 m2; L x = 2.03 m; L y = 3.10 m; M x = 800 kN-m; M y = 400 kN-m; N 1 = 600 kN; N 2 = 320.24 kN; N 3 = 279.76 kN; N 4 = 0 kN; P = 1200 kN; x 1 = 0.71 m; y 1 = 1.25 m.
Ahora, por las ecuaciones (3), (4), (5) y (6) los momentos se obtienen: M x1´-x1´ = 943.25 kN-m; M x2´-x2´ = 286.75 kN-m; M y1´-y1´ = 492.67 kN-m; y M y2´-y2´ = 179.33 kN-m. Por las ecuaciones (7), (8), (9) y (10) los cortantes por flexión se encuentran: V Fx1´-x1´ = 920.24 kN; V Fx2´-x2´ = 279.76 kN; V Fy1´-y1´ = 879.76 kN; y V Fy2´ y2´ = 320.24 kN. Por la ecuación (11) el cortante por punzonamiento para la columna se obtiene: V Pc = 1200 kN. Por la ecuación (12) el cortante por punzonamiento para el pilote se encuentra: V Pp = 600 kN.
En seguida, se sustituyen todos los valores correspondientes en la ecuación (13) para encontrar la función objetivo (costo mínimo), y también en las ecuaciones (14) a (27) para obtener las funciones de restricción.
La solución para el costo mínimo es: C min = 7.49Cc; A sx = 70.74 cm2; A sy = 46.32 cm2; d = 0.68 m; ρ x = 0.0033333; ρ y = 0.0033333. Ahora, si se observa la solución, la profundidad efectiva d es mayor que x 1 - b/2 (ubicación de los pilotes a partir de la cara de la columna sobre el eje Y), entonces los pilotes se ubican dentro de la sección crítica del cortante por flexión. Por lo tanto, los cortantes por flexión sobre el eje Y no existen y se considera 0.
Ahora, la nueva solución para el costo mínimo es: C min = 7.49Cc; A sx = 70.74 cm2; A sy = 46.32 cm2; d = 0.68 m; ρ x = 0.0033333; ρ y = 0.0033333.
Caso D
Este caso muestra el diseño de costo mínimo para un cabezal que soporta una columna en la parte superior y está apoyado sobre cinco pilotes (Figura 2d de la parte 1). La información para este caso es: P = 1200 kN, M x = 800 kN-m y M y = 400 kN-m.
Todos los valores correspondientes se sustituyen en la ecuación (47) para encontrar la función objetivo (área mínima), así como en las ecuaciones (48) a (57) para obtener las funciones de restricción (parte 1).
La solución para el área mínima es: A min = 8.89 m2; L x = 2.37 m; L y = 3.75 m; M x = 800 kN-m; M y = 400 kN-m; N 1 = 480 kN; N 2 = 254.07 kN; N 3 = 240 kN; N 4 = 225.93 kN; N 5 = 0 kN; P = 1200 kN; x 1 = 0.89 m; y 1 = 1.57 m.
Ahora, por las ecuaciones (3), (4), (5) y (6) los momentos se obtienen: M x1´-x1´ = 987.32 kN-m; M x2´-x2´ = 303.88 kN-m; M y1´-y1´ = 522.39 kN-m; y M y2´-y2´ = 188.01 kN-m. Por las ecuaciones (7), (8), (9) y (10) los cortantes por flexión se encuentran: V Fx1´-x1´ = 734.07 kN; V Fx2´-x2´ = 225.93 kN; V Fy1´-y1´ = 705.93 kN; y V Fy2´ y2´ = 254.07 kN. Por la ecuación (11) el cortante por punzonamiento para la columna se obtiene: V Pc = 960 kN. Por la ecuación (12) el cortante por punzonamiento para el pilote se encuentra: V Pp = 480 kN.
Enseguida, se sustituyen todos los valores correspondientes en la ecuación (13) para encontrar la función objetivo (costo mínimo), y también en las ecuaciones (14) a (27) para obtener las funciones de restricción.
La solución para el costo mínimo es: C min = 8.27Cc; A sx = 58.47 cm2; A sy = 59.63 cm2; d = 0.47 m; ρ x = 0.0033333; ρ y = 0.0053786.
Caso E
Este caso muestra el diseño de costo mínimo para un cabezal que soporta una columna en la parte superior y está apoyado sobre seis pilotes (Figura 2e de la Parte 1). La información para este caso es: P = 1200 kN, M x = 800 kN-m y M y = 400 kN-m.
Todos los valores correspondientes se sustituyen en la ecuación (59) para encontrar la función objetivo (área mínima), y en las ecuaciones (60) a (70) para obtener las funciones de restricción (Parte 1).
La solución para el área mínima es: A min = 8.82 m2; L x = 2.07 m; L y = 4.25 m; M x = 800 kN-m; M y = 400 kN-m; N 1 = 400 kN; N 2 = 218.92 kN; N 3 = 290.54 kN; N 4 = 109.46 kN; N 5 = 181.08 kN; N 6 = 0 kN; P = 1200 kN; x 1 = 0.74 m; y 1 = 1.83 m.
Ahora, por las ecuaciones (3), (4), (5) y (6) los momentos se obtienen: M x1´-x1´ = 993.37 kN-m; M x2´-x2´ = 290.63 kN-m; M y1´-y1´ = 514.26 kN-m; y M y2´-y2´ = 193.74 kN-m. Por las ecuaciones (7), (8), (9) y (10) los cortantes por flexión se encuentran: V Fx1´-x1´ = 618.92 kN; V Fx2´-x2´ = 181.08 kN; V Fy1´-y1´ = 790.62 kN; y V Fy2´ y2´ = 328.38 kN. Por la ecuación (11) el cortante por punzonamiento para la columna se obtiene: V Pc = 1200 kN. Por la ecuación (12) el cortante por punzonamiento para el pilote se encuentra: V Pp = 400 kN.
Enseguida, se sustituyen todos los valores correspondientes en la ecuación (13) para encontrar la función objetivo (costo mínimo), y también en las ecuaciones (14) a (27) para obtener las funciones de restricción.
La solución para el costo mínimo es: C min = 8.42Cc; A sx = 63.97 cm2; A sy = 63.25 cm2; d = 0.45 m; ρ x = 0.0033333; ρ y = 0.0067674.
Resultados
En esta sección se muestran los datos prácticos de los cinco ejemplos numéricos del costo mínimo para diseño de cabezales que soportan una columna en la parte superior y están apoyados sobre pilotes. Los casos A y B soportan las mismas cargas y momentos en una dirección. Los casos C, D y E soportan las mismas cargas y momentos en las dos direcciones.
Caso A
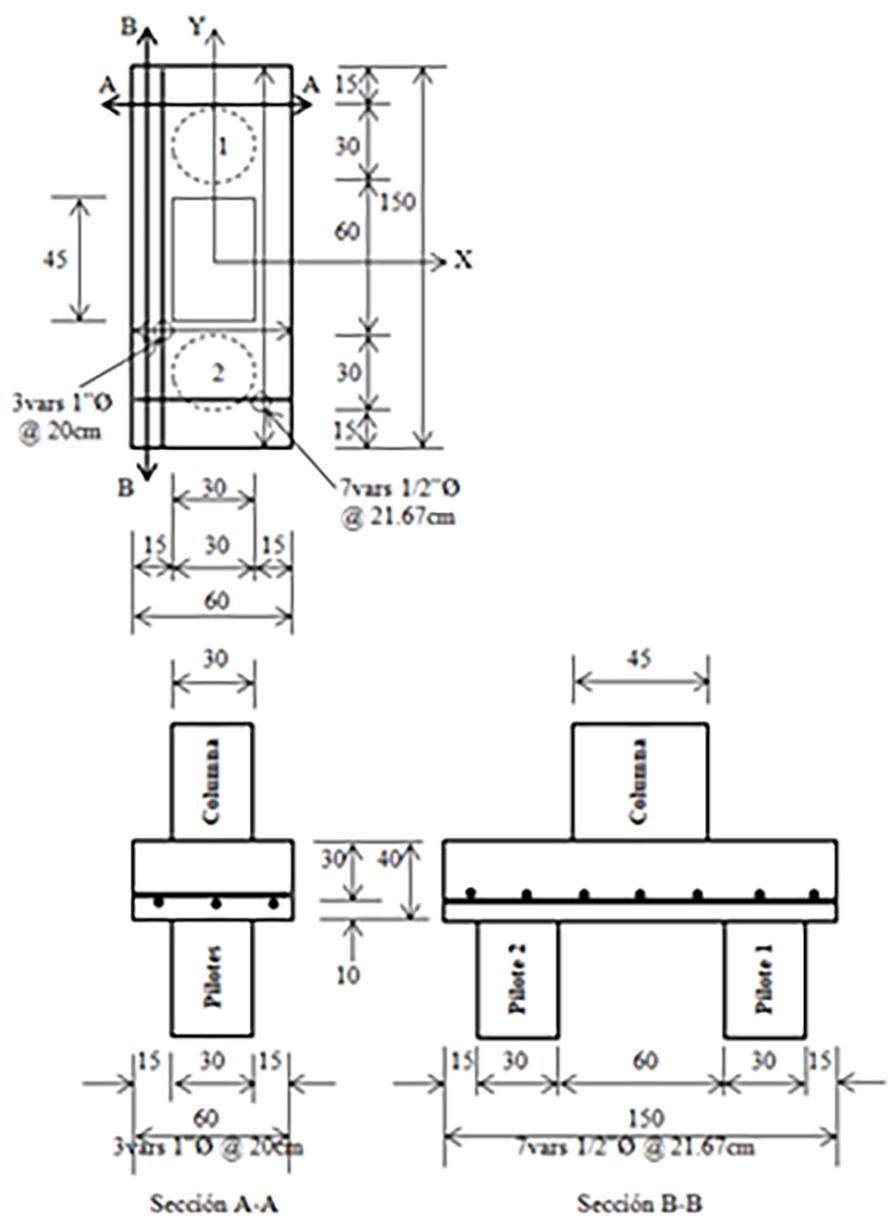
La solución obtenida para el costo mínimo es: C min = 0.58Cc; L x = 60 cm; L y = 150 cm; A sx = 8.10 cm2; A sy = 13.54 cm2; d = 30 cm; ρ y = 0.0075243. Las áreas de acero de refuerzo propuestas son A sx = 8.89 cm2 (7Ø1/2”) y A sy = 15.21 cm2 (3Ø1”). Ahora, se sustituyen las áreas de acero de refuerzo propuestas en la ecuación (13) para obtener el costo mínimo real C min = 0.61Cc.
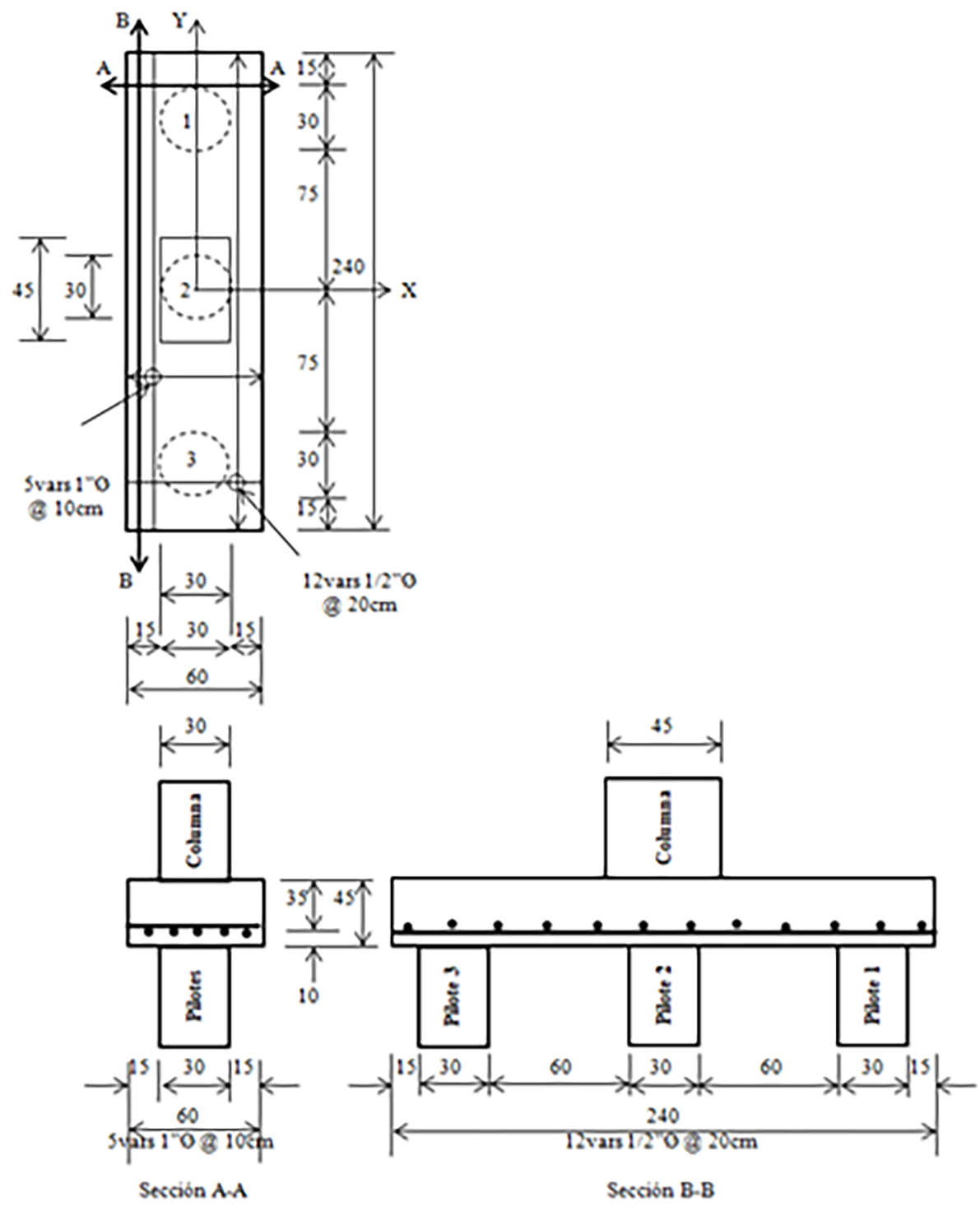
La Figura 5 muestra las dimensiones y el acero de refuerzo para el cabezal apoyado sobre dos pilotes.
Caso B
La solución obtenida para el costo mínimo es: C min = 0.78Cc; L x = 60 cm; L y = 240 cm; A sx = 15.05 cm2; A sy = 22.13 cm2; d = 35 cm; ρ y = 0.0105869. Las áreas de acero de refuerzo propuestas son A sx = 15.24 cm2 (12Ø1/2”) y A sy = 25.35 cm2 (5Ø1”). Ahora, se sustituyen las áreas de acero de refuerzo propuestas en la ecuación (13) para obtener el costo mínimo real C min = 0.82Cc.
La Figura 6 muestra las dimensiones y el acero de refuerzo para el cabezal apoyado sobre tres pilotes.
Caso C
La solución obtenida para el costo mínimo es: C min = 7.49Cc; L x = 203 cm; L y = 310 cm; A sx = 70.74 cm2; A sy = 46.32 cm2; d = 68 cm; ρ x = 0.0033333; ρ y = 0.0033333. Las áreas de acero de refuerzo propuestas son A sx = 70.98 cm2 (14Ø1”) y A sy = 50.70 cm2 (10Ø1”). Ahora, se sustituyen las áreas de acero de refuerzo propuestas en la ecuación (13) para obtener el costo mínimo real C min = 7.59Cc.
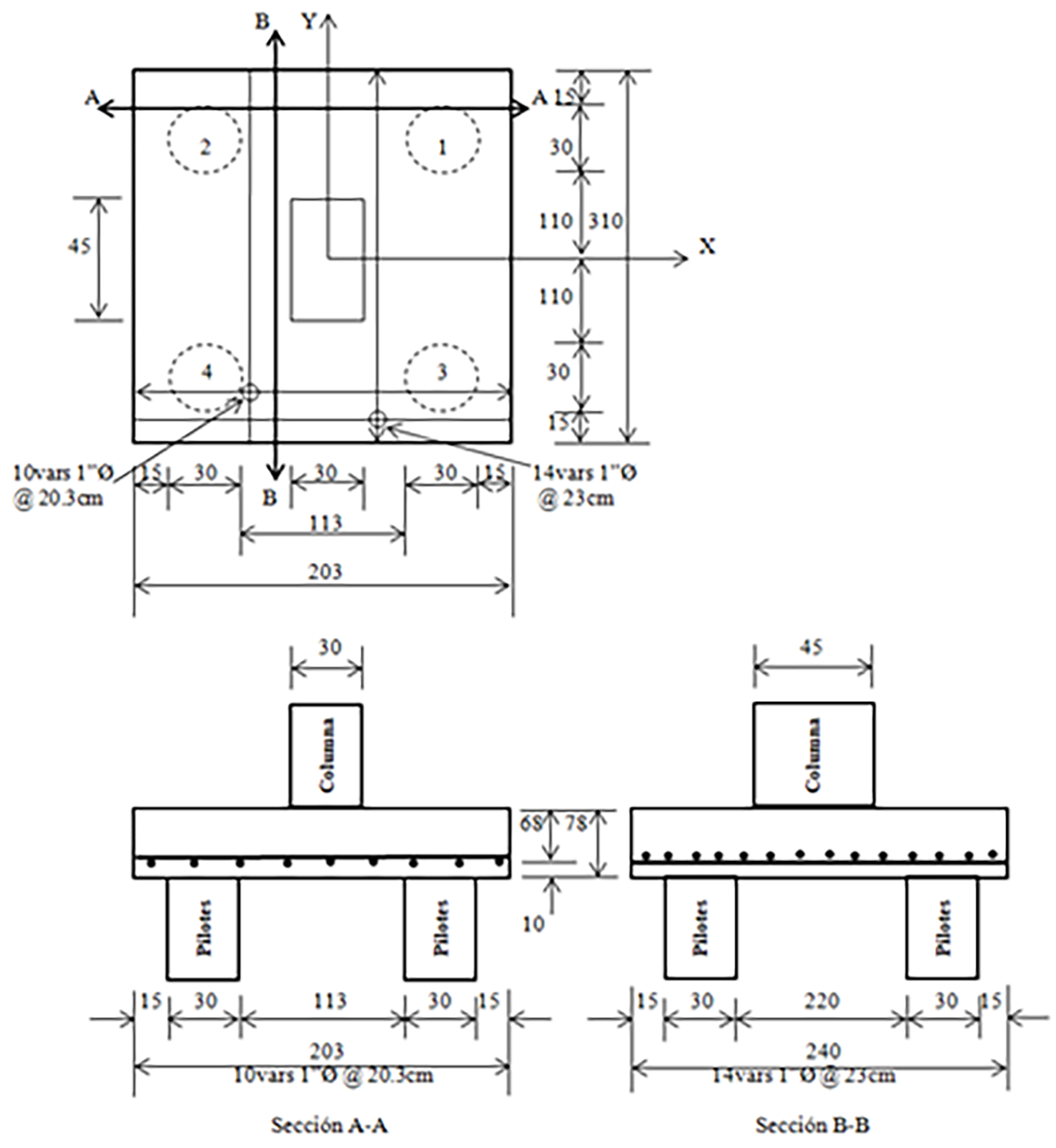
La Figura 7 muestra las dimensiones y el acero de refuerzo para el cabezal apoyado sobre cuatro pilotes.
Caso D
La solución obtenida para el costo mínimo es: C min = 8.27Cc; L x = 237 cm; L y = 375 cm; A sx = 58.47 cm2; A sy = 59.63 cm2; d = 47 cm; ρ x = 0.0033333; ρ y = 0.0053786. Las áreas de acero de refuerzo propuestas son A sx = 60.84 cm2 (12Ø1”) y A sy = 60.84 cm2 (12Ø1”). Ahora, se sustituyen las áreas de acero de refuerzo propuestas en la ecuación (13) para obtener el costo mínimo real C min = 8.38Cc.
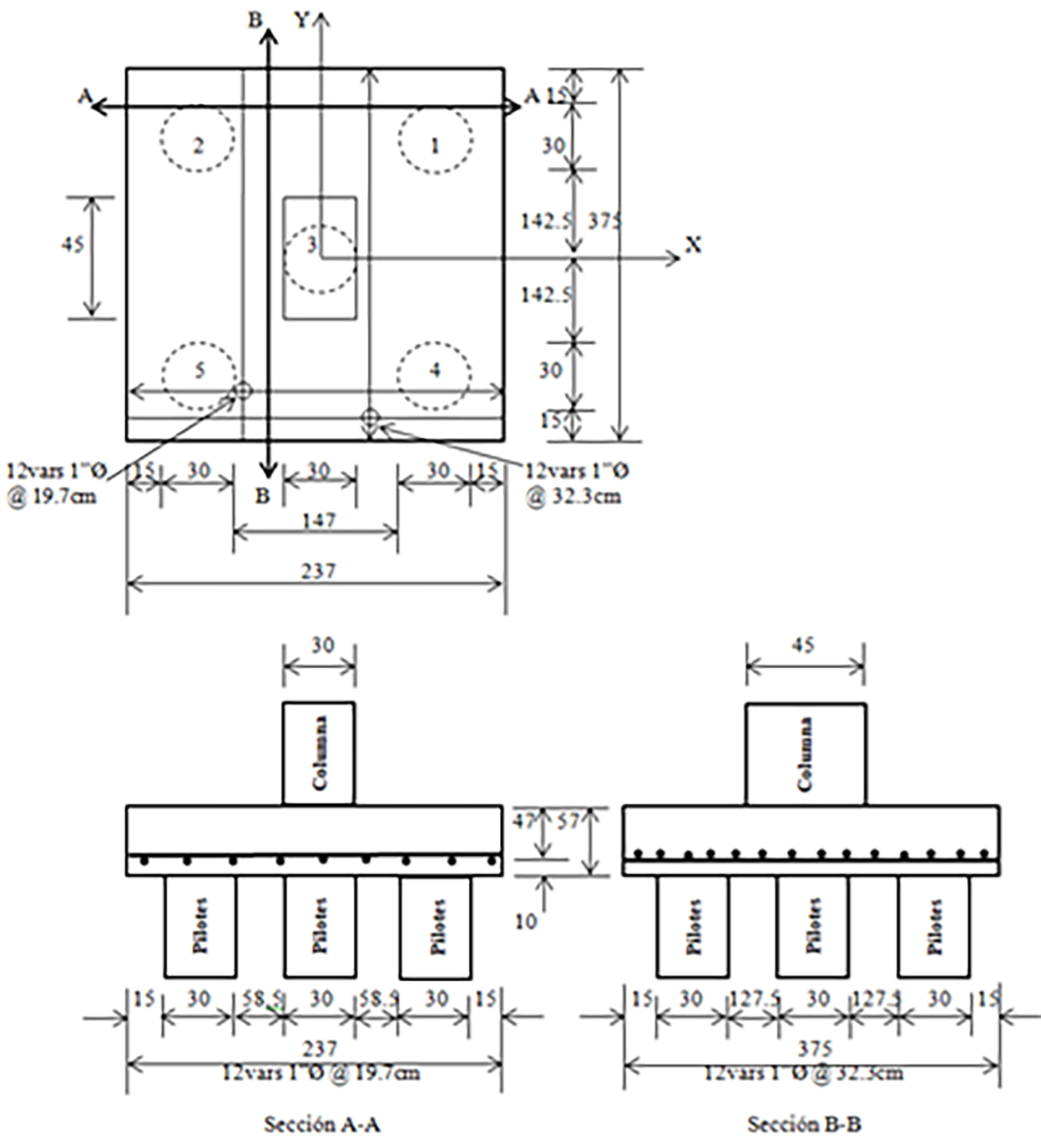
La Figura 8 muestra las dimensiones y el acero de refuerzo para el cabezal apoyado sobre cinco pilotes.
Caso E
La solución obtenida para el costo mínimo es: C min = 8.42Cc; L x = 207 cm; L y = 425 cm; A sx = 63.97 cm2; A sy = 63.25 cm2; d = 45 cm; ρ x = 0.0033333; ρ y = 0.0067674. Las áreas de acero de refuerzo propuestas son A sx = 65.91 cm2 (13Ø1”) y A sy = 65.91 cm2 (13Ø1”). Ahora, se sustituyen las áreas de acero de refuerzo propuestas en la ecuación (13) para obtener el costo mínimo real C min = 8.55Cc.
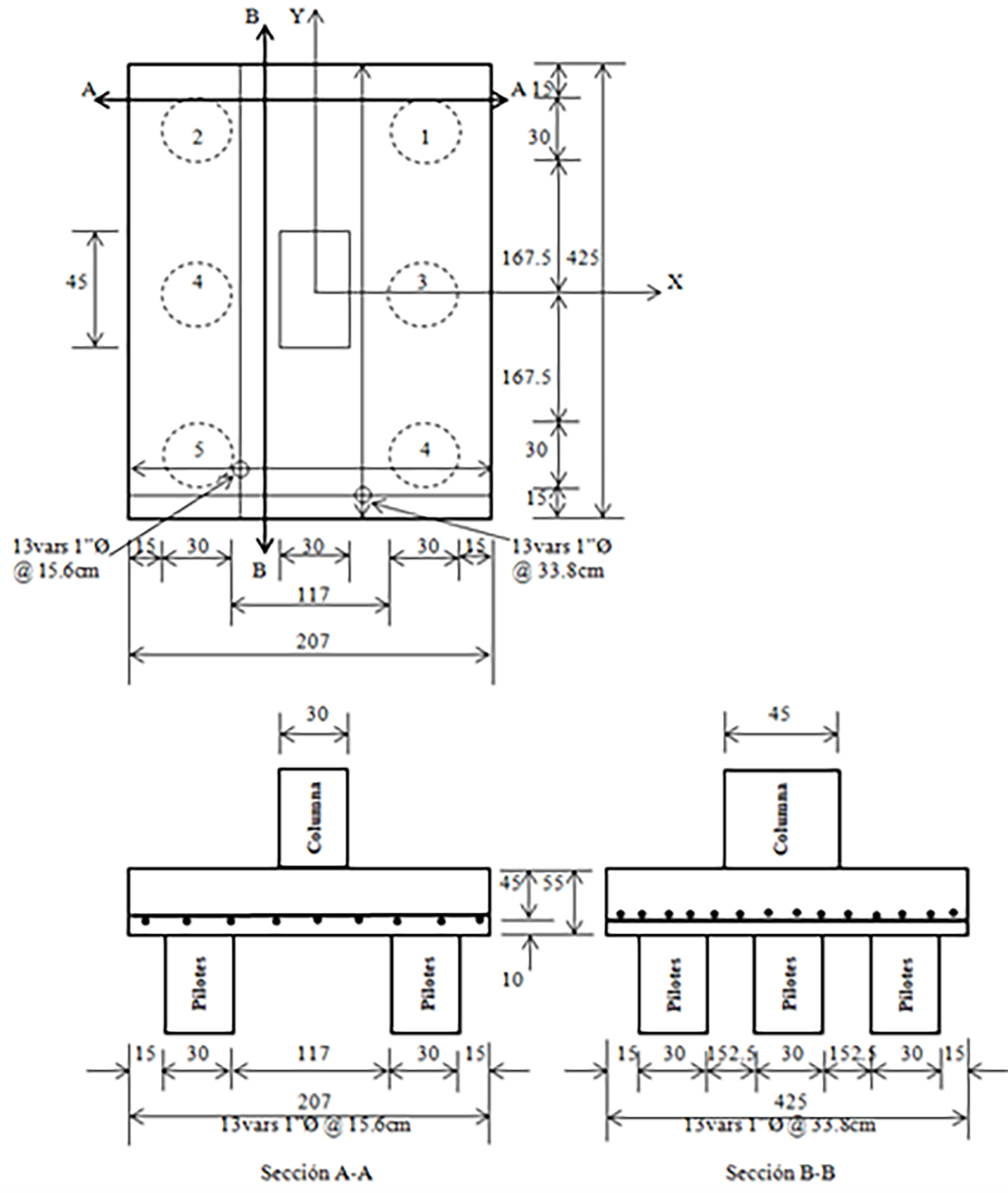
La Figura 9 muestra las dimensiones y el acero de refuerzo para el cabezal apoyado sobre seis pilotes.
La Tabla 1 muestra los resultados de los casos A, B, C, D y E.
Tabla 1 Resumen de los cinco casos para cabezales.
| Concepto | Casos | ||||
| A | B | C | D | E | |
| Cargas aplicadas | P = 800 kN; Mx = 200 kN-m | P = 1200 kN; Mx = 800 kN-m; My = 400 kN-m | |||
| Lx (cm) | 60 | 60 | 203 | 237 | 207 |
| Ly (cm) | 150 | 240 | 310 | 375 | 425 |
| x1 (cm) | 0 | 0 | 71 | 89 | 74 |
| y1 (cm) | 45 | 90 | 125 | 157 | 183 |
| Amin (m2) | 0.9 | 1.44 | 6.29 | 8.89 | 8.82 |
| Np1 (kN) | 622.22 | 377.78 | 600 | 480 | 400 |
| Np2 (kN) | 177.78 | 266.67 | 320.24 | 254.07 | 218.92 |
| Np3 (kN) | - | 155.56 | 279.76 | 240 | 290.54 |
| Np4 (kN) | - | - | 0 | 225.93 | 109.46 |
| Np5 (kN) | - | - | - | 0 | 181.08 |
| Np6 (kN) | - | - | - | - | 0 |
| d (cm) | 30 | 35 | 68 | 47 | 45 |
| Asx (cm2) | 8.89 | 15.24 | 70.98 | 60.84 | 65.91 |
| Asy (cm2) | 15.21 | 25.35 | 50.7 | 60.84 | 65.91 |
| Cmin ($) | 0.61Cc | 0.82Cc | 7.59Cc | 8.38Cc | 8.55Cc |
Fuente: Elaboración propia.
La Tabla 1 muestra la comparación de los casos A y B, así como de los casos C, D y E por tener la misma carga y momentos aplicados a los cabezales.
Para los casos A y B, el área de acero de refuerzo en la dirección del eje X para los dos casos es acero temperatura. El caso B presenta mayor superficie en planta, mayor profundidad efectiva y mayor área de acero de refuerzo en las dos direcciones que el caso A. Por lo tanto, el cabezal del caso A es más económico, pero el cabezal del caso A cuenta con dos pilotes que deben resistir mayor carga con respecto al caso B, el cual tiene tres pilotes.
Para los casos C, D y E, el área de acero de refuerzo en la dirección del eje X para los tres casos, y para el caso C en la dirección del eje Y, es acero mínimo. El caso C presenta menor superficie en planta y menor área de acero de refuerzo en la dirección Y. El caso D muestra la menor área de acero de refuerzo en la dirección X. El caso E presenta la menor profundidad efectiva. Por lo tanto, el cabezal para el caso C es más económico, pero el cabezal del caso C cuenta con cuatro pilotes que deben resistir mayor carga con respecto a los casos D (cinco pilotes) y E (seis pilotes).
Conclusiones
La cimentación de una estructura es la parte esencial para transmitir las cargas de columna o pared al terreno subyacente de la estructura. En el caso de cimentaciones profundas, las cargas que provienen de la estructura descansan sobre un miembro estructural llamado cabezal y, a su vez, las cargas se trasmiten a los pilotes que se apoyan directamente en un estrato más fuerte, que puede ubicarse a una profundidad significativa debajo de la superficie del suelo. La primera parte de esta investigación presenta el área óptima de los cabezales rectangulares utilizando las técnicas de optimización. La parte principal de esta investigación es obtener el diseño óptimo (costo mínimo) de los cabezales rectangulares utilizando las técnicas de optimización.
El modelo propuesto en esta investigación produce resultados que tienen una precisión sin precedentes para que se pueda aplicar a todos los problemas de ingeniería de cimientos.
Las cimentaciones profundas son necesarias cuando la capacidad de carga del suelo cerca de la superficie de este es demasiado baja.
El modelo propuesto presentado en este documento para obtener el diseño óptimo (costo mínimo) para los cabezales rectangulares bajo una carga concéntrica y momentos alrededor de los ejes X y Y debido a la columna, también se puede usar para los otros casos: 1) Cabezales o zapatas sometidos una carga concéntrica; 2) Cabezales o zapatas sometidos una carga concéntrica y un momento en una dirección.
Las principales conclusiones son:
La metodología mostrada en este documento es más precisa y converge más rápidamente.
El espesor de los cabezales es gobernado por el cortante por flexión, y las zapatas apoyadas sobre el suelo se rigen por el cortante por punzonamiento.
El modelo clásico no será práctico en comparación con esta metodología, ya que el modelo normalmente utilizado para obtener el diseño de los cabezales considera que todos los pilotes transmiten la misma carga vertical; esto funciona únicamente cuando la columna transmite carga axial y no momentos.
El modelo optimizado presentado en este artículo es aplicado solo para obtener el diseño óptimo (costo mínimo) para cabezales rectangulares apoyados sobre un grupo de pilotes, y este estudio considera que los cabezales son perfectamente rígidos y los pilotes están articulados en la unión con los cabezales y, por lo tanto, los pilotes transmiten solamente carga vertical.
Las sugerencias para las próximas investigaciones pueden ser: 1) El diseño óptimo para cabezales o zapatas apoyadas sobre pilotes de otro tipo de forma en planta como circular, triangular, pentagonal, hexagonal, etc.; 2) El diseño óptimo para cimentaciones profundas que incluya los cabezales y los pilotes.











 text new page (beta)
text new page (beta)