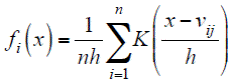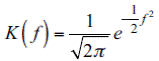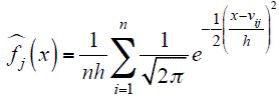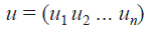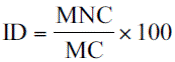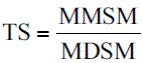1. Introducción
Este trabajo, predominantemente exploratorio y metodológico, tiene los siguientes objetivos: i) develar la redistribución de la atractividad migratoria entre los municipios de México desde 2000 y proyectarla para el largo plazo, y ii) generar evidencia de los procesos de convergencia/divergencia de la atractividad migratoria entre los municipios del país.
La migración intermunicipal es un proceso demográfico que refleja, en parte, el éxito o falla de los municipios como lugares para vivir y/o trabajar. Migrar implica diversos costos (objetivos y subjetivos, tangibles e intangibles), por lo que se migra sólo si se anticipa que la situación en el destino será más favorable (o menos desfavorable) que en el origen (Harris y Todaro, 1970; Faist, 2012). En México, se puede suponer que los municipios con altas tasas de inmigración (v. g., atractores) ofrecen mejores condiciones (reales o percibidas) para vivir/trabajar que otros (siempre en un marco de notables restricciones para los migrantes), principalmente en materia de suelo y vivienda asequible y de empleo en el lugar o accesible desde el lugar (véanse diversos factores clave para los flujos de migración interna en Pérez y Santos, 2008 y Sobrino, 2010). Por su parte, los municipios con altas tasas de emigración (v. g., expulsores) son los que no han sido capaces de generar o sostener las condiciones de residencia requeridas por su población original, en términos absolutos (v. g., en comparación con sí mismos) o relativos (v. g., en comparación con los demás municipios). La evidencia sobre esto es abundante para México (Arroyo y Rodríguez, 2014; Partida, 2010; Pérez y Santos, 2008, 2013; Sobrino, 2014).
En este trabajo evitamos utilizar conjuntos de indicadores económicos o de calidad de vida seleccionados por los analistas para representar la atractividad migratoria, porque la selección y el peso de las variables afecta los resultados (e. g., García-Verdú, 2005; Moncada e Hincapié, 2013). En su lugar, usamos las tasas netas de migración recientes (TNMR) intermunicipales como indicador de preferencia revelada condicionada de los migrantes respecto a la elección de destinos que ofrecen mejores condiciones (reales o percibidas) para vivir/trabajar.1 Es decir, consideramos que el comportamiento migratorio revelado de las personas es más confiable que utilizar variables seleccionadas por especialistas.
Las TNMR tienen varias ventajas sobre otros indicadores migratorios. Por ejemplo, si se usa el número absoluto de inmigrantes se incorpora información directa sobre el tamaño de la población del origen y del destino, lo que distorsiona las comparaciones de flujos migratorios entre unidades espaciales (e. g., país, región, municipio) de tamaños poblacionales diversos. En cambio, el efecto neto de la inmigración y la emigración de la población (v. g., la TNMR) refleja mejor la dinámica migratoria y las diferencias entre orígenes y destinos (NAS, 2016).2
Algunos antecedentes recientes, aunque indirectos, de nuestro trabajo son las investigaciones de López (2008), Gutiérrez et al. (2011), Moncada e Hincapié (2013) y Villaverde (2004). Estos análisis exploran la convergencia/divergencia económica en diferentes regiones de México. En nuestro trabajo retomamos muchas de sus ideas y las adaptamos al análisis de la convergencia/divergencia de la atractividad migratoria entre los municipios del país, utilizando como indicador clave las TNMR intermunicipales.
1.1. Estrategia de presentación
El resto del texto se divide en cinco secciones. En la sección 2 valoramos algunas ventajas y desventajas de utilizar la migración como un indicador alternativo de redistribución territorial de las condiciones para vivir/trabajar. En la sección 3 repasamos la literatura para comparar nuestro indicador alternativo con los indicadores socioeconómicos tradicionales. Concluimos que nuestro indicador migratorio ofrece ciertas ventajas para explorar los procesos de convergencia/divergencia territorial. Especialmente porque es un indicador de preferencia revelada condicionada sobre los territorios de destino, que incluye información objetiva y subjetiva, individual y grupal, y el acceso e interpretación de la información sobre los destinos en un entorno de asimetría informativa y en un marco de múltiples restricciones. Es decir, refleja las preferencias de la población en su espectro de limitantes y posibilidades, y no depende de variables seleccionadas por los analistas. En esta misma sección advertimos que no todos los procesos de convergencia son deseables, ni todos los de divergencia son indeseables. Todo depende de la trayectoria y velocidad (endógena y exógena) de los cambios de la atractividad migratoria en los territorios y de la estrategia de desarrollo a diversas escalas espaciales. Esta reflexión es clave para interpretar mejor los resultados del análisis. La sección 4 es breve y se enfoca a explicar la estrategia metodológica y reportar las fuentes de información utilizadas. En la sección 5 presentamos los métodos que aplicamos y los resultados del análisis, y en la 6 sintetizamos los principales hallazgos y aportaciones del trabajo. El documento concluye con un listado de la bibliografía consultada.
2. ¿Por qué usar la migración como un indicador de redistribución territorial de condiciones para vivir/trabajar?
Usualmente los procesos de convergencia/divergencia en el territorio se han analizado con indicadores económicos o con una mezcla de indicadores económicos y sociales, dejando de lado numerosos temas difíciles de medir, como los culturales o políticos, así como la manera como las personas acceden y procesan la información sobre diversos temas clave en sus vidas cotidianas (Magrini, 2004).
La migración, entonces, puede ser un buen indicador alternativo, porque es resultado de desigualdades económicas y sociales en el territorio y en el tiempo (diferencias reales e imaginadas, tangibles e intangibles, siempre inestables), que generan flujos de población que cambian su residencia habitual con el objetivo de mejorar o evitar mayor deterioro en sus condiciones para vivir/trabajar (véase el clásico trabajo de Ravenstein, 1885). Las desigualdades territoriales (en México algunas de las más relevantes serían el precio del suelo y la vivienda, y el acceso al empleo; véase Arroyo y Rodríguez, 2014) son incentivos para migrar o permanecer en un lugar. Nadie migra si no tiene expectativas de obtener algún beneficio (o evitar un perjuicio) en lo individual y en lo familiar (Massey et al., 1994), porque migrar implica un costo importante (objetivo y subjetivo, integrado de manera compleja: económico, anímico, en términos de riesgo, esfuerzo, desapego) que se espera superar una vez que se consolide la estancia en el destino (Hagen-Zanker, 2008, pp. 1-25).
En un territorio homogéneo (real o percibido) no se producirán flujos migratorios porque no existirían incentivos para migrar. Por lo tanto, la migración es un indicador sintético de desigualdades territoriales (reales o percibidas). En general, en los países como el nuestro, la población abandona territorios que ofrecen condiciones menos propicias para vivir/trabajar y se dirige a lugares que ofrecen condiciones más favorables (objetivas, percibidas; cuantitativas, cualitativas; para los que migran y/o para las familias que se quedan en el origen) (Brettell y Hollifield, 2014, pp. 3-36).
Una ventaja importante de utilizar la migración como indicador sintético de redistribución territorial de condiciones para vivir/trabajar es que condensa efectos de múltiples variables situadas en diversas dimensiones, pero interrelacionadas en formas complejas y desconocidas (e. g., económicas: PIB, ingreso; socioculturales: situación política, tradiciones, costumbres; sicológicas: soledad, nostalgia, depresión). La situación de estas variables puede ser real o percibida (a escala individual o colectiva) y se interrelacionan de manera dinámica en el tiempo y el espacio. Aún más, la migración es sensible a la disponibilidad y percepción de información compleja y diversa sobre las condiciones en el origen y en el destino -a escala individual, familiar y comunitaria-, y a la valoración subjetiva que las personas hacen de esa información (Hagen-Zanker, 2008). En cambio, los indicadores tradicionales socioeconómicos dependen de la selección de variables que hagan los analistas sobre los procesos de redistribución territorial de las condiciones para vivir/trabajar, y cada selección de variables puede generar resultados diferentes.
Sin embargo, también hay desventajas en utilizar la migración como indicador de redistribución territorial de condiciones para vivir/trabajar. Las primordiales: no arroja luz sobre la evolución de las variables específicas (e. g., PIB, ingreso, empleo, calidad de vida) y no es posible saber si las diversas dimensiones del desarrollo convergen o divergen de manera manifiesta. Adicionalmente, la forma de medir la migración es complicada y tiene serias debilidades (Garrocho, 2011), aunque lo mismo se puede decir de la medición de numerosos aspectos económicos y sociales utilizados tradicionalmente en los análisis de convergencia/divergencia (desde el PIB hasta la calidad de vida; véase Stiglitz et al., 2011).
Otra característica importante de explorar la convergencia/divergencia de la migración interna es que el sistema migratorio es un juego de suma cero. Es decir, el sistema migratorio compensa con exactitud la ganancia o pérdida de migrantes de un municipio, con las pérdidas o ganancias de los demás. Por tanto, no es posible que se logre un estado de convergencia municipal plena hacia la atracción o expulsión de población, porque, si todos los municipios son atractores de migrantes, ¿cuáles municipios expulsan población? Y en el caso contrario, si todos los municipios expulsan población, ¿cuáles atraen migrantes? La única posibilidad de convergencia plena es en la situación en la que todos los municipios mantengan un estado de equilibrio migratorio. Sin embargo, la convergencia plena es una posibilidad hipotética que rara vez se encontrará en la realidad. Lo que sí se va a encontrar son tendencias hacia la convergencia/divergencia.
Dos advertencias: i) no todos los procesos de convergencia son deseables, ni todos los de divergencia son indeseables, como se explicará más adelante, por lo que tratamos de no hacer juicios de valor al respecto; y, ii) las proyecciones de largo plazo que aquí se presentan no son pronósticos. Sólo son escenarios exploratorios que bosquejan tendencias y permiten detectar, de manera condicionada, algunas características del sistema migratorio (e. g., alta volatilidad migratoria, fuerte competencia intermunicipal) que pueden ser insumos para políticas públicas a diversas escalas espaciales (e. g., elevar la calidad de las instituciones municipales, promover alianzas estratégicas entre municipios).
3. Síntesis del debate sobre los procesos de convergencia/divergencia territorial: adaptación a la escala municipal
Se puede decir que existen dos corrientes teóricas principales en el debate conceptual sobre la existencia de procesos territoriales de convergencia/divergencia a escala de países o macrorregiones. La primera, de carácter neoclásico, propone que en el largo plazo los cambios y la difusión de la tecnología, sumados a diversos mecanismos del mercado, favorecen que los territorios con menor desarrollo logren tasas de crecimiento superiores a las de los territorios más desarrollados. Esto conduce a la hipótesis de convergencia catch-up, que propone que la diferencia tecnológica entre el territorio líder, que innova y genera avances tecnológicos, y los seguidores, que simplemente adoptan esa nueva tecnología, se irá reduciendo porque es más rápido y barato adoptar tecnología que generarla. Por tanto, “en el largo plazo las tasas de crecimiento de la productividad tienden a variar inversamente con los niveles de productividad inicial” (Abramovitz, 1986, p. 385). Esta tendencia de crecimiento apuntaría también a la convergencia del ingreso per cápita (Targetti y Foti, 1997, p. 29) y a las condiciones para vivir/trabajar. La convergencia puede ser débil o no ser plena y es complicado determinar qué se entiende por “largo plazo”, pero se propone que existen periodos en que existe cierto grado de convergencia. En la hipótesis de convergencia catch-up son más importantes las variables externas o exógenas al territorio (e. g., la tecnología generada por el líder), que las variables internas o endógenas (e. g., producir avances tecnológicos propios) (Serrano, 1998).
En la escala municipal el principal factor exógeno no sería el avance tecnológico, sino, principalmente, la diferencia entre las condiciones para vivir/trabajar del entorno (e. g., ciudades potentes) y las de cada municipio. Por ejemplo, en general los beneficios de vivir y trabajar en las grandes ciudades son mayores a los costos que eso implica, lo que genera ventajas exógenas a los municipios que pertenecen a grandes zonas urbanas. Las economías de aglomeración en territorios altamente urbanizados generan clusters de firmas en el espacio, lo que incrementa la productividad y los salarios. Esto explica en parte que los trabajadores de las grandes ciudades por lo regular ganen salarios más altos que los de las ciudades de menor tamaño (Gleaser, 2012). Sin embargo, conforme la urbe crece, el nivel del salario promedio más alto que ofrece la ciudad a sus residentes se ve afectado por diversas características indeseables de las grandes áreas urbanas; por ejemplo: largos viajes intraurbanos (al trabajo, a la escuela, principalmente), densidades de población muy altas que obligan a gran parte de los habitantes a vivir en edificios de departamentos pequeños y costosos, congestión de automóviles, contaminación, inseguridad, menor disponibilidad de tiempo para la convivencia familiar y el esparcimiento, entre otros (Storper, 2013). Incluso puede llegar un punto en que la utilidad de los trabajadores decrezca debido a que las economías de aglomeración se ven superadas por las deseconomías de la urbanización. En este caso, los trabajadores pueden incrementar su utilidad cambiando su localización residencial, lo que generaría procesos de convergencia territorial (e. g., a escala urbana, municipal) (O’Sullivan, 2011).
La otra vertiente teórica dominante de los análisis de convergencia/divergencia a escala de país (o regiones integradas por varios países) se apoya en las teorías de crecimiento endógeno, que proponen que los factores productivos acumulables (e. g., progreso tecnológico, capital humano, calidad de las instituciones) no necesariamente registran rendimientos decrecientes, lo que conduce a la hipótesis de divergencia. Así, los factores endógenos (v. g., los que son propios del territorio, como la competitividad, el capital humano, la disponibilidad de suelo, vivienda, empleo) y las fuerzas del mercado pueden favorecer una acumulación creciente de ventajas en ciertos territorios, aumentando la divergencia (Piketty, 2014; Pritchett, 1996). Por tanto, es posible que un territorio líder mantenga sus condiciones de ventaja, e incluso las incremente a lo largo del tiempo. La razón: los efectos de múltiples externalidades positivas, como la difusión del conocimiento en ciencia y tecnología entre los productores, y las derivadas de las economías de escala y aglomeración; por ejemplo, la tendencia a la baja de los costos unitarios conforme se incrementa la cantidad producida, o la existencia de clusters productivos o científicos que favorecen las interacciones empresariales (Moncayo, 2004). Desde esta perspectiva, la convergencia territorial no es ineludible en el largo plazo.
A escala municipal las ventajas crecientes de algunos municipios se relacionarían con externalidades positivas vinculadas con sus condiciones favorables para vivir/trabajar, pero también con economías de escala y de aglomeración. Si estas ventajas se sostienen en el tiempo, el resultado apuntaría en el sentido contrario a lo que pronostica el enfoque de convergencia catch-up. Las condiciones para vivir/trabajar son poderosos atractores o expulsores de población a escala municipal: un ejemplo claro de municipio atractor es Mérida (condiciones favorables), mientras los municipios expulsores son varios de Veracruz, Zacatecas o Guerrero (condiciones desfavorables) (Almejo y Campos, 2013). Si estas condiciones se mantienen en el tiempo, el resultado será un incremento en la divergencia municipal. Sin embargo, a escala de municipio las condiciones para vivir/trabajar son mucho más volátiles que a escala nacional. En México la violencia las afecta notablemente (Durin, 2012), aunque no es el único factor clave4.
Quizá la diferencia central entre los dos enfoques es que el de catch-up propone una convergencia casi natural en el largo plazo, mientras que en el enfoque de crecimiento endógeno ésta no es inevitable, e incluso existe una mayor probabilidad de que se mantengan y amplíen las divergencias territoriales.
3.1. No todos los procesos de convergencia son deseables, ni todos los de divergencia son indeseables
Al hacer comparaciones en el tiempo de la situación migratoria municipal es importante notar que los cambios pueden medirse en términos atomizados y sistémicos. Por atomizados nos referimos a cambios en el desempeño de los municipios en el momento (t) comparados con su propio desempeño en (t-1). Es decir, es una comparación de los municipios contra sí mismos. Por sistémicos nos referimos a los cambios en el desempeño de cada municipio respecto a los demás municipios, que son los otros integrantes del sistema migratorio (v. g., los competidores). En estos términos, un municipio puede mejorar notablemente su desempeño, pero si sus competidores registran una mejor actuación, no cambiará su situación migratoria (que refleja sus condiciones como lugar para vivir/trabajar en relación con los demás). En otras palabras, para ser municipio atractor no basta simplemente con mejorar las condiciones propias, se debe mejorar más que los demás.
Así, los cambios de la atractividad migratoria de los municipios pueden deberse a: i) cambios positivos o negativos de la atractividad migratoria (v. g., cambio de trayectoria), y ii) velocidad de cambio. En ambos casos nos referimos tanto al desempeño de cada municipio en lo particular, como a su desempeño comparado con el de los demás municipios del sistema migratorio. Esto significa que los municipios pueden incrementar o debilitar su atractividad de migrantes con relación a sí mismos y a los demás en un entorno sistémico de suma cero (porque hablamos de migración interna). Por ejemplo, puede haber convergencia en un contexto de debilitamiento de todos los municipios, pero con mayor intensidad entre los líderes (lo que podría ser indeseable) o en un contexto de avances de los más rezagados, pero de debilitamiento de los líderes (lo que también podría ser indeseable). Por el otro lado, podemos imaginar un escenario donde se aprovechan ciertas condiciones para intentar concentrar la población mediante la aglomeración del empleo (e. g., clusters tecnológicos, polos de conocimiento, distritos industriales). Esto podría generar divergencia, y aun así ser un escenario deseable, si estas concentraciones de inversión y empleo se consolidan como motores potentes del desarrollo con amplios efectos difusores (Krugman, 1995; Porter, 1998).
En conclusión, no todos los procesos de convergencia son deseables, ni todos los de divergencia son indeseables, a diferencia de lo que se proponía hasta hace relativamente poco, en que se hacía una defensa a ultranza del llamado “equilibrio regional” (De Mattos, 1990). Todo depende de la trayectoria y la velocidad del cambio en las dimensiones atomizada y sistémica, así como de los objetivos y estrategias de desarrollo a diferentes escalas espaciales.
4. Estrategia metodológica y fuentes de información
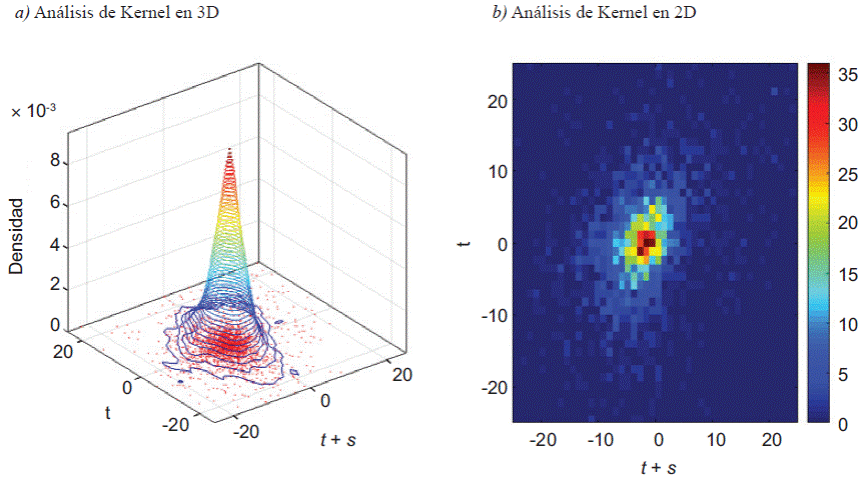
Estimamos funciones de densidad de Kernel y cadenas de Markov para examinar la convergencia/divergencia de las TNMR entre los 2 456 municipios de México5. Las funciones de densidad no paramétricas de Kernel las usamos para representar sintéticamente nuestro indicador clave de las condiciones para vivir/trabajar de los municipios: las TNMR. La aproximación de Kernel tiene la ventaja de no suponer ninguna forma de la distribución de la información estadística, facilita generar gráficos bi y tridimensionales y detectar la existencia de grupos de municipios con un comportamiento estadísticamente similar entre ellos y distinto del de los demás municipios (clubes de convergencia). Al final, este trabajo permite explorar la pregunta, ¿los municipios tienden a la convergencia/divergencia de sus condiciones para vivir/trabajar?
El análisis de Kernel genera información importante pero no suficiente para determinar la convergencia/divergencia de procesos en el territorio. Por eso complementamos el análisis de la dinámica de las TNMR con cadenas de Markov (CM), que permiten examinar, mediante matrices de transición, los cambios de situación migratoria de cada una de las categorías de municipios: si permanecen o cambian como expulsores o atractores de población. Este cambio de comportamiento migratorio es un síntoma de la redistribución de las condiciones para vivir/trabajar a lo largo del periodo analizado.6 Adicionalmente, las CM permiten perfilar el estado estacionario hipotético de la distribución de la atractividad migratoria entre los municipios en México en el largo plazo, considerando como base la situación inicial del sistema migratorio municipal. Con las cadenas de Markov exploramos la pregunta, ¿cuáles fueron las transiciones de los municipios entre las categorías de atracción/expulsión en el periodo analizado, y cuál es el estado más probable de la distribución de las condiciones para vivir/trabajar en el largo plazo?
La principal fuente de información fue la base de datos del Consejo Nacional de Población construida especialmente para este trabajo. El Consejo clasifica los municipios según su condición migratoria de la siguiente manera: i) expulsión elevada, ii) expulsión media, iii) equilibrio, iv) atracción media, y v) atracción elevada. El sistema de clasificación para este tipo de estudios depende de los objetivos de cada investigación (Gutiérrez et al., 2011, p. 149), por lo que esta categorización nos resultó adecuada. Para los cálculos del análisis de Kernel y de las cadenas de Markov se utilizó Matlab.
5. Métodos y análisis empírico
5.1. Análisis de Kernel: método
El análisis de Kernel es una alternativa al análisis no paramétrico tradicional de convergencia, ya que no requiere conocer o asumir la forma de la distribución estadística de los datos, sino que permite calcular una función de densidad en torno a valores muestrales. Es decir, la función de Kernel “deja que los datos hablen”7. Quizá por eso es uno de los métodos más utilizados para develar procesos de convergencia/divergencia (Terrell y Scott, 1992; Chow et al., 2016).
En el análisis de Kernel estimamos la siguiente función de densidad:
donde n es el número de unidades espaciales consideradas en el análisis (v. g., los 2 456 municipios de México), v ij se refiere a cada una de las observaciones de la variable j (v. g., las TNMR) y h es el parámetro que suaviza el comportamiento de los datos para ajustarlos a una función no paramétrica. La variable v ij se normaliza a partir de su media.
El análisis de Kernel ofrece distintas alternativas para la construcción de funciones de densidad. En este trabajo se recurrió al Kernel gaussiano, por su eficiencia de cálculo y por ser, quizá, el más utilizado en la literatura especializada (Silverman, 1986; Le Gallo, 2004)8.
Por facilidad de cálculo se supone aquí una distribución univariante que responde a la expresión:
Si la Ecuación 2 se sustituye en la Ecuación 1, se tiene:
Con lo que obtenemos la siguiente ecuación:
En este contexto, la tendencia a la convergencia implica que el cúmulo de datos de probabilidad esté cada vez más concentrado. La función Kernel detecta cómo se acumulan los datos al representar gráficamente la Ecuación 4 (Betancourt, 2013).
El resultado de la estimación depende de la acertada elección del parámetro h (ancho de banda) que suaviza el comportamiento de los datos para ajustarlos a una función no paramétrica (Salgado-Ugarte y Pérez-Hernández, 2003)9. Dada la importancia de la elección del parámetro h, la literatura sugiere diferentes criterios para determinarlo. La opción de Silverman (1986) es la más aplicada, como reportan diversos autores (López, 2008; Gutiérrez et al., 2011). Se estima de la siguiente forma (Brufman et al., 2005):
donde n es la cantidad de datos, σ es la desviación estándar de los datos y R es el rango intercuartil de los datos. Aplicando la Ecuación 5 se obtuvo que, para los datos de 2000, h = 0.82 y para los datos de 2010: h = 1.04.
Tomando como referencia el criterio de Silverman (1986), en la Figura 1 se observa el suavizado variando el parámetro h. La Figura 1 (c, d) corresponde a un estimador infrasuavizado h = 0.1 para los años 2000 y 2010, respectivamente. Estos gráficos registran un gran número de oscilaciones que corresponden a falsas modas. El número de éstas aumentaría si se disminuyera aún más el valor de h.
5.2. Resultados del análisis de Kernel
La Figura 1a sugiere una distribución unimodal de los datos en 2000, utilizando el ancho de banda h = 0.82. En el año 2000 la moda de la función de Kernel se ubicó en -2.1. El signo implica que prevalecen los municipios con condiciones adversas (v. g., no atractivos) como lugares para vivir y/o trabajar. En términos de población, el valor del pico se traduce como una disminución de la población de dos personas en promedio anual, por cada mil residentes10.
El análisis para 2010 también muestra una distribución unimodal utilizando un ancho de banda h = 1.04, con un Kernel centrado casi en el origen (Figura 1b). Los datos se agrupan en -1.1. Esto significa que los municipios siguen registrando tendencia a ser expulsores de población, como ocurría en 2000. Sin embargo, con menor intensidad, la disminución de la población en 2010 era de una persona en promedio anual por cada mil residentes. No obstante, se observa el surgimiento de un conjunto de datos alrededor de otro valor (+2.2), lo que sugiere la existencia de un grupo de municipios que atraen significativamente más población de la que expulsan (v. g., que mejoraron notablemente sus condiciones para vivir/trabajar). Obsérvese cómo la función gaussiana de 2000 se deforma para 2010 (donde señala la flecha en la Figura 1b).
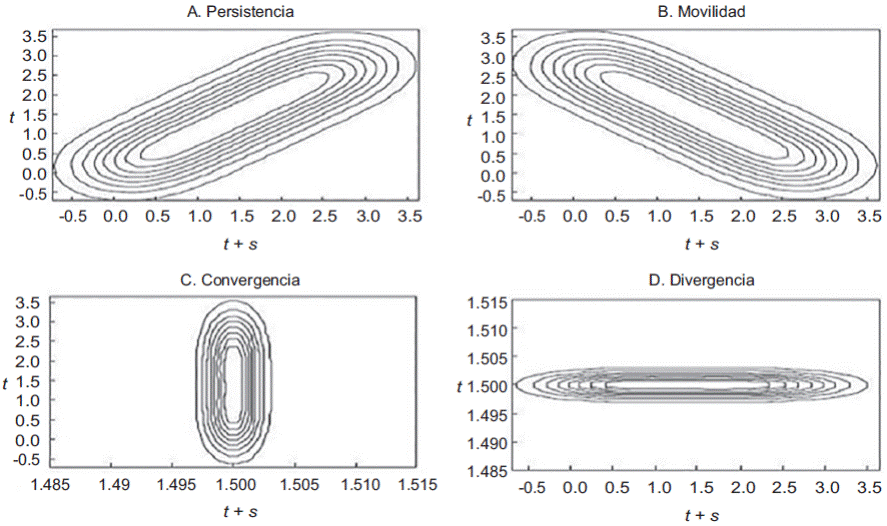
Una propiedad del análisis de Kernel es que permite estimar las llamadas líneas de contorno, que facilitan develar la dinámica de la distribución hacia la convergencia o divergencia. La Figura 2 muestra las superficies de densidad de referencia de los análisis de Kernel (Ardila Rueda, 2004, p. 245). Cada línea de contorno señala los puntos para los cualestiene un valor constante. Las superficies de referencia de la Figura 2 ofrecen un punto de comparación para los resultados obtenidos en nuestro análisis, en relación con cuatro posibilidades clave: persistencia, movilidad, convergencia y divergencia.
La Figura 2a sugiere persistencia y, en consecuencia, baja movilidad de los municipios entre categorías (e. g., de expulsores a atractores, o viceversa). La Figura 2b presenta la situación opuesta a la 2a: un comportamiento migratorio de los municipios en donde predomina la movilidad (v. g., un comportamiento migratorio cambiante) y, en consecuencia, una alta transición de los municipios entre categorías. No obstante, ninguna de las superficies representadas en las Figuras 2a y 2b implica convergencia/divergencia. La Figura 2c es la superficie típica de convergencia, ya que la distribución de los datos se concentra alrededor de un valor sobre el eje t + s (donde se registra el comportamiento de la variable: en nuestro caso las TNMR). Si las TNMR tienden a agruparse en una posición perpendicular al eje de las abscisas (t + s), existe convergencia porque se agrupan (v. g., convergen) en un cierto momento (t). Finalmente, la Figura 2d muestra la típica superficie de divergencia: las TNMR están totalmente dispersas en un momento (t), formando una línea perpendicular al eje de las ordenadas.
Con el apoyo de la Figura 2 (que es teórica) podemos analizar sistemáticamente la Figura 3, que muestra los resultados. Recordemos que la Figura 2 muestra casos típicos puros que difícilmente se van a encontrar en la realidad. Lo que se encuentra en el mundo real son matices de esas situaciones extremas.
La Figura 3 sintetiza las características clave de la dinámica de las TNMR de los municipios de México para el periodo de estudio: i) en 2000 predominan los municipios en los que la emigración es mayor que la inmigración, es decir, prevalecen los municipios no atractivos como lugares para vivir y/o trabajar (v. g., la moda es negativa); ii) para 2010 siguen predominando los municipios no atractivos, pero la diferencia con los municipios atractivos se reduce (la moda es negativa, pero de menor magnitud que en 2000); además, se registra un grupo de municipios que se destacan como atractores de población (la deformación de la curva 1b, correspondiente al periodo 2000-2010); iii) se registra un proceso de convergencia de las TNMR (v. g., las TNMR tienden a agruparse en una posición perpendicular al eje de las abscisas); y iv) la pendiente de la función de Kernel apenas es positiva, lo que sugiere una tendencia hacia la movilidad o transición entre estados migratorios.
5.3. Cadenas de Markov: método
Las cadenas de Markov son uno de los métodos más útiles para modelar procesos estocásticos y su evolución probabilística, conociendo solamente la situación presente. Los flujos migratorios (y muchos otros procesos) observados en el tiempo (y en el espacio) son a menudo modelados mediante procesos estocásticos, entendidos como cualquier colección de variables aleatorias {X (t)} dependientes del tiempo t (Cameron y Poot, 2011). El tiempo puede medirse en unidades discretas, por ejemplo t = 0, 1, 2,... o continuas: t ≥ 0. En cualquier momento, t describe la observación de una variable aleatoria que denotaremos X t o X(t). Sea {X n }n≥0 un proceso estocástico discreto con espacio de estados contable E = {i, j, k,…}.
Un proceso estocástico (X) es markoviano si la probabilidad condicional de un evento futuro en t +1 no depende de un evento pasado, sino sólo del evento presente del proceso. Esto se muestra en la Ecuación 6, donde ambos lados de la ecuación están bien definidos.
Este proceso estocástico se llama cadena de Markov. Se dice que dicha cadena es homogénea si el lado derecho de la Ecuación 6 es independiente de n. La Ecuación 7 muestra las propiedades de Markov para todas las variables i, j (Yin y Zhang, 2010).
donde P ij es la matriz de transición, en nuestro caso la matriz de cambios de estado (o situación migratoria) de los municipios; i es la clasificación inicial de los municipios según sus TNMR, y j la clasificación en 2010.
En este trabajo, el proceso estocástico X 1, X 2, X 3, ... representa grupos de municipios clasificados según el valor de su TNMR11. Dicho de otro modo, cada grupo X t representa una cierta relación de inmigración y emigración en la que puede ubicarse cada municipio (Arrufat et al., 2006). Así, p i = (p ij ) j∈E es un vector de probabilidades para cada i.12
El proceso de cadenas de Markov puede alcanzar una situación de equilibrio, es decir, confluir hacia un vector de categorías estacionarias en el largo plazo que se mantienen sin cambios. Esto se cumple cuando n → ∞, entonces p n tiende a una matriz como la que se muestra en la Expresión 8.
donde cada fila es igual al vector (Ecuación 9) y sus elementos suman uno:
En este caso, u es un vector de un grupo estacionario para cualquier vector de probabilidad x, xp n → u, cuando n → ∞. También el vector del grupo estacionario es único y satisface que up = u.
Con el vector de grupo estacionario se puede observar el comportamiento de las probabilidades de migración/emigración en el largo plazo. En consecuencia, las cadenas de Markov permiten conocer las probabilidades finales de que los municipios se mantengan en una u otra categoría migratoria, en un horizonte temporal lo suficientemente amplio como para validar la existencia de un proceso de convergencia/divergencia, si las condiciones iniciales se mantienen.
Para el análisis de convergencia/divergencia, Quah (1993) discretiza la distribución de la variable bajo análisis en cinco grupos mutuamente excluyentes, que en nuestro caso corresponden a la clasificación de los municipios que hace el Consejo Nacional de Población (Conapo, 2015) según la condición migratoria de cada municipio: i) expulsión elevada (EE), ii) expulsión media (EM), iii) equilibrio (EQ), iv) atracción media (AM), y v) atracción elevada (AE) (Cuadro 1).
Cuadro 1 Vectores de estado inicial, 2000-2010
| Año | EE | EM | EQ | AM | AE | Total |
|---|---|---|---|---|---|---|
| 2000 | 548 | 482 | 221 | 594 | 611 | 2 456 |
| % | 22.3 | 19.6 | 9.0 | 24.2 | 24.9 | 100.0 |
| 2010 | 850 | 754 | 205 | 301 | 346 | 2 456 |
| % | 34.6 | 30.7 | 8.3 | 12.3 | 14.1 | 100.0 |
EE: expulsión elevada; EM: expulsión media; EQ: equilibrio; AM: atracción media; AE: atracción elevada.
Fuente: Elaboración propia con datos del Conapo, 2015.
5.4. Resultados de las cadenas de Markov: dinámica de la atracción migratoria entre los municipios de México
La clasificación migratoria de los municipios que hace el Conapo es consistente con los propósitos de este estudio. Por tanto, las categorías migratorias del Conapo son las situaciones o estados entre los que transitan los municipios13. Los vectores iniciales totales (x 0) se construyeron a partir de los municipios que estaban en el año inicial en cada categoría, en relación con el total (Cuadro 1).
Lo primero que llama la atención de los vectores iniciales (Cuadro 1) es el incremento de los municipios de expulsión de 2000 a 2010. Los de expulsión elevada pasaron de 548 a 850 (un incremento de 55.1%) y los de expulsión media subieron de 482 a 754 (un aumento de 56.4%). En total, los municipios expulsores de población, es decir, los municipios no atractivos como lugares para vivir/trabajar, pasaron de 1 030 en 2000 a 1 604 en 2010 (un aumento de 574 municipios). Mientras al inicio del periodo los municipios no atractivos representaban 41.9% del total nacional, diez años después su proporción subía a 65.3% del total: en 2010 casi dos de cada tres municipios no eran lugares atractivos para vivir y/o trabajar (Cuadro 1).
Por su parte, los municipios en situación migratoria de equilibrio decrecieron ligeramente (de 9.0% en 2000 a 8.3% en 2010), por lo que podemos hablar de una situación estacionaria. Sin embargo, como era de esperarse, los municipios atractores de población (los municipios atractivos) disminuyeron notablemente. Los de atracción media se redujeron prácticamente a la mitad (una reducción de 49.3%) y los de atracción elevada ligeramente menos (reducción de 43.4%). En total los municipios atractivos se redujeron en la década de 1 205 a 647: una reducción porcentual de 46.3 por ciento.
En resumen, durante la primera década del siglo XXI se reconfiguró drásticamente el país en términos de la redistribución de la atractividad migratoria en el territorio a escala municipal. Aumentaron notablemente los municipios no atractivos y se redujeron drásticamente los atractivos. Esto se puede leer como un proceso de divergencia en el que se polarizan los municipios atractivos y no atractivos para vivir/trabajar, y en el que la mayoría de los municipios pierden potencia como lugares atractivos para vivir/trabajar.
Matrices de transición, 2000-2010
Mientras el análisis de Kernel permite examinar la evolución de la forma de la distribución estadística de las TNMR, no es útil para observar los cambios en el interior de la distribución a lo largo del tiempo. Una manera de subsanar este problema es aplicar cadenas de Markov para derivar matrices de probabilidades de transición, que representan la probabilidad de estar en un estado k en el periodo t+1, a partir de la distribución en el periodo t (Moncada e Hincapié, 2013).
Determinamos la construcción de las matrices de transición para 2000-2010 por conteo de cambios entre categorías de los municipios de un año a otro. Para esto no se requiere aplicar cadenas de Markov (que se aplicarán para la proyección del segundo estado de transición 2010-2020); basta consultar las fuentes de información y ordenarlas como en el Cuadro 2.
El Cuadro 2 (columna m) y la Figura 4 confirman la situación de divergencia en 2010: 65.3% de los municipios se concentraban en las dos categorías de expulsión. Sin embargo, si hacemos un zoom, se observa que entre 2000 y 2010 los municipios de expulsión elevada (EE) mostraron cierta capacidad de mejorar su situación migratoria (véase el renglón EE del Cuadro 2). Si bien más de un tercio permanecieron en la misma categoría (36.1%), casi 64% la mejoraron e incluso uno de cada tres (33.9%) pasaron de expulsores a atractores de población (351 municipios), de lo que se infiere que fueron capaces de mejorar de manera importante sus condiciones para vivir/trabajar en sólo una década. Esto sugiere dos cosas: i) un proceso de redistribución progresiva de las condiciones para vivir/trabajar que favorece a los municipios de EE, y ii) que existe la posibilidad real de revertir déficits de condiciones para vivir/trabajar en la escala municipal, incluso en una situación general de divergencia.
Si leemos la columna EE del Cuadro 2, observamos que las categorías de municipios que están en mayor riesgo de bajar a esa categoría son los de expulsión media (EM) y los de equilibrio (EQ), lo que es lógico; pero incluso alrededor de 12.3% de los municipios que registraban situaciones de atracción media (AM) y elevada (AE) pasaron a EE, lo que implica volatilidad de la redistribución de condiciones para vivir/trabajar en esa década de alta violencia en México (Durin, 2012). Esto es consistente con la pendiente apenas positiva de la función de Kernel, lo que indicaba una tendencia hacia la movilidad entre estados (véase la sección 5.2).
Cuadro 2 Matriz de transición, 2000-2010
| t+1 | ||||||||
|---|---|---|---|---|---|---|---|---|
| EE | EM | EQ | AM | AE | m | % | ||
| EE | 36.1 | 22.6 | 7.4 | 17.8 | 16.1 | 850 | 34.6 | |
| EM | 17.1 | 22.9 | 11.4 | 32.9 | 15.6 | 754 | 30.7 | |
| t | EQ | 15.6 | 22 | 9.3 | 28.3 | 24.9 | 205 | 8.3 |
| AM | 12.3 | 5 | 4.3 | 34.6 | 43.9 | 301 | 12.3 | |
| AE | 12.4 | 16.5 | 11.6 | 9.5 | 50.0 | 346 | 14.1 | |
| 2456 | 100.0 | |||||||
Fuente: Elaboración propia con datos del Conapo, 2015.
En la categoría de expulsión media (EM), 22.9% de los municipios registran una tendencia a mantenerse en ese mismo estado (173 municipios) y sólo 17.1% se convirtieron en municipios de expulsión elevada (EE). Esto significa que en este periodo era más probable que los municipios de EM pasaran a ser de atracción: 48.5% (366 municipios). Estos municipios, más los que mejoraron su situación migratoria convirtiéndose en municipios de equilibrio (11.4%: 86 municipios), suman 452, lo que significa que 60% de los municipios de expulsión media mejoraron su situación migratoria. Esto confirma que, al hacer un zoom sobre este entorno de divergencia, se insinúa una tendencia de redistribución progresiva de condiciones para vivir/trabajar en favor de los municipios más desaventajados.
En la categoría equilibrio (EQ), la perspectiva de permanecer en la misma categoría (19 municipios de 205) fue 9.3%. La mala noticia es que 37.6% (77 municipios) pasaron a las categorías de expulsión; 22% a expulsión media (45 municipios), y 15.6% a expulsión elevada (32 municipios). La buena noticia es que 53.2% de los municipios en EQ (sumaron 109) mejoraron su situación migratoria: 28.3% pasaron a atracción media (AM) (58 municipios) y 24.9% transitaron a atracción elevada (AE) (51 municipios).
Los municipios de atracción media fueron los más estables: 78.5% se mantuvieron en esa categoría o subieron a la de AE: 34.6% de los municipios permanecieron en la misma categoría (104 municipios) y 43.9% mejoraron su situación migratoria pasando a la categoría de atracción elevada (132 municipios). No obstante, uno de cada cinco municipios de AM (21.6%) pasaron a las categorías de expulsión (65 municipios). De cualquier manera, los municipios de AM tuvieron una mayor tendencia a mantener o mejorar su situación migratoria (236 municipios) que a debilitarla.
Vale la pena destacar la poca fortaleza de los municipios de atracción elevada (AE) para mantenerse como territorios con las mejores condiciones para vivir/trabajar. Sólo la mitad de los municipios de AE lograron permanecer en esa categoría y el resto bajó: 12.4% pasaron dramáticamente de atracción elevada a expulsión elevada (43 municipios que dañaron profundamente sus condiciones para vivir/trabajar), 16.5% transitaron a expulsión media (57 municipios), 11.6% se movieron a la categoría de equilibrio (40 municipios) y 9.5% evolucionaron a atracción media (33 municipios). En México parece complicado mantenerse entre los municipios líderes, lo que sugiere que los gobiernos municipales deben estar muy alertas porque su realidad es altamente cambiante: la competencia es intensa y la situación de violencia es muy dinámica.
La diagonal del Cuadro 2 indica que 774 municipios permanecieron en la misma categoría migratoria, y por tanto 1 682 municipios la cambiaron para mejorar o debilitar su situación. Con estos resultados podemos obtener un porcentaje que sería un indicador de la volatilidad o dinámica del sistema (ID). La estimamos de la siguiente forma: municipios que no cambiaron su situación migratoria (MNC), entre los municipios que la cambiaron (MC) multiplicado por 100. El ID se muestra en la Ecuación 12.
El ID es 46%, lo que devela que en la década de referencia casi uno de cada dos municipios se movió de categoría migratoria, lo que significa que el sistema es altamente volátil.
Otro indicador es el de tendencia del sistema (TS). Se calcula dividiendo los municipios que mejoran su situación migratoria (MMSM), entre los municipios que debilitaron su situación migratoria (MDSM) (no se consideran los que permanecen en equilibrio: Ecuación 13).
Dado que 1 235 municipios mejoraron su situación y 412 no, el indicador TS es igual a 3.0, lo que confirma una tendencia progresiva de redistribución territorial de la atractividad migratoria en favor de los municipios más desaventajados, aun si el contexto es de divergencia.
Segundo estado de transición, 2010-2020
El segundo estado de transición indica la probabilidad de que un municipio cambie de categoría en el periodo t+1 (que en este trabajo es 2020). Esta nueva matriz es una proyección de las categorías migratorias de los municipios, según sus TNMR previas, si se mantuvieran las condiciones de 2000-2010. Para realizar esta proyección se aplicaron cadenas de Markov (véase la Ecuación 6 y el Cuadro 3).
Cuadro 3 Matriz del segundo estado de transición, 2010-2020
| t+1 | |||||||
| EE | EM | EQ | AM | AE | m a | ||
| EE | 22.2 | 18.5 | 8.5 | 23.6 | 27.1 | 753 | |
| EM | 17.8 | 15.8 | 8.1 | 26.6 | 31.4 | 687 | |
| t | EQ | 17.4 | 16.1 | 8.6 | 24.8 | 33.1 | 188 |
| AM | 15.6 | 13.8 | 8.4 | 21.1 | 40.9 | 383 | |
| AE | 16.4 | 17.8 | 10.1 | 18.9 | 36.6 | 445 | |
| 2456 | |||||||
a El número de municipios se estimó mediante una proyección matricial. Véase Grossman y Soto (1983, pp. 240-249).
Fuente: Elaboración propia.
Principales cambios
En el periodo 2000-2010, 307 municipios se encontraban en la categoría de expulsión elevada (EE), lo que equivalía a 36.1% del total de la categoría (Cuadro 2)14. La proyección (Cuadro 3) indica que para 2020 la probabilidad de que los municipios de EE permanezcan en esa categoría se reduce a 22.2%. Debe destacarse que estas transiciones se registran sobre todo hacia las categorías de atracción media (AM) y, notablemente, atracción elevada (AE). La probabilidad de transitar a AM subiría de 17.8 a 23.6%, y la de pasar a AE se elevaría de 16.1 a 27.1%. En síntesis, la proyección sugiere una redistribución progresiva importante de condiciones para vivir/trabajar en beneficio de los municipios más débiles de la década anterior. Es decir, en términos endógenos y exógenos estos municipios serían mejores (o menos adversos) lugares para vivir/trabajar que en el periodo anterior.
La categoría de municipios de expulsión media (EM) mantiene casi la misma probabilidad de pasar a la categoría de expulsión elevada (EE) que en el decenio anterior. En 2010 era de 17.1% y en 2020 se proyecta a 17.8%. La probabilidad de permanecer como de EM se reduce drásticamente de 22.9 a 15.8%, y la de ascender a la categoría de equilibrio (EQ) se reduce al pasar de 11.4% en 2010 a 8.1% en 2020. Por su parte, la probabilidad de transitar a la categoría atracción moderada (AM) también se reduce levemente de 32.9 a 28.6%. En conjunto, estos datos sólo pueden indicar importantes transiciones hacia la categoría atracción alta (AA) para 2020. Así, mientras en 2010 la probabilidad de pasar de EM a AA era 15.6%, se proyecta que para 2020 será de 31.4%. De acuerdo con la proyección, se reducirían los municipios de EM y sus transiciones se concentrarían en las categorías de atracción más altas, lo que sugiere que mejorarían sus condiciones para vivir/trabajar.
En el marco de la proyección, los municipios en situación de equilibrio (EQ) mantienen más o menos estables sus probabilidades de transitar a la categoría de expulsión elevada (EE) y las de permanecer en la de EQ. En el primer caso las probabilidades pasan de 15.6% en 2010 a 17.4% en 2020, y en el segundo de 9.3 a 8.6%. Por el otro lado, bajan sus probabilidades de pasar de la categoría EQ a la de atracción media (AM): 28.3% en 2010 contra 24.8% en 2020; aunque elevan notablemente su probabilidad de transitar de EQ a atracción alta (AA): de 24.9% en 2010 a 33.1% en 2020, y también reducen de manera importante su probabilidad de pasar a la categoría expulsión media (EE): 22.0% en 2010 y 16.1% en 2020. Al final el saldo para los municipios de la categoría EQ tendería a la atracción.
Hasta ahora, la proyección sugiere una redistribución progresiva de las condiciones para vivir/trabajar hacia los municipios que estaban en situación más desaventajada en 2010, lo que los impulsa a transitar a mejores situaciones de atracción migratoria. Por tanto, podemos suponer que las categorías atracción media (AM) y atracción elevada (AE) registrarán pérdidas en su capacidad de atraer migrantes (por cambios atomizados o sistémicos de sus condiciones para vivir/trabajar), ya que la migración interna es un sistema de suma cero. En consecuencia, podemos decir que se insinúa una tendencia hacia la convergencia.
La proyección perfila que los municipios de atracción media (AM) registran cambios negativos en todas sus probabilidades de transición. Aumentan ligeramente sus probabilidades de ser de expulsión elevada (EE): de 12.3 a 15.6%; más que duplican sus probabilidades de ser de expulsión media (EM): de 5.0 a 13.8%; casi duplican sus probabilidades de transitar a la categoría equilibrio (EQ): de 4.3 a 8.4%; bajan notablemente sus probabilidades de permanecer como de AM (de 34.6 a 21.1%); y reducen, aunque marginalmente, sus probabilidades de pasar a la categoría atracción elevada (AE). La proyección sugiere que los municipios de AM son volátiles, a pesar de que, se infiere, son motores del desarrollo a diversas escalas espaciales.
Por su parte, los municipios de atracción elevada (AE) registran debilitamiento y también se les complica permanecer en su misma categoría: sus probabilidades bajan de 50.0% en 2010 a 36.6% en 2020. Esta pérdida de potencia se desplaza, sobre todo, a la categoría atracción media (AM), donde las probabilidades de transición casi se duplican: suben de 9.5% en 2010 a 18.9% en 2020. Los cambios en las demás probabilidades de transición son marginales. Esto se explica por la potencia inercial de los municipios de AE, que son menos volátiles que los de expulsión media en la proyección a 2020.
Con la estructura de la matriz de transición 2010-2020 (Cuadro 3), podemos obtener el indicador TS, que es igual a 2.1. Esto significa que el sistema sigue registrando una tendencia hacia la mejoría de la capacidad de atracción de los municipios, aunque menor a la de la década anterior. Como la migración interna es un sistema de suma cero, esto se traduce en un debilitamiento de los municipios atractores, especialmente de los de atracción media. Por su parte, el indicador de la movilidad o dinámica del sistema (ID) es 27.9%, mucho menor al de la década anterior, que fue 46%, lo que refleja una caída en la movilidad entre categorías del sistema migratorio, pero favoreciendo a los municipios expulsores.
La Figura 5 sintetiza la tendencia del cambio de perfil de la distribución de los municipios entre las categorías migratorias: entre 2010 y 2020 se registra un desplazamiento de los municipios de expulsión hacia las categorías de atracción. Seguramente esta tendencia será aún más clara en la proyección de largo plazo.
Vectores de convergencia: la situación de largo plazo
Iterar reiterativamente la matriz de transición original (Cuadro 2; Ecuación 11) permite estimar los vectores de estado estacionario (Ecuación 9), donde las probabilidades de transición ya no cambian aun si se realizan más interacciones. Ésta es la situación más probable en el largo plazo si permanecen las condiciones de 2000-2010. Los vectores de probabilidad de largo plazo se estacionaron en un número constante de siete decimales. Las distribuciones en el largo plazo no son pronósticos, pues el supuesto de que las condiciones iniciales no cambian es muy restrictivo. Son, simplemente, escenarios exploratorios que perfilan tendencias y permiten generar algunos insumos para políticas públicas, dado el entorno de alta volatilidad migratoria y fuerte competencia sistémica (además de la baja calidad de las instituciones municipales; véase Ziccardi y Saltalamacchia, 2016).
En el Cuadro 4, cada fila representa el vector de probabilidades de transición de largo plazo, también muestra la ergodicidad (E) en la última columna. Si se mantienen las condiciones de la distribución de municipios de 2010 en el sistema clasificatorio y se consideran las variaciones de 2020, después de seis periodos (o interacciones; en este caso cada iteración equivale a una década) 17.6% de municipios serían de expulsión elevada, 16.5% de expulsión media, 9.0% de equilibrio, 22.0% de atracción media y 34.7% de atracción elevada.
Este patrón de la distribución de los municipios por categoría migratoria es muy diferente del de 2010 y confirma la tendencia de 2020 de una redistribución progresiva de la atractividad migratoria (Figura 5). En 2010 el perfil era dominado por los municipios de expulsión elevada (EE) y expulsión media (EM). En cambio, en el estado estacionario de largo plazo, el perfil es casi una imagen espejo de la de 2010, dominado por las categorías de atracción elevada (AE) y atracción media (AM), que juntas concentran 57.0% del total: 1 400 municipios. La categoría equilibrio (EQ) queda prácticamente sin cambios: 205 municipios en 2020 y 221 en la situación estacionaria. Esto confirma un proceso de convergencia débil (se requirieron seis iteraciones o décadas), pero persistente hacia un estado migratorio de atracción, lo que indica una redistribución progresiva de largo plazo de las condiciones para vivir/trabajar entre los municipios de México. Sin embargo, como el sistema de migración interna es de suma cero, debe de llamar la atención el grupo de municipios que se verán cada vez más rezagados.
La diagonal del Cuadro 4 indica que, en el largo plazo, 576 municipios permanecen en la misma categoría migratoria y por tanto 1 880 municipios la cambian para mejorar o para debilitar su situación. El indicador de la dinámica del sistema es de 30.6%. Por otro lado, dado que 1 392 municipios mejoraron su situación (56.7%) y 837 no, el indicador de tendencia es 1.6. Esto indica que se debilita la tendencia progresiva de redistribución territorial de la atractividad migratoria.
Cuadro 4 Matriz de convergencia: estado estacionario de largo plazo
| t+1 | |||||||
|---|---|---|---|---|---|---|---|
| EE | EM | EQ | AM | AE | E | ||
| EE | 17.9 | 16.5 | 8.8 | 22.4 | 34.2 | 17.6 | |
| EM | 17.5 | 16.4 | 8.9 | 22.0 | 34.9 | 16.5 | |
| t | EQ | 17.5 | 16.5 | 8.9 | 22.0 | 34.9 | 9.0 |
| AM | 17.4 | 16.7 | 9.1 | 21.7 | 35.0 | 22.0 | |
| AE | 17.6 | 16.6 | 9.0 | 22.1 | 34.5 | 34.7 | |
Fuente: Elaboración propia.
Recapitulando, el análisis de cadenas de Markov sugiere que el perfil de la situación de largo plazo es casi el inverso del perfil de 2010. Esto implica un proceso de convergencia que cambia de trayectoria: de las categorías de expulsión a las de atracción (Figura 6). El sistema registra una tendencia hacia la mejoría de la capacidad de atracción de los municipios: los que mejoraron su situación migratoria pasaron de 26.3% en 2010 a 28.0% en 2020, y suben hasta 56.6% en el largo plazo. Estos cambios migratorios sólo pueden ocurrir en un marco de redistribución progresiva de las condiciones para vivir/trabajar. Sin embargo, hay que resaltar dos temas, por lo menos: i) el estado estacionario de las categorías migratorias de los municipios ocurre hasta la sexta iteración, lo que apunta, vale reiterarlo, a que el proceso de convergencia es débil, aunque persistente en el largo plazo, y ii) en este contexto en el que se detecta una redistribución progresiva, se debe estar muy atento a los municipios que inevitablemente quedarán rezagados (inevitablemente, porque la migración interna es un sistema de suma cero).
6. Conclusiones
Los objetivos de este trabajo, exploratorio y metodológico, fueron: i) develar la redistribución espaciotemporal de la atractividad migratoria entre todos los municipios de México, para el periodo 2000-2020 y su tendencia de largo plazo, y ii) explorar las tendencias de convergencia/divergencia de las TNMR a escala municipal. Ambos se cumplieron. Deliberadamente evitamos utilizar indicadores socioeconómicos tradicionales que requieren ser seleccionados por los analistas, porque esta selección determina los resultados. En su lugar, preferimos probar las TNMR como indicador indirecto del cambio en el espacio y el tiempo de las condiciones municipales como lugares para vivir/trabajar (v. g., atractividad migratoria).
Consideramos a las TNMR un indicador de preferencia revelada condicionada de los migrantes respecto a la elección de su territorio de destino. La población en los países emergentes (como México) migra, principalmente, para mejorar su ingreso y sus condiciones de vida. Por tanto, la población migrante se dirige a destinos que ofrecen mayores oportunidades y mejores condiciones (reales o percibidas) para vivir/trabajar, tanto para ellos como para sus familias, en un contexto plagado de restricciones. En consecuencia, para cumplir los objetivos de nuestro texto, supusimos que el comportamiento migratorio revelado de las personas es más confiable que utilizar variables basadas en la selección de expertos.
No todo está a favor de utilizar indicadores de migración, porque su medición registra serios problemas conceptuales y metodológicos. Pero lo mismo se puede decir de múltiples indicadores socioeconómicos. Una consideración adicional: al menos en el campo de las previsiones, la demografía ha demostrado ser, quizá, la más exacta de las ciencias sociales.
Quedó claro que no todos los procesos de convergencia son deseables, ni todos los de divergencia son indeseables. Todo depende de la trayectoria y la velocidad del cambio en las dimensiones atomizada y sistémica, así como de las estrategias de desarrollo a diferentes escalas espaciales. Por eso evitamos, de manera deliberada, hacer juicios de valor a lo largo del texto sobre las tendencias de convergencia/divergencia.
También se advirtió que las proyecciones de largo plazo que presentamos no son pronósticos, sino escenarios que delinean tendencias, pero, más importante, permiten revelar algunas características importantes del sistema migratorio. En este caso, su alta volatilidad migratoria (especialmente la de los municipios de atracción media, en la proyección de largo plazo) y la intensa competencia intermunicipal. Estas características pueden ser retomadas para alimentar políticas públicas a diversas escalas (e. g., elevar la calidad de las instituciones municipales, promover alianzas estratégicas entre municipios, afinar el desarrollo local).
El sistema migratorio municipal refleja objetivos locales, regionales y nacionales que pueden ser mutuamente incompatibles. Más en espacios metropolitanos donde usualmente se registran serios conflictos entre gobiernos de diversos partidos políticos que “conducen” la misma ciudad, sin considerarla como una totalidad. Esto sugiere la urgencia de discutir seriamente los gobiernos metropolitanos y la prevalencia de la planeación espacial sobre la sectorial, entre otros temas (Sobrino et al., 2015). La competencia intermunicipal es inevitable y no se puede eliminar por decreto, pero quizá se podría avanzar hacia un esquema de competencia cooperativa (Feiock, 2010), para lo que se requiere contar con instituciones locales fuertes y de calidad (Ziccardi y Saltalamacchia, 2016).
Las principales herramientas que utilizamos fueron el análisis de densidad de Kernel y las cadenas de Markov. Sus resultados fueron consistentes entre sí, reforzándose mutuamente y, aún más, son coherentes con: i) el intenso proceso de urbanización y metropolización que registra el país, y ii) la volatilidad de la violencia, lo que seguirá modificando de manera importante los patrones de migración y movilidad, en respuesta a la redistribución territorial de las condiciones para vivir/trabajar en la escala municipal.
Con todas sus limitaciones y restricciones, este trabajo permite atisbar que el perfil de la situación de largo plazo de las TNMR es casi el inverso del perfil de 2000, lo que implica un proceso de convergencia positiva (en el que la mayoría gana, seamos reiterativos, la migración interna es un fenómeno de suma cero) que cambia de trayectoria: de las categorías de expulsión a las de atracción. Estos cambios migratorios develan un proceso de redistribución progresiva de las condiciones para vivir/trabajar en el territorio y en el tiempo, que favorece a los municipios más desaventajados. El proceso de convergencia parece débil, pero persistente en el largo plazo.











 nueva página del texto (beta)
nueva página del texto (beta)