Services on Demand
Journal
Article
Indicators
Related links
Share
Contaduría y administración
Print version ISSN 0186-1042
Contad. Adm vol.64 n.1 Ciudad de México Jan./Mar. 2019
https://doi.org/10.22201/fca.24488410e.2018.1286
Articles
The demand for employment in the manufacturing industry in Mexico
1Universidad Autónoma de Baja California, México.
The purpose of the document is to analyze the demand for employment in the manufacturing industry in Mexico, during the period from 2007 to 2015, considering 19 subsectors of the manufacturing industry. The effect that economic performance variables have as the gross domestic product, as well as wages, is analyzed. Labor productivity and manufacturing exports are also considered as explanatory variables. With information from the INEGI Monthly Industrial Survey, different models with panel data are estimated and the most suitable one is selected based on specification tests. It is found that the demand-product elasticity is the most relevant of all. The demand elasticity - wages is negative, and it is only significant to explain the demand for specialized work. Labor productivity and exports are significant and have a negative and positive effect, respectively, on the demand for total, specialized and non-specialized work.
Keywords: Employment; Manufacturing; Panel data
JEL Codes: J23; J24; J31
El propósito del documento es analizar la demanda de empleo en la industria manufacturera de México, durante el periodo de 2007 a 2015, considerando 19 subsectores de la industria manufactura. Se analiza el efecto que tienen variables de desempeño económico como el producto interno bruto, así como los salarios. También se consideran como variables explicativas, la productividad laboral y las exportaciones de la manufactura. Con información de la Encuesta industrial Mensual del INEGI, se estiman distintos modelos con datos de panel y se selecciona el más idóneo con base a pruebas de especificación. Se encuentra que la elasticidad demanda-producto es la más relevante de todas. La elasticidad demanda - salarios es negativa, y sólo es significativa para explicar la demanda de trabajo especializado. La productividad laboral y las exportaciones son significativas y tienen un efecto negativo y positivo respectivamente, sobre la demanda de trabajo total, especializado y no especializado.
Palabras clave: Empleo; Industria manufacturera; Datos de panel
Códigos JEL: J23; J24; J31
Introduction
Currently in the national sphere, there is a series of phenomena that describe the macroeconomic and sectorial performance of the economy such as inflation, labor informality, slow growth, and income inequality, all of which have effects on the productive and social sphere at a national, regional, and local level. However, it is also important to point out that there are important challenges in the labor market, since there is an urgent need for the productive apparatus to develop a greater capacity to generate formal jobs and thus respond to the demand for employment exhibited by the economically active population (EAP). From this perspective, it is also important to rethink public policies that help trigger employment from the business and sectoral structure and thereby encourage social welfare conditions, minimizing the levels of poverty that prevail in the Mexican economy.
In this framework, it is worth noting that the figures of employed personnel reported by the Monthly Industrial Survey of the National Institute of Statistics and Geography (INEGI, by its acronym in Spanish), indicate that the largest amount of the workforce is found in the tertiary sector, while the secondary and primary sectors are located in a lower position respectively. Taking the above into consideration, it is considered urgent to estimate an employment demand function related to the manufacturing sector of the Mexican economy during the 2007-2015 period. The idea of contemplating a level of disaggregation by subsectors came to be with the purpose of studying the asymmetries manifested within the manufacturing sector in terms of employment, salaries, and wages, but also with the expectation of integrating a database that allows analyzing the analytical relations between the variables, capturing the temporal and cross-sectional part of the object of study.
Studies such as that by the World Bank (2012) note that the analysis of employment is fundamental because it is an indicator that directly affects the economic and social development of a country, since through a wage income a certain level of subsistence and quality of life can be guaranteed, which means mitigating the degree of poverty in households. Consequently, the aim is to investigate the behavior of the demand for employment in the manufacturing industry, a sector that throughout the years has been fundamental and linked to the processes of economic growth and commercial opening. Although it is possible to affirm that the national economy registers a process of tertiarization with respect to employment, it is also true that the secondary sector is not the most contracted in terms of employed personnel, since it registers a participation rate in the total economy higher than that presented by the primary sector. In the specific case of trade and services, as well as the manufacturing industry, it is specified that prior to the 2008 crisis, the participation of employed personnel in manufacturing was higher than that reflected after said year, while services and trade were already reflecting an upward trajectory. However, according to information from the Monthly Industrial Survey, manufacturing employment is recovering after the crisis episode, which means that it is having a favorable impact on the labor market and reversing its growth path. According to figures from the national accounts of the INEGI, the secondary sector is comprised of mining and the generation, transmission, and distribution of electricity, water, and gas supply through pipelines for final consumption, as well as the construction and manufacturing industry, the latter having the greatest weight in the secondary sector. Manufacturing, in particular, recorded a variation of 7.1% in the last quarter of 1995 and of -10.6% in the first quarter of 2009. Nevertheless, since the second quarter of 2009 and until now, it reports a recovery trajectory with a similar trend to the one after the 1994 crisis.
In this context, the objective of this research is to estimate a job demand function for the manufacturing industry in order to identify those factors that may be relevant to detonate employment levels in an environment of slow growth and deep social inequalities. While there is a vast body of literature associated with the topic, it is also true that it is a core issue in economic analysis that requires further study. The empirical work separately analyzes the segment of workers and employees for whom the industrial survey provides information on a quarterly basis. The purpose is to evaluate the same econometric function in both cases and to identify possible differentiated effects, considering both segments as non-specialized and specialized labor force respectively. The findings will make it possible to reflect on the topic of study and outline elements that may contribute to the design of policies and/or programs in the area of sectoral economic development. What underlies the empirical work is the contrast of the working hypothesis, which establishes that the demand for employment in the manufacturing sector essentially responds to the dynamics of the product and the external sector and not so much to wage costs as the conventional theory postulates.
The work is structured in three sections. The first provides an overview of the performance of the manufacturing industry on an aggregate scale and by subsector, with the aim of identifying distinguishing characteristics among the economic activities that comprise the industry. The outline focuses on indicators such as employed personnel, share of manufacturing and subsectors in the total gross domestic product, salaries, wages, and remunerations. This section seeks to better understand the sectors that are now empirically analyzed. The second section presents the theoretical arguments that comprise the working hypothesis and reviews empirical literature that deals reflectively with the topic of employment demand, thus attempting to contextualize the findings. The third section presents the econometric methodology of the data panel, highlighting its relevance given the nature of the information and justifying its instrumentation, as well as discussing the main findings in light of the working hypothesis. Finally, the conclusions derived from the empirical work are presented.
Performance of labor indicators
This section expos the behavior of a set of labor market indicators such as employed personnel, salaries, wages, and remunerations with the interest of having an approach to the performance of the manufacturing industry and its subsectors, considering that they are relevant variables in the dynamics of said market. Although other variables are involved in the empirical analysis, they are omitted in this section for reasons of space and the focus is on those already referred to. According to information available from the National Institute of Statistics and Geography (INEGI for its acronym in Spanish), during the fourth quarter of 2015, 61.33% of Employed Personnel (EP) was located in the tertiary sector, while 24.71% and 13.37% in the secondary and primary sectors, respectively. This distribution by activity sectors shows that, in terms of employment, the national economy is practically tertiarized, noting a clear asymmetry between them. In this regard, Loria (2010) states that there has been a process of job destruction; a fact that undoubtedly implies challenges in terms of economic policy and the capacity to generate more jobs.
Figure 1 shows in more detail its evolution over time, but also in comparative terms. For example, from the first quarter of 2005 to the fourth quarter of 2015, around 60% of employed personnel are in the tertiary sector and less than 30% in the secondary sector. On the other hand, the primary sector is the most contracted in terms of its capacity to generate employment and the marked gap between the three sectors is visible. In this context, Ruiz (2005) states that in Mexico it was expected that the process of labor emigration from the primary sector to the urban centers would be absorbed by the industries, triggering a growth in the level of labor occupation. It is noted that the use of labor-saving technology probably explains the phenomenon under study.
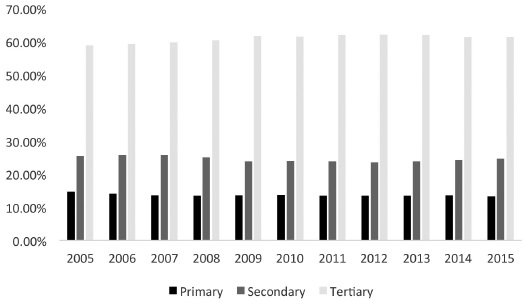
Source: own elaboration with data from the INEGI.
Figrue 1 Average total annual participation of the sectorial employed personal between 2005-2015.
In this context of large sector performance in the national economy, Ros (2005) empirically proves, for a group of Latin American countries, that the fall in unemployment has improved in those cases where exports and manufacturing employment have performed well. For his part, Moreno (2016) argues that having a manufacturing industry with export potential and the capacity to generate employment is urgent in order to achieve a viable and sustainable economic development. In other studies, such as that of Loria and Ramos (2007), it is argued that there is a need to implement an active industrial policy that encourages manufacturing sectors with a high added-value. Although Ruiz (2005) associates the loss of dynamism in the labor market with low investment and the use of labor-saving technologies, there are also other authors such as Peralta (2010), who have similar arguments regarding the explanation of a contracted labor market. In an analysis carried out by economic branches, Dussel (2003) points out that since 1988 the country has specialized in a set of export-oriented activities that are capital-intensive, which has led to a reduced process of employment generation. It is noted that non-tradable sectors have been the main activities that have generated employment. In this discussion, Samaniego (2014) points out that, in the first ten years of the 21st century, there has been a destruction of employment in net terms. It is pointed out that in 2009 the level of formal employment reached its lowest level compared to previous years.
In order to analyze in more detail the dynamics of the EP in the manufacturing industry, an analysis by subsector is carried out with the purpose of identifying contrasts between them. According to information from the Monthly Industrial Survey of the INEGI, the manufacturing sector is divided into 21 subsectors: 311 Food industry; 312 Manufacture of beverages and tobacco; 313 Manufacture of textile inputs and finishing of textiles; 314 Manufacture of textile products, except clothing; 315 Manufacture of clothing; 316 Tanning and finishing of leather and fur, and manufacture of leather products, fur, and substitute materials; 321 Wood industry; 322 Paper industry; 323 Printing and related industries; 324 Manufacture of petroleum and coal products and derivatives; 325 Chemical industry; 326 Plastics and rubber industry; 327 Manufacture of non-metallic mineral products; 331 Basic metal industries; 332 Manufacture of metal products; 333 Manufacture of machinery and equipment; 334 Manufacture of computer, communication, measuring, and other electronic equipment, components, and accessories; 335 Manufacture of accessories, electronic devices, and electricity generating equipment; 336 Manufacture of transport equipment; 337 Manufacture of furniture, mattresses, and blinds; and 339 Other manufacturing industries (INEGI, 2013).
The data reported in Table 1 show the percentage of EP by subsector with regard to the total of the manufacturing industry. The figures show the distribution of employment generated in a disaggregated manner and allow identifying sectors with greater and lesser potential to absorb work force from the economically active population, EAP. The subsectors that report the greater amount of EP, specifically in 2015, were 336 (Manufacture of transport equipment) with 22.31% and 311 (Food industry) with 18.77%, both amounting to a participation of 41.08%, followed by 334 (Manufacture of computer, communication, measurement, and other electronic equipment, components, and accessories) with 7.46% and all the others with very small ratios in relation to the total. In contrast, the subsectors with the lowest ratio in the same year were 321 (Wood industry) and 314 (Manufacture of textile products, except clothing) with 0.41% and 0.57%, respectively.
Table 1 Ratio of total personnel employed by subsector in the manufacturing industry.
| Period | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 |
|---|---|---|---|---|---|---|---|---|---|
| 311 | 18.95 | 19.49 | 21.50 | 20.64 | 20.02 | 19.71 | 19.73 | 19.01 | 3.53 |
| 312 | 4.18 | 4.22 | 4.65 | 4.27 | 4.05 | 3.90 | 3.68 | 3.55 | 1.63 |
| 313 | 2.20 | 2.04 | 2.04 | 1.96 | 1.87 | 1.80 | 1.76 | 1.67 | 0.57 |
| 314 | 0.71 | 0.67 | 0.66 | 0.60 | 0.57 | 0.57 | 0.55 | 0.57 | 4.19 |
| 315 | 6.04 | 5.75 | 5.72 | 5.26 | 4.91 | 4.59 | 4.56 | 4.36 | 1.86 |
| 316 | 2.01 | 1.95 | 1.99 | 2.03 | 2.01 | 2.03 | 2.00 | 1.90 | 0.41 |
| 321 | 0.57 | 0.56 | 0.56 | 0.51 | 0.48 | 0.47 | 0.45 | 0.43 | 2.03 |
| 322 | 2.09 | 2.16 | 2.29 | 2.28 | 2.21 | 2.15 | 2.13 | 2.08 | 0.85 |
| 323 | 1.00 | 1.02 | 1.05 | 1.04 | 1.04 | 0.97 | 0.91 | 0.87 | 0.83 |
| 324 | 0.86 | 0.90 | 0.95 | 0.94 | 0.93 | 0.91 | 0.90 | 0.89 | 4.35 |
| 325 | 4.90 | 4.93 | 5.28 | 5.11 | 5.02 | 5.02 | 4.78 | 4.60 | 5.59 |
| 326 | 5.31 | 5.38 | 5.27 | 5.56 | 5.60 | 5.66 | 5.64 | 5.55 | 2.81 |
| 327 | 3.11 | 3.12 | 3.07 | 3.02 | 3.00 | 2.96 | 2.90 | 2.85 | 2.47 |
| 331 | 2.28 | 2.35 | 2.38 | 2.37 | 2.45 | 2.50 | 2.51 | 2.50 | 5051 |
| 332 | 7.12 | 7.60 | 7.61 | 7.46 | 7.16 | 6.79 | 6.62 | 6.64 | 1088 |
| 333 | 2.58 | 2.64 | 2.46 | 2.66 | 2.82 | 2.86 | 2.93 | 2.94 | 7.46 |
| 334 | 8.90 | 8.62 | 7.91 | 8.24 | 7.94 | 7.59 | 7.61 | 7.34 | 4.87 |
| 335 | 5.59 | 5.39 | 5.11 | 5.23 | 5.05 | 4.81 | 4.70 | 4.84 | 22.31 |
| 336 | 15.93 | 15.46 | 13.69 | 14.93 | 17.02 | 18.88 | 20.22 | 21.57 | 1.39 |
| 337 | 1.69 | 1.67 | 1.59 | 1.55 | 1.43 | 1.40 | 1.39 | 1.37 | 4.49 |
| 339 | 3.98 | 4.08 | 4.21 | 4.35 | 4.41 | 4.43 | 4.37 | 4.46 | 100 |
| Total | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
Source: own elaboration with data from INEGI.
If the information is analyzed over time, it is possible to identify that the most outstanding subsectors in terms of employment are 326, 331, 333, 336, and 339, as these are the ones with the highest ratio of EP in 2015 but with respect to 2007. Within this group, subsector 336 (Manufacture of transport equipment) stands out, being the one that registers the greatest increase in the whole period. It is observed that 315 (Manufacture of clothing) is the one that exhibits the greatest decrease between both years.
A variable that is closely linked to the evolution of the labor market is the product of labor. According to McConell and Macpherson (2003), labor demand is a derived demand because it responds to the level of product or generation of services. In this sense, it is established that there is a positive relationship between the variations of the product and the level of employment of an economy. Economic growth brings about positive effects on the entire population, thus leading to a greater generation of jobs (Isaza and Meza, 2004). Therefore, an increase in output is expected to lead to an increase in the demand of workers, since producing larger production units would require a larger amount of labor input, especially in less specialized sectors. Within this framework, it is important to observe the evolution of the GDP in the manufacturing sector at the sub-sector level (see Table 2). The data make it possible to see the subsectors that have decreased their participation in the total GDP of the manufacturing industry and those that have had a greater impact. The case of subsector 311 (Food industry) stands out because it represents the largest amount of product in the whole period and, although it is not the one that generates the most employment, it has been one of the subsectors that has stood out. It is interesting to note that in the years when other sub-sectors were affected by the crisis, it maintained a growth rate. For example, in 2009 its ratio to total GDP was 24.23%. Also noteworthy is subsector 336 (Manufacture of transport equipment), which is characterized by the fact that it generates the most employment. It is also identified that subsector 325 (Chemical industry), has decreased its representation in the total GDP over the course of the study period.
Table 2 Ratio of the manufacturing industry GDP in 2008 prices (thousands)
| Period | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | Average |
|---|---|---|---|---|---|---|---|---|---|---|
| 311 | 21.80 | 22.27 | 21.23 | 22.70 | 22.17 | 21.84 | 21.82 | 21.10 | 20.84 | 2209 |
| 312 | 4.94 | 5.11 | 5.60 | 5.18 | 5.19 | 5.11 | 5.03 | 5006 | 5.22 | 5016 |
| 313 | 0.87 | 0.82 | 0.83 | 0.85 | 0.77 | 0.77 | 0.74 | 0.69 | 0.68 | 0.78 |
| 314 | 0.68 | 0.64 | 0.64 | 0.60 | 0.56 | 0.54 | 0.55 | 0.56 | 0.60 | 0.60 |
| 315 | 2.69 | 2.79 | 2.78 | 2.68 | 2.57 | 2.46 | 2.51 | 2.34 | 2.44 | 2.58 |
| 316 | 0.89 | 0.85 | 0.89 | 0.88 | 0.84 | 0.83 | 0.82 | 0.77 | 0.77 | 0.84 |
| 321 | 1.02 | 0.95 | 0.99 | 0.96 | 0.96 | 1.04 | 1.01 | 0.98 | 0.98 | 0.99 |
| 322 | 1.94 | 2.01 | 2.18 | 2.08 | 1.97 | 1.99 | 2.01 | 1.99 | 2.00 | 2.02 |
| 323 | 0.77 | 0.81 | 0.83 | 0.84 | 0.83 | 0.77 | 0.71 | 0.67 | 0.65 | 0.76 |
| 324 | 4.25 | 4.28 | 4.69 | 4.01 | 3.69 | 3.59 | 3.67 | 3.37 | 3.03 | 3.84 |
| 325 | 13.43 | 13.25 | 14.01 | 12.86 | 12.28 | 11.76 | 11.73 | 22.19 | 10.77 | 12.37 |
| 326 | 2.79 | 2.72 | 2.68 | 2.80 | 2.86 | 2.99 | 2.90 | 2.94 | 2.99 | 2.85 |
| 327 | 5.77 | 5.61 | 5.54 | 5.34 | 5.30 | 5.21 | 4.99 | 4.90 | 5.01 | 5.30 |
| 331 | 7.24 | 7.24 | 6.60 | 6.83 | 6.81 | 6.79 | 6.74 | 7.05 | 6.59 | 6.88 |
| 332 | 3.47 | 3.48 | 3.26 | 3.27 | 3.35 | 3.34 | 3.19 | 3.26 | 3.35 | 3.33 |
| 333 | 3.22 | 3.25 | 2.84 | 3.85 | 4.17 | 4.23 | 4.22 | 4.04 | 5.90 | 3.75 |
| 334 | 4.80 | 4.43 | 4.34 | 4.15 | 4.23 | 4.08 | 4.19 | 4.46 | 4.64 | 4.37 |
| 338 | 3.30 | 3.24 | 3.16 | 3.20 | 3.03 | 2.96 | 2.87 | 2.99 | 3.08 | 3.09 |
| 336 | 12.54 | 12.68 | 10.18 | 13.34 | 14.87 | 16.26 | 16.99 | 18.32 | 19.05 | 14.91 |
| 337 | 1.39 | 1.35 | 1.37 | 1.36 | 1.31 | 1.30 | 1.21 | 1.14 | 1.19 | 1.29 |
| 339 | 2.20 | 2.27 | 2.36 | 2.22 | 2.23 | 2.15 | 2.13 | 2.17 | 2.20 | 2.21 |
| Total | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
Source: own elaboration with data from the INEGI.
Other important variables closely linked to the labor market are salaries, wages, and remunerations by subsector. Table 3 shows the average of these variables by worker and sub-sector for the 2007 to 2015 period1. The first thing that is observed is precisely the difference between salaries and wages, which is very marked in practically all subsectors. It is important to consider that, in the case of salaries, we are basically talking about a specialized labor force while, in the case of wages, we speak of the personnel directly involved in production tasks and whose level of specialization and human capital stock is, on average, lower. In this sense, the information in Table 3 tries to illustrate the differences in income that exist in two different segments of the labor market of the manufacturing industry.
Table 3 Average wages, salaries, and remunerations per worker and sub-sector during the 2007-2015 period.
| Subsector | Wages | Salaries | Remunerations |
|---|---|---|---|
| 311 Food industry | 4.03 | 8.50 | 6.57 |
| 312 Beverages and tobacco industry | 4.94 | 9.35 | 8.65 |
| 313 Manufacture of textile inputs and finishing of textiles | 4.63 | 9.77 | 7.06 |
| 314 Manufeture of textile products, except clothing | 3.85 | 8.34 | 6.10 |
| 315 Manufacture of clothing | 3.70 | 8.21 | 5.29 |
| 316 Tanning and finishing of leather and fur, and manufacture of leather products, fur, and substitute materials | 4.20 | 8.19 | 6.14 |
| 321 Wood industry | 4.07 | 7.43 | 6.03 |
| 322 Paper industry | 5.80 | 14.46 | 10.66 |
| 323 Printing and related industries | 5.54 | 10.00 | 8.52 |
| 324 Manufacture of petroleum and coal products and derivatives | 17.18 | 33.06 | 32.90 |
| 325 Chemical industry | 10.03 | 18.03 | 17.41 |
| 326 Plastic and rubber industry | 4.42 | 11.37 | 7.69 |
| 327 Manufacture of non-metallic mineral products | 5.44 | 15.52 | 9.92 |
| 331 Basic metal industries | 7.15 | 16.11 | 12.88 |
| 332 Manufacture of metal products | 4.78 | 12.31 | 7.86 |
| 333 Manufacture of machinery and equipment | 6.10 | 18.33 | 11.90 |
| 334 Manufacture of computer, communication, measuring, and other electronic equipment, components, and accessories | 5.27 | 18.16 | 9.96 |
| 335 Manufacture of accessories, electrical devices, and electricity generating equipment | 4.92 | 18.31 | 9.50 |
| 336 Manufacture of transport equipment | 5.10 | 16.62 | 10.05 |
| 337 Manufature of furniture, mattresses, and blinds | 4.91 | 12.95 | 7.83 |
| 339 Other manufacturing industries | 5.38 | 18.31 | 9.63 |
Source: own elaboration with data from the EMIM (2007-2015).
The data indicate that subsector 324 (Manufacture of petroleum and coal products) records higher wage levels than the others, even the wage per worker exceeds the salary per worker in several subsectors with the exception of subsectors 324 (Manufacture of petroleum and coal products), 325 (Chemical industry), 333 (Manufacture of machinery and equipment), 334 (Manufacture of computer, communication, measuring and other electronic equipment, components, and accessories), 335 (Manufacture of accessories, electronic devices, and electricity generating equipment), and 339 (Other manufacturing industries). On the other hand, it is identified that the subsectors with the lowest wages are 314 (Manufacture of textile products, except clothing) and 315 (Manufacture of clothing), which also have the lowest amount of EP in the analysis period. Regarding remunerations, it is observed that subsector 324 is where the highest remunerations are registered per worker, linked again to the manufacture of petroleum and coal products, while the subsector that registers the lowest level in the indicator is 315, related to clothing.
Review of the literature: a theoretical and empirical perspective
The objective of this section veers in two directions: first, a presentation of the theory that underpins the research work and, subsequently, a review of empirical literature related to the study of employment demand. The literature related to international experience and the case of the Mexican economy is analysed, emphasizing the most important findings. The factors that are taken into account in the estimation work are framed in two theoretical aspects that allow establishing the link between employment demand and the dynamics of economic growth, remunerations, wages, and salaries. The working hypothesis discussed theorizes that the demand for labor in the manufacturing industry is more sensitive to changes in economic growth than to movements in wages. However, it is also argued that changes in labor productivity work against the level of manufacturing employment, since it generates a displacement effect derived from a bias possibly caused by technological change, which is more accentuated in the segment of workers.
The neoclassical approach states that the labor market operates an adjustment mechanism between demand and labor supply, since wages are flexible and do not face rigidities. This condition is what makes it possible to reach a state of equilibrium and to converge to a level of full employment. Furthermore, it is argued that the market is competitive, which means that wages are adjusted naturally without regulatory actions by the State. From this perspective, it is estimated that there is virtually no involuntary unemployment and that there can only be voluntary and temporary unemployment. It is, therefore, an approach that assumes that there are no rigidities that can impede the free adjustment of wages. It is stated that as wages fall, there will be a greater demand for labor. In Martínez et al. (2001) it is pointed out that when external agents intervene in some way, free competition in the labor market is not allowed and efficiency is lost. Therefore, the key variable that would explain the dynamics of employment would be wages, which is why it is considered to be a factor that explains the demand for employment.
On the other hand, Argoti (2011) explains that Keynesian theory arises in the context of the economic crisis of 1929, a period during which high rates of unemployment were registered that were not explained by adjustments in wages, but by a level of insufficiency of demand that was not capable of triggering a greater level of occupation. In this theoretical approach it is maintained that, in reality, wages are rigid and that conditions of perfect competition are not fulfilled, in addition it is indicated that the lack of flexibility in wages does not guarantee the automatic balance of the labor market, producing a situation where involuntary unemployment prevails. In this sense, it is stated that the intervention of the State in the economy, the fixing of a minimum wage, or the role of trade unions in collective bargaining processes are rigid factors that explain why the labor market does not automatically regulate itself, guaranteeing a condition of full employment. From the sphere of the normative economy, the Keynesian explanation regarding unemployment argues that it can be reduced to the extent of the role played by the State through a public expenditure policy affecting effective demand and, with it, the level of economic activity. Therefore, the relevant variable that would explain the demand for employment would be an indicator of demand or economic activity, with a positive relationship between the level of employment and the growth of the national product.
A review of specialized literature in the field of interest is carried out using the object of study as well as the previous theoretical outline as reference. Although employment may have different explanations and characteristics from one country to another and in different periods, it is important to highlight some empirical findings. For example, in Hamermesh (1993) it is affirmed that the employment-wage elasticity oscillates in the long-term within a range of -0.15 to -0.75; considering the value of -0.3 as a good result. In a more current review of labor demand for seven countries in Latin America and the Caribbean, including Mexico, Hamermesh (2003) himself explores some work that has been carried out on labor demand functions, in which product and wage are considered fundamental determinants. In general, it is observed that the employment-wage elasticities are negative, as would be expected according to the theory. One feature that is identified is that elasticity is greater in the case of skilled workers than unskilled workers, regardless of whether the data are aggregated, by establishment or by company.
In the case of Argentina, Lanteri (2013) investigates the main factors that explain the level of employment, particularly the employment-real wages link and the employment-long-term product elasticity. Using quarterly data for the 1994/03 to 2011/02 period, he estimates a vector error correction model (VEC) that allows him to estimate short-term dynamic adjustments and long-term relationships between variables. He finds that although economic growth and productive restructuring operate in favor of labor-intensive sectors, it does not appear to be sufficient to reduce unemployment.
Bencosme’s study (2008) estimates labor demand for the Dominican Republic for the 1991-2006 period using panel data. Its objective is to contrast whether the employment-product elasticity changed over time. It is found that there was a decrease in the employment-product elasticities in 2000 in the capital-intensive sectors. In the case of wages, it is noted that it has a significant and negative impact on employment; however, its elasticity is low in comparison with other countries. Medina et al. (2012) estimate a Panel-VAR model to analyze the main variables that influence the dynamics of labor demand in the Colombian manufacturing industry for the 1993-2009 and 2000-2009 periods. It is argued that Panel-VAR models may yield better results than a standard methodology that can present a possible simultaneous bias. It is determined that industrial (worker) employment presents a strong persistence and that the demand for employment is sensitive to shocks on the production of a company. It is also found that the response of worker employment to their wages is significantly greater than that found in the case of non-worker employment.
In the case of the research by Castillo (2006) a function of industrial labor demand is estimated in the metropolitan area of Cali, Colombia, for the 1995-2001 period; a panel data fixed effects model is executed on 17 sectors and a negative employment-wage elasticity and a positive employment-product elasticity are obtained. It is also determined that the generation of jobs is determined mainly by the product rather than by the wages and that the subsectors that generate more employment are those that use more technology.
For the case of Chile, Martínez et al. (2001) investigate possible structural changes in labor demand for the quarterly period 1986:1-2000:4; they estimate two models to evaluate a possible decrease in the relationship between employment and product. Using the co-integration methodology based on autoregressive vector models and carrying out structural change tests, it is demonstrated that the employment-product elasticity has not decreased, but there is evidence of instability in demand since there is a structural change for the year 2000.
In the work of Tangarife (2013), the factors that influence the demand for labor in the manufacturing industry in Colombia for the period 2002-2009 are analyzed. Based on a model with panel data, it is pointed out that the increase in GDP has not led to a proportional increase in employment. Special emphasis is put on the productivity factor that may be relevant when explaining the mismatch between employment and economic growth. The estimates show that wage growth has a positive effect on the increase in labor demand and add that, in recent years, there has been a difference in the impact of productivity on labor demand.
In the same line of analysis, Roberts and Skoufias (1997) estimate demand functions for worker and non-worker employment in manufacturing plants in Colombia using panel data. They find employment-product elasticities of 0.89 for non-worker employment and of 0.76 for the worker segment. The employment-wage elasticity is of -0.42 for non-worker employment and of -0.65 for worker employment. The results show that the employment-wage elasticity of unskilled work is greater than that of skilled work. The employment-product elasticity is higher for skilled work than for unskilled work. This means that unskilled workers are more sensitive to wage changes than skilled workers. It also shows that skilled workers are sensitive to changes in the product.
In the case of Mexico, there are also several studies that have focused on studying labor demand. Lechuga and Varela (2001) estimate a manufacturing employment function for the 1990-1998 period using quarterly data. Explanatory variables such as the GDP of the sector, labor productivity, and gross fixed capital formation as an investment proxy are considered. Estimates indicate that increases in productivity do not determine sustained increases in remunerations, but it is also claimed that they lead to a slow employment dynamic. It is also pointed out that investment has a positive but inelastic effect on employment behavior. Regarding labor, an additional function of wages is estimated and, in both exercises, the method of Ordinary Least Squares with autocorrelation correction is used. It is important to point out that in the employment function the wage variable is not used, and it is an estimate with strictly temporal information and at an aggregate level.
The work of Loria and Brito (2001) demonstrates the impact that foreign direct investment has on employment in 9 sectors of the Mexican economy. It estimates a manufacturing employment function that is determined by employment lagging in one period, manufacturing output, real average wages, intermediate and capital goods, and gross fixed capital formation. In another work by Ríos and Carrillo (2014), a demand function for skilled and unskilled employment in Mexico is estimated with annual data for 2005-2009. It has been shown that in periods of crisis, companies retain skilled work and tend to lay off unskilled workers, with the maquiladora and traditional industries being more affected.
For their part, Almonte et al. (2013) estimate an employment function for the state of Mexico with manufacturing industry data by economic activity for the 1999-2008 period. Based on a panel data methodology, they specify that manufacturing employment is a function of GDP, productivity, and wages. Their results suggest that increases in productivity cause decreases in the level of employment and that the variable with the greatest influence on employment is the product.
In the work developed by Félix and Castro (2015) a dynamic labor demand model is estimated for the industries integrated to the international value chains. Data from the automotive industry are used and through an error correction model they obtain a wage-labor demand elasticity of 0.54. They also estimate the speed of adjustment for any deviation from the long-term optimum and determine that any deviation is corrected in approximately 21 months. The results illustrate the dependence of much of the manufacturing employment of Mexico on labor costs, as well as on the evolution of the world market.
In the work by Fajnzylber and Maloney (2005) the demand for labor by types of employment is analyzed. Worker and non-worker employment demands are estimated using the Arellano and Bond methodology, which is based on the Generalized Method of Moments; employment-product elasticities are obtained according to the theory. Data from Colombia, Chile, and Mexico in the 1980s and early 1990s are considered for the purpose of analyzing changes in labor demand in the face of trade liberalization policies. In the case of Isaza and Meza (2004), the employment-wage elasticities for Mexico allow the authors to conclude that higher levels of trade openness lead to significant changes in labor markets and that international trade affects the relative demands of skilled and unskilled employment.
From the previous review it can be noted that the results vary according to the case study and the methodology used. For the case of Mexico, some findings highlight that the effect of the product level and wages agree with the theory; however, it can be seen that the magnitude of the effect varies according to the level of aggregation of the study. In this sense, the purpose of this work is to evaluate the effect of wages, product, and productivity in the demand of employment, considering the 2007-2015 period. It is important to point out that this work presents variants with respect to the work by Lechuga and Varela (2001). The first of said variants is that in this reference the variable of wages is not integrated in the econometric function; second, the estimates are based on a data structure of time series and the study focuses on the aggregate of the manufacturing industry. It is considered that studying industry at the subsector level and introducing the variables of wages, salaries, and remunerations can lead to different results in terms of their magnitude, but in the same direction, once the unobservable heterogeneity in the panel model is contemplated. Furthermore, estimates are made for two different segments of the labor market, specialized and non-specialized work, taking the workers and employees variables, respectively, from the Monthly Industrial Manufacturing Survey as proxies.
Estimation methodology and results
This section present the econometric methodology and uses an integrated database with information on 19 manufacturing subsectors in Mexico during the 2007-2015 period. The estimation of a model with panel data basically consists of following the same units of analysis or cross-section along a time horizon (Wooldridge, 2007). According to econometric theory, a model grouped with panel data is expressed as:
where i represent the individual or the study unit, t refers to the dimension of the information in time, α is a common intercept, β is a k parameter vector, xit is the i-th observation at moment t for the contemplated explicative k variables, and uit is a random error term. The total sample of the observations is given by N cross-sectional observations and T observations in time (Pindyck and Rubinfeld, 2001). Equation [1] represents a grouped regression with a common intercept for all elements i. A second estimation possibility is to consider that the intercept varies in each analysis unit, which would entail the specification of i. In this case there would be differential intercepts given by (α + αi). The term i indicates a dummy variable vector associated to each unit of the cross-sections.
The previous estimation entails the estimation of fixed effects in time, but with variants in i. A third possibility is to estimate the same model [1] but considering that the intercept changes both for each study unit i and in the time horizon, in which case the correct term is αit. The implication is that degrees of freedom may be reduced if the total number of observations is not very large. In any of the last two cases we speak of a fixed effects model and the value of α would represent the intercept of the reference category or base, in such a way that we would have in the regression N-1 dummy variables to avoid the problem of perfect multicollinearity. It is also possible to estimate a random-effects model based on y it = αi + βxit + μit, that is, instead of considering αi as a fixed effect, it would be defined as a random variable with a mean value equal to α and the value of the intercept for each unit of analysis would be defined as αi = α + εi with εi being a random error term with a mean equal to zero and constant variance (Gujarati and Porter, 2010). Taking into consideration the last equation and substituting terms, we have:
where the compound error is defined as υit = εi +μit . Therefore, equation [2] is re-expressed in the following manner:
The term υit is called compound random error and is composed of the component εi that expresses the random cross-sectional error, and μit is interpreted as the combination of the time series error and the cross-sectional error. From the previous theoretical specifications, a regression is estimated with a common intercept that serves as the basis for the subsequent estimation of a fixed and random effects model. In the specific case of a fixed effects over time model, but variants in each unit of analysis, models [4], [5], and [6] would include αi instead of α0, and in relation to the random effects model the term α0 would be replaced by α1= α + εi. The initial models would be:
The variable L1it expresses the total employed personnel of the manufacturing industry in thousands of workers, Yit is the real gross product of the manufacturing industry in 2008 prices. Pit expresses an index of real labor productivity in 2008 prices and Eit is the manufacturing exports. The variables L2it and L3it are the number of workers and employees, respectively. W1it is the remunerations of employed personnel, W2it expresses the wages of workers, and W3 it the salaries of employees, all three variables are expressed at constant 2008 prices. The information for these variables was obtained from the Monthly Industrial Manufacturing Survey. The real gross domestic product by subsector was obtained from the National Accounts System of the INEGI, while labor productivity was obtained from the same Monthly Industrial Manufacturing Survey following the methodology of INEGI (2012). Once the variables of the model have been defined, the aim is to find relations that are consistent with the theory, but also to corroborate the working hypothesis that the demand for employment is more sensitive to changes in the product than to changes in remunerations, salaries, and wages. In the case of productivity, a negative relationship is expected, as it is considered that it may have implications for a lower demand for labor and, above all, more notoriously in the segment of less qualified employees, such as workers. Exports are introduced with the purpose of capturing the effects that the external sector of the economy has on the labor market. It is clarified that net exports, which are the difference between exports and imports, are not included in the analysis. In reality, the balance of the trade balance or of the current account of the balance of payments is not considered. Since net exports are not considered, it is feasible to introduce them in the function of employment demand without generating problems of collinearity with the gross product.
Prior to the estimation and discussion of results, a diagnosis is made of the possible existence of collinearity between the variables. The results reported in Table 4 correspond to Pearson’s bivariate correlation coefficients, their magnitude and sign suggest that there is no severe problem of collinearity since in general the values are really low. The variables W1it, W2it, and W3it correspond to the remunerations, wages, and salaries of the total number of people employed, workers, and employees. The correlation between exports and the product can be considered relatively low as it does not approximate the unit.
Table 4 Correlation matrix.
| Yit | W1it | W2it | W3it | PRODit | EXPit | |
|---|---|---|---|---|---|---|
| Yit | 1.00 | -0.14 | 0.14 | -0.08 | -0.01 | 0.52 |
| W1it | -0.14 | 1.00 | - | - | -0.08 | -0.04 |
| W2it | 0.14 | - | 1.00 | - | -0.29 | 0.11 |
| W3it | -0.08 | - | - | 1.00 | 0.26 | 0.15 |
| PRODit | -0.01 | -0.08 | -0.29 | 0.26 | 1.00 | 0.18 |
| EXPit | 0.52 | -0.04 | 0.11 | 0.15 | 0.18 | 1.00 |
Source: own elaboration with data from the INEGI.
Once a multicollinearity problem has been ruled out, a diagnosis is made as to whether or not the level series have a unit root problem. In Table 5, the results of the Levine - Lin - Chu (LLC) unit root test are reported for panel data. The null hypothesis stipulates that there is unit root and the results suggest that in all cases it is rejected, because the p-value is less than 0.05. In this sense it is concluded that the series at level are integrated of order zero, I(0). Based on this, it is not necessary to differentiate them or to implement any co-integration methodology for panel data, since the standard estimation allows for a reliable statistical inference analysis. In addition, it is specified that to perform a co-integration analysis the series should be integrated in order one, I(1).
Table 5 Unit Root Test for Panel Data
| Level | Levin-Lin-Chu | ||
|---|---|---|---|
| Notation | Variables | Statistic | Prob. |
| L1 it | Employed Personnel | -8.2847 | 0.0000 |
| L2it | Workers | -9.1587 | 0.0000 |
| L3it | Employees | -6.2570 | 0.0000 |
| W1it | Remunerations | -4.4103 | 0.0000 |
| W2it | Wages | -4.9846 | 0.0000 |
| W3it | Salaries | -6.0176 | 0.0000 |
| Yit | Manufacturing GDP | -13.488 | 0.0000 |
| PRODit | Productivity | -1.8796 | 0.0301 |
| EXPit | Exports | -4.7562 | 0.0000 |
| Null Hypothesis: unit root | |||
| Newey-West automatic bandwidth selection and Bartlett Kernel | |||
Source: own estimates with data from the INEGI.
Once the above has been determined with regard to the integration order of the series of the model, we proceed to carry out the estimations for the total employed personnel and subsequently for the segment of workers and employees. For each of the three groups, four panel models are estimated: 1) common intercept model, 2) model with fixed effects in t and variants in i, 3) model with fixed effects in i but variants in t, and 4) a model with random effects (see Table 6) The corresponding tests to select the ideal model are also illustrated. For example, statistic F is estimated to choose between a model with a common intercept or a grouped regression and a model with fixed effects. The Hausman test is also carried out to determine which model is the most suitable between the fixed-effect and random-effects models. The results of the Breusch - Pagan contrast are also reported to choose between a common intercept model and the random-effects model. In all panel regressions, robust standard errors are obtained for the purpose of obtaining reliable results.
Table 6 Estimation results.
| Total Employed Personnel | Workers | Employees | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L1it | L2it | L3it | ||||||||||
| Variable | M1 | M2 | M3 | M4 | M1 | M2 | M3 | M4 | M1 | M2 | M3 | M4 |
| C | 12.52 | 5.521 | 12.36 | 5.459 | 23.15 | 5.216 | 23.22 | 5.322 | -1.017 | 7.457 | -5.466 | 6.777 |
| 5.43 | 0.928 | 14.57 | 0.660 | 4.123 | 0.852 | 9.331 | 0.765 | 2.771 | 0.558 | 5.939 | 0.642 | |
| Yit | 0.540 | 0.615 | 0.543 | 0.620 | 0.499 | 0.664 | 0.500 | 0.653 | 0.780 | 0.454 | 0.795 | 0.538 |
| 0.009 | 0.023 | 0.173 | 0.020 | 0.010 | 0.027 | 0.165 | 0.023 | 0.008 | 0.060 | 0.124 | 0.050 | |
| W1it | -2.35 | -0.075 | -2.526 | -0.086 | ||||||||
| 1.165 | 0.160 | 2.852 | 0.178 | |||||||||
| W2it | -4.278 | -0.199 | -4.359 | -0.224 | ||||||||
| 0.807 | 0.120 | 1.171 | 0.175 | |||||||||
| W3it | -0.408 | -0.487 | 0.265 | -0.504 | ||||||||
| 0.582 | 0.103 | 1.385 | 0.114 | |||||||||
| PRODit | -0.032 | -0.447 | 0.169 | -0.454 | -0.501 | -0.467 | -0.438 | -0.467 | 0.435 | -0.373 | 0.711 | -0.423 |
| 0.071 | 0.060 | 0.659 | 0.063 | 0.192 | 0.066 | 0.612 | 0.070 | 0.072 | 0.066 | 0.668 | 0.071 | |
| EXPit | 0.307 | 0.127 | 0.305 | 0.134 | 0.355 | 0.144 | 0.355 | 0.153 | 0.159 | 0.101 | 0.151 | 0.106 |
| 0.003 | 0.011 | 0.083 | 0.010 | 0.007 | 0.009 | 0.079 | 0.009 | 0.008 | 0.013 | 0.080 | 0.020 | |
| Adjusted R2 | 0.83 | 0.90 | 0.82 | 0.70 | 0.83 | 0.90 | 0.82 | 0.72 | 0.84 | 0.99 | 0.84 | 0.52 |
| Test F = 655.8 prob. 0.0000 | Test F = 655.5 prob. 0.0000 | Test F = 422.77 prob. 0.0000 | ||||||||||
| Ho: β0i = β0 (common intercept) | Ho: β0i =β0 (common intercept) | Ho: β0i = β0 (common intercept) | ||||||||||
| Test F = 0.494 prob. 0.858 | Test F = 0.248 prob. 0.980 | Test F = 1.058 prob. 0.395 | ||||||||||
| Ho: β0t = β0 (common intercept) | Ho: β0t = β0 (common intercept) | Ho: β0t = β0 (common intercept) | ||||||||||
| Hausman Test, Chi-Sq = 6.85 prob. 0.143 | Hausman Test, Chi-Sq = 12.80 prob. 0.012 | Hausman Test, Chi Chi-Sq = 13.87 prob.0.007 | ||||||||||
| Ho: Ɛi are not correlated with Xit | Ho: Ɛi are not correlated with Xit | Ho: Ɛi are not correlated with Xit | ||||||||||
| Test Breuch - Pagan, LM = 618.67 prob. 0.000 | Test Breuch - Pagan, LM = 2.826 prob. 0.000 | Test Breuch - Pagan, LM = 587.24 prob 0.000 | ||||||||||
| Ho: σ2εi=0, random effects equal to zero | Ho: σ2εi=0, random effects equal to zero | Ho: σ2εi=0, random effects equal to zero | ||||||||||
| Selection of the model | Selection of the model | Selection of the model | ||||||||||
| yit = α + βxit + Ɛi + μit | yit = αi + βxit + μit | yit = αi + βxit +μit | ||||||||||
| (M1): Grouped regression with a common intercept (White cross-section standard error & covariance). | ||||||||||||
| (M2): Fixed effects, cross-section dummy variables (White cross-section standard error & covariance). | ||||||||||||
| (M3): Fixed effects, dummy variables in the period, (White period standard error & covariance). | ||||||||||||
| (M4): Random effects, (White period standard error & covariance | ||||||||||||
Source: own elaboration with data from the INEGI.
The estimation results reported in Table 6 correspond to four different specifications from which the most appropriate standard model is chosen based on fundamental econometric tests. In the particular case where the dependent variable is the total employed personnel, the restricted F test, which contrasts the common intercept model with that of fixed-effects over time, suggests that the latter is better. However, Hausman’s test, which contrasts the fixed-effects over time model and the random-effects model, indicates that the most appropriate model is the random-effects model. The Breusch - Godfrey test also points out that the random effects model is better than the common intercept model, since the hypothesis that the effects are zero is rejected. In this sense, the regression that best explains L1it corresponds to the M4 random-effects model.
The estimates suggest that the elasticity of labor-product demand is positive, and the elasticity of real remunerations-labor demand is negative. In both cases, the sign of the parameters is determined to be consistent with Keynesian and neoclassical theory, respectively. However, it is appropriate to point out that the evolution of GDP has a greater impact on employment than the reduction of remunerations. Moreover, the latter variable is not statistically significant at a standard of 95% confidence level. The coefficient of the elasticity of employment-product demand is 0.62, indicating that if the gross domestic product increases by 1% the demand for employment will increase on average by 0.62%. Although the relationship is less than proportional, it is admitted that the sensitivity of employment is marked with respect to the level of economic activity. Therefore, any effort to generate employment must necessarily involve actions, strategies, plans, and programs aimed at strengthening economic growth. A country with low growth rates will not only face restrictions to boost the demand for formal employment but will also create the conditions for continued growth in labor informality, poverty levels, and inequality in household income.
For the same segment of total employment demand (workers and employees), it is found that labor productivity has a negative effect on labor demand. The coefficient of -0.454 suggests that if productivity increases by 1%, total employment demand will decrease by 0.45%. Although said magnitude is lower in absolute value than that reported for the gross domestic product, it is recognized that it shows an important sensitivity before the percentage changes in productivity. In this context, it is pertinent to formulate the question of whether productivity increases are good or bad. It is argued that productivity improvement is good, as it can contribute to triggering long-term economic growth and is also a factor of competitiveness in an environment of internal and external competition. However, it should be noted that the workers who constitute the unskilled labor force have a greater weight in the total employed personnel. Therefore, it is inferred that if labor productivity improves, what fundamentally decreases is the demand for workers, given the relative weight they have in the demand for total employment. For this and other reasons previously explained, it is justified to estimate labor demand functions for the two segments of the labor force (workers and employees). It would be understood that the negative effect of productivity on the demand of total employment would be explained in part, so it has been discussed in the literature and has to do with a process of biased technological change that does not favor the demand of less qualified work.
Concerning exports, it is also determined that it is a relevant variable. Although it is specified that the magnitude of its coefficient is lower than that of gross domestic product and productivity, it reveals that if the exports of the manufacturing industry increase by 1%, the total employment demand would grow by 0.134%. From this perspective, it is proposed that the dynamics of the external sector are fundamental to explain the demand for labor. Having a strong export sector not only strengthens the aggregate demand of an economy or can become an important source of foreign exchange generation but can also boost employment in a situation where the domestic market may be contracted. Therefore, promoting the external sector by subtracting imports from the domestic market or vice versa should not be a mutually exclusive process or a dilemma in the field of economic policy, but rather two complementary and indispensable processes in a strategy for generating employment in the medium and long term.
In the case of the worker segment, the respective econometric tests were also performed to decide which type of panel model is the most appropriate to explain the L2 it variable. The restricted F test with fixed time effects but variants in the cross-sectional unit suggests that the fixed-effects model is better than the common intercept or grouped regression model. For its part, Hausman’s test suggests that the null hypothesis that states that random effects are not correlated with the X variables is rejected, thus determining that it is better to estimate fixed effects than random effects. Finally, the Breusch - Pagan contrast demonstrates that a random-effects model is better than a fixed-effects model. Once evaluating these tests as a whole and the significance of the variables and the model, the M2 model that corresponds to a specification of fixed effects with dummy variables for the cross-sections (see Table 6) was chosen. It can be seen that of all the coefficients, the elasticity of labor-product demand is the highest, being equal to 0.66. As in the previous model, it is suggested that the real growth of the Mexican economy is an important factor that explains the demand for labor (workers). It is emphasized that it is essential that the real gross domestic product increases if the demand for less specialized labor is to be increased, pointing out that the growth of economic activity should surely be registered in those sectors that have a stronger link to traditional activities that do not necessarily demand specialized labor or that exhibit less technological development. In this case, the variables related to labor costs are no longer total remunerations, but real wages, whose coefficient is -0.199, which suggests that if they are increased by 1% the demand for workers would decrease by 0.199%, clarifying that it is a series that is statistically significant only at 90% confidence, but much more relevant than in the case of total employed personnel.
Regarding productivity, the fixed effects model reports an elasticity of -0.46, indicating that if it increases by 1%, then the demand for workers in the manufacturing industry will decrease by an average of 0.46%. This information is relevant in the sense that the improvements in productivity are not accompanied by a greater demand for workers, but on the contrary, the efforts made in the different sectors will have on average a negative effect on the demand for less qualified labor. Reversing the effect, of course, would not discourage productivity, but rather, strengthen the levels of general training and specialization of the workers, so that their performance and demand is consistent with improvements in labor productivity. In the case of manufacturing exports, a coefficient of 0.144 is obtained, which shows that if they grow by 1%, then the response of the demand for workers will increase by 0.144%. Although it is the variable that reports the smallest magnitude of the set of coefficients, it is also encouraging to know that an improvement in manufacturing exports can translate into a positive growth in the demand for less skilled jobs, although it would be expected that the external sector would have a more noticeable effect on the demand for skilled labor, as confirmed by the following results.
Finally, with regard to the role of employees in approximating what can be considered demand for skilled labor, the overall analysis of statistics and econometric tests suggests that the ideal specification for modeling the L3 it variable is a time-fixed effects model and variant in each cross-sectional unit, M2. The results of this regression stand apart from the two models previously chosen in a fundamental aspect, this being that all variables are relevant. Salaries as opposed to remunerations and wages are statistically significant at 95% confidence level and, in addition, their coefficient of -0.487 is much higher than that of the total employed personnel of -0.086 and of the workers of -0.199. This means that if the salaries in the manufacturing industry increase by 1%, on average the demand for employees will decrease by 0.487%. In this framework of analysis, it is observed that labor costs do play an important role in the labor demand of the manufacturing industry. Since this is a more specialized segment, it is inferred that higher salaries can reduce the competitiveness of the industry and thereby reduce the potential demand. However, it should be emphasized that a strategy of competitiveness based on the long term in low labor costs is not desirable, on the contrary, other aspects related to product differentiation should be improved, or a higher level of skills should be encouraged, thus considering the possibility of paying efficiency wages. Another aspect that derives from the results is that contemplating the three estimates referenced (total personnel, workers, and employees), the increase in salaries has a smaller effect on the reduction of employees than that of remunerations and wages on the total employed personnel and workers, respectively. This would be understood as the degree of specialization represented by each segment and, above all, that of the workers and employees in a disaggregated manner.
Regarding the variable of economic activity measured through the real gross domestic product of manufacturing, it is significant and has a positive sign. The coefficient indicates that if the GDP increases by 1%, the demand for specialized labor (employees) will increase by 0.454%. However, it is worth noting that unlike the two previous estimates, for the case of total employed personnel and workers, the effect of the economic growth of manufacturing is lower than that registered in the previous cases. The elasticity of the demand for employment-manufacturing exports suggests that if export activity increases by 1%, then the demand for specialized labor will increase by an average of 0.10%. In this case, there is a close relationship between the performance of the manufacturing export sector and employment with a higher degree of specialization, a link that is not entirely surprising considering that the external sector is precisely the demand for greater labor skills. For its part, the productivity variable continues to have a negative impact on employment demand, although less than that reported in the previous two regressions. That is to say, it is determined that productivity improvements not only reduce the demand for workers, but also the demand for employees, but to a lesser extent, as would be expected, since more productive manufacturing activities somehow demand a more specialized workforce.
As a reflection derived from the empirical contrast, it is necessary to consider that the choice of each of the models was not made arbitrarily, but rather it was based on evidence suggested by the standard econometric theory. It is stressed that the purpose of running different regressions for each segment of the labor market responds to the interest of evaluating different estimation possibilities and subjecting them to conventional tests that allow discrimination given the nature of the data. In the three case studies, the most restrictive panel estimate has been discarded, which assumes that intercepts are constant with respect to sub-sectors and time. On the other hand, it is necessary to consider that the dimension of the information does not strictly correspond to a macro-panel; therefore, avoiding a reduction in the degrees of freedom is desirable in order to not weaken the process of estimation and statistical inference. For this reason, differential intercepts are only contemplated in fixed-effect models (workers and employees). In the case of total employed personnel, which is estimated to be a random effects model, the intercept for each unit of analysis would be given by an average intercept value plus a random error term. Therefore, in the estimated models, changes in the intersection coefficients have been considered through additive dummy variables that yield differential intercepts. In the case of slope coefficients, they have remained constant, mainly due to the lack of a macro-panel. To have one would imply including interactive dummy variables, which would yield numbers of differential slope coefficients, with the implication that the degrees of freedom NT -K would be reduced too much, in addition to generating a possible problem of multicollinearity as postulated by the panel data theory (Wooldridge, 2007).
Conclusions
The manufacturing industry has proven to be one of the most important sectors of the Mexican economy and represents an important part of the total product and employment. Since the opening of the national economy, the performance of the manufacturing industry has become a preponderant sector. However, it is also observed that its participation in the total economic activity and employment generated has been exhibiting a less dynamic evolution. It should also be considered that it has been a sector that has been significantly affected by the aftermath of the 2008-2009 crisis in the United States, which undoubtedly had far-reaching international repercussions.
It could be said that a process of technological change that affects productivity improvement could lead to lower demand for workers. However, the results suggest that the adverse effect occurs with greater notoriety in the segment of the labor force than in that of the employees, who are considered to have a greater degree of specialization. In this sense, the need for the segment of workers to improve their levels of labor productivity, in order to be less affected by the evolution of technical change and what it implies in terms of productivity in the labor market, is noted. It is also observed that the growth of total employed personnel, as well as the set of workers and employees separately, is very sensitive to the behavior of the gross domestic manufacturing product as an indicator of economic activity. It is determined that domestic economic activity is a fundamental determinant of employment demand, even more than wage levels as the standard theory assumes. In this sense, the challenges that the Mexican economy must face in order to achieve greater economic growth within the manufacturing industry are urgent, which implies not only diversifying the external market, but also boosting the domestic market through greater productive investment, both public and private.
In contrast, it was determined that real remunerations, wages, and salaries, although showing a coefficient in line with what was expected with respect to their relationship to total employed personnel, workers, and employees, are not statistically relevant variables in the model, with the exception of the case of employees. This result suggests that the evolution of employment is not essentially determined by the costs of the labor force, or by those actions of flexibilization of the labor market. On the contrary, it is proven that a labor market in full recovery is more linked to the degree of economic performance. Therefore, in order to achieve higher employment rates in the manufacturing industry, it is essential to have a higher rate of economic growth in the manufacturing sector and, in general, to improve the well-being of households through consumption and access to greater infrastructure that provides better public services. These results should lead to reflection on the challenges of stimulating economic growth. These can be situated at national, regional, and local levels. At the different levels of public administration, business development plans that favor economic activity should be developed and monitored, taking into consideration local and regional productive vocations, thus taking advantage of and developing innovation processes and human capital assets. Fostering domestic consumption and productive investment together with the development of public infrastructure can create conditions that will trigger the business environment, medium and long-term investment plans, and sectoral competitiveness. All of these are indispensable elements for improving economic activity and fostering the growth of formal and quality employment. Finally, it should be noted that manufacturing exports are also a variable that triggers employment and that strengthening the domestic market does not discourage export activity, on the contrary, it continues to promote it and see both processes as complementary.
REFERENCES
Almonte, L. Carbajal, S. Y. Valverde, V. C. (2013). El empleo manufacturero en el estado de México: estimación por división de actividad económica, 1999-2008. Economía UNAM, vol. 10, núm. 29, 56-73. https://doi.org/10.1016/s1665-952x(13)72195-9 [ Links ]
Argoti (2011). Algunos elementos sobre la teoría clásica del empleo y la versión keynesiana. Tendencia, revista de la Facultad de Ciencias Económicas y Administrativas. Universidad de Nariño, vol. XII, no. 2, segundo semestre. Disponible en: https://dialnet.unirioja.es/servlet/articulo?codigo=3854586 y consultado: 05/03/2016. [ Links ]
Banco Mundial (2012). Informe sobre el desarrollo mundial 2013. Panorama general: Empleo. Washington, DC: Banco Mundial. Licencia: Creative Commons Atribucion CC BY 3.0. Disponible en: http://siteresources.worldbank.org/EXTNWDR2013/Resources/8258024-1320950747192/8260293-1322665883147/Overview_Spanish.pdf y consultado: 9/9/2015. [ Links ]
Bencosme, G. P. (2008). Estimación de la demanda por trabajo en la economía dominicana. Unidad Asesora de Análisis Económico y Social, Secretaria de Estado de Economía, Planificación y Desarrollo, texto de discusión no. 12, 1-20. Disponible en: http://economia.gob.do/despacho/unidad-asesora-de-analisis-economico-y-social/textos-de-discusion/ y consultado: 24/11/2015. [ Links ]
Castillo, C. M. (2006). Demanda laboral industrial en el área metropolitana de Cali: Un análisis entre 1995 y 2001. Revista Sociedad y Economía, núm. 11, julio-diciembre, 40-64. Disponible en: http://www.redalyc.org/pdf/996/99616177002.pdf y consultado: 07/10/2015. [ Links ]
Dussel, E. (2003). Características de las actividades generadoras de empleo en la economía mexicana (1988-2000). Investigación Económica, vol. LXII, núm. 243, enero-marzo, 123-154. Disponible en: http://www.redalyc.org/articulo.oa?id=60124304 y consultado: 10/03/2016. [ Links ]
Fajnzylber, P. y Maloney, W. (2005). Labor demand and trade reform in Latin America. Journal of International Economics, 66, 423-446. https://doi.org/10.1016/j.jinteco.2004.08.002 [ Links ]
Félix, G., y Castro, L.D. (2015). Demanda laboral en las industrias integradas a cadenas de valor internacionales. Un análisis regional con panel dinámico no estacionario para el caso de México. Centro de Investigaciones Socioeconómicas. Universidad Autónoma de Coahuila-México. Disponible en: https://www.researchgate.net/publication/291829419_Felix-Castro2015_ICRS y consultado: 17/03/2016. [ Links ]
Hamermesh, D. (1993). Labor Demand. Princeton, Princeton University Press, 1993. [ Links ]
Hamermesh, D. S. (2004). Labor Demand in Latin America and the Caribbean: What Does It Tell Us? In Law and employment: Lessons from Latin America and the Caribbean, cords. James J. Heckman y Carmen Pages. Chicago Scholarship Online. https://doi.org/10.7208/chicago/9780226322858.003.0012 [ Links ]
Hsiao, C. (2003). Analysis of panel data. Cambridge University Press. 2nd ed., United Kingdom. [ Links ]
INEGI (2013). Encuesta Mensual de la Industria Manufacturera 2013. Instituto Nacional de Estadística y Geografía. México, INEGI. [ Links ]
INEGI (2012). Cálculo de los índices de productividad laboral y del costo unitario de la mano de obra. Instituto Nacional de Estadística y Geografía. México. [ Links ]
Isaza, J. y Meza, C. (2004). La demanda de trabajo Teoría y evidencia empírica para el caso colombiano. Revista Equidad y Desarrollo, núm. 2. Julio, 35-64 https://doi.org/10.19052/ed.392 [ Links ]
Lanteri, L. (2013). Determinantes económicos del nivel de empleo. Alguna evidencia para Argentina. Ensayos Revista de Economía, vol. XXXII, núm. 1, 73-100. Disponible en: https://ideas.repec.org/a/ere/journl/vxxxiiy2013i1p73-100.html y consultado: 2/03/2016. [ Links ]
Lechuga, M. J. y Varela, O. M. (2001). Empleo Manufacturero en México, 1990-1998. Análisis económico, vol. XVI, núm. 33, segundo semestre, 2001, 215-234. Disponible en: http://www.redalyc.org/pdf/413/41303308.pdf y consultado: 26/02/2016. [ Links ]
Loría, E. (2010). Sobre el lento crecimiento económico de México. Una explicación estructural. Investigación Económica, vol. LXVIII, 270, octubre-diciembre de, 37-68. http://dx.doi.org/10.22201/fe.01851667p.2009.270.16681 [ Links ]
Loría, E., & Brito, L. (2005). El impacto de la inversión extranjera directa en el empleo sectorial en México: Un análisis de prospección. Análisis económico, vol. XX, núm. 44, segundo cuatrimestre, 5-34. Disponible en: http://www.redalyc.org/pdf/413/41304402.pdf y consultado: 24/02/2016. [ Links ]
Pindyck R. y Rubinfeld D. (2001). Econometría: modelos y pronósticos. Cuarta edición, editorial Mc Graw-Hill. México D.F. [ Links ]
Martínez, C. Morales, G. y Valdés, R. (2001) Cambios Estructurales en la demanda por trabajo en Chile. Economía Chilena, vol. 4, núm. 2, 5-25. Disponible en: https://dialnet.unirioja.es/servlet/articulo?codigo=965028 y consultado: 09/09/2015. [ Links ]
McConnell C. Brue S. y Macpherson D. (2003). Economía laboral, Sexta Edición. (Contemporary Labor Economics) Traducción al español de Esther Rabasco y Luis Toharia, McGraw-Hill, Madrid. [ Links ]
Medina, C.; Posso, C.; Tamayo, J. y Monsalve, E. (2012). Dinámica de la demanda laboral en la industria manufacturera colombiana 1993-2009: Una estimación panel VAR. Borradores de economía Núm. 694. Banco de la Republica. Disponible en: http://www.banrep.gov.co/docum/ftp/borra694.pdf y consultado: 07/10/2015. [ Links ]
Moreno, B. J. C. (2016). Política macro e industrial para un cambio estructural y crecimiento: gran pendiente de la economía mexicana. Revista problemas del desarrollo. Revista latinoamericana de economía, vol. 47, núm. 185, jun, 59-80. https://doi.org/10.1016/j.rpd.2015.10.013 [ Links ]
Peralta, E. (2010). Perspectiva Laboral en Mexico 2008-2030. Comercio Exterior, 60(3), 195-208. Disponible en: http://revistas.bancomext.gob.mx/rce/magazines_en/123/2/195_Peralta_LABORAL.pdf y consultado: 25/02/2016. [ Links ]
Ríos J. y Carrillo S. (2014). El empleo calificado y no calificado en la manufactura de México ante la crisis de 2009. Economía, Sociedad y Territorio, vol. XIV, núm.46, septiembre-diciembre, 687-714. https://doi.org/10.22136/est002014393 [ Links ]
Roberts M. y Skoufias E. (1997). The Long-Run Demand for Skilled and Unskilled Labor in Colombian Manufacturing Plants. The Review of Economics and Statistics, 79(2), may, 330-334. https://doi.org/10.1162/003465397556700 [ Links ]
Ros, J. (2005). El desempleo en America Latina desde 1990. CEPAL Serie estudios y perspectivas. Unidad de desarrollo economico. Serie Estudios y Perspectivas, núm 29, 1-34. Disponible en: https://repositorio.cepal.org/handle/11362/4949 y consultado: 13/03/2015. [ Links ]
Ruiz, D. C. (2005). El reto del empleo en Mexico. Comercio Exterior, 55(1), 6-15. Disponible en: http://revistas.bancomext.gob.mx/rce/magazines/74/2/RCE.pdf y consultado: 10/09/2015. [ Links ]
Pindyck R.S. y Rubinfeld D.L. (2001). Econometría, modelos y pronósticos. Cuarta edición, Mc Graw Hill, 1-639. [ Links ]
Samaniego, B. N. (2014). La participación del trabajo en el ingreso nacional: el regreso a un tema olvidado. Economiaunam, 11(33), 52-77. https://doi.org/10.1016/s1665-952x(14)72181-4 [ Links ]
Tangarife, Carmen Lucía, (2013). La economía va bien pero el empleo va mal: factores que han explicado la demanda de trabajo en la industria colombiana durante los años 2002-2009. Perfil de Coyuntura Económica, núm. 21, enero-junio, 2013, pp. 39-61 Universidad de Antioquia Medellín, Colombia. Disponible en: http://www.redalyc.org/pdf/861/86129819003.pdf y consultado: 16/09/2015. [ Links ]
INEGI (2013). Síntesis Metodológica de la Encuesta Mensual de la Industria Manufacturera. [ Links ]
Wooldridge M. Jeffrey (2007). Introducción a la econometría, un enfoque moderno. 2da edición, editorial Thomson. España. [ Links ]
1According to the EMIM (2013), wages are the payments made by the establishment to remunerate the ordinary and extraordinary work of the workers, before any deduction withheld by the employers, while salaries are the payments made by the establishment to remunerate the ordinary and extraordinary work of the employees. Remunerations are payments and contributions before any deduction, to remunerate the work of the staff, whether this payment is cal culated on the basis of a working day or for the amount of work performed (piecework), or by means of a basic wage that is complemented with commissions for sales or other activities. Salaries, wages, and remunerations are recorded in thousands of pesos (MXN).
Received: October 31, 2016; Accepted: June 07, 2018











 text in
text in 


