1. Introduction
A spherical object observed at a distance in its longitudinal (||) and transversal (⊥) dimensions, should provide a test of different cosmological models, as first proposed by Alcock & Paczyński (1979). The Alcock-Paczyński parameter, hereafter AP, basically the ratio of || to ⊥ dimensions, takes a value of one at redshift zero, and increases with z with a strong dependence on the value of the cosmological parameters that make up the Hubble function, introducing a cosmological distortion to the large scale structure observations. This apparently simple comparison is, however, greatly complicated by several factors. First, real-space measurements are not directly attainable and one has to rely on redshift-space. Then, if the proposed object consists of a cluster of quasars or galaxies, or a statistical ensemble of such, proper motions of its constituents (either derived from gravitational collapse or virialized conditions) distort redshift-space measurements causing a degeneracy problem (e.g., Hamilton 1998). On cosmological scales, clusters of galaxies or quasars are among the simplest geometric structures that one may conceive. Even if single clusters should have non-spherical or filamentary structures, those should be randomly oriented. As we probe more distant clusters, observations become biased towards brighter and widely separated members, and the numbers become statistically insignificant. A superposition of many such clusters may reduce the problem while retaining spherical symmetry. For more than 40 years the two-point correlation function (2PCF), and its Fourier transform, the power spectrum, have been fundamental tools in these studies (e.g., Peebles 1980).
Overdense clusters or associations separate from the Hubble flow due to their own gravity, which results in peculiar velocities of its members that distort redshift-space observations. When gravitational fields are small, velocities are well described by the linear theory of gravitational collapse (Peebles 1980). In the study of these clusters, the 2PCF was initially conceived as a single entity ξ that could be evaluated in either real (r−) or redshift (s−) space (Peebles 1980). Davis & Peebles (1983) even mentioned that when observing the local universe, if the peculiar velocities were relatively small, s−space would directly reproduce r−space and one would have ξ(r)= ξ(s). That should be the case for distant objects, although one should be careful not to mix up the notions of distant from each other and distant from the observer. In the case of the CfA Redshift Survey (e.g., Huchra et al. 1983), as described in Davis & Peebles (1983) peculiar velocities were significant, and the authors chose to go from real ξ(r) to observable ξ(s) by means of a convolution with a pair-wise velocity distribution, tailored to approach the Hubble flow at large distances, known as the streaming model. The convolution integral would at the same time convert r−space to s−space coordinates. However, the same function ξ would be obtained as a result of the convolution of ξ with a function of velocity, which constitutes an inconsistency. Later on, Kaiser (1987), hereafter K87, showed that gravitationally induced peculiar velocities by gravitational collapse of overdense structures in the linear regime produced a power spectrum P
(s)
for s−space different from the one P
(r)
for r−space, that is, two different functions for the power spectrum. Both are, however, functions of the r−space Fourier frequency k. Then, while P
(r)
(k) is a spherically symmetric function, P
(s)
(k) shows an elongation along the line of sight (LoS) direction. Later on, Hamilton (1992) translated these results to configuration space obtaining the 2PCF in its two flavors: ξ(r)(r) and ξ(s)(r). Again ξ(r)(r) is symmetric and the possibility of a power-law r
−γ is considered, as had been historically accepted (e.g., Peebles 1980, who favored γ = 1.8 ). Also, in perfect agreement with K87, ξ(s)(r) shows a squashing along the LoS direction. Hamilton (1998) presented in great detail the assumptions that led to his results. He started by defining selection functions n
(r)
(r) and n
(s)
(s) for r−space and s−space and by numerical conservation obtained a complicated high order expression (his equation 4.28) for the density contrast δ(s). From that one can obtain the 2PCF, but a series of approximations are needed (the linear case) to reduce the right hand side of the equation and to obtain his equation 4.30 for δs(s). Then, he introduced one extra assumption, δs(r) = δs(s), which is not justified by the linear approximation. This changes the left hand side of the equation directly to δs(r). It may be argued that this approximation is valid in the distant case mentioned above. Consequently, one could easily write ξ(s)(s) in place of ξ(s)(r), shifting between one form and the other as needed. That is an imperative because observable 2PCF are inevitably obtained in s−space.
Since then many authors have tried the Kaiser linear approximation facing this dilemma and have introduced similar approximations. In the description of 2PCF in redshift-space, due to the multipole expansion of the inverse Lagrangian operator derived from the corresponding power spectrum in Fourier space (Hamilton 1992), there appears a dependence with µ, the cosine of the angle between the r (real space) vector and the LoS: μr=r∥/r. However, it has been a common practice to approximate µ from redshift-space coordinates as either μs=s∥/s or μ(cs)=c||s||/c⊥2s⊥2+c||2s||2 (e.g., Matsubara & Suto 1996; Nakamura et al. 1998; López-Corredoira 2014). Yet in some other cases the approximation r||=s|| is specifically made (e.g., Tinker et al. 2006) calling it the “distant observer" approximation. But, as mentioned above, this is really intended to mean a wide separation approximation and does not apply in the small scale regime. Furthermore, the “distant observer" name is also used for the plane-parallel case (e.g., Percival & White 2009), adding to the confusion. In some other cases the substitution r||=s|| is just performed with no further comment (e.g., Hawkins et al. 2003). Another facet of the same problem has been to expand the redshift-space correlation function as a series of harmonics of that same µ(s), rather than the actual µ(r) derived in linear theory (e.g., Guo et al. 2015; Chuang & Wang 2012; Marulli et al. 2017). While this is certainly a valid approach, the conclusions of linear theory, like the existence of only monopole, quadrupole and hexadecapole terms in the Legendre polynomial expansion, are not really applicable to the µ(s) case. All these forms of the approximation are really one and the same, and to avoid further confusion (like the term “distant observer") we decided to call it the µ(s) approximation.
When observational data are used to construct the 2PCF ξ(s)(s) , it is generally true that simple linear theory predictions are not kept. On one hand, the predicted compression along the viewing direction is observed, but as one approaches the LoS axis the observed structure is mostly dominated by an elongated feature (e.g., Hamaus et al. 2015), usually called Finger of God (Huchra 1988), hereafter FoG. Prominent examples of FoG were found in the Coma Cluster by de Lapparent et al. (1986) and in the Perseus cluster by Wegner et al. (1993). The FoG feature is also commonly observed in the 2PCF of statistical aggregates (e.g., Hawkins et al. 2003), making it a common feature of large scale structures.
Many studies have been conducted to explain this discrepancy. In general, non-linear processes are invoked. Sometimes the non-linearities are assigned to virial relaxation in the inner regions of clusters, while others explore the non-linear terms of the approximation in the derivation of the K87 result. In these categories, we mention a small sample of the representative literature. Kinematic relaxation, like the virialized motion of cluster members in the inner regions (Kaiser 1987; Hamaus et al. 2015), are explored by introducing a distribution of pair-wise peculiar velocities for cluster components. There are at least two ways of doing so: First, the streaming model where a velocity distribution f(V) is convolved with ξ(r)(r) to obtain ξ(s)(s), without using the K87 result, similar to Davis & Peebles (1983) but differentiating ξ(s) from ξ(r). More recent work on distribution functions take great care of this issue (Seljak & McDonald 2011; Okumura et al. 2012a,b) by directly obtaining the power spectra in redshift-space as a function of the s−space wave-number. Unfortunately, the expression that results for the power spectra is rather complicated, even when it is conveniently expressed as a series of mass weighted velocity moments. However, it is possible to obtain FoG structures in ξ(s)(s) maps by the convolution with simple velocity distributions, at the same time that a mapping from r− to s−space takes place (e.g., Scoccimarro 2004). Paradoxically, it is not that easy to obtain the traditional peanut-shape structure that is generally recognized as the K87 limit in ξ(s)(s), unless the limit s ∼ r is once again invoked. Second, in the phenomenological dispersion model (c.f., Scoccimarro 2004; Tinker et al. 2006) a linear K87 spectrum is multiplied in Fourier space by a velocity distribution. This can be seen as a convolution in configuration space, as in Hawkins et al. (2003), but the procedure has the disadvantage that it obtains the same function ξ(s) as the result of the convolution of ξ(s) and f (V). It has to be noted, however, that very good fits to the observed data are obtained by this procedure. The same is true for the fits to numerical simulation results at mid spatial frequencies obtained by similar procedures in e.g., Marulli et al. (2017). In the streaming model, the velocity distribution function can also be obtained from the interaction of galaxies with dark mater halos (e.g., Tinker et al. 2006; Tinker 2007), via the halo occupation distribution formalism.
Apart from kinematics, non-linear terms also arise in the expansion of the mass conservation or continuity equation in r− and s−spaces to obtain the power spectrum or the 2PCF (e.g., Matsubara 2008; Taruya et al. 2010; Zheng & Song 2016). Preserving only first order terms yields the K87 result. However, a full treatment of all the terms is possible with the use of perturbative methods. There are diverse techniques: standard, Lagrangian, renormalized, resumed Lagrangian (for a comparison see Percival & White 2009; Reid & White 2011). The latter authors however, conclude that the failure of these methods to fit the l=2 and 4 terms in the expansion ξl(s)(r) on quasi-linear scales of 30 to 80 h
−1 Mpc, must be due to inaccuracies in the mapping between r- and s-spaces. So, they favor again the streaming model. Clearly, there is still substantial debate on this subject.
In most of these works the necessity to translate their results to observable 2PCFs, ξ(s)(s), is not really addressed. Most authors prefer to display their results in Fourier space as s-space power spectrum P
(s)
(
k
r
) (e.g., Matsubara 2008; Okumura et al. 2012a), but with k
r
in r-space; or display its moments Pls(kr) (e.g., Taruya et al. 2010; Zheng & Song 2016); or the power spectra with k
s
in s−space P
(s)
(
k
s
, µ
s
) (e.g., Okumura et al. 2012b). Other authors display the correlation function in r-space, either as ξ(r)(r) (e.g., Matsubara 2008) or ξ(s)(r) (e.g., Tinker 2007; Reid & White 2011; Okumura et al. 2012a), or its moments ξls(s) (e.g., Taruya et al. 2010) for l=2. Few works try to display directly the 2PCFs ξ(s)(s) (e.g., Matsubara & Suto 1996; Nakamura et al. 1998; Tinker et al. 2006; López-Corredoira 2014), but as already mentioned above, usually perform the µ(s) approximation; this amounts to really obtaining ξ(s)(r) instead.
To further complicate matters, redshift-space distortions are often treated separately from the cosmological distortions. Both are not easily discernible because both produce stretching or squashing in the LoS direction (Hamilton 1998; Hamaus et al. 2015). This degeneracy could in principle be resolved because the cosmological and peculiar velocity signals evolve differently with redshift, but in practice the uncertain evolution of bias (the dimensionless growth rate for visible matter, see equation 26) complicates the problem (Ballinger et al. 1996). Furthermore, Kaiser (1987) and Hamilton (1992, 1998) do not consider cosmological distortions in their analysis of peculiar motions. Since the earlier works, the inclusion of cosmological distortions has been attempted by several authors (e.g., Matsubara & Suto 1996; Hamaus et al. 2015).
In this paper, we show that a structure quite similar to FoG can be obtained in ξ(s)(s) directly in the linear theory limit of K87. That is, without invoking virial relaxation or the streaming model, nor the non-linearities studied in perturbation theory, but just by avoiding the µ(s) approximation, in any of its forms (μ=s||/|s|, “distant observer" or r||=s||), the FoG structure is recovered. This will be accomplished by solving for the function r(s) with the aid of the projected correlation function of both 2PCFs : ξ(s)(s) and ξ(r)(r). We will stay on the academic power-law approximation ξ(r)(r)~r-γ in order to be able to show a closed form for the result, and to prove the main point of this paper, i.e. that the FoG feature is derived in the simplest case.
We start with a detailed definition of r− and s−space, noting that frequently s−space is expressed in distance units as is r−space. But in doing so, one multiplies by a scale factor that invariably introduces a cosmological parameter in the definition; and as a result the named s−space is no longer purely observational. Later on, the factor is solved by introducing a fiducial cosmology and solving for the real values. An example can be seen in the analysis made by Padmanabhan & White (2008) in Fourier space and Xu et al. (2013) in configuration space. The latter recognize the need of introducing a two-step transformation, one isotropic dilation and one warping transformation, to transform from real fiducial to real space. However, the real fiducial space is actually redshift-space, and this identification is missing in these works.
Therefore, we argue (c.f., § 2) that it is convenient to define the observable-redshift-space σ (σ-space) given by the simple redshift differences and subtended angles that are truly observable, and that do not depend on any choice of cosmological parameters. Multiplying by a unit function (scale factor) produces the physical redshift-space (s−space): s=KΩ,zσ, that is isomorphic to the observable σ-space, but has actual distance units that are dependent on a particular cosmological set of parameters Ω and on the redshift z. The K(Ω, z) function is chosen so that the physical redshift-space is related to real space r by a unitary Jacobian independent of redshift. So, no additional scaling is needed, and the only remaining difference will be precisely in shape. That is why σ and s are more alike, and thus can both be named redshift-space; σ is the observable redshift-space while s is the physical redshift-space. Then, the transformation to real-space necessarily goes through redshift distortions.
Furthermore, when we introduce peculiar non-relativistic velocities in this scheme, we will show that it is possible to keep the same relation between observable and physical redshift-spaces, s and σ, and that the Kaiser (1987) effect is recovered independently of redshift (see § 3). That is, now redshift-space will also show an additional gravitational distortion with respect to real-space.
To solve for the relation between real-space and redshift-space, we will rely on projected correlations. Projections of the 2PCF in the plane of the sky have been widely used to avoid the complications of dealing with unknown components in redshift-space (e.g., Davis & Peebles 1983). This has the advantage that in the case of a symmetric 2PCF in real-space, the 3-D structure can be inferred from the projection. We will show in § 4 that since the projections of the 2PCF in real-space and in redshift-space are bound to give the same profile, a relationship can be obtained for the real-space coordinate r|| as a function of the corresponding one in redshift-space s||. From this, we solve for µ(r) in real-space, and show that a different view of the redshift-space 2PCF emerges. The main result is that the redshift-space 2PCF presents a distortion in the LoS direction which looks similar to the ubiquitous FoG. This is due to a strong anisotropy that arises purely from linear theory and produces a change in scale as one moves into the on-axis LoS direction. As we move out of the LoS, a structure somewhat more squashed than the traditional result by the µ(s) approximation is obtained. As this effect has been missed before (to the best of our knowledge), we provide a detailed derivation in § 2 to 4, and show examples of the derived 2PCFs in redshift-space (§ 5). Finally, in § 6 we summarize our main conclusions.
2. Redshift-space
Consider the Friedmann-Lemaître-Robertson-Walker metric (e.g., Harrison 1993) written in units of distance and time as follows:
ds2= c2dt2-dr2= c2dt2-a(t)2dχ2+Sk(χ)2dθ2+sin2(θ)dφ2,
(1)
with S
k
= (sin, Identity, sinh) for k = (1, 0,−1). Then the co-moving present-time length of an object dr
0 that is observed longitudinally is related to a variation in the observed redshift dz by
dr||0=cdzH(z),
(2)
where H(z) is the Hubble function and the 0 superindex is used to define the present time t
0. Similarly, an object with a transversal co-moving dimension dr⊥0 subtends an angle dθ given by the angular co-moving distance (e.g., Hogg 1999) as
dr⊥0dθ=a0Skca0∫0zdz'H(z'),
(3)
where a
0 is the present day scaling parameter of the metric.
Observationally one measures redshift differences dz and subtended angles dθ. We then define the observable redshift-space adimensional quantities (dσ|| ,dσ⊥) as
dσ||=dz,
(4)
and
dσ⊥=zdθ.
(5)
The physical redshift-space sizes ds|| and ds⊥ can then be defined in terms of σ as
ds||=K(Ω, z)dσ||,
(6)
and
ds⊥=K(Ω, z)dσ⊥,
(7)
where K(Ω, z) has distance units and depends on the cosmology, represented here symbolically by the Ω terms. The relation between real-space and physical redshift-space is then obtained from equations (2) to (7), that is:
dr∥0=c∥ds∥,
(8)
and
dr⊥0=c⊥ds⊥,
(9)
with
c∥=cKΩ, z H(z)
(10)
and
c⊥=a0z KΩ, zSkca0∫0zdz'Hz'.
(11)
It is clear then that the Alcock & Paczyński (1979) function AP(z), that tests redshift distortions of a particular cosmology, can be written as
AP(z)=c⊥(z)c||(z)=a0c H(z)z Skca0∫0zdz'H(z').
(12)
Furthermore, from the transformation of physical redshift-space with coordinates (ds⊥,ds⊥,ds||) into real-space (dr⊥0,dr⊥0,dr||0) we get a Jacobian
d3sd3r=1c||(z) 1c⊥2(z).
(13)
In order for this transformation to preserve scale we need a unitary Jacobian. This condition can be achieved simply by the following condition:
KΩ,z=cHzAP(z)2/3,
(14)
as can be seen from equations (10) to (12). Here the dependence on the cosmology is made explicit through the Hubble function. Note that the resulting scale factor KΩ,z approaches the Hubble radius aH=c/H0 as z→0 and decreases approximately as 1/(1+z) thereafter. Also note that for redshift z>0, the physical scale that transforms all dimensions of redshift-space contracts isotropically. Also we remark that c|| and c⊥ are of order unity as z→0, and satisfy c⊥/c||=AP(z) for all z. In fact we have (see also Xu et al. 2013):
c||(z)=AP(z)-2/3,
(15)
and
c⊥(z)=AP(z)1/3.
(16)
Peculiar velocities modify the observed redshift, and therefore alter the relation between real-space and redshift-space giving rise to kinematic distortions. Suppose the near-end of an object is at rest at redshift z, while the far-end is moving with peculiar non-relativistic velocity v→. Then it will appear Doppler shifted to an observer at rest at the far-end position, causing equation (2) to get the form (see also Matsubara & Suto 1996; Hamaus et al. 2015):
cdz=Hzdr∥0+1+zv→∙r^,
(17)
where r^ points in the direction of the far-end, at an angle dθ from the near-end. Since v→∙r^=v∥+v⊥dθ, then for small angular separations (dθ<<1) the perpendicular component of the peculiar velocity may be trivialized.
dr∥0=c||(ds||-dsV).
(18)
where ds
v (in physical redshift-space) is given by
dsv=KΩ,zdσv,
(19)
and dσv (in observable redshift-space) is given by
dσv=(1+z)v||c.
(20)
Through the similarity of equations (19) and (20) with equations (6) and (4), we note that the concepts of observable redshift-space and physical redshiftspace can be extended to include peculiar motions as well.
3. Two point correlation function
Let r be real-space Euclidean co-moving coordinates in the close vicinity of a point at redshift z, defined as dr in the previous section. Then for azimuthal symmetry around the line of sight (aligned to the third axis) we have r=(dr⊥0,dr⊥0,dr||0). Let s denote physical redshift-space coordinates around the same point (in the same tangent subspace), with the third axis along the line of sight. Then, from equations (9) and (18), the Jacobian is
d3sd3r=1c||(z)c⊥2(z) 1+1+zHz ∂v||∂r||=1+1+zHz ∂v||∂r||,
(21)
where we have used the unitary condition on equation (13) to eliminate the c||(z) c⊥2(z) term. In going from r to s space, the density change can be related to the change in volume V, and the Jacobian by the equation
dρρs-r=-dVV=1-d3sd3r.
(22)
This can also be expressed in terms of the contrast density ratios in s and r spaces defined such that
dρρs-r=δ(s)-δr,
(23)
where δ(s) and δ(r) are two distinct scalar functions of position in either space. This particular definition of δ(s) requires knowledge of the real-space selection function (Hamilton 1998), which makes it rarely a first choice. However, the procedure given below allows us precisely to solve for the function
r
(s).
In linear theory, Peebles (1980) shows by equations 14.2 and 14.8 that an overdensity of mass δ(r) creates a peculiar velocity field similar to the acceleration field produced by a mass distribution. As such, it can be derived from a potential function whose Laplacian is the overdensity itself (e.g., Thornton & Marion 2004) times a constant which is time (or redshift) dependent. That is
vr=-Hz fz1+z∇∇-2δmrr,
(24)
where ∇ is the gradient, ∇-2 is the inverse Laplacian, and
f(z)=a(z)D(z)dDda.
(25)
Here D(z) is the growth factor, the temporal component of density. Note that in Peebles (1980) coordinates are given in the expanding background model x, which relate to present time real-space coordinates by r=a0x; this brings about the (1 + z) factor in equation (24). The m subscript to δ emphasizes that all mass is responsible for the velocity field, while δ without the subscript refers to visible mass in the form of galaxies or quasars. To account for the difference, it is customary to introduce a bias factor b(z) and to define the dimensionless growth rate for visible matter
β(z)=f(z)b(z).
(26)
Then from equations (21) to (24) we get:
δsr=1+βz∂||2∇-2δrr,
(27)
where ∂|| denotes ∂/∂r|| in real space. Note that if we had not required a unity Jacobian (c.f., equation 13), then equations (21) and (22) would not have canceled out the 1-c||(z)-1c⊥(z)-2 term. We note that this term is not small when K(Ω,z) is a constant, and will vary by one order of magnitude as z→1, and up to three orders of magnitude as z→10. So the transformation between observable and physical redshift-spaces cannot be neglected (contrary to the assumption of Matsubara & Suto 1996).
The square modulus of the Fourier transform of equation (27) gives an expression for the power spectrum, or the Fourier transform of the autocorrelation function (2PCF) ξ, which generalizes results for any redshift z
ξs~k=(1+βz μk2)2 ξr~k,
(28)
where μk=kr3/|kr| is the cosine of the angle between the kr3 component and the wave number vector
k
r
in real-space; it arises by the Fourier transform property of changing differentials into products. Note that wave number vectors in real-space also differ from their counterparts in redshift-space by the unknown velocity field in equation (17).
Fourier transforming back into coordinate space gives the Hamilton (1992) result:
ξsr=(1+β(z)∂||2∇-2)2 ξrr
(29)
Note that this equation is written in a way that all terms in the right hand side are real-space coordinates
r
dependent, as is the case for the derivatives and inverse Laplacian. Recalling that the solution of the Laplace equation in spherical coordinates consists of spherical harmonics in the angular coordinates and a power series in the radial part, one can write for the case of azimuthal symmetry
ξsr=∑l=0ξlrPl(μr)
(30)
where P
l
(μ(
r
)) are the Legendre polynomials,
μr=r|||r|,
(31)
explicitly defined for real-space coordinates, and the harmonics are given by the coefficients ξl(r) that can be obtained from equation 30 through orthogonality properties as
ξlr=(2l+1)2∫⊢11Pl(μr) ξsr dμr.
(32)
Substituting equation (29) in (32) for the case of spherical symmetry in real-space (ξrr=ξrr), one gets by direct evaluation the classical result given by Hamilton (1992), see also Hawkins et al. (2003). That result consists of only three terms: monopole, quadrupole and hexadecapole (l = 0, 2, 4), all the others evaluate to zero. It is important to note that this is not true when the expansion of equation (30) is done in μ(s) as assumed by several authors (e.g., Guo et al. 2015; Chuang & Wang 2012; Marulli et al. 2017).
When the 2PCF can be approximated by a power-law, ξ(r)(r)=(r/r0)-γ, the solution for equation (29) can be written as
ξsr=gγ,β,μr ξrr.
(33)
where gγ,β,μr has been written in several equivalent forms (Hamilton 1992; Matsubara & Suto 1996; Hawkins et al. 2003). One of these is the following:
gγ,β,μr=1+21-γμr23-γβz+γ(γ+2)μ(r)4-6γμ(r)2+33-γ5-γβ(z)2.
(34)
This function takes values greater than 1 for the equatorial region (μ(r)→0), and less than 1 for the polar axis (μ(r)→1). Alternatively, it has been mentioned that the quadrupolar term in the multipole expansion dominates the hexadecapole. As a result of either argument the 2PCF ξsr seems squashed with a peanut shape when displayed in r-space , in agreement with common knowledge.
However, we will show below that the stretching of redshift scale along the LoS will counteract this apparent squashing producing a structure similar to a FoG. In order to stay within the linear regime, we ensure not to reach the turnaround velocity by keeping gγ,β,μr positive in the polar region. In that case β is limited from 0 to an upper limit which is a function of γ, and equals 2/3 when γ=1.8. The β=0 case gives the no gravity one in which ξsr=ξrr.
We now remark that μr=r∥/|r| (see equation 31). But in some works it has been approximated as μr=s∥/|s| or as μ(cs)=c||s||/c⊥2s⊥2+c||2s||2, or even as r||=s||. We have referred to this as the μs approximation. In principle, given that μ is a scalar function, either form should be acceptable as long as the
s
and
r
vectors refer to the same point. However, we remark that r|| differs from c||s|| (see equation 18), and that it is usually unknown, since in order to obtain it from s||, the infall velocity field must be known. So these approximations should be carefully used.
The result in our equation (33) has been derived for r-space, profiting from the difference between r- and s- spaces. Plotting this function directly in r-space as the independent variable produces a squashed structure for ξsr. However, one wants to display the correlation function in s-space to compare it with observations, not in r-space. In order to do so, some authors perform the μs approximation while others may plainly substitute s for r all the way in equation (33) and write ξss=gγ,β,μs ξrs to be able to display ξ(s) in s-space. This is certainly wrong because
s
and
r
are not just independent names for position, and there exists a relation s(
r
) between them that is not linear. Specifically, the parallel component is s||∼r||+v|| (equation 18), with v|| also a (yet unknown) function of position
r
. In the case of small disturbances we expect small velocities (below turnover) that result in a bi-univocal map s(
r
) and its inverse. So, if we want to display the resulting ξ(s) in
s
space, we must proceed first to evaluate r = r (
s
) and then ξsr via equation (33), or in short ξsr(s)=gγ,β,μr(s) ξrr(s). We can therefore informally define ξss≡ξrr(s). and we claim that this is the correct way to evaluate the two-point correlation function on a grid in s-space.
On the other hand, if the µ(
s
) approximation is used one obtains structures that are squashed in the LoS direction, and with a characteristic peanut-shaped geometry close to the polar axis (see for example Hawkins et al. 2003). One concludes that this geometry fails to reproduce the structure known as “Finger of God" (FoG). The consequence is that other processes are called upon to account for it, such as random motions arising in the virialized inner regions of clusters. We show below that avoiding this approximation allows us to obtain a geometrical structure quite similar to the FoG feature.
4. Projected correlation function
In order to avoid the complications that redshift-space distortions introduced in the correlation function, such as those produced by gravitationally induced motions or virialized conditions, the projected correlation function w⊥(r⊥) is frequently preferred in the analysis. This approach was first suggested in the analysis of CfA data by , who mention that at small redshift separations peculiar velocities may cause ξ(s) to differ from ξ(r). To avoid this effect, they integrate ξ(r) along the redshift difference to obtain the projected function w⊥(r⊥) on the plane of the sky. Then, from it, they recuperate ξ(r) inverting the problem by solving Abel’s integral equation (Binney & Tremaine 1987) numerically. See also Pisani et al. (2014) for other possibilities. In the case where ξ(r) is a power-law, w⊥(r⊥) will be one as well, and the relation between them is analytical (e.g., Krumpe et al. 2010).
We will show that the projected correlation function can be used to obtain the r||(s||) function that allows us to calculate µ(
r
). We start by noting that the projection on the plane of the sky may be performed either by using the ξ(s) function or its real space counterpart ξ(r). Then we define the projected correlation functions as
w⊥(s)(s⊥,s||*)=∫0s||*ξs(r(s⊥,s||)) ds||,
(35)
and
w⊥(r)(r⊥,r||*)=∫0r||*ξ(r)(r⊥,r||) dr||,
(36)
where ξs(r(s⊥,s||), given by equation (33), may be understood as ξs(s), as mentioned above.
The integral limits should go to infinity to get the total projected functions. However, one can project the correlation function up to a particular real space distance r||*. Furthermore, if we assume that there exists a biunivocal function s||(r||), then we can find the corresponding s||*=s||(r||*). Boundary conditions are thus well defined (e.g., Nock et al. 2010). On the one hand, slices in r-space (equation 36) do not depend on the observer’s perspective, while on the other (equation 35) the limit of the integral (boundary condition) becomes a function that is precisely going to be evaluated. Carrying on, due to number conservation, the projections in redshift- and real-space multiplied by the corresponding area elements that complete the volume where the number of pairs are counted, must be equal. This leads to
w⊥(s)(s⊥,s||*) ds⊥2=w⊥(r)(r⊥,r||*) dr⊥2,
(37)
for all values of r⊥ (or its corresponding s⊥, see equation 9). Inverting the s||(r||) map and using equations (35) to (37), together with (33) and (9) we obtain
∫0s||*gγ,β,μr ξr(r⊥,r||) ds||=c⊥2∫0r∥(s||*)ξ(r)(r⊥,r||) dr||.
(38)
Then, changing variables to r|| in the left (ds||=ds||dr||dr||), and noting that the equality holds for all values of s||*, the integral signs can be omitted. Furthermore, using equations (15) and (16) the equation simplifies to
c|| ds||=dr||gγ,β,μ(rr⊥,r∥) ,
(39)
where the dependence µ(r(r⊥, r∥)) = r∥/r⊥2+r∥2 has been emphasized for clarity. Equation (39) completes the metric transformation between redshift- and real-spaces. As a consistency test, we note that in the limit of no gravitational disturbance (β = 0) we have g(γ, β, µ(r)) = 1 and equation (8) is recovered.
5. Resulting redshift-space and real-space relation
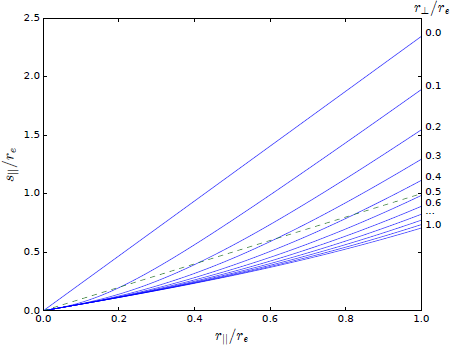
We integrate equation (39) numerically using equation (34), to obtain the s||(r||) function shown in Figure 1 for different values of r⊥/re, indicated for each curve in the figure, where re is an arbitrary scaling parameter, γ=1.8, β=0.4, and c||=1. Note that the relation is not linear. If we compare it to the identity line (s||=r||) shown as a dashed line, we note that sometimes the curves of constant r⊥ lie above or below the identity line, or even cross it.
So, it can be noted that for on-axis separations (where r⊥=0), the spatial scale in redshift space is stretched, i.e. s||>r||, effectively opposing the squashing effect obtained by the rough µ(
s
) approximation. On the other hand, for r⊥→1 a squashed structure is seen (even more so that the one obtained by the µ(
s
) approximation) that ultimately converges to the limit s||→r|| as we approach the plane of the sky (r||=0).
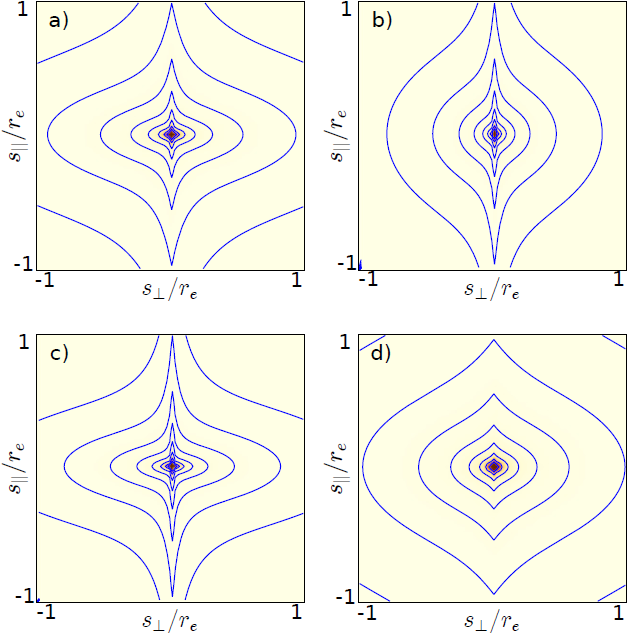
These geometrical distortions can be better appreciated by their effect on the 2PCF presented in Figure 2. Here we start from a grid in s−space, and transform to r-space using the integral relation (equation 39) for the parallel component and equation (9) for the perpendicular one. From there, we calculate µ(
r
) (equation 31), g(γ, β, µ(r)) (equation 34), assuming that ξ(r)(r) = (r/r0)-γ; and finally, ξ(s)(s) (i.e. ξsrs ) from equation (33). The cosmological distortion is governed by the c|| and c⊥ parameters that depend on the Alcock-Paczyński function AP (see equation 12). Its value depends on the cosmological parameters Ω=(Ωm,Ωk,ΩΛ) and increases with the redshift z (see Figure 1 in Alcock & Paczyński 1979).
Figure 2 (a) shows the case that corresponds to the parameters used for Figure 1: γ= 1.8, β= 0.4 and AP = 1, where the geometrical distortions produced are evident, an elongation in the polar direction and a squashing in the equatorial direction. As can be noted the polar elongation resembles the structure known as FoG.
In the other three Figures, 2(b), 2(c) and 2(d), we explore the effect of cosmological and gravitational alterations. Figure 2 (b) shows that the effect of increasing AP is a geometrical distortion that concentrates the structure towards the polar axis direction for AP = 2 that corresponds to ΛCDM cosmology at z = 2.6. In Figure 2 (c) we explore the effect of changing the dimensionless growth-rate for visible mater β. This gravitational effect is to enhance the FoG structure as its value increases (recall that its limit value is 2/3). On the other hand, if β decreases the structure becomes rounder and the FoG fainter, as is shown in Figure 2 (d). By comparing Figures 2 (b) and 2(c) relative to 2(a), we note that the same enhanced strength of the FoG feature is obtained in the small scale regions, but the large scale structure is quite different. This is because in the first case the distortion is cosmological while on the second it is gravitational.
Although it has not been the purpose of this paper, we may consider different values of the power-law index γ and we obtain figures similar to those shown in Figure 2. In some cases they might even resemble some of the cases depicted here. It turns out that lower values may accommodate rounder 2PCFs at mid scales, while a steeper γ may also concentrate the structure towards the LoS. Note, however, that it is easy to discern those cases by a simple projection on the plane of the sky, as depicted through § 4. This is because such a projection will erase redshift distortions, both gravitational (β) and cosmological (AP), while preserving the radial structure γ.
As we have indicated, a rounder 2PCF at mid spatial scales is favored by some works that use the µ(s) approximation. As can be seen in Figure 2 (b), rounder figures can be obtained with lower values of β. We have estimated that a β = 0.25 produces a 2PCF which is squashed equally to that obtained by the µ(s) approximation for the case β = 0.4 for most points in the s-space plane, those with s⊥ > s||. An increase in the AP parameter may also contribute to alleviate the situation.
Another possibility, that was not intended to be covered here, is the case of a more realistic 2PCF ξ(r)(r) such as the ones inferred from baryon acoustic oscillations (BAOs) (e.g. Slosar et al. 2013) or those obtained by the CAMB code (Seljak & Zaldarriaga 1996). In order to apply the results of this paper to such cases, one could try breaking the inferred ξ(r)(r) profile into a series of power-laws, and then apply equation (39) to each section. If this is not possible, then we would have to give up equations (33) and (34) as a way of simplifying ξ(s)(r). However, the projections on the plane of the sky, i.e. equations (35) and (36) are still valid, and instead of using equation (33) to simplify, we would have to go back to the expansion of ξ(s)(r) in multipoles (equation 30). In that case one would end up with the following equation:
c∥ds∥=ξ(r)(r)∑l=0,2,4ξlrPl(μr)dr∥
(40)
instead of equation (39). We would also have to find a way to estimate the multipole moments ξl(r). Another possibility is to leave ξ(s)(r) in the denominator. Considering these possibilities seems like an interesting task for future works, but it is beyond the scope of this paper.
We conclude that a whole range of possibilities in shape and strength of the FoG structure and the squashing of the equatorial zone can be obtained by tuning the parameters γ, β, and AP . This may provide a path towards solving the usual degeneracy problem between cosmological and gravitational distortions, which can still be seen at a level of 10% in 1σ correlated variations in recent work (e.g. Satpathy et al. 2017).
6. Conclusions
We emphasize the importance of distinguishing three spaces in cluster and large scale structure studies: the observable redshift-space σ, the physical redshift-space
s
, and the real-space
r
. The transformation between σ and s is an isotropic dilation that introduces a scale factor dependent on the cosmology.
On the other hand, the transformation between
s
and
r
occurs through a unitary Jacobian independent of redshift, and only distorts the space by factors related to the Alcock-Paczyński AP function (c.f., equations 15 and 16).
Furthermore, when we introduce non-relativistic peculiar velocities in this scheme, we demonstrate that the same relation between observable and physical redshift-spaces s = K(Ω, z) σ is kept. In the analysis of the 2PCF in the physical redshift-space s, we recover the Kaiser (1987) effect independent of redshift in Fourier space, and Hamilton (1992) results in configuration space.
We remark that a dependence with µ in real-space (µ(r) = r||/|r|) appears, and that it has been a common practice to approximate it from redshift-space coordinates as either µ(s) = s||/|s| or μ(cs)=c||s||/c⊥2s⊥2+c||2s||2 or r||=s||, sometimes called the“distant observer approximation", or simply to substitute
s
for
r
in the equations. To avoid further confusion we have called this the µ(s) approximation in any of its forms. We argue that this wrong assumption produces either a squashed or a peanut-shaped geometry close to the LoS axis, for the 2PCF in redshift-space.
Since r|| is usually unknown, we propose a method to derive it from s|| using number conservation in the projected correlation function in both real- and redshift-spaces. This leads to a closed form equation (39) for the case where the real 2PCF can be approximated by a power-law. From this, we solve for µ(
r
) in real-space, and show that a different view of the redshift-space 2PCF emerges. The main result is that the redshift-space 2PCF presents a distortion in the LoS direction which looks quite similar to the ubiquitous FoG. This is due to a strong anisotropy that arises purely from linear theory and produces a stretching of the scale as one moves into the on-axis LoS direction. Moving away from the LoS the structures appear somewhat more squashed than those obtained by the µ(s) approximation for equivalent values of β. The implications of this remains an open question.
The development presented here produces structures that qualitatively reproduce the observed features of the 2PCF of galaxies and quasars large scale structure. A squashing distortion in the equatorial region is attributed to a mixture of cosmological and gravitational effects. The FoG feature that is usually attributed to other causes is instead ascribed to the same gravitational effects derived from linear theory.
We conclude that a whole range of possibilities in shape and strength of the FoG structure, and the squashing of the equatorial zone, can be obtained by tuning the parameters γ, β, and AP . This provides a path towards solving the usual degeneracy problem between cosmological and gravitational distortions. In a future paper (Salas & Cruz-González in preparation) we will apply these results to the galaxies and quasar data obtained by current large scale surveys.
I.C.G. acknowledges support from DGAPA-UNAM (Mexico) Grant IN113417.
References
Alcock, C. & Paczyński, B. 1979, Natur, 281, 358
[ Links ]
Ballinger, W. E., Peacock, J. A., & Heavens, A. F. 1996, MNRAS, 282, 877
[ Links ]
Binney, J. & Tremaine, S. 1987, Galactic Dynamics (Princeton, NJ: PUP)
[ Links ]
Chuang, C.-H. & Wang, Y. 2012, MNRAS, 426, 226
[ Links ]
Davis, M. & Peebles, P. J. E. 1983, ApJ, 267, 465
[ Links ]
de Lapparent, V., Geller, M. J., & Huchra, J. P. 1986, ApJL, 302, L1
[ Links ]
Guo, H., Zheng, Z., Zehavi, I., et al. 2015, MNRAS, 446, 578
[ Links ]
Hamaus, N., Sutter, P. M., Lavaux, G., & Wandelt, B. D. 2015, JCAP, 11, 036
[ Links ]
Hamilton, A. J. S. 1992, ApJ Letters, 385, L5
[ Links ]
Hamilton, D. 1998, Astrophysics and Space Science Library, 231, Linear Redshift Distortions: a Review, ed. D. Hamilton, 185
[ Links ]
Harrison, E. 1993, ApJ, 403, 28
[ Links ]
Hawkins, E., Maddox, S., Cole, S., et al. 2003, MNRAS, 346, 78
[ Links ]
Hogg, D. W. 1999, ArXiv Astrophysics e-prints /9905116
[ Links ]
Huchra, J. P., Davis, M., Latham, D., & Tonry, J. 1983, ApJS, 52, 89
[ Links ]
Huchra, J. P. 1988, in ASPC 5, The Minnesota lectures on Clusters of Galaxies and Large-Scale Structure, ed. J. M. Dickey, (San Francisco, CA: ASP), 41
[ Links ]
Kaiser, N. 1987, MNRAS, 227, 1
[ Links ]
Krumpe, M., Miyaji, T., & Coil, A. L. 2010, ApJ, 713, 558
[ Links ]
López-Corredoira, M. 2014, ApJ, 781, 96
[ Links ]
Marulli, F., Veropalumbo, A., Moscardini, L., Cimatti, A., & Dolag, K. 2017, A&A, 599, A106
[ Links ]
Matsubara, T. 2008, PhRvD, 77, 063530
[ Links ]
Matsubara, T. & Suto, Y. 1996, ApJ Letters, 470, L1
[ Links ]
Nakamura, T. T., Matsubara, T., & Suto, Y. 1998, ApJ, 494, 13
[ Links ]
Nock, K., Percival, W. J., & Ross, A. J. 2010, MNRAS, 407, 520
[ Links ]
Okumura, T., Seljak, U., & Desjacques, V. 2012a, JCAP, 11, 014
[ Links ]
Okumura, T., Seljak, U., McDonald, P., & Desjacques, V. 2012b, JCAP, 2, 010
[ Links ]
Padmanabhan, N. & White, M. 2008, PhRvD, 77, 123540
[ Links ]
Peebles, P. J. E. 1980, The large-scale structure of the universe, (Princeton NJ: PUP)
[ Links ]
Percival, W. J. & White, M. 2009, MNRAS, 393, 297
[ Links ]
Pisani, A., Lavaux, G., Sutter, P. M., & Wandelt, B. D. 2014, MNRAS, 443, 3238
[ Links ]
Reid, B. A. & White, M. 2011, MNRAS, 417, 1913
[ Links ]
Satpathy, S., Alam, S., Ho, S., et al. 2017, MNRAS, 469, 1369
[ Links ]
Scoccimarro, R. 2004, PhRvD, 70, 3007
[ Links ]
Seljak, U. & McDonald, P. 2011, JCAP, 11, 039
[ Links ]
Seljak, U. & Zaldarriaga, M. 1996, ApJ, 469, 437
[ Links ]
Slosar, A., Iršič, V., Kirkby, D., et al. 2013, JCAP, 4, 026
[ Links ]
Taruya, A., Nishimichi, T., & Saito, S. 2010, PhRvD, 82, 3522
[ Links ]
Thornton, S. T. & Marion, J. B. 2004, Classical Dynamics of Particles and Systems, (5th ed. Brooks/Cole, a division of Thomson Learning Inc.)
[ Links ]
Tinker, J. L. 2007, MNRAS, 374, 477
[ Links ]
Tinker, J. L., Weinberg, D. H., & Zheng, Z. 2006, MNRAS, 368, 85
[ Links ]
Wegner, G., Haynes, M. P., & Giovanelli, R. 1993, AJ, 105, 1251
[ Links ]
Xu, X., Cuesta, A. J., Padmanabhan, N., Eisenstein, D. J., & McBride, C. K. 2013, MNRAS, 431, 2834
[ Links ]
Zheng, Y. & Song, Y.-S. 2016, JCAP, 8, 050
[ Links ]











 text new page (beta)
text new page (beta)


