1. INTRODUCTION
The search for orbital maneuvers that minimize fuel consumption is a very important topic in astrodynamics. Several solutions are available in the literature; they consider high and low thrusts, as well as some options using the gravity of a celestial body to give energy to the spacecraft. Several missions used this technique in the past, like the missions Mariner (Dunne & Burgess 1978), Voyager (Flandro 1966; Kohlhase & Penzo 1977), BepiColombo Messenger (Solomon et al. 2007), MESSENGER Team et al. (2006), Grard (2006), Jehn et al. (2008). The pure gravity assisted maneuver is a powerful technique to change the energy of a spacecraft travelling in the Solar System, but several options are also considered in the literature with the goal of increasing the variations of energy of this maneuver. The goal of the present paper is to study a maneuver called “powered aero-gravity-assisted maneuver”. The origin of this name stems from the three different aspects that are involved in this orbital maneuver: (i) the rotation of the velocity vector of the spacecraft with respect to the largest primary of the system, the Sun, due to the effect of the gravity field of Venus (Hollister & Prussing 1965; Uphoff 1989; Broucke 1988; Broucke & Prado 1993; Qi & Xu 2015; Prado 2007; Gomes & Prado 2010); (ii) the deviations in the trajectory of the spacecraft due to the drag and lift forces generated by the atmosphere of Venus (Solomon et al. 2007; MESSENGER Team et al. 2006; Grard 2006); (iii) the application of an impulsive maneuver at the time when the spacecraft passes by the point of the closest approach to Venus (Prado 1996; Casalino et al. 1999b; Silva et al. 2015; Silva et al. 2013a, b; Gomes et al. 2016). There is a large number of studies related to each of these points, as well as to combinations of two or more of them. The consideration of those three effects combined in a single maneuver has not been well studied and is very recent in the literature. Some examples consider maneuvers around the Earth (Murcia & Prado 2017b) and Mars (Murcia et al. 2018). In the case of Mars (Murcia et al. 2018), emphasis is placed on comparing direct and retrograde orbits, showing their existence and the differences among them. In the present paper, the maneuvers are made using Venus.
The present paper has the goal of making a detailed verification of the effects of each force involved in the dynamics. The objective is to understand the indirect effects of the impulse, that not only change the velocity vector, but also change the trajectory. The modification made in the trajectories can increase or decrease the contributions of the atmospheric forces, further changing the results obtained. The idea is to perform numerical integrations of the accelerations given by each force, to reveal the individual contribution of each of them in the maneuver. In particular, the contribution of lift and drag due to the modification of the trajectories caused by the application of the impulsive maneuver is studied. This study considers the planet Venus for the close approach. This planet is selected because it is in a strategic position in the Solar System for missions going to the inner and outer planets. Besides this important location, Venus has a very dense atmosphere, which allows large variations of energy, as well as a high risk of collision with the planet. The results will show that Venus can give up to eight times the variations of energy when compared to Earth, for similar maneuvers. Regarding Mars, another planet that can be used for maneuvers of this type, variations of energy can be up to four times larger. Due to the complex dynamics involved in this maneuver, only numerical simulations can identify the best trajectories for specific goals of a mission, and general results are not available, not even based on comparisons with similar studies made for other planets.
The pure gravity maneuver has received more attention in the literature. The physical reason for the energy gains is the rotation of the velocity vector of the spacecraft with respect to the inertial frame. This maneuver changes the energy of the spacecraft with respect to the primary body of the system. This change can increase or decrease the energy, depending on the geometry of the passage. A trajectory that passes in front of the celestial body reduces the energy, while a passage behind the body can increase the energy of the spacecraft (Broucke 1988; Broucke & Prado 1993). There are several examples of applications of this maneuver, like shown in Flandro (1966) and Kohlhase & Penzo (1977), related to the Voyager mission. Missions to Mercury are also considered in the literature using this type of maneuver (Solomon et al. 2007; MESSENGER Team et al. 2006; Grard 2006; Jehn et al. 2008). The Galileo spacecraft also benefited from this maneuver, like shown in D’Amario et al. (1981, 1982). Maneuvers for the Mariner mission are described in reference (Dunne & Burgess 1978). It is also possible to modify the orbital plane of a spacecraft, as shown in Carvell (1986) for the Ulysses mission. A series of close approaches can also be used by a spacecraft, as detailed in Dunham & Davis (1984). The planet Venus has been used for a pure gravity-assisted maneuver in Striepe & Braun (1989), as well as in Hollister & Prussing (1965). More distant planets can be visited using this concept, like in a mission to Pluto, as described in Longuski & Williams (1991). Using a more generic approach, Prado & Broucke (1995a) mapped orbits around the Moon. Felipe & Prado (1999) studied maneuvers around Jupiter in the three-dimensional space. Strange & Longuski (2002) built a graphical method that is able to find optimal trajectories for a spacecraft. Trips to study Europa can be found in Heaton et al. (2002).
Extending those basic studies, the concept of applying an impulse combined with the close approach also has some published studies, like Prado (1996); Casalino et al. (1999b); Silva et al. (2013a, b); Silva et al. (2015). They used the Moon as the body for the close approach and indicated the best geometry to apply the impulse. Clouds of particles are also studied, with the goal of finding the evolution of the individual members of the clouds and the new distribution of particles after a close approach (Gomes et al. 2013b, a; Gomes & Prado 2008). Maneuvers that use low thrust and close approaches are also possible, like shown in Casalino et al. (1999a); McConaghy et al. (2003); Okutsu et al. (2006). The use of the atmosphere of a celestial body to change the maneuver is also possible. References (Gomes et al. 2013b) and (Prado & Broucke 1995b) study this problem taking into account the effects of drag.
The more complete maneuver, including the atmosphere of the planet, called “aero-gravity assisted” (AGA) maneuvers, also including the effects of the lift force, can increase or decrease the variations of energy obtained from the maneuver. It depends on the direction of this force, which can points to the planet or opposite to it. Several results are available in Murcia & Prado (2017b); Murcia et al. (2018). Even inclination changes are possible using this technique (Murcia & Prado 2017a).
Several other researches can be linked to the present paper, like McRonald & Randolph (1992), which used high values of the ratio lift to drag, with values up to 10. They used the planets Mars, Venus and Earth. Sims et al. (1995, 2000) showed that the losses of energy due to drag are not large in this type of maneuvers, when realized with high lift/drag ratio. Bongfilio et al. (2000) and Lavagna et al. (2005) also worked in this problem, building solutions for trajectories using the same planets Earth, Mars and Venus. Strange & Longuski (2002) designed missions to Pluto, also using high values for the ratio lift/drag during the passages by the atmospheres of the intermediate planets. Armellin et al. (2007) designed maneuvers also using the planet Mars. Returning missions are also possible, as shown in Henning et al. (2014), as is a double-flyby mission in Mars, as explained in Jesick (2015). A study of a Mars freereturn mission is described in Hughes et al. (2015).
Considering all those aspects, the present paper has two objectives: (i) finding powered aero-gravity assisted trajectories around the planet Venus, because this planet has a very dense atmosphere; (ii) making, for the first time, a detailed study of the contribution of each force involved in the dynamics, to be able to show in detail their relative importance. The main goal of this topic is to understand the variations in the contributions of lift and drag due to the modifications of the trajectories made by the impulsive maneuver. This study is made by integrating the cumulative effects of the accelerations coming from each force along time, as done before in the literature on similar problems (Prado 2013; Lara 2016).
The equations of motion are derived from the restricted three-body problem (Szebehely 2012) with the inclusion of the atmosphere of Venus. This atmosphere is modeled using an exponential approximation. Besides those terms, an impulse is added to the velocity vector when the spacecraft passes by the periapsis of its orbit around the planet. This combined maneuver is more efficient compared to other options in terms of fuel consumption, if the best geometry can be found.
The study of the effects of each force is then performed, along with the discovered trajectories using the planet Venus, which were not studied before, and that turned out to provide variations of energy up to eight times larger than the ones given by the Earth, and four times the results obtained from Mars. The participation of the atmosphere is indexed by the ballistic coefficient, which ranges from zero (when there is no atmosphere) up to 5.0 × 10−7km2/kg. It is also necessary to assume values for the lift-to drag ratio (L/D). The values used here for L/D are: 0, which represent trajectories without lift; 1, which represents the situation where lift is equal to drag, with a component pointing opposite to Venus; −1, representing the same situation just described, but with the lift having a component pointing to Venus; the maximum values 9 and −9, the best scenarios for a higher lift, representing the situations where the lift has components pointing opposite to Venus or in the direction of Venus, respectively. Those maximum values are valid for Waveriders, as shown in the references (Lewis & McRonald 1992, 1991). They are constant during the whole trajectory. So, this research is a continuation of previous researches considering maneuvers without the presence of the impulse, and the complete maneuver using the planets Earth (Murcia & Prado 2017b), and Mars (Murcia et al. 2018).
Of course it is known that this type of maneuver has difficulties in practical implementations, always presenting risks of collision. Therefore, the goal of the present paper, similarly to the papers cited before, is to show a potential available in nature to provide help in interplanetary maneuvers. It can be used when necessary for the mission, after a detailed study of the risks and benefits involved. It is also expected that improvements in the accuracy of propulsion systems, as well as in guidance and control techniques available to interplanetary spacecraft, may make this type of maneuver more popular in the future.
2. DYNAMICAL MODEL
The dynamical system is constituted by three bodies: the largest one is called M1 (the Sun in this research), the second more massive body is called M2 (Venus in our simulations) and a third body with negligible mass is called M3 (the spacecraft travelling around Venus). The spacecraft is moving around the Sun when it passes near Venus. This passage modifies the orbit of the spacecraft around the Sun in a maneuver called Swing-By. The mathematical model is based on the restricted three-body problem (Szebehely 2012) adding the terms derived from the atmosphere of Venus. Equations (1-4) describe the motion of the spacecraft, where FxAtm and FyAtm are the horizontal and vertical components (in the orbital plane), respectively, of the forces giving by the atmosphere of Venus. Ω is the potential.
In those equations →L is lift, which is a force in the orbital plane of the spacecraft and perpendicular to its motion; →D is drag, a force in the direction opposite to the motion of the spacecraft. Because the trajectories are analyzed in the orbital plane, acceleration and velocity in the Z direction are null. Drag and lift are functions of the projected area in the direction of the motion of the spacecraft (A), the drag and lift coefficient [(CD), (CL), respectively], the density of the atmosphere and the velocity spacecraft-atmosphere of Venus (Vw). Equation (5) shows this dependency.
To follow the usual nomenclature available in the literature, it is possible to combine m, the mass of the spacecraft, A and CD in the so called ballistic coefficient CB. It is also useful to define the coefficient CBL = CB (CL/CD). In this way, equations (6-7) define those coefficients. The ratio CL/CD, and hence L/D, is a function of the incidence angle of the spacecraft, or angle of attack. In the present paper it is assumed that the spacecraft attitude keeps an incident angle such that the ratio L/D is constant, and this value is used as an independent parameter, replacing the incident angle.
The variations of energy can be obtained, in the inertial frame, by equations (8-10), representing the energy before and after the passage by Venus, respectively (Prado 2007).
The numerical simulations are made using a periapsis altitude fixed at 330 km, so as to reduce the number of parameters. Of course the variation of this parameter changes the results, but the general behaviors are the same, not affecting the conclusions obtained here. If the variations are not too large the results are close to linear. Regarding the geometry of approach, the two extreme values in terms of variations of energy are used: 90º(minimum variation) and 270º(maximum variation) (Broucke 1988). After defining the initial conditions, numerical integrations are made using negative time steps (Neto & Prado 1998) with the spacecraft starting at the periapsis of its orbit around Venus without including the effects of the atmosphere (CB = 0). The integration is performed until the spacecraft reaches a location that can be assumed to be far enough from Venus and the system spacecraft-Sun can be modeled by Keplerian orbits. The initial position and velocity vectors of the spacecraft are the initial conditions used for the numerical integrations. So, this is the starting point of all the trajectories simulated in the present paper. In the case of the gravity-assisted maneuvers, the trajectories of the spacecraft pass near Venus, but not inside the atmosphere of the planet, and then proceed to another point that is very far from Venus. From those extreme points it is possible to obtain the variations of energy provided by the gravity-assist maneuver.
After that, comes the aero-gravity-assist maneuver. In this type of maneuver the spacecraft comes from the same point, but now passes the atmosphere of Venus. The ballistic coefficient has values in the range from 0.0 to 5.0×10−7km2/kg. The same technique used in the pure gravity-assisted maneuvers is applied to calculate the energy variations. Numerical tests are made to verify captures of the spacecraft by the planet and those trajectories are excluded from the present study. The maneuvers including the application of the impulse at the periapsis of the orbit of the spacecraft around Venus is the main objective of this paper and it is described next. It is similar to the aero-gravity-assist maneuver just explained, but there is an impulse applied at the periapsis. A graphical representation is shown in Figure 1.
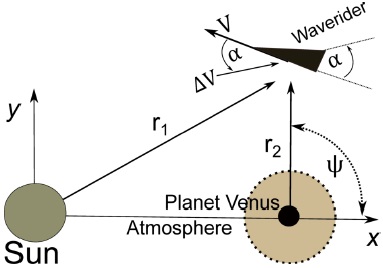
Fig. 1 Powered-aero-gravity-assisted maneuver around Venus (Gomes et al. 2016). The color figure can be viewed online.
The complete system has Venus orbiting the Sun in a circular orbit and the spacecraft travelling around those two celestial bodies. The motion is assumed to be planar, with the spacecraft constrained to the plane of the motion of the primaries. The atmosphere of Venus is modeled by an exponential, expressed by ρ = 65 exp (−h/15.9) kg/m3, where h represents the altitude of the spacecraft with respect to the surface of Venus1, in km (see Table 1). A Runge-Kutta-Fehlberg 7/8 method with adaptative step size (Fehlberg 1968) is implemented for the numerical integrations performed here.
3. RESULTS
The results consist of a large number of simulations that can show the influence of the atmosphere of Venus on the trajectories obtained by the maneuver that combines impulse, close approach and passage through the atmosphere of the planet. The velocity at periapsis used in the present research is 17.5 km/s (0.5 canonical units), the same value (in canonical units) used in simulations made using the Earth (Murcia & Prado 2017b) and Mars (Murcia et al. 2018). It is a value that allowed to generate maneuvers with significant variations of energy, but that do not have a large number of captures or collisions. The simulations also used a constant number for the altitude of the periapsis, which is 330 km. This value is used based on the same criterion of having significant variations of energy and a small number of captures and collisions. The use of fixed values for those parameters simplifies the study, since this problem has already a large number of parameters to be considered. The use of different values for these parameters modifies the results, but the general behaviors are the same, not affecting the main conclusions. In Table 1 are presented the Venus parameters selected for the simulations. Fig. 1. Powered-aero-gravity-assisted maneuver around Venus (Gomes et al. 2016). The color figure can be viewed online.
The simulations considered values for the angle of approach of 90º, the region with maximum losses of energy, and 270º, the region with maximum gains of energy (Broucke 1988). The lift/drag (L/D) ratio assumed five different values: −9, one of the maximum values cited in the literature and pointing to Venus (Lavagna et al. 2005; Lewis & McRonald 1992, 1991; Randolph & Mcronald 1992); −1, when drag and lift are equal, with the lift pointing towards Venus; 0, when there is no lift; 1, when drag and lift are equal, with lift pointing in the direction opposite to Venus; 9, one of the maximum values cited in the literature for L/D and pointing in the direction opposite to Venus (Lavagna et al. 2005). Regarding the magnitude of the impulse, the values used are 0.0 and 0.5 km/s, representing an unpowered maneuver and a powered maneuver with a value for the magnitude of the impulse that is possible to reach with current technology.
3.1. Variations of Energy Obtained from Venus
The first set of results shows the variations of energy per mass unit, in canonical units. A color code is used, where the ballistic coefficient is represented in the horizontal axis, while the vertical axis shows the direction of the impulse. The other parameters are kept constant for each plot: the L/D ratio, the magnitude of the impulse, and the angle of approach. In this way, graphs are made to show the effects of those variables in the maneuvers around Venus. The full range of possible directions for the impulse is used, going from −180º to 180º. The values of CB are inside the interval starting at zero (no atmosphere) and going up to 5.0 × 10−7 km2 /kg, as used in similar studies (Prado 1996; Murcia & Prado 2017b; Murcia et al. 2018). The results are shown in Figures 2 to 9. The reference for the direction of the impulse defines the angle 0º, when the direction of the impulse is against the motion of the spacecraft and 180º, when it is in the opposite direction. The values for this angle increase in the clockwise sense. In this way, an angle of 90º means that the impulse is made in the direction of Venus, while −90º indicates an impulse in the direction opposite to Venus.
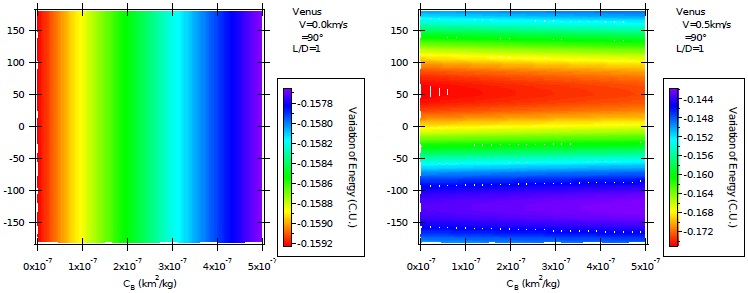
Fig 2 Variation of energy per unit of mass as a function of the direction of the impulse for AGA with L/D = 1 and ψ = 90º for unpowered (left) and powered (right) maneuvers. The color figure can be viewed online.
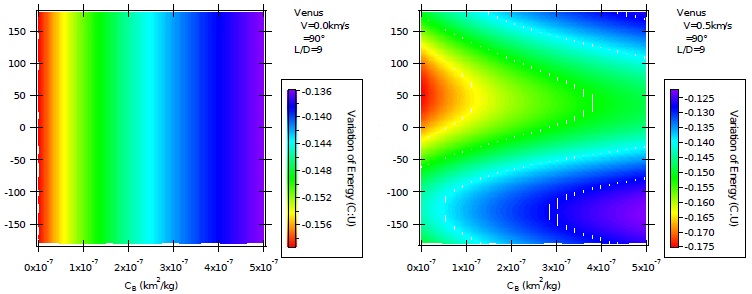
Fig 3 Variation of energy per unit of mass as a function of the direction of the impulse for AGA with L/D = 9 and ψ = 90º for unpowered (left) and powered (right) maneuvers. The color figure can be viewed online.
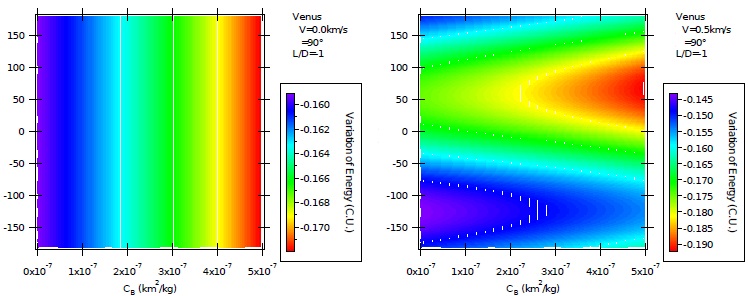
Fig 4 Variation of energy per unit of mass as a function of the direction of the impulse for AGA with L/D = −1 and ψ = 90º for unpowered (left) and powered (right) maneuvers. The color figure can be viewed online.
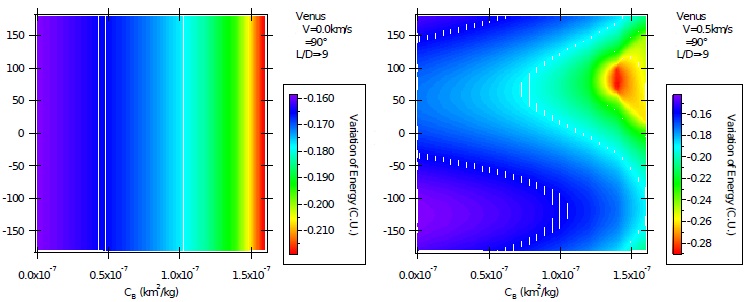
Fig 5 Variation of energy per unit of mass as a function of the direction of the impulse for AGA with L/D = −9 and ψ = 90º for unpowered (left) and powered (right) maneuvers. The color figure can be viewed online.
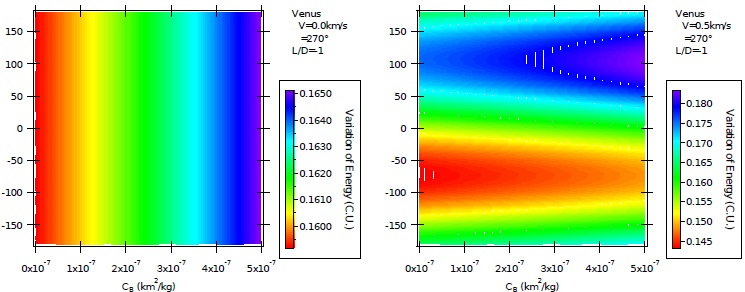
Fig 6 Variation of energy per unit of mass as a function of the direction of the impulse for AGA with L/D = −1 and ψ = 270º for unpowered (left) and powered (right) maneuvers. The color figure can be viewed online.
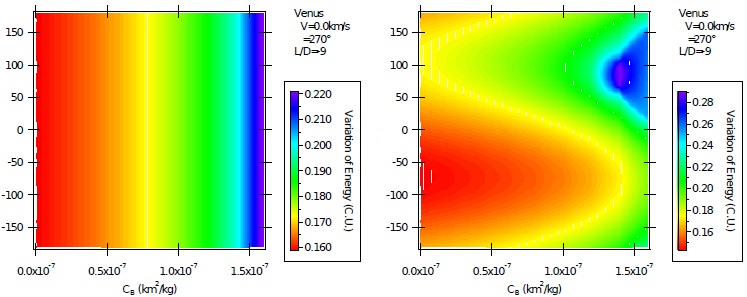
Fig 7 Variation of energy per unit of mass as a function of the direction of the impulse for AGA with L/D = −9 and ψ = 270º for unpowered (left) and powered (right) maneuvers. The color figure can be viewed online.
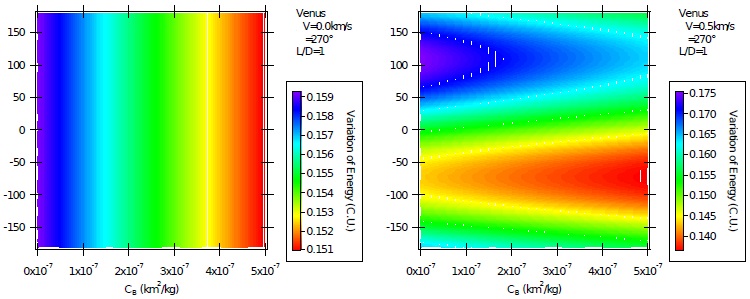
Fig 8 Variation of energy per unit of mass as a function of the direction of the impulse for AGA with L/D = 1 and ψ = 270º for unpowered (left) and powered (right) maneuvers. The color figure can be viewed online.
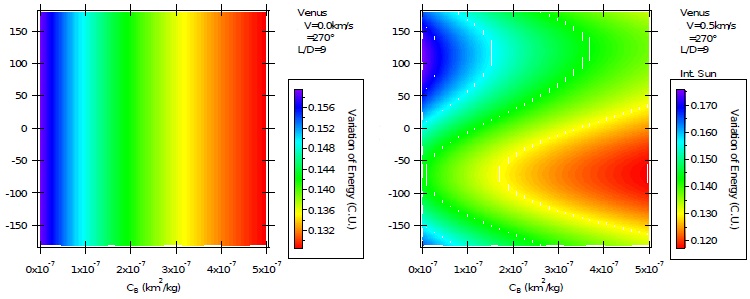
Fig 9 Variation of energy per unit of mass as a function of the direction of the impulse for AGA with L/D = 9 and ψ = 270º for unpowered (left) and powered (right) maneuvers. The color figure can be viewed online.
Figures 2 and 3 show the results when L/D = 1 and 9 with ψ = 90º, (maneuvers where the spacecraft looses energy [Broucke 1988]), for both powered (right side) and unpowered (left side) maneuvers. The powered maneuvers use a magnitude of 0.5 km/s. The unpowered orbits show that the removal of energy decreases with the ballistic coefficient, so the maneuver removes less energy with the increase of the atmospheric forces. This is the final result of the compensations that occur due to the extra energy that is removed by drag and the smaller reductions of the energy variations obtained due to the smaller effects from the gravity of Venus, since lift is pointing opposite to Venus, which decreases the angle of curvature. Of course, there is also the effect of moving the angle of approach from the optimal value, but this is a small effect compared to the others. The direction of the impulse (angle α) gives important effects on the maneuvers. For values of α larger than 120º, the plots are dominated by the green and blue colors, which mean smaller reductions of energy. It is also seen that the regions in the interval from zero to 120º have the largest values for the loss of energy, with the maximum occurring around α = 60º. This is the case where the impulse has a component pointing to Venus, which increases the effects of the gravity of the planet, as well as the atmospheric forces. This direction also gives a component opposite to the motion of the spacecraft, which directly removes energy from the spacecraft. The intervals below −60º have mainly a blue color, indicating the minimum removal of energy. This is a region where the propulsion is applied with a component pointing against the motion of the spacecraft, and another sending the spacecraft away from Venus, which reduces the gravity part of the maneuver. These results have the same general behavior for the maneuvers using the Earth (Murcia & Prado 2017b) and Mars (Murcia et al. 2018), but the magnitudes of the energy variations are very different. To perform the necessary conversions to show the results in the same units (the canonical systems are not the same for all the three systems), it is necessary to use the orbital velocities of the planets around the Sun. This is done because the unit of energy per unit of mass is the unit of the square of the velocity. The values for the orbital velocities are 29.78 km/s for the Earth, 24.07 km/s for Mars and 35.20 km/s for Venus. This means that the variations of energy in the maneuvers around the Earth have to be divided by 1.3971 (35.20/29.78)2 and the variations of energy obtained from Mars have to be divided by 2.1386 (35.20/24.07)2 to be compared with the equivalent results for Venus. The variations of energy obtained in the maneuvers around the Earth lie in the interval −0.0269 to −0.0275 canonical units of the Earth-Sun system (Murcia & Prado 2017b), which means −0.0192 to 0.0301 in the equivalent canonical system of units used for Venus. Regarding Mars, the variations of energy lie in the interval −0.0809 to −0.0813 canonical units of the Mars-Sun system (Murcia et al. 2018), which means −0.0378 to 0.0380 in the equivalent canonical system of units used for Venus. The present research indicates that the variations of energy given by Venus lie in the interval from −0.1592 to −0.1578 canonical units. Those values are much larger compared to the other two planets, about eight times the effects obtained when using the Earth and four times the variations giving by Mars. Those variations are functions of the combination of the values of the masses, radii and density profiles of the atmospheres of the planets, which makes it difficult to predict this type of results without performing the simulations made here. The results shown in the present paper indicate that Venus is the best planet of the three ones compared here, with Mars in second place. The Earth is the one that shows the smaller variations of energy in this type of maneuver.
Next, Figure 3 shows the equivalent results for the maneuvers around Venus when L/D = 9 and ψ = 90º, which is a situation of very high lift pointing opposite to Venus. The behavior of the unpowered maneuvers is similar, with the energy losses decreasing when the ballistic coefficient is increased. The new aspect is the larger interval of the energy variations, which is now from −0.1580 to −0.1360 canonical units. The higher lift takes the spacecraft away from Venus, which decreases the energy removal made by the maneuver. Powered maneuvers are shown in the right side of the figure. The direction of the impulse has the same important effects observed when L/D = 1, with the maximum loss of energy around α = 60º. In this geometry the impulses have components pointing towards Venus and against the motion of the spacecraft. The interval below −60º is where the impulses point against Venus and opposite to the motion of the spacecraft, so smaller effects from the maneuver are obtained. The literature (Murcia & Prado 2017b; Murcia et al. 2018) shows similarities with the results for the Earth and Mars, but with different values for the magnitudes of the energy variations. In particular, maneuvers using the Earth indicate the possibility of zero variations of energy, which does not occur for Venus and Mars. In terms of canonical units for the Venus-Sun system, the variations obtained from the Earth range from 0.0000 to −0.0280 canonical units. The similar results for Mars lie in the interval from −0.0234 to −0.0468 canonical units (Murcia et al. 2018). Figure 3 shows that the equivalent results for Venus vary from −0.1750 to −0.125 canonical units, which are much larger values. This confirms and quantifies how much better is Venus for this type of maneuver, even in the powered case. Another fact noted is the stronger effects of the atmosphere. This point can be observed in the inclinations of the lines separating two neighboring colors. The yellow lines dividing the green and red regions are good examples. They were almost horizontal when L/D = 1, but are very inclined for L/D = 9. Following a line of constant α (horizontal line), it is easy to see that the larger values for the ballistic coefficient correspond to smaller losses of energy. This happens because the positive sign for the lift force reduces the gravity effects of the maneuver, because the spacecraft is moved away from Venus.
Figure 4 considers the situation of negative values for the lift to drag ratio (L/D = −1 and ψ = 90º), indicating that lift is pointing now to Venus. This situation causes the spacecraft to stay longer in the atmosphere, so reducing the periapsis altitude. Therefore, drag has a higher influence, which removes more energy directly from the spacecraft. The unpowered maneuvers now have a different behavior, when compared with maneuvers with positive lift, and the energy losses increase with the ballistic coefficient, since lift now points to Venus. In this situation, drag (directly) and lift (indirectly, by increasing the effects of gravity) remove more energy from the spacecraft.
The powered maneuvers (right side) also show interesting results. The maximum and minimum variations of energy occur at the same locations, as already explained. The larger effects of the atmosphere can be observed in the inclinations of the lines separating two adjacent colors. As mentioned before, the yellow lines are very good examples, since they are no longer horizontal, as they were when L/D = 1. Following again a horizontal line (α constant), the borderlines between two colors show that increasing the ballistic coefficient can give larger values for the losses of energy. This happens because the negative values for the lift to drag ratio indicate that lift is pointing to Venus, so lift sends the spacecraft toward Venus, which increases the effect of the gravity part of the maneuver. Since this is a maneuver that reduces the energy of the spacecraft, the effects are combined with drag, both of them removing energy from the spacecraft. The consequence is that lift causes the maneuver to be very dependent on the ballistic coefficient.
Figure 5 considers the situation of negative large lift to drag ratio, with L/D = −9, again in the geometry where ψ = 90º. It is shown that the unpowered maneuvers have the same behavior, just with different magnitudes for the variations of energy. It is a situation with stronger effects from the lift force, which makes the interval of variations of energy wider. It now goes from −0.2200 to −0.1600 canonical units, compared to an interval that goes from −0.172 to −0.160 canonical units when L/D = −1. The powered maneuvers (right side of the figure) also identify the stronger atmospheric effects. Just look at the more inclined lines. In both Figures 4 and 5, the triangular forms visible in the plots are due to the stronger effects of the atmosphere. There are now larger increases in the losses of energy with the increase of the ballistic coefficient. It is seen that the plot is now dominated by the blue color, in particular dark blue, which indicates smaller values for the variations of energy.
We now consider geometries to increase the energy of the spacecraft, so ψ = 270º (Murcia & Prado 2017b). Figure 6 shows the results of the simulations for L/D = −1. Unpowered maneuvers show plots composed by vertical lines, as expected, because there are no impulses. The increases of energy are stronger when using larger values for the ballistic coefficients. Note that red colors are now located at the left sides of the plots. This direction of the lift force moves the spacecraft closer to Venus, which increases the gains of energy from the gravity part of the maneuver. They are larger compared to the extra losses of energy from the increased drag. The variations lie now in the interval from 0.1595 to 0.1650 canonical units. The powered maneuvers (right side of the figure) show nearly horizontal lines with little dependency on the ballistic coefficient. The impulses are strong, so they dominate the maneuvers in this situation. The maximum variation of energy is around α = 120º, for the reasons explained before. In this geometry, the impulses have components pointing to Venus, which increase the effects of the gravity of Venus; and another component in the direction of the motion of the spacecraft, which directly gives energy to the spacecraft. On the opposite side, the minimum variations occur around α = −75º. In this case the impulses have components pointing opposite to Venus and against the motion of the spacecraft, both of them removing energy from the spacecraft.
Figure 7 shows the results when L/D = −9 and ψ = 270º, the situation of extreme lift and gains of energy. The general behavior is the same, showing only differences in the magnitudes of the variations. They are higher due to the increase of the lift force. The values for the variations of energy are now in the interval from 0.1600 to 0.2200 canonical units in the unpowered case, compared to the interval from 0.1595 to only 0.1650 canonical units, when L/D = −1. For the powered maneuvers, the range is now from 0.15 to 0.28 canonical units, against an interval from 0.1450 to 0.1800 canonical units for L/D = −1. Note the existence of triangular forms in the plots made for the powered maneuvers, which is due to the stronger effects of the atmospheric forces. Note also that the energy gains increase with the ballistic coefficient, since the maneuver gets stronger effects from the atmosphere.
The results for lift pointing opposite to Venus and ψ = 270º are shown in Figures 8 and 9, when L/D = 1 and 9, respectively. The increases in the energy are now reduced by the decrease of the ballistic coefficient in the case of unpowered maneuvers. This is due to drag, which removes energy directly from the spacecraft, and lift, which moves the spacecraft away from Venus, so decreasing the effects of the gravity of Venus. It is the same behavior observed in the powered maneuvers. The atmospheric contributions to the maneuvers are very small when L/D = 1, which can be observed by the horizontal border lines between two adjacent colors. Larger effects can be seen in the situation where L/D = 9, because the same lines are now inclined and the triangular shapes are again present.
3.2. Identifying the Contribution of Each Force in the Maneuvers
This section has the goal of measuring the effects of each force involved in the dynamics. Special attention is given to the variation of the contribution of lift and drag in the powered maneuvers. The application of the impulse changes the orbit directly by modifying the velocity vector instantaneously, but it also changes the orbit indirectly, because the new trajectories may stay for a longer or shorter time inside the atmosphere, so increasing or decreasing the contribution of lift and drag. This measurement is done by performing numerical integrations of the accelerations given by each force included in the mathematical model. It is an idea similar to that of Sanchez et al. (2014), where the accelerations from each term of the gravity field of the Earth are numerically integrated to show the contribution of each term on the trajectories of the spacecraft. These integrations made over the whole trajectory of the spacecraft give the total increase of velocity that each force delivers to the spacecraft. The literature has several papers studying different forms of integral indexes to quantify the perturbation level of orbits (Lara 2016; Prado 2013), similar to the idea used in the present session. The contribution of each force involved in the dynamics (FC) is measured as the integration of the acceleration of each force (ac) during the total time interval of the trajectory, as shown by equation (11). This gives the total variation of velocity given to the spacecraft by each force.
The results are shown in Figures 10 to 12, where a color code indicates the value of the integral of the acceleration from a given force as a function of the ballistic coefficient in the horizontal axis and the angle that defines the direction of the impulse in the vertical axis. The magnitude of the impulse, the angle of approach and the lift to drag ratio are kept constant for each plot.
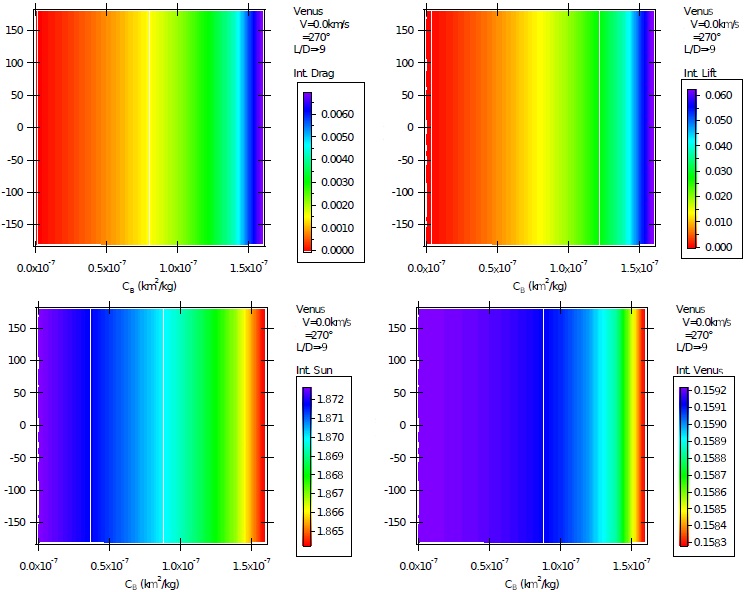
Fig. 10 Contributions of the accelerations from drag, lift, gravity of the Sun and gravity of Venus, in CU, for unpowered maneuvers with ψ = 270º and L/D = −9. The color figure can be viewed online.
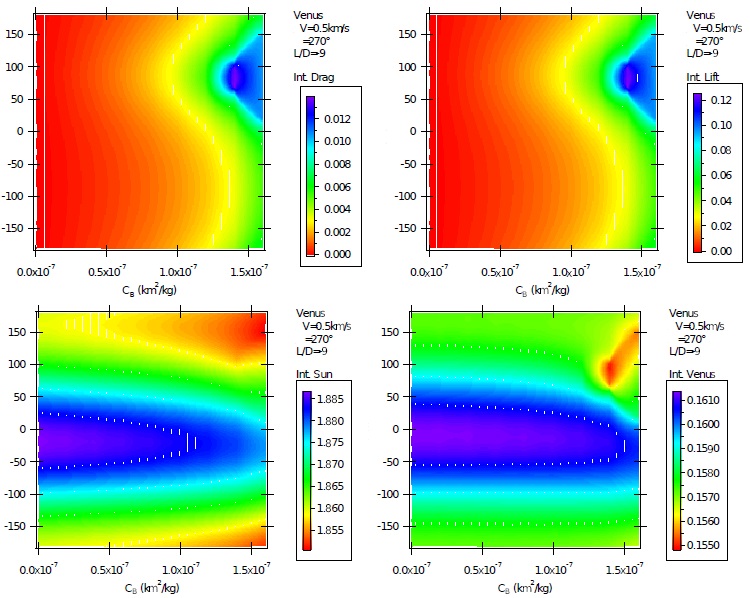
Fig. 11 Contributions of the accelerations from drag, lift, gravity of the Sun and gravity of Venus, in CU, for powered maneuvers using an impulse with magnitude of 0.5 km/s with ψ = 270º and L/D = −9. The color figure can be viewed online.
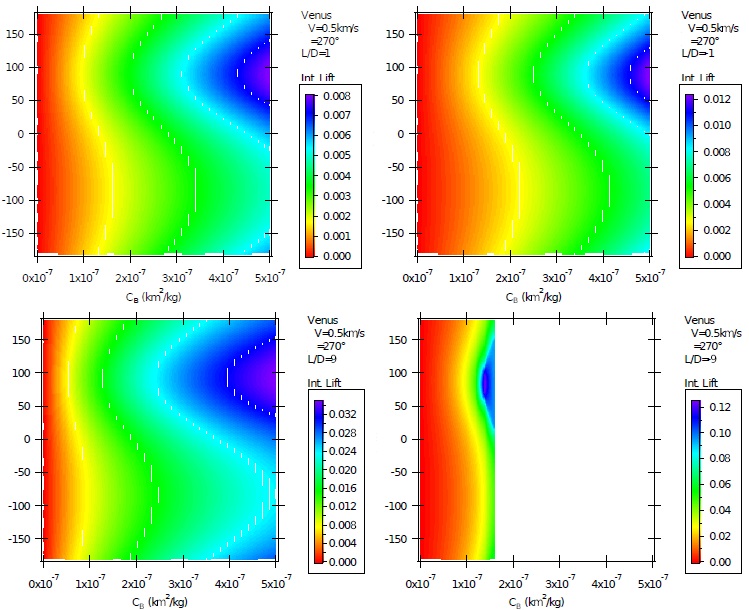
Fig. 12 Contributions of the accelerations from drag, lift, gravity of the Sun and gravity of Venus, in CU, for powered maneuvers using an impulse with magnitude of 0.5 km/s with ψ = 270º and L/D = 9. The color figure can be viewed online.
The results quantify the contributions of lift, drag, gravity of the Sun and gravity of Venus for each trajectory. Of course the gravity of the Sun dominates the motion, because the passage by Venus is short and the Sun is always acting on the system. This is clearly shown in Figure 10, made for the unpowered maneuvers with ψ = 270º and L/D = −9. This figure is very typical for all the simulations, making unnecessary the reproduction of similar results. It shows that the gravity of Venus has contributions in the interval from 0.1583 to 0.1592 C U , about 8.5% of the contribution of the Sun, which is in the interval from 1.8650 to 1.8720 C U (C U denotes canonical units). The contribution of Venus, in metric units, amounts to 5.6 km/s in order of magnitude, more than eleven times the impulse applied. This shows the importance of the gravity assisted maneuvers. These variations are functions of the ballistic coefficient, because the increase of the atmospheric forces reduces the velocity of the spacecraft, which increases the integration time, since the integration is stopped when the spacecraft reaches a fixed distance from Venus. Since this is the unpowered maneuver, the angle α does not play any role in the results. The lift force has a contribution in the range from 0.00 to 0.06 CU, of course depending strongly on the ballistic coefficient. This means that its contribution goes from zero to about 37% of the contribution of the gravity of Venus, which indicates an important role in the dynamics. The contribution of drag is similar, just with the magnitudes divided by 9, since L/D = 9.
Next, Figure 11 is obtained for powered maneuvers using a magnitude of impulse of 0.5 km/s, with ψ = 270º and L/D = −9. The effect of the direction of the angle that defines the direction of the impulse (α) is clear. The maximum effects for lift and drag are located near α = 90º and the minimum around α = −90º. This is expected, since α = 90º means that the impulse is applied in the direction of Venus, so increasing the atmospheric flight; while α = −90º means that the impulse is applied in the direction opposite to Venus, so decreasing the atmospheric flight. The increase of the contributions with the ballistic coefficient is of course confirmed. It is important to note the magnitudes of the maximum effects compared to those of the unpowered maneuvers. The maximum is now 0.12 C U , twice the value showed by the unpowered maneuvers. This means that the lift force can now contribute about 75% of the variation of velocity given by the gravity of Venus, a very large and important contribution. Drag has the same behavior, just divided by the factor 9. This is an interesting explanation of the indirect effects of the impulse that changes the trajectory of the spacecraft and, if the direction is properly used, it can increase the atmospheric flight and the effects of lift and drag. The effects of the gravity of the Sun and Venus show small increases, due to the larger integration times caused by the stronger effects of lift and drag that slow down the spacecraft, as already explained.
The final step of the present study shows the variations of the contribution of the lift force as a function of the lift to drag (L/D) ratio (Figure 12). This is the only force showed here, because drag follows the same behavior, just with the magnitudes divided by 9, and the contributions of the gravity of the Sun and Venus have only small variations. The upper plots consider the values of L/D = 1 and −1, and they show the behavior already explained. The main fact to be noted is that the contribution of lift is increased by 50% (from 0.008 to 0.012 C U ) when the negative lift to drag ratio is used. This means a contribution of 0.42 km/s, about the same value used in the impulse applied. This increase is expected, because the negative lift to drag ratio sends the spacecraft in the direction of Venus, so increasing the atmospheric flight. The quantification of this increase is important and it is shown in Figure 12. In the same way, the increase of lift from L/D = ±1 to ± 9 enlarges the contribution of this force. The maximum goes from 0.008 CU, when L/D = 1, to 0.012 C U , when L/D = −1. When considering higher values for the lift, the maximum contributions go from 0.033 CU, when L/D = 9, to 0.120 CU, when L/D = −9. These values indicate a contribution around 4.22 km/s, more than eight times the impulse applied. These numbers show the high relative importance of lift in this situation. This figure shows a complete quantification of the effects of lift in the powered maneuvers. It also shows the problem of collisions with Venus. They are expected to appear when using a high negative lift to drag ratio, but it is important to define the limit of the ballistic coefficient that causes this problem. Figure 12 shows that this limit is around 1.5 × 10−7 km2 /kg. After this point there is a blank region in the plot, which indicates the occurrence of collisions with Venus due to the very strong effect of its atmosphere. The maneuvers using ψ = 90º have exactly the same results, for the same reasons, so they are not repeated in the present paper.
4. CONCLUSIONS
This paper presents a study of powered-aerogravity-assist maneuvers around Venus. This is a maneuver that uses the lift and drag forces from the atmosphere of Venus, an impulsive maneuver, and the gravity field of Venus to modify the trajectory of a spacecraft. The objective is to measure the variations of energy of a spacecraft passing by Venus as a function of the parameters that describe the maneuver, like the direction and magnitude of the impulse applied to the spacecraft; the periapsis distance of the close approach; the velocity and the angle of approach of the spacecraft; and the ballistic coefficient, which is a quantity that defines the effects of the atmosphere. The results are expressed in figures where the colors show the energy variations as a function of those parameters. Two particular geometries are used to obtain the results, the one with maximum gains and the one with maximum losses of energy.
The results identified clearly the effects of the atmosphere in maneuvers around Venus, showing that this planet gives better results compared to Earth and Mars for this type of maneuver. The variations of energy given by Venus are about eight times the values obtained using the Earth, and four times the equivalent results verified in Mars.
The importance of using lift pointing to Venus (negative values of L/D) is shown, and the increases in the energy variations compared to positive lift are detailed. This geometry increases the effects obtained from the gravity part of the maneuver.
The maximum losses of energy occur for impulses with direction around α = 60º, with a component against the motion of the spacecraft and another component sending the spacecraft toward Venus, to increase the effects of the gravity maneuver. In the situations where the goal is to increase the energy of the spacecraft, the maximum values occur for impulses with directions near α = 120º, because they have one component pointing to Venus and another component in the direction of the motion of the spacecraft, so both components help to increase the energy of the spacecraft.
The use of low values for the lift force (when L/D = 1) generates maneuvers dominated by the impulse, while large values for the lift force (when L/D = 9) generate maneuvers where the impulse and passage by the atmosphere of Venus have similar contributions.
The analysis of the contribution of the forces involved in the dynamics shows that the gravity of Venus has contributions around 0.159 C U , which is about 8.5% of the contribution of the Sun, which is near 1.870 CU. This value confirms the importance of the gravity field of Venus, which gives a contribution more than eleven times the velocity increment given by the impulse.
In the unpowered maneuvers, when L/D = −9, lift has a contribution in the range from 0.00 to 0.06 CU, depending on the ballistic coefficient. This implies a maximum contribution of around 37% of the contribution of the gravity of Venus, an important value. The contribution of drag is similar, just with the magnitudes divided by 9, since L/D = 9.
The powered maneuvers show that the maximum effect for lift and drag is located near α = 90º (when the impulse is applied in the direction of Venus) and the minimum near α = −90º (opposite direction). The maximum effects increase to 0.12 CU, twice the value showed by the unpowered maneuvers. The contribution of lift increases to about 75% of the contribution of the gravity of Venus. Drag has the same behavior, just divided by the factor 9, because L/D is constant for all the trajectories analyzed. Those numbers are an illustration of the indirect effects of the impulse; larger effects are obtained from the atmosphere due to the modification of the trajectory of the spacecraft.
This analysis also shows that the contribution of lift is increased by 50%, from 0.008 to 0.012 C U , when negative L/D is used, in the case where lift is equal to drag. In the same way, when lift is nine times larger than drag, the increase of the lift contribution goes from 0.032 CU to 0.120 CU, when a negative lift to drag ratio is used. Those numbers show the importance of lift, which gives a contribution more than eight times larger than the velocity increment given by the impulse.
The problem of collisions with Venus is also studied, and the results show that, when using L/D = −9, this problem appeared beyond a limiting value for the ballistic coefficient around 1.5×10−7km2/kg.











 text new page (beta)
text new page (beta)


