1. INTRODUCTION
Galaxies are complex systems, formed mainly from the cold gas captured by the gravitational potential of dark matter halos and transformed into stars, but also reheated and eventually ejected from the galaxy by feedback processes (see for a recent review Somerville & Davé 2015). Therefore, the content of gas, stars, and dark matter of galaxies provides key information to understand their evolution and present-day status, as well as to constrain models and simulations of galaxy formation (see e.g., Zhang et al. 2009; Fu et al. 2010; Lagos et al. 2011; Duffy et al. 2012; Lagos et al. 2015).
Local galaxies fall into two main populations, according to the dominance of the disk or bulge component (lateand early-types, respectively; a strong segregation is also observed by color or star formation rate). The main properties and evolutionary paths of these components are different. Therefore, the present-day stellar, gaseous, and dark matter fractions are expected to be different among latetype/blue/star-forming and early-type/red/passive galaxies of similar masses. The above demands that the gas-to-stellar mass relations be determined separately for each population. Morphology, color and star formation rate correlate among them, though there is a fraction of galaxies that skips the correlations. In any case, when only two broad groups are used to classify galaxies, the segregation in the resulting correlations for each group is expected to be similar for any of these criteria. Here we adopt the morphology as the criterion for classifying galaxies into two broad populations.
With the advent of large homogeneous optical/infrared surveys, the statistical distributions of galaxies, for example the galaxy stellar mass function (GSMF), are now very well determined. In the last years, using these surveys and direct or statistical methods, the relationship between the stellar, M∗, and halo masses has been constrained (e.g., Mandelbaum et al. 2006; Conroy & Wechsler 2009; More et al. 2011; Behroozi et al. 2010; Moster et al. 2010; Rodríguez-Puebla et al. 2013; Behroozi et al. 2013; Moster et al. 2013; Zu & Mandelbaum 2015). Recently, the stellar-to-halo mass relation has been even inferred for (central) galaxies separated into blue and red ones by Rodríguez-Puebla et al. (2015). These authors have found that there is a segregation by color in this relation (see also Mandelbaum et al. 2016). The semi-empirical stellar-to-halo mass relation and its scatter provide key constraints to models and simulations of galaxy evolution. These constraints would be stronger if the relations between the stellar and atomic/molecular gas contents of galaxies were included. With this information, the galaxy baryonic mass function can be also constructed and the baryonic-to-halo mass relation can be inferred, see e.g, Baldry et al. (2008).
While the stellar component is routinely obtained from large galaxy surveys in optical/infrared bands, the information about the cold gas content is much more scarce due to the limits in sensitivity and sky coverage of current radio telescopes. In fact, the few blind HI surveys, obtained with a fixed integration time per pointing, suffer from strong biases, and for H2 (CO) there are no surveys. For instance, the HI Parkes All-Sky Survey (HIPASS; Barnes et al. 2001; Meyer et al. 2004) or the Arecibo Legacy Fast ALFA survey (ALFALFA; Giovanelli et al. 2005; Haynes et al. 2011; Huang et al. 2012a), miss galaxies with low gas-to-stellar mass ratios, specially at low stellar masses. Therefore, the HI-to-stellar mass ratios inferred from the crossmatch of these surveys with optical ones should be regarded as an upper limit envelope (see e.g., Baldry et al. 2008; Papastergis et al. 2012; Maddox et al. 2015). In the future, facilities such as the Square Kilometre Array (SKA; Carilli & Rawlings 2004; Blyth et al. 2015), or precursor instruments such as the Australian SKA Pathfinder (ASKAP; Johnston et al. 2008) and the outfitted Westerbork Synthesis Radio Telescope (WSRT), will bring extragalactic gas studies more in line with optical surveys. Until then, the gas-to-stellar mass relations of galaxies can be constrained: (i) from limited studies of radio follow-up observations of large optically-selected galaxy samples or by crosscorrelating some radio surveys with optical/infrared surveys (e.g., Catinella et al. 2012; Saintonge et al. 2011; Boselli et al. 2010; Papastergis et al. 2012); and (ii) from model-dependent inferences based, for instance, on the observed metallicities of galaxies or from calibrated correlations with photometrical properties (e.g., Baldry et al. 2008; Zhang et al. 2009).
While this paper does not present new observations, it can be considered as an extension of previous efforts to attempt to determine the HI-, H2- and cold gas-to-stellar mass correlations of local galaxies over a wide range of stellar masses. Moreover, here we separate galaxies into at least two broad populations, late and early-type galaxies (hereafter LTGs and ETGs, respectively). These empirical correlations are fundamental benchmarks for models and simulations of galaxy evolution. Our main goal here is to constrain these correlations by using and uniforming large galaxy samples of good quality radio observations with confirmed optical counterparts. Moreover, the well determined local GSMF combined with these correlations can be used to construct the galaxy HI and H2 mass functions, GHIMF and GH2MF, respectively. As a test of consistency, we compare these mass functions with those reported in the literature for HI and CO (H2).
Many of the samples compiled here suffer from incompleteness and selection effects or, in many cases, the radio observations provide only upper limits to the flux (non-detections). To provide reliable determinations of the HI and H2-to-stellar mass correlations, for both LTGs and ETGs, here we homogenize as much as possible the data, check them against selection effects that could affect the calibration of the correlations, and take into account adequately the upper limits. We are aware of the limitations of this approach. Note, however, that in absence of large homogeneous galaxy surveys reporting gas scaling relations over a wide dynamical range and separated into late- and early-type galaxies, our approach is well supported as well as its fair use.
The plan of the paper is as follows. In § 2 and Appendices A and B, we present our compilation and homogenization of local galaxy samples with available information on stellar mass, morphological type, and HI and/or H2 masses from the literature. In § 3, we test the different compiled samples against possible biases in the gas content due to selection effects. In § 4, we describe the strategy to infer the gas-tostellar mass correlations taking into account upper limits, and present the determination of these correlations for the LTG and ETG populations (mean and standard deviations). Further, in § 5 we constrain the full distributions of the gas-to-stellar mass ratios as a function of M∗. In § 6 we explore the consistency of the determined correlations with the observed HI and H2 mass functions, by using the GSMF as an interface. In § 7.1 we discuss the H2-to-HI mass ratios of LTGs and ETGs inferred from our correlations; § 7.2 is devoted to a discussion on the role of the environment, and § 7.3 presents comparisons with some previous attempts to determine the gas scaling relations. A summary of our results and the conclusions are presented in § 8. Finally, Table 1 lists all the acronyms used in this paper, including the ones of the surveys/catalogs used here.
Table 1 List of acronyms used in this paper
| BCD | Blue compact dwarf |
| ETG | Early-type galaxy |
| GHIMF | Galaxy HI Mass Function |
| GH2MF | Galaxy H2 Mass Function |
| GSMF | Galaxy Stellar Mass Fu/nction |
| IMF | Initial Mass Function |
| LTG | Late.type galaxy |
| MW | Milky Way |
| RHI and RH2 | HI- and H2-to stellar mass ratio |
| SB | Surface brightness |
| SFR | Star formation rate |
| ALFALFA | Arecibo Legacy Fast ALFA survey |
| ALLSMOG | APEX Low-redshift Legacy Survey for Molecular Gas |
| AMIGA | Analysis of the interstellar Medium of Isolated Galaxies |
| ASKAP | Australian SKA Pathfinder |
| ATLAS3D | (A volume-limited survey of local ETGs) |
| COLD GASS | CO Legacy Database for GASS |
| FCRAO | Five College Radio Astronomy Observatory |
| GALEX | Galaxy Evolution Explorer |
| GAMA | Galaxy And Mass Assembly |
| GASS | GALEX Arecibo SDSS Survey |
| HERACLES | HERA CO_Line Extragalatic Survey |
| HIPASS | HI Parkes All-Sky Survey |
| HRS | Herschel Reference Survey |
| NFGS | Nearby Field Galaxy Catalog |
| NRTA | Nancay Radio Telescope |
| SDSS | Sloan Digital Sky Survey |
| SINGS | Spitzer Infrared Nearby Galaxies Survey |
| SKA | Square Kilometre Array |
| THINGS | The HI Nearby Galaxy Survey |
| UNAM-KIAS | UNAM-KIAS survey of SDSS isolated galaxies |
| UNGC | Updated Nearby Galaxy Catalog |
| WRST | Westerbork Synthesis Radio Telescope |
2. COMPILATION OF OBSERVATIONAL DATA
The main goal of this section is to present our extensive compilation of observational studies (catalogs, surveys or small samples) that meet the following criteria:
Include HI and/or H2 masses from radio observations, and luminosities/stellar masses from optical/infrared observations.
Provide the galaxy morphological type or a proxy of it.
Describe the selection criteria of the sample and provide details about the radio observations, flux limits, etc.
Include individual distances to the sources and corrections for peculiar motions/large-scale structures for the nearby galaxies.
In the case of non-detections, provide estimates of upper limits for HI or H2 masses.
The observational samples that meet the above criteria are listed in Table 2. In Appendices A and B, we present a summary of each one. We have found information on colors (g − r or B − K) for most of the samples. For M∗ > 109 M⊙, the galaxies in the color-mass diagram segregate into the so-called red sequence and blue cloud. Excluding those more inclined than 70 degrees, we find that ≈ 83% of LTGs (≈ 80% of ETGs) have colors that can be classified as blue (red) by using a mass-dependent (g − r) criterion to define blue/red galaxies. At masses lower than M∗ ≈ 109 M ⊙, the overwhelming majority of galaxies are of late types and are classified as blue.
Table 2 Observational samples
| Sample | Selection | Environment | HI | Detections/Total | H2 | Detections/Total | IMF | Category |
|---|---|---|---|---|---|---|---|---|
| UNGC | ETG-LTG | local 11 Mpc | Yes | 407/418 | No | - | diet-Salpeter | Gold |
| GASS/COLD GASS | ETG-LTG | no selection | Yes | 511/749 | Yes | 229/360 | Chabrier (2003) | Gold |
| HRS-field | ETG-LTG | no selection | Yes | 199/224 | Yes | 101/156 | Chabrier (2003) | Gold |
| ATLAS3D-field | ETG | field | Yes | 51/151 | Yes | 55/242 | Kroupa (2001) | Gold |
| NFGS | ETG-LTG | no selection | Yes | 163/189 | Yes | 27/31 | Chabrier (2003) | Silver |
| Stark et al. (2013) compilation* | LTG | no selection | Yes | 62/62 | Yes | 14/19 | diet-Salpeter | Silver |
| Leroy+08 THINGS/HERACLES | LTG | nearby | Yes | 23/23 | Yes | 18/20 | Kroupa (2001) | Silver |
| Dwarfs-Geha+06 | LTG | nearby | Yes | 88/88 | Yes | - | Kroupa et al. (1993) | Silver |
| ALFALFA dwarf | ETG-LTG | no selection | Yes | 57/57 | Yes | - | Chabrier (2003) | Silver |
| ALLSMOG | LTG | field | Yes | - | Yes | 25/42 | Kroupa (2001) | Silver |
| Bauermeister et al. (2013) compilation | LTG | field | Yes | - | Yes | 7/8 | Kroupa (2001) | Silver |
| ATLAS3D-Virgo | ETG | Virgo core | Yes | 2/15 | Yes | 4/21 | Kroupa (2001) | Bronze |
| AMIGA | ETG-LTG | isolated | Yes | 229/233 | Yes | 158/241 | diet-Salpeter | Bronze |
| HRS-Virgo | ETG-LTG | Virgo core | Yes | 55/82 | Yes | 36/62 | Chabrier (2003) | Bronze |
| UNAM-KIAS | ETG-LTG | isolated | Yes | 352/352 | No | - | Kroupa (2001) | Bronze |
| Dwarfs-NSA | LTGs | isolated | Yes | 124/124 | No | - | Chabrier (2003) | Bronze |
*From this compilation, we considered only galaxies that were not in GASS, COLD GASS and ATLAS3D samples.
2.1. Systematic Effects on the HI and H2 -to-Stellar Mass Correlations
To reduce potential systematic effects that can bias how we derive the HI and H2-to-stellar mass correlations we homogenize all the compiled observations to the same basis. Following, we discuss some potential sources of bias/segregation and the calibration that we apply to the observations. It is important to stress that to infer scaling correlations, as those of the gas fraction as a function of stellar mass, it is important to have a statistically representative and unbiased population of galaxies in each mass bin. Thus, there is no need to have mass limited volume-complete samples (see also § 4.1). However, a volume-complete sample assures that possible biases of the measure in question due to selection functions in galaxy type, color, environment, surface brightness, etc., are not introduced. The main expected bias in the gas content at a given stellar mass is due to the galaxy type/color; this is why we need to separate the samples at least into two broad populations, LTGs and ETGs.
2.1.1. Galaxy Type
The gas content of galaxies, at a given M∗, segregates significantly with galaxy morphological type (e.g., Kannappan et al. 2013; Boselli et al. 2014c). Thus, information on morphology is necessary in order to separate galaxies at least into two broad populations, LTGs and ETGs. Apart of its physical basis, this separation is important to avoid introducing biases in the obtained correlations due to selection effects related to the morphology of the different samples used here. For example, some samples are only of late-type or star-forming galaxies, others only of early-type galaxies, etc., so that combining them without a separation by morphology would yield correlations that are not statistically representative. We consider as ETGs those classified as ellipticals (E), lenticulars (S0), dwarf E, and dwarf spheroidals or with T < 1, and as LTGs those classified as spirals (S), irregulars (Irr), dwarf Irr, and blue compact dwarfs or with T ≥ 1. The morphological classification criteria used in the different samples are diverse, ranging from individual visual evaluation to automatic classification methods, as the one by Huertas-Company et al. (2011). We are aware of the high level of uncertainty introduced by using different morphological classification methods. However, in our case the morphological classification is used to separate galaxies just into two broad groups. Therefore, such an uncertainty is not expected to affect significantly any of our results. It is important to highlight that the terms LTG and ETG are useful only as qualitative descriptors. These descriptors should not be applied to individual galaxies, but instead to two distinct populations of galaxies in a statistical sense.
2.1.2. Environment
The gas content of galaxies is expected to depend on the environment (e.g., Zwaan et al. 2005; Geha et al. 2012; Jones et al. 2016; Brown et al. 2017). In this study we are not able to study in detail such a dependence, though our separation into LTG and ETG populations partially takes into account this dependence because these populations segregate by environment (e.g., Dressler 1980; Kauffmann et al. 2004; Blanton et al. 2005a; Blanton & Moustakas 2009, and references therein). In any case, in our compilation we include three samples specially selected to contain very isolated galaxies and one subsample of galaxies from the Virgo Cluster central regions. We will check whether or not their HI and H2 mass fractions significantly deviate from the mean relations.
2.1.3. Systematical Uncertainties on the Stellar Masses
There are many sources of systematic uncertainty in the inference of stellar masses related to the choices of: initial mass function (IMF), stellar population synthesis and dust attenuation models, star formation history parametrization, metallicity, filter setup, etc. For inferences from broad-band spectral energy distribution fitting and using a large diversity of methods and assumptions, Pforr et al. (2012) estimate a maximal variation in stellar mass calculations of ≈ 0.6 dex. The major contribution to these uncertainties comes from the IMF. The IMF can introduce a systematic variation of up to ≈ 0.25 dex (see e.g., Conroy 2013). For local normal galaxies and from UV/optical/IR data (as it is the case of our compiled galaxies), Moustakas et al. (2013) find a mean systematic difference between different massto-luminosity estimators (fixed IMF) of less than 0.2 dex. We have seen that in most of the samples compiled here, the stellar masses are calculated using roughly similar mass-to-luminosity estimators, but the IMF are not always the same.Therefore, we homogenize the reported stellar masses in the different compiled samples to the mass corresponding to a Chabrier (2003) initial mass function (IMF), and neglect other sources of systematic differences.
2.1.4. Other Effects
We also homogenize the distances to the value of H0 = 70 kms−1 Mpc−1. In most of the samples compiled here (at least the most relevant ones for our study), distances were corrected for peculiar motions and large-scale structure effects. When the authors included helium and metals to their reported HI and H2 masses, we take care of subtracting these contributions. When we calculate the total cold gas mass, then helium and metals are explicitly taken into account.
2.1.5. Categories
The different HI and H2 samples used in this paper are widely diverse, in particular they were obtained with different selection functions, radio telescopes, exposure times, etc. We have divided the different samples into three categories according to the feasibility of determining from each one robust and statistically representative HIor H2-to-stellar mass correlations for the LTG and ETG populations. We will explore whether or not the less feasible categories should be included for determining these correlations. The three categories are:
Golden: It includes datasets based on volume complete (above a given luminosity/mass) samples or on representative galaxies selected from volume-complete samples. The Golden datasets, by construction, are unbiased samples of the distribution of galaxy properties.
Silver: It includes datasets from galaxy samples that are not volume complete, but that are intended to be statistically representative at least for their morphological groups, i.e., these samples do not present obvious or strong selection effects.
Bronze: This category includes samples selected deliberately by environment, and it will be used to explore the effects of environment on the LTG and ETG HIor H2-to-stellar mass correlations.
2.2. The Compiled HI Sample
Appendix A presents a summary of the HI samples compiled in this paper (see also Table 2). Table 3 lists the total numbers and fractions of compiled galaxies with detection and non-detection for each galaxy population. Table 4 lists the number of detected and non-detected galaxies for the golden, silver, and bronze categories listed above (§ 2.1.5).
Table 3 Number of galaxies with detections and upper limits by morphology.
| Morphology (%) | Detections (%) | Upper limits(%) | Total |
|---|---|---|---|
| HI data | |||
| LTG (78%) | 1975 (94%) | 121 (6%) | 2096 |
| ETG (22%) | 292 (50%) | 288 (50%) | 580 |
| H2 data | |||
| LTG (63%) | 533 (75%) | 180 (25%) | 713 |
| ETG (37%) | 124 (29%) | 298 (71%) | 422 |
Table 4 Number of galaxies with detections and upper limits by category
| Category (%) | Detections (%) | Upper limits (%) | Total |
|---|---|---|---|
| HI data | |||
| Golden (58%) | 1168 (76%) | 374 (24%) | 1542 |
| Silver (16%) | 391 (94%) | 26 (6%) | 417 |
| Bronze (26%) | 708 (99%) | 9 (!%) | 717 |
| H2 data | |||
| Golden (67%) | 385 (51%) | 373 (49%) | 758 |
| Silver (10%) | 91 (76%) | 29 (24%) | 120 |
| Bronze (23%) | 181 (70%) | 76 (30%) | 257 |
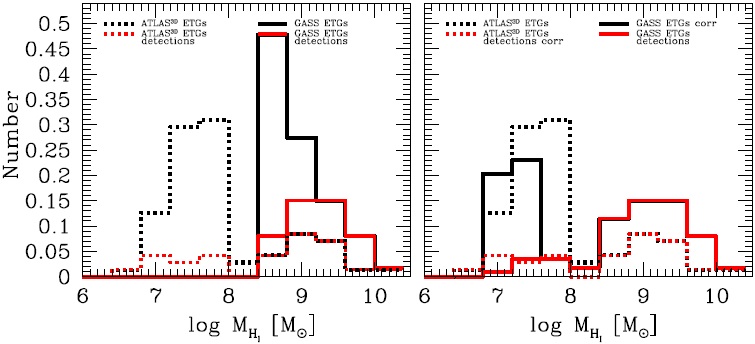
Figure 1 shows the mass ratio RHI ≡ MHI /M∗ vs. M∗ for the compiled samples. Note that we have applied some corrections to the reported samples (see above) to homogenize all the data. The upper and bottom left panels of Figure 1 show, respectively, the compilations for LTGs and ETGs. The different symbols indicate the source reference of the data and the downward arrows are the corresponding upper limits of the HI-flux for non-detections. We also reproduce the mean and standard deviation of different mass bins as reported in Maddox et al. (2015) for a cross-match of the ALFALFA and SDSS surveys. As mentioned in the Introduction, the ALFALFA survey is biased to high RHI values, specially towards the low mass side. Note that the small ALFALFA subsample of dwarf galaxies by Huang et al. (2012b, dark purple dots) was selected mainly as an attempt to take into account low-HI mass galaxies at the low-mass end.

Fig. 1 Atomic gas-to-stellar mass ratio as a function of M∗. Upper panels: Compiled and homogenized data with information on RHI and M∗ for LTGs (the different sources are indicated inside the left panel; see Appendix A for the acronyms and authors); downward arrows show the reported upper limits for non-detections. The blue triangles with thin error bars are mean values and standard deviations from the v.40 ALFALFA and SDSS crossmatch according to Maddox et al. (2015); the ALFALFA galaxies are biased toward high values of RHI (see text). Right panel is the same as left one, but with the data separated into three categories: Golden, Silver, and Bronze (yellow, gray, and brown symbols, respectively). The red and blue lines are Buckley-James linear regressions (taking into account non-detections) for the high- and low-mass regions, respectively; the dotted lines show extrapolations from these fits. Squares with error bars represent the mean and standard deviation of the data in different mass bins, taking into account non-detections by means of the Kaplan-Meier estimator. Open circles with error bars show the corresponding median and 25-75 percentiles. Estimates of the observational uncertainties are shown in the panel corners (see text). Lower panels: Same as upper panels but for ETGs. In the right panel, we have corrected for distance the galaxies with upper limits from GASS to make them consistent with the distances of the ATLAS3D sample (see text); the upper limits from the latter were increased by a factor of two to homogenize them to the ALFALFA instrument and signal-to-noise criteria. For the bins where more than 50% of the data are upper limits, the median and percentiles are not calculated. The color figure can be viewed online.
2.3. The Compiled H2 Sample
Since the emission of cold H2 in the ISM is extremely weak, a tracer of the H2 abundance should be used. The best tracer from the observational point of view is the CO molecule due to its relatively high abundance and its low excitation energy. The H2 mass is related to the CO luminosity through a CO-to-H2 conversion factor: MH2 = αCO LCO. This factor has been determined in molecular clouds in the Milky Way (MW), αCO,MW = 3.2 (K km s−1 pc−1)−1, with a systematic uncertainty of 30%. It was common to assume that this conversion factor was the same for all galaxies. However, several pieces of evidence show that αCO is not constant, and that it depends mainly on the gas-phase metallicity, increasing as the galaxy metallicity decreases (e.g., Boselli et al. 2002; Schruba et al. 2012; Narayanan et al. 2012; Bolatto et al. 2013, and references therein). At firstorder, αCO changes slowly for metallicities larger than 12 + log10(O/H) ≈ 8.4 (approximately half the solar one) and increases considerably as the metallicity decreases. Here, we combine the dependence of αCO on metallicity given by Wolfire et al. (2010) and the observed mass-metallicity relation to obtain an approximate estimation of the dependence of αCO on M∗ for LTGs; see Appendix C for details. We are aware that the uncertainties involved in any metallicity-dependent correction remain substantial (Bolatto et al. 2013). Note, however, that our aim is to introduce and explore at a statistical level a reasonable mass-dependent correction to the CO-to-H2 factor, which must be better than ignoring it. In any case, we present results both for αCO = αCO,MW and our inferred mass-dependent αCO factor. In fact, the mass-dependent factor is important only for LTGs with M∗ ≲ 3 × 1010 M⊙; for larger masses and for all ETGs, αCO ≈ αCO,MW1.
Appendix B presents a description of the CO (H2) samples that we utilize in this paper. Table 3 lists the number of galaxies with detections and upper limits in the compilation sample in terms of morphology. Table 4 lists the number of detections and upper limits for the golden, silver, and bronze categories mentioned above (§ 2.1.5).
Figure 2 shows the mass ratio RH2≡ MH2 /M∗ vs. M∗ for the compiled samples. Similarly to the RHI vs. M∗ relation, we applied some corrections to observations in order to homogenize our compiled sample and to allow a more consistent comparison between the different samples. The upper and bottom left panels of Figure 2 show, respectively, the compiled datasets for LTGs and ETGs.
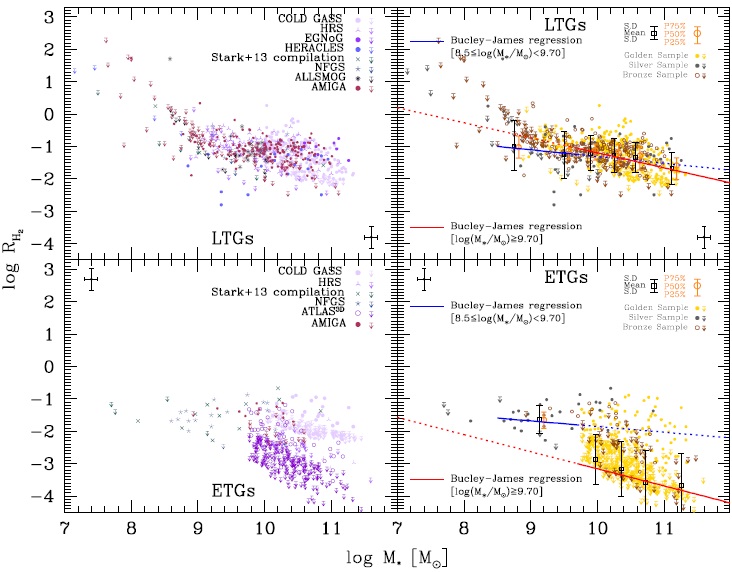
Fig. 2 Molecular gas-to-stellar mass ratio as a function of M∗. Upper panels: Compiled and homogenized data with information on RH2 and M∗ for LTGs (see inside the panels for the different sources; see Appendix B for the acronyms and authors); downward arrows show the reported upper limits for non-detections. Right panel is the same, but with the data separated into three categories: Golden, Silver, and Bronze (yellow, gray, and brown symbols, respectively). The red and blue lines are Buckley-James linear regressions (taking into account non-detections). The dotted lines show extrapolations from these fits. The green dashed line shows an estimate for the RH2 -M∗ relation inferred from combining the empirical SFR MH2 and SFR-M∗ correlations for blue/star-forming galaxies (see text for details). Squares with error bars are the mean and standard deviation of the data in different mass bins, taking into account non-detections by means of the Kaplan-Meier estimator. Open circles with error bars are the corresponding median and 25-75 percentiles. Estimates of the observational/calculation uncertainties are shown in the panel corners (see text). Lower panels: The same as upper panels but for ETGs. In the right panel, we have corrected for distance the galaxies with upper limits from COLD GASS to make them consistent with the distances of the ATLAS3D sample (see text). For the bins where more than 50% of the data are upper limits, the median and percentiles are not calculated. The color figure can be viewed online.
3. TESTS FOR SELECTION EFFECTS AND PRELIMINARY RESULTS
In this section we check the gas-to-stellar mass correlations from the different compiled samples for possible selection effects. We also introduce, when possible, a homogenization at the upper limits of ETGs. The reader interested only in the main results can skip to § 4.
As seen in Figures 1 and 2 there is a significant fraction of galaxies with no detections in radio, for which the authors report an upper limit for the flux (converted into an HI or H2 mass). The non-detection of observed galaxies gives information that we cannot ignore, otherwise a bias towards high gas fractions would be introduced in the gas-to-stellar mass relations to be inferred. To take into account the upper limits in the compiled data, we resort to survival analysis methods for combining censored and uncensored data (i.e., detections and upper limits for non-detections; see e.g., Feigelson & Babu 2012). We will use two methods: the BuckleyJames linear regression (Buckley & James 1979) and the Kaplan-Meier product limit estimator (Kaplan & Meier 1958). Both are survival analysis methods commonly applied in astronomy.2The former is useful for obtaining a linear regression from the censored and uncensored data. Alternatively, for data that cannot be described by a linear relation, we can bin them by mass, use the Kaplan-Meier estimator to calculate the mean, standard deviation,3 median, and 25-75 percentiles in each stellar mass bin, and fit these results to a function using conventional methods, e.g., the Levenberg-Marquardt algorithm. For the latter case, the binning in log M∗ is started with a width of ≈ 0.25 dex but if the data are too scarce in the bin, then its width is increased so as to have no less than 25% of galaxies in the most populated bins. Note that, for detection fractions smaller than 50%, the median and percentiles are very uncertain or impossible to be calculated with the Kaplan-Meier estimator (Lee & Wang 2003), while the mean can still be estimated for fractions as small as ≈ 20%, though with a large uncertainty. In the case of the Bukley-James linear regression, reliable results are guaranteed for detection fractions larger than 70 − 80%.
When the fraction of non-detections is significant, the inferred correlations could be affected by selection effects in the upper limits reported in the different samples. This is the case for ETGs, where a clear systematical segregation between the upper limits of the GALEX Arecibo SDSS Survey (GASS) and ATLAS3D or Herschel Reference Survey (HRS) surveys is observed in the log RHI − log M* plane (see the gap in the lower left panel of Figure 1), as well as between the CO Legacy Database for GASS (COLD GASS) and ATLAS3D or HRS surveys in the log RH2 − log M* plane (see the gap in the lower left panel of Figure 2). The determination of the upper limits depends on distance and instrumental/observational constraints (telescope sensitivity, integration time, spatial coverage, signalto-noise threshold, etc.). The HI observations of GASS and ATLAS3D were carried out with different radio telescopes: the single-dish Arecibo Telescope and the Westerbork Synthesis Radio Telescope (WRST) interferometer array, respectively. Serra et al. (2012) discussed the differences between detections by single- and multiple-beam observations. From some galaxies from ATLAS3D that they observed also with the Arecibo telescope, they concluded that the upper limits should be increased by a factor of ≈ 2 in order to agree with the ALFALFA survey sensitivity and the signal-to-noise threshold they used for declaring non-detections in their multiple-beam observations. Thus, to homogenize the upper limits, we corrected the ATLAS3D upper limits by this factor. In the case of RH2, the CO observations in the ATLAS3D and COLD GASS samples were obtained with the same radio telescope (IRAM).
The GASS (COLD GASS) samples are selected to include galaxies at distances between ≈ 109 and 222 Mpc, while the ATLAS3D and HRS surveys include only nearby galaxies, with average distances of 25 and 19 Mpc, respectively. Since the definition of the upper limits depends on distance, for the same radio telescope and integration time, more distant galaxies have systematically higher upper limits than nearer galaxies. This introduces a clear selection effect. When we have information for a sample of galaxies nearer than another sample, and under the assumption that both samples are roughly representative of the same local galaxy population, a distance-dependent correction to the upper limits of the non-detected galaxies in the more distant sample should be introduced. In Appendix D, we describe our approach to apply such a correction to GASS (COLD GASS) ETG upper limits with respect to the ATLAS3D ETGs. We test our corrections by using a mock catalog. This correction for distance is an approximation based on the assumption that the (COLD)GASS and ATLAS3D ETGs are statistically similar populations. In any case, we will present the correlations for ETGs for both cases, with and without this correction.
Note that after our corrections for distance and instrumental effects, the upper limits of the massive ETGs in the GASS/COLD GASS sample are now consistent with those in the ATLAS3D (as well as HRS) samples, as seen in the right panels of Figures 1 and 2 to be described below, and in Figure 17 in Appendix D. In the case of LTGs, there is no evidence of much lower values of RHI and RH2 than the upper limits given in GASS and COLD GASS for galaxies nearer than those in these samples.
In the right panels of Figures 1 and 2, all the compiled data shown in the left panels are again plotted with dots and arrows for detections and non-detections, respectively. The yellow, dark gray, and brown colors correspond to galaxies from the Golden, Silver, and Bronze categories, respectively (see § 2.1.5). The above mentioned corrections to the upper limits of GASS/COLD GASS and ATLAS3D ETG samples were applied. Note that the large gaps in the upper limits between the GASS/COLD GASS and ATLAS3D (or HRS) samples tend to disappear after the corrections.
We further group the data in logarithmic mass bins and calculate in each mass bin the mean and standard deviation of log R HI and log RH2 (black circles with error bars), taking into account the upper limits with the Kaplan-Meier estimator as described above. The orange squares with error bars show the corresponding medians and 25-75 percentiles, respectively. In some mass bins the fraction of detections is smaller than 50% for ETGs. Therefore, the medians and percentiles cannot be estimated (see above). However, the means and standard deviations can still be calculated, though they are quite uncertain.
As seen in the right panels of Figures 1 and 2, the logarithmic mean and median values tend to coincide and the 25-75 percentiles are roughly symmetric in most of the cases. Both facts suggest that the scatter around the mean relations (at least for the LTG population) tends to follow a nearly symmetrical distribution, for instance, a normal distribution in the logarithmic values (for a more detailed analysis of the scatter distributions see § 5).
In the following, we check whether each one of the compiled and homogenized samples deviate significantly from the mean trends. This could be due to selection effects in the sample. For example, we expect systematical deviations in the gas contents for the Bronze samples, because they contain galaxies in extreme environments. As a first approximation, we apply the Buckle-James linear regression to each one of the compiled individual samples, taking into account in this way the upper limits. When the data in the sample are too scarce and/or are dominated by non-detections, the linear regression is not performed, but the data are plotted.
3.1. RHI vs. M∗
In Figure 3, results for log RHI vs. log M∗ are shown for LTGs (upper panels) and ETGs (lower panels). From left to right, the regressions for samples in the Golden, Silver, and Bronze categories are plotted. The error bars correspond to the 1σ scatter of the regression. Each line covers the mass range of the corresponding sample. The blue/red dashed lines and shaded regions in each panel correspond to the mean and standard deviation values calculated with the Kaplan-Meier estimator in mass bins for all the compiled LTG and ETG samples, previously plotted in Figures 1 and 2, respectively. However, the yellow, gray, and brown dots connected with thin solid lines in each panel are the mean values in each mass bin calculated only for the Golden, Silver, and Bronze samples, respectively. The standard deviations are plotted as dotted lines. In the following, we discuss the results shown in Figure 3.
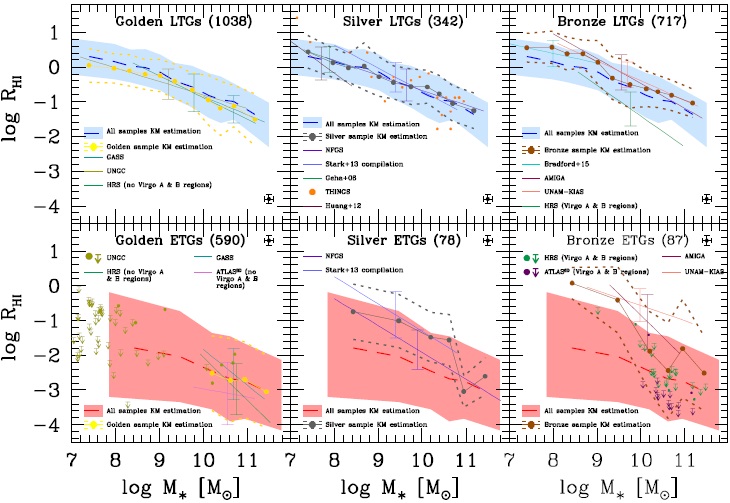
Fig. 3 Atomic gas-to-stellar mass ratio as a function of M∗ for the Golden, Bronze, and Silver LTGs (upper panels) and ETGs (lower panels). The mean and standard deviation in different mass bins, taking into account upper limits by means of the Kaplan-Meier estimator, are plotted for each case (filled circles connected by a dotted line and dotted lines around, respectively). For comparison, the mean and standard deviation (dashed lines and shaded area) from all the LTG (ETG) samples are reproduced in the corresponding upper (lower) panels. For each sample compiled and homogenized from the literature, the Buckley-James linear regression is applied, taking into account upper limits. The lines show the result, covering the range of the given sample; the error bars show the corresponding standard deviations obtained from the regression. When the data are too scarce and dominated by upper limits, the linear regression is not applied but the data are plotted. The numbers of LTG and ETG objects in each category are indicated in the respective panel. The color figure can be viewed online.
Golden category: For LTGs, the three samples grouped in this category agree well among themselves in the mass ranges where they overlap; even the 1σ scatter of each sample does not differ significantly4. Therefore, as expected, these samples provide unbiased information for determining the RHI -M∗ relation of LTGs from log(M∗/M⊙ )≈ 7.3 to 11.4. For ETGs, the deviations of the Golden linear regressions among themselves and compared to all galaxies are within the 1σ scatter, which is actually large. If no corrections to the upper limits of the GASS and ATLAS3D are applied, then the regression for the former would be significantly above the regression for the latter. Within the large scatter, the three Golden samples of ETGs seem not to be particularly biased, and they cover a mass range from log(M∗/M⊙)≈ 8.5 to 11.5. At smaller masses, the Updated Nearby Galaxy Catalog (UNGC) sample provides mostly only upper limits to RHI.
Silver category: The LTG and ETG samples in this category, as expected, show more dispersed distributions in their respective RHI-M∗ planes than those from the Golden category. However, the deviations of the Silver linear regressions among themsleves and compared to all the galaxies are within the corresponding 1σ scatter. If any, there is a trend of the Silver samples to have mean R HI values above the mean values of all galaxies especially for ETGs. Since the samples in this category are volume-complete, (they were specially constructed to study HI gas content), a selection effect towards objects with non-negligible or higher than the mean HI content can be expected. In any case, the biases are small. Thus, we decided to include the Silver samples to infer the RHI-M∗ correlations in order to slightly increase the statistics (the number of galaxies in this category is actually much smaller than in the Golden category), specially for ETGs of masses smaller than log(M∗/M⊙)≈ 9.7 (see Table 4).
Bronze category and effects of the environment: The very isolated LTGs (from the UNAMKIAS and Analysis of the interstellar Medium of Isolated GAlaxies -AMIGAsamples) have HI contents higher than the mean of all the galaxies, especially at lower masses: log RHI is 0.1 − 0.2 dex larger than the average at log(M∗/M⊙)>∼ 10 and these differences increase up to 0.6 − 0.3 dex for 8 < log(M∗/M⊙) < 9, though the number of galaxies at these masses is very small. The HI content of the Bradford et al. (2015) isolated dwarf galaxies is also larger than the mean of all the galaxies but not by a factor larger than 0.4 dex. For isolated ETGs, the differences can attain an order of magnitude and are at the limit of the upper standard deviations around the means of all the ETGs. Thus, while isolated LTGs have somewhat larger RHI ratios on average than galaxies in other environments, in the case of isolated ETGs, this difference is very large; isolated ETGs can be almost as gas rich as LTGs. In the Bronze group we have included also galaxies from the central regions of the Virgo Cluster, as reported in HRS and ATLAS3D (only ETGs for the latter). According to Figure 3, the LTGs in this high-density environment are clearly HI deficient with respect to LTGs in less dense environments. For ETGs, the HI content is very low but only slightly lower on average than the HI content of all ETGs. It should be noted that ETGs, in particular the massive ones, tend to be located in high-density environments.
We conclude that the HI content of galaxies is affected by the effects of extreme environments. The most remarkable effect occurs for ETGs, which in a very isolated environment can be as rich in HI as LTGs. Therefore, we decided not to include galaxies from the Bronze category to determine the RHI-M∗ correlation of ETGs. In fact, our compilation in the Golden and Silver categories includes galaxies from a range of environments (for instance, in the largest compiled catalog, UNGC, 58% of the galaxies are members of groups and 42% are field galaxies, see Karachentsev et al. 2014) in such a way that the RHI-M∗ correlation determined below should represent an average of different environments. Excluding the Bronze category for the ETG population, we avoid biases due to effects of the most extreme environments. For LTGs, the inclusion of the Bronze category does not introduce significant biases in the RHI-M∗ correlation of all galaxies but it helps to improve the statistics. The mean values of R HI in mass bins above ≈ 109 M⊙ are actually close to the mean values of the entire sample (compare the brown solid and blue dashed lines); at smaller masses the deviation increases, but the differences are well within the 1σ dispersion.
3.2. RH2 vs. M∗
In Figure 4, we present plots similar to Figure 3 but for log RH2 vs. log M∗. The symbol and line codes are the same in both figures. In the following, we discuss the results shown in Figure 4.
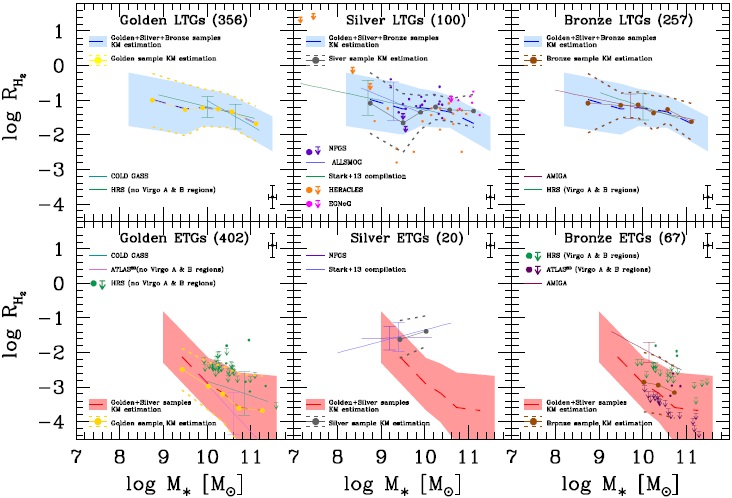
Fig. 4 Same as Figure 3 but for the molecular gas-to-stellar mass ratio. The color figure can be viewed online.
Golden category: For LTGs, the two samples grouped in this category agree well among themsleves and with the overall sample, though for masses < 1010 M⊙, where the Golden galaxies are only those from the HRS sample, the average RH2 values are slightly larger than those from the overall LTG sample (compare the solid yellow and dashed blue lines), but still well within the 1σ scatter (shaded area). For ETGs, the deviations of the linear regressions of the Golden samples among themselves, and compared to all ETGs, are within the respective 1σ scatters, which are actually large. If no corrections to the upper limits of the GASS and ATLAS3D were applied, then the regression for the former would be significantly above the regression for the latter. Summarizing, the Golden samples of LTGs and ETGs do not show particular shifts in their respective RH2 - M∗ correlations. Therefore, the combination of them is expected to provide reliable information for determining the respective RH2 - M∗ correlations: for LTGs in the ≈ 108.5 − 1011.5 M⊙ mass range, and for ETGs, only for M∗ ≳ 1010 M⊙.
Silver category: The LTG samples present a dispersed distribution in the log RH2 -logM∗ plane but well within the 1σ scatter of the overall sample (shaded area). The mean values in mass bins from samples of the Silver category are in reasonable agreement with the mean values from all the samples (compare the gray solid and blue dashed lines). Therefore, the Silver samples, though scattered and not complete in any sense, seem not to exhibit a clear systematical shift in their H2 content. We include these samples to infer the RH2 - M∗ correlation of LTGs. For ETGs, the two Silver samples provide information for masses below M∗ ≈ 1010 M⊙, and both are consistent with each other. Therefore, we include these samples to infer the ETG RH2 -M∗ correlation down to M∗ ≈ 108.5 M⊙.
Bronze category and the effects of environment: The isolated (from the AMIGA sample) and Virgo central (from the HRS catalog) LTGs have H2 contents similar to the mean in different mass bins of all the galaxies. If any, the Virgo LTGs have on average slightly higher values of RH2 than the isolated LTGs, especially at masses smaller than M∗ ≈ 1010 M⊙. Given that LTGs in extreme environments do not segregate from the average RH2 values at different masses of all galaxies, we include them for calculating the RH2 -M∗ correlation of LTGs. For ETGs, the AMIGA isolated galaxies have on average values of RH2 significantly higher than the mean of other galaxies, while those ETGs from the Virgo central regions (from HRS and ATLAS3D; mostly upper limits), seem to be on average consistent with the mean of all the galaxies, though the scatter is large. Given the strong deviation of isolated ETGs from the mean trend, we prefer to exclude galaxies from the Bronze category to determine the ETG RH2 -M∗ correlation. We conclude that the H2 content of LTGs is weakly dependent on the environment of galaxies, but in the case of ETGs, very isolated galaxies have systematically higher RH2 values than galaxies in more dense environments.
4. THE GAS-TO-STELLAR MASS CORRELATIONS OF THE TWO MAIN GALAXY POPULATIONS
4.1. Strategy for Constraining the Correlations
In spite of the diversity in the compiled samples and their different selection functions, the exploration presented in the previous section shows that the HI and H2 contents as a function of M∗ for most of the samples compiled here do not segregate significantly among them. The exception are the Bronze samples for ETGs. Therefore, the Bronze ETGs are excluded from our analysis. The strong segregation is actually by morphology (or color, or star formation rate), and this is why we have separated from the beginning the compiled data into two broad galaxy groups, LTGs and ETGs.
To determine gas-to-stellar mass ratios as a function of M∗ we need (1) to take into account the upper limits of undetected galaxies in radio, and (2) to evaluate the correlation independently of the number of data points in each mass bin. If we have many data points in some mass bins and only a few ones in other mass bins (as would happen if we use, for instance, a mass-limited volume-complete sample, with many more data points at smaller masses than at larger masses), then the overall correlation of RHI or RH2 with M∗ would be dominated by the former, probably giving incorrect values of RHI or RH2 at other masses. In view of these two requirements, our strategy to determine the logR HI-logM∗ and log RH2 -logM∗ correlations is as follows:
Calculate the logarithmic means and standard deviations (scatter) in stellar mass bins obtained from the compiled data taking into account the non-detections (upper limits) by means of the Kaplan-Meier estimator.
Obtain an estimate of the intrinsic standard deviations (scatter), taking into account estimates of the observational errors.
Propose a function to describe the relation given by the mean and intrinsic scatter as a function of mass (e.g., a single or double power law).
Constrain the parameters of this function by performing a formal fit to the mean and scatter calculated for each mass bin; note that in this case the fitting gives the same weight to each mass bin, irrespective of the number of galaxies in each bin.
4.2. The HI-to-Stellar Mass Correlations
In the upper left panel of Figure 5, along with the data from the Golden, Silver, and Bronze LTG samples, the mean and standard deviation (squares and black error bars) calculated for each mass bin with the Kaplan-Meier method are plotted. In the lower left panel, the same is plotted but for the Golden and Silver ETG samples (recall that the Bronze samples are excluded in this case). We see that the total standard deviations in log RHI, σdat, do not evidence a systematical dependence on mass both for LTGs and ETGs. Then, we can use a constant value for each case. For LTGs, the standard deviations have values around 0.45-0.65 dex with an average of σdat ≈ 0.53 dex. For ETGs, the standard deviations are much larger and more dispersed than for LTGs (see § 4.4 below for a discussion on why this could be). We assume an average value of σdat = 1 dex for ETGs.

Fig. 5 Left panels: The RHI-M∗ correlation for LTGs (upper panel) and ETGs (lower panel). Dots are detections and arrows are upper limits for non-detections (for ETGs the Bronze sample was excluded). The squares and error bars show the mean and standard deviation in different mass bins calculated by means of the Kaplan-Meier estimator for censored and uncensored data. The thin error bars correspond to our estimate of the intrinsic scatter after taking into account the observational errors (shown in the panel corners). The solid and long-dashed lines in each panel are respectively the best double- and single-power law fits. The shaded areas show the intrinsic scatter; to avoid overcrowding, for the single power-law fit, the intrinsic scatter is plotted only at one point. The dotted lines are extrapolations of the correlations to low masses, where the data are scarce and dominated by upper limits. Middle panels: Same as in the left panels but for RH2. For the ETG population, the double power-law fit was performed with the conservative constraint that below M∗ = 109 M⊙, the low-mass slope is zero. Right panels: The Rgas-M∗ correlations for LTGs and ETGs as calculated from combining the respective double- and single-power law RHI-M∗ and RH2 -M∗ correlations and taking into account helium and metals (see text). The shaded area and error bar are the (1σ) intrinsic scatter obtained by error propagation of the intrinsic scatter around the corresponding R HI-M ∗ and RH2 -M∗ relations. For completeness, the data from our compilation that have determinations of both HI and H2 masses are also plotted (the obtained correlations are not fits to these data). Dotted lines are extrapolations of the inferred relations to smaller masses. The short dashed lines show the best fits using the double power-law function. The color figure can be viewed online.
The intrinsic standard deviation (scatter) can be estimated as σ2intr≈σ2dat-σ2err (this is valid for normal distributions), where σerr is the mean statistical error in the log R HI determination due to the observational uncertainties. In Appendix E we present an estimate of this error, σerr ≈ 0.14 dex. Therefore, σintr ≈ 0.52 and 0.99 dex for LTGs and ETGs, respectively. These estimates should be taken only as indicative values given the assumptions and rough approximations involved in their calculations. For example, we will see in § 5 that the distributions of log R HI (detections and non-detections) in different mass bins tend to deviate from a normal distribution, in particular for ETGs.
Next, we propose that the HI-to-stellar mass relations can be described by the general function:
where y = RHI, C is the normalization factor, a and b are the low and high-mass slopes of the function and Mtr* is the transition mass. This function is continuous and differentiable. If a = b, then equation (1) describes a single power law, or a linear relation in logarithmic scales. In this case, the equation remains as y(M∗) = C′(M∗/M⊙)−a. For a ≠ b, the function corresponds to a double power law.
We fit the logarithm of function, equation (1), to the mean values of logRHI as a function of mass (squares in the left panels of Figure 5) with the corresponding (constant) intrinsic standard deviation as estimated above (thin blue/red error bars). For LTGs, the fit is carried out in the range 7.3 ≲ log(M∗/M⊙ )≲ 11.2, and for ETGs in the range 8.5 ≲ log(M∗/M⊙)≲ 11.5. The Levenberg Marquardt method is used for the fit (Press et al. 1996). First, we perform the fits to the binned LTG and ETG data using a single power law, i.e., we fix a = b. The dashed orange and green lines with an error bar in the left panels of Figure 5 show the results. The fit parameters are given in Table 5. We note that these fits and those of the Buckley-James linear regression for all the data (not binned) in logarithm are very similar.
Table 5 Best fit parameters to the single power law (equation 1, a = b)
| log C' | a | σdat | σintr | |
|---|---|---|---|---|
| RHI-M∗ | ||||
| LTG | 3.77 ± 0.22 | -0.45 ± 0.02 | 0.53 | 0.52 |
| ETG | 1.88 ± 0.33 | -0.42 ± 0.03 | 1.00 | 0.99 |
| ETGndc | 1.34 ± 0.46 | -0.37 ± 0.05 | 1.35 | 1.34 |
| RH2 -M∗ | ||||
| LTG | 1.21 ± 0.53 | -0.25 ±0.05 | 0.58 | 0.47 |
| ETG | 5.86 ± 1.45 | -0.86 ± 0.14 | 0.80 | 0.72 |
| ETCndc | 5.27 ± 1.78 | -0.80 ± 0.17 | 0.95 | 0.88 |
| Rgas-M∗ | ||||
| LTG | 4.76 ± 0.05 | -0.52 ±0.03 | - | 0.44 |
| ETG | 3.70 ± 0.07 | -0.58 ± 0.01 | - | 0.68 |
∙ The suffix "ndc" indicates that for the ETG correlations, no distance correction was applied to the upper limits in the (COLD) GASS samples.
∙ σdat and σintr are given in dex.
Then, we fit to the binned data the logarithm of the double power-law function given in equation (1). The corresponding best-fit parameters are presented in Table 6. We note that the fits are almost the same if the total mean standard deviation, σdat, is used instead of the intrinsic one. The reduced χ2red are 0.01 and 0.03, respectively. The fits are actually performed to a low number of points (the number of mass bins) with large error bars; this is why the χ2red are smaller than 1. Note, however, that the error bars are not related to measurement uncertainties but correspond to the population scatter of the data. Therefore, in this case χ2red < 1 implies that while the best fit is good, other fits could be also good within the scatter of the correlations. In the case of the single power-law fits, the χ2red are 0.03 and 0.01, respectively for LTG and ETG.
Table 6 Best fit parameters to the double power law (equation 1, a ≠ b)
| C | a | b | log( Mtr* /M⊙) | σdat | σintr | |
|---|---|---|---|---|---|---|
| RHI-M∗ | ||||||
| LTG | 0.98 ± 0.06 | 0.21 ± 0.04 | 0.67 ± 0.03 | 9.24 ± 0.04 | 0.53 | 0.52 |
| ETG | 0.02 ± 0.01 | 0.00 ± 0.15 | 0.58 ± 0.03 | 9.00 ± 0.30 | 1.00 | 0.99 |
| ETGndc | 0.02 ± 0.01 | 0.00 ± 0.55 | 0.51 ± 0.05 | 9.00 ± 0.60 | 1.35 | 1.34 |
| RH2 -M∗ | ||||||
| LTG | 0.19 ± 0.02 | -0.07 ± 0.18 | 0.47 ± 0.04 | 9.24 ± 0.12 | 0.58 | 0.47 |
| ETG | 0.02 ± 0.01 | 0.00 ± 0.00 | 0.94 ± 0.15 | 9.01 ± 0.12 | 0.80 | 0.72 |
| ETGndc | 0.02 ± 0.03 | 0.00 ± 0.00 | 0.88 ± 0.18 | 9.01 ± 0.15 | 0.92 | 0.88 |
| R gas-M ∗ | ||||||
| LTG | 1.69 ± 0.02 | 0.18 ± 0.01 | 0.61 ± 0.02 | 9.20 ± 0.04 | - | 0.44 |
| ETG | 0.05 ± 0.02 | 0.01 ± 0.03 | 0.70 ± 0.01 | 9.02 ± 0.05 | - | 0.68 |
∙ The suffix "ndc" indicates that for the ETG correlations, no distance correction was applied to the upper limits in the (COLD) GASS samples.
∙ σdat and σintr are given in dex.
The double power-law RHI-M∗ relations and the estimated intrinsic (1σ) scatter for the LTG (ETG) population are plotted in the left upper (lower) panel of Figure 5 with solid lines and shaded areas, respectively. From the fits, we find for LTGs a transition mass Mtr* = 1.74 ×109 M⊙, with R ∝ M∗ −0.21 and M∗ −0.67 at masses much smaller and larger than this, respectively. For ETGs, Mtr* = 1×109 M⊙, and RHI ∝ M∗ 0.0 and M∗ -0.58, at masses much smaller and larger than this, respectively.
Both the double and single power laws describe well the HI-to-stellar mass correlations. However, the former could be more adequate than the latter. In Figure 1 we plot the Buckley-James linear regressions to the RHI vs. M∗ data for the low and high mass regions (below and above log(M∗/M⊙)≈ 9.7; for ETGs the regression is applied only for masses above 108 M ⊙); the dotted lines show the extrapolation of the fits. The slope at low masses for LTGs, −0.36, is shallower than the one at high masses, −0.55. For ETGs, there is even evidence of a change in the slope sign at low masses. A flattening of the overall (late + early type galaxies) correlation at low masses has been also suggested by Baldry et al. (2008), who have used the empirical mass- metallicity relation coupled with a metallicity-to-gas mass fraction relation (which can be derived from a simple chemical evolution model) to obtain a gasto-stellar mass correlation in a large mass range. Another evidence that at low masses the RHI-M∗ relation flattens is shown in the work by Maddox et al. (2015) already mentioned (see also Huang et al. 2012a). While the sample used by these authors does not allow to infer the RHI-M∗ correlation of galaxies due to its bias towards high R HI values (see above), the upper envelope of this correlation can be actually constrained; the high-RHI envelope does not suffer from selection limit effects. As seen for the data from Maddox et al. (2015) reproduced in the left upper panel of our Figure 1, this envelope tends to flatten at M∗ ≲ 2 × 109 M⊙,5 which suggests (but does not demonstrate) that the mean relation can also exhibit such a flattening. Another piece of evidence in favor of the flattening can be found in Huang et al. (2012b), and more recently in Bradford et al. (2015) for their sample of low-mass galaxies combined with larger mass galaxies from the ALFALFA survey.
4.3. The H2 -to-Stellar Mass Correlations
In the upper middle panel of Figure 5, along with the data from the Golden, Silver, and Bronze LTG samples, the mean and standard deviation (error bars) calculated in each mass bin with the KaplanMeier method are plotted. In the lower panel, the same is plotted but for the Golden and Silver ETG samples (recall that the Bronze samples are excluded in this case). The poor observational information at stellar masses smaller than ≈ 5 × 108 M⊙ does not allow us to constrain the correlations at these masses, both for LTG and ETGs. Regarding the total standard deviations, for both LTGs and ETGs, they vary from mass bin to mass bin but without a clear trend. Then we can use a constant value for both cases. For LTGs, the total standard deviations have values around 0.5-0.8 dex with an average of σdat ≈ 0.58 dex. For ETGs, the average value is roughly 0.8 dex. As in the case of HI (previous subsection), we further estimate indicative values for the intrinsic population standard deviations (scatter). For this, we present in Appendix E an estimate of the the mean observational error of the log RH2 determination, σerr ≈ 0.34 dex. Therefore, the estimated mean intrinsic scatters in log RH2 are σintr ≈ 0.47 and 0.72 dex for LTGs and ETGs, respectively. Given the assumptions and approximations involved in these estimates, they should be taken with caution. For example, we will see in § 5 that the distributions of log RH2 (detections and non-detections) in different mass bins tend to deviate from a normal distribution, in particular for the ETGs.
We fit the logarithm of function equation (1), y = RH2, to the mean values of log RH2 as a function of mass (squares in the left panels of Figure 5) with their corresponding scatter as estimated above (thin blue/red error bars), assumed to be the individual standard deviations for the fit. Again, the Levenberg-Marquardt method is used to perform the fit. The fits extend only down to M∗ ≈ 5 × 108 M⊙. First, the fits are performed for a singe power law, i.e., we fix a = b. The dashed orange and green lines in the middle panels of Figure 5 show the results. The parameters of the fit and their standard deviations are given in Table 5. The fits are very similar to those obtained using the Buckley-James linear regression to all (not binned) logarithmic data.
Then, we fit the binned LTG and ETG data to the double power-law function equation (1). In the case of the ETG population, we impose an extra condition to the fit: that the slope of the relation at masses below ≈ 109 M⊙ be flat. The few data at these masses clearly show that RH2 does not increase for smaller M∗; it is likely that it even decreases, so that our assumption of a flat slope is conservative. The corresponding best-fit parameters are presented in Table 6. As in the case of the RHI −M∗ correlations, the reduced χ2red are smaller than 1 (0.04 and 0.10, respectively), which implies that while the best fits are good, other fits could describe reasonably well the scattered data. In the case of the single power-law fits, χ2red were 0.04 and 0.07, respectively for LTG and ETG. The double power-law RH2 -M∗ relations and their (1σ) intrinsic scatter for the LTG (ETG) population are plotted in the middle upper (lower) panel of Figure 5 with solid lines and shaded areas, respectively. We note that the fits are almost the same if the total mean standard deviation, σdat, is used instead of the intrinsic one.
From these fits, we find for LTGs, Mtr* = 1.74 × 109 M⊙, with RH2 ∝ M∗ −0.07 and M∗ −0.47 at much smaller and larger masses than this, respectively. For ETGs, Mtr* = 1.02 × 109 M⊙, with RH2 ∝ M∗ 0.00 and M∗ −0.94 at much smaller and larger masses than this, respectively. In the middle upper panel of Figure 5, we plot also the best double power-law fit to the RH2 -M∗ correlation of LTGs when the αCO factor is assumed constant and equal to the MW value (purple dashed line).
Both the single and double power-law functions describe equally well the RH2 -M∗ correlations for the LTG and ETG population, but there is some evidence of a change of slope at small masses. In Figure 2, the Buckley-James linear regressions to the RH2 vs. M∗ data below and above log(M∗/M⊙)≈ 9.7 are plotted (in the former case the regressions are applied for masses only above 108 M⊙); the dotted lines show the extrapolation of the fits. The slopes in the small mass range at low masses for LTGs/ETGs are shallower than those at high masses. Besides, in the case of ETGs, if the single power-law fit shown in Figure 5 is extrapolated to small masses, ETGs of M∗ ≈ 107 M⊙ would be dominated in mass by H2 gas. Red/passive dwarf spheroidals are not expected to contain significant fractions of molecular gas. Recently, Accurso et al. (2017) have also reported a flattening in the H2-to-stellar mass correlation at stellar masses below ≈ 1010 M⊙.
4.4. The Cold Gas-to-Stellar Mass Correlations
Combining the RHI-M∗ and RH2 -M∗ relations presented above, we can obtain now the Rgas-M∗ relation, for both the LTG and ETG populations. Here, Rgas = Mgas/M∗ = 1.4(RHI + RH2), where Mgas is the galaxy cold gas mass, including helium and metals (the factor 1.4 accounts for these components). The intrinsic scatter around the gas-tostellar mass relation can be estimated by propagating the intrinsic scatter around the HI and H2 to-stellar mass relations. Under the assumption of null covariance, the logarithmic standard deviation around the logRgas -logM∗ relation is given by
The obtained cold gas-to-stellar mass correlations for the LTG and ETG populations are plotted in the right panels of Figure 5. The solid lines and shaded bands (intrinsic scatter given by the error propagation) were obtained from the double powerlaw correlations, while the solid green lines and the error bars were obtained from the single power-law correlations. For completeness, we also plot in Figure 5 those galaxies from our compilation that have determinations for both the HI and H2 masses. Note that a large fraction of our compilation has no determinations for both quantities at the same time. We fit the results obtained for the single (double) power-law fits, taking into account the intrinsic scatter, to the logarithm of the single (double) power law function given in equation (1) with y = R gas and report in Table 5 (Table 6) the obtained parameters for both the LTGs and ETGs. The fits for the double power-law are shown as dotted lines in Figure 5. The standard deviations σlog Rgas change slightly with mass; we report an average value for them in Tables 5 and 6. Both for LTGs and ETGs, the mass at which the Rgas-M∗ correlations change slope is Mtr* ≈ 1.7 × 109 M⊙, the mass that roughly separates dwarf from normal galaxies.
According to Figure 5, the LTG and ETG Rgas- M∗ correlations are significantly different. The gas content in the former is at all masses larger than in the latter, the difference being maximal at the largest masses. For the LTG population, Mgas ≈ M∗ on average at log(M∗/M⊙) ≈ 9, and at smaller masses, these galaxies are dominated by cold gas; at stellar masses around 2 × 107 M⊙ , Mgas is on average three times larger than M∗. For ETGs, there is a hint that at ≈ 109 M⊙, Rgas changes from increasing as M∗ is smaller to decreasing at larger masses.
5. THE DISTRIBUTIONS OF THE SCATTER AROUND THE GAS-TO-STELLAR MASS RELATIONS
To determine the correlations presented above, we have made use only of the mean and standard deviation of the data in different mass bins. It is also of interest to learn about the scatter distributions around the main relations. Furthermore, in the next section we will require the full distributions of RHI(M∗) and RH2 (M∗) in order to generate a mock galaxy catalog through which the HI and H2 mass functions will be calculated. The Kaplan-Meier estimator provides information to construct the probability density function (PDF) at a given stellar mass including the uncensored data. By using these PDFs we explore the distribution of the RHI and RH2 data (detections + upper limits). Given the heterogeneous nature of our compiled data, these “scatter” distributions should be taken just as a rough approximation. However, when the uncensored data dominate (this happens in most of the mass bins for the ETG samples), the Kaplan-Meier estimator cannot predict well the distribution of the uncensored data.
Late-type galaxies. Figures 6 and 7 present the R HI and RH2 PDFs in different M∗ bins for LTGs. Based on the bivariate HI and stellar mass function analysis of Lemonias et al. (2013), who used the GASS sample for (all-type) massive galaxies, we propose that the PDFs of R HI and RH2 for LTGs can be described by a Schechter (Sch) function (equation 3 below; x denotes either RHI or RH2). By fitting this function to the RHI data in each stellar mass bin we find that the power-law index α weakly depends on M∗, with most of the values being around −0.15 (see also Lemonias et al. 2013), while the break parameter x* varies with M∗. A similar behavior was found for RH2, with most of the values of α around −0.10. We then perform for each case (RHI and RH2) a continuous fit across the range of stellar-mass bins rather than fits within independent bins. The general function proposed to describe the RHI and RH2 PDFs of LTGs, at a fixed M∗ and within the range log x ± d log x/2, is:

Fig. 6 Distributions (PDFs) of the LTG HI-to-stellar mass ratios in different stellar mass bins (indicated inside the panels). The gray histograms show results from the Kaplan-Meier estimator applied to the data (detections + upper limits), and the solid blue line corresponds to the best fitted number density-weighted distribution within the given mass bin (equation 6); the constrained parameters of the mass-dependent PDF (equation 3) are given in Table 7. The red dotted line shows the constrained function equation (3) evaluated at the mass corresponding to the logarithmic center of each mass bin. The color figure can be viewed online.

Fig. 7 Same as Figure 6 but for the H2-to-stellar mass ratios. The color figure can be viewed online.
with the normalization condition, ϕ∗ = 1/Γ(1 + α), where Γ is the complete gamma function, which guarantees that the integration over the full space in x is 1. The parameters α and x* depend on M∗. We propose the following functions for these dependences:
and
The parameters c, d, x0, mtr, e, and f are constrained from a continuous fit across all the mass bins using a Markov Chain Monte Carlo method, following Rodríguez-Puebla et al. (2013). Since the stellar mass bins from the data have a finite width, for a more precise determination we convolve the PDF with the GSMF over a given bin. Therefore, the PDF of x averaged within the bin ∆M ∗ =[M∗1,M∗2] is:
where Φlate (M∗) is the GSMF for LTGs (see § 6). The constrained parameters are reported in Table 7. The obtained mass-dependent PDFs are plotted in the panels of Figures 6 and 7. The solid blue line corresponds to the number density-weighted distribution within the given mass bin (equation 6), while the red dotted line shows the function equation (3) evaluated at the mass corresponding to the logarithmic center of each bin. As seen, the Kaplan-Meier PDFs obtained from the data (gray histograms) are well described by the proposed Schechter function averaged within the different mass bins (blue lines), both for RHI and RH2.
Table 7 Best fit parameters to the full distributions
| c | d | x 0 | Log( mtr* /M⊙) | e | f | g | h | i | j | |
|---|---|---|---|---|---|---|---|---|---|---|
| P(RHI|M∗) distributions | ||||||||||
| LTG | 1.11±0.35 | -0.11±0.04 | 2.45±0.76 | 8.77±0.45 | 0.002±0.10 | 0.61±0.07 | - | - | - | - |
| ETG | -0.42±0.80 | -0.02±0.08 | 2.15±0.55 | 8.30±0.38 | -0.43±1.10 | 0.52±0.09 | -0.22±0.37 | -0.07±0.04 | -1.62±1.08 | -0.13±0.11 |
| P( RH2 |M∗) distributions | ||||||||||
| LTG | 0.70±1.28 | -0.07±0.13 | 0.15±0.03 | 10.37±0.31 | 0.19±0.17 | 0.19±0.16 | - | - | - | - |
| ETG | -0.52±1.19 | -0.01±0.11 | 0.71±0.27 | 7.90±1.09 | 0.42±0.50 | 0.21±0.28 | 0.24±0.97 | 0.04±0.09 | 5.74±3.17 | -0.86±0.29 |
For LTGs the distributions are given by equation (3), for ETGs, by equation (7).
Early-type galaxies.- We present the RHI and RH2 PDFs for ETGs in Figures 8 and 9, respectively. The distributions are very extended, implying a large scatter in the RH2 -M∗ correlations, as discussed in § 4.2 and 4.3.6 The distributions seem to be bimodal, with a significant fraction of ETGs having gas fractions around a low limit (≈ 10−4) and the remaining galaxies with larger gas fractions, following an asymmetrical distribution. The low limit is given by the Kaplan-Meier estimator and it is associated with the reported upper limits of non-detections. We should keep in mind that when non-detections dominate, the Kaplan-Meier estimator cannot provide a reliable PDF at the low end of the distribution. From a physical point of view, we know that ETGs are in general quiescent galaxies that likely exhausted their cold gas reservoirs and did not accrete more gas. However, small amounts of gas can still be available from the winds of old/intermediate-age stars. For instance, Sun-like stars can lose ≈ 10−4 − 10−5 of their masses in 1 Gyr; more massive stars lose higher fractions. A fraction of the ejected material is expected to cool efficiently and ends up as HI and/or H2 gas. However, those ETGs that have larger fractions of cold gas could acquire it by radiative cooling from their hot halos, or by accretion from the cosmic web, and/or by accretion from recent mergers (see for a discussion Lagos et al. 2014, and references therein). The amount of gas acquired depends on the halo mass, the environment, the gas mass of the colliding galaxy, etc. The range of possibilities is large; hence the scatter around the ETG RHI − M∗ and RH2 -M∗ relations is expected to be large, as semi-analytic models show (Lagos et al. 2014).

Fig. 8 Distributions (PDFs) of the ETG HI-to-stellar mass ratios in different stellar mass bins (indicated inside the panels). The gray histograms show results from the Kaplan-Meier estimator applied to the data (detections + upper limits), and the solid red line corresponds to the best fitted number density-weighted distribution within the given mass bin (equation 8); the constrained parameters of the mass-dependent PDF (equation 7) are given in Table 7. The red dotted line shows the constrained function equation (7) evaluated at the mass corresponding to the logarithmic center of each mass bin. The colorfigure can be viewed online.

Fig 9 Same as Figure 8 but for the H2-to-stellar mass ratios. The color figure can be viewed online.
To describe the PDFs seen in Figures 8 and 9, we propose a (broken) Schechter function plus a uniform distribution. The value of RHI or RH2 where the Schechter function breaks and the uniform distribution starts, x2, seems to depend on M∗ (see Figures 8 and 9). The lowest values where the distributions end, x1, are not well determined by the KaplanMeier estimator, as mentioned above. To avoid un necessary sophistication, we just fix x1 as one tenth of x2. This implies physical lowest values for RHI and RH2 of 10−4÷−5, which are plaussible according to our discussion above. The value of the Schechter parameter α shows a weak dependence on M∗ for both HI and H2. However, the fraction of galaxies between x 1 and x2, F, seems to depend on M∗. For the uniform distribution, this fraction is given by F = P(< x2|M∗)−P(< x1|M∗) = ∫x2x1Cd log x, where C = F /(log x2 − log x1); given our assumption of logx2 −logx1 = 1 dex, then C = F(M∗). We parametrize all these dependences on M∗ and perform a continuous fit across the range of stellar-mass bins, both for the RHI and RH2 data. The general function proposed to describe the PDFs of ETGs as a function of M∗ within the range log x ± d log x/2 is the sum of a Schechter function, PSch (x|M∗), and a uniform function in x but dependent on M∗, C = F(M∗):
where the parameters x* and α in PSch (x|M∗) are described by equation (3) with the normalization condition ϕ* =(1−F)/Γ(1+α), and logx 1 =logx2−1. The parameters x0, mtr, e, and f of the broken Schechter function and the parameters g, h, i, and j of the uniform distribution are constrained as described for LTGs above, from a continuous fit accross all the mass bins using the number density-weighted PDFs at each stellar mass bin:
where Φearly (M∗) is the GSMF for ETGs (see § 6). The constrained parameters are reported in Table 7, both for RHI and RH2. The mass-dependent distribution function obtained is plotted in the panels of Figures 8 and 9 The solid red line corresponds to the number density-weighted distribution within the given mass bin (equation 8), while the red dotted line shoes the proposed broken Schechter + uniform function evaluated at the mass corresponding to the logarithmic center of each bin. As seen, the Kaplan-Meier PDFs obtained from the data (gray histograms) are reasonably well described by the proposed function (equation 7) averaged within the different mass bins (red lines), both for RHI and RH2.
Finally, in Figures 10 and 11 we reproduce from Figure 5 the means and standard deviations obtained with the Kaplan-Meier estimator in different M∗ bins (gray dots and error bars) for LTG and ETGs, respectively, and compare them with the means and standard deviations of the general mass-dependent distributions functions given in equations (3) and (7) and constrained with the data (black solid line and the two dotted lines surrounding it). The agreement is rather good in the log-log RHI-M∗ and RH2 -M∗ diagrams both for LTGs and ETGs. Black dashed lines are extrapolations of the mean and standard deviation inferences from the distributions mentioned above, assuming they are the same as in the last mass bin with available gas observations. We also plot in these figures the respective mean double power-law relations determined in § 4.2 and 4.3 (dashed blue or red lines, for LTGs and ETGs respectively; dotted blue or red lines are extrapolations.).

Fig. 10 Mean and standard deviation as a function of stellar mass (solid and dotted black lines) from the distributions of RHI (upper panel) and RH2 (lower panel) for LTGs as given by equation (3) (see Table 7 for the constrained parameters). When the data are insufficientat small masses, the distributions are assumed to be the same as in the last mass bin (dashed black lines). The gray dots with error bars are the mean and standard deviation obtained with the Kaplan-Meier estimator applied to the data (detections + upper limits) in different mass bins, as shown in Figure 5. The double-power law fits to these data as reported in § 4 are reproduced with the blue dashed lines (the blue dotted lines are extrapolations of these fits). The color figure can be viewed online.
In conclusion, the RHI and RH2 distributions as a function of M∗ described by equations (3) and (7) (with the parameters given in Table 7) for LTGs and ETGs, respectively, are fully consistent with the corresponding RHI-M∗ and RH2 -M∗ correlations determined in § 4.2 and 4.3. Therefore, equations (3) and (7) provide a consistent description of the HI- and H2 -to-stellar mass relations and their scatter distributions for LTGs and ETGs, respectively.
6. CONSISTENCY OF THE GAS-TO-STELLAR MASS CORRELATIONS WITH THE OBSERVED GALAXY GAS MASS FUNCTIONS
The HI- and H2-to-stellar mass relations can be used to map the observed GSMF into the HI and H2 mass functions (GHIMF and GH2MF, respectively). In this way, we can check whether the correlations we have inferred from observations in § 4.2 and 4.3 are consistent with the GHIMF and GH2MF obtained from HI and CO (H2) surveys, respectively. In order to carry out this check of consistency, we need, on the one hand, a GSMF defined in a volume large enough to include massive galaxies and to minimize cosmic variance, and on the other hand, complete down to very small masses. As a first approximation to obtain this GSMF, we follow here a procedure similar to Kravtsov et al. (2014, see their Appendix A). We use the combination of two GSMFs: Bernardi et al. (2013) for the large SDSS volume (complete from M∗ ≈ 109 M⊙), and Baldry et al. (2012) for a local small volume but nearly complete down to M∗ ≈ 107 M⊙ (GAMA). In Appendix F we describe how we apply some corrections and homogenize both samples to obtain an uniform GSMF from M∗ ≈ 107 to ≈ 1012 M⊙.
Figure 12 presents our combined GSMF (solid line) and some GSMFs reported in the literature: the two used by us (see above), and those from Wright et al. (2017), Papastergis et al. (2012), and Baldry et al. (2008) in small but deep volumes, and D’Souza et al. (2015) in a large volume. We plot both the original data from Bernardi et al. (2013) (pink symbols) and after decreasing M∗ by 0.12 dex (blue symbols) to homogenize the stellar masses to the BC03 population synthesis model (see Appendix F). There is very good agreement between our combined GSMF and the recent GSMF reported in Wright et al. (2017) for the GAMA data.

Fig. 12 Our GSMF obtained from the combination of three observational GSMFs following Kravtsov et al. (2014) (thick solid line): first from the large SDSS DR7 volume but complete only down to ≈ 109 M⊙ (Bernardi et al. 2013, pink open circles with error bars; the orange open circles with error bars were obtained after correcting M∗ by 0.12 dex, see text); and then, two complete GSMFs down to smaller masses but drawn from a very local volume (Wright et al. (2017), Papastergis et al. 2012 and Baldry et al. 2012). We also plot for comparison, the GSMFs reported in Baldry et al. (2008) and D’Souza et al. (2015). The lower panel shows the fraction of ETGs as a function of mass inferred by Moffett et al. (2016), using GAMA galaxies and their visual morphological classification. The color figure can be viewed online.
Since the GSMF will be used as an interface for constructing the HI and H2 mass functions, the assumption that each galaxy with a given stellar mass has its respective HI and H2 content is implicit. Hence, the gas mass functions presented below exclude the possibility of galaxies with gas but no stars, and are equivalent to gas mass functions constructed from optically-selected samples (as in e.g., Baldry et al. 2008; Papastergis et al. 2012). In any case, it seems that the probability of finding only-gas galaxies is very low (Haynes et al. 2011).
We generate a volume complete mock galaxy catalog that samples the empirical GSMF presented above, and that takes into account the empirical volume-complete fraction of ETGs, fearly, as a function of stellar mass (the complement is the fraction of LTGs, flate =1 − fearly). The catalog is constructed as follows:
A minimum galaxy stellar mass M∗,min is set (= 107 M⊙). From this minimum we generate a population of 5 × 106 galaxies that samples the GSMF presented above.
Each mock galaxy is assumed to be either an LTG or an ETG. For this, we use the results reported in Moffett et al. (2016), who visually classified galaxies from the GAMA survey. They considered ETGs those classified as Ellipticals and S0-Sa galaxies. The fearly fraction as a function of M∗ is calculated as Φearly(M∗)/Φall(M∗), with Φearly(M∗) = ΦEll(M∗) + ΦS0−Sa(M∗), using the fits to the respective GSMFs reported in Moffett et al. (2016).7
To each galaxy RHI is assigned randomly from the conditional probability distribution Pj (RHI|M∗) that a galaxy of mass M∗ and type j =LTG or ETG lies in the RHI ±dRHI/2 bin. Then, MHI=RHI×M∗. The probability distributions for LTGs and ETGs are given by the mass-dependent PDFs presented in equations (3) and (7), respectively (their parameters are given in Table 7).
The same procedure as in the previous item is applied to assign MH2 ≡ RH2 ×M∗, by using for the Pj ( MH2 |M∗) probability distributions the corresponding mass-dependent PDFs for LTGs and ETGs presented in equations (3) and (7), respectively (their parameters are given in Table 7).
Our mock galaxy catalog is a volume-complete sample of 5×106 galaxies above M∗ = 107 M⊙, corresponding to a co-moving volume of 5.08 × 107 Mpc3. Since the HI and H2 mass functions are constructed from the GSMF, the mass limit M∗, min will propagate in a different way from that of these mass functions. The co-moving volume in our mock galaxy catalog is big enough to avoid significant effects from Poisson noise. This noise affects specially the counts of massive galaxies, which are the less abundant objects.
6.1. The Mock Galaxy Mass Functions
6.1.1. Stellar Mass Function
The mock GSMF is plotted in panel (a) of Figure 13 along with the Poisson errors given by the thickness of the gray line; except for the highest masses, the Poisson errors are actually thinner than the line. The mock GSMF is an excellent realization of the empirical GSMF (compare it with Figure 12). We also plot the corresponding contributions to the mock GSMF of the LTG and ETG populations (blue and red dashed lines). As expected, LTGs dominate at small stellar masses and ETGs dominate at large stellar masses. The contribution of both populations is equal (fearly = flate = 0.5) at Mcross* = 1010.20 M⊙ (recall that the fraction fearly used here comes from Moffett et al. (2016), who included Sa galaxies as ETGs; if consider Sa galaxies as LTGs, then Mcross* would likely be higher). In order to predict accurate gas and baryonic mass functions, the present analysis will be further refined in Rodriguez-Puebla et al. (in prep.), where several sources of systematic uncertainty in the GSMF measurement and in the definition of the LTG/ETG fractions will be taken into account. Our aim here is only to test whether the empirical correlations derived in § 4 are roughly consistent with the total HI and H2 empirical mass functions.
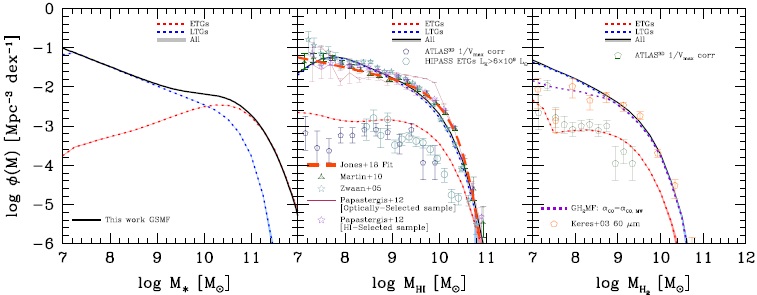
Fig. 13 Panel (a): Total GSMF from the mock catalog that reproduces the empirical GSMF of Figure 12 (solid line). The gray shadow represents the Poisson errors (except for large masses, these errors are thinner than the line thickness). The GSMF from the mock catalog samples very well the empirical GSMF used as input. The blue/red dotted lines and shadows correspond to the LTG/ETG mass function components, using the empirical ETG fraction as a function of M∗ shown in Figure 12. Panel (b): Same as Panel (a) but for atomic gas, using the mean R HI-M∗ relation and its scatter distribution as given in § 5. Several observational GHIMF’s from blind HI samples, and the ETG GHIMF from ATLAS3D and HIPASS surveys are reproduced (see labels inside the panel). Panel (c): Same as Panel (a) but for molecular gas. The GH2MF calculated from the Keres et al. (2003) LCO function is reproduced. The dotted purple line is the total GH2MF from the mock catalog using a RH2 -M∗ correlation obtained from our compilation, but assuming that αCO=αCO,MW=const., as done in Keres et al. (2003). The color figure can be viewed online.
6.1.2. HI Mass Function
In panel (b) of Figure 13, we plot the predicted GHIMF for our mock galaxy catalog using the mean (LTG+ETG) RHI -M∗ relations and their scatter distributions as given in § 5 (black line, the gray shadow shows the Poisson errors). For comparison, we plot also the HI mass functions estimated from the blind HI surveys ALFALFA (Martin et al. 2010; Papastergis et al. 2012, for both their HIand optically-selected samples; and the latest results from Jones et al. 2018) and HIPASS (Zwaan et al. 2005). At masses larger than M HI ≈ 3 × 1010 M⊙ , our GHIMF is in vey good agreement with those from the ALFALFA survey but significantly above that from HIPASS. Martin et al. (2010) argue that the larger volume of the ALFALFA survey compared to HIPASS, makes ALFALFA more likely to sample the mass function at the largest masses, where objects are very rare. The volume of our mock catalog is even larger than the ALFALFA one. At intermediate masses, 9 ≲ log(MHI /M⊙)≲ 10.5, our GHIMF is in reasonable agreement with the observed mass functions but it has in general a slightly less curved shape. At small masses, log(MHI /M⊙)≲ 8, the observed GHIMF’s flatten more than our predicted mass function. It could be that the blind surveys start to be incomplete due to sensitivity limits in the radio observations. Note that Papastergis et al. (2012) imposed additional optical requirements to their HI blind sample (see their § 2.1), which flatten the low-mass slope. Regarding the optically-selected sample of Papastergis et al. (2012), since it is constructed from a GSMF that starts to be incomplete below log(M∗/M⊙)≈ 8 (see Figure 12), one expects incompleteness in the GHIMF starting at a larger HI mass. Since our GHIMF is mapped from a volume complete GSMF from M∗,min ≈ 107 M⊙, “incompleteness” in MHI is expected to start from the HI masses corresponding to M∗,min × P(RHI|M∗,min), where the latter is the scatter around the RHI-M∗ relation. This shows that our GHIMF can be considered complete from log(MHI/M⊙)≈ 8. The slope of the GHIMF around this mass is −1.52, steeper than the slope at the low-mass end of the corresponding GSMF (α = −1.47).
In Figure 13 are also plotted the LTG and ETG components of the GHIMF as obtained from our mock catalog. The GHIMF is totally dominated by the contribution of LTGs. Our ETG GHIMF is compared with the ones obtained from observations using the ATLAS3D and HIPASS surveys as reported in Lagos et al. (2014).
6.1.3. H2 Mass Function
In Panel (c) of Figure 13, we plot the predicted GH2MF from our mock galaxy catalog using the mean (LTG+ETG) RH2 -M∗ relations and their scatter distributions as given in § 5 (black line, the gray shadow shows the Poisson errors). We compute the H2 mass function from the CO luminosity function derived by Keres et al. (2003), who used the small and incomplete FCRAO CO survey (Young et al. 1995) and combined it with the volume-complete FIR survey. We adopt the MW H2-to-CO conversion factor and correct their h parameter to 0.7. Unfortunately, this derivation is highly uncertain since is based on a empirical correlation between the 60μm and CO luminosities, and the selection effects in both surveys introduce several biases. The GH2MF obtained is plotted in Figure 13. Our GH2MF decreases faster than the one by Keres et al. (2003) at large masses, roughly agrees with it at intermediate masses, and for masses below log(RH2 /M⊙)≈ 8.5, our mass function is steeper. The reason for this latter difference seems to be the mass-dependent CO-to-H2 conversion factor introduced by us (see Appendix C). This factor increases as M∗ decreases while in the case of Keres et al. (2003) it is constant. We recalculate the GH2MF by using in the conversion from LCO to MH2 a constant CO-to-H2 factor equal to the MW value, and plot it as the purple dotted line; the mass function at the small-mass side is now in good agreement with that of Keres et al. (2003). In Figure 13 are also plotted the LTG and ETG components of the GH2MF as obtained from our mock catalog. The GH2MF is totally dominated by the contribution of LTGs. Our ETG GH2MF is compared with the one obtained from observations by using the ATLAS3D survey as reported in Lagos et al. (2014).
7. DISCUSSION
7.1. The H2 -to-HI Mass Ratio
The global H2-to-HI mass ratio of a galaxy characterizes its global efficiency of converting atomic into molecular hydrogen. This efficiency is tightly related to the efficiency of large-scale SF in the galaxy (see e.g., Leroy et al. 2008). From the empirical correlations inferred in § 4, we can calculate MH2 /M HI as a function of M∗ for both the LTG and ETG populations. We do this by using our double power-law fits to the data. The left panel of Figure 14 presents the obtained MH2 /MHI -M∗ relations and their 1σ H2 HI scatter calculated by propagating the dispersions in the assumption of null covariance. In this sense, the plotted scatters are upper limits, since there is evidence of some (weak) correlation between the HI and H2 content of galaxies, in particular among those deficient in HI and H2 (Boselli et al. 2014c). We can plot the same correlations for the mock catalog presented in § 6, which samples the observed GSMF, the LTG and ETG fractions as a function of M∗, and the empirical correlations inferred by us. The middle panels of Figure 14 present our measures from the mock catalog for LTG (blue), ETG (red), and all galaxies (gray). The lines are the logarithmic means in small mass bins and the shaded regions are the corresponding standard deviations. At small masses, LTGs dominate, so the correlation of all galaxies is practically the one of LTGs. At large masses, ETGs become more important.
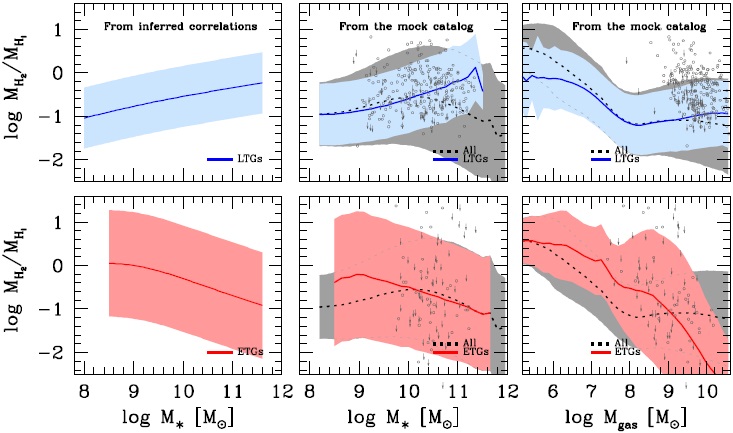
Fig. 14 Left panels: Molecular-to-atomic mass ratio, MH2 /MHI, for LTGs (upper panel) and ETGs (lower panel) inferred from our double power-law fits to the R HI-M∗ and RH2 -M∗ correlations. The shaded areas are the 1σ scatter obtained by error propagation of the scatter around the RHI-M∗ relations. Middle panels: Same as left panels, but from our mock catalog generated to sample the empirical GSMF, volume-complete ETG/LTG fractions as a function of mass, and RHI-M∗ and RH2 -M∗ correlations. The dotted line surrounded by the gray area is the total MH2 /MHI ratio and the 1σ scatter as a function of stellar mass. Right panels: Molecular-to-atomic mass ratio as a function of the cold gas mass, Mgas, from the mock catalog for LTGs (upper panel) and ETGs (lower panel). We plot available detected and undetected cold gas observational data as gray unfilled circles and downward arrows respectively. The color figure can be viewed online.
According to Figure 14, the molecular-to-atomic mass ratio of LTGs increases with M∗, albeit with a large scatter. On average, MH2 /MHI increases from ≈ 0.1 to ≈ 0.8 for masses ranging from M∗ = 108 M⊙ to 3 × 1011 M⊙. Given that the surface density of LTGs correlates significantly with M ∗, one can expect this dependence of MH2 /MHI on M∗ at least from two arguments: (1) Disk instabilities, which drive the formation of molecular clouds (e.g., the Toomre criterion Toomre 1964), are more probable to occur as the disk surface density is higher. (2) The H2-to-HI mass ratio in galaxies has been shown to be directly related to the hydrostatic gas pressure (Blitz & Rosolowsky 2006; Krumholz et al. 2009), and this pressure depends on the (gas and stellar) surface density (Elmegreen 1989). In fact, the physics of H2 condensation from HI is very complex and it is expected to be driven by local parameters of the ISM (see e.g., Blitz & Rosolowsky 2006; Krumholz et al. 2009; Obreschkow & Rawlings 2009). Therefore, the dependence of the H2-to-HI mass ratio on M∗ should be understood as consequence of the correlations of these parameters (their mean values along the galaxy) with M∗, introducing this actually large scatter in the dependence of MH2 /MHI on M∗. Indeed, several authors have shown that MH2/MHI correlates better with the mean gas-phase metallicity or mean stellar surface density than with M∗ (e.g., Saintonge et al. 2011; Boselli et al. 2014a).
For ETGs, the trend of the H2-to-HI mass ratio is inverse to the one of LTGs and shows a very large scatter. The ETGs more massive than ≈ 1011 M⊙ have mean ratios around 0.15 and a 1-σ scatter of ≈ ±1 dex; for intermediate masses, this ratio increases on average, and for ETGs with masses M∗ ≈ 109 M⊙, which are actually very rare, their mean H2-to-HI mass ratios are ≈ 1 with the same scatter of ≈ ±1 dex. Even though the gas fraction in ETGs is much smaller than in LTGs at all masses (see Figure 5), the former are also typically more compact than the latter, resulting probably in similar or higher gas pressures on average, and consequently similar or even higher MH2 /MHI ratios, especially at masses smaller than M∗ ≈ 1010 M⊙. In fact, given the large scatter in MH2 /MHI for ETGs, this ratio depends likely on many other internal and external factors (mergers, environment, etc.) that do not correlate significantly with M∗.
Regarding MH2/MHI vs. Mgas, for LTGs, which for M∗ > 107 M⊙ have mostly gas masses > 108 M⊙, there is no significant dependence, while for ETGs, which are almost inexistent with Mgas ≳ 109 M⊙, MH2/MHI is larger on average for lower values of Mgas. This can be seen in the right panel of Figure 14, where the mock catalog has been used. Basically, for a given Mgas, in the mass range Mgas ≈ 107 − 109 M⊙, ETGs have typically larger H2-to-HI mass ratios than LTGs. In combination, the H2-to-HI ratio appears to be larger for lower values of M gas. Such a dependence has been reported by Obreschkow & Rawlings (2009) for their compiled sample of galaxies, and predicted by these authors for a physical model.
The dependences of the H2-to-HI mass ratio on M∗, Mgas, and morphological type discussed above are in qualitative agreement with several previous observational works, which actually are part of our compilation (Leroy et al. 2008; Obreschkow & Rawlings 2009; Saintonge et al. 2011; Boselli et al. 2014a; Bothwell et al. 2014). However, our results extend to a larger mass range and separate explicitly the two main populations of galaxies.
7.2. The Role of Environment
There are several pieces of evidence that the atomic gas fraction of galaxies is lower in higherdensity environments (e.g., Haynes & Giovanelli 1984; Gavazzi et al. 2005; Cortese et al. 2011; Catinella et al. 2013; Boselli et al. 2014c). The fact that the ETG population has lower HI gas fractions than the LTG one (§ 4), the former being commonly found in higher-density environments, agrees with the mentioned environment trends. Thus, due to the morphology-density relation, our determinations of the RHI-M∗ (as well as RH2-M∗ and Rgas-M∗) correlations for the LTG and ETG populations, partially account for the dependence of these correlations on environment. Moreover, for the very isolated LTGs and for the subsample of LTGs in the Virgo cluster central regions, we confirm higher and lower HI-to-stellar mass ratios than the average of the overall LTG sample, respectively (see § 3.1). However, this systematic difference according to the environment is within the 1σ scatter of the RHI-M∗ correlation of LTGs (see Figure 3). Instead, in the case of ETGs, the isolated galaxies have much larger RHI values than the mean of all ETGs, above the 1σ scatter; isolated ETGs are almost as HI gas rich as the mean of LTGs.
Regarding the molecular gas fraction, the observational results are controversial in the literature. Recent studies seem to favor the the fact that galaxies in clusters are actually H2-deficient compared to similar galaxies in the field. However, the deficiencies are smaller than in the case of HI (Boselli et al. 2014c, and references therein). Here, for isolated and Virgo-center LTGs, we do not see any systematical segregation of RH2 from the rest of our compiled LTGs (Figure 4), but in the case of ETGs, the isolated galaxies have on average larger values of RH2.
In summary, the results from our compilation point out that the HI content of LTGs has a (weak) dependence on environment, mainly due to the fact that at high densities LTGs are HI deficient. However, the H2 content of LTGs seems not to change on average with the environment. In the case of ETGs, those very isolated are significantly more gas rich (both in HI and H2) than the average at a given mass.
An important aspect related to the environment is whether a galaxy is central or satellite. The local environmental effects once a galaxy becomes a satellite inside a halo. Ram pressure, viscous stripping, starvation, harassment and tidal interactions work in the direction of lowering the gas content of the galaxy, likely more the more massive the halo is (Boselli & Gavazzi 2006; Brown et al. 2017). Part of the scatter in the gas-to-stellar mass correlations is probably due to the external processes produced by these local-environment mechanisms. A result in this direction has been recently shown for the RHI-M∗ correlation by Brown et al. (2017). These authors have found that the HI content of satellite galaxies in more massive halos has, on average, lower HI-tostellar mass ratios at fixed stellar mass and specific SFR. According to their analysis, the systematic environmental suppression of the HI content at both fixed stellar mass and fixed specific SFR in satellite galaxies begins at halo masses typical of the group regime (> 1013 M⊙), and fast-acting mechanisms such as ram-pressure stripping are suggested to explain their results. In a future study, we will attempt to characterize the central/satellite nature of our compiled galaxies, as well as calculate a proxy to their halo masses, in order to clarify this question.
7.3. Comparisons with Previous Works
In Figure 15 we compare our results with those of previous works. When necessary, the data are corrected to a Chabrier (2003) IMF. Most of the previous determinations of the HI- and H2-to-stellar mass correlations are not explicitly separated for the two main galaxy populations as done here, and in several cases non-detections are assumed to have the values of the upper limits, or are not taken into account.
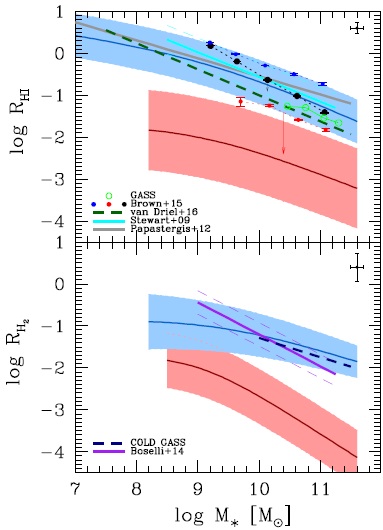
Fig. 15 Upper panel: Our empirical HI-to-stellar mass correlations for LTGs and ETGs (blue and red shaded areas, respectively) compared with some previous determinations (see labels inside the panel and details of each determination in the text). Previous determinations are based on compilations typically biased to late-type, blue galaxies, and/or do not take into account non-detections. The blue and red arrows correspond to estimates of the difference between the logarithm of the mean (the stacking technique provides the equivalent of the mean value) and the logarithmic mean (our determinations are for this case) for standard deviations of 0.52 and 0.99 dex, respectively (see text for more details). Lower panel: Our empirical molecular H2-to-stellar mass correlations for LTGs and ETGs (blue and red shaded areas, respectively) compared with very rough previous determinations not separated into LTGs and ETGs (see labels inside the panel and details of each determination in the text). The color figure can be viewed online.
In the upper panel, our empirical RHI-M∗ correlations for LTGs and ETGs are plotted along with the linear relations given by Stewart et al. (2009) (cyan line, the dashed lines show the 1σ scatter) and Papastergis et al. (2012) (gray line). The former authors used mainly the observational data presented in McGaugh (2005) for disk-dominated galaxies, and the latter authors used samples from Swaters & Balcells (2002), Garnett (2002), Noordermeer et al. (2005), and Zhang et al. (2009), which refer mostly to late-type galaxies. Their fits are slightly above the mean of our LTG RHI-M∗ correlation. This is likely due to their ignoring non detections. We also plot the logarithmic average values in mass bins reported by Catinella et al. (2013) for GASS (green open circles). Since ETGs progressively dominate in number as the mass increases, our total (density-weighted) RHI-M∗ correlation would fall below the one by Catinella et al. (2013), especially at the largest masses. Note that for the data plotted from Catinella et al. (2013), the HI masses of non-detections were set equal to their upper limits. Therefore, the plotted averages are biased to high values of RHI, specially for ETGs which are dominated by non-detections. Furthermore, recall that we have corrected the upper limits of GASS for distance to make them compatible with those of the nearer ATLAS3D survey.
More recently, Brown et al. (2015) have used the HI spectral stacking technique for a volume-limited, stellar mass selected sample from the intersection of SDSS DR7, ALFALFA, and GALEX surveys. With this technique the stacked signal of co-added raw spectra of detected and non-detected galaxies (about 80% of the ALFALFA selected sample) is converted into a (lineal) average HI mass. The authors have excluded from their analysis HI-deficient galaxies - typically found within clusters- because of their significant offset to lower gas content. The black dots connected by a dotted line show the logarithm of the average RHI values reported at different stellar mass bins in Brown et al. (2015). Since HI-deficient galaxies -which typically are ETGs- were excluded, the Brown et al. (2015) correlation should be compared with our correlation for LTGs. Note that with the stacking technique it is not possible to obtain the population scatter in R HI because the reported mean values come from stacked spectra instead of from averaging individual values of detections and nondetections. However, the stacking can be applied to subsets of galaxies, for example, selected by color. Brown et al. (2015) have divided their sample into three groups by their NUV−r colors: [1,3), [3,5), and [5,8]. The average RHI values at different masses corresponding to the bluest and reddest groups are reproduced in Figure 15 with the blue and red symbols, respectively. Note that the logarithmic mean is lower than the logarithm of the mean. For a lognormal distribution, 〈logx〉=log〈x〉-0.5×σ2logx ln10 (see e.g., Rodríguez-Puebla et al. 2017). Then, for the typical scatter of 0.44 dex corresponding to LTGs, the logarithm of the stacked values of RHI should be decreased by ≈ 0.2 dex to compare formally with our reported values of logarithmic means; this is shown with a black arrow in Figure 15. If the reddest galaxies in the Brown et al. (2015) stacked sample are associated with ETGs (which is true only partially), then for them the correction to a logarithmic mean is of ≈ 1 dex, shown with a red arrow.
Finally, recently van Driel et al. (2016) reported the results for HI observations at the Nancay Radio Telescope (NRT) of 2839 galaxies selected evenly from SDSS. The authors present a Buckley-James linear regression to their data (long-dashed green line in Figure 15), taking into account this way upper limits for non-detections (though their upper limits are quite high given the low sensitivity of NRT). They fitted the entire sample, that is, they do not separate into LTG/ETG or blue/red groups. In a subsequent paper (Butcher et al. 2016), the authors obtained ≈ 4 times more sensitive follow-up HI observations at Arecibo for a fraction of the galaxies that were either not detected or marginally detected; 80% of them were detected with HI masses ≈ 0.5 dex smaller than the upper limits in van Driel et al. (2016), and the rest, mostly luminous red galaxies, were not detected. If this trend is representative of the rest of the NRT undetected galaxies, Butcher et al. (2016) expect the fit plotted in Figure 15 to be offset toward lower RHI values by about 0.17 dex and even more at the highest masses. This fit lies between a density-weighted fit to our two correlations when taking into account that at large masses the fraction of ETG/red galaxies increases and at small masses LTG/blue galaxies dominate.
The lower panel of Figure 15 is similar to the upper panel, but for the RH2-M∗ correlations. Regarding the molecular gas content, there are only a few attempts in the literature to determine the relation between MH2 and M∗. In fact, those works that report approximate correlations are included in our compilation: Saintonge et al. (2011) for COLD GASS, and Boselli et al. (2014a) for HRS. The former authors report a linear regression to their binned data assuming H2 masses for non-detection set equal to their upper limits. The latter authors present a bisector fit using only detected, late-type gas-rich galaxies. Therefore, in both cases the reported relations are clearly biased to LTGs and toward high RH2 values.
The differences we find between our correlations and those plotted in Figure 15, as discussed above, can be understood on the basis of the different limitations that are present in each of the previous works. Bearing in mind these limitations we can conclude that the correlations presented here are in rough agreement with previous ones, but compared to them (i) they extend the correlations to a larger mass range, (ii) they separate explicitly galaxies into their two main populations, and (iii) they take into account adequately the non-detections.
8. SUMMARY AND CONCLUSIONS
The fraction of stars and atomic and molecular gas in local galaxies is the result of complex astrophysical processes along their evolution. Thus, the observational determination of how these fractions vary as a function of mass provides key information on galaxy evolution at different scales. Before the new generation of radio telescopes becomes available, which will bring extragalactic gas studies more in line with optical surveys, the main way to get this kind of information are studies based on radio follow-up observations of (small) optically-selected galaxy samples. In this work, we have compiled and homogenized samples from the literature with information on M∗ and MHI and/or MH2 for galaxies that can be identified to belong to two main (in a statistical sense) groups: the LTG and ETG populations. To estimate MH2 from CO observations, we have introduced a mass-dependent CO-to-H2 conversion factor in agreement with studies that show that this factor is not constant and depends on metallicity (hence, statistically, on mass). Results using a constant CO-to-H2 factor were also presented. Figures 1 and 2 summarize our compilation in the RHI vs. M∗ and RH2 vs. M∗ logarithmic diagrams.
Before inferring the correlations, we have tested how much each one of the compiled samples deviates from the rest and have classified them into three categories: (1) samples complete in limited volumes (or selected from them) without selection effects that could affect the calibration of the correlations (Golden); (2) samples that are not complete but are representative of the average galaxy population, without obvious selection effects (Silver); and (3) samples selected by their environment (Bronze). We showed that most of the samples, after our homogenization, are suitable to infer the RHI- M∗ and RH2 -M∗ correlations, except those from the Bronze category in the case of ETGs. These galaxies in extreme environments show significant deviations from the mean trends, and are not taken into account in our determinations. From the combination of all the chosen samples, we have calculated the mean, standard deviation, and percentiles of the logarithms of the RHI and RH2 mass ratios in several stellar mass bins, taking into account non-detected galaxies and their reported upper limits, which are a non-negligible fraction of the data, especially for the ETG population. Taking into account non-detected galaxies and their homogenization among different samples is relevant for determining the gas-to-stellar mass correlations of ETGs.
The mean logarithmic values in mass bins, ⟨log RHI⟩ and ⟨log RH2 ⟩, with the corresponding (intrinsic) standard deviations calculated by means of the Kaplan-Meier estimator were fitted to the logarithm of single and double power-law functions (equation 1). The parameters of the best fits to these functions, both for LTGs and ETGs, are reported in Tables 5 and 6, respectively. We highlight the following results from our analysis:
The RHI-M∗ and RH2 -M∗ correlations for the LTG and ETG populations can be described roughly equally well by a single or a double power law at masses larger than log(M∗/M⊙)≳ 9. For smaller masses, we see some hints of a flattening in these correlations. LTGs have significantly higher HI and H2 gas fractions than ETGs, the differences increasing at the high- and low-stellar mass ends. For the ETG population, the scatters of the RHI-M∗ and RH2 -M∗ correlations are much larger than for the LTG population.
Combining the RHI-M∗ and RH2-M∗ correlations and propagating errors, we calculated the cold gas (Mgas =1.4[MHI + MH2 ])-to-stellar mass correlations of the LTG and ETG populations. For the former, Rgas is around 4 on average at M∗ = 107 M⊙ and ≈ 1 at M∗ = 1.60 × 109 M⊙. At larger masses, Rgas continues to decrease significantly. For the ETG population, Rgas on average is smaller than 1 even for the smallest galaxies. Galaxies as massive as M∗ = 1011 M⊙ have on average Rgas ratios smaller than 2.5 × 10−3. The intrinsic standard deviation of the Rgas-M∗ correlation of the LTG population is ≈ 0.44 dex while for ETG it is larger, around 0.68 dex.
The H2-to-HI mass ratio implied by our correlations is such that for LTGs it increases on average with M∗, from ≈ 0.1 to 0.8 for masses ranging from M∗ = 108 M⊙ to 3×1011 M⊙. For ETGs, the trend is the opposite but with a large scatter (standard deviation of ≈ ±1 dex). While ETGs have much less gas content than LTGs, the H2-to-HI mass ratio at intermediate and small masses is higher on average in the former than in the latter, and lower at large masses.
In an attempt to describe the full distributions of RHI and RH2 as a function of M∗ for both the LTG and ETG populations, the respective PDFs from the censored+uncensored data in different mass bins provided by the Kaplan-Meier estimator were used. For LTGs, we found that a Schechter function with their parameters depending on M∗ offers a good description of the RHI and RH2 distributions as a function of M∗ (equation 3). For ETGs, these distributions look bimodal, with a (broken) Schechter function and a uniform distribution at the low-end side providing an approximate description of them (equation 7). These mass-dependent PDFs offer a full description of the RHI-M∗ and RH2 -M∗ relations and their scatter distributions for both LTGs and ETGs. Their first and second moments agree very well with our previously determined double power- law correlations (Figures 10 and 11).
The mass-dependent distribution functions of RHI and RH2 were used to map the GSMF into the corresponding HI and H2 mass functions, both for LTGs and ETGs. We use an empirical GSMF from the combination of GSMFs from a low-z survey and from the overall DR7 sample, following Kravtsov et al. (2014). The fractions of LTGs/ETGs as a function of M∗ are calculated from the fitted mass functions of ETGs obtained by Moffett et al. (2016) using the GAMA survey. The predicted total HI and H2 mass functions agree with those obtained from empirical determinations in the mass ranges where these determinations are reliable.
Our (marginal) finding of a flattening in the HI- and H2-to-stellar mass correlations at small masses has been suggested in some previous works (see § 4 for references). For our double power-law fits (equation 1), we find that the transition mass Mtr* is around 1 − 2 × 109 M⊙ for both the RHI-M∗ and RH2 -M∗ correlations and for both the LTG and ETG populations. Interestingly enough, this is the mass that roughly separates normal and dwarf galaxies.
We are aware that our determination of the gasto-stellar mass relations is based on an heterogeneous mix of samples. However, we have shown that there are no significant differences in the RHI and RH2 values as a function of M∗ for volume-limited complete and incomplete samples. Significant differences are observed only for samples selected by environment in the case of ETGs. On the other hand, our correlations for ETGs (and LTGs in the case of molecular gas), are very limited at small masses. They are actually just extrapolations for stellar masses below several 108 M⊙, but we have checked them to be consistent with the very few available determinations (mostly non-detections) below these masses.
In spite of these shortcomings, it is encouraging that the correlations (in fact, the full mass- dependent distributions), when mapped onto the HI and H2 mass functions using the observed GSMF as an interface, are consistent with the mass functions determined from observational radio surveys, at least in the mass ranges where these surveys do not suffer strong selection, volume, and cosmic variance effects. Such a self-consistency between the gas-tostellar correlations and mass functions supports the reliability of our results, which help to pave the way for the next generation of radio telescopes.
The empirical gas-to-stellar mass correlations and the approximate scatter distributions presented in this paper for the two main populations of galaxies are useful for understanding global aspects of galaxy evolution as a function of mass. We encourage the use of these correlations (or the full mass-dependent PDFs) for comparisons with predictions of models and simulations of galaxy formation and evolution.
Finally, we provide upon request to A. R. Calette a Python-based code that allows to generate plots and electronic tables for both LTGs and ETGs of (1) the R HI-M∗ and RH2 -M∗ double power-law relations and their 1σ intrinsic scatters as presented in Figure 5 and Table 6; and (2) the mass-dependent full RHI and RH2 PDFs as constrained in § 5, including the first and second moments (mean and standard deviation) of these PDFs.











 text new page (beta)
text new page (beta)