1 Introduction
Strontium ruthenate (Sr2RuO4) [1], a ternary body-centered tetragonal crystal with a layered square structure for the ruthenium atoms has a normal state described by a Fermi liquid model [2], with three FS metallic conduction sheets, namely the α and β (1D), and γ (2D) ones. Moreover, Sr2RuO4 belongs to the family of low temperatures unconventional superconductors, with Tc ≈ 1.5 K, but strongly depending on non-magnetic disorder [3]. Furthermore, Sr2RuO4 is an unconventional superconductor with triplet pairing and some type of nodes in the order parameter for each sheet of the FS [4]. In addition, the symmetry of the superconducting gap breaks the time reversal symmetry [5-7].
The discovery of several superfluid phases at ultralow temperatures in the liquid isotope 3He in 1972 by Lee, Oshero and Richardson was an initial point of remarkable investigations in unconventional superconductors [8]. 3He atoms are naturally fermionic, and thus the formation of Cooper pairs in 3He, provides a system similar to bulk superconductors but with some differences. 3He is superconducting in a liquid state at ultralow temperatures with Tc ~ 2.6 mK, the order parameter (OP) shows an odd momentum k-pairing dependence in one of the phases of 3He, namely in the A phase with a p-wave spin triplet broken state with jumps observed in specific heat in an external magnetic field [9].
In 1994 the discovery of the low temperature unconventional bulk superconductor Sr2RuO4 has since then attracted a lot of attention [1] due to the similarities with the A phase of the isotope 3He [4]. Strontium (stoichiometry) ruthenate is isostructurally similar to the the HTSC compounds but without copper. In contrast to the HTSC, it shows triplet odd pairing with a p-wave order parameter and k-dependence similar to the OP proposed in phase A of fermionic 3He. A recent review favoring this argumentation is given in [38].
We use the elastic scattering cross-section in our work to study strontium ruthenate in order to obtain a classical window [18] to the quantum effects in the unitary limit [41] for the FS γ-sheet, therefore we consider our work important, since this approach was previously not considered to be relevant in this compound, even it was used widely for HTSC in the past, mainly by Carbotte and collaborators [22]. Additionally, we use a couple of TB Wigner distribution probabilities aiming at helping to clarify and to contrast visually the location of the nodes.
This communication concerts the 2D γ sheet of the FS in Sr2RuO4. We investigate using a tight binding approach (TB) [10], the conjecture of nodes position, due to the fact that it continues to be a matter of intense discussions among the scientific community, despite it was experimentally discovered 27 years ago [11-17] and references there in.
As in previous works using a Wigner probabilistic distributions macroscopic approach [18], in this numerical study, we use a TB first nearest neighbor expression for the dispersion law ξγ(kx,ky) in order to model the FS γ sheet, which is centered at (0,0) in the first Brillouin zone. We extend our previous phenomenological works [19-20] by varying and analysing the behavior of one of the TB parameters, i.e., specifically the Fermi energy |ϵF| accordingly to table 1.
Table I TB Parameter and dispersion law values and limits for the quasi-point and point models nodes in the γ sheet of Sr2RuO4.
|
t,ϵF,Δ0γ
|
type of nodes |
dispersion law limit |
Figure |
| (0.4, 0.4, 1.0) (meV) |
4 quasi-point nodes |
strong disperse law |
Figures 1 and 3
|t|≈|ϵF|
|
| (0.4, 0.04, 1.0) (meV) |
4 point nodes |
flat non-disperse law |
Figures 2 and 4
|t|≫|ϵF|
|
Following this idea, we have noticed that by making the Fermi energy TB parameter |ϵF| very small in absolute value for the γ sheet, we get point nodes (shown in Fig. 2) in the MN model instead of quasi-point nodes of Fig. 1. Therefore, the case shown in Fig. 2 corresponds to the half-filling metallic limit with one electron per site, and with almost not dispersion, the so called flat band limit, and where the ground state of Sr2RuO4 has the lowest N states occupied. In this case, superconducting Sr2RuO4 is therefore gapless, i.e., is is a metallic unconventional system, meaning that it can be excited above the ground state by any infinitesimal energy/temperature value, and it correspond to a point nodes model as we numerically aim at showing in this work.
We also notice, that the quantum mechanics dispersion effect is caused by the hopping integral between local orbitals, is the one that makes the energy of the γ sheet with values |t|≈|ϵF| to have quasi-node points, but as it was note in [21] in some cases, i.e., with only first neighbors hopping there are bands with no dispersion, and these bands are called flat bands. It is very interesting to notice that in reference [21], it is state that these compounds do not include magnetic elements, such as transition or rare-earth elements, but we point out that the element Strontium (Sr) is non-magnetic, therefore is not excluded from their approach.
In this research, we set up a new numerical study with almost non dispersion in ξγ(kx,ky), i.e., when |t|≫|ϵF|, in contrast with our previously studied [19-20] where we used |t|≈|ϵF|.
In other order of ideas, the 2D TB normal state electronic energy expression in a first neighbor approximation is given by ξγkx,ky=-ϵF+2t coskxa+coskya, which follows electron-hole symmetry. The 2D TB OP expression in a first neighbor approximation, corresponds to the MN model [16]. These equations allow the study of the triplet time symmetry broken state in the FS γ-sheet of Sr2RuO4 i.e., Δγkx,ky=Δ0 dγkx,ky, with dγ(kx,ky)=[(sin(kxa)+i sin(kya)] z and Δ0γ=1.0 meV, according to experimental measurements in impurity samples [3].
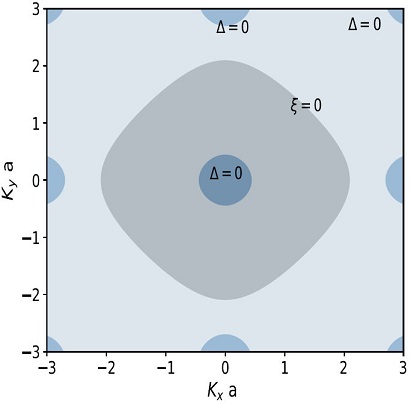
The nine points where the order parameter dγ(kx,ky) has zeros are sketched in both, Figs. 1 and 2. From nine OP zeros only 4 points, symmetrically distributed in the {10} and {01} planes at k-points (0, ±π) and (±π, 0) give symmetric point nodes, according to group theoretical considerations, when ϵF<<1 and when |t|≫|ϵF|. The other five points in Fig. 1, do not touch the γ sheet, i.e., the 4 points symmetrically distributed in the {11} planes at k-points (±π, ±π), and 1 point in the {00} plane at k-point (0,0).
As noticed firstly in [16] and also by us in [19-20], the gap on the γ sheet is very anisotropic and leaves a tiny gap Δ0γ around four points (0, ±π) and (±π, 0), but now we state that when |t|≫|ϵF| there is not such a gap. According to group theory considerations, in this case as in the tiny gap MN model, the imaginary OP has two components which belong to the irreducible representation E2u of the tetragonal point group D4h[17]. It also corresponds to a triplet odd paired state dγ(-kx,-ky)=-dγ(kx,ky) with the same basis functions sin(kxa) and sin(kya) and Ginzburg-Landau coefficients (1, i) [17,39].
We ought to emphasize that the difference with our previous work [19], consists in using the metallic ground state, which is given by decreasing an order of magnitude of the Fermi energy for the γ sheet, with a new value ϵF=0.04 meV, as can be observed in Fig. 2, giving us a new model with natural point nodes, that intercept the gap in 4 points on the γ-sheet, making it gapless, namely, (0, ±π) and (±π, 0) arriving to a 2D non disperse flat 𝛾 sheet model for Sr2RuO4 .
We use a numerical methodology able to control the non-magnetic disorder values, proposed by J. Carbotte and E. Schachinger [22], i.e., we vary first the inverse of the strength parameter c from 0 to 1 and second, we vary the value of the parameter concentration Γ+, from optimal to dilute doping in the function in the imaginary part of the scattering cross-section. The numerical analysis is performed in the reduced elastic scattering phase-space (RPS), giving us two families of Wigner distribution macroscopic probabilities. This methodology resembles an analysis using quantum collision theory with a phase-space scattering space with a Wigner probabilistic distribution, where those represent a classical window to study the quantum world [18]. This numerical approach agrees with a previous theoretical formalism, such as the work developed by I. M. Lifshitz and collaborators on disordered systems [23].
In the following sections, we report first, a theoretical derivation of the scattering cross-section formalism, and second, a visual numerical analysis of the imaginary part of the elastic scattering cross-section on Sr2RuO4 at the phenomenological level, using the gapless point nodes model of Fig. 2 and comparing it, with the quasinodal case previously studied [19-20].
2 Non-magnetic impurity scattering, the Edwards-Nambu-Gorkov formalism
It is known that non-magnetic elastic scattering destroys the coherence of the Cooper pairs in unconventional superconductors. The decrease of Tc is a function of the concentration of non-magnetic impurities (nimp). Thus, the maximum transition temperature Tc is given for the case when nimp = 0 and is denoted as
Tc0.
S. Edwards in 1961 (see [24] for a summary and original references) introduced the technique that allowed the use of Feynman diagrams to include the Hamiltonian that would describe the effect of static impurities in a normal metal, his model assumes the following physical conditions: at T = 0, the N impurities are equal and independent, they are randomly distributed in the normal metal (however on a macroscopic scale the metal is homogeneous), and finally, a very important point, this is a quantum model, since impurities scatter electrons elastically and there is no loss of energy in collisions.
A dressed normal metal Green function (GF) is defined as an averaged by non-magnetic impurities GF, in Fourier components and its self-consistent form is given as follows
G(k,ε)=G0(k,ε)+G0(k,ε)Σ(k,ε)G(k,ε).
(1)
In this case, the average represents a sum over all the electronic momenta k and for all the points j locating at each of the N impurities.
...=∑k,j
(2)
The solution to Eq. (1), which represents the GF normalized by the effects of the scattering by non-magnetic impurities is
G(k,ε)=1G0(k,ε)-Σ(k,ε)-1,
(3)
with an undressed normal metal GF given by:
G0(k,ε)=1iε-ξk.
(4)
On the other hand, the GF in a superconductor for a Cooper pair in the presence of a non-magnetic impurity potential is known as the Edwards-Nambu-Gorkov GF [25] and is defined as
G^(ε,k)=G^0(ε,k)+G^0(ε,k)T^(ε)G^0(ε,k).
(5)
The symbol ∧ introduced by Y. Nambu above the GF means that the superconducting state is described by a two-dimensional Pauli Matrix basis, since it takes into account the spin space, in addition to the momentum space. Any function in the spin space can be decomposed in terms of the Pauli matrices, and it becomes a scalar for a normal metal [24].
The normal GF in the superconducting state is given by the expression G^0(ε,k) (We will not use in this work, the anomalous F^(ε,k) Green function introduced by L. Gorkov [25] and references therein, since the anomalous F Green function has the kernel Δ - gap as a function of temperature, and it is useful for a study of impurities temperature dependence on the gap, which is not the scope of this research), therefore G^0(ε,k) is written as
G^0(ε,k)=εσ^0+ξkσ^3+Δ(k)σ^1ε2-ξk2-|Δ(k)|2.
(6)
The array T^ has the following general form
T^(ε)=U^0⋅σ^0-U^0∑kG^0(ε,k)-1,
(7)
with the impurity potential matrix U^0=U0σ^3. Since we want to use a tight binding numerical formalism, it is convenient to define an average where the sums in the space k will be now averages over the Fermi Surface for each component of the GF is described by the Pauli matrices in the following way:
∑kG^0(ε,k)=∑k(G00(ε,k)σ^0+G01(ε,k)σ^1+G03(ε,k)σ^3).
(8)
Studying each component separately we have the following relations:
∑kG00(ε,k)=-iπNFεε2-|Δ(k)|2FS,
(9)
∑kG01(ε,k)=-iπNFΔ(k)ε2-|Δ(k)|2FS,
(10)
and
∑kG03(ε,k)=-iπNFξkε2-|Δ(k)|2FS.
(11)
Integrating over the space k for the energy of the metal and averaging in our TB model on the Fermi surface, assuming electron-hole symmetry, we have two important conditions: ∑kG01(ε,k)=0 for a superconductor in a triplet state with D4h symmetry, since the order parameter has odd parity Δ-kγ=-Δkγ. In addition, the value of ∑kG03(ε,k)=0 means that in the metallic system there is a symmetric electron-hole physical system ξkγ=ξ-kγ, as we pointed out in the introduction. With these two conditions, we rewrite (8) with a new function that we call g(ε)
∑kG^0(ε,k)=∑kG00(ε,k)σ^0=-i π NF g(ε) σ^0,
(12)
where g(𝜺) is given by the equation
g(ε)=εε2-|Δ(k)|2FS.
(13)
Now with this result, we calculate the inverse matrix of the array T^
T^(ε)=U0σ^3⋅σ^0+iπNFU0σ^3⋅(g(ε)σ^0)-1,
(14)
and,
σ^0+iπNFU0g(ε)σ^3-1=σ^0+iπNFU0g(ε)σ^31-(iπNFU0g(ε))2 ,
(15)
to get
T^(ε)=U0σ^3+iπNFU02g(ε)σ^01-(iπNFU0g(ε))2.
(16)
Instead of using the impurity potential U0, we use the parameter c inverse to the strength U0. The parameter c which is defined as c=(π NF U0)-1=cotδ0 is related to the phase shift δ0 of the Cooper pair wave function. Recalling that by assuming e-h symmetry, it is obtained that the component T3ε=0, and
T^(ε)=i(πNF)-1g(ε)c2+|g(ε)|2σ^0.
(17)
The self-energy induced by the concentration of impurities nimp is denoted by Σϵ=nimpTϵ, where Γ+=nimp/(π NF), and where finally the renormalized self-energy due to the presence of non-magnetic impurities is given by
t(ε)=ε+Σ(t(ε)).
(18)
Since we use Planck units ℏ=kB=c=1, then Eq. (18) can be converted according to the following self-consistent expression which finally, allow us to have an expression for the scattering cross-section parameterized as function of c and Γ+[22]
ω~( ω+i0+) =ω+iπΓ+g(ω~)c2+|g(ω~)|2.
(19)
The first thing to notice is that they represent a classical set of Wigner distribution probabilities, the second issue about (19) is that it describes both the Born classical elastic scattering and also the coherent phase (unitary) limit for which c = 0. Thirdly, it should be noted that the real part of the equation represents the energy ℏω. Fourthly, the imaginary part of Eq. (19) defines the inverse of the quasiparticle dressed lifetime τ-1(ω) in a RPS according to the expression
τ-1 (ω) =2I[ω~ω+i0+].
(20)
Therefore, we have theoretically derived the main equation for the elastic scattering cross-section formalism ω~ ( ω +i 0+) in the case of non-magnetic disorder, in order to model low energy self-consistent frequencies in the unitary region of the reduced scattering phase space, by varying the tight binding parameters, to obtain several families of the macroscopic Wigner probability distributions.
For very large values of U0, the unitary limit (l kF∼l a-1∼1 & c=0) in Eq. (19) is given by the expression
ω~(ω+i0+)=ω+iπΓ+1g(ω~) .
(21)
The function g(ω~) in Eq. (19) is given by
g(ω~)=〈ω~ω~2-|Δ|2(kx,ky)〉FS,
and the average over the γ sheet of the FS 〈 …〉FS is performed following an integration over the FS according a numerical technique successfully used to fit experimental low temperatures data with an accidental 3D point nodes TB model, i.e, the ultrasound attenuation, the electronic heat transport, and the electronic specific heat in Sr2RuO4
[26-28]. This kind of approximation is indeed characterized by root singularities at the edges of the dependence for the unitary case, i.e., where g(ω~) can go to zero within the model, following Lifshitz disorder system theory [23].
Born’s approximation applies and if c≫1 (i.e. U0≪1) with a disorder renormalized doping parameter ΓB+=Γ+/c2≪1, with is proportional to the square of the strength potential U0, and to nimp. However, as we recently reported [20], Born scattering does not play a role in the low temperature properties of Sr2RuO4 it has a RPS window of Δ0= 1.0 meV. At this point we also emphasize, that for the case of the lines nodes superconductor La2-xSrxCuO4, we reported that this compound can be numerically be in the Born limit with a RPS scattering window if Δ0= 33.9 meV, for it we found another family of Wigner probabilistic distributions [20,29].
On the other hand, the unitary limit has a unique feature which is the resonance at zero frequency, that is, ω~ (0)=i γ, where γ defines the “impurity averaged” zero energy elastic scattering rate [22], and determines the crossover energy scale separating several scattering limits (Born, intermediate and unitary). Finally, impurity effects within unitary scattering has been widely investigated in several works [30-36] among other references, but not exactly within the TB macroscopic Wigner probabilistic distribution approach, we perform here.
3 The unitary limit for the case of quasinodal points in the FS gamma-sheet of Strontium ruthenate
In this section, we calculate numerically and visualize the behavior of the imaginary part of the elastic scattering cross-section in the unitary limit (c = 0) for different values of the impurities concentration parameter Γ+, starting at very dilute disorder (turquoise line), to an optimal disorder (gray line) as it was done in our previous publications [19-20] but with a different purpose, the study of the flat γ sheet limit. We use the following TB parameters (|t|,|ϵF|)=(0.4,0.4) meV given in Table I, where there is anisotropic dispersion reflected in the normal state electronic energy that can be seen in Fig. 1.
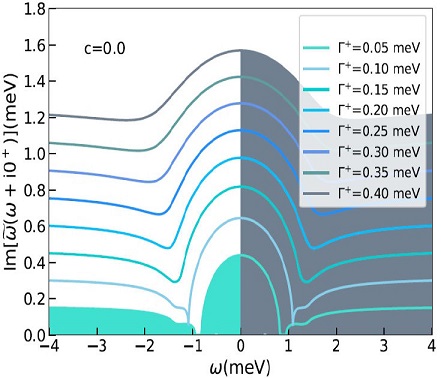
The unitary limit means that the dressed normal state quasiparticles have an ill-defined momentum between elastic collisions, but the energy is conserved [41]. In addition, the signature of the unitary state is the resonance at zero frequency with the parameter c = 0, in the imaginary part of the scattering cross-section as can be seen from all Wigner distribution functions of Fig. 3.
If |ϵF|≈t, as in Fig. 1, the unitary regime in the elastic scattering due to non-magnetic disorder is so strong that the mean-free path l becomes comparable to the inverse Fermi momentum kF-1, and to the lattice parameter a, and it has two macroscopic phases, the tiny gap phase ( Γ+=0.05 meV - dilute levels of non magnetic disorder, turquoise line and region in phase scattering space shaded turquoise in Fig. 3) where the energy interval between 0.85 and 1.0 meV is composed only by Cooper pairs (ω~(ω+i0+)=0 meV), and the mixed phase with both, Cooper and normal state quasiparticles for the whole range of energies from 0 to 4 meV (from pale blue to gray color lines and a maximum region in scattering space shaded gray in Fig. 3 and Γ≥0.10 meV).
This corresponds to the quasinodal point nodes model as was previously reported in [19-20]. We also observe the smooth resonance centered at zero frequency for all values, with smaller values of residual zero energy γ for very dilute values of disorder Γ+.
4 The unitary limit for the case of nodal points and a flat dispersion law in the FS gamma-sheet of strontium ruthenate, and the metallic half filling ground TB state.
If |ϵF|≈(|t|/10), i.e., ϵF≪t, the unitary regime and the family of Wigner distribution functions of Fig. 4, show a different behavior from the one studied in the previous section. It resembles a gapless node points in unconventional superconductors (also it resembles the line nodes points model of high Tc compounds we previously calculated for La2-xSrxCuO4 in [29]). This intuitively means that the half filling ground state in the unitary limit gives point nodes and a flat dispersion law if the TB parameters are appropriately chosen.
Therefore, the normal state quasiparticles with a flat γ-sheet in the unitary region for Sr2RuO4 , and with a gapless behavior have also an ill-defined momentum quasiparticles between elastic collisions, can be studied using the scattering cross-section following the same methodology. The signature of the unitary state still corresponds to the resonance at zero frequency in the imaginary part of the scattering cross-section, as it can be seen from the Wigner distribution probabilities functions, obtained self-consistently in Fig. 4, but in this case there is not a tiny gap as in the previous section, as should be, since the superconducting regime is gapless in the case of point nodes.
In this case, there is only one macroscopic phase in Sr2RuO4 , for both, the dilute levels of non-magnetic disorder composed by Cooper pairs and the normal state quasiparticles (turquoise line and region in phase scattering space shaded turquoise in Fig. 4), and where the following identity holds: (ω~[ω+i0+]≠0) meV, for the whole range of energies from 0 to 4 meV (with a minimum region shaded turquoise, and maximum region in scattering reduced phase space shaded gray in Fig. 4.
This is a new class of Wigner probabilistic distributions family found for Sr2RuO4 in the case of point nodes for the γ-flat Fermi sheet, and it shows how numerically depending on the values of the TB parameter ϵF there can be point nodes in this compound as well, and not only a tiny gap family of Wigner distribution functions [20]. We wish to point out, that the use of the symmetric point group D4h and the symmetry broken state in the case of strontium ruthenate is also supported by recently review works [37-39], and the flat bands approach is widely discussed for heavy fermions compounds in the monograph [40].
5 Conclusions
This communication was aimed at investigating numerically the behavior of the non-magnetic disordered imaginary part of the elastic scattering cross-section in the unitary metallic limit for two cases in the FS γ-sheet of Sr2RuO4 . One case with TB parameters for the dispersion law ξγ(kx,ky) given by |ϵF|≈|t| with represents a dispersed quantum mechanical (QM) electronic behavior, and the case with |ϵF|≪|t| with a flat γ QM sheet behavior.
First we found and discuss an interesting feature, the MN tiny gap model at half filling in the γ sheet disappears, and converts into a point nodes case in the RPS with D4h symmetry, if in the TB first neighbor approximation, we use for an almost flat sheet the parameter value |ϵF|=0.04 meV, otherwise is |ϵF|=0.4 meV for quasinodal behavior. In Fig. 1 and Fig. 2 we illustrate and compare the two cases mentioned above, using an implicit function scheme for both, the dispersion law and gap symmetry equations with the corresponding TB parameters. In addition in Sec. 2, we briefly introduced the Edwards-Nambu-Gorkov formalism needed for a TB analysis of the RPS.
Second, in Fig. 3, we numerically calculate and sketch a first family of eight Wigner distributions, where the region corresponding to optimal levels of disorder, i.e., Γ+=0.4 meV, has been shaded gray in the right side of the plot. In addition, the regions corresponding to dilute levels of disorder with Γ+=0.05 meV, has been shaded turquoise in the left side of the plot. The Miyake-Narikiyo tiny gap that corresponds to 4 quasi-nodal points in the order parameter, and graphically is showed in Fig. 3 as a turquoise line in the left side.
Third, in Sec. 4, the behavior of the disordered non magnetic matrix I[ω~]( ω+i 0+) inside the unitary (c = 0) RPS was studied for eight values of Γ+, starting at very diluted disorder, optimal disorder values, and finally an enriched disorder concentration. In Fig. 4, the region corresponding to optimal levels of disorder, i.e., Γ+=0.4 meV, has been shaded gray in the right side of the figure. In addition, in this case the MN tiny gap does not appear in the imaginary part of the scattering cross-section, i.e., it represents the case of the 4 point nodes with a flat FS γ-sheet, which is shaded turquoise in Fig. 4 on the left side, and corresponds to the turquoise line at value Γ+=0.05 meV.
We find according to Fig. 3, that for the case of the MN tiny gap, there are two phases: a phase in the RPS with doping Γ+≥0.1 meV where Fermion dressed RPS quasiparticles are mixed with Cooper pairs. This can be seen in Fig. 3 (gray region). We also found the MN tiny gap phase for Γ+=0.05 meV, in that region only Cooper pairs exist for an energy window between 0.85 and 1.0 meV as is seen in Fig. 3, left side (turquoise line) as noticed previously [20].
Also, we find according to Fig. 4, that for the case point nodes, exists macroscopically only one phase with both, Cooper pairs and normal state point nodal quasiparticles, reflecting a new family of Wigner probabilistic distributions in the RPS with doping Γ+≥0.05 meV, for the whole energy window, i.e., (-4 meV, +4 meV), this can be seen in Fig. 4 (turquoise and gray regions). This phase resembles High Tc cuprates. In the case, we conclude that there is always a minimum amount of Fermi dressed quasiparticles interacting elastically due to a small amount of non-magnetic disorder Γ+=0.05 meV, the main difference with lines nodes case [29] is that here, Δ0γ=1.0 meV (an smaller RPS window (-4 to +4.0 meV [20]) and in the line nodes high Tc case, Δ0γ=33.9 meV (bigger RPS window (-33.9 to +33.9 meV [20,29]) .
We end this communication pointing out that the Miyake-Narikiyo gap expression using a tight binding model is very useful for setting up numerical studies in triplet superconductors such as Sr2RuO4 , as we have demonstrated in this and previous studies on the subject [19-20]. This approach uses a macroscopic Wigner distribution probabilities phenomenological approach obtained from the analysis of the imaginary part of the scattering cross-section, helping undoubtedly to resolve the actual conjecture of the location of the nodes in Sr2RuO4.
Our studies involve using several families of TB Wigner distribution probabilities with the Miyake Narikiyo model obtained self-consistently, aiming at clarifying the location of point nodes in the FS γ-sheet broken symmetry state. They could be used to study other irreducible representations belonging to different point symmetry groups in other crystalline structures, so far, we have considered 2 of them, remaining several more to be studied.
The existence of a link of our phenomenological TB approach with the quasi-classical approach to the strong coupling theory in unconventional superconductors proposed in [42] and recently discussed in [43] could improve the development of the use of Wigner distributions probabilities [18,44] in order to study new unconventional superconductors with a reduced scattering phase space with dressed quasiparticles and their quantum DOS states.
Acknowledgements
We thank conversations with Dr E. Beliayev and Prof. Sh. M. Ramazanov about the use of quantum distribution functions to study macroscopic properties in unconventional superconductors. Also we thank an anonymous reviewer whose technical comments helped improve and clarify this manuscript. The authors did not receive any financial support for research, authorship and/or publication of this article.
References
1. Y. Maeno et al., Superconductivity in a layered perovskite
without copper, Nature
372 (1994) 53, https://doi.org/10.1038/372532a0.
[ Links ]
2. C. Bergemann, A. P. Mackenzie, S. R. Julian, D. Forsythe, E.
Ohmichi, Quasi-two-dimensional Fermi liquid properties of the unconventional
superconductor Sr2RuO4, Advances
in Physics
52 (2003) 639,
https://doi.org/10.1080/00018730310001621737.
[ Links ]
3. M. Suzuki, M. A. Tanatar, N. Kikugawa, Z. Q. Mao, Y. Maeno, and
T. Ishiguro, Universal Heat Transport in Sr2RuO4,
Phys. Rev. Lett. 88 (2002) 227004,
https://doi.org/10.1103/PhysRevLett.88.227004.
[ Links ]
4. T. M. Rice and M. Sigrist, Sr2RuO4: an
electronic analogue of He3?, Journal of
Physics: Condensed Matter 7 (1995) L643,
http://dx.doi.org/10.1088/0953-8984/7/47/002.
[ Links ]
5. K. Ishida, H. Mukuda, Y. Kitaoka et al., Spin-triplet
superconductivity in Sr2RuO4 identified
by 17O Knight shift, Nature
396 (1998) 658, https://doi.org/10.1038/25315.
[ Links ]
6. G. Luke, Y. Fudamoto, K. Kojima et al., Time-reversal
symmetry-breaking superconductivity in Sr2RuO4,
Nature
394 (1998) 558, https://doi.org/10.1038/29038.
[ Links ]
7. J. A. Duffy, S. M. Hayden, Y. Maeno, Z. Mao, J. Kulda, and G. J.
Mclntyre, Polarized-Neutron Scattering Study of the Cooper-Pair Moment in
Sr2RuO4, Phys. Rev. Lett.
85 (2000) 5412,
https://doi.org/10.1103/PhysRevLett.85.5412.
[ Links ]
8. D. Osheroff, W. Gully, R. Richardson, and D. Lee, New Magnetic
Phenomena in Liquid 3He below 3 mK. 1972. Phys. Rev. Lett.
29 (1972) 920,
https://link.aps.org/doi/10.1103/PhysRevLett.29.920.
[ Links ]
9. V. Ambegaokar and N.D. Mermin, Thermal Anomalies of 3He: Pairing
in a Magnetic Field. Phys. Rev. Lett. 30 (1973)
81-84, https://link.aps.org/doi/10.1103/PhysRevLett.30.81.
[ Links ]
10. W. A. Harrison, Electronic Structure and Properties of Solids (Dover, New York, 1980).
[ Links ]
11. A. P. Mackenzie and Y. Maeno, The superconductivity of
Sr2RuO4 and the physics of
spin-triplet pairing, Rev. Mod. Phys. 75 (2003)
657, https://doi.org/10.1103/RevModPhys.75.657.
[ Links ]
12. C. W. Hicks, D. O. Brodsky, E. A. Yelland et al., Strong
Increase of Tc of Sr2RuO4
Under Both Tensile and Compressive Strain, Science
344 (2014) 283,
https://www.science.org/doi/10.1126/science.1248292.
[ Links ]
13. S. Benhabib, C. Lupien, I. Paul et al., Ultrasound evidence for
a two-component superconducting order parameter in
Sr2RuO4, Nat. Phys.
17 (2021) 194,
https://doi.org/10.1038/s41567-020-1033-3.
[ Links ]
14. S. Ghosh, A. Shekhter, F. Jerzembeck et al., Thermodynamic
evidence for a two-component superconducting order parameter in
Sr2RuO4, Nat. Phys.
17 (2021) 199,
https://doi.org/10.1038/s41567-020-1032-4.
[ Links ]
15. V. Grinenko, D. Das, R. Gupta et al., Unsplit superconducting
and time reversal symmetry breaking transitions in
Sr2RuO4 under hydrostatic
pressure and disorder. Nat Commun 12 (2021) 3920,
https://doi.org/10.1038/s41467-021-24176-8.
[ Links ]
16. K. Miyake and O. Narikiyo, Model for Unconventional
Superconductivity of Sr2RuO4: Effect of
Impurity Scattering on Time-Reversal Breaking Triplet Pairing with a Tiny Gap,
Phys. Rev. Lett. 83 (1999) 1423,
https://doi.org/10.1103/PhysRevLett.83.1423.
[ Links ]
17. M. B. Walker and P. Contreras, Theory of elastic properties of
Sr2RuO4 at the superconducting
transition temperature, Phys. Rev. B
66 (2002) 214508,
https://doi.org/10.1103/PhysRevB.66.214508.
[ Links ]
18. P. Carruthers and F. Zachariasen, Quantum collision theory with
phase-space distributions, Rev. Mod. Phys.
55 (1983) 245,
https://doi.org/10.1103/RevModPhys.55.245.
[ Links ]
19. P. Contreras, D. Osorio and S. Ramazanov, Non-magnetic tight
binding effects on the 𝛾 sheet of
Sr2RuO4.
Rev. Mex. Fis.
68 (2022) 1,
https://doi.org/10.31349/RevMexFis.68.020502.
[ Links ]
20. P. Contreras, Dianela Osorio, and E Beliayev, Dressed behavior
of the quasiparticles lifetime in the unitary limit of two unconventional
superconductors, Low Temp. Phys.
48 (2022) 187, https://doi.org/10.1063/10.0009535.
[ Links ]
21. Hase, I., Yanagisawa, T., and Kawashima, K. Computational Design
of Flat-Band Material. Nanoscale research letters,
13 (2018) 63,
https://doi.org/10.1186/s11671-018-2464-y.
[ Links ]
22. E. Schachinger and J. P. Carbotte, Residual absorption at zero
temperature in d-wave superconductors, Phys. Rev. B
67 (2003) 134509,
https://doi.org/10.1103/PhysRevB.67.134509.
[ Links ]
23. I. M. Lifshitz, S. A. Gredeskul and L. A. Pastur, Introduction to the theory of disordered systems (John Wiley and Sons, 1988).
[ Links ]
24. J. M. Ziman, Models of Disorder: The Theoretical Physics of Homogeneously Disordered Systems, (Cambridge University Press, Cambridge, 1979).
[ Links ]
25. V. Mineev and K. Samokhin, Introduction to Unconventional Superconductivity, (Amsterdam, Gordon and Breach Science Publish, 1999).
[ Links ]
26. P. Contreras, M. Walker, and K. Samokhin, Determining the
superconducting gap structure in from sound attenuation studies below
Tc, Phys. Rev. B
70 (2004) 184528,
https://doi.org/10.1103/PhysRevB.70.184528.
[ Links ]
27. P. Contreras, Electronic heat transport for a multiband
superconducting gap in Sr2RuO4, Rev. Mex.
Fis.
57 (2011) 395.
[ Links ]
28. P. Contreras, et al., A numerical calculation of the electronic
specific heat for the compound Sr2RuO4
below its superconducting transition temperature. Rev. Mex.
Fis. 60 (2014) 184.
[ Links ]
29. P. Contreras, and D. Osorio, Scattering Due to Non-magnetic
Disorder in 2D Anisotropic d-wave High Tc
Superconductors, Engineering Physics
5 (2021) 1,
https/doi.org/10.11648/j.ep.20210501.11.
[ Links ]
30. P. J. Hirschfeld, P. Wolfle, and D. Einzel, Consequences of
resonant impurity scattering in anisotropic superconductors: Thermal and spin
relaxation properties, Phys. Rev. B
37 (1988) 83,
https://doi.org/10.1103/PhysRevB.37.83.
[ Links ]
31. K. Maki and H. Won, Why d-wave superconductivity?,
Journal de Physique I
6 (1996) 2317,
https://doi.org/10.1051/jp1:1996220.
[ Links ]
32. C. J. Pethick and D. Pines, Transport processes in heavy-fermion
superconductors, Phys. Rev. Lett. 57 (1986) 118,
https://doi.org/10.1103/PhysRevLett.57.118.
[ Links ]
33. S. Schmitt-Rink, K. Miyake, and C. M. Varma, Transport and
Thermal Properties of Heavy-Fermion Superconductors: A Unified Picture,
Phys. Rev. Lett.
57 (1986) 2575,
https://doi.org/10.1103/PhysRevLett.57.2575.
[ Links ]
34. A. V. Balatsky, M. I. Salkola, and A. Rosengren,
Impurity-induced virtual bound states in d-wave superconductors, Phys.
Rev. B
51 (1995) 15547,
https://doi.org/10.1103/PhysRevB.51.15547.
[ Links ]
35. L. P. Pitaevskii, Superfluid Fermi liquid in a unitary regime,
Phys.-Usp. 51 (2008) 603,
https://doi.org/10.1070/PU2008v051n06ABEH006548.
[ Links ]
36. Stefan Kasen, Response functions of strongly correlated electron systems: From perturbative to many-body techniques. Ph.D. Graduate Theses and Dissertations, 2020.
[ Links ]
37. V.G. Yarzhemsky, Multiplicity, Parity and Angular Momentum of a
Cooper Pair in Unconventional Superconductors of D4h Symmetry:
Sr2RuO4 and Fe-Pnictide
Materials. Symmetry, 13 (2021) 1435,
https://doi.org/10.3390/sym13081435.
[ Links ]
38. A. Leggett, and Y. Liu, Symmetry Properties of Superconducting
Order Parameter in Sr2RuO4. J Supercond Nov
Magn
34 (2021) 1647,
https://doi.org/10.1007/s10948-020-05717-6.
[ Links ]
39. P. Contreras, J. Florez and R. Almeida, Symmetry Field Breaking
Effects in Sr2RuO4, Rev. Mex. Fis.
62 (2016) 442.
[ Links ]
40. V. Shaginyan and M. Amusia, Strongly Correlated Fermi Systems: A New State of Matter (Springer, 2020).
[ Links ]
41. L. Landau and E. Lifshitz, Quantum Mechanics, Non-relativistic theory (Pergamon, 1965).
[ Links ]
42. D. Rainer and J. A. Sauls. Strong Coupling Theory of
Superconductivity in Superconductivity: From Basic Physics to the Latest
Developments, World Scientific: 45, (1995).
https://doi.org/10.1142/9789814503891.0002.
[ Links ]
43. Stefan Kasen. Response functions of strongly correlated electron systems: From perturbative to many-body techniques. Ph.D. Graduate Theses and Dissertations, 2020.
[ Links ]
44. M. Hillery, R.F. O’Connell, M.O. Scully, and E.P. Wigner,
Distribution functions in physics: Fundamentals, Physics
Reports, 106 (1984) 121,
https://doi.org/10.1016/0370-1573(84)90160-1.
[ Links ]













 text new page (beta)
text new page (beta)


