1 Introduction
Due to numerous works on chaos in recent years, current research on this topic comprises chaotic systems in diverse areas such as lasers, chemical reactions, electronic circuits, biological systems, among others. The work of Pecora and Carroll on synchronization [1] and experiments with circuits operating in a chaotic regime give a great impulse to the study of chaotic systems. Particularly, low-dimensionality systems have been of interest in order to understand the synchronization and chaotic behavior in nature. The most studied and representative systems are the Lorenz, Chua, Rössler, van der Pol and Duffing ones [2-7].
The van der Pol and Duffing oscillators are the paradigmatic circuits to study chaos in systems of low-dimensionality. These systems give rise to limit cycles and prototypes of strange attractors. Studies focused on the van der Pol oscillator reveal that the system possess an interesting dynamical structure when the oscillator is under an external forcing. In fact, the system exhibits complex bifurcation structures with an important number of periodic states, a chaotic region and islands of periodic states, showing, in addition, transitions from chaos to stable states [8]. On the other hand, the Duffing oscillator presents damping oscillations when the system is autonomous. In the presence of an external harmonic forcing, the system leads to hysteresis, multistability, period-doubling, and intermittent scenarios of chaos. In addition, we can mention that two coupled van der Pol oscillators give a rich fractal structure. Moreover, other systems based on this oscillator, such as identical oscillators, have also been analyzed. The dynamics based on identical or distinct linear oscillators presenting the same kind of attractors is still under study [8]. The dynamics of these systems in states of different attractors is of current interest and it could originate important information. A model of coupled oscillators, each being in its own attractor regime, could be useful to represent hysteresis or resonant phenomena founded in biological or electromechanical systems [9]. Some applications of the van der Pol and Duffing oscillators go from physics to biology, electronics, chemistry and many other fields. For instance, a possible application of synchronization in chaotic signals, is for implementing secure communication systems, since chaotic signals are usually broadband, noise-like, and difficult to predict their behavior [10-12]. In robotics, the oscillators have been included to control hip joints and knees of human-like robots to synchronizing the mechanical system, giving approximate paths to the robot legs. The signals generated can also be used as trajectories of reference for the feedback control [13-14]. Other applications are in artificial intelligence. In fact, the oscillators show usefulness to training neuronal network and recognition of chaotic systems [15-16].
The synchronization is observed in several natural and technical systems, going from cardiac cells to coupled lasers [17-18]. Thus, the comprehension of mutual interactions between coupled oscillators and their synchronization results an important issue. As far as the coupling between the van der Pol and Duffing oscillators is concerned, we can mention three different couplings, namely: gyroscopic, dissipative and elastic [19-24]. Among the diverse way of coupling, the most used are the elastic and dissipative ones [25-26]. In a previous work [24], it is analyzed a different approach of synchronizing two distinct oscillators of low-dimensionality, by using the aforementioned couplings. In this work, we study and compare three types of couplings by using the van der Pol-Duffing system; the elastic, the dissipative and the used previously by Uriostegui et al. [24], in order to achieve synchronization in a master-slave system. It is important to remark that the studies in the literature on this kind of synchronization is based only on one coupling.
An outline of this work is as follows. In Sec. 2, it is briefly studied the main features of the van der Pol and Duffing oscillators. In Sec. 3, we study and compare three types of couplings using the van der Pol-Duffing system in the master-slave configuration to achieve synchronization. In Sec. 4, the final remarks and an outlook are presented.
2 Dynamics of the systems
As a dynamical system, the van der Pol oscillator is one with nonlinear damping. The evolution is governed by
where, as usual, the x variable denotes the position, t the time, and μ is a parameter that governs the nonlinearity and damping of the system. The external forcing is given by the harmonic function, with amplitude A2 and frequency ω2. In order to identify the potential, we cast Eq. (1) as
where we have defined the function
as the energy potential of the van der Pol oscillator, which represents a simple well (see Fig. 1a)). The potential has a minimum located at x = 0. In order to express Eq. (1) as a dynamical system and to analyze the fixed points, we set
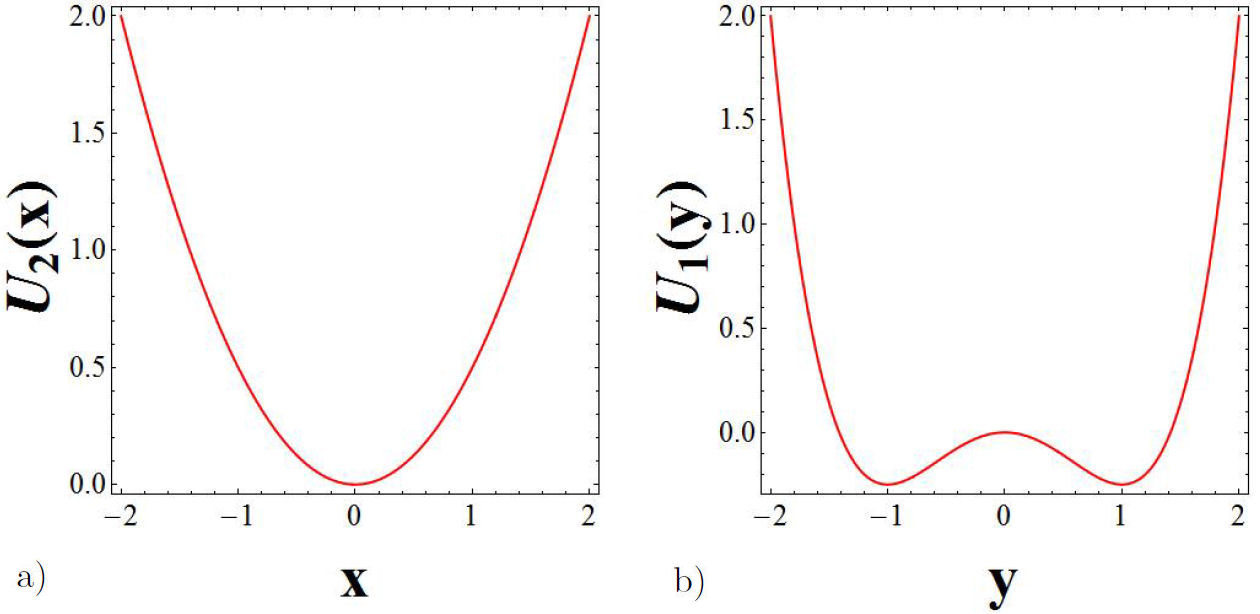
Figure 1 The potentials
As it is well known, for a dynamical system with n degrees of freedom,
On the other hand, the Duffing oscillator is a nonlinear dynamical system governed by
where α is the damping parameter, ε is a positive constant that controls the nonlinearity of the system, A1 and ω1 are the amplitude and frequency, respectively, of the external forcing. As before, we can identify a potential U1(y) in the Duffing system given by
The potential represents a double well shown in Fig 1b). The local minima of this potential are located in
The fixed points for this system are located in the phase space at (0, 0) and
3 Master-slave synchronization in the van der Pol-Duffing system
In this section, three different couplings for the van der Pol-Duffing system are studied and compared among themselves, namely: the elastic, the dissipative and the one that combines an elastic and dissipative couplings employed by Uriostegui et al., [24]. Let us stress that most of the research on synchronization is based on autonomous systems of three dimensional or higher [27-29]. It is important to mention that the synchronization between coupled forced systems of low-dimensionality has been hardly studied [30,31] since there are few low-dimension chaotic systems with forcing known in the literature. Three of the most studied nonautonomous systems of low-dimensionality with forcing are the Duffing, van der Pol, and Rayleigh, since much of the dynamical features embedded in the physical systems can be realized on these systems [32-34]. One important implication is that a two dimensional continuous dynamical system cannot give rise to strange attractors. In particular, chaotic behavior arises only in continuous dynamical systems of three dimensions or higher. Most of the research on synchronization is based on autonomous systems that satisfy the Poincaré-Bendixson theorem.
The dynamics of the oscillators under study is described by Eqs. (1) and (5). The values of the parameters we use to carry out the numerical study are as follows: μ = 0.8, α = 0.25, ε = 1, A1 = 0.3, ω1 = 1, A2 = 1 and ω2 = 0.4. In Fig 2. it is displayed the respective trajectories with the initial conditions x(0) = 0.8, y(0) = 2.0, u(0) = 1 and v(0) = -1. In addition, we would like to mention that the differential equations are numerically solved by using the Runge-Kutta method of fourth order.
In the configuration master-slave, the Duffing oscillator acts as master and the van der Pol oscillator as slave. For this case we have
In this instance, the coupling corresponds to an elastic one and it is represented by k(y - x), being K a coupling parameter to be varied. For the K = 0 case, the system decouples. The coupling is a lineal feedback to the slave oscillator and it can be seen as a perturbation for each oscillator in the system, proportional to the difference of the position, what is called in literature an elastic coupling. We are interested in to study how the dynamics of the system evolves as the constant coupling K changes.
In particular, let us consider the
which represents a simple harmonic oscillator with an external forcing. The solutions to the equation are harmonic functions, whose amplitudes can be as large as the corresponding to the particular solution provided by the forcing, particularly by the term Ky due to the master oscillator. This implies that total synchronization could not be possible for values of K large enough.
In general, the synchronization problem reduces to finding a suitable value of the coupling strength K, (denoted as K*) being in the range K ≥ K* > 0, such that the master and slave systems synchronize. Thus, for a coupling strength K*, when the synchronization is reached, the error function goes to zero:
When the system is partially synchronized, for a certain value of K*, the error functions satisfy
for given positive values δ, τ >0. In some cases, it can be reached total synchronization in only one channel while in the other, it can be only obtained partial or null synchronization.
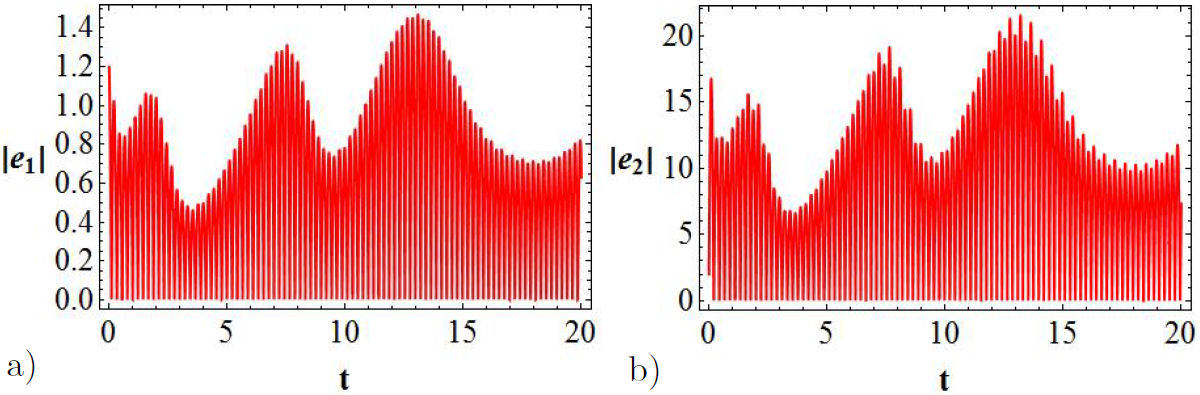
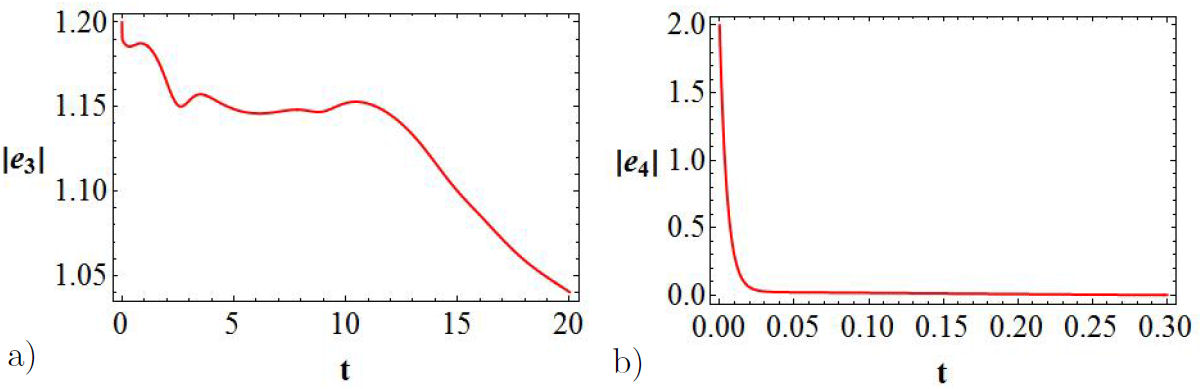
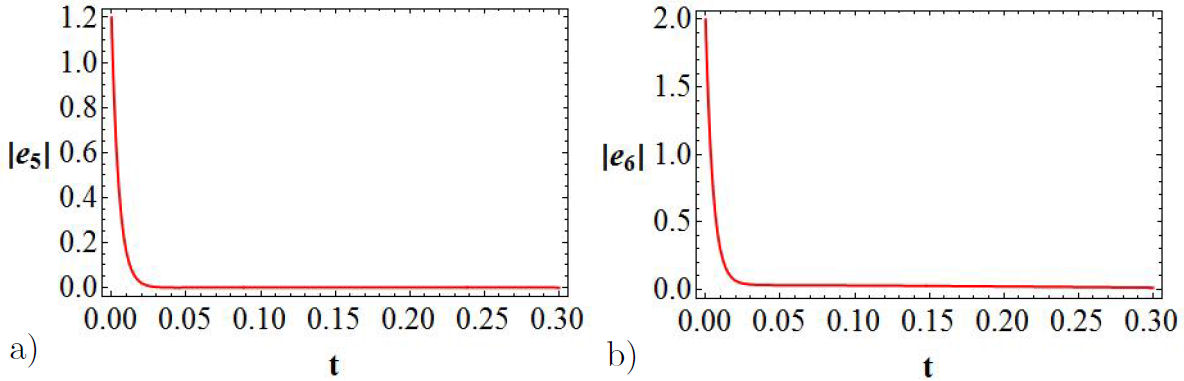
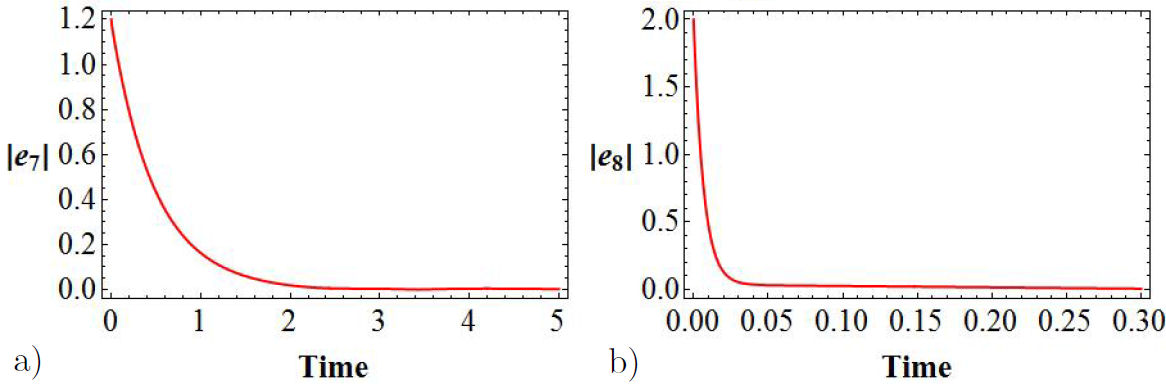
The bifurcation diagrams are achieved by means of the error functions
whose behavior is displayed in Fig. 3 as a function of t, for a value of K = 200.

Figure 3 Bifurcation diagrams for the error functions: in (a) it is represented
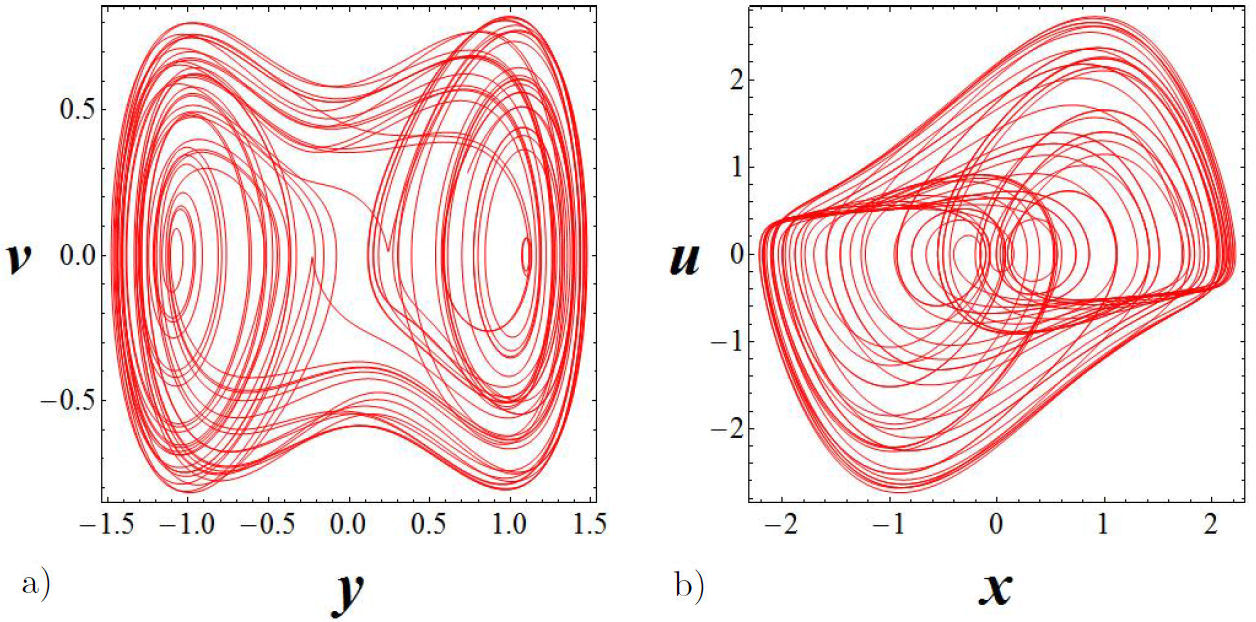
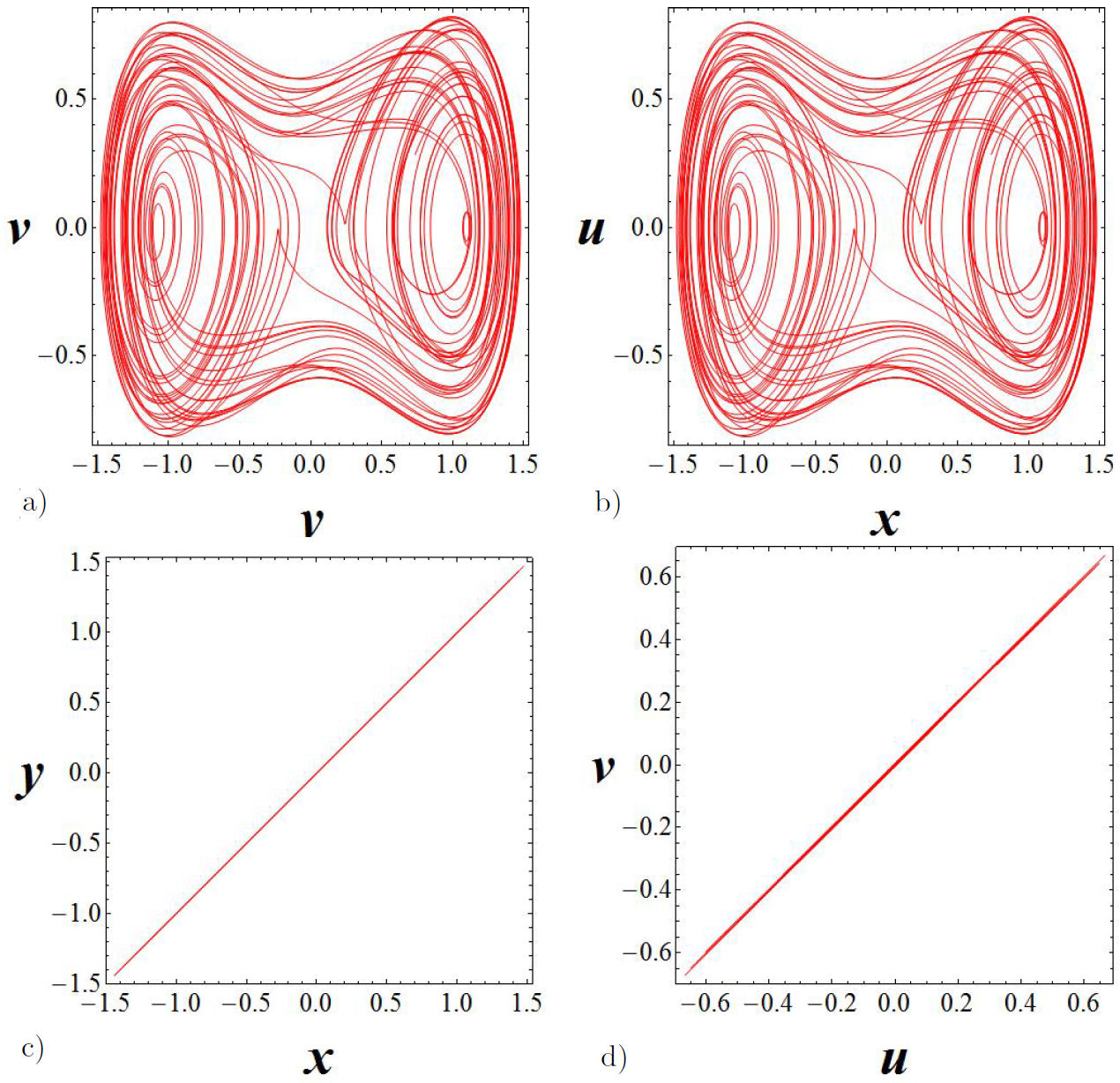
In order to numerically corroborate that there is not synchronization in any of the channels under study, let us analyze the phase space in the y - x and v - u channels for a particular value K = 200. For which, the master system (Duffing oscillator) is working in the chaotic regime and the dynamics of the van der Pol oscillator is not being controlled by Duffing oscillator as it can be observed from Figs. 5c) and d). If we had have synchronization we could observe a straight line at 45o on both channels, but it is not the case.
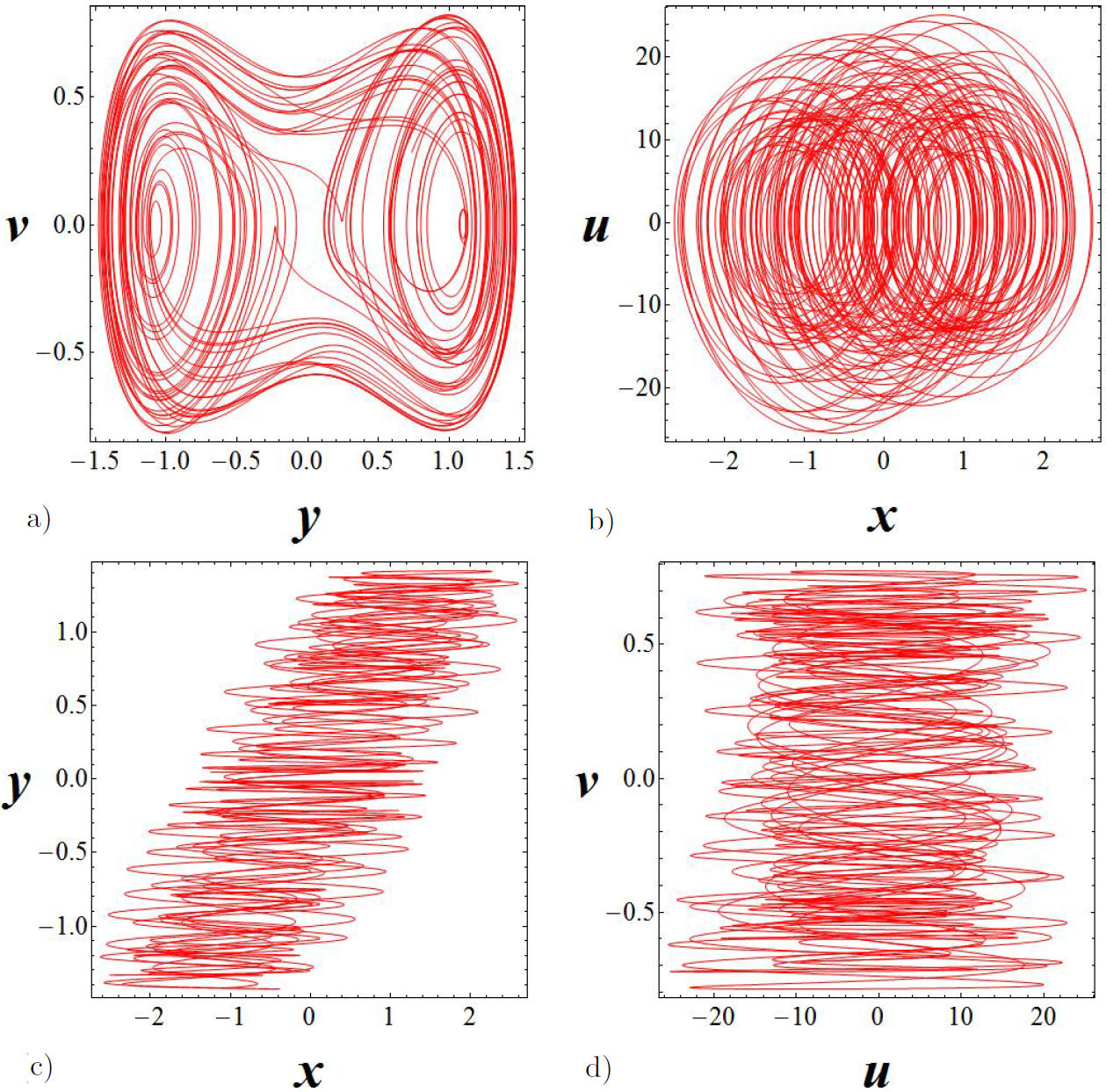
Figure 5 Elastic coupling, for a parameter control of K = 200. In a) the Duffing oscillator. In b) the van der Pol oscillator. In c) and d) the phase space for the y - x and v - u channels.
Let us now discuss the synchronization when the oscillators are interacting through a dissipative coupling, represented by
where H(v - u) represents the dissipative
coupling, being H used as a parameter. As before, for the case in
which H = 0, the oscillators become to be decoupled. Similar to the
elastic coupling, the term, H(v -
u), used in this case, is a lineal feedback to the slave
oscillator. Physically, the dissipative coupling
H(v - u) drives the two
interacting systems to a more homogeneous regime where their states coincide. As a
result, this coupling directly favors synchronization of the oscillators. In order
to get more insight in the solution, let us consider the case of H
large enough such that
This equation represents a damped harmonic oscillator with forcing, where the term
We study the evolution of the system by varying the H parameter. The
bifurcation diagrams are obtained by means of the error functions
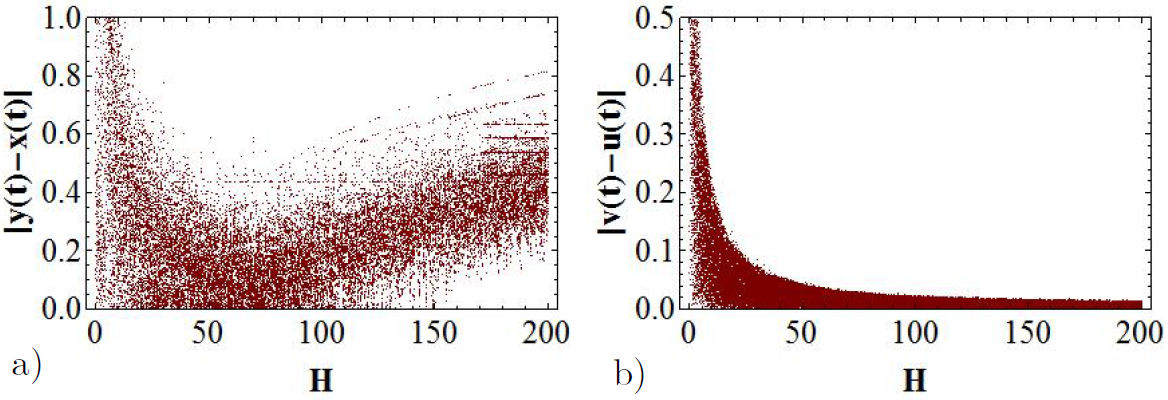
Figure 6 Bifurcation diagrams for the error functions: In a) it is displayed
The behavior of these functions is shown in Fig. 7 for a value of H = 200.
Let us analyze the space phase for the y - x and v - u, channels for a specific value of H = 200. In this case, the Duffing oscillator is in a chaotic regime. In Fig. 8c) we can appreciate the fact that in the y - x channel there is no synchronization, while in v- u channel there is total synchronization fig. (8d)).
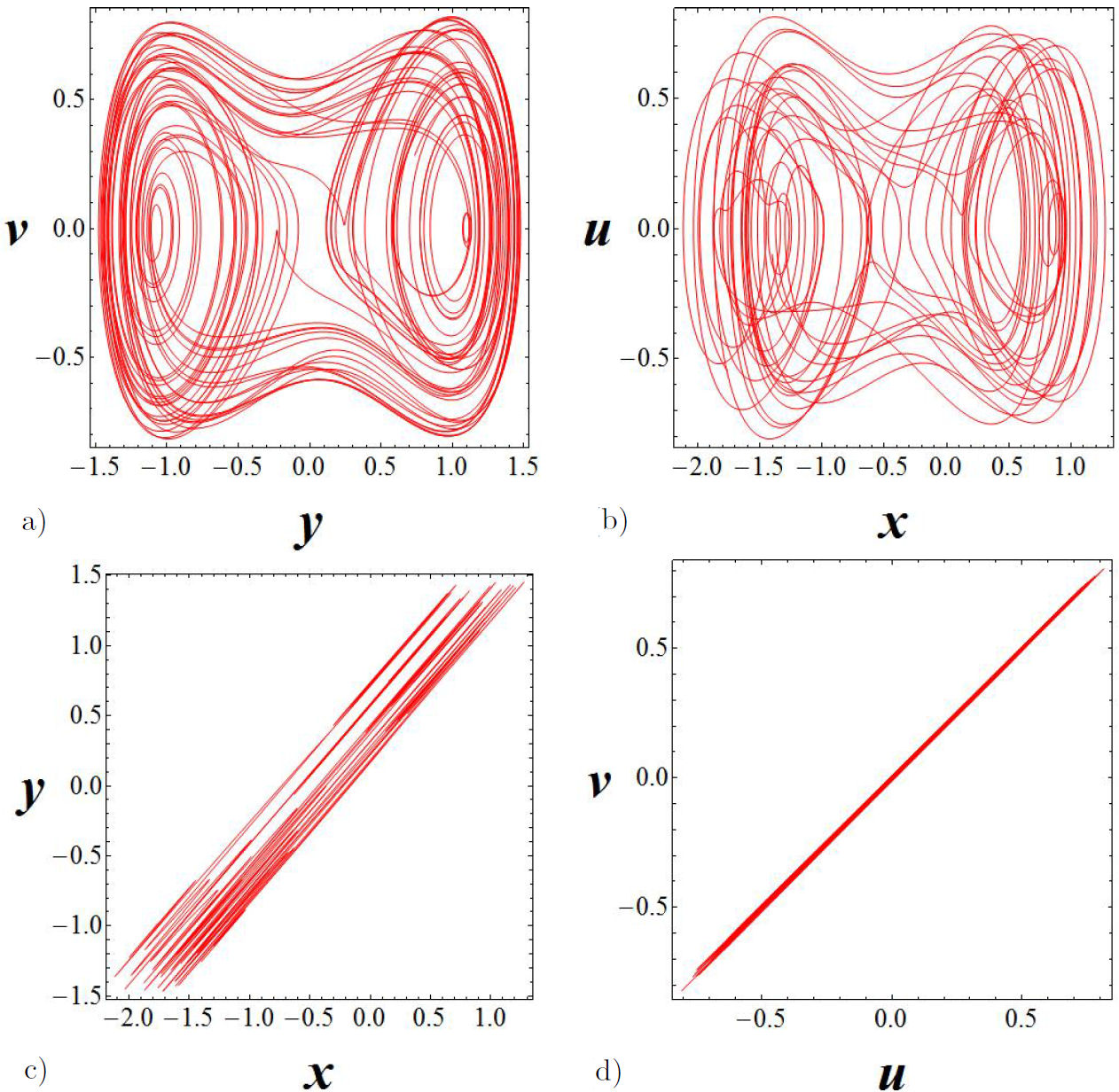
Figure 8 Dissipative coupling case, for H = 200. In a) The Duffing oscillator (master) and in b) the van der Pol oscillator (slave). In c) and d) the phase space for the y - x and v - u channels respectively.
For certain systems, it is not possible to reach synchronization when the classical master-slave scheme is used. Specifically, there are cases where it is impossible to find a coupling constant K such that the systems reach synchronization, as it occurs for the systems described by Eqs. (8) and (9). In some cases, the systems reach partial or total synchronization in only one channel as it occurs for the dynamics contained in Eqs. (15) and (16), depending of the value H. Variations to the master-slave scheme for some systems have been proposed to solve certain kind of problems [35-38].
In particular, in Ref.[24] a modified master-slave scheme is considered that leads to synchronization even in the cases where the classical master-slave scheme fails. The approach used in Ref. [24] uses a non conventional coupling, where a linear feedback occurs. The coupling can be seen as a perturbation to each oscillator proportional to the difference of the position (elastic coupling), G(y - x), which is introduced in the velocity of the slave system. The coupling also uses another linear feedback, that can be seen as perturbation to each oscillator proportional to the difference of the velocity (dissipative coupling), G(v - u), introduced in the acceleration in the slave system. For the van der Pol-Duffing system, the equations read as
Notice, again, that for G = 0, the equations decouple. In order to get more
insight in the physical meaning of this case, let us assume that
The left hand side of the equation depends only on the x while the right hand side depends only on y, except for the external harmonic forcing. Thus, the oscillators synchronize in both channels y - x and v - u. In the last case, we have
that is, if there is synchronization in the y - x channel (both oscillators follow the same dynamics) then in the v - u channel there is also synchronization. We should emphasize that, by comparing with the former cases, in the dissipative coupling only was possible to reach synchronization in the v - u channel, and in the elastic coupling no synchonization exists.
We study the dynamics of the system varying the coupling constant G. In order
to analyze the bifurcation diagrams, let us consider the error functions
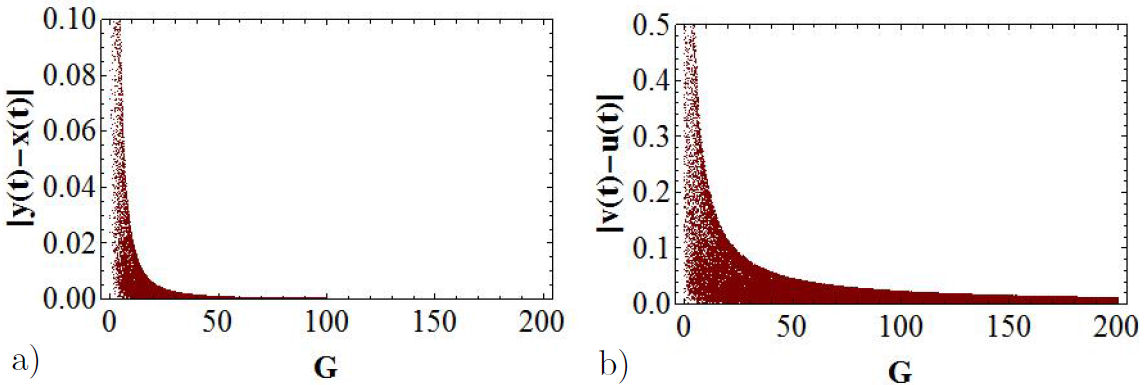
Figure 9 Bifurcation diagrams for the error functions. In a) it is represented
The plots of
Let us now analyze the phase space for the y - x and v - u channels for the value G = 200. In Figs. 11c) and d) it can be observed that total synchronization is reached since the error function in the phase space is represented by a straight line at 45o in both channels.
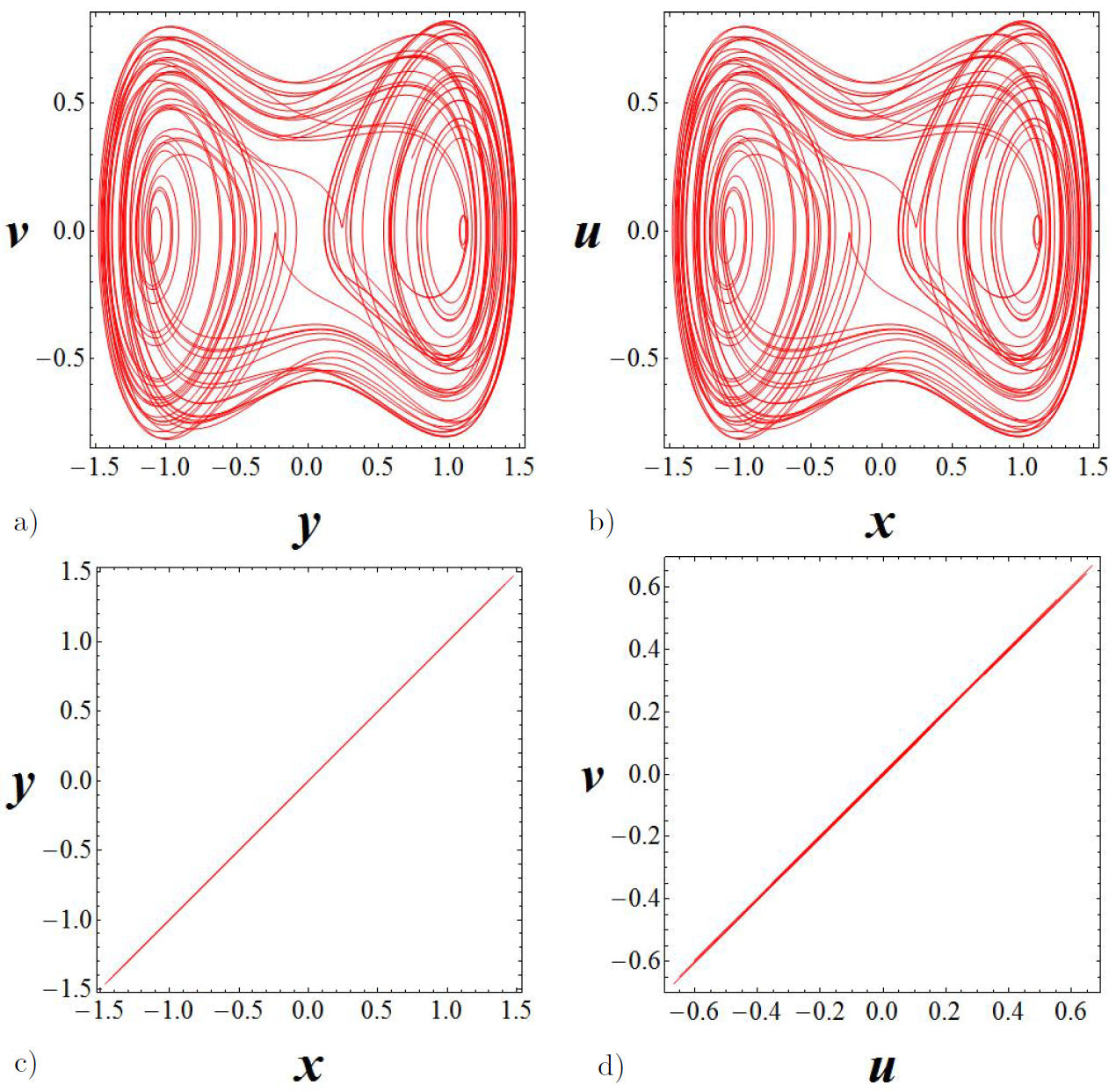
Figure 11 Elastic and dissipative couplings for G = 200. In a) the Duffing oscillator (master). In b) the van der Pol oscillator (slave). In c) and d) the phase space for the y - x and v - u channels.
By comparing the three different coupling above mentioned, we observed that the coupling used by Uriostegui et al. gives the best results. In fact, by using the former coupling, we observed that total synchronization in both y - x and v - u channels is achieved.
In order to analyze the case of two different values in the couplings its is convenient, for
our discussion, to express the couplings in terms of the errors: for the elastic
coupling we have
As before, let us assume that
Once again, by comparing with Eq. (20), we observe that, to obtain synchronization, we must assume
The errors
The constant G1 corresponds to the elastic coupling and
G2, to the dissipative coupling. Hence,
The first vectors in the right hand side of Eqs. (26) and (27) contain the nonlinearity
information of the system, while the second ones contain the information of the
external forcing. The last vector in Eq. (27) is the so-called control vector, which
contains the coupling we propose. Notice that the control depends on the error and
its derivative. For the case G1 =
G2 = 0 de system decouples. In order to study the
dynamics of the system, we vary the couplings G1 or
G2 keeping one constant. To analyze the bifurcation
diagrams, let us consider the error functions
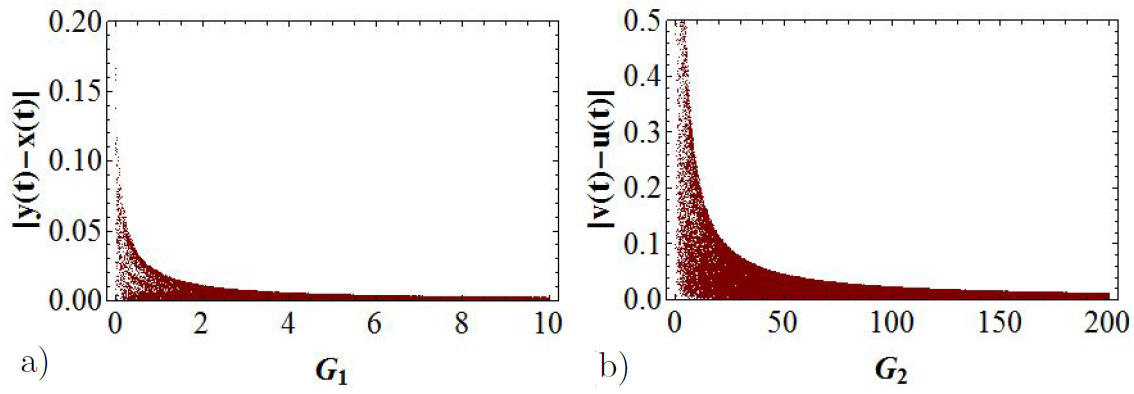
Figure 12 Bifurcation diagrams for the error functions. In (a) it is represented
Let us now analyze the phase space for the the y - x and v - u channels, for values of G1 = 2 and G2 = 150. In Figs. 14c) and d), we can observe that total synchronization is reached, since the error functions in the phase space is represented by a straight line at 45o in both channels.
4 Final remarks and outlook
The van der Pol and Duffing are nonautonomous systems of low-dimensionality that present chaos and have been well studied. One of the conclusions presented in the literature related to these systems is that the elastic coupling does not lead to synchronization. For this same system, when the dissipative coupling is used, only synchronization in one channel can be obtained. In this paper, we have analyzed the synchronization in the van der Pol-Duffing system based on two different couplings simultaneously employed, namely the elastic and dissipative. We used the error function by varying the control parameters, K, H, G or G1 and G2 (depending on the coupling used), which enabled us to obtain the range for which the synchronization takes place. We found that the synchronization was favored for rather large values of the control parameter.
We also observed that, the coupling that blend the elastic and dissipative, leds to total
synchronization in the y - x and
v - u channels. In this case the
synchronization was obtained for values of G large enough (in our
numerical simulations, we took G = 200). For small values, we
obtained partial synchronization. For the general case, when two constants coupling
are used, G1 (elastic) and
G2 (dissipative), with
The possibility of using two coupling constant instead of only one, allows the system a more interesting dynamics and a broad range for the control parameters. It is well known that synchronization in communication systems needs a large range for the control parameter, such as the obtained, for the van Pol-Duffing system, by employing our approach of coupling. Consequently, the system studied could be of usefulness in this communication systems. The coupling studied in this work will be applied in others systems of low-dimensionality that do not present synchronization through the classical master-slave configuration.











 nova página do texto(beta)
nova página do texto(beta)