Research
Solid State Physics
Optimal electronic doping in p-wave
superconductors
B. Millána
I. J. Hernández-Hernándezb
L. A. Pérezc
J. Samuel Millánd
aInstituto de Investigaciones en Materiales,
Universidad Nacional Autónoma de México, Apartado Postal 70-360, 04510, Ciudad
de México, México.
bInstituto Nacional de Investigaciones
Nucleares, Carretera México-Toluca km. 36.5, La Marquesa, 52750, Ocoyoacac,
Estado de México, México.
cInstituto de Física, Universidad Nacional
Autónoma de México, Apartado Postal 20-360, 04510, Ciudad de México,
México.
dFacultad de Ingeniería, Universidad Autónoma
del Carmen, 24180, Cd. del Carmen, Campeche, México. e-mail:
smillan@pampano.unacar.mx
Abstract
Recently, within a generalized Hubbard model which includes correlated nearest
(Δt) and next-nearest hopping interactions
(Δt3), a comparative study between d- and s*- wave superconducting
ground states on a square lattice was performed. It was found that the critical
temperature of transition T
c
(n), as a function of the electron concentration
n, reaches a maximum (T
c-max
) at a given optimal doping (n
op
) for each value of the ratio t´/t, where t and
t´ are the tight-binding nearest and next-nearest hopping
parameter of a square lattice, respectively. From all values obtained for
Tc-max(t'/t,nop) a global minimum one was encountered for both symmetries. Likewise,
in the same space, a minimal ground state energy Eg was also
obtained. For d-wave channel both minima are localized around
the same optimal doping. However, for s* symmetry, the two minima are located at
different electron concentrations. In this work, we additionally study how the
p-wave ground-state energy and the critical temperature
depend on the hoppings parameters and the electron concentration. The results
show that for p-wave, minimum global values of
T
c-max
and Eg in the (t'/t,nop) space do exist too, and are found around half filling but, as occurs
for s *- wave, the minimum of T
c-max
does not occur at the same point as Eg. Moreover, we present a
ground-state phase diagram in the space (t'/t,nop) where it is possible to find zones of coexistence and competition
between the s*-, p- and d-wave symmetries.
Also, an analysis of the shape of the Fermi surface and the single-particle
energy, as functions of the wave vector of an electron in the Cooper pair, has
been done for different regions of the mentioned space.
Keywords: Theories and models of superconducting state; pairing symmetries (other than s-wave); pseudogap regime.
PACS: 74.20.-z; 74.20.Rp; 74.72.Kf
1.Introduction
The possibility of realization of anisotropic superconductivity with triplet pairing
has been subject of interest since the 1970s, when the discovery of superfluity was
found in the fermionic isotope 3He, with p -wave Cooper
pairs of atoms and a critical transition temperature of about 1 mK 1. In 1994, Y. Maeno 2 reported that strontium ruthenate
(Sr2RuO4), with a critical temperature of 1.5 K, could
possess a superconducting gap with p -wave symmetry. In this
system, the critical temperature of the superconducting state cannot be tuned by
changing the electron density or concentration as in cuprate superconductors such as
La2-xSrxCuO43, where an optimal doping of holes xop≈0.15 from half filling leads to a maximum critical temperature Tc-max≈40 K. Nevertheless, Sr2RuO4 (SRO) and
La2-xSrxCuO4 (LSCO) have similar tetragonal
crystal structures but, in the former, the planes where the particles flow without
any resistance are RuO2, whereas in the latter are CuO22. Although Ru atoms may play an
analogous role for electronic pairing as Cu in LSCO, these systems SRO and LSCO have
very distinct superconducting properties; in particular, the former could have
p -wave Cooper pairs and the latter has a d-wave
superconducting gap. It has been suggested that in the underdoping regime, for
𝑑-wave superconductors, the antiferromagnetic state could be a precursor of the
superconducting state 4, whereas
the ferromagnetic state would be appropriate for 𝑝-wave superconductors, as
possibly occurs in the family of superconductors compounds with uranium (U), such as
Ute2, UGe2, URhGe2 and UCoGe 5, with critical temperatures around
1.5 K. A model which accounts for both p- and 𝑑-wave superconductivity, within the
same theoretical framework, is the generalized Hubbard model (GHM) 6-8, where nearest and next-nearest-neighbor correlated
hoppings (bond-charge interactions) can lead to the formation of Cooper pairs with
different symmetries. For SRO an infinitesimal distortion of the RuO2
square lattice is also considered. This distortion leads to an asymmetry between the
second-neighbor correlated hoppings along the two diagonals of the former square
lattice, which give rise to two 𝑝-wave superconducting states of different energies
6. In previous works, we have
studied the dependence of the p-wave ground-state critical temperature and p-wave
gap amplitude on the electron density (n) and the electron-electron interaction
parameters within the generalized Hubbard model, maintaining the ratio between
first- (t) and second-neighbor (t´) single-electron hoppings constant 6,7,13. Also, we have studied the temperature dependence of
the p-wave gap amplitude for a fixed set of Hamiltonian parameters which allows the
calculation of the temperature behavior of the electronic specific heat, which has
shown a good agreement with that experimentally obtained for SRO 13. However, in a square lattice the
ratio t´/t determines the energy at which the van Hove singularities occur, that in
turn affect the optimal electron density where the maximum T
c
(n) is attained for a given set of electron-electron interaction parameters.
Hence, in this work, in a similar manner as was recently done for d- and s*-wave
superconductors 9,10, the superconducting critical
temperature (T
c
) versus the electron density (n) and the ratio t´/t is calculated for a set
of electron-electron interaction parameters. In particular, for the optimal electron
density (n
op
), i.e., that n where the critical temperature attains its maximum T
c,max
with the other Hamiltonian parameters fixed, the corresponding ground state
energy was determined for different values of t´. For a given set of
electron-electron interaction parameters, the results show that the largest T
c,max
occurs at low electron densities, and the minimum of T
c,max
can be encountered close to half filling (n = 1). Moreover, there could be a
competition between s*-, d- and p-wave superconducting states around half filling.
Finally, this study suggest that the values of the optimal doping (n
op
) and second-neighbor hopping (t´) that lead to a critical temperature
Tc≈1.5 K, which matches with that of the SRO, are found close to have filling
(nop∼1) and for t´< 0, in agreement with first-principles studies performed
for SRO 11. Finally, an analysis
of the corresponding Fermi surfaces and the single-particle excitation energy were
performed.
2. The model
We start from a single-band generalized Hubbard model on-site (U) and
nearest-neighbor (V) Coulombic interactions, first- (t) and second-neighbor (t´)
hopping parameters, and first- (Δt) and second-neighbor (Δt3) correlated
hopping interactions 6,7
H=t∑<i,j>,σciσ†cjσ+∑≪i,j≫,σ(t'+χijδ)ciσ†cjσ+U∑ici↑ci↓+V2∑<i,j>,σninj+Δt∑<i,j>,σciσ†cjσ(ni,-σ+nj,-σ)+∑<i,l><j,l>≪i,j≫,σ(Δt3+χijδ3)ciσ†cjσnl,
(1)
where ni=ni,↑+ni,↓, ni,σ=ci,σ†ci,σ, and ci,σ†ci,σ, is the creation (annihilation) operator with spin σ=↓ or ↑ at site i. < i,j > and << i,j >> denote nearest-
and the next-nearest neighbour sites, respectively. In the case of SRO, a surface
distortion of the RuO2 square lattice has been observed by using X-ray
diffraction 12. Hence, we
considered an infinitesimal distortion of the square lattice that leads to an
asymmetry between the second-neighbor hopping (t´) and correlated hopping
(Δt3) along the two square diagonals. The former undisturbed
second-neighbour hopping (t´) and second-neighbor correlated hopping
(Δt3) of a non-distorted square lattice respectively become t'+χijδ and Δt3+χijδ3, where χij=+1 if second-neighbour sites i and j are along the x^-y^ direction, and χij=-1 if they are along the x^+y^ direction. Here δ and δ3 characterize the degree of asymmetry
between the mentioned hoppings along the two square diagonals. The expressions for
the model parameters are given in Table I in
terms of Wannier functions [φ(r-Ri)] centred at lattice site R
i.
Table I Expressions for the Hubbard model parameters.
|
Single-particle parameters
tij=∫d3r φ*r-Ri-ℏ2∇22m+urφr-Ri,u(r) is the lattice periodic potential
t = tij for < i,j >
t´ = tij for << i ,j >>
|
|
Electron-electron interaction parameters
Uijkl=∫d3rd3r´σ*(r-Rj)φ*(r´-Rj)v(r-r´)φ(r-Rk)φ(r´-Rl)
u (r - r´) is the interaction
potential between two electrons in the lattice
U=Uiiii;∆t=Uiiii with < i, j >; ∆t3=Uljil with < i, l >, < j, l > and <<
i,j >>
|
The real-space Hamiltonian ((1)) can be transformed into reciprocal space by
performing a Fourier transform of the electron operators ck,σ†=(1/Ns)∑jexp(ik⋅Rj)cjσ†. After a mean-field Hartree decoupling, the reciprocal-space Hamiltonian
can be written as:
H¯=∑k,σεMF( k )ck,σ†ck,σ†+1Ns∑k,k',q,σWk,k',qck+q,σ†c-k+q,σ†c-k´+q,σck´+q,σ
(2)
where the Fourier transform of the electron-electron interaction for electrons with
the same spin component is given by:
Wk,k',q =V2β(k-k')+Δt3+γ( k +q,k'+q)+Δt3-ζ(k+q,-k'+q)
(3)
With
β(k)=2(cos[kxa]+cos[kya]),
(4)
γ(k,k’)=2cos(a[kx+k'y])+2cos(a[k'x+ky]),
(5)
ζ(k,k’)=2cos(a[kx-k'y])+2cos(a[k'x-ky]),
(6)
where α is the lattice parameter and Δt3±=Δt3±δ3. Notice that the real-space term Δt3+χijδ3 in Eq. (1) leads, after the Fourier transform, to Δt3+ and Δt3- depending on the value of χij(±1). Also, εMF(k) is the mean-field dispersion relation and Ns is the total
number of lattice sites. In this case, εMF(k) is given by:
εMF(k)=EMF+2tMF(cos[kxa]+cos[kya])+2tMF,+'cos(a[kx+ky])+2tMF,-'cos(a[kx-ky]),
(7)
With
EMF=U2+4Vn,
(8)
tMF=t+nΔt,
(9)
tMF,±'=t±'+2nΔt3±=t'±δ+2n(Δt3±δ3),
(10)
where n is the electron density and t'±=t'±δ. Notice that the mean-field single-particle hoppings t
MF
and t'MF,±, depend on the electron density (n) and correlated hoppings (Δt,Δt3), in particular on the distorted values of the second-neighbor
correlated hopping (Δt3±=Δt3±δ3).
In general, the BCS coupled integral equations can be written as 6,7:
Δ(k)=-12NS∑k'Wk,k',0Δ(k')E(k')tanhE(k')2kBT,
(11)
and
n-1=-12NS∑k'εMF(k')-μE(k')tanhE(k')2kBT,
(12)
whose solution gives the chemical potential (μ) and the amplitude of the
superconducting gap for given n and T. For the particular case of an interaction
Wk,k’,q given by Eq.(3), Eq. (11) and (12) admit a solution for the
superconducting gap (Δ(k)) of the form:
Δp(k)=Δp(sin[kxa]±sin[kya]),
(13)
known as p-wave superconducting gap, where Δp is the temperature-dependent
superconducting gap amplitude and the sign ± indicates the direction of the
real-space distortion. It is worth mentioning that, in general, the gap of a
superconducting state formed by triplet Cooper pairs could have another symmetry
different from p-wave, such as f-wave symmetry, and the possible symmetries depend
on the form of the electron-electron interaction potential Wk,k’,q.
By substituting (13) in (11) and (12) we obtain:
1=-(V∓4δ3)a24π2∬1BZ(sin[kxa]±sin[kya])22E(k)×tanhE(k)2kBTdkxdky,
(14)
1-n=-a24π2∬1BZεMF(k)-μE(k)×tanhE(k)2kBTdkxdky,
(15)
where the sums over the first Brillouin zone (1BZ), defined as
-πa,πa⊗-πa,πa
have been transformed into integrals. Here E(k) is the quasi-particle
energy given by:
E(k)=(εMF(k)-μ)2+∆p2(k).
(16)
It is important to mention that the chiral p-wave gap given by
Δchi-p(k)=Δchi-p(sin[kxa]±isin[kya]),
(17)
also satisfies (11) and (12) with Wk,k’,q given by (3), where the second term in the square root of (16) is
Δchi-p(k)Δchi-p*(k)=Δ2chi-p×(sin2[kxa]+sin2[kya]),
(18)
instead of
∆p2(k)=∆p2(sin[kxa]±sin[kya])2.
(19)
However, in this work, the chiral case will not be considered because it does not
seem to successfully apply to SRO 13.
The critical temperature Tc can be determined from (14) and (15)
considering that Δp(T=Tc)=0. In this case, these equations transform into:
1=-(V±4δ3)a24π2∬1BZ(sin[kxa]±sin[kya])22|εMF(k)-μ|×tanh|ϵMF(k-μ|2kBTcdkxdky,
(20)
n-1=-a24π2∬1BZεMF(k)-μ|εMF(k)-μ|×tanh|εMF(k)-μ|2kBTcdkxdky.
(21)
Here, for given Hamiltonian interaction parameters and n, the two-coupled equations
determine the values of T
c
and μ. Moreover, the ground state energy (Eg) per site is given by
14:
Eg=1Ns∑k(εMF(k)-μ)-1Ns∑kE(k)+1Ns∑kΔ2(k)2E(k)+μN-U4+2Vn2,
(22)
which, in the case of a p-symmetry superconducting gap Eq. (13) can be simplified
to:
Eg=1Ns∑k[εMF(k)-E(k)]+Δp24δ3-V+(n-1)μ-U4+2Vn2.
(23)
It is important to mention that for p-wave superconductors, U plays a similar role in
the superconducting gap equation as for d-wave ones, i.e., it does not affect the
shape of εMF, and only modifies the electron self-energy (EMF) shifting
the numerical value of the superconducting chemical potential (μ) without changing
the superconducting critical temperature. Therefore U can be taken equal to zero.
Moreover, to obtain a solution for the superconducting gap equation 7, (V-4δ3) should be negative and therefore the condition V<4δ3 must to be satisfied. In order to keep a minimum set of parameters but
considering that a p-wave superconducting gap can be generated from δ3, V
will be set to zero too. It is worth mentioning that models which consider a
negative V can lead to triplet pairing in frustrated lattices 15, however, this term would also lead to a phase
separated state, where electrons double occupy sites over a macroscopic region of
the lattice, which would strongly compete with the superconducting state 16.
3.Results
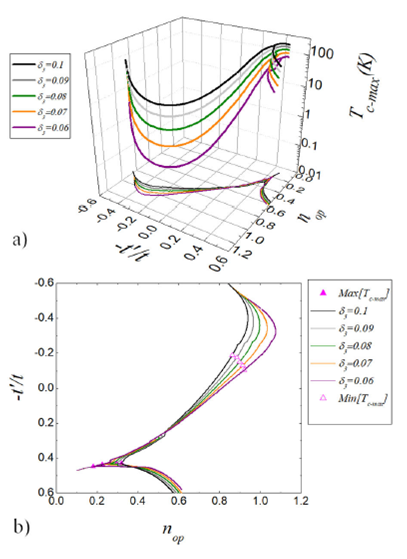
Figure 1a) shows the critical temperature T
c
of p-wave superconducting states as a function of the electron concentration
n and the second-neighbor hopping parameter t´ for Δt=0.5|t|, Δt3=δ=0.05|t|, and δ3=0.08|t|. Likewise, 1b) shows the critical temperature versus the electronic
density (n) for a particular value of -t'/t=-0.15. The value of n, where the maximum critical temperature (T
c-max
) is attained for each value of t´/t is called the optimal electron density n
op
.
The p-channel maximum critical temperature (T
c-max
) versus the optimal electronic density (n
op
) and t´/t, for the same interaction parameters Δt and Δt3 can be
obtained from Fig. 1a). These curves are shown
in Fig. 2a) for different values of
δ3. The projections of these curves Tc-max(nop,t'/t) on the (nop,t'/t) plane are presented in Fig. 2b).
For a given δ3, a global maximum of T
c-max
can be found for t´> 0 (solid magenta triangles) within of the intervals
nop-max∈[0.08,0.32] and t'∈[0.47,0.43]. The latter interval is very narrow. On the other hand, for a given
δ3, minimum values of T
c-max
can be found for t´< 0. These minima are located within the intervals
nop∈[0.863,0.921] and t'∈[-0.190,-0.105] (open magenta triangles). The values of n
op
and t´ where the global maxima and minima of T
c-max
occur, for each δ3, are shown in Table II.
Table II Maximum and minimum values of T
c−max with the corresponding ground state
energies for p-wave superconductors with ∆t = 0.5 eV, δ = ∆t3
= 0.05 eV and different values of δ3
| δ3 (eV) |
nop
|
−t´/t |
Max [Tc−max] (K) |
Eg (meV) |
nop |
−t´/t |
Min [Tc−max] (K) |
Eg (meV) |
| 0.100 |
0.320 |
0.429250 |
285.18 |
-554.862 |
0.863 |
-0.190 |
6.14 |
-1035.20 |
| 0.090 |
0.295 |
0.429625 |
228.55 |
-515.152 |
0.884 |
-0.175 |
3.00 |
-1003.648 |
| 0.080 |
0.265 |
0.431875 |
177.77 |
-467.880 |
0.898 |
-0.150 |
1.24 |
-973.712 |
| 0.070 |
0.225 |
0.437500 |
133.57 |
-404.334 |
0.913 |
-0.130 |
0.40 |
-946.0469 |
| 0.060 |
0.185 |
0.445550 |
96.34 |
-338.897 |
0.921 |
-0.105 |
0.09 |
-923.498 |
It is important to underline that for t´< 0, n
op
is close to half filling and, in this region, T
c-max
abruptly diminishes. Moreover, as shown below, in this zone p-wave
superconducting states compete with extended s-wave (s*) and d-wave ones.
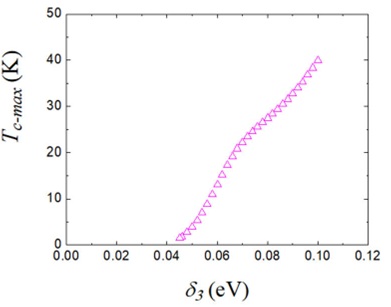
It is also worth mentioning that close to (nop,-t'/t)=(0.868,-0.57), n
op
is almost the same for all δ3. Figure 3 shows T
c-max
versus δ3 at this point.
Moreover, when δ3 = 0.045 eV, the maximum critical temperature (T
c-max
) of the state (nop,-t'/t)=(0.868,-0.57) agrees with the critical temperature of SRO, i.e., Tc≈1.5 K. Other points that satisfy Tc-max≈1.5 K with different values of δ3 are summarized in Table III. Two cases correspond to t´> 0:
(nop,-t'/t)=(0.684,0.115) with δ3 = 0.07 eV; and (nop,-t'/t)=(0.586,0.210) with δ3 = 0.06 eV. The other cases correspond to t´< 0.
Taken into account that the distortion of the square lattice is assumed to be very
small, it is expected that the parameter δ3 should be very small. Hence,
according with the results of this work, the smaller value of δ3
satisfying Tc-max≈1.5 K, corresponds to δ3 = 0.045 eV, which is attained at
(nop,-t'/t)=(0.868,-0.57). However, it has been estimated, by using first-principles calculations
11, that the first- and
second-neighbor hoppings of SRO on the RuO2 planes satisfy -t'/t=-0.3 and then, the states (nop,-t'/t)=(0.960,-0.26) with δ3 = 0.08 and (1.027, -0.385) with δ3 = 0.07
eV, both of which also have small values of δ3 and optimal electron
concentrations (dopings) close to half-filling, are good candidates to be the
experimentally observed p-wave ground state of SRO.
The p-wave gap amplitude (Δp-max) and the ground state energy (Eg) of the systems depicted in
Fig. 2a) are shown in Fig. 4a) and 4b),
respectively. Notice that, although there is a global minimum of T
c-max
and Δp-max, and a local minimum of Eg, they are not located at the same
(nop,-t'/t) point as occurs for d-wave superconducting states 9.
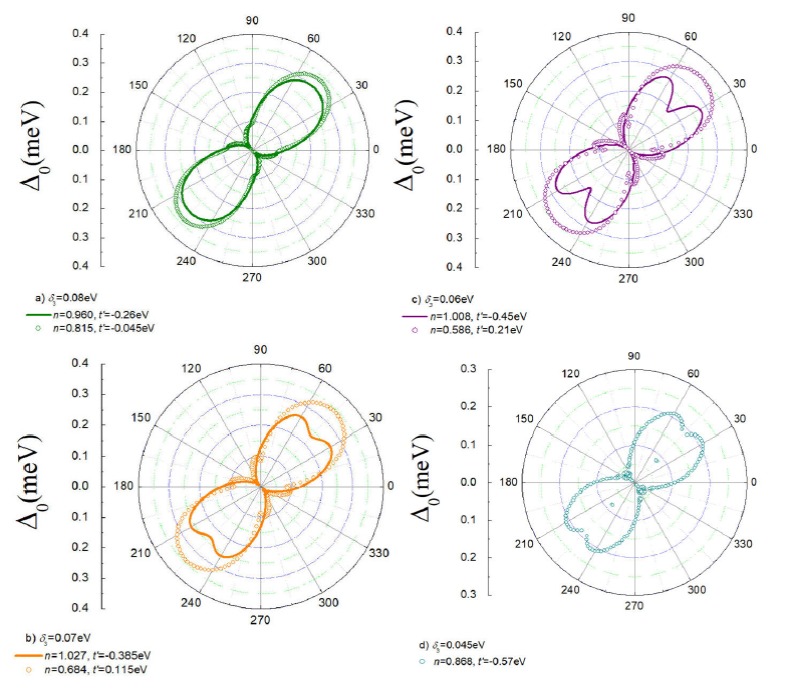
Figures 5a)-d) show the Fermi surfaces (FS)
corresponding to the states listed in Table
III. Likewise, 6a)-d) show the corresponding single-particle excitation
energies (Δ0). This energy is defined as the minimum energy necessary to
break a Cooper pair when the momentum k of the pairing electrons are
along the angle θ=ky/kx. Notice that the FS are symmetric with respect to the k
x + k
y diagonal. It is also important to point out that the states (nop=0.586, t'=0.2|t| eV), (nop=0.684, δ3 = 0.07 eV), (δ3=0.06, δ3 = 0.08 eV) whose single-particle excitation gaps are
depicted in Fig. 6a)-6c), Δ0≈2Δp at the antinode. However, for the other cases, the FS is more elongated
along the k
x + k
y diagonal, and the relation Δ0≈2Δp is not fulfilled at the antinode. In the case (nop=0.868,t'=-0.570|t| δ3 = 0.045eV), the FS is disconnected, see Fig. 5d).
Table III Superconducting physical properties of (n
op
, −t´/t) p-wave states satisfying T
c−max
= 1.5 K.
| δ3 (eV) |
nop
|
−t´/t |
Tc−max (K) |
∆p−max (meV) |
∆0 (meV) |
Eg (meV) |
E(con) (meV) |
EF (meV) |
| 0.08 |
0.815 |
-0.045 |
1.50 |
0.169 |
0.335 |
-981.456 |
-0.007 |
-322.263 |
| 0.08 |
0.960 |
-0.260 |
1.50 |
0.174 |
0.302 |
-960.071 |
-0.214 |
265.916 |
| 0.07 |
0.684 |
0.115 |
1.47 |
0.171 |
0.341 |
-925.830 |
-51.9 |
-811.084 |
| 0.07 |
1.027 |
-0.385 |
1.52 |
0.178 |
0.233 |
-924.312 |
6.0 × 10−6 |
494.374 |
| 0.06 |
0.586 |
0.210 |
1.46 |
0.179 |
0.347 |
-849.282 |
−3.7 × 10−6 |
-1108.611 |
| 0.06 |
1.008 |
-0.450 |
1.49 |
0.182 |
0.183 |
-962.571 |
-0.036 |
498.879 |
| 0.045 |
0.868 |
-0.570 |
1.50 |
0. 121 |
0.335 |
-1174.628 |
-0. 0145 |
364.411 |
Besides p-wave superconducting ground states, the first- (Δt) and second-neighbor
(Δt3) correlated hoppings can also induce extended s-wave (s*) and
d-wave superconducting states 7,
where the respective gaps (order parameters) are given by Δs*(k)=Δs+Δs*[cos(kxa)+cos(kya)] and Δd(k)=Δd(cos[kxa]-cos[kya]). To compare the behavior of p-wave superconducting systems with those
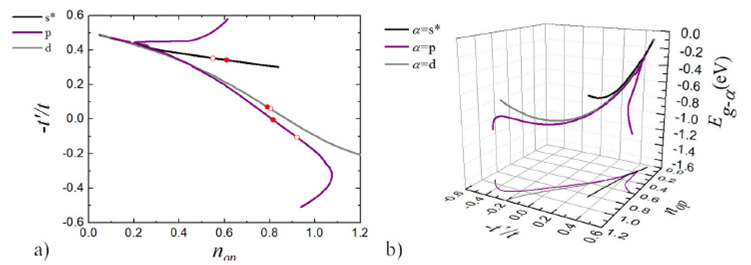
with extended s- and d-wave superconducting gaps, Fig.
7a) shows those points (nop,-t'/t) where the critical temperature is maximum, for s*- (black line), p-
(purple line), and d-wave (gray line) superconductors. The depicted d- and s*-wave
states have Δt=0.5|t| and Δt3=0.05|t|
9,10, whereas the p-wave ones have, in addition, δ =
0.05 eV and δ3 = 0.06 eV. In each curve, the red open and solid circles
correspond to those states where T
c-max
, and Eg, respectively attain their minimum values. Figure 7b) shows the corresponding ground state
energies for the same systems as in Fig. 7a).
Notice that, at low densities, around the point (nop,-t'/t)=(0.14,0.455), all the curves coincide, and the ordering from lowest to highest value
of Eg correspond to s*-, p- and d-wave symmetries. However, for higher
densities, the maximum critical temperatures for the different superconducting
symmetries are located in different regions, and can be distinguished two crossing
points; one around (nop,-t'/t)=(0.260,0.415), where the s* channel curve crosses with the p-channel one, and other at
(nop,-t'/t)=(0.459,0.310), where the d-channel crosses with the p-channel one. Close to these
points it is expected that the different possible superconducting symmetries could
coexist, if they had similar ground state energies.
Table IV summarizes the superconducting
physical properties of the mentioned points of possible coexistence.
Table IV Superconducting physical properties of s∗, p and d-wave
superconducting states with ∆t = 0.5 eV, ∆t3 = 0.05 eV, U =
2.0 eV and δ = δ3 = 0 (s∗- and d-wave) or δ = 0.05 eV,
δ3 = 0.06 eV (p-wave).
| Symmetry α |
nop
|
−t´/t
|
Tc (K) |
Eg (meV) |
∆α (meV) |
Econd (meV) |
EF (meV) |
| s∗
|
0.140 |
0.455 |
162.53 |
-613.027 |
-022.126, |
0.700 |
-1707.073 |
| s |
|
|
|
|
16.962 |
|
|
| p |
0.140 |
0.4572 |
93.87 |
-262.703 |
14.559 |
0. 245 |
-1863.602 |
| d |
0.140 |
0.455 |
129.36 |
-260.216 |
14.501 |
0.241 |
-1844.425 |
| s* |
0.260 |
0.414 |
168.50 |
-690.708 |
-17.926 |
1.839 |
-1447.564 |
| s |
|
|
|
|
13.993 |
|
|
| p |
0.260 |
0.415 |
77.8 |
-456.167 |
10.753 |
0.152 |
-1723.577 |
| d |
0.455 |
0.310 |
126.14 |
-700.532 |
11.630 |
0.152 |
-1410.959 |
| p |
0.459 |
0.310 |
10.31 |
-719.364 |
1.3490 |
0.001 |
-1421.150 |
4.Conclusions
For the first time, by means of the generalized Hubbard model, we have studied the
variation of the maximum critical temperature (T
c-max
), the gap amplitude (Δ
p
) and the ground state energy (Eg) of p-wave superconducting
ground states in a square lattice within the (nop,t'/t) space for fixed values of the electron-electron interaction parameters,
where n
op
denotes the optimal electron density where the maximum Tc is
attained for a given value of the second-neighbor hopping (t´). In contrast to
previous studies, here the effects of different values of t´ on the superconducting
properties were analyzed. The ground state energies (Eg) were obtained
for all optimal electron concentrations (n
op
) where the critical temperature (Tc) is maximum, for systems with
given values of the second-neighbor hopping (t´) and δ3 and with Δt = 0.5
eV, δ = Δt3 = 0.05 eV. It is important to emphasize that it is not
possible to define a supremum value for the set of maximum critical temperatures (T
c-max
), as occurs for 𝑑-wave superconducting states 9, where the minimum ground state energy is found for
that state with the minimum value of T
c-max
. Moreover, the results presented in this work suggest that the p-wave
superconducting ground states that reproduce ecuacion K, are found close to half
filling (nop∼1), and should posses t ´< 0, in agreement with first-principles
calculations. In addition, in this parameter zone the Fermi surface is close and the
single-particle excitation energy [ Δ0(θ)] possess a clear p-wave
pattern. Moreover, within this zone, the p-wave ground state energies are lower than
the surrounding d- and s*-wave superconducting states. In contrast to previous works
6,7,13, this study indicates that the
Hamiltonian-parameter zone where stable p-wave superconductivity with low critical
temperatures can be found embraces positive and negative values of t´, and thus
other superconducting materials whose pairing symmetry has not been established can
be studied under the framework considered in this work. For example the iron-based
superconductors, where the K-doping of Sr1-xK-xFe−2As2,
modifies the former lattice and electronic structure 17. In addition, we can also investigate compounds such
as RuSr2-xBaxGdCu2O8 which contains both
Ru-O and Cu-O planes, and could have superconducting gaps with different symmetries
18.
Acknowledgments
This work has been supported by UNACAR-2020 project, ENERXICO Project No. B-S-69926,
and UNAM-PAPIIT IN109320. The authors thankfully acknowledge the computer resources
provided by Laboratorio Nacional de Supercómputo del Sureste de México (LNS) and
DGTIC-UNAM (project LANCAD-UNAM-DGTIC-180).
References
1. A. J. Leggett, A theoretical description of the new phases of
liquid 3He, Rev. Mod. Phys. 47 (1975) 331,
https://doi.org/10.1103/RevModPhys.47.331.
[ Links ]
2. Y. Maeno et al., Superconductivity in a layered perovskite
without copper, Nature 372 (1994) 532,
https://doi.org/10.1038/372532a0.
[ Links ]
3. T. Matsuzaki, N. Momono, M. Oda, and M. Ido, Electronic Specific
Heat of La
2-x
SrxCuO4: Pseudogap Formation and Reduction of the
Superconducting Condensation Energy, J. Phys. Soc. Jpn. 73 (2004) 2232,
https://doi.org/10.1143/JPSJ.73.2232.
[ Links ]
4. M. Schmid, B. M. Andersen, A. P. Kampf, and P. J. Hirschfeld,
d-Wave superconductivity as a catalyst for antiferromagnetism in underdoped
cuprates, New J. Phys. 12 (2010) 053043,
https://doi.org/10.1088/1367-2630/12/5/053043.
[ Links ]
5. S. Ran et al., Nearly ferromagnetic spin-triplet
superconductivity, Science 365 (2019) 684,
https://doi.org/10.1126/science.aav8645.
[ Links ]
6. J. S. Millán, L. A. Pérez, and C. Wang, p-wave superconductivity
in a twodimensional generalized Hubbard model, Phys. Lett. A 335 (2005) 505,
https://doi.org/10.1016/j.physleta.2004.12.080.
[ Links ]
7. L. A. Pérez, J. S. Millán, and C. Wang, Spin singlet and triplet
superconductivity induced by correlated hopping interactions, Int. J. Mod. Phys.
B 24 (2010) 5229, https://doi.org/10.1142/S0217979210057353.
[ Links ]
8. J. S. Millan, I. R. Ortiz, L. A. Pérez, and C. Wang,
First-Brillouin-zone integration areas for anisotropic superconducting states,
J. Phys. Conf. Ser. 490 (2014) 012221,
https://doi.org/10.1088/1742-6596/490/1/012221.
[ Links ]
9. B. Millán, L. A. Pérez, and J. S. Millán, Optimal doping for
d-wave superconducting ground states within the generalized Hubbard model, Rev.
Mex. Fis. 64 (2018) 233,
https://doi.org/10.31349/RevMexFis.64.233.
[ Links ]
10. B. Millán, I. J. Hernández-Hernández, L. A. Pérez, and J. S.
Millán, A comparison of optimal doping behaviors between d- and s*-wave
superconducting ground states, Rev. Mex. Fis. 67 (2021) 312,
https://doi.org/10.31349/RevMexFis.67.312.
[ Links ]
11. I. I. Mazin and D. J. Singh, Ferromagnetic Spin Fluctuation
Induced Superconductivity in Sr2RuO4, Phys. Rev. Lett. 79
(1997) 733, https://doi.org/10.1103/PhysRevLett.79.733.
[ Links ]
12. R. Matzdorf et al., Ferromagnetism Stabilized by Lattice
Distortion at the Surface of the p-Wave Superconductor
Sr2RuO4, Science 289 (2000) 746,
https://doi.org/10.1126/science.289.5480.746.
[ Links ]
13. J. S. Millán, L. A. Pérez, and C. Wang, Chiral and non-chiral
p-wave superconducting states from correlated hopping interactions, Phys. Status
Solidi B 251 (2014) 2302,
https://doi.org/10.1002/pssb.201451107.
[ Links ]
14. L. A. Pérez, Ph. D. thesis, Superconductividad con simetíıa d en
el modelo de Hubbard, Universidad Nacional Autónoma de México, 2002, p.
66.
[ Links ]
15. L. A. Pérez, O. Navarro, and C. Wang, Nonperturbative results
for attractive Hubbard pairings in triangular lattices, Phys. Rev. B 53 (1996)
15389, https://doi.org/10.1103/PhysRevB.53.15389.
[ Links ]
16. E. Dagotto, A. Nazarenko, and A. Moreo, Antiferromagnetic and
van Hove Scenarios for the Cuprates: Taking the Best of BothWorlds, Phys. Rev.
Lett. 74 (1995) 310,
https://doi.org/10.1103/PhysRevLett.74.310.
[ Links ]
17. M. Pan et al., The Doping Effect on the Lattices and Electronic
Structure in Superconducting Fe-based Compounds Sr
1-x
KxFe2As2, J. Supercond. Nov. Magn. 23
(2010) 985, https://doi.org/10.1007/s10948-010-0693-0.
[ Links ]
18. L. T. Yang et al., Enhancement of superconducting transition
temperature via Ba doping in RuSr
2-x
BaxGdCu2O8 (x ·≤ 0:1), J. Appl. Phys. 95
(2004) 1942, https://doi.org/10.1063/1.1636829.
[ Links ]














 text new page (beta)
text new page (beta)


