text new page (beta)
English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Similars in
SciELO 
Permalink
1. Introduction
Nonlinear partial differential equations (PDEs) are largely used to model various physical events such as shallow water waves, hydrodynamic, physics of plasmas, solid state physics, fluid mechanics, kinematics in chemistry, optic fibers, and chemistry among others. As consequence, the solutions of such equations and, particularly, the traveling wave equation solutions are of interest and become more significant when the impact in these fields is considered. The mathematical theory of these solutions is also significant to support the reliability of the proposed methods. Some recent approaches have begun to draw attention, for example; the exp(ϕ(χ))-expansion method [1], the modified Khater method [2], the symmetry analysis and fractional logistic function methods [3], the modified exponential expansion approach [4], the Sardar-subequation method [5], the extended rational sine-cosine and rational sinh-cosh methods [6], the Nucci’s reduction method [7], simple hyperbolic function ansatzes [8] and so on [9-26].
Here, we plan to employ the method of functional variable to set solutions of the following equations
and
where α,β and n are arbitrary chosen nonzero constants and 0 < µ ≤ 1. In recent years, some exact solutions for GZKE have been obtained by using different methods; for example, Wazwaz [27] used the extended form of the tangent hyperbolic method to construct solutions to the GZKE describing plasma waves. By the extended type trial equation method, new solitary solutions for the GZKE were obtained in [28]. Mothibi and Khalique [29] used the method based on the simplest equation to report some solutions to the GZKE in new forms. El-Ganaini [30] used the transform defined by ColeHopf with the method of first integral to obtain the complex solutions of the Eq. (1). Deng [31] expressed the solutions of the GZKE in travelling wave forms by the hyperbolic function method in extended form. Furthermore, some exact solutions of the GZK-BBM equation have also been found in some more studies using extended form of the trial equation method, the approach of sine-cosine functions, method of tanh-expansion, and G 0 /G-expansion approach [28,32,33].
In Refs. [34,35], Zerarka et al. defined the method based on functional variable to determine solutions for a many classes PDEs in linear or nonlinear forms. The technique of functional variable has been successfully employed to nonlinear problems. Aminikhah et al., [36] employed it to solve the system of generalized form of the Drinfel’d-Sokolov- Wilson (DSW), Davey-Sterwatson (DS) and Bogoyavlenskii models. Liu and Chen [37] found solutions to the Klein- Gordon (KG) model, and the Hirota-Satsuma (HS) coupled- KdV model with both time conformable derivatives by using the same method. In another study, the solutions to the general forms of KG equation, the Camassa-Holm(CH) in two space dimensions, the Kadomtsev-Petviashvili and the Schrodinger equations are reported in [38] by the same approach. Eslami et al., [39] applied the method of functional variable to construct the solutions of some problems such as Zakharov model in general aspect, general evolution term K(m,n) model, long-short wave resonance interaction model defined in two space dimensions, and power law nonlinear Schrodinger equation.
Some required definitions of the recently defined derivative, namely Khalil’s derivative (KCD), and some significant properties are briefly given below. Significant properties like chain rule or derivative of power functions are also given without proofs. The proofs can be found in the recent related literature.
Definition 1. Suppose f : (0,∞) →
in the whole positive half space for the order µ ∈ (0,1]. Some significant properties of the KCD can be summarized below.
Theorem 3. Let µ ∈ (0,1], and f and g be differentiable for the order µ at a point t. Then,
Moreover, if f is differentiable in classical meaning, then the relation is valid D t µ f(t) = t 1−µ (df/dt).
In Ref. [8], the rule of chain for the KCD was established.
Theorem 4. Suppose f : (0,∞) →R be a function satisfying the required conditions to derivative it of order µ and differentiable in classical meaning and assume that g is another function that satisfies differentiability conditions in classical sense in the range of f; then,
2. The method of functional variable
Consider the nonlinear time-conformable PDE, whose time derivatives are KCD,
where u = u(x,y,t) solves Eq. (5), the subscripts denote derivatives in partial sense.
The wave transform
and consequently, the partial differential equation (5) transforms to the ordinal differential equation
Then, assume that the unknown function denoted by capital U is the functional variable satisfying
and the derivatives of U in various orders are
where F 0 = dF/dU, F 00 = d 2 F/dU 2 and so on.
The Eq. (7) is an ODE and it can be reduced by employing U,F and its derivatives given in Eq. (9) into Eq. (5) to give
This form admits to generate solutions in wide classes covering many traveling waves described by trigonometric or hyperbolic functions. Integrating Eq. (10) gives some new expressions in terms of F. Combining Eq. (8) and other relations satisfying required conditions leads to set the solutions of the focused initial problem.
3. The GZKE with time conformable derivatives
In the present section, we derive solutions in traveling various wave forms of the GZKE with time conformable derivatives by using the method of functional variable described in Sec. 2.
Using the transform u(x,y,t) = u(ξ), where ξ is defined in Eq. (6), the Eq. (1) is transformed to an ODE
or
Following Eq. (9), one can easily deduce
from Eq. (12) . The integral of Eq. (13) with zero integral constant yields
or
From (8) and (15) we find that
where ξ 0 is a constant of integration. Finally, by completing the integration in Eq. (16), two cases of solutions of the time-conformable GZKE after a straightforward algebraic manipulation.
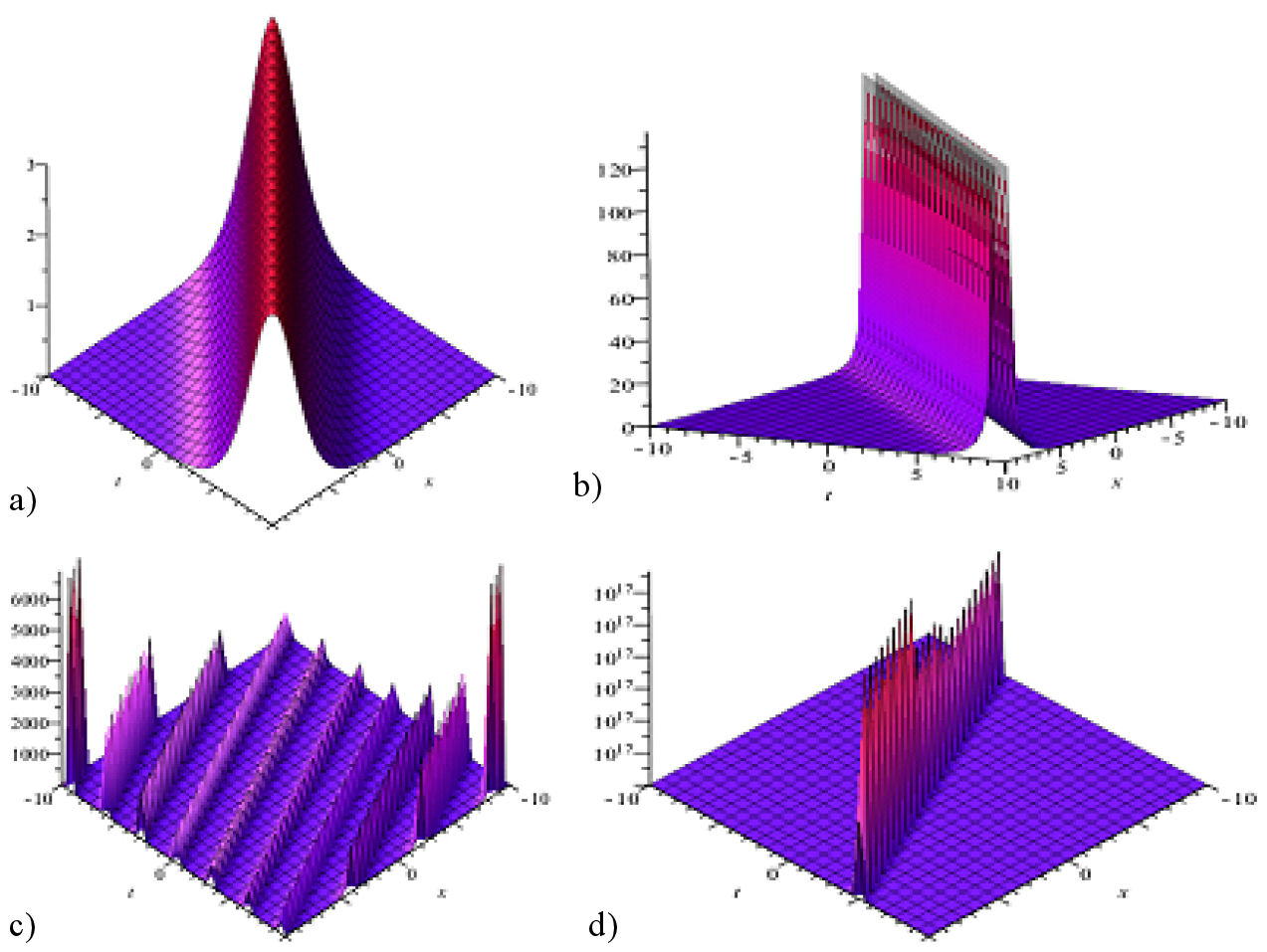
FIGURE 1 The graphical representations of a) bright and b) singular soliton solutions given in Eq. (17) and (18) with the suitably chosen parametric values n = 1,a = 1,b = 1,c = 1,y = 0,m = 1 are given respectively. The graphical representations of c) bright and d) singular soliton solutions given in Eq. (19) and (20) with the suitably chosen parametric values n =2,a =1,b =1,c =2,y =0,m =1 are.
The case c/β > 0 gives the hyperbolic traveling wave solutions u(x,y,t)
The case c/β < 0 gives the periodic traveling wave solutions u(x,y,t)
It should be noted that the solutions given in Eq. (17) and Eq. (18) are soliton solutions, in bright and in singular forms, respectively, whilst Eq. (19) and Eq. (20) are singular periodic solutions.
4. Time-conformable GZK-BBM equation
In the present Section, we set solutions of the timeconformable GZK-BBM equation by using the method of functional variable described in Sec. 2.
The two dimensional wave transform u(x,y,t) = u(ξ), where ξ is defined in Eq. (6), the Eq. (7) is
Following Eq. (9) results from Eq. (22) in an expression for the function F(U)
or
FIGURE 2 The graphical representations of a) bright and b) singular soliton solutions given in Eq. (27) and (28) with the suitably chosen parametric values n = 2,a = 1,b = −2,c = 0.5,y = 0,m = 1 are. The graphical representations of c) bright and d) singular soliton solutions given in Eq. (29) and (30) with the suitably chosen parametric values n =2,a =1,b =1,c =2,y =0,m =1 are.
From Eqs. (9) and (26) we deduce that
where ξ 0 is a constant of integration. Finally, by completing the integration in Eq. (26), two cases of travelling wave solutions of the GZK-BBM equation with conformable time derivatives after a straightforward algebraic manipulation.
Case 1/β < 0 gives the hyperbolic traveling wave solutions u(x,y,t)
which represent bright and singular soliton solutions, respectively.
Case 1/β > 0 gives the periodic traveling wave solutions u(x,y,t)
which are singular periodic solutions.
5. Conclusion
In this paper, the hyperbolic and trigonometric wave-type solutions are constructed for the time conformable forms of the GZK and the time-conformable GZK-BBM equations. The compatible traveling wave transforms defined in two space dimensions reduce the governing equations to some ODEs. Defining a new variable in function form modifies the resulted ODE. The following effort is to solve these ODEs by integration techniques. Due to the good performance of the method of functional variable, it is believed that this method is a promising technique in handling a wide variety of timeconformable PDEs.
