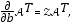1.Introduction

Differential geometric tools such as surfaces and curves have been appeared in many disciplines of theoretical and practical areas of science ranging from thermodynamics ¹ to high energy strings ², and from general relativity ³ to solitons ⁴, or even in plasma physics (5) and liquid crystals ⁶. The motion of curves and the concept of the Frenet-Serret frame are the main common ingredient in all these applications.

These tools have also been considered in the research of magnetic structures significantly. Recently, many authors have focused on the subject of magnetic curves and investigate many important results. In these studies, one common approach has been used extensively. According to this approach, it is generally assumed that magnetic curves are trajectories of the time-independent moving charged particle on geometric manifolds or physical spacetime structures. This motion of the particle is specifically determined by the Lorentz force equation. Once the Lorentz force equation is managed to solve successfully, then many interesting characterizations have been developed from the geometric and physical points of view. Körpinar and Demirkol investigated electromagnetic curves, their geometric phases, and their transportation laws, along with the linearly polarized light coupling into the optical fiber in a three-dimensional semi-Riemannian manifold ⁷.Körpinar and Demirkol also obtained frictional and magnetic curves by using the anti-symmetric Lorentz force operator and Frenet-Serret equations to characterize their physical and geometric properties ^8,9. Kazan and Karadağ computed magnetic vector fields of magnetic non-lightlike curves in terms of parallel transport frames in three-dimensional Minkowski space ¹⁰. Güvenç and Özgür determined necessary and sufficient conditions for being slant normal magnetic curves in (2n +1) -dimensional S-manifolds ¹¹ Cabrerizo studied the magnetic flow lines and associated Killing magnetic fields in three-dimensional space ¹² Sun established the connection between geometric invariants of the magnetic curves and magnetic normal binormal surfaces (13). Körpinar et al. investigated a new kind of evolution equation for electric and magnetic fields satisfying the Maxwell equations along with the uniform optical fiber in three-dimensional ordinary space and Minkowski space ^14,15.

These structures are implemented by many authors to define magnetic flux-tubes in the case of inflexional configuration and inflectional disequilibrium. In the presence of a magnetic field, the magnetic flux-tube is defined by the cylindrical-thin tube of circular cross-section having a positive radius. The cases of twisted magnetic flux-tube and straight flux-tube are investigated separately in various studies. The geometric formulation of these tubes is derived by the Lorentz force equation and used to determine generic characterizations associated with the several useful applications to astrophysical flows, solar corona loops, etcetera. Nested toroidal flux surface is described due to the motion curves in magnetohydrostatic. It can be considered as a generalization of the magnetic flux-tube. All these results have been obtained through the Riemannian and non-Riemannian geometric data and facts. Ricca studied generic behavior and equilibrium conditions of the magnetic flux-tube by considering the Lorentz force equations ¹⁶. Ricca also presented new consequences concerning inflexional and evolution instability of magnetic flux tubes when the curvature of the tube axis vanishes ¹⁷. De Andrade obtained a non-Riemannian geometrical characterization of the magnetic flux-tube and the fluid rotation by using the Da Rios equation ¹⁸. De Andrade showed that the twist of the magnetic flux tube could be computed in terms of the torsion of the tube axis under a special evolution equation ¹⁹. De Andrade considered the Heisenberg spin equation and Gauss-Mainard-Codazzi equations to observe the influence of torsion and curvature of the magnetic flux-tube axis in magnetic filament acting as dynamos evolution ^20.

The wider geometric importance of the moving curves is appeared in vortex filament motion, magnetic dynamics, kinematics of interfaces. The relationship between the motion of curves and the integrable evolution equation is the main subject focused on by many researchers. As a result of this effort, the equation of the motion of curve or vortex filament is linked by many geometric and physical evolution equations such as the Landau-Lifshitz equation, non-linear Schrödinger equation, localized induction equation, Heisenberg antiferromagnetic and ferromagnetic equation, binormal equation, Da-Rios equation. Guo and Ding classified explicit or approximate boundary value solutions or initial value problems together with their physical or geometric flow models²¹. Vieria and Horley used binormal, normal, and tangent vectors of the Frenet-Serret system in such a successful way that they extracted significant data regarding the dynamics of the magnetization vector ²² Hasimoto described an intrinsic equation governing the torsion and curvature of a vortex to define the propagation of a hump or loop of helical flow ²³. Anco and Myrzakulov generalized Heisenberg spin models and Schrödinger maps from geometric surface flows and Hamiltonian flow through Frenet-Serret equations of surfaces and curves ²⁴ Erdoğdu and Özdemir discussed Hasimoto surfaces and their geometric properties such as mean and Gaussian curvature of these surfaces for each case in Minkowski space ²⁵. Ricca realized a correlation among localized induction approximation, Betchov-Da Rios equation, and nonlinear Schrödinger equation for extracting pseudo-helicity, energy, and associated Lagrangian for the motion of a thin vortex filament ²⁶. Balakrishnan et al. derived the geometric phase, gauge potential, and the anholonomy density of general space curves by employing Lamb’s formulation for time evolution systems ²⁷. Barros et al. computed soliton solutions of the Betchov-Da Rios equation explicitly in the anti-De Sitter and Lorentzian space forms ^28,29. Arroyo studied binormal flow with torsion and curvature to investigate the evolution of filaments ³⁰.

These flow models and nonlinear evolution equations can be related to soliton propagation. In many cases, they are used to explain the notion of parallel transportation and geometric phase along with that propagation. For example, the effect of this phase is observed along with the rotational direction of polarized light rays propagating through the optical fiber. If the solid angle observed by the turning of the tangent vector of optical fiber is equal to the angular rotation of light rays, then it implies that the polarization has been parallel transported. Subsequent studies have shown that particular equations such as Maxwell’s equations, spin equations, Lorentz equations, etcetera. contain the rotational effect of the polarization of light. Köpirnar et al. studied soliton propagation of electromagnetic field vectors of the polarized light ray traveling along with the coiled optical fiber in different geometric structures ^31-33. Balakrishnan formulated path dependence of the rotation and the geometric phase of the moving orthonormal vectors by considering continuous, classical, antiferromagnetic Heisenberg flow ³⁴. Bliokh reviewed the spin-orbit propagation along with the light with the emphasis of the Berry phase and spin Hall effect carried by the wave ³⁵. Bliokh et al. also measured the precession of the Stokes vector and the spin-dependent deflection along the coiled ray trajectory in an excellent accuracy with theoretical estimations ³⁶. Wassmann and Ankiewicz improved an alternative method allowing one to derive Berry’s topological phase in terms of both planar and solid angles ³⁷. Balakrishnan characterized a special type of geometric phase depending on a family of soliton-based equations ³⁸. Samuel and Nityananda explained a new transportation rule for polarization vectors and their integrability conditions while these vectors are assumed to define along with non-geodesic null curves ³⁹. Balakrishnan and Dandoloff generalized the classical evolution equation for a spae curve to demonstrate traditional analogs of the Heisenberg and Schrödinger pictures seen in the quantum theory ⁴⁰.

This paper investigates another aspect of the moving curve evolution. We define magnetic field lines governed by the inextensible Heisenberg antiferromagnetic flow in relation to the total geometric phase and apply these to characterize the Lorentz magnetic flux surfaces in the binormal direction. Thus, we aim to derive the geometric relationship between magnetic flux surfaces and magnetic field lines in the binormal direction. The theoretical and numerical accuracy of the methodology is proved through the inextensible Heisenberg antiferromagnetic flow of magnetic vector fields, the evolution anti-symmetric Lorentz force field operator, and the conformable fractional derivative method when these fields are transformed under the traveling wave hypothesis. Thus, we aim to develop a novel approach for gaining a better insight into the nature of potential geometric and physical properties in interacting magnetic field lines and their flow models in the binormal direction.

The organization of the paper is as follows. In Sec. 2, we present differential geometric structures of orthonormal Frenet-Serret vectors and their directional derivatives. In Sec. 3, we compute magnetic and electric b-lines in terms of orthonormal vector fields and associated geometric quantities in the binormal direction. In Sec. 4, we describe a new type of inextensible Heisenberg antiferromagnetic flow model for the magnetic lines and associated magnetic vector fields in the binormal direction. In Sec. 5, the results and potential research topics are specialized. We conclude the paper by the appendix, which includes approximate solutions of some equations computed through the manuscript.

2.Differential Geometry of Frenet-Serret Vectors

In the introduction, we state that the motion of curves and the concept of the Frenet-Serret frame are the main common ingredient in many applications. The orthonormal Frenet-Serret frame governing the intrinsic characterization of the vector triple A=(e1⃗, e2⃗, e3⃗) is given in the compact shape by

∂∂bAT=ZAT,

where X, Y, Z can be written in the following skew-symmetric matrix form

respectively. Here, T denotes the transpose of the matrix A=(e1⃗, e2⃗, e3⃗). Furthermore, ∂/∂s, ∂/∂n, ∂/∂b represent directional derivatives in the tangent direction, normal direction, and binormal direction, respectively. By assumption, in the tangent direction, we know that the tangent vector of s-lines is denoted by e1⃗i.e.

where ς is assumed to represent s-lines. In the normal direction, the tangent vector of 𝑛-lines is denoted by  e2⃗ i.e.

where ϖ is assumed to represent n-lines. In the binormal direction, the tangent vector of b-lines is denoted by  e3⃗ i.e.

where θ is assumed to represent b-lines. The gradient operator is written by

Hence, the vector analysis formulas can be expressed by

where

The curl operator is written by

Hence, the other vector analysis formulas can be expressed by

Where

In the end, we remind that each vector or geometric quantity depends on the three variables of (s, n, b). For the brevity purpose, we rather choose using e1⃗=e1⃗s,n,b, κ1=κ1s,n,b, etc. type of notation. We will continue to apply a similar notation for any function associated with the above vectors or geometric quantities. We also think that repeated statements of smoothness conditions and excessive repetition that certain parameters are supposed to be non-vanishing may seem obscure. Accordingly, we suppose that all functions are sufficiently smooth as required by the calculation unless stated otherwise.

3.Magnetic and electric 𝐛-lines in the binormal direction

An important relation between electromagnetism and differential geometry can be established when the moving positively charged particle under the action of the Lorentz force and its trajectory is observed. This trajectory is represented by electromagnetic lines such that they are assumed to the composition of magnetic lines and electric lines. Lorentz force has a crucial role to describe the behavior of these lines. In the differential geometric viewpoint, the magnetic s-lines, magnetic n-lines, magnetic b-lines satisfy the following types of Lorentz force equations in the tangent direction, normal direction, and binormal direction, respectively

where Ms, Mn, Mb are divergenceless magnetic vector fields associated with each magnetic line given directions ⁴¹. By using the language of differential geometry, we aim to simplify the calculation and formalization of the magnetic field lines and provide various other physical understanding more simply. In this section, we obtain magnetic lines under the action of the Lorentz force equation by using the Frenet-Serret formalism in the binormal direction. Later on, these lines will be used derived magnetic flux surfaces when their motions are governed by the inextensible Heisenberg antiferromagnetic flow.

First, we consider Eqs. (5,23) to obtain Lorentz force fields of Frenet-Serret vectors. Then we should also take into account the following well-known facts of the inner product

So, from Eqs. (5,23,24), Lorentz force fields of Frenet-Serret vectors are obtained in the following way

where ρ is a well-defined arbitrarily chosen sufficiently smooth function along with magnetic b-lines. It is already known that divergenceless magnetic vector field Mb is spanned by the (e1⃗, e2⃗, e3⃗). Therefore, it should also be true that

where ϕb(Mb)=0. Here, m₁, m₂, and m₃ are also sufficiently smooth functions along with magnetic b-lines. As a result of Eqs. (23,25,26,27), the magnetic vector field of magnetic b-lines in the binormal direction is computed by

The electromagnetic force equation in the binormal direction can be expressed by

where En denotes electric n-lines defined along with the motion of the positively charged particle. Thus, by using Eqs (28,29), it is obtained that

Eb=-κbs1+mqe1⃗-κ1+dive2⃗1+mqe2⃗.

4.Inextensible Heisenberg antiferromagnetic flow model in the binormal direction

The inextensibility of the mechanism is an important tool to seek the relation between the geometric motion of space or plane curves and integrable equations. Apart from the traditional inextensible flows in the tangent direction, we identify time-dependent evolution equations satisfied by the geometric quantities of magnetic b-lines under inextensible flows in the binormal direction.

In the binormal direction, the most generalized form of the inextensible flow can be represented by

where λ₁, λ₂, and λ₃ are sufficiently smooth coefficients of the tangent, normal, and binormal vectors along magnetic b-lines in the binormal direction. ∂/∂u is used to represent the time derivative. Here, one should also recall that the binormal vector is assumed to satisfy the following identity

where ϖ denotes the family of magnetic b-lines in the binormal direction. Now, if basic compatibility conditions and properties of the inner product are applied to Eqs. (5,31,32) then we may write that

where σ is a sufficiently smooth function defined along with the magnetic b-lines in the binormal direction. Eqs. (32-34) are given the most generalized form of the evolution equation for time derivative in the normal direction. Now, we define the particular case of the inextensible evolution of magnetic b-lines in the binormal direction. This particular case is known as the Heisenberg antiferromagnetic flow in the binormal direction. It is defined by

or equivalently

From Eqs. (5,35,36), it can easily be computed that

By comparing Eqs. (32-34) and Eq. (37), we can conclude that the inextensible flow and Heisenberg antiferromagnetic flow of b-magnetic lines coincide in the binormal direction when the following equalities satisfy

Thus, the inextensible Heisenberg antiferromagnetic flow of Frenet-Serret vectors can be induced to

where σ is a sufficiently smooth function defined along with the magnetic b-lines in the binormal direction. Time-dependent evolution equations of Frenet-Serret vectors may also be written by only using the vector calculus identities in the following way

The inextensible soliton surface associated with the Heisenberg antiferromagnetic flow of magnetic b-lines can be constructed once the coefficients of the fundamental forms are derived. Coefficients of the first fundamental form can be computed by

Thus, we find that

The binormal vector of the inextensible soliton surface associated with the Heisenberg antiferromagnetic flow of magnetic b-lines is calculated as

Then, coefficients of the second fundamental form can be computed by

A direct computation of the above equation yields that

Thus, we find that

GII=1(κbs)2+(κ1+dive2→)2-σ{κbs}2+{κ1+dive2→}2-κbs∂∂uκ1+dive2→+κ1+dive2→∂∂uκbs.

As a result, the Gauss curvature and mean curvature of the inextensible soliton surface associated with the Heisenberg antiferromagnetic flow of magnetic b-lines are given by using Eqs. (45-52) in the following way

Now, we can present some further geometric properties of magnetic b-lines lying on the inextensible soliton surface associated with the Heisenberg antiferromagnetic flow in the binormal direction.

A curve lying on any surface is called a geodesic if and only if the normal vector of the surface coincides with the principal normal of the curve. Based on this fact, we get the following two results.

⬧ b -parameter magnetic b-lines of the inextensible soliton surface associated with the Heisenberg antiferromagnetic flow in the binormal direction are geodesics.

⬧ u -parameter magnetic 𝑏-lines of the inextensible soliton surface associated with the Heisenberg antiferromagnetic flow in the binormal direction are geodesics if and only if

A curve lying on any surface is called an asymptotic if and only if along the curve the surface normal vector field is orthogonal to the principal normal vector field of the curve. Based on this fact, we get the following two results.

⬧ b -parameter magnetic b-lines of the inextensible soliton surface associated with the Heisenberg antiferromagnetic flow in the binormal direction are asymptotics if and only if

κ1=-dive2⃗.

⬧ u -parameter magnetic 𝑏-lines of the inextensible soliton surface associated with the Heisenberg antiferromagnetic flow in the binormal direction are asymptotics if and only if

κbs=σ(κ1+dive2⃗).

As a result, we conclude that magnetic b-lines are lines of curvature if and only if the following equality holds

An exclusive case is that for which the inextensible soliton surface associated with the Heisenberg antiferromagnetic flow of magnetic b-lines is developable. For that, we first assume that magnetic b-lines are lines of curvature. Then, the soliton surface is developable if and only if

Equations (56,57) may be used to derive such a relation in a way that emphasizes the physical aspect of the soliton surface through the geometric quantities of the Heisenberg antiferromagnetic flow of magnetic b-lines. This relation is written by Laplacian-like differential equations in the following way

In the appendix section, we will investigate approximate solutions and their numerical demonstrations of some special cases of the Laplacian-like formalism given by Eqs. (58,59).

5.Magnetic Flux Surfaces of the Inextensible Heisenberg Antiferromagnetic Flow

In this section, new developments of the research recently proposed by many authors on the generalization of time evolution equations on geometric quantities are investigated. Particularly, we consider applications to three-dimensional inextensible Heisenberg antiferromagnetic flow dynamics, including the case of a magnetic flux surface and the flow rotation in the binormal direction. Integrals on the total geometric phase are proved to be related to the integrals, which represent the geometric characterization of the magnetic flux surface in continuous Heisenberg antiferromagnetic spin of magnetic b-lines in the binormal direction.

Let us first consider the Lorentz force fields of magnetic b-lines given by Eq. (26) .

Now, we are ready to compute the evolution equations of Lorentz force fields for both and u parameters. The evolution equations of the Lorentz force fields for the arc-length parameter in the binormal direction are written by using Eqs. (5,60) in the following way

The evolution equations of the Lorentz force fields for the time parameter obtained through the inextensible Heisenberg antiferromagnetic flow are given by using Eqs. (39-41,60) in the following way

Considering (61-66) with the general reference frame given by (5), we can identify the geometric phase of magnetic b-lines in which their evolution equations are dependent on both b and u parameters. In this way, we can observe the effect of the rotational flow of magnetic b-lines in the binormal direction while they evolve in time through the inextensible Heisenberg antiferromagnetic evolution and Frenet-Serret equations. Accordingly, this phase becomes

This is the statement for the geometric phase of the inextensible Heisenberg antiferromagnetic flow of magnetic b-lines in the binormal direction. We use an efficient technique that is based on the certain evolution system of the spin configuration, which allows the system to return to its original shape and position after a time interval. This technique also provides to determine necessary and sufficient conditions that have to be satisfied by the geometric quantities associated with the magnetic b-lines to define the Lorentz magnetic flux surfaces. Finally, it can be considered to compute the magnetic flux density of the Lorentz magnetic flux surfaces obtained through the evolution of magnetic 𝑏-lines based on the inextensible Heisenberg antiferromagnetic flow model.

The magnetic vector field of magnetic b-lines in the binormal direction has already computed by Eq. (28) in the following way

Using the Lorentz force equations and inextensible Heisenberg antiferromagnetic evolution equations of magnetic b-lines with appropriate boundary conditions given by Eqs. (60-66), the necessary and sufficient conditions for the existence of the Lorentz magnetic flux surfaces are stated by

As a result, the magnetic flux density of the Lorentz magnetic flux surfaces obtained through the evolution of magnetic b-lines based on the inextensible Heisenberg antiferromagnetic flow model is computed by