2.1.Numerical methods

We solve the time dependent GPP system of equations which in code units is written as

that describes the evolution of the fuzzy dark matter. Here, Ψ represents the wave function of the system and |Ψ|2 is interpreted as the macroscopic density of the condensate and V is the gravitational potential sourced by the condensate itself. We solve these equations for Ψ in a cubic finite domain, with initial data for Ψ consistent with the potential V. In this system, Poisson equation is a constraint that has to be solved on the fly as the bosonic gas density evolves.

We solve the Gross-Pitaevskii equation numerically in 3D using the method of lines for the evolution across spatial slices separated by intervals of time Δt. The spatial domain D=xmin,xmax×ymin,ymax×[zmin,zmax]> is described with a Cartesian and uniformly discretized grid defined by xi,j,k=xmin+iΔx, yi,j,k=ymin+jΔy and zi,j,k=zmin+kΔz, for i=0,...,Nx, j=0,...,Ny, k=0,...,Nz, with an isotropic resolution Δx=Δy=Δz=(xmax-xmin)/Nx.

We discretize the equations with second order accurate finite difference stencils for spatial derivatives. For the sake of accuracy in the region of the merger, we use fixed mesh refinement based on the Berger-Oliger algorithm ²⁸, with concentric refinement boxes. The resolution factor between successive refinement levels is one half. Considering that for the stability of the evolution, time and space resolution are limited by the condition C=Δt/Δx2<0.25/3, we choose the value of C to be that corresponding to the most refined level.

We solve Poisson equation for V with a Multigrid algorithm with subcycles that use the Successive Over Relaxation method. This equation is solved at initial time and during the evolution. Due to its computational cost, the integration of Poisson equation represents the major bottleneck of the code during the simulations.

Since we want to avoid reflections of matter from the boundary of the numerical domain, and because the Gravitational Cooling depends on the emission of matter that carries kinetic energy with it, we implement a sponge consisting of the addition of an imaginary potential such that V→V+Vim, acting as a sink of particles following the recipe in ²⁹. We make sure that the transition region of the sponge lies exclusively in the coarsest refinement level.

2.2.Initial conditions

We assume the colliding objects are equilibrium configurations, which are spherical stationary solutions, constructed by assuming a harmonic time dependence of the wave function Ψ=e-iωtψ(r), where ω is the eigenvalue of the Sturm-Liouville problem resulting from the spatial and time symmetries of Ψ as described in ²⁹.

The initial wave function for the collision of two configurations is the superposition of the wave functions of two of these equilibrium configurations with different masses and linear momentum. For the superposition we use the method in ¹⁴, specifically, we do not solve the Sturm-Liouville problem for two equilibrium configurations with different masses. Instead, we exploit the scale invariance of the GPP system of equations ²⁹, namely that by scaling physical quantities as t=λ2t^, x=λx^, Ψ=Ψ^/λ2, V=V^/λ2, where x represents any of the spatial coordinates and λ is a number, the GPP system ([eq:gpp]) remains unchanged. Thus, the solution of the GPP system for a given configuration means one can construct all other equilibrium configurations using this scaling property. In fact, a consequence of this scaling is that density and mass also scale as ρ^=λ4ρ, M^=λM which are important physical parameters of a scaled configuration used below.

In practice the typical equilibrium configuration is that with the central value of the wave function ψ(r=0)=1 that we will call ψ(r)1 and has mass we call M₁. We choose one of the two configurations that will collide, to be precisely this standard configuration.

The second configuration that will collide, is a configuration constructed with the scaling relations above, represented by the wave function ψ(r)λ=λ2ψ(r)1, with mass Mλ=λM1. Notice that the scaling parameter happens to be the mass ratio λ=Mλ/M1=λ=MR between the first and the second configurations used for the collision. In the analysis we consider the convention 0<λ<1 in all cases, so that Mλ<M1 always.

We then interpolate and superpose the two configurations in the numerical domain D. In order to maintain the system evolving within the numerical domain, we set the center of mass of the configuration at the coordinate origin. We parametrize the initial conditions by fixing the coordinates of the lighter configuration with mass M_λ at (x₀, y₀,0) with x₀,y₀ > 0. Then, in order for the center of mass to lie at the origin, the center of the heavy configuration with mass M₁ must be centered at coordinates (-λx₀, -λy₀,0). In this set up y₀ will play the role of impact parameter prior to merger.

The angular momentum is added through the imprint of linear momentum to the configurations along the x direction only. For this, we parametrize the momentum with the x-component of the heavy configuration with mass M₁ that we set to p_x0. Then again, in order to keep the center of mass approximately at the coordinate origin, the momentum of the light configuration must be px0/λ. The momentum is applied to each of the configurations by redefining ψ1→eipx0xψ1 and ψλ→e-ipx0xψλ. Finally the wave function of the binary system at initial time is Ψ=ψ1+ψλ and the scheme in Fig. 1 illustrates the initial conditions.

Figure 1 Scheme of the initial conditions on the xy-plane, for the two configurations described by ψ₁ and ψ_λ. It illustrates the initial position and momentum in terms of the mass ratio λ, which are defined such that the center of mass is located at the origin and is expected to remain there. 

2.3.Diagnostics

We monitor the dynamics of the system by evaluating some macroscopic variables. These include the mass M, kinetic energy K, gravitational energy W and the z component of the angular momentum L_z. These quantities are

where the integrals are calculated using the second order accurate trapezoidal rule. A first important quantity is the total energy E = K + W, whose sign determines when a system is bounded (E < 0) or unbounded (E > 0). A second one is Q = 2K + W which should be zero for a virialized system and allows one to determine when a system is near, tends to or is far from a virialized state.

3.1.Parameter space

There is a wide variety of possible configurations that can be explored. However, three parameters influence the behavior of the configuration resulting from the interaction between the two cores, namely, the mass ratio MR momentum p_x0, and impact parameter. These three parameters determine wide ranges of angular momentum and total energy values at initial time. It would be ideal to have the possibility of exploring a wide range of this parameter space. Nevertheless, due to the expensive computational cost of simulations, we restrict the exploration to illustrate the influence of some parameters using specific values.

First, we set two possible values of the mass ratio MR = λ = 0.5,1, which are the equal mass scenario and the two to one mass ratio case, which will illustrate well the behavior of the system in unequal mass encounters.

Second, we consider various values of the impact parameter y₀. The radius of the configuration with mass M₁ is r₉₅ ∼ 3.93 in code units , whereas that of mass M_1/2 is twice as big. Thus we study the range of values y₀ = 1,2,…,10 that accounts for scenarios ranging from nearly head-on to a separation various times bigger than the size of the structures.

Third, we distinguish between merger and unbounded scenarios. In the first scenario the two configurations end up together and form a final configuration. In the second scenario, either the configurations flyby each other or behave as solitons. The momentum p_x0 is useful to generate the two scenarios, because it sets the amount on kinetic energy K of the two configurations together. With a low value of this parameter the gravitational energy W dominates, implying that E < 0, otherwise a high momentum contributes to K that can contribute importantly to the energy to be positive and produce unbounded configurations. The threshold value for the head-on scenario is found to be p_x0 ∼ 0.7 ³⁰ which serves as a guide to avoid non-merging cases.

We empirically found a range of values of p_x0 for which at initial time the total energy is negative for the two values of MR and all the values of y₀. Values in the range px0∈[0,0.3] produce configurations with negative energy. In what follows we use the case p_x0 = 0.1 to illustrate the generic properties of mergers.

The values of these physical parameters suggest the numerical parameters to be used. The first parameter is the location of the lighter configuration at (x₀, y₀,0) with x₀ = 10 in all cases. We use this value because the interference at the origin between ψ₁ and ψ_A, ⟨ψ1,ψλ⟩ is less than 10^-8. We consider the domain to be the box D=[-40,40]3 and cover it with two refinement levels, and maximum resolution Δx=0.1r95 in the inner box, which covers the region where the dynamics is more important Dh=[-20,20]3.

3.2.Global quantities

In a merger scenario, the two cores collide and form a single final configuration whose density profile can eventually be fitted with a simple function that can be further used to understand and analyze the physics of different processes.

We study now this scenario using p_x0 = 0.1 for the two values of MR and all the values of the impact parameter y₀. The system of Eq. (1) is solved numerically for the initial conditions described above and we show the evolution of some of the scalars defined in Sec. II.C in Fig. 2, for the ten values of y₀ = 1,…,10.

Figure 2 For the case p _x0 = 0:1, we show the total energy E, the total mass M and L _z for the two mass ratios considered MR = 0:5; 1 and the ten impact parameter values y₀ = 0; :::; 10. Labels are used only for the two extreme values of y₀ = 1; 10, whereas the unlabeled curves correspond to the other eight intermediate values of y₀. 

The energy E is shown normalized with the absolute value of its initial value. Notice that the total energy becomes more negative than at initial time, which indicates that the gravitational energy plays a more important role with time. The energy is also lost in a bigger proportion for smaller impact parameter y₀, and for MR = 1 than for MR = 0.5.

The mass is normalized with the mass of the standard equilibrium configuration M₁, therefore for MR = 1 the total mass is initially M = 2, whereas for MR = 0.5 the initial mass is M = 1.5. Notice that the mass decreases because matter is ejected and eventually captured by the numerical sponge. The combination of these two observations indicates that the mass lost during the process carries kinetic energy with it, exemplifying the Gravitational Cooling process ^11,31.

Notice also that for MR = 1, the total mass is higher at initial time, but is also lost in a bigger percentage compared to the case of MR = 0.5. It can also be seen that the bigger the impact parameter y₀, the smaller the mass ejected during the process. For MR = 1 the final mass converges to the same value independently of y₀, or equivalently to the initial angular momentum of the pre-merger configuration as discovered in ¹⁹. Nevertheless for MR = 0.5 this is not the case, at least within the time window of our simulations.

Another interesting result is that the matter also carries angular momentum with it. In the bottom panel of Fig. 2, the proportion of angular momentum during the merger is shown.

The evolution of angular momentum shows an interesting behavior. For MR = 0.5 the amount of L_z released is between ∼20% for y₀ = 1 and ∼40 % for y₀ = 10. In this sense, the simulations indicate that the merger process can produce final configurations with a wide range of values of angular momentum that could give origin to rotating galactic cores. However, for MR = 1 the loss of angular momentum radiated away is of ∼65% for y₀ = 10 and even turns negative for y₀ = 1,2,3 in the time window of the simulations and could hold also for other values in a bigger time domain. This result is interesting and the reason for the change of sign is that small values of y₀ correspond to nearly head-on situations. Since y₀ is the value of the impact parameter only at the center of each configuration, part of the matter ejected should be that initially located farther from the x-axis which carries angular momentum with it when it abandons the domain. This turn in the direction of rotation could be an interesting sign that eventually may provide restrictions to the model or predictions.

3.3.Equal mass case

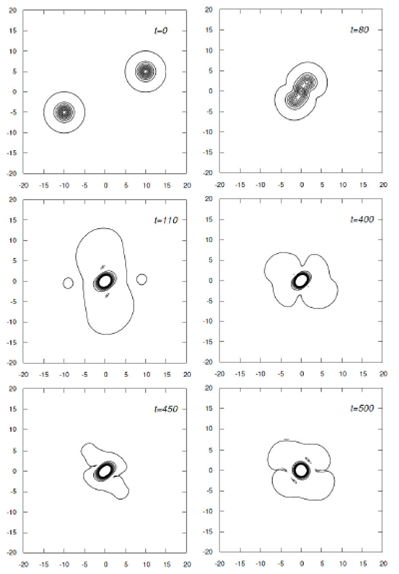
The evolution of a specific simulation is shown in Fig. 3 for the equal mass case. The final configuration remains centered at the coordinate origin, rotates and has an ellipsoidal density profile. Animations of this and cases with various other parameter values are available in the supplemental material ³².

Figure 3 Density contours on the xy-plane for the equal mass merger with p _x0 = 0:1 and y₀ = 5. 

In order to learn more about the dynamical behavior of the final configuration, we track the value of the central density and Q = 2K + W as functions of time that are shown in Fig. 4 for the two extreme values of the impact parameter y₀ = 1, 10. It can be seen that the quantity Q oscillates around zero with a decreasing amplitude as expected for the Gravitational Cooling ¹⁴.

Figure 4 For the case p _x0 = 0:1 and MR = 1, we show Q = 2K +W and the central value of the density as a function of time for y₀ = 0 and y₀ = 10. Oscillations are smaller for y₀ = 10 than for the nearly head-on case y₀ = 1. 

The central density oscillates changing values by factors between two and three in the nearly head-on case y₀ = 1 and smaller oscillations for y₀ = 10. Figure 4 suggests that the amplitude of the oscillations and the central value of the density depend on the impact parameter. In order to find a dependency on y₀ we calculated the average density ρavg and its standard deviation to have a measure of the amplitude variation around the average ρdev, for t > 200. The results are shown in Fig. 5, which suggest that both, the central density and oscillation amplitude depend on y₀ linearly. Finally, calculating a Fourier Transform within the same time domain, we obtain the peak frequency associated to the dominant density oscillation mode, which also depends on the impact parameter as shown in the third panel of Fig. 5. Knowing that the final mass is the same for all values of y₀, the oscillation frequency is genuinely different for different values of y₀.

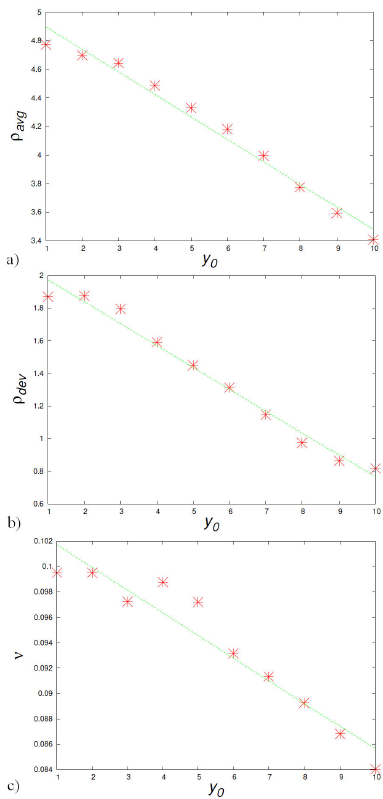
Figure 5 For the case p _x0 = 0:1, MR = 1, the stars indicate the average in time of the central density of the final configuration ρ _avg , its standard deviation ρ_dev dev and the peak frequency v for the ten values of y₀ used. For each of these quantities we show a linear fit, suggesting the dependency on y₀ can be linear. 

In structure formation simulations ^7,8,12,18,19 the density distributions resulting from the interaction of two or more configurations are associated to density profiles with a solitonic core and a tail, however it is not quite specified whether these are final, relaxed configurations or not. As far as we can tell, the oscillations shown in Fig. 4 do not correspond to a relaxed structure. Even though the density profile can be fitted with the core profile

as indicated in ^7,12, where p₀ is the central density and r_c is a core radius.

The issue is that the density is oscillating with considerable amplitude as seen in Fig. 4. Nevertheless, the fitting was performed on the density profile when the central density is at a local maximum and at a local consecutive minimum. The fitting parameters results appear in Table I for the projection of p along the x-axis. Notice that the central density changes by a factor between two and three from a minimum to a maximum, whereas the core radius changes by nearly 50%. An example of how the density profile changes in time is illustrated in Fig. 6, where the projection of the density along x is shown at two specific times for y₀ = 10 at a minimum (t = 254) and at a maximum (t = 261).

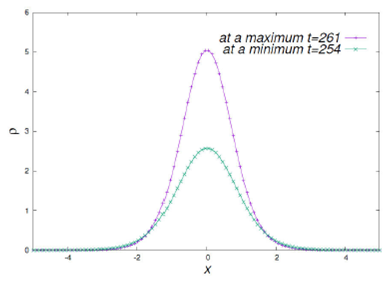
Figure 6 Density profile at two different times for the case p _x0 = 0:1, MR = 1 and y₀ = 10. The dynamics can be seen in the corresponding animation within supplemental material ³². 

In order to have an idea of the physical time scale of these oscillations, we use the recipe in ¹². Considering a boson mass value 2.5 x 10^-22 eV and that core radius of the final configuration is converging to r_c = 1 kpc, using the range of frequencies ν∈(0.084,0.1) from Fig. 5, the period of the density oscillations is in the range T ∼ 0,76 - 0.91 Gyr. If the core radius is considered to be r_c = 0.25 kpc the period is within the range T ∼ 47- 57 Myr.

3.4.Unequal mass case

As described before, the case we look at in detail corresponds to MR = 0.5. The time dependence of M, Q and L_z appears in Fig. 2. General properties are very similar to those of the equal mass case. The loss of mass and angular momentum is smaller when the impact parameter is bigger.

Snapshots of the unequal mass MR = 0.5 merger with y₀ = 7 are presented in Fig. 7. The resulting high density region wobbles around the origin due to the asymmetric distribution of matter and at some point evolves toward the coordinate origin. Animations for other values of the parameters are also shown in the supplemental material ³².

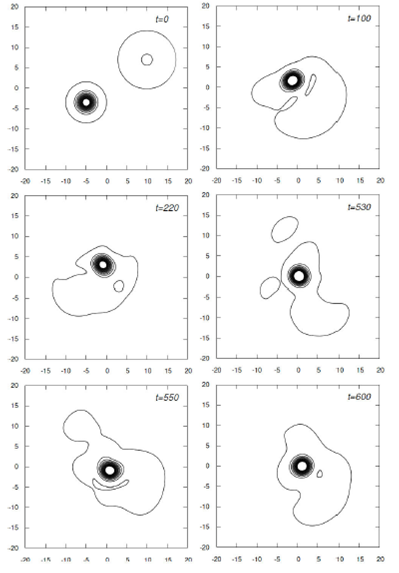
Figure 7 Density isocontours on the xy-plane for the collision for MR = 0:5 with p _x0 = 0:1 and y₀ = 7. 

What is different from the equal mass case is the relaxation process. The evolution of Q = 2K + W and the central value of the density are shown in Fig. 8 for the two extreme values of the impact parameter y₀ =1,10. The value of Q oscillates around zero with amplitude an order of magnitude smaller than in the equal mass case. For density, on the other hand, since the configuration is wobbling around the coordinate origin, instead of tracking the central value of the density we track its maximum value ρmax. The result in Fig. 8 is the generic behavior for the unequal mass cases with values of MR between 0.5 and 1 we experimented with. The highly dynamical behavior is due to the fact that the small configuration with mass M_λ approaches with a higher velocity and the distribution is much less symmetric than for MR = 1. This explains a quick ejection of kinetic energy so that Q acquires small values.

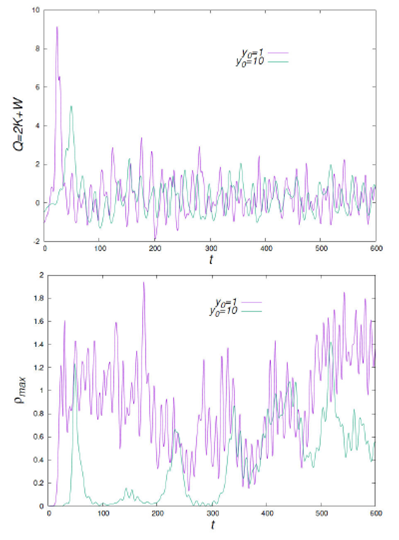
Figure 8 For the case p _x0 = 0:1 and MR = 0:5, we show Q = 2K +W and the maximum value of the density as a function of time for the cases y₀ = 1 and y₀ = 10. 

The density does not show any clear sign of relaxation or a particular dominant mode during the time window used in the simulations. This is perhaps a major obstacle when the density is fitted with a space-dependent density fitting function. Unlike the equal mass case, where the average of the density is a good estimate of the asymptotic value, here the expected value of the central density is uncertain. Nevertheless, Fig. 8 indicates that the central density of the final configuration depends on the impact parameter y₀.