1. Introduction
A significant restriction on quantum devices for information processing and communication is environmental noise. Up to now, the effects of several archetypal quantum operations on a qubit, the depolarizing, phase-damping (or phase-flip), and amplitude damping channels have been studied on different quantum information processing protocols and quantum correlations. They have been widely applied for the implementation of quantum information processing. However, a real quantum system is, in general, influenced by its surrounding environment [1-6]. As a result, the communication accomplished under noisy channels may not be trustable because the receiver may obtain partial or degrade information different from the sender’s information. Studying how decoherence affects quantum correlations has been investigated in several quantum systems [7-12].
Quantum teleportation is an extensively applied principle for quantum information technologies, including quantum communication and quantum computing [13,14]. It is the process in which two spatially separated parties Alice and Bob share an entangled bipartite resource, and Alice transmits the unknown state of a qubit to Bob. If they share a maximally entangled state, then Alice can transmit the state successfully with unit fidelity following some set of protocols. The main problem of quantum teleportation is related to generate nearly perfect entangled states between distant sites. One of the simplest theoretical models in quantum optics is known as the Jaynes-Cummings model [15-19]. It has been used extensively to describe the quantum features of the interaction of a single two-level atom with a single cavity mode. This model has been investigated not only theoretically but also experimentally [18-20]. Many beautiful experiments lead to creating entangled states which are obtained from atom-photon interactions in optical and microwave cavities. Hence, as one of the promising candidates engineering quantum entanglement and quantum channel, the cavity quantum electrodynamics (QED) system has received much attention [21,22]. Entanglement states are useful tools for the implementation of quantum information protocols such as quantum key distribution, quantum teleportation [23,24], super dense coding [23] and quantum computation. Therefore, generating entangled states and keeping them surviving for a long time is an important task. For this aim, many efforts have been devoted to the study of the manipulation of quantum entanglement with atoms and photons in cavities. They have been widely applied for the implementation of quantum information processing. However, a real quantum system is, in general, influenced by its surrounding environment [1-3]. As a result, the communication accomplished under noisy channels may not be trustable because the receiver may obtain partial or degrade information different from the sender’s information.
The study of correlations between quantum systems has received great attention at the beginning of the last century. In the bipartite system, no matter whether it is separable or entangled, one can exploit quantum discord (QD) measures [25] and super quantum discord (SQD) measures [26] for quantifying the quantum correlations. The QD can be described as a difference between classical correlation and quantum mutual information, which is captured by the strong (projective) measurements. When the quantum and classical correlations are the same, QD is zero. It is shown that separable states can be applied to distribute entanglement [27]. It is illustrated that QD is the resource that causes this process feasible and enables entanglement distribution without actually sending an entangled state. Moreover, the measurement of an arbitrary quantum state with using projective measurement will result in coherence loss [1,28-30]. However, the system will be perturbed softly, and may not lose its coherence entirely, if the measurement device couples to the system weakly [31-35]. Weak measurements performed on one of the subsystems can lead to SQD that is always larger than QD. The amount of information extracted using weak measurements can be tunable in some cases. This feature is helpful in protecting quantum entanglement from decoherence [36]. Recently, it was shown that weak measurements also help to protect quantum entanglement from the decoherence [37]. In the present work, we investigate quantum teleportation through noisy channels by creating entangled states between atom and field. We obtain the fidelity of quantum teleportation and quantum correlations as a function of decoherence time. We display that noisy quantum channels always diminish the range of states to be accurately teleported.
The layout is as follows: In Sec. 3, we present the Hamiltonian of the Jaynes-Cummings model and noisy channels. In Sec. 4, we pay attention to the effect of noise on teleported states that have been created using the Jaynes Cummings model. Finally, the main results will be summarized in Sec. 5.
2. Description of the model and noisy channels
In the following we investigate the Jaynes Cummings model of a single-two level atom interacts with a single cavity mode. The Hamiltonian of this system by considering the rotating wave approximation has the form [37,38]:
where ω
0 is the atomic transition frequency, ω is the field frequency and α†(α) is the annihilation (creation) operator,
Let us define the joint atom-field initial states as the following relation:
which the first and second states denote field and atom, respectively. We consider that atom is initially in the excited state |e〉, where Pn = exp(-ˉn/2)√n-n / n! is for a coherent state of mean photon number
where U is the time evolution operator. Using the relation U(t) = exp(- iHt), it can be shown in the atom basis |e〉 and |g〉 and for the case of resonance that it takes the form [39]:
which τ =
The density state of the atom-field is in a 2× ∞ dimensional space. For such states, we are interested in the 2 × 2 systems. By a local action, we project the entire atom-field into a subspace equivalent to 2 × 2 system. Following this protocol in a two-dimensional space, the density operator ρaf = |ψ(t)〉af 〈ψ(t)| is,
where the matrix elements can be written as,
where,
The interaction of a noisy environment with a qubit can be represented by a quantum operation acting only on the Hilbert space associated with the qubit if we use the operator-sum representation formalism. Based on the Kraus operator approach, decoherence channels for a density matrix ρ can be given as [40-43]:
where ε(ρ) represents the evolved state of the system under suitable local decoherence channels and the Kraus operators Ei satisfy the completeness relation:
and I is the 2 × 2 identity matrix. Kraus operators for noisy channels are given by Table I, where 0 ≤ λ ≤ 1 represents the decoherence parameter and expressing the probability of losing a system excitation to the environment. A description of the physical meaning of each kind of noise, as well as its Kraus operators, are given below and we also effects these noisy channels on the teleportation process by using entangled states given by Eq. (6).
Table I Kraus operators for phase flip (PF) channel, amplitude damping (AD) channel, phase damping (PD) channel, and depolarizing (De) channel, where λ represents the decoherence parameter.
| Channel description | Kraus operators |
| PD channel |
|
| AD channel |
|
| PF channel |
|
| PF channel |
|
2.1. Phase damping
A type of noise due to environmental interaction can be modeled as the following phase damping (PD) channel. In this case, the relative phase between the energy eigenstates of the system is lost, decaying the off-diagonal elements of the density matrix of the system. In other words, the loss of quantum information occurs without loss of energy. Substituting Kraus operators of noisy channels given by Table I, and combining Eq. (6)-(8), the elements of the density matrix for the evolution of the PD channel can be represented form X-state as follows:
where
where, ϱ = ρ11 + ρ22 (1 + λ) + ρ33 (1 - λ) + ρ44. The matrix of Eq. (11) has an X structure, which will turn out to be very useful to compute the dynamics of QD and SQD.
2.2. Amplitude damping
Now, we consider the interaction of the system with the amplitude damping channel. A quantum system dissipating energy to (or receiving energy from) its environment-such as an atom losing (or receiving) a photon can be modeled as damping (or amplification) in its amplitude. In this case, the Kraus operators of the amplitude damping channel for a single qubit are given by Table I. Where λ is the probability of decay from upper-level |1〉 to the lower level |0〉. Using Eq. (8) and Table I it is straightforward to find the elements of the density matrix under noise as follows:
2.3. Phase-flip
Another noisy channel is phase-flip channel. The effect of the phase-flip channel is to destroy the information contained in the phase relations without an exchange of energy, which applies ρ to the first qubit with probability 1 − λ and leaves it alone with probability λ. Using the Kraus operators describing the phase flip channel and Eq. (6)-(7), given by Table I, we obtain the elements of density matrix for the phase-flip channel as:
where, α = (κ2 + κ4)(1 - λ) and β = (κ1 + κ5) (1 - λ).
2.4. Depolarizing channel
Finally, we are interested in examining the effect of depolarizing (De) channel on the system. A d-level quantum system under depolarizing channel is depolarized with some probability, i.e., is replaced by the maximally mixed state 1/d with some probability or left untouched. The Kraus operators of depolarizing channel for a single qubit are given by in Table I. The evolved state of the system is governed by the depolarizing channel as follows:
where p is decoherence strength.
3. Noisy teleportation
Teleportation is a critical way of transfer information separated spatially by qubit, which is an unknown state. In this study, we investigate the effect of the cavity Fock state n on the quantum correlation of the teleported state. Let us assume that we have two users, Alice and Bob, who share an entangled state given by Eq. (6). Alice is given pure state ρin = |ψin〉〈 ψin|, where,
where 0 ≤ θ ≤ π and 0 ≤ φ ≤ 2π. Alice aims to send this state to Bob using Eq. (6). The output state can be achieved as follows [44]:
where
where
and
are bell states. Using the computational basis, we replace |n, g〉, |n, +1, e〉 with |00〉, |11〉 and |n + 1, g〉, |n, e〉 by |10〉, |01〉. Therefore, the density operator on Bob’s hand (out state), ρout, is given by:
the elements of this matrix are:
The quality of Bob’s state will be measured in terms of the fidelity and quantum correlations. Fidelity measures how is close the final state, to the initial state which is defined by [45]:
It is a useful indicator of the teleportation performance of a quantum channel when the input state is pure. Since the transported state is pure, the efficiency of quantum communication is characterized by the average fidelity, which describes the fidelity averaged over all possible pure input states in the Bloch sphere formulated as [46]:
If our model is used as a quantum channel for teleporting an entanglement state, Fα can be expressed as:
In a common situation, 0 ≤ Fα ≤ 1, information is distorted to some extent after being transmitted. For quantum communication, Fα can be larger than 2/3, which is the maximum of classical communication so that in order to transmit |ψin〉 with better fidelity than any classical communication protocol, we require the value of Fα to be strictly greater than 2/3.
Let us now investigate what happens if one of the qubits belonging to the quantum channel is also subjected to noise. In the following, we intend to study the effect of local noisy environments on the evolution of teleported states through joint atom-field. Most often, the uncontrollable interaction with the environment leads to decoherence. Studies of decoherence and teleported state dynamics in a quantum system are believed a major subjects in quantum information processing. The following work will investigate how teleported states by the Jaynes-Cummings model are influenced by four different types of noisy channels, such as phase-flip, amplitude damping, phase-damping, and depolarizing channels. In further calculations, using the computational basis, we replace |n, g〉, |n, + 1, e〉 with |00〉, |11〉, and |n, + 1, g〉, |n, e〉 by |10〉, |01〉. To see this matter, we assume that we want to send teleported states given by Eq. (17) to Bob and Charlie through noisy channels.
Considering the Eqs. (11)-(14), we will focus on the dynamics of average fidelity of quantum teleportation, QD and SQD for the obtained states that are presented under named noisy channels. The dynamics of average fidelity for the four different types of noisy channels versus τ and decoherence strength are plotted in Fig. 1. It can be seen that in the phase-damping channel and phase-flip channel, the teleported state can have average fidelity larger than 2/3 in the interval of time [4, 5] for λ → 0 and λ → 1. It is not difficult to find that the teleported state can have the valid average fidelity for the phase damping channel and phase-flip channel, the teleported state has an average fidelity greater than 2/3, for values of the scaled time close to 4.5. In the case of phase damping channel, validity fidelity is independent of the decoherence strength in the interval of time [4,5]. In other words, the dynamics of average fidelity oscillates with time and indicates more robust concerning the noisy of phase damping channel in the interval of time [4,5]. Moreover, the teleported state is not sensitive to any change in this noisy channel for this interval of time. Comparing dynamic properties of the quantum channel and average fidelity leads to an interesting outcome, that the teleported state can be safe against phase damping noise in some interval of times. It is immediately seen that the dynamics of average fidelity declines rapidly to no valid value (average fidelity less than 2/3) and revives increasingly to its initial values in the phase-flip channel (see Fig. 1c) with increasing the decoherence strength in the interval of time [4,5]. Therefore, one can observe that the presence of noise in the channel can lead to a revival of average fidelity. While for AD channel and depolarizing (De) channel average fidelity can not maintain its valid limit with growth decoherence. This indicates that noisy channels are not always destructive and teleported states can be immune against decoherence channel.
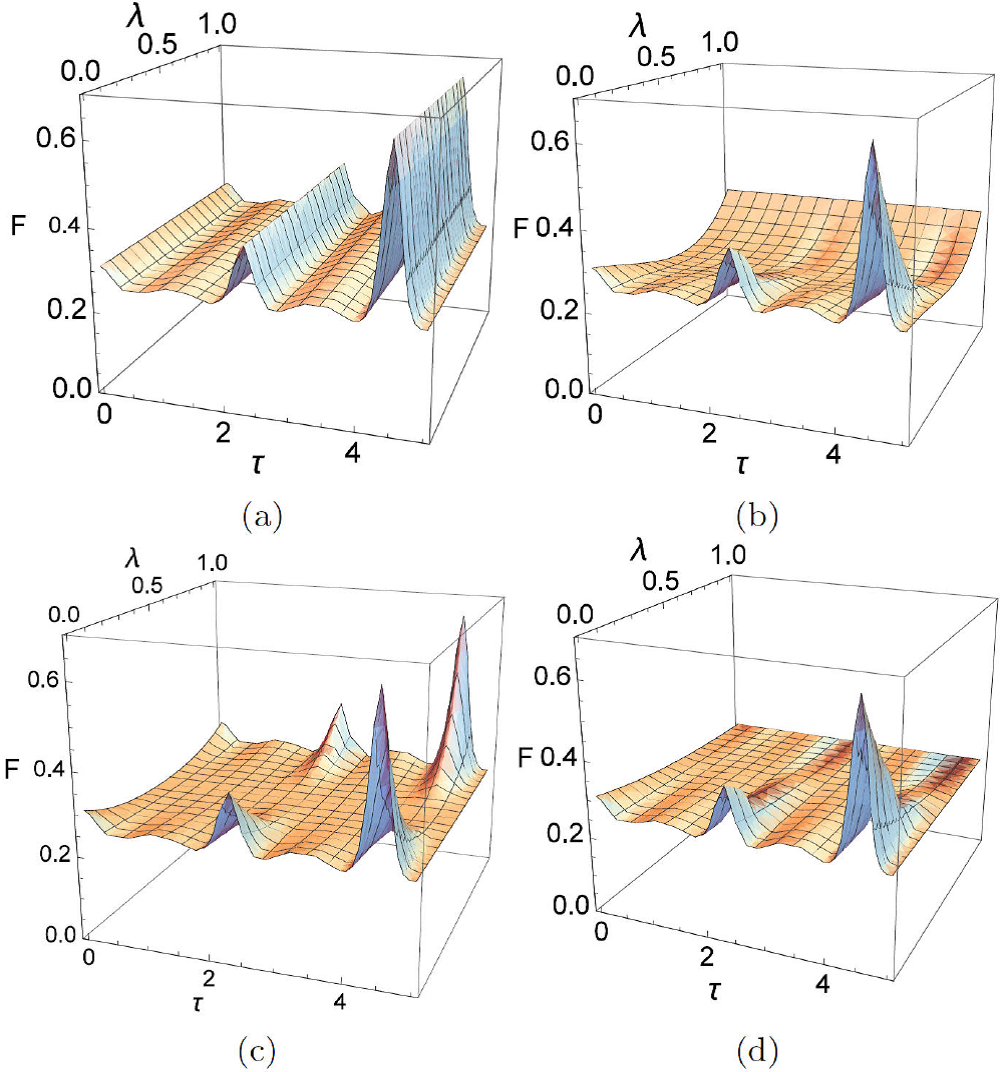
Figure 1 Teleported average fidelity of (a) phase damping channel (b) AD channel (c) phase flip channel (d) depolarizing (De) channel versus scaled time τ and λ with the mean photon numbers n = 2 when the cavity fock states are n = 2 for φ = θ = π/2.
In the following, we are interested in comparing the dynamical properties of the quantum correlation of the channel with average fidelity. The matrix of Eq. (18) has an X structure, which will turn out to be very useful to compute the dynamics of QD and SQD. For different channels, we plot simultaneously QD, SQD and average fidelity of the teleported state in terms of τ for λ = 0.01with cavity Fock state n = 2 and given n¯ = 2, in Fig. 2 and Fig. 3. They show that the degree of quantum correlation for the teleported state which is generated in the interval of time [0,5]. Figures indicate that for some intervals time average fidelity has not a valid value. However, in this case, the QD and SQD can still capture correlation for the teleported state. Also, despite the lack of QD and valid value for fidelity for some intervals time, we still have the SQD (see Fig. 3). A noteworthy point, in this case, is that quantum correlations (especially SQD) are more robust than average fidelity against the decoherence channels.

Figure 2 Teleported average fidelity (Purple, Dashed), quantum discord (red, solid) and super quantum discord (green, dashed) of the atom-field (a) phase damping channel (b) AD channel (c) phase flip channel (d) depolarizing (De) channel versus scaled time τ versus scaled time τ with the mean photon numbers n = 2 when the cavity fock states are n = 2 for λ = 0:02 and φ = θ = π=2.
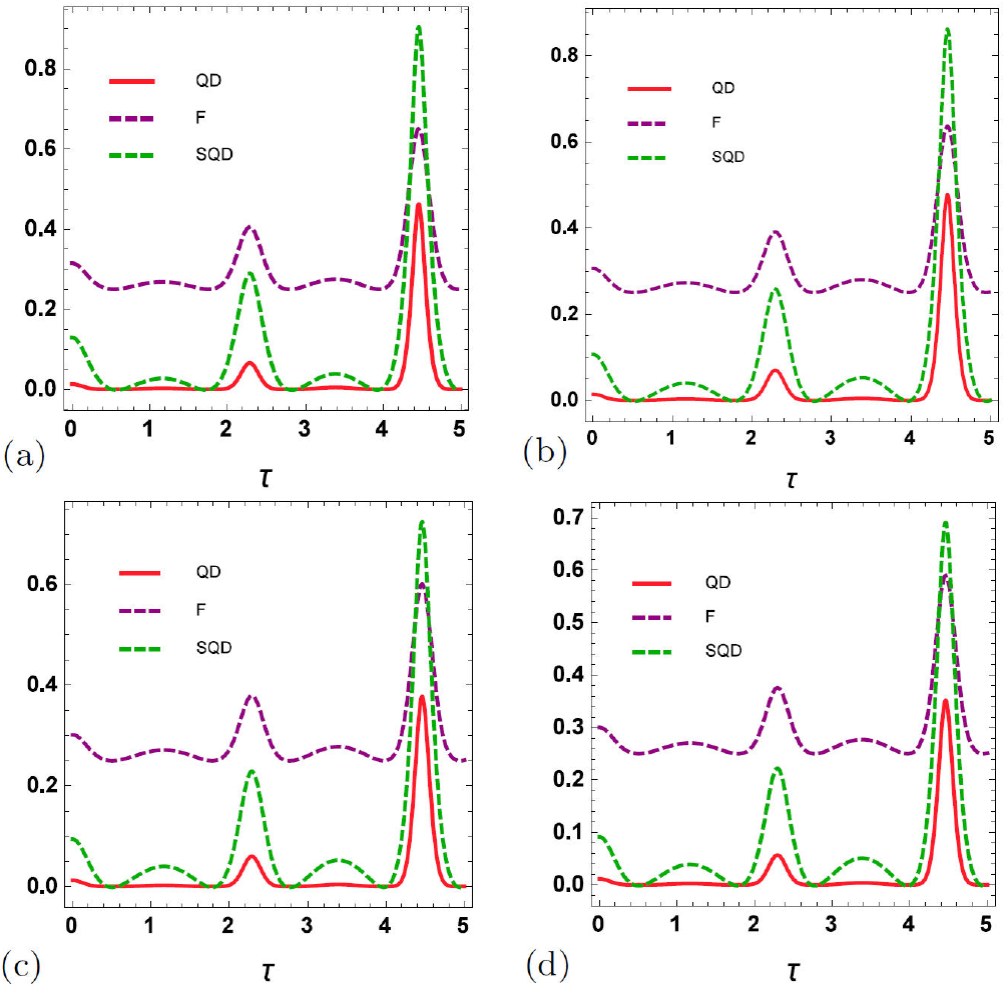
Figure 3 Teleported average fidelity (Purple, Dashed), quantum discord (red, solid) and super quantum discord (green, dashed) of the atom-field (a) phase damping channel (b) AD channel (c) phase flip channel (d) depolarizing (De) channel versus scaled time τ versus scaled time τ with the mean photon numbers n = 2 when the cavity fock states are n = 2 for λ = 0:02 and φ = π/2; θ = π=4.
In the following, we are interested in comparing the dynamical properties of the quantum correlation of the channel with average fidelity. The matrix of Eq. (18) has an X structure, which will turn out to be very useful to compute the dynamics of QD and SQD. For different channels, we plot simultaneously QD, SQD and average fidelity of the teleported state in terms of τ for λ = 0.01 with cavity Fock state n = 2 and given n¯ = 2, in Fig. 2 and Fig. 3. They show that the degree of quantum correlation for the teleported state which is generated in the interval of time [0,5]. Figures indicate that for some intervals time average fidelity has not a valid value. However, in this case, the QD and SQD can still capture correlation for the teleported state. Also, despite the lack of QD and valid value for fidelity for some intervals time, we still have the SQD (see Fig. 3). A noteworthy point, in this case, is that quantum correlations (especially SQD) are more robust than average fidelity against the decoherence channels.
4. Conclusions
The effects of quantum noise on the quantum correlations of teleported states generated by atom and photon interaction are analyzed. We calculated the QD, SQD, and the average fidelity of quantum teleportation subject to various types of noises during the teleportation. We examined the range of states that can be accurately teleported. Among states to be teleported, the phase damping channel and depolarizing (De) channel are less sensitive to the noise. So that, average fidelity is smaller than that of ideal one in all intervals of time. While, quantum correlations generated by the Jaynes-Cummings model when subjected to phase damping channel and phase flip channel, as decoherence starts and increases, teleported states are immune to the quantum noise. The average fidelity of values larger than 2/3 in a certain interval of time may be one representation indirectly showing how the teleportation process is possible under these channels. Therefore, we found the dependence of the average fidelity and quantum correlations on the type of noise affecting the quantum channel. On the other hand, if the noisy quantum channel is described by a phase damping channel and phase
flip channel, the average fidelity is always greater than the value of 2/3, the best possible value that can be obtained only by the classical communication. Also, quantum correlations of teleported states and average fidelity comparisons showed that quantum correlations were more resistant to noise than average fidelity.











 text new page (beta)
text new page (beta)


