1. Introduction
Spontaneous imbibition is the main mechanism of enhanced oil recovery in many subterranean reservoirs, particularly on those where water injection technology is used. Since the classical approach of Lucas-Washburn [1,2], who established that the liquid travel distance (x) in a capillary tube is proportional to the square root of time (√t); extensive theoretical and experimental studies have been performed to understand the imbibition phenomena. Based on experimental data of imbibition in paper [3,4], textile [5], glass beads [6], and berea [7] it was shown that the wetting front rises as [5,8]
Being 0.25 ≤ m ≤ 0.5 the scaling exponent and Ω is a constant that is linked to porous media and liquid properties and interactions. The range of m matches with the analytical approach of [9], x∝t 1/2dτ , where d τ is the fractal dimension of flow tortuosity (see [10] for a quick review) in capillary tubes with fractal path [11]. The exact value of m can be found using the fractal theory as an analysis tool. It depends on the intrinsic topology of individual porous medium.
The scaling exponent of the relationship between recovery by spontaneous imbibition x and the production time t by permeable materials possesses a fractal architecture and is characterized as [12]
with the value of the Hausdorff dimension of the porous medium satisfying d t < d Ⱨ < d e , where d t is the topological dimension and d e is the embedded dimension of the fractal object. Notice that the scaling exponent given in Eq. (2) is presumed to be applicable on imbibition processes. Hence, it is employed to fit data of field measurements.
However, there is a set of dimension numbers that describe the scaling properties of a fractal domain, see for example [13-16] and references therein. Accordingly, authors of [17] have introduced a new dimension number d tⱧ termed the topological Hausdorff dimension, in order to further characterize the fractal geometry.
Besides, it is frequently supposed that the “Hausdorff dimension” is equal to the “topological Hausdorff dimension” [12,18]. But, it has been proved that for path-connected fractals,
Thereupon, this manuscript has as a main aim to theoretically verify Eq. (2) and the assumption that d Ⱨ = d tⱧ for infinitely ramified fractals in imbibition studies. These imbibition studies were performed on samples of deterministic fractals (Menger sponge and Cantor Tartans), which are exactly self-similar fractals. It was found that the liquid travel distance through the pre-fractal network is a topological Hausdorff dimension function rather than a Hausdorff dimension function. This contradicts the assumption that the Hausdorff dimension and the topological Hausdorff dimension always have the same value. Consequently, we argue that the penetration of the fluid on fractal porous media by spontaneous imbibition is governed by the topological Hausdorff dimension. Analytic results are brought to comparison with previous experimental works in order to validate the proposed imbibition model.
The structure of this paper is as follows. In Sec. 2 the fractal theory and the basic tools required are reviewed. Details of the material and methods used are described in Sec. 3. Section 4 is devoted to describe illustrative examples and some physical implications are discussed. Section 5 finishes the paper with conclusions.
2. Theoretical considerations
In what follows, some basic tools and properties of spontaneous imbibition in porous media with fractal porosity are recalled (for review, see [10-12] and references therein).
2.1. Naturally fractured subterranean reservoirs
Many naturally fractured reservoirs exhibit fractal features. The complex network of pores possesses scale invariance over a lot of length scales. Suchlike a pore space can be similar to pre-fractal, e.g., Cantor Tartan and Menger sponge.
2.2. Fractal model of spontaneous imbibition
The oil production rate q by spontaneous imbibition can be expressed as dx/dt, from Eq. (1):
considering the fractal model proposed in [19] for the production rate
and relating Eqs. (3) and (4), the Eq. (2) is obtained. So, Eq. (1) can be written as a function of the Hausdorff dimension of the porous medium and the Li-Zhao’s fractal-model to predict spontaneous imbibition in porous media is obtained [12]
here, 2 < d Ⱨ < 3 describing the heterogeneity of porous rock. It is a straightforward matter to understand that if 0.5 < d Ⱨ < d e , the behaviour of Eq. (5) may be inconsistent with the physical situation. In this regard, it is pertinent to mention that the scaling exponent from Eq. (5) was questioned in [10,20].
2.3. Topological Hausdorff dimension
On the other hand, authors of [17] proposed a new dimension number, the well-celebrated topological Hausdorff dimension d tⱧ that provides a further insight into the geometry of path-connected fractals.
The value of the topological Hausdorff dimension quantifies the ramification of a fractal and its transport properties. Such that, for totally disconnected fractals d tⱧ = 0; for path-connected but finitely ramified fractals d tⱧ = d t = 1 and for infinitely ramified fractals d t < d tⱧ < d Ⱨ (for details see [16,21-23]).
Generally, the topological Hausdorff dimension is
Regarding the imbibition rate in a fractally permeable medium in [16] was established that it is controlled by its fractal ramification, characterized by d tⱧ , rather than the corresponding Hausdorff (mass fractal) dimension d Ⱨ > d tⱧ . So, Eq. (5) can be rewritten as
differentiating Eq. (7) with respect to time t, the recovery rate for a porous medium with fractal porosity considering its topological Hausforff dimension, results in
2.4. Topological connectivity dimension
It is known that d Ⱨ and d tⱧ are defined with respect to the Euclidean metric L in the embedding Euclidean space. Nevertheless, there always exists the geodesic metric associated with the fractal topology [24,25], characterized by the connectivity dimension d Ɩ , which is independent of the embedding [25]. It allowed to introduce the topological connectivity dimension d tƖ to the authors of [15], in order to characterize the fractal mass with respect to the geodesic metric Ɩ min , where d tⱧ ≤ d tƖ ≤ d Ɩ (for further details see [15]). It is relevant to note that when the geodesic and Euclidean metrics are equivalent Ɩ min ∞L, the Hausdorff and connectivity dimensions are equal d Ⱨ (F) = d Ɩ (F), implying that d tⱧ (F) = d tƖ (F). Resulting in the possibility of writing Eq. (7) as:
2.5 Deterministic fractals with known scaling properties
The imbibition processes were performed on fractal objects as a physical representation of core samples with exact fractal parameters such as Menger sponge and Cantor Tartans.
The Menger sponge Μ is a three-dimensional generalization of the Cantor set C. It is constructed starting from a unit cube [0,1]3 which is divided into n × n × n sub cubes of equal size, after that, the interior of m 3 sub cubes is deleted and so on. The Hausdorff dimension of the Menger sponge is given by
and its topological Hausdorff dimension is [17]
where d Ⱨ (C) is the Hausdorff dimension of the corresponding Cantor set C. The Cantor Tartan CT is a fractal recently introduced by authors of [26,27]. It is established in ℜ3 as a union of three orthogonal Cartesian products (C × C ) × [0,0,1], (C × C ) × [0,1,0], (C × C ) × [1,0,0]. It constitutes a special class of infinitely ramified fractals, where its Hausdorff dimension is equal to its topological Hausdorff dimension:
In order to solve Eqs. (10) and (11) one must know the Hausdorff dimension of the corresponding Cantor set C.
Note that the three-dimensional Cantor set generalization is a fractal dust with totally path-disconnected [28], but the Cantor Tartan is a path-connected fractal, as it is shown in the following figures.
For the case of the Cantor middle sets its Hausdorff dimension is defined as:
For another special cases of Cantor sets see [29].
With the aim of construct three-dimensional fractals with d Ⱨ similar to the core samples experimentally studied in [12] and in order to validate the theoretical model proposed, we use the Cantor set shown in Fig. 1 (a), where n = 9 and m = 5 as the corresponding Cantor set of the Menger sponge, this for the modeling of Geyser’s rock core sample.
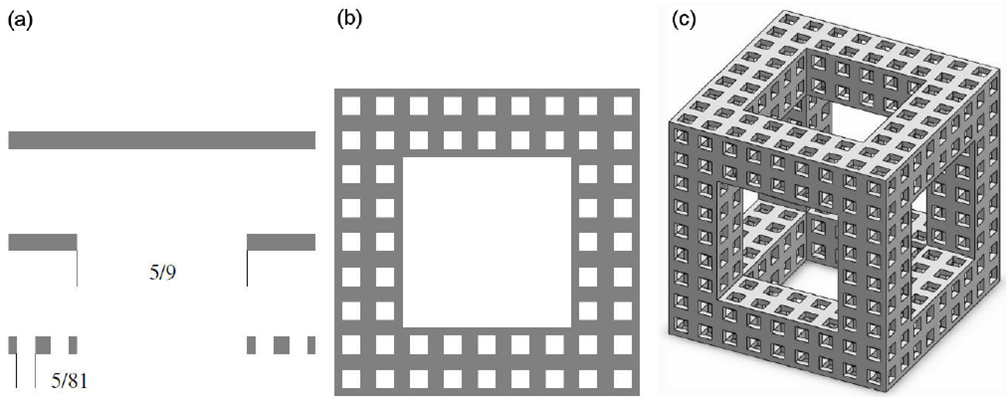
Figure 1 Generation process of Menger sponge. (a) Cantor set. i = 0; 1; 2, (b) Sierpinksi carpet. i = 2, (c) Menger sponge. i = 2.
For the modelling of the Glass bead core sample, the Cantor Tartan (CT) is constructed with the generator from the corresponding Cantor set (n = 13 and m = 9) drawn in Fig. 2 (a) of [29].
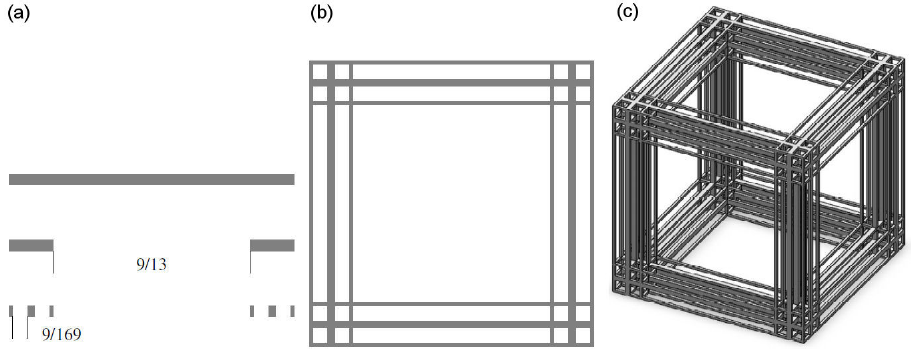
Figure 2 Generation process of Cantor Tartan CT 1. (a) Cantor set, i = 0; 1; 2, (b) Two-dimensional Cantor Tartan, i = 2. (c) Three dimensional Cantor tartan (CT 1), i = 2.
Now for the modeling of the Berea sandstone core sample, the Cantor Tartan (CT 2) depicted in Fig. 3 is a generalization to the three-dimensional Euclidean space of the Sierpinski carpet given in the Fig. 2 (b) of [16].
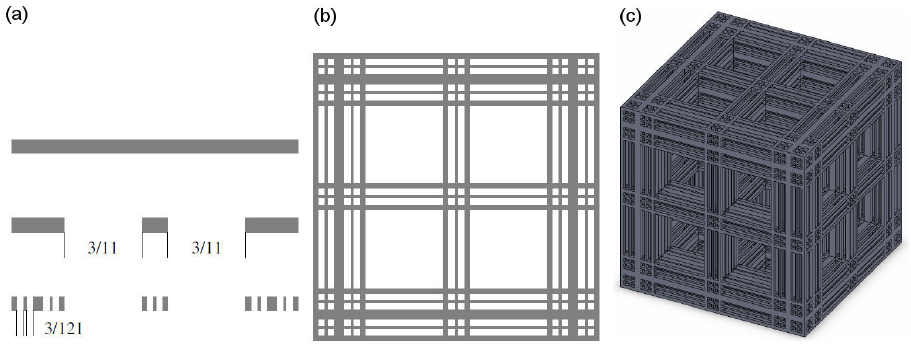
Figure 3 Generation process of Cantor Tartan CT 2. (a) Cantor set, i = 0; 1; 2, (b) Two-dimensional Cantor Tartan i = 2, (c) Three dimensional Cantor tartan CT 2, i = 2.
Finally for the modeling of the Chalk core sample, the Cantor Tartan (CT 3) (see Fig. 4), is constructed in a similar way as (CT 2), where its correspondent Cantor set has d Ⱨ = In4/In7 [29]. All the values of the dimension numbers of these fractals are given in Table I. Fractal data of core samples are taken from [12,18].
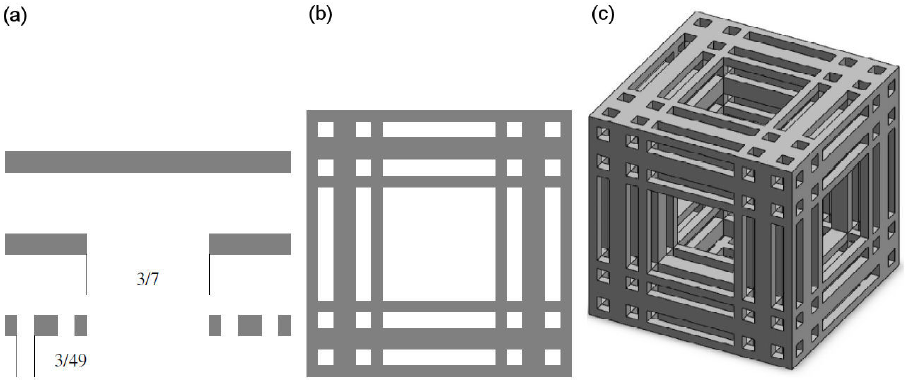
Figure 4 Generation process of Cantor Tartan CT 3. (a) Cantor set i = 0; 1; 2. (b) Two-dimensional Cantor Tartan i = 2, (c) Three-dimensional Cantor tartan CT 3 i = 2.
Table I Fractal parameters and scaling exponents for Menger sponge, Cantor Tartan, and core samples.
| Fractal matrix | Dimension numbers | ||||||
| dt | dⱧ | dtⱧ | de | m | dⱧ(C) | dtU | |
| Cantor Tartan CT1 [16,26] | 1 | 2.08 | 2.08 | 3 | 0.08 | 0.54 | 2.08 |
| Glass bead packa [12] | 1 | 2.07 | 2.07 | 3 | 0.07 | - | 2.07 |
| Cantor Tartan CT2 [16,26] | 1 | 2.15 | 2.15 | 3 | 0.15 | 0.57 | 2.34 |
| Berea sandstonea [12] | 1 | 2.16 | 2.16 | 3 | 0.16 | - | 2.16 |
| Cantor Tartan CT3 [16,26] | 1 | 2.42 | 2.42 | 3 | 0.42 | 0.71 | 2.42 |
| Chalka [12] | 1 | 2.40 | 2.40 | 3 | 0.40 | - | 2.40 |
| Menger sponge M [30,31] | 1 | 2.60 | 2.26 | 3 | 0.26 | 0.63 | 2.26 |
| The Geysers rockb [12] | 1 | 2.60 | - | 3 | 0.60 | - | - |
a Similar to the Cantor-Tartan geometry.
b. Menger-sponge-like.
3. Materials and methods
This section presents the physical models of naturally fractured reservoirs where the previous equations are applied.
3.1. Materials
All of the theoretical parameters of the fractals defined in the previous section are given in Table I. The process of spontaneous imbibition is carried out with gas-water displacement in materials taken from [12,18].
3.2. Methods
The expressions given in Eqs. (7) and (8) have analytical solutions. This implies that they can be solved when the boundary conditions and the fractal parameters are given to be applied. The topological Hausdorff dimension is determined by Eq. (10) and (11) for Menger sponge and Cantor Tartans, respectively or it can be calculated by many estimation methods of fractal dimension (see [32-34]).
4. Results and discussions
The objective of this section is to discuss some physical implications of the phenomenon under study based in the results found.
4.1. Analytic findings
Figure 5 shows the liquid travel distance on Cantor Tartan fractals. The behaviour is in accordance with previous results published in literature and described with Eqs. (1) and (5). The discrete data is from experimental results of tests conducted on the core samples published in [12].
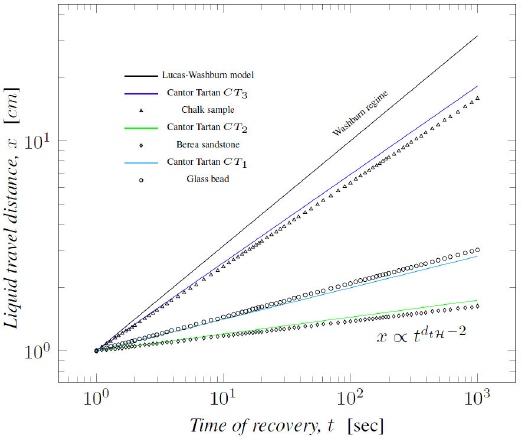
Figure 5 Liquid travel distance versus imbibition time in Cantor Tartan (d tH = d H ) and core samples.
The results obtained for Cantor Tartans from Eq. (8) are in agreement with the experimental data given in previous reports as it is shown in Fig. 6. Representing the recovery rate q by spontaneous water imbibition versus time production, the linear curves enact the theoretical results of different versions of the Cantor Tartan; depicted with green, cyan and blue lines (see Table I). Meanwhile, the rest of the curves are experimental test results given in [12,18]. The core samples heterogeneity is similar to path-connected fractals, whose topological Hausdorff dimension is equal to its Hausdorff dimension.

Figure 6 Comparison of theoretical water imbibition rate and experimental test in Cantor Tartan and core samples, respectively, where d tH = d H .
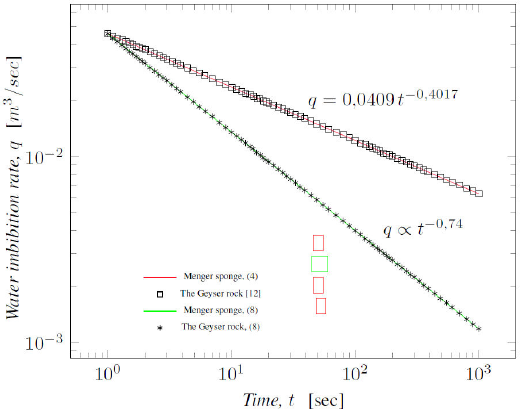
The Fig. 7 presents the imbibition process behaviour on Menger sponge fractal. It has two different curves; on one hand, the curve depicted in topological Hausdorff dimension function (d tⱧ ) is the olive one; on the other hand, the liquid travel distance graph obtained with the Hausdorff dimension function (d Ⱨ ) is the red one.

Figure 7 Liquid travel distance versus imbibition time in Menger sponge (d tH < d H ) and core samples.
The recovery rate (q) by spontaneous water imbibition shown in Fig. 8 (green and red lines), is a characterization of the curves describing the Menger sponge behaviour with both dimension numbers d tⱧ and d Ⱨ according to Eq. (8). The recovery behaviour in Geyser rock core sample (squares) from experimental tests is also shown, as well as the theoretical approach (stars) using the dimension number d tⱧ rather tan d Ⱨ for Geyser rock.
4.2. Discussions
In the Fig. 5, the scaling exponent of the curves is in topological Hausdorff or Hausdorff dimension function, since d tⱧ = d Ⱨ is true for all Cantor Tartans. Their upper and lower cut-off being 2 < d tⱧ < 0.5. The slopes obtained with Eq. (7) on Cantor Tartan fractals match with those obtained on core samples [12].
The physical behaviour of spontaneous imbibition is well-described when the time scale is a topological Hausdorff dimension function (olive curve in Fig. 7). If the imbibition is computed with the Hausdorff dimension a physical inconsistency is obtained (red color data). The value of m is greater than the Washburn regime. The slope found with Eq. (7) on the Menger sponge fractal is in accordance with the physical situation, and this is attributed to the introduction of the topological Hausdorff dimension in Eq. (2).
The results found with Eq. (8) are in agreement with experimental results given in a previous report as shown in Fig. 6 on the Cantor Tartan. Also, the Fig. 8, presents a curve in green color that is the real rate recovery q on the Menger sponge (obtained with d tⱧ ), while the curve in red color is a non-consistent behaviour (obtained as a d Ⱨ function).
In this regard, we argue that the Geyser’s rock core has a fractal structure very similar to the Menger sponge shown in Fig. 7 with the topological Hausdorff dimension of d tⱧ ≈ 2.26.
The time scaling exponent on Eq. (1) is in d tⱧ function rather tan in d Ⱨ function as is depicted in graph of previous figures. The behaviour found in this paper is in agreement with the reported results in [12]. These results validate the model proposed in Eq. (7). Even the apparent physical inconsistency plotted in Fig. 7 from [12] can be explained by Eq. (8); in this regard, it is not difficult to see that d tⱧ < d Ⱨ becomes true for the Geyser’s sample, similar to the Menger sponge; meanwhile the rest of the samples from [12] have a behaviour as an infinitely ramified fractal network Cantor-Tartan-like, where d tⱧ = d Ⱨ .
We would like to point out that the proposed model in [12] is a particular case of our model given in Eq. (7) that can be applied when the porous media have d tⱧ = d Ⱨ .
Nonetheless, the time scaling exponent m can take another forms, depending on the fractal structure F. Such that when d Ⱨ (F) = d l (F), i.e. Menger sponge and Cantor Tartan, the liquid travel distance is computed by Eq. (9).
It is known that d tl characterizes the fractal mass in regard of the geodesic metric [15], consequently, only for Cantor Tartans, d Ⱨ (F) = d l (F) = d tⱧ (F) = d tl (F) holds, and the liquid travel distance is obtained by Li-Zhao model, given in Eq. (5).
Ultimately, if 1 ≤ d Ⱨ (F) < 2 for lineal deterministic finitely ramified fractals, i.e. Koch curve, Mikonswki sausage, and time series type functions see [9,11] and references therein, Eq. (1) can be written as the Jianchao Cai model x = Ωt 1/2dτ [9,35,36].
In this theoretical approach of spontaneous imbibition in actual fluid-rock systems and simulated fractal structures, we can establish the following:
The generalized equation proposed to describe the imbibition processes given in Eq. (7) is modeled using the fractal ramification d tⱧ [16,17], which quantifies the interconnected pores and channels network in a porous medium (fluid-rock system), rather than using the Hausdorff dimension d Ⱨ (also simply called the fractal dimension d f ) that quantifies the fractal mass, as the classic fractal model does.
The fractality of Eqs. (5), (7) and (9) is bounded to a range of time scales, where the lower cutoff is when the initial contact between the water reservoir and the porous medium occurs (t = 0), and the upper cutoff is characterized by the instant in which the equilibrium height on spontaneous imbibition is reached (t = t eq ) [11].
5. Conclusions
In this work it has been put forward the analytic expression
The topological Hausdorff dimension allows further characterization of the transport properties of flow on infinitely ramified fractals. The time scale m = d tⱧ - 2 is a generalized model that can be employed for modeling spontaneous imbibition in naturally fractured reservoirs, even when the real medium has d tⱧ ≠ d Ⱨ .
Illustrative examples of spontaneous imbibition in Menger sponge and Cantor Tartan using the proposed model were presented. Specifically, the Menger sponge and the Geyser rock are well-described using the topological Hausdorff dimension given in (8), instead of using the Hausdorff dimension, (4). Results obtained are in agreement with the previously reported findings on fractal calculations by Li and Zhao.
This results provide a more detailed description of the physical phenomena of the spontaneous imbibition in fractal matrix with complex porosity using another dimension number that characterize the fractal structure.











 nueva página del texto (beta)
nueva página del texto (beta)