1. Introduction
Polyethylene (PE) is a thermoplastic material used in various products such as plastic bottles, shopping bags, toys, plastic tubes, kitchen utensils, insulating layer of coaxial cables, etc. and is obtained from the polymerization of ethylene with different kinds of techniques. PE is a polymer half permeable, light, elastic, durable to the chemical effects, easily produced, and its color is close to white. Chemical formulation of PE is (C n H4) n , here n represents the degree of polymerization. PE was discovered coincidentally in the 1930's. PE, was obtained under very high pressure at the beginning, has been obtained under lower pressure in the following years and has become the most widely used plastic material in the world today. The transparency of PE is in direct proportion to the density. Low-density polyethylene (LDPE) and high-density polyethylene (HOPE) have a density between 0.90 - 0.94 g/cm3 and 0.94 - 0.97 g/cm3 respectively [l].
PE based structures are well-known materials for the application of shielding radiation in space technologies be- cause of their high content of hydrogen [2]. PE material has been chosen by NASA as the reference material for the accelerator-based radiation test of multi-functional composites being developed [3]. PE-boron carbide composites have been produced using standard polymer techniques and their radiation shielding properties have been studied by Harrison et al. [2]. They have compared this new produced composite material with HOPE material and have also concluded that PE-boron carbide composites are very important for the application of space radiation shielding. Monte Carlo simulations of radiation shielding properties of polyethylene materials have been performed by Guetersloh et al. While making Monte Carlo calculations, they have also simulated the flux of galactic cosmic rays (GCR) [3]. Toe first space test results about the radiation shielding performance of Kevlar have been explained by Narici et al. and they have concluded that Kevlar has comparable radiation shielding performance with PE [4].
Different kinds of radiation permeability, attenuation coefficients, and half-value thicknesses are the subject of many studies for the PE which has such a wide usage area from daily life to space technologies [5-10]. Toe transport of beta particles from PE and its derivatives also have been investigated in different studies. The relation between the number of beta particles passing through different thicknesses of PE material and energy distribution of beta particles have been determined by Yalçim et al. Thus, they have developed a method that can find the unknown thickness of an absorber material by using the energy distributions of beta particles [11]. The number of particles passing through the polymer composite materials have been measured experimentally by Al-Rawi and linear attenuation coefficients have been calculated [12]. The relationship between the obtained linear attenuation coefficients and absorber thicknesses has also been investigated. The mass attenuation coefficients by examining the beta particle transition experimentally from poly vinyl chloride materials have been determined by Alshabander and Jaafer [13]. The attenuation coefficients and the transport of beta particles have been investigated with many methods for different absorber materials like Al, Cu, Au, Pb, Ag, Bakelite, Plexiglas, etc. [14-19].
In our previous works [20,21], the absorption of beta particles in aluminum absorbers using different beta sources has been investigated experimentally. Toe attenuation coefficients and half-value thicknesses of aluminum absorbers have been measured. An inconsistency has been observed between the experimental results for half-value thickness and values obtained from the standard attenuation equation. To avoid this inconsistency, the standard attenuation equation has been redefined and solved with the help of fractional calculus. New fractional half-value thicknesses have been obtained equivalent to the experimental half-value thicknesses for around 0.3 value of the order of fractional derivative for all beta sources.
In this work, we have investigated the absorption of beta particles from PE materials for 99 Tc, 147Pm, 137Cs, 2º4Tl, 210Pb and 36 Cl beta sources theoretically and experimentally. The attenuation coefficients and half value thicknesses of PE materials have been measured and calculated. It has been seen that there is no agreement between half-value thick- nesses which is obtained from standard attenuation equation and experimental ones. To overcome this inconsistency be- tween experimental and theoretical half-value thicknesses for PE absorber, the fractional attenuation equation was obtained from our previous work [20, 21] and its solution has been used. As with the same aluminum absorber, even if different beta sources are used also for PE absorbers, the experimental and fractional half-value thicknesses have been obtained almost equivalent to around 0.3 value of fractional derivative order.
2. Fractional attenuation equation
The range of charged particles in absorber material depends on the type of the particle, the structure of the material and the energy of the particle. When a heavy charged particle collides with an electron it scatters with a negligible angle, but if a beta particle collides with an electron in material, it scatters sharply. While the heavy particles move through in the material have almost a linear way, beta particles follow irregular trajectories. Because of the process of energy losing or interactions with the material of beta particles that influence to the absorber material are different from each other, the distance of each beta particle in the material is different from each other. The distance of a beta particle in a material is generally longer than the average range of the beta beam. Therefore, it is hard to define a clear range for a single beta particle. Instead of this, an average range can be calculated from the dependence of the number of beta particles entering the material to the thickness of the material. For this aim, the intensity of beta radiation is considered as a function of the distance of the beta particles within the material [22].
When beta particles pass through a material, some of them are absorbed. The absorption rate of particles depends on both the energies of the particles and the thickness of absorber material. The relationship between the intensity of the beta particle and the thickness of absorber material as follows [23]:
where I(x) is the intensity of beta particle, µm is the mass attenuation coefficient and x is the thickness of absorber material. The standard solution of this equation is
where, 1 0 is the intensity of beta particles before they are absorbed by the absorber material. The half-value thickness of absorber material is the absorber thickness that required to halve the initial intensity of the beta particle and is defined as
Standard attenuation equation, Eq. (1), is defined as an exponential behavior corresponding to the average trend of the observations. The solution of the standard attenuation equation corresponds to a simple idealization of the physical process and defines an average over the spectrum of attenuation coefficients. For a more realistic description, also processes of energy losing of beta particles must be taken into account. In standard approximation, experimental results cannot be predicted as theoretical because of the energy losing of beta particles are not involved to the calculations. We have observed that, theoretical half-value thicknesses have been obtained from Eq. (1) and experimental half-value thicknesses of absorber material are different from each other in our previous studies examining the interaction of beta particles with aluminum absorbers [20,21]. We have used fractional calculus to avoid this inconsistency in these works. Thus, the energy loss processes of beta particles have been also included in the calculation.
Research and detailed information about fractional calculus and its application in science and engineering can be found in the literature such as electric circuits, quantum mechanics, statistical physics, and nuclear physics [24-33]. There are many definitions of fractional derivatives or integrals in literature [34-37]. The most common ones are Grünwald-Letnikov, Riemann-Liouville (RL) and Caputo. Caputo fractional derivative definition is commonly used in the solution of differential equations and applications in physics. Although the RL fractional derivative operator plays an important role in fractional mathematics, it is not as useful as the Caputo fractional derivative operator in modeling physical systems. When solving a fractional differential equation, it is important to use boundary values and initial conditions to describe and analyze the system. The use of the RL derivative operator for this purpose is not suitable for a physical approach. However, the derivative of a constant that can be used as the initial condition according to the derivative definition of RL is not zero. The Caputo fractional derivative has been used to address the fractality (non-locality) of the medium. Thus, it has been aimed to define fractality by fractional derivative operators. The important thing is not the kind of definition of the fractional derivative operator, but also to be able to model the fractal-like paths of beta particles as they pass through the material and correlate their physical meaning. Caputo fractional derivative is defined as,
Here, m is positive integer, a is the order of the fractional derivative, r is the gamma function, Dg is Caputo derivative operator, and f (t) is a time variable function that can be integrated over [a, b] e R.
If Eq. ( 1) is redefined using Caputo fractional derivative,
is obtained. By using the Laplace transform and properties of the Caputo fractional derivative, the solution for the equation above is found to be
The details of this solution were given in our previous work [20, 21]. Equation (7) is a solution of fractional attenuation equation defined with Eq. (5). Here,
is the Mittag-Leffier function. Fora = l,E 1(z) = exp(z) is obtained.
3. Experimental results and calculations
The experiments have been made in the Nuclear Research Laboratory of Physics Department of Kütahya Dumlupmar University. 99 Tc, 147Pm, 137 Cs, 2º4TI, 210Pb, and 36 Cl beta sources have been used and their properties have been given in Table I. The measurements have been taken with a 11.25 x 3.5 Geiger-Müller (GM) Paseo SN-7970A probe has a 2 mg/cm2 mica window device. During measurements, the different PE absorbers with a thickness of 9.6 mg/cm to 14.1 mg/cm2 and dimensions 7 x 7 cm have been used. The properties of used absorbers have been given in Table II. The distance between absorber materials and beta sources is 2 cm and also the distance between the counter and sources is 4 cm. The corrections of dead time and background have been added to the results.
TABLE I Properties ofbeta sources used in experiments.
| Sources | Emax (keV) | Activity (µCi) | Half-life (year) |
| 99Tc | 294 | 0.01 | 2.13 X 105 |
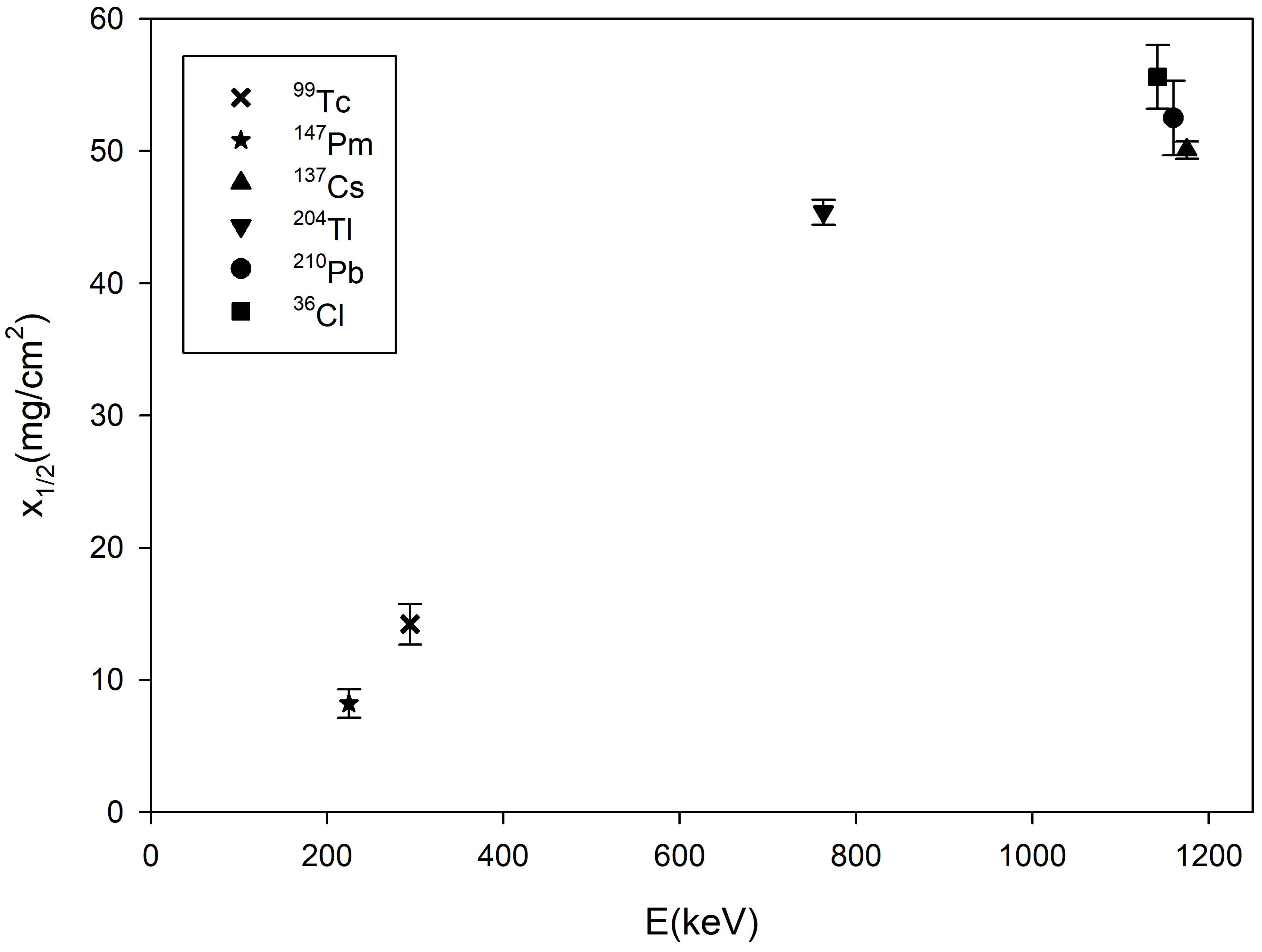
| 147pm | 225 | 0.01 | 2.62 |
| 13 7c s | 1175 | 1.0 | 30.2 |
| 204Tl | 763 | 1.0 | 3.78 |
| 2 10Pb | 1160 | 0.01 | 22.3 |
| 36Cl | 1142 | 0.01 | 3.01 X 105 |
TABLE II Properties of the PE absorber.
| Absorber | Density (g/cm3 ) | Element | weight (%) |
| H | C | ||
| Polyethlene | 0.92 | 14.4 | 85.6 |
In Fig. 1, experimental results that give the intensity of beta ray on the detector screen corresponding to change of absorber material thickness are shown. Initial beta intensity values, half-values of beta intensity, and half-value thicknesses of PE absorber obtained from Fig. 1, have been given in Table III.
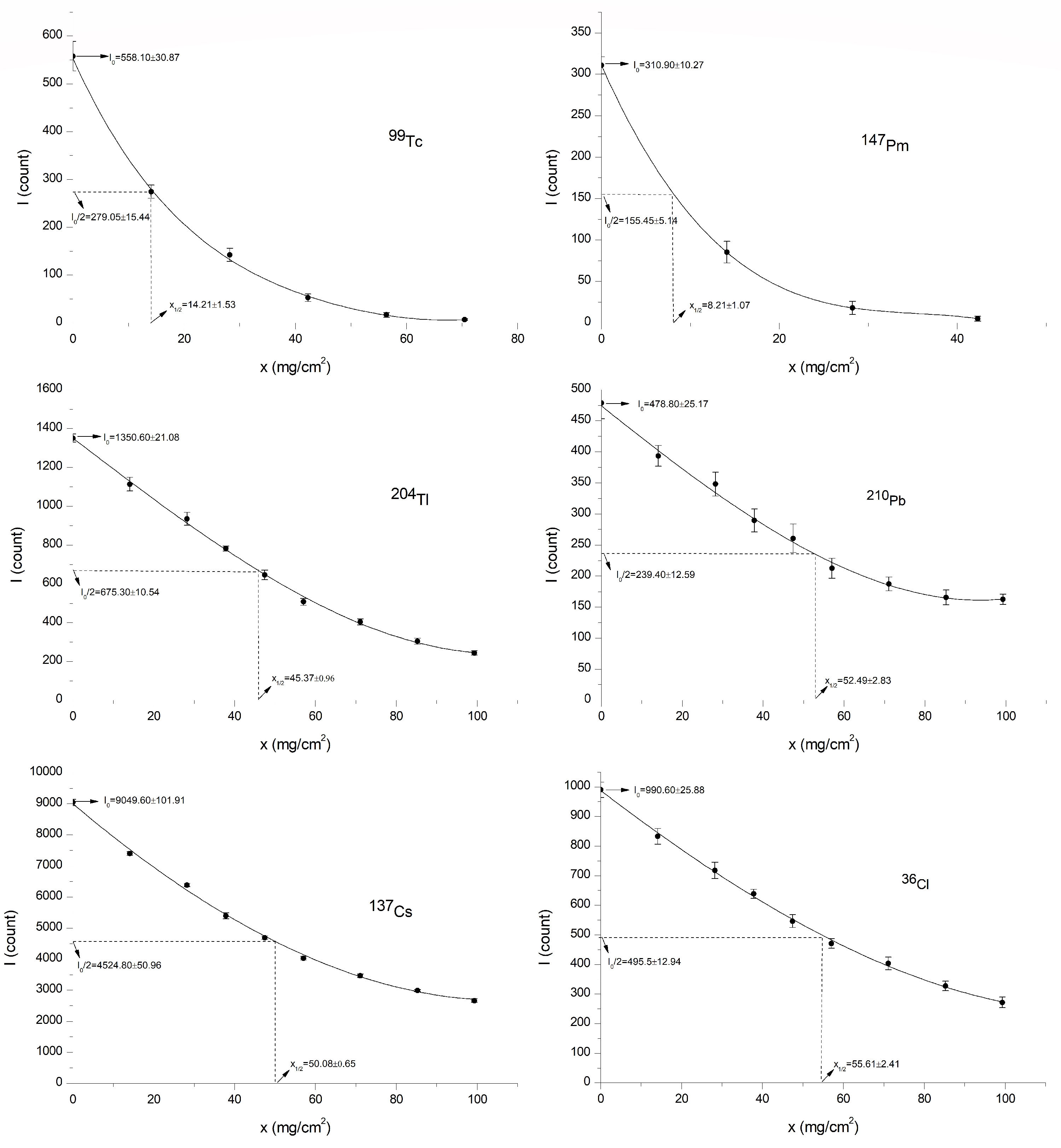
FIGURE 1 Results for the intensity of beta particle with respect to changing of thickness of the PE absorber for 99 Tc, 147 Pm, 137 Cs, 2º4TI, 210 Pb, and 36 Cl beta sources.
TABLE III Experimental lo, lo/2, and x1¡ 2 values in Fig. 1 for PE absorber.
| Sources |
lo (count/min) |
lo/2 (count/min) |
X1/2 (mg/cm2) |
| 99Tc | 558.10±30.87 | 279.05±15.44 | 14.21±1.53 |
| 147pm | 310.90±10.27 | 155.45±5.14 | 8.21±1.07 |
| 13 7Cs | 9049.60±101.91 | 4524.80±50.96 | 50.08±0.65 |
| 204Tl | 1350.60±21.08 | 675.30±10.54 | 45.37±0.96 |
| 210Pb | 478.80±25.17 | 239.40±12.59 | 52.49±2.83 |
| 36Cl | 990.60±25.88 | 495.30±12.94 | 55.61±2.41 |
In Fig. 2, variation of experimental ln(J/ 10) values ac- cording to absorber thickness for each beta source is presented. Mass attenuation coefficients have been obtained from the slope of this change and have been given in Table IV.
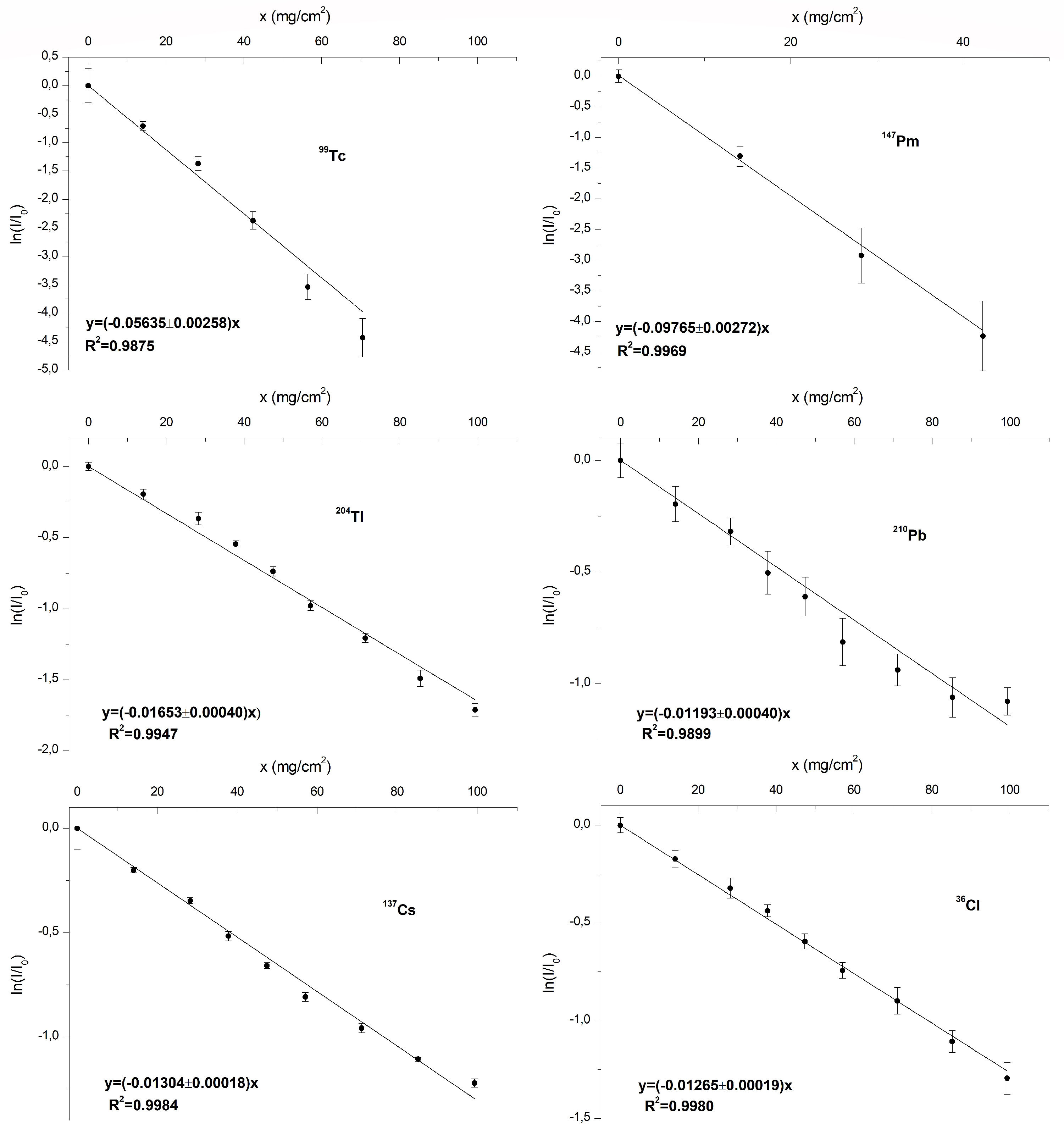
FIGURE 2 The results of ln(J / 10) with respect to changing of thickness of PE absorber for 99 Tc, 147Pm, 137 Cs, 2º4 TI, 210 Pb, and 36 Ci beta sources.
TABLE IV Mass attenuation coefficients of PE absorber for 99Tc, 147Pm, 137 Cs, 2 º4Tl, 210Pb and 36Cl beta sources.
| Sources | µm (cm2/mg) |
| 99Tc | 56.35±2.58 |
| 147pm | 97.65±2.72 |
| 131Cs | 13.04±0.18 |
| 204Tl | 16.53±0.40 |
| 2 10Pb | 11.93±0.40 |
| 36Cl | 12.65±0.19 |
In Table V, experimental, standard, and fractional half- value thicknesses of PE absorber for different six beta sources have been given. In the first and second columns of Table V, beta sources and experimental half-value thicknesses that obtained from Fig. 1 have been given, respectively. In the third column, half-value thicknesses obtained from Eq. (3) which are the solutions of the standard attenuation equation given by Eq. (1) are conveyed. One can easily see from the table that there is a discrepancy between this standard calculated results and the experimental ones. In the fourth column, half-value thicknesses obtained from Eq. (7), which is the solution of fractional attenuation equation defined by Eq. (5) are given. During these calculations, the first 10 terms for the series representation of the Mittag-Leffier function, which has an infinite series opening, have been taken into account in order to obtain physically meaningful results. Calculated fractional half-value thicknesses that are given in the fourth column with experimental half-value thicknesses for orders of fractional derivative that are given in the fifth column are in statistical agreement. The aim of this study is to eliminate the discrepancy between experimental and standard half-value thickness. For this purpose, fractional derivative orders that give experimental values have been calculated by fractional manner. In other words, the same results with experimental values have been obtained using fractional calculus. Toe solution of the attenuation equation represents the ideal situation and gives a variation of intensity of beta rays according to only absorber material thickness. In reality, the absorption of beta particles by a material depends on not only on the thickness of the material but also the mechanism by which beta particles loose energy. There is a lot of research in the literature about energy dependence of mass attenuation coefficients [14,15,38-41]. These studies have also focused on taking beta particle energies into consideration. How- ever, beta particles loose their energy due to the interaction with the material as they move through. This particle intensity change with energy may not explain using the standard attenuation equation given by Eq. (1). While the standard attenuation equation cannot provide the experimental results as seen in Table V, the fractional attenuation equation with around 0.3 value of fractional derivative order can reproduce the experimental results. In our previous works, similar calculations have been studied for aluminum absorbers [20,21] and some construction materials [42] and we have found the order of fractional attenuation equation to be around 0.3, which reproduces experimental results. In the present study, we have obtained approximately the same value for the fractional derivative order in PE absorbers. Obtaining similar results for two different absorber materials suggests that even if beta sources are different, the equation describes that the absorption of beta particles from a material should be a fractional attenuation equation with an order of the fractional derivative of around 0.3. Thus, it can be predicted that similar results can be obtained for future studies for different sources and materials as Ref. [20,21,42].
TABLE V Experimental, standard and fractional half-value thick- ness (mg/cm2) of PE absorber.
| Sources | Xl/2 experimental |
Xl/2 standard |
Xl/2 fractional |
α |
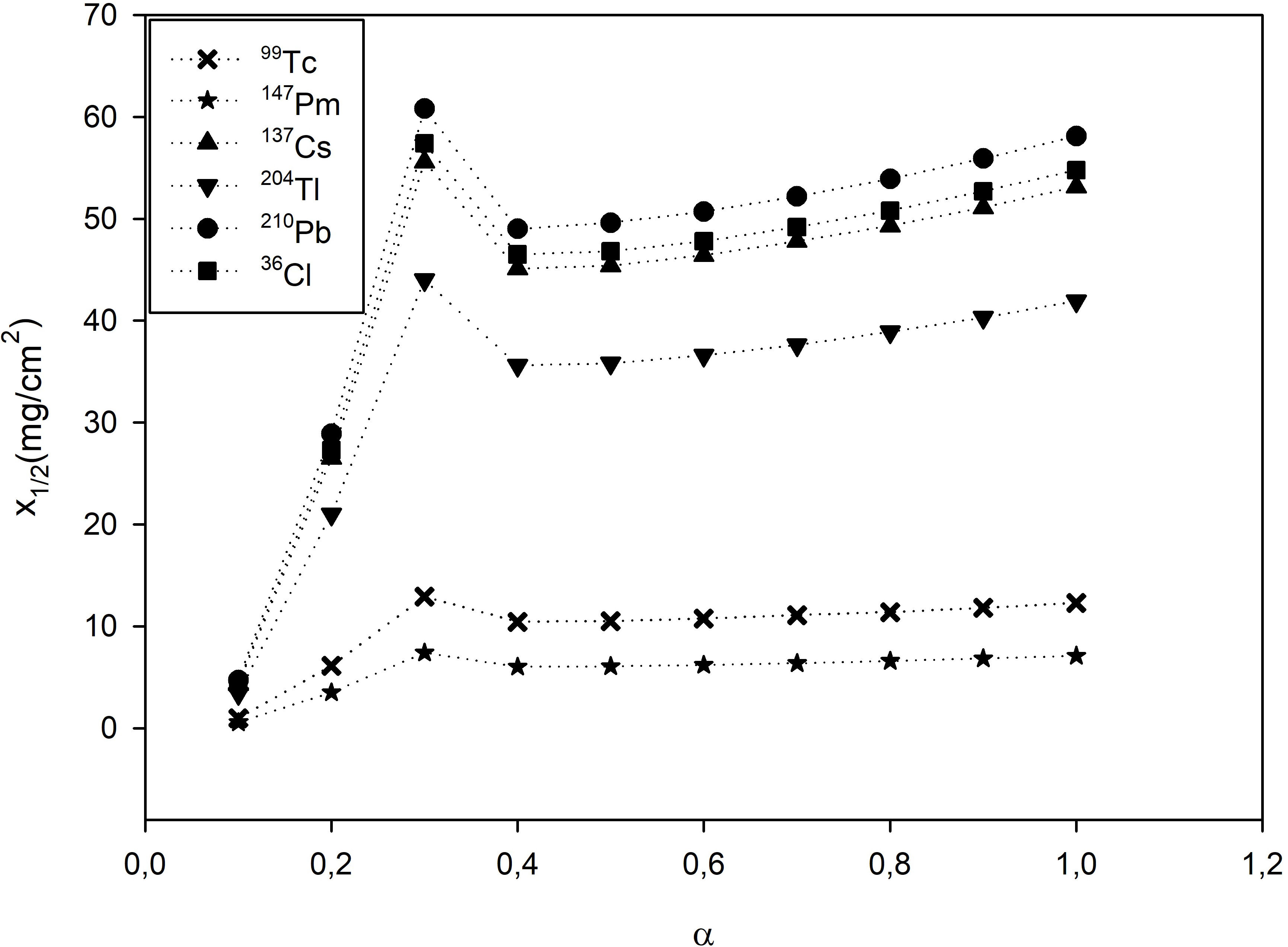
| 99Tc | 14.21±1.53 | 12.30±0.56 | 14.21±1.53 | 0.31 |
| 147pm | 8.21±1.07 | 7.10±0.20 | 8.21±1.07 | 0.31 |
| 131Cs | 50.08±0.65 | 53.14±0.72 | 50.08±0.65 | 0.32 |
| 2 04Tl | 45.37±0.96 | 41.91±1.02 | 45.37±0.96 | 0.31 |
| 2 10Pb | 52.49±2.83 | 58.09±1.95 | 52.49±2.83 | 0.34 |
| 36Cl | 55.61±2.41 | 54.78±0.81 | 55.61±2.41 | 0.31 |
The variation of half-value thicknesses according to the beta energies have been given in Fig. 3. As seen in Fig. 3, half-value thicknesses increase with increasing values of beta energies. Half-value thicknesses are close to each other naturally because of the energy values of 137 Cs, 147Pm and 36 Cl sources are approximately equal. Meanwhile, the moving of beta particles through the material depends on their energies. Calculated half-value thicknesses versus the different fractional derivative orders have been given in Fig. 4. Half-value thicknesses take the maximum values at the order of the fractional derivative of around 0.3. Calculated half-value thicknesses are equal to standard ones for a = 1 as expected because of the Mittag-Leffler function generalization of the exponential function. As seen in Fig. 4, variations of half-value thicknesses have similar behavior for beta sources with close energies.
4. Conclusion
In the present study, the interaction of beta particles from different beta sources with the PE absorbers in different thick- nesses have been investigated and half-value thicknesses of the absorber materials have been compared with experimental results. The standard solution of the attenuation equation represents the ideal situations and an average of attenuation coefficients. The energy losing processes of beta particles should be included in the calculations for describing a more realistic situation. In this context, a more realistic approximation has been done using fractional calculus instead of the standard differential equation, where the intensity of the beta particle varies only with distance.
Beta particles follow different paths like a fractal because of the structure of the absorber material and different interactions of beta particles. Therefore, the internal structure of the absorber material can be considered as a fractal space that is non-Euclidean for beta particles. In this fractal space, energy losing processes are repeated on similar but different scales on the different paths that follow of beta particles. The reduction of the intensity of beta rays in the absorber material can be considered as a multi-fractal physical process. The order of fractional derivative a in the fractional attenuation equation represents this fractality. Thus, the energy losing processes of beta particles have been also included in the calculations without any fitting parameter. The order of the fractional derivative is not an adjust parameter, it has been obtained from fractional calculations, naturally. So the or- der of fractional derivative can be considered as a measure of fractality.
Although different beta sources and different absorbers are used in previous and present studies, the experimental results are in statistical agreement with the fractional results for the around 0.3 value of the fractional derivative order. In other words, the order of the fractional derivative is not de- pendent on the type of beta source. Consequently, we can conclude that, the interaction of beta particles with material have been described much better with a fractional differential equation that is given by Eq. (5) instead of Eq. (1).











 text new page (beta)
text new page (beta)