1. Introduction
The nonlinear dynamics that describes the propagation of pulses in optical metamaterials (MMs) is given by the nonlinear Schrödinger equation (NLSE). In the presence of parabolic law nonlinearity, with an additional anti-cubic nonlinear term and perturbation terms that include inter-modal dispersion (IMD), self-steepening (SS) as well as nonlinear dispersion (ND), the governing equation reads [1-6]
In Eq. (1), the unknown or the dependent variable q(x, t) represents the wave profile, while x and t are the spatial and temporal variables respectively. The first and second terms are the linear temporal evolution term and group velocity dispersion (GVD), while the third term introduces the anti-cubic nonlinear term, fourth and fifth terms account for the parabolic law nonlinearity, and sixth, seventh and eighth terms represent the IMD, SS, and ND respectively. Finally, the last three terms with 𝜃 k for k = 1, 2, 3 appear in the context of metamaterials [7, 8].
Metamaterials are basically artificially structured materials which are made from assemblies of multiple elements fashioned from composite materials such as metals or plastics. In just a few years, the field of optical metamaterials has emerged as one of the most exciting topics in the science of light, with stunning and unexpected outcomes that have fascinated scientists and the general public alike. Its applications' include superlenses, super-resolution devices, and negative-indexed materials. Such applications necessitate the presence of unnatural materials with properties that can fit into these applications and others. The study of solitons in optical metamaterials is trending as a hotspot in the field of optical materials. There has been a significant amount of results that are reported in this field. However, there is still a long way to go. There are many unanswered questions than answers. This paper will quell the thirst partially. In the past, solitons in optical metamaterials have been studied with various forms of non-Kerr laws of nonlinearity where several integration schemes have been implemented [10-28]. The interested reader also read herein references [29-45]. This paper is going to revisit the study of solitons in optical metamaterials for a specific form of nonlinear medium. This is of anti-cubic (AC) type. There are three forms of integration algorithms that will be applied to extract soliton solutions to metamaterials with AC nonlinearity. These schemes will retrieve bright, dark and singular soliton solutions that will be very important in the study of optical materials. These solitons will appear with constraint conditions that are otherwise referred to as existence criteria of the soliton parameters. After a quick introduction to the model, the integration techniques will be applied and the details are enumerated in the subsequent sections.
In order to solve Eq. (1), the starting hypothesis is [7, 8]
where
and the phase component 𝜙 is given by
In Eqs. (2) and (3), u(x,t) represents the amplitude portion of the soliton, and k and v are inverse width and velocity of soliton. From (4), κ is the frequency of the soliton, ω is the wave number of the soliton and finally θ is the phase constant. Inserting (2) into (1) and then decomposing into real and imaginary parts yield a pair of relations. Imaginary part gives
and
while real part leads to
To acquire an analytic solution, the transformations θ 1 = 0 and θ 2 = - θ 3 are applied in Eq. (7), and gives
where
In order to obtain closed-form solutions, we employ the transformation given by
that will reduce Eq. (8) into the ordinary differential equation (ODE)
The generalized (G'/G)-expansion approach [29-31] will now be applied, in the subsequent section, to Eq. (11) to retrieve bright, dark and singular soliton solutions to the NLSE with AC nonlinearity (1). Biswas and coworkers investigated the extended nonlinear Schrödinger equation [49], the nonlinear Schrödinger equation with parabolic law nonlinearity [50], the perturbed nonlinear Schrödinger equation with five different forms of nonlinearity [51], the Schrödinger-Hirota equation in birefringent fiber [52], the Gerdjikov-Ivanov equation [53], the complex Ginzburg-Landau equation [54] and obtained new exact solutions including different forms of optical solitons. Also, authors of [55-57] studied the nonlinear Schrödinger equation and obtained optical solitons with help of the trial and extended trial equation methods. Finally, bright optical soliton solutions from resonant nonlinear Schrödinger's equation has been gained by the aid of semi-inverse variational principle by Biswas et al. [58].
This paper is organized as follows: Sec. 2 presented a brief discussion about the improved exp(-Ω(η))-expansion method and its application for solving the aforementioned equation. Moreover, Sec. 3 and its sub-sections deal with the applications of the extended sinh-Gordon equation expansion method (EShGEEM) to look for new singular, kink-singular, and combined dark-bright soliton solutions. Physical significance by graphical presentation of some of the obtained solutions is given in Sec. 4. Also, a conclusion is given in Sec. 5.
2. The improved method exp(-Ω(η))-expansion
This section elucidates a systematic explanation of exp(-Ω(η))-expansion method [59, 60] so that it can be further applied to optical metamaterials with anti-cubic non-linearity in order to furnish its exact solutions:
Step 1. The following nonlinear partial differential equation (NLPDE)
can be transformed into an (ODE)
by using the suitable transformation η = B (x - vt), where B and v are the free parameters which would be calculated subsequently.
Step 2. Assuming the solution of the ODE to be of the form:
where F (η) = exp (-Ω(η)) and A j (0 ≤ j ≤ N ),B j (0 ≤ j ≤ M), are constants to be determined, such that A N , BM ≠ 0, and, Ω = Ω(η) satisfying the ODE given below
The special cases formed from the solutions [61, 62] of the ODE given in Eq. (15) are mentioned below:
Solution-1: If μ ≠ 0 and λ 2 - 4μ > 0, then we have
where E is integral constant.
Solution-2: If μ ≠ 0 and λ2 - 4μ < 0, then we have
Solution-3: If μ = 0, λ ≠ 0, and λ2 - 4μ > 0, then we get
Solution-4: If μ ≠ 0, λ ≠ 0, and λ2 - 4μ = 0, then we get
Solution-5: If μ = 0, λ = 0, and λ2 - 4μ = 0, then we get
where A j (0 ≤ j ≤ N), B j (0 ≤ j ≤ M), λ and μ are also the constants to be explored later. The values N and M are determined by equalizing the maximum order nonlinear term and the maximum order partial derivative term appearing in (13). If N and M are the rational, then the appropriate transformations can be applied to conquer these hurdles.
Step 3. Putting (14) into Eq. (13) as well as the values of N and M determined in previous step into (14). Gathering coefficients of all the powers of F (η), then equating every coefficient with zero, we derive a set of over-determined nonlinear algebraic equations for A 0 , B 0 , A 1 , B 1,... , A N , B M , λ, and μ.
Here, it is important to note that E is the integration constant. We have the following relations as
where 𝛿 = (An/Bm). Balancing v' 2 with v 4 in Eq. (11) yields
We can determine values of N and M as follows:
Case I: N=2, M=1
The improved exp(-𝜙)-expansion method (IEFM) allows us to recruit the substitutions
Plugging (27) along with (15) into Eq. (11) and equating all the coefficients of powers of F (η) to be zero, one gains a system of algebraic equations. Solving this system by the help of Maple yields
Set I:
where A1 , A2 , B0 and B1 are arbitrary constants. Imposing the solution set (28) into (27), the solution formula of Eq. (11) can be concluded in the following cases:
Subcase IA:
By the help of (16), the exact solutions to the model are deducted as
where
It should be noted that these solitons exist for
Subcase IB:
By the help of (17), the exact solutions to the model are deducted as
where
It should be noted that these solitons exist for
Subcase IC:
By the help of (18), the exact solutions to the model are obtained as
where
It should be emphasized that these solitons exist for λ ≠ 0.
Subcase ID:
By the help of (19), the exact solutions to the model are gained as
where
It should be noted that these solitons exist for
Subcase IE:
By the help of (20), the exact solutions are obtained as
where
It should be pointed out that these solitons exist for
Set II:
where A 1, A 2, B 0 and B 1 are arbitrary constants. Plugging the solution set (34) into (27), the solution formula of Eq. (11) can be concluded in the following:
Subcase IIA:
By the help of (16), the exact solutions are in the following:
where
It should be emphasized that these solitons exist for
Subcase IIB:
By the help of (17), the exact solutions are concluded in the form:
where
It should be noted that these solitons exist for
Subcase IIC:
By the help of (18), the exact solutions are given as
where
It should be pointed out that these solitons exist for λ = 0.
Subcase IID:
By the help of (19), the exact solutions are gained as
where
It should be noted that these solitons exist for
Subcase IIE:
By the help of (20), the exact solutions are concluded as
where
It should be noted that these solitons exist for
Set III:
where A 0 , A 1 and A 2 are arbitrary constants. Substituting the solution set (40) into (27), the solution formula of Eq. (11) can be written in the following cases:
Subcase IIIA:
By the help of (16), the exact solutions can be stated as
where
and A 0 A 2 > 0.
Subcase IIIB:
By the help of (17), the exact solutions can be obtained as
where
with A0A<0.
Subcase IIIC:
By the help of (20), the exact solutions to the model as follows:
where
It should be pointed out that these solitons for A 0 = 0.
3. Algorithm of the extended sinh-Gordon equation expansion method
Take the sinh-Gordon equation as:
where u=u(x,t) and α is a constant. By utilizing the relations u(x,t) =U(ξ) and ξ = kx - ωt, then Eq. (44) transforms to the following NODE:
By using of the integrating process of Eq. (45) gets
where p is an integration constant.
Putting U2 = 𝜔(ξ), and - α/kω = q in Eq. (46), we gain
by choosing the parameters p and q in Eq. (47) can be found the further results of solutions [63-67]:
Case-I: Take p = 0 and q = 1, then Eq. (47) gets
Simplifying Eq. (48), the following results are gained [63]:
and
where,
Case-II: Take p = 1 and q = 1 , then Eq. (47) gets
Again, simplifying Eq. (51), the following results are achieved [63]:
and
We assume that the given nonlinear PDE
In Eq. (54), u = u(x, t) is an unknown function, F is a polynomial in u(x, t) and its various partial derivatives are involved. Consider the following transformation:
Implementing the transformation of (55) into Eq. (54), then Eq. (54) converted to the following NODE
where G is a polynomial of U = U (ξ) and its derivatives with respect to ξ.
Suppose the exact solution be as
Base on the relations (48)-(50), then (57) can be written in the following forms
and
Similarly, base on the relations (51)-(53), then (57) can be written in the following forms
and
the value of N can be determined by using the homogeneous balance principle.
3.1. The EShGEEM
3.1.1. For Case-I: Eq. (48)
Base on the Eqs. (57)-(59), the solution of Eq. (11) can be presented as
and
and so
where A 1 ≠ 0 or B 1 ≠ 0.
Inserting (64) and its derivatives into Eq. (11), we can obtain the following results by solving the nonlinear algebra system with the help of symbolic computation package as:
Set I-1:
The bright and singular soliton solutions for the Eq. (1) are achieved as
and
Set I-2:
The bright and singular soliton solutions for the Eq. (1) are presented as
and
Set I-3:
Therefore, we conclude the following dark and singular soliton solutions for the Eq. (1) respectively:
and
Set I-4:
The dark and singular soliton solutions for the Eq. (1) are deduced as
and
Set I-5:
The combined dark-bright and singular soliton solutions for the Eq. (1) are concluded as
and
Set I-6:
Thus, we deduce the following combined dark-bright and singular soliton solutions for the Eq. (1) respectively:
and
3.1.2. For Case-II: Eq. (48)
Base on the Eqs. (60)-(61), the solution of Eq. (11) can be presented as
And
and so
where A 1 ≠ 0 or Bi ≠ 0.
Plugging (94) and its derivatives into Eq. (11), we can gain the following results by solving the nonlinear algebra system with the help of symbolic computation package as:
Set I-1:
The periodic and singular periodic solutions for the Eq. (1) are shown as
and
Set I-2:
Therfore, we conclude the following periodic and singular periodic solutions for the Eq. (1) respectively:
and
Set I-3:
The periodic and singular periodic solutions for the Eq. (1) are presented as
And
Set I-4:
The periodic and singular periodic solutions for the Eq. (1) are shown as
and
Set I-5:
Therefore, we conclude the following combined periodic-singular and singular periodic solutions for the Eq. (1) respectively:
and
Set I-6:
Thus, we deduce the following combined periodic-singular and singular periodic solutions for the Eq. (1) respectively:
and
3.1.3. For Case-II: Eq. (48)
Base on the Eqs. (60)-(61), the solution of Eq. (11) can be presented as
and
and so
where A 1 ≠ 0 or B 1 ≠ 0.
Plugging (94) and its derivatives into Eq. (11), we can gain the following results by solving the nonlinear algebra system with the help of symbolic computation package as:
Set I-1:
The periodic and singular periodic solutions for the Eq. (1) are shown as
and
Set I-2:
Therfore, we conclude the following periodic and singular periodic solutions for the Eq. (1) respectively:
and
Set I-3:
The periodic and singular periodic solutions for the Eq. (1) are presented as
And
Set I-4:
The periodic and singular periodic solutions for the Eq. (1) are shown as
and
Set I-5:
Therefore, we conclude the following combined periodic-singular and singular periodic solutions for the Eq. (1) respectively:
and
Set I-6:
Thus, we deduce the following combined periodic-singular and singular periodic solutions for the Eq. (1) respectively:
and
4. Physical significance by graphical presentation of some of the obtained solutions
In this portion of the paper, we seek to draw attention on the physical conduct of some of the obtained solutions. We have examined the nature of the solutions by assuming appropriate values of involved unknown parameters and plotted these solutions graphically. Resultant solutions for the Eq. (1) consist of kink, singular, dark, combined dark-bright, kink-singular, and bell soliton solutions as well as periodic solutions. Solitons are a unique kind of solitary wave having a very important property of not losing its identity upon the interaction with various other solitons. Particle-like structures and extended structures such as magnetic monopoles, domain walls as well as cosmic strings, whose repercussions lie in the cosmology of the early universe, are exhibited by soliton solutions. The obtained solutions including the bright soliton (65), singular soliton (66), dark soliton (69), combined dark-bright soliton (73), periodic wave solutions (95) and (99), and periodic-singular wave solution (103). Graphical representations of the accomplished solutions are as follows Figs. (1-7):
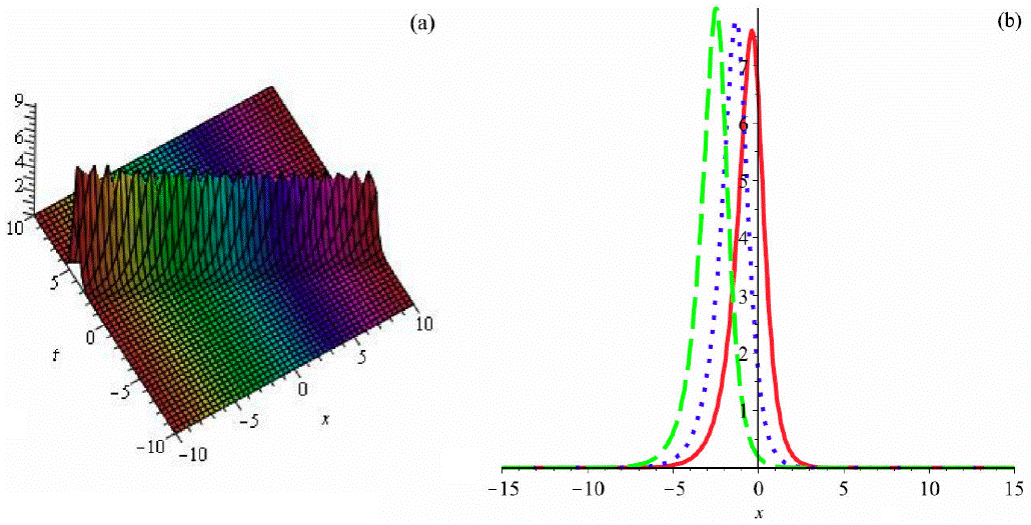
Figure 1 Graph of (65) by taking B 1 = 1, a = 1, b 2 = 0.5, b 3 = -0.6, α = 2, β = 3, θ = 1 (a) 3D plot and (b)) 2D plot (red (t = 0.1), blue (t = 0.5) and green (t = 1)).
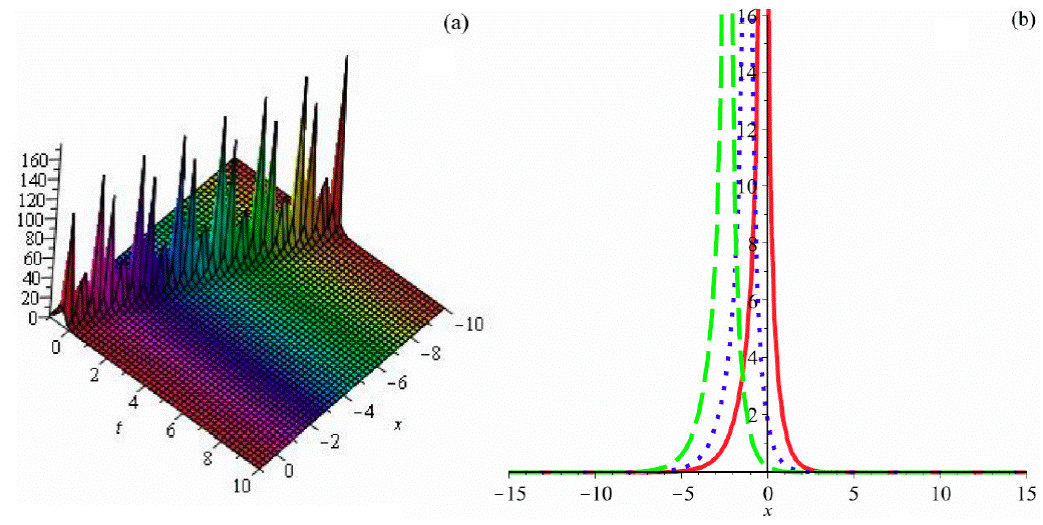
Figure 2 Graph of (66) by taking B 1 = 1, a = 1, b 2 = 0:5, b 3 = -0:6, α = 2, β = 3, θ = 1 (a) 3D plot and (b)) 2D plot (red (t = 0:1), blue (t = 0:5) and green (t = 1)).
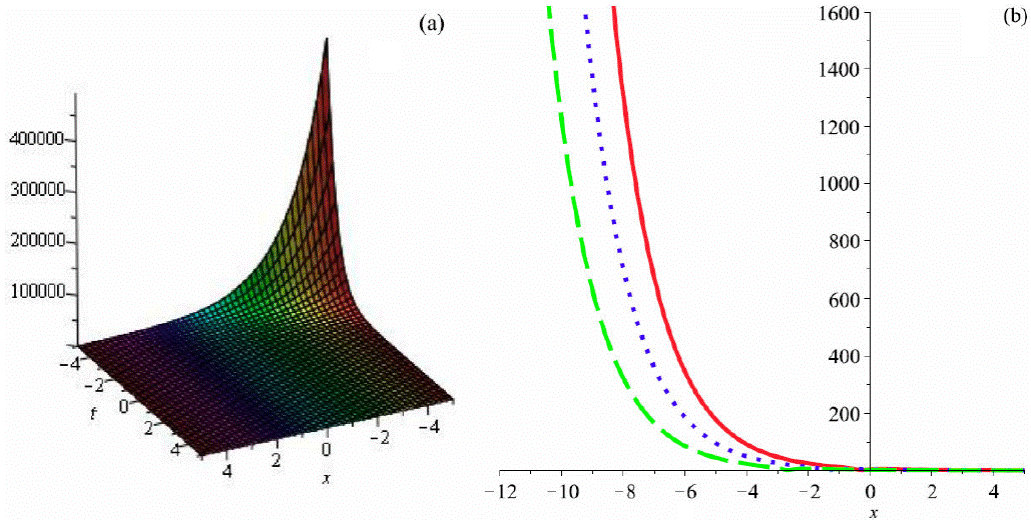
Figure 3 Graph of (69) by taking A 1 = 1, a = 1, b 2 = 0.5, b 3 = -0.6, α = 2, β = 3, θ = 1 (a) 3D plot and (b)) 2D plot (red (t = 0.1), blue (t = 0.5) and green (t = 1))
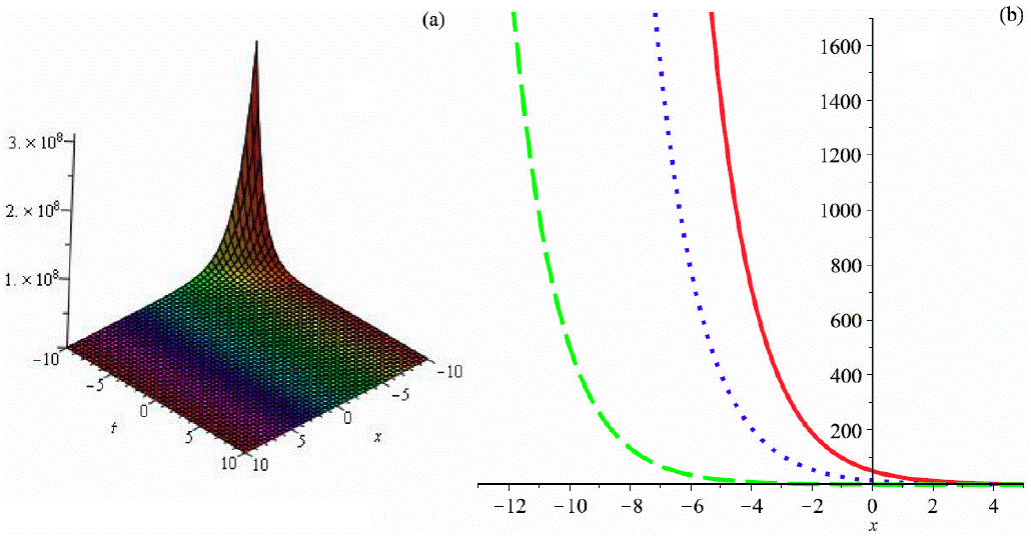
Figure 4 Graph of (73) by taking A 1 = 1, a = 1, b 2 = 0.5, b 3 = -0.6, α = 2, β = 3, θ = 1 (a) 3D plot and (b)) 2D plot (red (t = 0.1), blue (t = 1.5) and green (t = 5)).
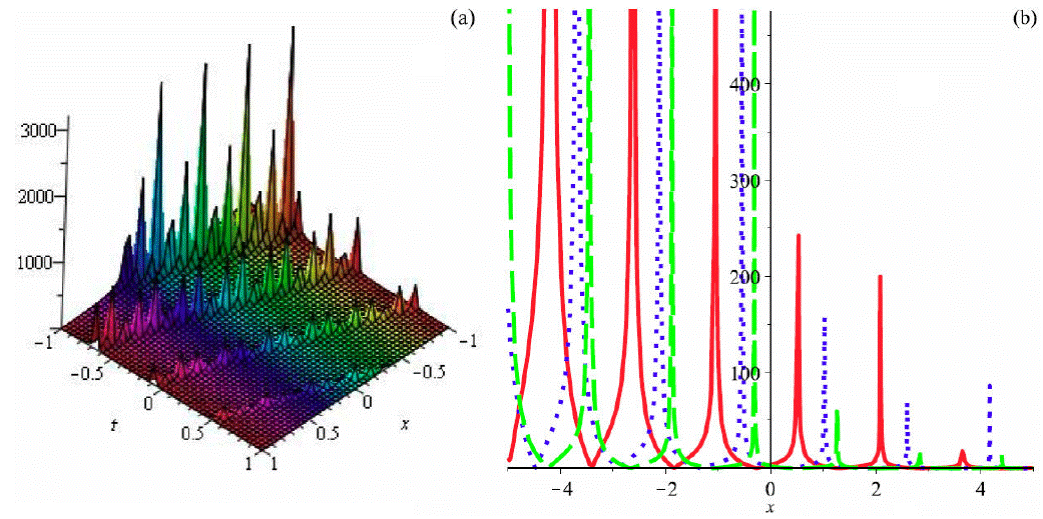
Figure 5 Graph of (95) by taking A 1 = 1, a = 1, b 2 = 0.5, b 3 = -0.6, α = 2, β = 3, θ = 1 (a) 3D plot and (b)) 2D plot (red (t = 0.1), blue (t = 0.5) and green (t = 1)).
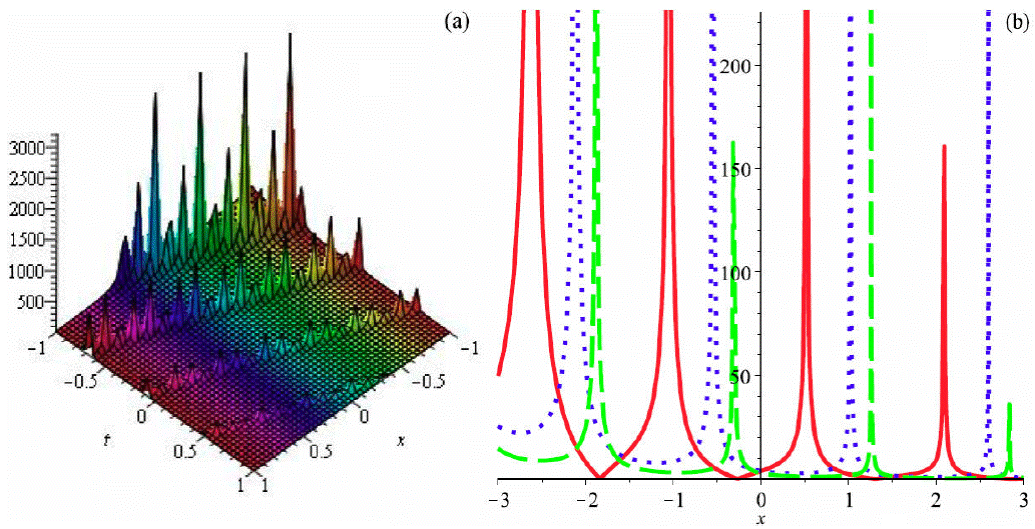
Figure 6 Graph of (99) by taking A 1 = 1, a = 1, b 2 = 0.5, b 3 = -0.6, α = 2, β = 3, θ = 1 (a) 3D plot and (b)) 2D plot (red (t = 0.1), blue (t = 0.5) and green (t = 1)).
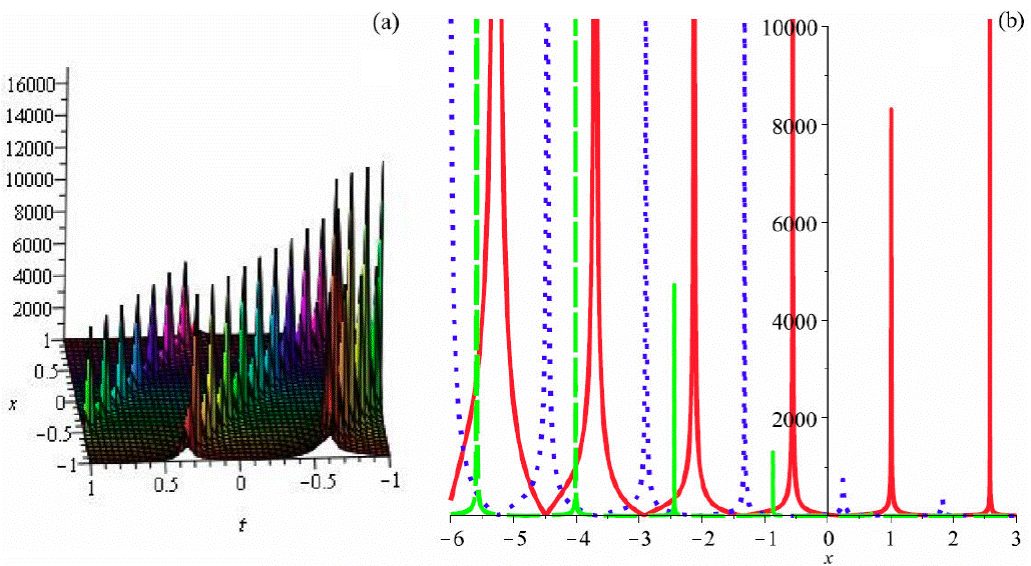
Figure 7 Graph of (103) by taking B 1 = 1, a = 1, b 2 = 0:5, b 3 = -0:6, α = 2, β = 3, θ = 2 (a) 3D plot and (b)) 2D plot (red (t = 0:1), blue (t = 0:5) and green (t = 1)).
Remark 4.1
Foroutan et al. [4] employed the generalized G'/G-expansion method to obtain the solitary wave solutions of the NLSE with dual power law nonlinearity. On the other hand, authors of [5] have used improved tan (𝜙(𝜉)/2)-expansion method with the aim of exploring new solutions of Eq. (1). The two methods mentioned above assume different forms of solutions which contain functions of ξ. These functions of η in exp (-Ω(η)) satisfies an ODE with hyperbolic, trigonometric, and rational functions. On the other hand, the ODE used in improved tan(𝜙(𝜉)/2) -expansion method and the generalized G ' /G-expansion method contain polynomial functions and all the cases of solutions of the ODE have not been explored in [4, 5]. Some of the obtained complex exponential solutions are in harmony with the already existing solutions [5]. The number of arbitrary constants in the solutions mentioned in [5] is less than those obtained in this paper. The extra arbitrary parameters might have potential applications in various fields of science which would make our solutions better than the already published ones. Thus, it can be stated that solutions obtained in this manuscript bestow valuable supplements to the existing literature.
5. Conclusion
In this work, we have investigated the nonlinear Schrödinger equation with anti-cubic nonlinearity by employing the improved exp(-Ω(η))-expansion method and extended sinh-Gordon equation expansion method. These methods have been lately augmented in order to explore more and more exact solutions for various NLPDEs. The richness of these obtained solutions lies in the existence of abundant arbitrary constants, having local structures, whose numerous applications prevail in various fields namely; signal propagation in optical fibers, wave propagation, IMD, SS as well as ND etc. It is worthy to note that several already published solutions of optical metamaterials, with anti-cubic nonlinearity, can be recovered by taking appropriate values of the involved arbitrary constants. Various explicit physical structures such as solitary wave, kink, and bell-shaped wave solutions are graphically represented distinctly which reveal the competence and high applicability of the obtained solutions. These solutions may be helpful in validating several numerical schemes and their accuracy.











 text new page (beta)
text new page (beta)



