1. Introduction

In nonlinear positive Kerr media light pulses break into solitons and radiation part. The number, powers, and velocities of obtained solitons for situations described by the nonlinear Schrödinger equation (NLS) are governed by eigenvalues of the Zakharov-Shabat (ZS) scattering problem [¹, ²]. The ZS equations are not self-adjoint, and in most cases of interest can be solved only numerically. On the other hand, the qualitative understanding of emerging soliton parameters is often important for applications. It is known that real pulses with one hump produce solitons only with zero velocities [³] (all ZS eigenvalues are purely imaginary), however for chirped pulses, and for more complicated (e.g two-hump) real pulses this is not true [⁴, ⁵]. There are numerical and analytical studies of soliton parameters for diffirent initial pulse shapes [⁶-⁸], but most analytic work is limited to real pulses. Here we propose a simple analytic method, which permits an estimation of ZS eigenvalues with big imaginary part (high power solitons) for multisoliton pulses with one intensity maximum. These eigenvalues are mostly determined by the function shape in a vicinity of the maximum, thus the situation of parabolic pulse is quite general. For the approximation we systematically use the relation between ZS and Schrödinger equation eigenvalue problem, which was first mentioned in an approximate form in the original Zakharov-Shabat paper [¹] . In mathematical literature it is also known, that for real pulses q(x), an equivalent Schrödinger equation with complex potential (SCP) exists, for the potential Q(x) = -q ² ±i𝜕 _x q [⁹]. The SCP gives the same eigenvalues after taking the square root. The relation can be established for complex q(x) as well, but in general it seems, that the inverse scattering technique is needed to reconstruct the corresponding Q(x), and the resulting potential can have singularities. However, it is relatively easy to obtain an equivalent SCP potential, which itself has an eigenvalue as a parameter. If the initial pulse has small variations in phase, the SCP potential depends on the parameter only quite weakly, and useful approximations can be constructed by iterations.

The link between SCP and ZS scattering problem is interesting not only mathematically. Recently, there is a lot of interest in PT symmetric physical systems with loss, described by SCP [¹⁰-¹²] . In optics, such systems correspond to media with locally distributed loss and gain, and such systems are not easily realized in experiment. But, once the equivalence between CS and ZS is established, the particular complex potential can be modelled with a certain distribution of light amplitude either in fiber (temporal domain) or in the bulk nonlinear medium such as photorefractive crystal (spatial domain) - parameters of solitons emerging from pulse breaking will correspond to SCP eigenvalues. PT symmetry breaking will correspond to the appearance of fiber soliton pairs with nonzero velocity, or spatial soliton pairs propagating with an angle to the symmetry axis.

2. The relation of ZS and SCP problems

The Zakharov-Shabat scattering problem is written as [¹,²]:

If v ₁ (x) → exp (-i𝜆x), v ₂ (x) → 0 for x → -∞, the solution will be limited only for a finite number of eigenvalues λ _n in the upper complex plane, with Im(𝜆) > 0 (we consider continuous functions q(x) on the compact support which are zero for |x| > R).

The eigenvalues define soliton parameters for the nonlinear Schrödinger equation

with the initial condition 𝜓(x, 0) = q(x).

If the pulse is symmetric, q(-x) = q(x), PT symmetry exists, and corresponding eigenvalues are either purely imaginary or obtained in pairs with opposite real parts.

The relation of ZS and SCP for real ZS potential q can be established as follows:

Start with equations:

After taking second derivatives it is transformed to the Schrödinger eigenvalue problem :

which has potential Q = P ² -𝜕P. For v ₂ the term with derivative 𝜕P has opposite sign. Now, make the transformation of Eqs. (4-5) with a constant matrix SU S ^-1 , where

and denote iP = p. Then we obtain AKNS scattering problem [²]:

It is seen, that when q is real, this is equivalent to Eqs. (1-2). In this case the corresponding CS potential is Q = P ² -𝜕P = -q ² + i𝜕q. Genarally, one has for ZS -q* as lower off-diagonal element, and in this case we were unable to find simple general correspondence between ZS and SCP problems. However, formally one can reconstruct a ZS pulse, which has the same spectral data in a sense of inverse scattering problem, as a Schrödinger equation with complex potential. For this, the scattering data of (Eq. (8-9)) can be used to reconstruct ZS potential Eq. (1-2) with one of known integral equation methods, taking into account different symmetry for two cases. The theory of inverse scattering for both ZS problem and Eq. (8-9) can be found in the book of Ablowitz [²]. The reconstruction of SCP from ZS can be problematic, since for Eq. (8-9) even one-soliton solution can produce potentials with singularity [²]. This procedure, however, does not seem practical for pulses with varying phase, because for reduction to SCP we need to solve the problem itself first.

Now, rewrite Eqs. (1-2) for v± = v ₁ ± v₂, and using real and imaginary part of pulse q(x) = q _R + iqI (both q _R , qI are real functions):

From Eq. (10),

and by taking second derivatives in Eqs. (10 -11 ), we obtain

where |q| ² =qR2+qI2. Denote

and use expression Eq. (12) in Eq. (13). The resulting equation can be reduced with standard method to Schrödinger form by taking v ₊ = u exp(1/2 ∫g ), which finally gives:

The expression in brackets gives the equivalent SCP potential, valid for any q, but the potential depends on eigenvalue according to Eq. (14). It is seen, that for purely imaginary q(x) = iq _I (x), we obtain 𝜆-independent potential, which is the same as for purely real pulse. If in some sense q _I ≫ q _R , we can approximate 𝜆 by iterations. It is also seen, that additions to SCP potential become bigger for small 𝜆, in particular one can expect strong distortions and even singularities for purely imaginary eigenvalues when Im(𝜆) ≈ q _R.

3. Approximations to soliton parameters

Mathematically, the reduction of ZS to SCP does not solve the problem, but it suggests that in some cases it is possible to develop approximations which start from known solutions of Schrödinger equation. We use here ZS and SCP relation to calculate approximate eigenvalues. For this, some simple Schrödinger potential is taken as a starting point, and the rest is treated as perturbation. As a test system we take a pulse with parabolic intensity distribution. It approximates pulses with one hump close to their intensity maximum. The corresponding Schrödinger problem is that one of quantum oscillator, and matrix elements for perturbation can be calculated explicitly for a number of cases. Other potentials which are analytically solved (Poschl-Teller, Morse, square pulse, etc) can be used as well, but it seems to us that the parabolic pulse presents good balance between practical interest and analytic difficulties.

Thus, for pulses of interest the amplitude is given by:

for |x| < A, and q(x) = 0, for |x| ≽ A, C is small real parameter, and f _k are complex functions. The resulting -qq* potential for Schrödinger operator is close to harmonic, - A ² + x ² , but it is true only for |x| < A, thus we assume in the following A ≫ 1 , and consider 𝜆 with big imaginary part.

The eigenfunctions ψ _n , where n = 0,1,2... of Schrödinger equation with potential -A ² + x ² are Hermite functions given by

where H _n are Hermite polynomials. The corresponding eigenvalues are

For the unperturbed matrix we take a diagonal matrix with a _n . As Hermite functions form orthogonal basis, the perturbation matrix elements are given by

where U (x) is the potential in Eq. (15), except for harmonic part -A ² + x ² . Note, that δ are generally complex and the resulting matrix is non-Hermitian. Thus, even for corrections of the lowest order in C it is necessary to take into account non-diagonal elements, as well as diagonal ones δ _n1n1 .

In what follows we assume that δ are small. Consider two diagonal elements with numbers n ₁ , n ₂ , where n ₂ > n ₁ and corresponding off-diagonal element. Then, the matrix reduced to the interaction of these two elements is:

Its eigenvalues are trivially found as a _n1 + n ₂ - n ₁ ±(n1-n2)2+δn1, n22 . For small δ, and n ₁ ≠ n ₂ the lower eigenvalue becomes

and the higher one has opposite sign displacement. For purely imaginary δ they are mutually attracted. To the lowest order in δ the energy additions to each level can be obtained by adding contributions from each pair involved.

The matrix elements for terms U = x ⁿ can be calculated using n times recursion equation for Hermite functions:

together with their orthogonality property.

Let us begin with a simple example of a pulse with slightly distorted amplitude, and no phase changes.

The SCP potential Eq. (15) expanded to terms x ³ is given by

The additions to diagonal matrix elements δ _η,η are C ² (n +1/2)+iC, but the dominant term iC is not physically valid; it is known that ZS eigenvalues for this potential are purely imaginary [³]. This term is eliminated when the elements δ _n,n+1 are taken into account. The elements δ _n,n+2 and δ _n,n+3 give corrections of higher order in small parameters C,A ^-1, and the result is

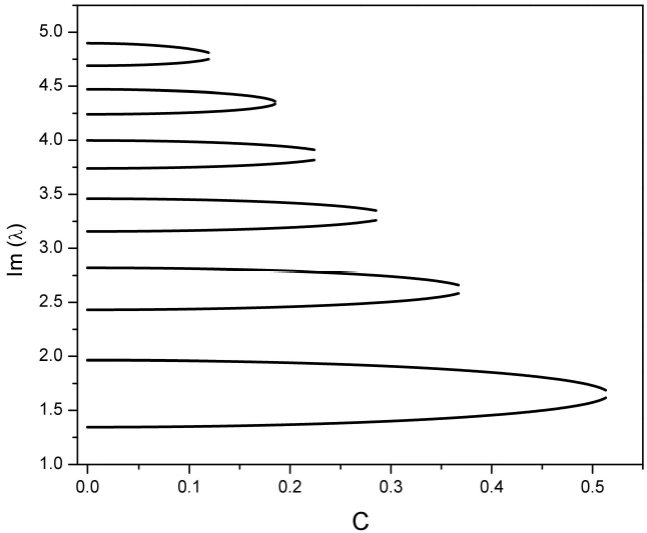
The comparison with numerical solution for ZS is given in Fig. 1. It is seen that upper eigenvalues are well approximated. The approximation breaks for two cases: for small X, and for big C when off-diagonal elements become important, and Eq. (21) is no more valid. For big amplitude the leading term is A ² C ², but the next order correction C ² (2n + 1) is also important (here we neglected C ² A ^-2 terms). To calculate eigenvalues exactly it is necessary not only to find exact eigenvalues for matrix, but also to take into account transitions to continuous spectrum of unperturbed operator.

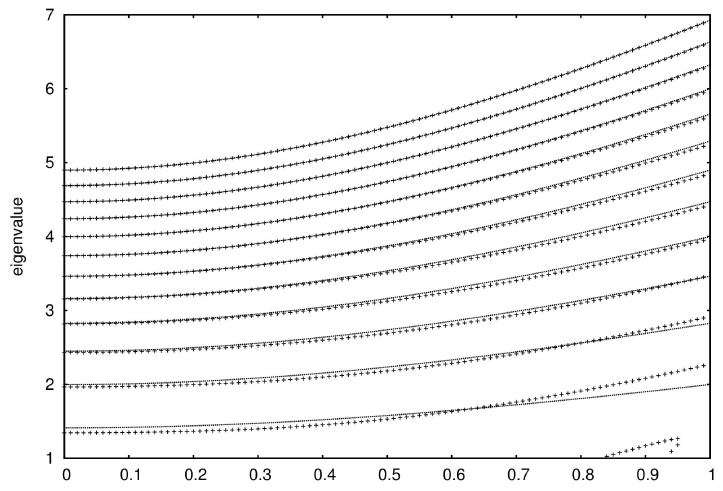
Figure 1 Numerically calculated imaginary parts of eigenvalues for parabolic pulse with addition to amplitude Eq. (23) (crosses), and the approximation of Eq. (25) (lines) in function of small parameter C. The amplitude is A = 5. 

A simple pulse with real part is given by:

It is easy to see from ZS equations, that in this case 𝜆 (C) = 𝜆 (0) + C/2, thus it can be used as a test. The result by perturbation, if terms proportional to C ² , CA ^-2 are neglected, really can be written in this form for

Thus the exactitude of this approximation is determined by the exactitude of eigenvalues for C = 0, as seen in Fig. 1. A pulse with chirp is represented by

The approximation for eigenvalues is:

and 𝜆 _n in the right hand side is taken from Eq. (27). The validity range of this approximation is determined by the leading gq _I term 2C Ax/(i𝜆). This term gives off-diagonal matrix element

and Eq. (21) loses validity for δ ≈ 1, which gives an estimation for C. For n = 7 we have C _max ≈ 0.15, in agreement with Fig. 2 data. It is possible to solve Eq. (29) with respect to X exactly, but this gives important corrections only for big C and two lowest eigenvalues, which already have an error because of the above mentioned restriction.

Figure 2 Imaginary part of eigenvalues for q(x) = i52+x2+ Cx ² (crosses) and approximation (lines). 

This is an example of PT-symmetric pulse, the eigenvalues for small C are purely imaginary, for bigger chirp eigenvalue pairs with opposite real parts are possible. Again we have reasonable approximation for big 𝜆 and small C.

The cubic variation in phase qx=iA2-x2+Cx3 to the first order gives a real addition to eigenvalue

thus with cubic chirp smaller solitons have higher velocities. The SCP potential in this case has a leading C-dependent term -3i(CA/i𝜆)x ² , thus formally the potential is close to ax ² , with complex a. The eigenvalues are simply calculated by considering x along a straight line in complex plane - the spectrum of harmonic oscillator is just rotated in complex plane, which agrees with Eq. (31). Such potentials are known to have interesting instability properties related to so called pseudospectra [¹³]; in particular, higher eigenvalue displacement with perturbation scales as exp(n) . The discussion of this topic is out of the scope of this paper.

One can formulate approximate criteria for level collisions close to the maximum of the real pulse with high amplitude and weak phase modulation

for PT symmetric q, when f (x) and q ₀ (x) are even real functions, and q ₀ (0) = A is big. If only the most important term for big A is considered in SCP potential we get an addition -igq_I of an order of -i(CA/i𝜆)𝜕f. Then the coefficient with C ² in level displacement for 𝜆n is determined by offdiagonal terms δ _n,n + _k . The "natural" case of |q| ² ≈ A ² - x ², and quadratic chirp iCx ² for this approximation is neutral -all levels are displaced to the same amount with C. The chirp f = x ⁴ gives both δ _n,n + ₁ proportional to (n + 1)^3/2 , thus all eigenvalues become lower for bigger C, and the distance between them grows, collisions are avoided. The combination of x ² + ßx ⁴, however, can produce collisions for negative β. Making chirp, that grows slower as x ², for example saturates x ² /(1 + Bx ²), or behaves as |x| ^a for a < 2 favours collisions, because then for big n matrix elements δ grow slower with n. With quadratic chirp, it is possible to manipulate level spacing by changing pulse intensity. If the distance between levels grows with n, as it happens for supergaussian and square pulses, the collisions are also favoured. Two-hump potentials have even-odd pairs nearly degenerate, thus those levels tend to collide with chirp. This explains qualitatively numerics of Klaus and Shaw [⁶]. However, for moderate values of A, as those considered here for numerical examples, the leading term quite rapidly becomes insufficient for bigger n, The corrections, as it is seen from e.g. Eq. (29) have n/A ² as a small parameter.

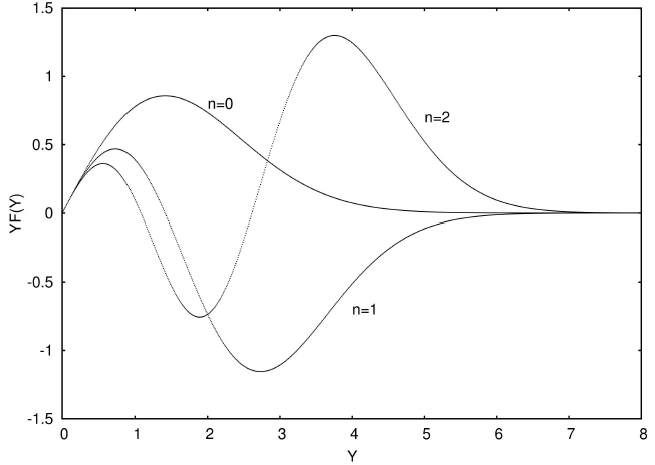
A curiuos case is f (x) = log(|x|) chirp. Then the term iCA/x is obtained in derivative. The odd Hermite functions, if divided by x, give a polynomial one degree lower, thus they are expanded in only lower functions. For even polynomials this is not true. Thus, all odd eigenvalues diminish with C, and all even eigenvalues grow. This gives characteristic neat pairwise collision picture (Fig. 3).

Figure 3 Eigenvalues for qx=52-x2exp⁡(iClog⁡z+0.001) . 

From a practical point of view, it is also interesting to consider sinusoidal chirp and amplitude patterns, since they are naturally produced in nonlinear media by interference fringes. As an example, we consider here q(x) of the type given by Eq. (32) with q0=A2-x2 and f (x) = cos(Yx), sin(Yx). First, consider phase perturbation f (x) = sin(Yx). The leading term in correction for λn2, is here purely imaginary, linear with C , and can be expressed as i(CA)YF _n (Y), and the displacement YF _n (Y) is shown in Fig. 4. The matrix elements are given by Fourier transform of products of Hermite functions, and expressed in Laguerre polynomials [¹⁴], but practically it is easier to calculate them directly with Eq. (19). For small Y we have nearly equal velocities for all three solitons, but for bigger spatial frequencies they behave quite differently. Thus, it is possible to separate the solitons by choosing an appropriate Y, for example for Y ≈ 3.5, the soliton with n = 0 has small velocity, and solitons with n = 1 and n = 2 are deflected in opposite directions. The behaviour for small Y can be obtained from above discussed cases of linear and cubic additions to real part of potential. For f (x) = cos(Yx), the lowest addition to λn2 is real and proportional to C ² . Again, relative magnitudes of displacement are oscillating functions of Y, and by choosing different spatial frequencies it is possible to obtain collisions of different pairs in function of C parameter. For big Y δ _n,n + _k with big k become more important here.

Figure 4 Relative soliton velocities for 3 biggest solitons with sine law phase modulation. 

For real sinusoidal additions to potential qx=i(A2-x2+C sin⁡(Yx)) and qx=i(A2-x2+C cos⁡(Yx)), the eigenvalue shift is proportional to C ² , and the coefficient is complicated oscillating function of Y, n. The behaviour for sin(Yx) and small Y is reduced to the case of Fig. 1, the amplitude of higher intensity solitons grows with YC product.

4. Discussion and conclusion

The reduction of ZS scattering problem to Schrödinger equation with complex potential permits to use known exact solutions, which are more numerous, than for ZS. We use here the approximate equivalence; the exact correspondence exists between Satsuma and Yajima solution of ZS equation [¹⁵] with q(x) = A/ cosh(x) and complex Scarf potential of Schrödinger equation a/ cosh ² (x) + iß sinh(x) / cosh² (x). This case, however, seems to be more complicated, than the harmonic oscillator.

For multisoliton pulses with small chirp, the proposed method gives reasonable estimation for parameters of the biggest solitons, and the approximations serve as a useful guide for numerics. In particular, it is possible to predict to some extent if the solitons from a symmetric initial pulse will or not diverge on propagation (PT symmetry breaking). Parabolic pulses are analysed in detail, but similar analysis can be made for A/ cosh(x) and square pulses, also leading to analytically solvable Schrödinger problems. We also establish a relation of SCP and ZS, which can be interesting for testing experimentally SCP equations.