1. Introduction
In the past few decades, researchers are interested in several aspects of the non-Newtonian fluid which represents the non-linear relation between shear stress and shear rate. The flow diversity of non- Newtonian fluid model leads to uncertainty related to rheological features. One cannot explain the complete phase through single constitutive equation which establish the relation between deformation rate and shear stress. Shear thinning is the non-Newtonian behaviour of fluids whose viscosity decreases under shear strain. The non-Newtonian behaviour of fluids are of huge importance because of its usage at industrial and technological scales such as melting of polymers, paints, asphalts and glues. In view of its importance, many recent studies have been found on the flow of Newtonian and non-Newtonian fluids. One of the most commonly used rheological model and has certain advantages over non-Newtonian fluid models. Further, non-Newtonian flows from wedge phenomena arise in a number of chemical engineering systems. The Carreau (1972) viscosity model is known to be a good approximation for a large number of shear-thinning fluids due to its capability to catch the rheological behaviour at very low and very high shear rates, while other idealized models, like the widely used Ostwald de Waele power-law model, are valid only in a limited range of operational conditions. An analysis is carried out in order to highlight the importance of boundary layer flow in various industrial applications such as the condensation process of metallic plate in a cooling bath and glass, extrusion of plastic sheets, aerodynamic and also polymer industries. Mehta and Rao [1] had given the remarkable conclusions about non-Newtonian fluids in a porous medium past a vertical flat plate with non-uniform surface heat flux. Pascal and Pascal [2] give their analysis on non-Newtonian fluids along with some non-linear shear flows. Pressure drop through porous media in non-Newtonian purely viscous fluid flow examined by Sabiri and Comiti [3]. Some later works on the boundary layer flow of non-Newtonian fluids are presented in Refs. [4-10]. Etemad [11] explored the non-Newtonian fluid flow and heat transfer in three dimensional laminar phenomena. In case of ducts and porous media, Liu and Masliyah [12] gave their analysis on non-Newtonian fluid flow. Turbulent flow in a membrane tube with mass transfer in Newtonian and non-Newtonian fluids studied by Parvatiyar [13]. Slip-flow boundary conditions for non-Newtonian lubrication layers has been studied by Anderson and Valnes [14]. Also, some useful applications regarding non-Newtonian flow is observed by Hoyt [15]. Papalexandris [16] elaborates the study of wedge-induced detonations in numerical aspects. The theme beyond the flow of viscous incompressible fluid with thermal conductivity and temperature dependent viscosity past a permeable wedge aside by uniform surface heat flux is studied by Hossain et al. [17]. In Carreau model, fall of non-spherical particles in a liquid is studied by Machac et al. [18]. Moreover, various aspects regarding Carreau fluid models are investigated in Refs. [19-25]. The effects of peristaltic transport with magnetic field in a Carreau fluid is reported by Hayat et al. [26]. A numerical analysis is carried out upon sheardependent non-Newtonian fluids in compliant vessels reported by Hundertmark-Zauskova and Lukacova-Medvid’ova [27].
The Fourier laws are used frequently, to determine the characteristics of heat transfer phenomena. Cattaneo-Christov heat flux model is the rectified form of the Fourier law which is used to determine the specifications of heat flux model. A useful results regarding thermal convection in a Newtonian fluid with Cattaneo-Christov heat flux equations are explored by Straughan [28]. He observed that thermal relaxation parameter is notable as Cattaneo number increases Also, Straughan extended his work by considering the Cattaneo-Christov heat flux model in transverse waves [29]. Cattaneo equations with thermal stratification are analysed and their closed form solutions are discussed by Al-Qahtani and Yilbas [30]. The Cattaneo-Christov heat flux is applied to Newtonian fluids and uniqueness solutions are discussed by Tibullo and Zampoli [31]. The analytical solutions of thermal slip effects of a Maxwell fluid along with Cattaneo-Christov heat diffusion are discussed by Han et al. [32]. Also, the effects of elasticity, slip coefficient, and Prandtl number are shown through graphical representation. Haddad [33] examined the heat flux in a Brinkman porous channel embedded with fluid inertia. Shivakumara et al. [34] observed the thermal convection with Cattaneo effects in the solid and found that its impacts on the nature of convective instability are efficient. Mustafa et al. [35] studied the rotating flow upon linearly stretching disk. Nanofluids are taken into account to determine the behaviour of heat transfer rate through Cattaneo-Christov heat diffusion formula. Various specifications of Cattaneo-Christov heat flux model are discussed by Hayat et al. [36-37]. The characteristics of heat flux through Cattaneo-Christov model in a porous stretching sheet is analysed by Nadeem and Muhammad [38]. The Cattaneo-Christov model with non-Newtonian fluids through stretching regimes is carried out by Abbasi and Shehzad [39]. A theoretical approach for Cattaneo-Christov model embedded with different geometries are observed by Reddy et al. [40]. Li et al. [41] examined the heat flux for magneto-hydrodynamic (MHD) viscoelastic fluid through stretching sheet. Here, the energy equation have been obtained with the help of Cattaneo-Christov theory. Ramzan et al. [42] observed the homogenous-heterogeneous reactions for the third grade fluid merged with Cattaneo-Christov heat flux model. The specifications of heat transfer via Cattaneo-Christov model induced by a stretching cylinder is studied by Malik et al. [43]. The numerical scheme for Williamson fluid is discussed and Cattaneo-Christov model is applied to extract the characteristics of heat transfer Salahuddin et al. [44]. The heat conduction via Cattaneo-Christov heat flux through parallel plates in the presence of MHD is observed by Dogonchi and Ganji [45]. Upadhya et al. [46] studied the Cattaneo-Christov heat flux on time dependent fluids with MHD effects. The numerical approach for MHD fluid flow induced by a cone emerged with Cattaneo-Christov heat flux model is examined by Kumar et al. [47]. Further, the importance of Cattaneo-Christov heat diffusion is highlighted in Refs. [48-51].
As the heat conduction laws given by the French mathematician named Jean-Baptiste Joseph Fourier (1768-1830) have been used to investigate the heat transfer mechanism since two centuries in suitable conditions. Later on it was analysed that this law is not applicable in the case when the initial state is disturbed because it affects the whole system. To overhaul this problem, Cattaneo (1911-1979) had played his role to modify the Fourier law to get the hyperbolic equation by invoking thermal relaxation time. The above literature tells us that no work is done on Cattaneo-Christov heat diffusion model with heat generation and chemical reaction in concern with the motion of the Carreau nano-fluid. To fill the gap, this report is presented in order to ascertain the heat and mass flux rate through Cattaneo-Christov heat and mass diffusion formulas. In Sec. 1, the relevant literature survey is presented in order to enhance the importance of current work. In Sec. 2, the flow describing equations are modelled mathematically and the numerical technique i.e. Runge-Kutta Fehlberg method along with shooting scheme is applied to sort out the governing partial differential equations in Sec. 3. The impacts of various physical parameters upon fluid velocity, temperature and concentration are presented through graphs. Also, the numerical values for the skin friction coefficient and local Nusselt number are offered in Sec. 4. In Sec. 5, the results and discussion for the impacts of aforementioned physical parameters are exhibited. Finally, the concluding remarks are done in Sec. 6.
2. Mathematical formulation
The beauty of mathematics allows us to express the upper-convective material derivative for any vectors as follows.
where
where normal heat and mass flux are denoted by q and J, k
f
is the thermal conductivity, D
B
is the Brownian diffusion, λ
H
and λ
M
are the relaxation time of heat flux and mass flux. It is important to note down that λ
H
= 0 and λ
M
= 0 lead (2) and (3) to classical Fouriers law and Fick’s law, respectively. Now by inserting the condition for incompressible fluids i.e.
later on we will deduce the energy and mass equations with the help of Eq. (4) and (5). Consider the boundary layer flow for an incompressible Carreau fluid model impinged on a stretching surface where the flow is launched by the stretched sheet. The coordinate system is designed in a way that x-axis is taken to be along stretching sheet whereas y-axis is perpendicular to the sheet and the fluid overcomes at y > 0. The uniform magnetic field B 0 is invoked along y-direction whereas the induced magnetic field B 0 is supposed to be negligible for lesser magnetic Reynold’s number. The sheet velocity is considered as u w (x) = cx with c > 0 as stretching rate and the exterior velocity as u ∞ = ax where a is constant. The constitutive equations for the generalized Carreau model are taken as
where
By manipulating the above assumptions and usual boundary layer approximations, the governing equations for current problem are given as
where
The following dimensionless quantities are used to change the governing partial differential equations into scheme of ordinary differential equations.
where ψ is to notify as stream functions which is supposed to be satisfied by the continuity equations with u = ∂ψ/∂y and v = −∂ψ/∂x. By using the above transformations, the momentum and energy and mass equations with the concerned boundary conditions are
here,
are the velocity ratio parameter, magnetic field parameter, Weissenberg number, Prandtl number, Brownian diffusion coefficient, thermophoresis parameter, temperature relaxation time parameter, nanoparticle volume fraction, Lewis number, heat generation parameter and chemical reaction parameter.
The corresponding boundary conditions are as follows:
The involved physical quantities of engineering are skin friction coefficient and local Nusselt number and is defined as
where τ w is the surface shear stress and q w the surface heat flux given by
the dimensionless form of the local skin friction coefficient and the local Nusselt number are defined as:
where Re x = xu w /υ is the Reynolds number.
3. Computational algorithm
The governing equations Eqs. (11)-(13) are highly nonlinear in coupled form. The shooting algorithm with fourth-fifth or-der Runge-Kutta integration scheme is proposed in order to get the solution of this system. In this regard, we consider the following steps as follows:
The above set of higher order differential equations descend to a set of first order ordinary differential equations, we introduce new variables as follows.
by substituting these expressions, we get
the transformed boundary conditions are
the initial guesses for the values of f’’(0), θ ’ (0) and φ ’ (0) are y 3(0) = u 1, y 5(0) = u 2, y 7(0) = u 3.
The following procedure is done in order to solve the above system of equations by shooting method:
Firstly, choose the values of η ∞ between 5 and 10.
Then we pursue the initial guesses for y 3(0), y 5(0) and y 7(0). Initially, y 3(0) = y 5(0) = y 5(0) =1 are adopted.
Then we sort out the ODE’s by considering fourth-fifth order Runge-Kutta technique.
Finally, the absolute variations in the given and calculated values of y 3(∞), y 5(∞), and y 7(∞) that is boundary residuals are calculated. The solution is said to be convergent if it lies below the tolerance error, which is considered to be 10 -5 .
5. Results and discussion
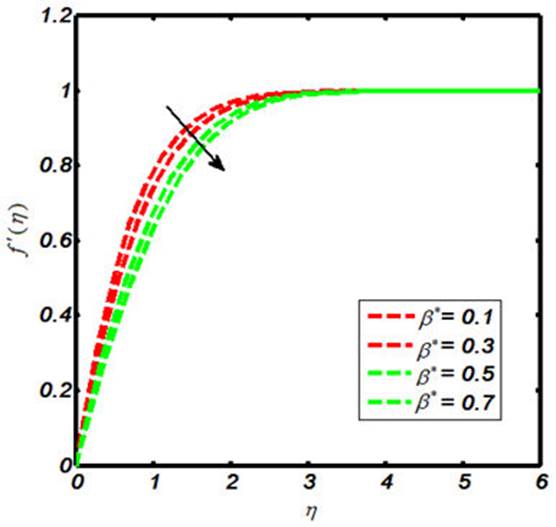
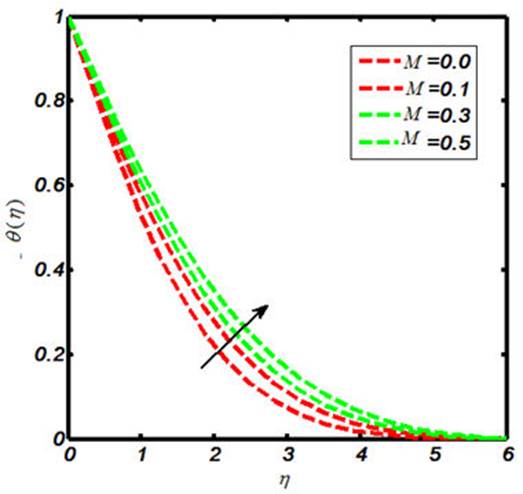
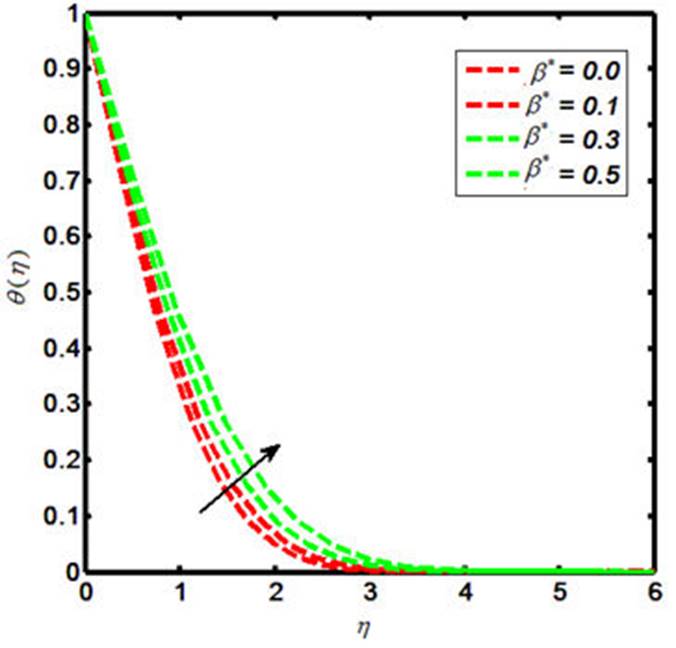
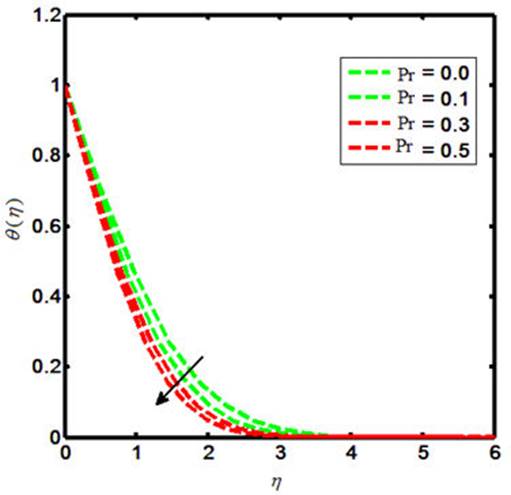
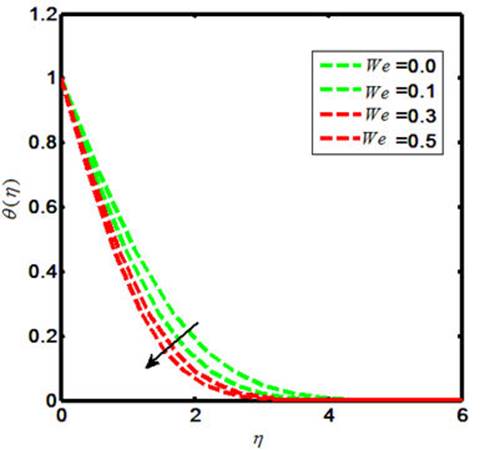
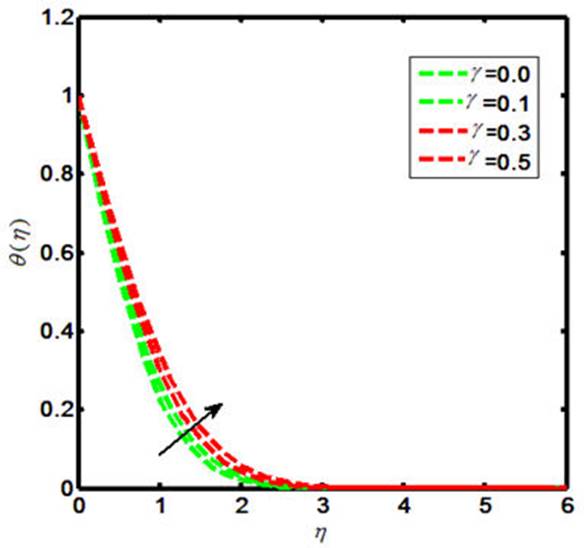
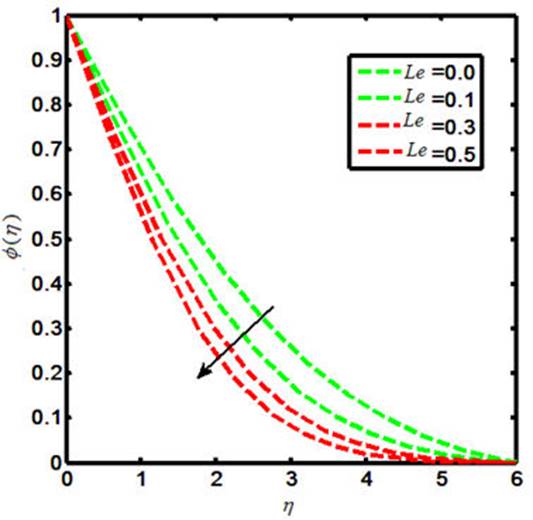
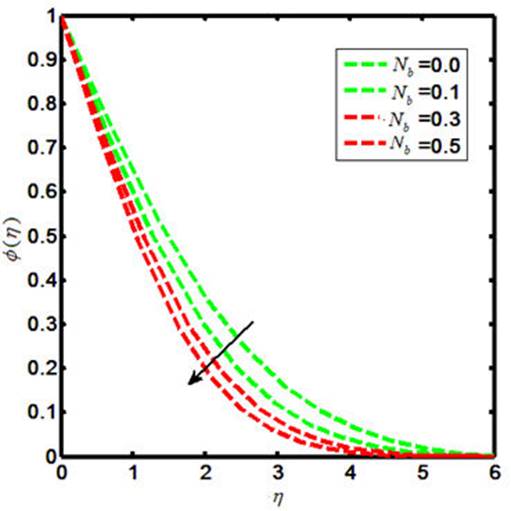
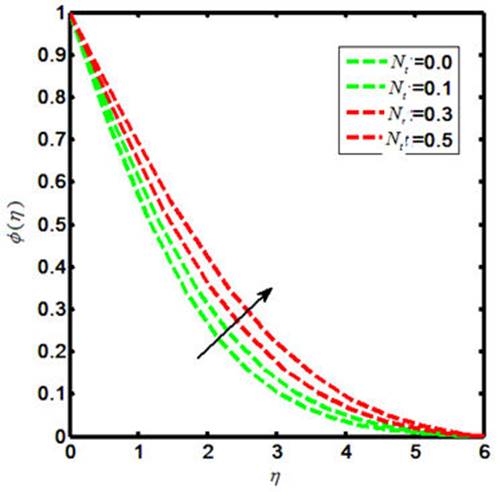
The Carreau nano-fluid with stagnation point flow towards a stretching sheet is debated in the present report. The Carreau nano-flow model is manifested with externally applied magnetic field. The energy and mass equations are presumed by the Cattaneo-Christov heat and mass flux model. The thermal boundary layer is executed with heat generation and chemical reaction. The laws of conversation of momentum and energy are used to describe the flow field that can be shown in the form of coupled partial differential equations. Later on, such equations are further reformed to coupled ordinary differential equations by declining the independent variables. The similarity transformation is considered in order to reduce the number of independent variables. The numerical results for the reduced system are sorted out by means of shooting technique with Runge-Kutta Fehlberg method. The involved physical parameters are M (magnetic field parameter), β* (viscosity ratio parameter), N B (Brownian motion parameter), N t (thermophoresis parameter), γ (heat generation parameter). The impacts of both the M and β* on the Carreau fluid velocity are investigated and provided by means of Figs. 1-2. Further, the influences of M, β*, Pr, W e and γ on the Carreau fluid temperature are explored and the results in this context are presented in Figs. 3-7. Also, the fluctuation in Carreau fluid concentration towards Le, N b and N t is acquired and shown in the form of Figs. 8-10. Now in detail, Fig. 1 indicates the influence of M on Carreau fluid velocity. It is testified that the fluid velocity shows the decline values towards M when M(= 0.0, 0.1, 0.3, 0.5) and this is due to the fact that increasing the values of M causes the enhancement of Lorentz force. This is a kind of resistive force that oppose fluid particles to move in a free manner and as result the average velocity of the Carreau fluid gets diminished. The influence of β* on a Carreau fluid velocity is observed and the fluctuation in this regard is captured in Fig. 2. When we iterate β*(= 0.1, 0.3, 0.5, 0.7), the velocity profile declines. The Carreau fluid temperature relies upon the variation of M, β*, Pr, W e, γ. To be more specific, the effects of M on a Carreau fluid temperature is inspected and the results are presented in the form of Fig. 3. The enhancing values of causes uplift in the Carreau fluid temperature. Figure 4 indicates the fluctuation in Carreau fluid temperature due to β* and thus testifies that the temperature enlarges as β*(= 0.1, 0.3, 0.5, 0.7). Figures 5-6 show the impacts of Pr and W e upon Carreau fluid temperature. This presents the picture of temperature profile getting decline towards Pr = (0.0, 0.1, 0.3, 0.5) and W e = (0.0, 0.1, 0.3, 0.5). Figure 7 is prepared to describe the link between heat generation and Carreau fluid temperature. On iterating the values of γ i.e. γ(= 0.0, 0.1, 0.3, 0.5), one can observe that Carreau fluid temperature enhances. This is due to the fact that the production of heat energy emits heat particles that causes increase in temperature. The influence of Carreau fluid concentration towards Le is offered in Fig. 8. This picture shows the decaying trend for Carreau fluid concentration towards Le(= 0.0, 0.1, 0.3, 0.5). Figure 9 depicts the fluctuation in the fluid concentration corresponding to multiple values of Brownian motion parameter N b . The larger values of N b (= 0.0, 0.1, 0.3, 0.5) causes reduction in the fluid concentration as well as the related boundary layer thickness. This is because of the Brownian force confined the fluid particles to move in the reverse direction of the concentration gradient and causes the fluid more consistent. Thus, the uplifting values of N b causes the lower concentration gradient and more uniform concentration profile. Figure 10 delineated the impacts of N t on the Carreau fluid concentration φ(η). Here the fluid concentration and the corresponding boundary layer thickness increases for higher values of N t i.e. N t (= 0.0, 0.1, 0.3, 0.5). Physically the thermophoretic force implies to oppose the nanoparticles against the direction of temperature gradient. This may also cause the nano-particles in a fluid concentration to be more non-unifrom. Thus the concentration gradient enhances for large values of N t and causes for more non-uniform fluid concentration. The variation of skin friction coefficient corresponding to various values of M, W e, α and β* are shown in Table I. It is testified that excellent match is captured for current results with the existing literature [52]. Also, the numerical values for the local Nusselt number towards various values of Pr, Nt and N b are delineated in Table II.
Table I The numerical values for the skin friction in comparison with [52].
| M | W e | α | β * |
|
Current results |
|---|---|---|---|---|---|
| n = 1.75 | n = 1.75 | ||||
| 0 | 3 | 0.3 | 0.001 | -1.053800 | -1.0537 |
| 0.3 | 3 | 0.3 | 0.001 | -1.090060 | -1.0901 |
| 0.6 | 3 | 0.3 | 0.001 | -1.194930 | -1.1954 |
| 0.8 | 3 | 0.3 | 0.001 | -1.298290 | -1.29830 |
| 0.3 | 2 | 0.3 | 0.001 | -1.012570 | -1.0126 |
| 0.3 | 3 | 0.3 | 0.001 | -1.090060 | -1.0901 |
| 0.3 | 3.5 | 0.3 | 0.001 | -1.125350 | -1.1252 |
| 0.3 | 4 | 0.3 | 0.001 | -1.158450 | -1.1586 |
| 0.3 | 3 | 0.7 | 0.001 | -1.090060 | -1.0901 |
| 0.3 | 3 | 1.3 | 0.001 | -0.490977 | -0.4910 |
| 0.3 | 3 | 0.3 | 0.001 | 0.598867 | 0.5989 |
| 0.3 | 3 | 0.7 | 0.001 | 1.827620 | 1.8277 |
| 0.3 | 3 | 1.3 | 0.001 | -1.090210 | -1.0901 |
| 0.3 | 3 | 1.7 | 0.001 | -1.059190 | -1.0592 |
| 0.3 | 3 | 0.3 | 0.0 | -1.024390 | -1.0244 |
| 0.3 | 3 | 0.3 | 0.2 | -1.007155 | -1.0073 |
Table II The numerical values of local Nusselt number (-θ 0 (0)) towards various values of Pr, N t and N b .
| Pr | N t | N b | Re -1/2 Nu x = -θ ’ (0) |
|---|---|---|---|
| 1.0 | 0.2 | 0.3 | 0.31492 |
| 1.0 | 0.2 | 0.3 | 0.2141 |
| 1.0 | 0.2 | 0.3 | 0.2765 |
| 1.0 | 0.2 | 0.3 | 0.3166 |
| 3.0 | 0.3 | 0.3 | 0.3234 |
| 3.0 | 0.3 | 0.3 | 0.2902 |
| 3.0 | 0.3 | 0.3 | 0.2861 |
| 3.0 | 0.3 | 0.3 | 0.2397 |
| 5.0 | 0.5 | 0.3 | 0.2921 |
| 5.0 | 0.5 | 0.3 | 0.3327 |
| 5.0 | 0.5 | 0.3 | 0.2690 |
6. Concluding remarks
The current report elaborates the specification of Cattaneo-Christov heat diffusion formula merged with the Carreau nano-fluid flow at a stagnation point. The energy and mass equations are manifested with heat generation and chemical reaction whereas the flow is caused by the stretching sheet. The governing PDE’s descend to ODE’s through similarity transformations. The numerical results are deduced with the aid of Runge-Kutta Fehlberg technique with shooting proficiency. The numerical findings for the skin friction coefficient and the local Nusselt number are deduced. The key points are as follows:
The Carreau fluid velocity trend is observed as declined towards M.
The higher values of β* causes the decreasing trend for Carreau velocity profile.
The Carreau fluid temperature enhances corresponding to higher values of M.
It is observed that the Carreau fluid temperature increases by uplifting β* and γ.
The temperature trend for the Carreau fluid model testifies the decline towards Pr and W e.
The Carreau fluid concentration profile decreases for growing values of Le.
The investigation tells us that Carreau concentration trend diminish when enlarging N b .
On uplifting the values of N t , we get the increasing trend for Carreau concentration profile.
Nomenclature
u, v |
Velocity component in x-, y-directions (m/s) |
x |
Direction along the surface (m) |
y |
Direction normal to the surface (m) |
T |
Temperature of the fluid (K) |
T w |
Temperature at sheet (K) |
μ |
Dynamic viscosity (Ns/m2) |
c p |
Specific heat capacity at constant pressure (J/ KgK) |
λ H |
Relaxation time of heat flux |
k f |
Thermal conductivity (W/mK) |
(pc p ) f |
Effective heat capacity (Kg/ m3K) |
T ∞ |
Temperature away from the sheet (K) |
ρ |
Density of the fluid (Kg/m3) |
D B |
Brownian diffusion coefficient |
|
Brownian motion parameter |
|
Relaxation time parameter of temperature |
|
Coefficient for thermal diffusion (m2/s) |
f ’ (η) |
Dimensionless velocity |
φ(η) |
Dimensionless temperature |
σ |
Electrical conductivity |
q |
Heat flux |
|
Lewis number |
|
Nano-particle volume fraction |
Γ |
Material time constant |
|
Magnetic field parameter |
υ |
- Kinematic viscosity (m2/s) |
γ, δ |
- Dimensionless parameter |
η |
- Similarity variable |
k o |
- Reaction rate |
|
Reynold number |
|
Ratio of nanoparticles heat capacity and the base fluid heat capacity |
q w |
Surface heat flux |
τ w |
Surface shear stress |
D T |
Thermophoresis diffusion coefficient |
|
Thermophoresis parameter |
|
Viscosity ratio parameter |
|
Velocity of exterior flow |
|
Velocity ratio parameter |
|
Weissenberg number |
μ 0 , μ ∞ |
Zero and infinite shear rate viscosity |
|
Prandtl number |











 text new page (beta)
text new page (beta)