1. Introduction
Recently, the discoveries of the giant magnetoresistance (GMR) and tunneling magnetoresistance (TMR) [1,2] opened the line of research called spintronics. Spintronics are composed of materials for which only one spin channel presents a gap at the Fermi level, while the other has a metallic character, leading to 100% carrier spin polarization at the Fermi energy (E F ) [3]. Therefore, these materials utilize the spin in addition to the charge of electrons to carry the current. These remarkable materials, and their relatives (a vast collection of more than 3000 compounds) are today known as Heusler and half-Heusler compounds, have been discovered in 1903 when Friedrich Heusler had shown that Cu2MnAl alloy behaves ferromagnetically even though none of its constituent elements are magnetic [4]. In 1983, de Groot et. al. [5] discovered half-metallic ferromagnetism in semi-Heusler compound NiMnSb by using first-principle calculation based on density functional theory. They first attracted interest of the magnetism community due to their high Curie temperatures [6] and being predicted to be half metallic ferromagnets [7]. In recent years, Heusler compounds are investigated due to their potential application in spintronics, green-energy-related fields, such as solar cells or thermoelectrics, superconductors [8], ferromagnetic shape memory alloys [9] and magnetic actuator [10].
Cu2MnZ compounds have attracted much theoretical and experimental attention [11-13] for magneto-resistive device applications. The results, of Oxley et al. [14], are given of comprehensive measurements on the magnetic and crystallographic properties of the ferromagnetic Heusler alloys Cu2MnZ (Z = Al, In, Sn, Ge, Sb, Bi and Ga), and they also discussed the indierct exchange effects which may give rise to ferromagnetism and antiferromagnetism in Heusler alloys. Dunlap et. al. [15] have studied the effects of rapid quenching on the structural and magnetic properties of the Heuler alloy Cu2MnSn. Buschow et. al. [16] have studied the magneto-optical properties of metallic ferromagnetic materials Cu2MnZ (Z = Al, Sn and In). Entel et. al. [17] computed the lattice parameters, magnetic moments, types of magnetic order and valence electron to atom ratios for series of Heusler compounds with the L21 structure, such as Cu2MnZ (Z = Al, Ga and In). Hamri et. al. [18] illustrated that all the studied ferromagnetic systems X2MnSn (X = Cu, Ni, Pd) exhibit a metallic character and possess an interesting elastic constants.
Besides ternary X2YZ compounds, there exist also large assortments of substitutional quaternary alloys of the type X2Y 1-x Y’ x Z, (X 1-x X’ x )2YZ and X2YZ 1-x Z’ x . One of the substitutional series that attracted interest as potential material for magneto-electronics was Co2Cr 1-x Fe x Al [19]. Drawback of these series is that it is hard to be stabilised in the L21 structure. Later, Seema et. al. [20] have investigated the effect of substitution of main group element on the electronic structure and magnetic properties of Co-based quaternary Heusler compounds Co2CrGa 1-x Ge x (x = 0-1) using first-principles density functional theory. Paudel et. al. [21] have studied the mechanical stability and physical properties of Co2V 1-x Zr x Ga (x = 0, 0.25, 0.50, 0.75, 1) by utilizing ab-initio calculations based on density functional theory within GGA-PBE, GGA+U and the quasi-harmonic Debye model.
Recently, Benichou et. al. [22] have investigated the structural, elastic, electronic and magnetic properties of quaternary Heusler alloy Cu2MnSi 1-x Al x (x = 0 - 1) using a first-principles calculation by substituting the main group element (Si by Al) in this compound. The Cu2MnSi 1-x Al x alloy is found to be ferromagnetic, metallic compound and has a ductile behavior. In this paper, we systematically study the effect of alloying Cu2MnSn full Heusler alloy with In, namely, Cu2MnSn 1-x In x (x = 0, 0.25, 0.5, 0.75, 1) alloy. To the best of our knowledge, there are no experimental and theoretical works exploring Cu2MnSn 1-x In x quaternary alloy. The study was based on a full-potential augmented plane wave method within the framework of density functional theory.
The remainder of this paper is arranged as follows : In Sec. 2, we give with a brief description of the method used and details of the calculations. Section 3 deals with the crystal structural aspects. In Sec. 4, the structural parameters, elastic constants, magnetic and the electronic properties, for the full-Heusler compounds of the type Cu2MnZ, where Z stands for Sn and In, and their quaternary alloy Cu2MnSn 1-x In x (x = 0.25, 0.5, 0.75), are presented and analyzed. Finally, conclusions are summarized in the last section. The present calculations provide predictions and may serve for a reference.
2. Computational details
In the present study, the first principles calculations are performed within the full potential linearized augmented plane wave (FP-LAPW) method [23] as implemented in the WIEN2k code [24], based on the density functional theory (DFT) [25,26]. The exchange and correlation potential was calculated using the generalized gradient approximation [27]. The plane wave parameter R MT × K max was 7.0, and to ensure the correctness of the calculations, we have taken l max = 10. The G max parameter was taken to be 12.0. The separation energy between the core and the valence states has chosen as -7.0 Ry. Thus, the atomic sphere radii were set to 2.2, 2.0, 2.0 and 2.5 a.u. (atomic unit) for Cu, Mn, Sn and In atoms, respectively. The number of k-points used in the irreducible part of the Brillouin Zone are 286 and 4 for ternary and quaternary alloys respectively, which give convergence of 10-4 Ry in the total energy.
3. Crystal Structure
Full-Heusler alloys are represented by the generic formula X2YZ, where X and Y denote transition metals and Z is an s - p element. The atomic positions described with the Wyckoff coordinates for X (Cu) atoms are (1/4,1/4,1/4), (3/4,3/4,3/4), while (1/2,1/2,1/2) for Y (Mn) and for Z (Sn, In) it is (0,0,0). In Fig. 1, we show the crystal structure of Cu2MnSn 1-x In x (x = 0, 0.25, 0.5, 0.75, 1) alloys, where the present structures composed of four interpenetrating face-centered-cubic (fcc) sublattices, with L21 phase and F m - 3m, space group no. 225. To simulate Cu2MnSn 1-x
Figure 1 Crystal structure of the Cu2MnSn 1-x In x (x = 0, 0.25, 0.5, 0.75, 1) alloys obtained with XCrysDen.
Al x quaternary alloys, we consider a (2 × 2 × 2) supercell eight times greater than L21 unit cell. The supercell is then constituted of 32 atoms; 16 Cu, 8 Mn and 8 Sn/In, as shown in Fig. 1. The Sn atoms are replaced by In atoms to simulate dif-ferent concentrations. Replacement of 2, 4, 6 and 8 number of those eight Sn atoms by In atoms leads to Cu2MnSn 1-x In x (x = 0.25, 0.5, 0.75, 1) respectively.
4. Results and discussion
4.1. Structural properties
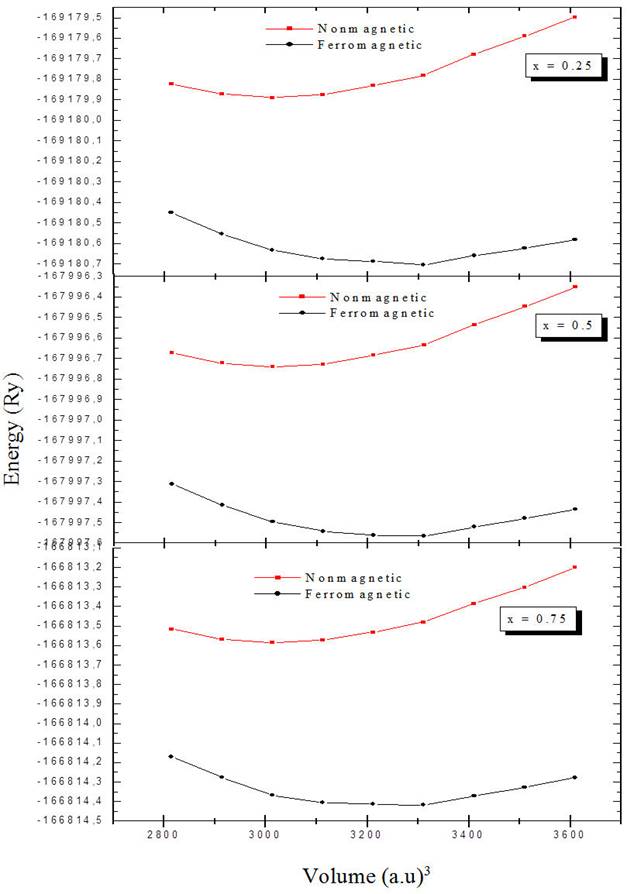
The equilibrium lattice constants, bulk modulus and their first pressure derivatives, which are quoted in Table I, are fitting by the computed total energies to the empirical Murnaghan’s equation of state [28]. We have done structural optimization of Cu2MnSn 1-x In x (x = 0.25, 0.5, 0.75) Heusler alloys by using nonmagnetic (NM) and ferromagnetic (FM) states. The plot of total energy variation versus volume under both non-magnetic and ferromagnetic phases with different concentrations is shown in Fig. 2. Clearly FM state is favorable in energy than the corresponding NM state. The optimized lattice constants for Cu2MnSn and Cu2MnIn alloys, which are also given in Table I, are in fairly good accordance with available experimental data [14,19] and previous theoretical calculations [16-18]. The maximal error for lattice parameters is less than 1.0%. To the best of our knowledge, there are no comparable studies about Cu2MnSn 1-x In x (x = 0.25, 0.5, 0.75) in literature, so we estimated the lattice parameters, for the selected concentrations 0.25, 0.5 and 0.75 by using the Vegard’s law [29] in Eq. (1).
Table I Calculated lattice parameter (a), bulk modulus (B), its pressure derivative (B’), and equilibrium energy for the Cu2MnSn 1-x In x (x = 0.25, 0.5, 0.75, 1) Heusler alloy.
| Compounds | a 0 (Å) | B (GPa) | B’ | E FM (Ry) |
|---|---|---|---|---|
| Cu2MnSn | 6.2432 | 100.9400 | 4.8760 | -21295.589815 |
| 6.24 [18] | 105.33 [18] | |||
| 6.2337 [30] | 101.31 [30] | |||
| 6.26 [Theo,31] | ||||
| 6.17 [Exp,32] | ||||
| 6.168 [16] | ||||
| 6.1674 [17] | ||||
| 6.173 [Exp,14] | ||||
| Cu2MnSn 1-0.25 In 0.25 | 6.22075 | 103.0271 | 3.0794 | -169180.697401 |
| Cu2MnSn 1-0.5 In 0.5 | 6.21615 | 109.5466 | 2.9170 | -167997.563381 |
| Cu2MnSn 1-0.75 In 0.75 | 6.202 | 113.0188 | 4.4334 | -166814.419381 |
| Cu2MnIn | 6.1957 | 107.8258 | 4.1911 | -20703.994345 |
| 6.2021 [Theo,30] | 106.96 [Theo,30] | |||
| 6.206 [16] | ||||
| 6.206 [Exp,14] |
4.2. Elastic properties
We now discuss the mechanical properties of the parent compounds Cu2MnSn, Cu2Mnln and Cu2MnSn 1-x In x (x = 0.25, 0.5, 0.75) quaternary alloy, in order to confirm their mechanical stability in a cubic structure via calculation of the elastic constants (C ij ). These constants are fundamental and indispensable for describing the mechanical properties of materials because they are closely related to various fundamental solid-state phenomena, such as the stuctural stability, the bonding character between adjacent atomic planes and anisotropic character. The elastic constants require knowledge of the derivative of the energy as a function of lattice strain. In the case of cubic system, there are only three independent elastic constants, namely, C 11, C 12 and C 44. The traditional mechanical stability conditions for a cubic stucture, which are known as the Born Huang criteria [33], are defined as follows: C 11 - C 12 > 0, C 11 > 0, C 44 > 0, C 11 + 2C 12 > 0 and C 12 < B < C 11. The obtainted elastic constants C ij , summarized in Table II, are calculated by using a numerical first-principles method within GGA approximation in the WIEN2k package. The bulk modulus calculated from the theoretical values of the elastic constants B = (1=3)(C 11 + 2C 12) are listed in Table II too, and it has nearly the same values as the ones obtained from energy minimization. As seen from Table II, the computed elastic constants of Cu2MnSn 1-x In x for all compositions are positive and satisfy the above mechanical stability criteria indicating that the structures under study are elastically stable phases. The obtained results for Cu2MnSn and Cu2MnIn alloys agree quite well with earlier ab-initio calculation in Ref. [18] and that of Ref. [30] respectively. Within best of knowledge, there is no report on the experimental and theoretical elastic constants on the quaternary alloy. Therefore, our results are considered as purely predictive.
Table II Calculated elastic constants (in GPa), and elastic moduli B (in GPa), G (in GPa), B/G, E (in GPa), v, A, ξ for Cu2MnSn 1-x In x (x = 0, 0.25 0.5, 0.75, 1).
| Compounds | C 11 | C 12 | C 44 | B | G | B/G | E | v | A | ξ |
|---|---|---|---|---|---|---|---|---|---|---|
| Cu2MnSn | 118.654 | 95.908 | 65.330 | 103.319 | 37.344 | 2.766 | 99.987 | 0.338 | 5.74 | 0.866 |
| 102.03 [18] | 91.71 [18] | 66.81[18] | ||||||||
| 105.93 [30] | 99.00 [30] | 64.75 [30] | ||||||||
| Cu2MnSn 1-0.25 In 0.25 | 244.905 | 48.936 | 191.087 | 114.085 | 146.153 | 0.780 | 307.254 | 0.051 | 1.95 | 0.351 |
| Cu2MnSn 1-0.5 In 0.5 | 319.038 | 14.453 | 220.733 | 115.666 | 190.228 | 0.608 | 368.609 | 0.031 | 1.44 | 0.192 |
| Cu2MnSn 1-0.75 In 0.75 | 261.499 | 91.386 | 131.115 | 147.994 | 110.231 | 1.342 | 264.920 | 0.201 | 1.54 | 0.493 |
| Cu2MnIn | 121.635 | 101.562 | 74.228 | 108.489 | 34.705 | 3.125 | 94.084 | 0.355 | 7.39 | 0.885 |
| 114.45 [30] | 103.22[30] | 78.26 [30] |
Besides this, we have also calculated various combinations of elastic moduli such as, Voigt’s shear (G V ), Reuss’s shear (G R ), Shear modulus (G), Young’s modulus (E), Poisson’s ratio (V), anistropy factor (A) and Kleinman parameter (ξ), which are listed in Table II, using the following equations [34-36]:
where G is the shear modulus, G V is Voigt’s shear modulus corresponding to the upper bound of G values and G R is Reuss’s shear modulus corresponding to the lower bound of G values.
In order to predict the brittle and ductile behavior of materials, Pugh [37] proposed an approximate criterion by the ratio B/G. Higher (lower) B/G ratio corresponds to ductile (brittle) behavior, and the critical value that separates brittle and ductile materials is about 1.75. The calculated values, listed in Table II, indicate that the B/G ratios are 2.766 and 3.125 for Cu2MnSn and Cu2MnIn respectively, suggesting the ductile nature of the parent ternary alloys, but for Cu2MnSn 1-x In x quaternary alloys, the values of B/G ratio are between 0.608 and 1.342 indicating their brittle nature.
The Young’s modulus (E) characterizes the stiffness of a material. The higher value of E, stiffer is the material. It can be seen, from Table II, that Cu2MnSn is stiffer than Cu2MnIn, and Cu2MnSn 1-x In x quaternary alloy is also stiffer for the concentration x = 0.5 than x = 0.25 and 0.75. We also note that this quaternary alloy has a high Young’s modulus, what classifies the studied compound as a strong incompressible material. The value of Poisson’s ratio (v) is indicative of the degree of directionality of the covalent bonds. Its value for covalent materials is small (v < 0.1), whereas the typical value for ionic materials is 0.25. Our calculated Poisson’s ratios vary from 0.201 to 0.355, so the contribution in the intra-atomic bonding for Cu2MnSn, Cu2MnIn and Cu2MnSn 1-0.75 In 0.75 alloys is ionic, whereas for Cu2MnSn 1-x In x (x = 0.25 and 0.5), v is less than 0.1 suggesting a covalent material. Elastic anisotropy factor (A) is equal to one for completely isotropic nature, while any different value shows anisotropy. The magnitude of the deviation from 1 is the measure of the degree of elastic anisotropy of the crystal. The calculated values of A factor shows that Cu2MnSn 1-x In x alloy is anisotropic by nature. It is seen from the Table II that all the herein materials are anisotropic in nature but both the parent ternary compounds are more anisotropic than their quaternary alloy.
4.3. Electronic properties
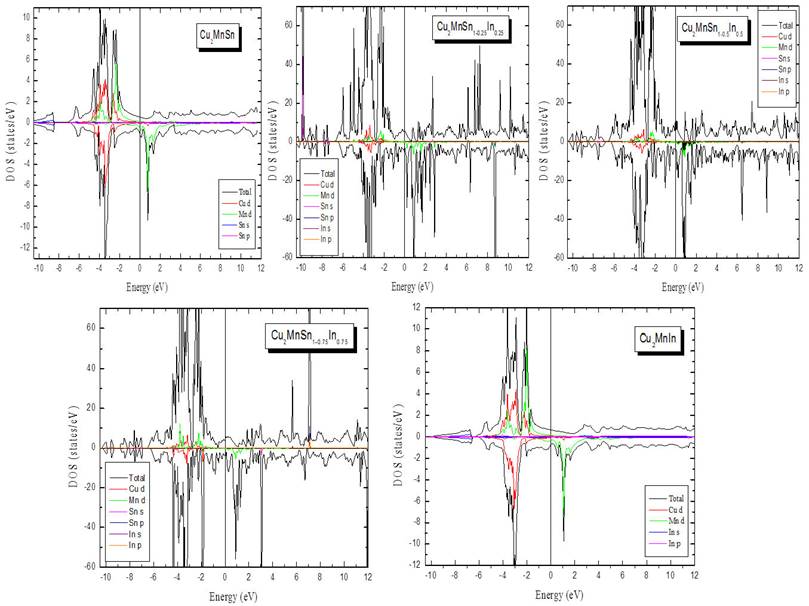
Here, we study our results of electronic properties of Cu2MnSn 1-x In x alloys by calculating the density of states (DOS) which is important for understanding the bonding properties. Therefore, the total (TDOS) and partial (PDOS) densities of states for spin-up and spin-down, using the GGA approximation, are calculated and depicted in Fig. 3. It is clear from Fig. 3 that both majority (up) and minority (down) spin band structures of Cu2MnSn 1-x In x are strongly metallic. As seen from Fig. 3, there are two distinct regions in the spin-up and spin-down states of DOS of the parent Heusler alloys. The lowest valence bands below -8 eV for Cu2MnSn (below -6 eV for Cu2MnIn) are formed entirely from the s-states of Sn/In, while the bands from -6 to 4 eV for both Cu2MnSn and Cu2MnIn are principally caused by the Cu and Mn 3d-states. Our results for Cu2MnSn are in quite good agreement with earlier ab-initio calculations [18]. Morever, for Cu2MnSn 1-x In x quaternary alloy, the mainly parts of the total densities of states localized around -4 to 3 eV are chiefly governed by the 3d-states of Cu/Mn atoms.
4.4. Magnetic properties
The calculated total and local spin magnetic moments for Cu2MnSn 1-x In x quaternary Heusler alloys are reported in Table III. It is clear from this table that our predictive results show that the total magnetic moments, which include the contribution from the interstitial region, comes mainly from the Mn atom, while the Sn, In and Cu atoms have a very small moment. Actually in Ni2MnZ and Cu2MnZ alloys, the magnetic moment cannot be substantial larger than the magnetic moment on Mn atoms because only Mn determined the magnetic behavior of these alloys [38]. Morever, in case of ternary parent Cu2MnSn and Cu2MnIn full-Heusler alloys, the calculated value of spin magnetic moments 3.91483 and 3.75798 respectively, are listed in Table III which are close to earlier obtained theoretical data [30,14] and experimental result by Webster et al., [39] which are also reported in Table III. The local spin magnetic moment on the non-transition metal atoms Sn (In) is small and aligned parallel (anti-parallel) to that of the Cu and Mn atoms. As far as we are aware, there are no reports on the magnetic moments for the quaternary alloy.
Table III Calculated values of total and partial spin magnetic moments (in μ B ) of Cu2MnSn 1-x In x (x = 0, 0.25, 0.5, 0.75, 1).
| Compounds | M Cu | M Mn | M Sn | M In | Minterstitial | Mtotal |
|---|---|---|---|---|---|---|
| Cu2MnSn | 0.040 | 3.507 | 0.00004 | − | 0.327 | 3.914 |
| 0.03 [18] | 3.73 [18] | 3.93 [18] | ||||
| 4.11 [Exp,39] | ||||||
| 0.04 [Theo,40] | 3.79 [Theo,40] | 3.81 [Theo,40] | ||||
| 3.89 [17] | ||||||
| Cu2MnSn 1-0.25 In 0.25 | 0.057 | 3.529 | 0.001 | -0.030 | 0.375 | 4.012 |
| Cu2MnSn 1-0.5 In 0.5 | 0.053 | 3.500 | 0.002 | -0.039 | 0.344 | 3.933 |
| Cu2MnSn 1-0.75 In 0.75 | 0.030 | 3.426 | 0.003 | -0.053 | 0.279 | 3.726 |
| Cu2MnIn | 0.037 | 3.490 | − | -0.052 | 0.245 | 3.757 |
| 3.7879[Theo,30] |
5. Conclusion
In summary, we have extensively investigated the structural parameters, elastic and mechanical, electronic and magnetic properties of the Cu2MnSn 1-x In x quaternary alloy by utilizing first-principle calculations based on density functional theory within GGA-PBE. The optimized lattice parameters and spin magnetic moments for the parent full-Heusler alloys Cu2MnSn and Cu2MnIn were in qualitative agreement with the available experimental and theoretical data. Also, our predicted lattice constants of the quaternary alloy, in the stable magnetic configuration, exhibit a high tendancy with the estimated values by Vegard’s law. The spin resolved density of states revealed that all the herein studied compounds have a perfect ferromagnetic and metallic character. The magnetic properties show that for these ferromagnetic compounds, the partial moment of In being antiparallel to the Cu, Mn and Sn atoms. The Mn atom is responsible for large magnetic moment in case of the ternary and quaternary Heusler alloys under study. Furthermore, according to mechanical stability conditions, our obtained elastic constants indicate that the Cu2MnSn 1-x In x quaternary Heusler alloy is mechanically stable, anisotropic and has a brittle behavior. Most of the studied properties for Cu2MnSn 1-x In x (x = 0, 0.25, 0.5, 0.75, 1) Heusler alloys, reported in this work, have not previously been established experimentally or theoretically. Finally, we hope that our results could provide baseline data for future investigations.











 text new page (beta)
text new page (beta)