1. Introduction
Deformations of phase space have been studied extensively since the first proposal by Heisenberg and formalized by Snyder [1], this to understand the effects of noncommutativity in many physical theories [2-4], where most of the arguments are motivated from string theory [5]. Topics of noncommutative deformations of gravity have been proposed in [6,7], the Seiberg-Witten map in [8,9] is used consistently to write a noncommutative theory of gravity. In [10-12] the authors consider an alternative to incorporate noncommutativity to cosmological models, this through deforming the minisuperspace variables. Apart from the advances mentioned, noncommutativity has been included in the context of classical and quantum mechanics [13], performing explicit calculations devoted to noncommutativity of the cannonical type was presented by [14,15]. In this sense, noncommutative Minkowski space satisfy the commutation relations
where xμ, μ = 0, ldots, 3 and θμv is an antisymmetric tensor. In the most of literature it is quite common to consider only space coordinate deformed. Nevertheless, in this work will be considered space-space coordinate variables and momentum-momentum as noncommutative, this as an alternative to study quantum mechanical effects. In particular, we present a two-dimensional anharmonic oscillator in noncommutative coordinates and momentum variables and show the eigenvalues correction Enx,ny versus the noncommutative parameters θ and ϕ. Excited states are graphically illustrated. Section 2 is devoted to the study of the anharmonic oscillator under the influence of the noncommutative variables, Sec. 3 to discussion and conclusions.
2. The Model
In quantum mechanics, there are only few problems whose Hamiltonians can be solved exactly, for example the Harmonic oscillator. However, small perturbations in the Hamiltonian may result the problem have no longer an exact solution, in these cases we have to use perturbation theory which is one of the methods of approximation for solution to eigenvalue problems in quantum mechanics [16,17]. The two dimensional oscillator have many symmetries which are manifest as degeneration in the energy levels. Nevertheless, perturbations and noncommutativity could break these symmetries and produce energy level splitting. In this perturbation theory one needs to solve the Hamiltonian of the type:
where H0 is the unperturbed Hamiltonian, which can be solved exactly and αH1 the perturbation term. However, for any arbitrary Hamiltonian, one has to use methods of approximations [16], as in the special case of the anharmonic oscillator
which is used frequently to test new approximation techniques since the calculation of the fundamental physics as the eigenvalues and eigenfunctions leads to challenging mathematical problems.
For our purpose, the noncommutative quantum oscillator is characterized by a generalized canonical structure of the form:
with i,j = 1, 2, ∈
i,j
is totally antisymmetric tensor in two dimensions, θ and
ϕ are the noncommutative parameters in phase space, [18-21] and σ = ħ + (θϕ /
4ħ). Further
In noncommutative space where the motivations are mainly theoretical, one replaces the ordinary product between functions by the Moyal or star product as in [13]. The noncommutative variables can be solved in terms of the ordinary quantum mechanics variables
where xi and pi satisfy the Heisenberg usual algebra and xi, pi θ and ϕ are the noncommutative variables and parameters respectively.
In two dimensional noncommutative phase space, the coordinates operators (5) are expressed in terms of commuting coordinates and their momenta as:
For the very specific case where a d-dimensional (2 ≤ d) oscillator with the phase space variables deformed, we can construct the two-dimensional noncommutative quantum mechanical anharmonic oscillator as:
where p̑x,
p̑y , x̑ and ŷ are the
noncommutative terms expressed by (6)
and
Now let us first begin with the noncommutative unperturbed Hamiltonian which can be viewed in terms of usual quantum mechanics variables in the form:
where M, Ω and k are defined as:
In order to find the eigenvalues of H0 it is convenient to introduce the ladder operators:
Hence the unperturbed non-diagonal Hamiltonian is given by:
The products ax ax† and ay ay† are number operators and the Hamiltonian is non-diagonal by the mixing term ax† ay ─ ay† ax. To diagonalize (11) we make use of unitary transformations
then the Hamiltonian (11) becomes:
The operators a’i and a’†j satisfy the same relations of commutation as ai and a†j , therefore we can identify a’i a’†j as number operators. The eigenvalues of this unperturbed Hamiltonian are therefore:
where nx ,ny are non-negative integers. We observe that these eigenvalues are non-degenerated.
Even in the commutative theory the anharmonic term is non-diagonal and can’t be solve exactly, this is studied in perturbation theory. In view that energies are non-degenerated we can use non-degenerated perturbation theory. To first order the shifts of the energies are given by the expectation value:
The action of α(x̑2 + x̑2)2 on the element | nx ,n y 〉(0) of the Fock basis contains a superposition of states, and one of them is the proper | nx, ny 〉(0)
The correction to the energies are C(0)nx,ny. To find this we write (x̑2 + ŷ2) in function of the ladder operator under the unitary transformation (12)
where β and γ are:
Next, we apply (x̑2 + ŷ2) two times on |nx, ny 〉(0). The result is:
Choosing m = ℏ = ω = 1, the nth energy level is given by:
where:
As stated above, the energy levels of the unperturbed Hamiltonian are non-degenerated, this new feature generated by the two-dimensional oscillator in a noncommutative plane could have an important impact on our conception of the quantum structure of physical systems. This deserves further investigation to give an appropriate interpretation. However, the fundamental idea is to assume that both eigenvalues and eigenvectors of the Hamiltonian under consideration can be expanded in powers of the perturbation parameter α to determine the coefficients in the perturbative expansions. In this way, we show the effects of noncommutativity on energy levels corrected to first order in perturbation theory performing the spectrum of energies in terms of the noncommutative parameters, this energy can be written as:
An exhaustive analysis of quantum operators in the noncommutative plane are treated in [22,23].
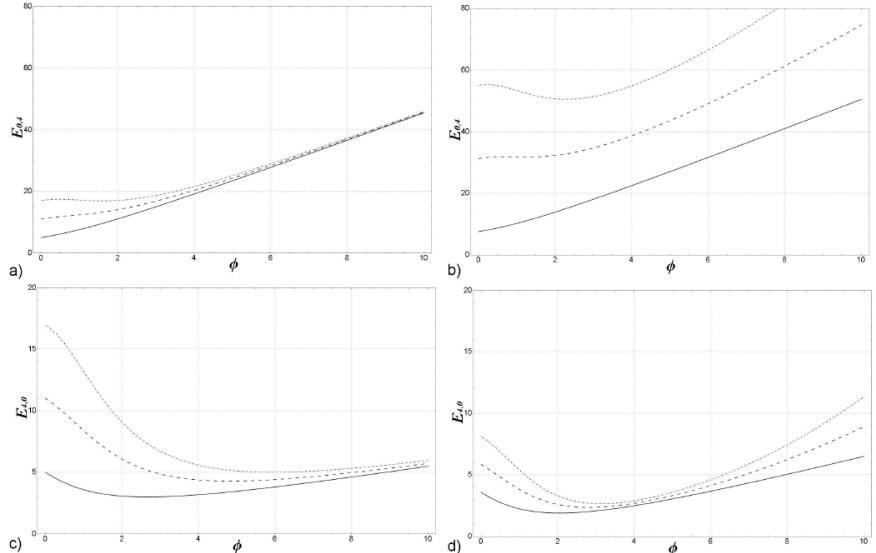
To illustrate the effects of the noncommtativity on this energies we consider a particular interesting example, when the states are nx + ny = 4, which in the absence of noncommutativity and perturbation term are degenerated. In the Fig. 1 we see how the energy levels are splitting as the θ, Φ and α parameters turn on. Values of the parameters θ, Φ and α are shown in the Table I.
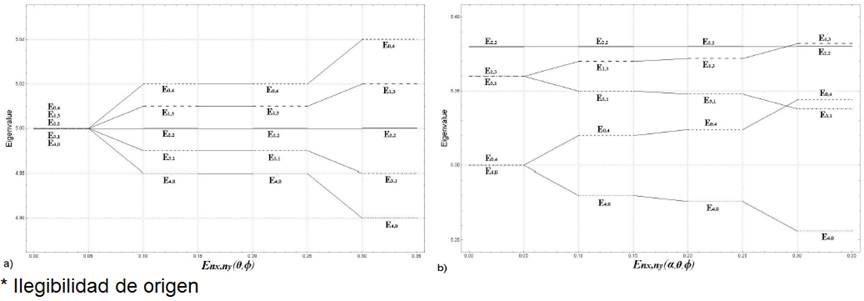
Figure 1 Level energy effects of the noncommutativity (a) Enx,ny with α = 0, (b) Enx,ny with α = 0:01. E4,0 (dashing ─ tiny), E3,1 (dotdashed), E2,2 (solid ─ line), E1,3 (dashing ─ large) and E0,4 (dashing ─ medium).
Table I Values of θ, Φ and α.
| A | B | C | D | E | F | G | H | |
| α | 0 | 0 | 0 | 0 | 0.01 | 0.01 | 0.01 | 0.01 |
| θ | 0 | 0 | 0.01 | 0.01 | 0 | 0 | 0.01 | 0.01 |
| φ | 0 | 0.01 | 0 | 0.01 | 0 | 0.01 | 0 | 0.01 |
In Fig. 1 a) column A, we show the effects of noncommutativity when the perturbation parameter is off (α = 0), then the effect of noncommutativity in the momentum column B is the same as that of the noncommutativity of the coordinates as shown in column C, breaking the degeneration in the energy levels by the same value. This because in the absence of perturbation, the Hamiltonian is symmetric under the exchange between coordinates and moments. The combination of θ an Φ, column D only amplifies the effect of splitting the energy levels.
The effect of nonconmutativity is more significative when the perturbation term is present Fig. 1 b). The presence of this term breaks partially the degeneration when the noncommutative parameters are zero, column E. On the other hand, column F and G exhibit a difference between the noncommutative parameters. The difference between these effects is small, nonetheless it allows to decide in a particular situation if any effect on the energy levels is due to the noncommutative space variables, momentum variables or both. Finally, column H shows the combined effect of both noncommutative parameters θ and Φ, the effect is strong in this case as we show in the third term of the Eq. (22).
To illustrate the dependence of the energy levels in the noncommutative parameters (θ and Φ), we show Fig. 2 for the levels E4,0 and E0,4. It can be seen that energy increase with the noncommutative parameter θ and the perturbation parameter α = 0,0.2 and 0.4. Also it can be noticed a slight increases in the energy for Φ = 1, Fig. 2 (b) and (d).
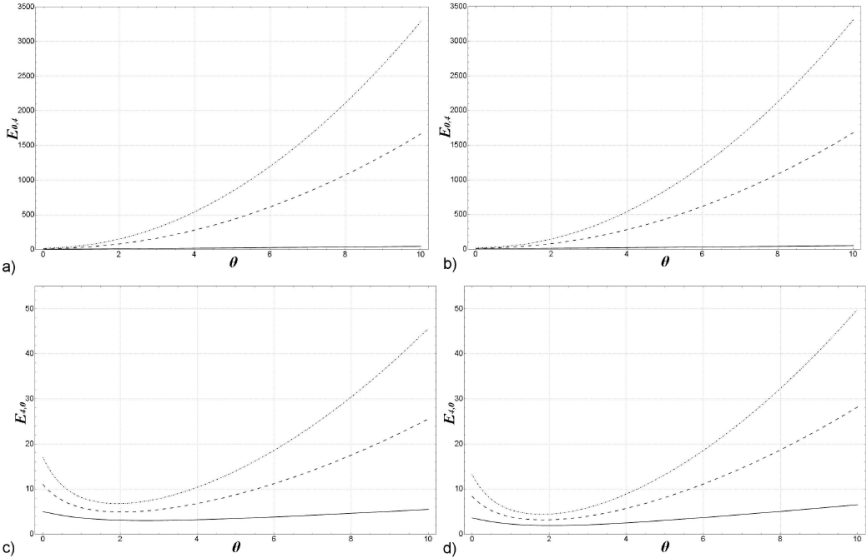
Figure 2 Enx,ny versus θ, solid line correspond to α = 0, dotted line to α = 0:2, dotdashed to α = 0:4. Figures (a) and (b) correspond to (nx,ny) → (0; 4), (c) and (d) to (nx ,ny) → (4; 0).
Figure 3 illustrates the dependence of the energy levels E4,0 and E0,4 for Φ and the perturbation parameter α = 0,0.2 and 0.4. When θ = 0 we can appreciate that the effect of perturbation increases the energy of the levels for small values of Φ(Φ > 4), for higher values, around 4, the energy is also increased, but this is slightly noticeable in the graphs, furthermore with θ = 1 there is a remarkable increase in the energy. Another characteristic to be highlighted is that for large values of Φ the energy grows suggestively linearly with Φ, although in reality is a quadratic behavior.
3. Conclusions
In this letter we have constructed the two-dimensional an- harmonic oscillator model and studied in a noncommutative phase space, i.e. making the transformation (6) on the phase space we work out a Hamiltonian that depends on the noncommutative variables x̑i and p̑i , allowing us to obtain the equations of the two-dimensional anharmonic oscillator. Based in previous work [14] and [15], we have found the eigenvalues of the anharmonic oscillators in noncommutative phase space with perturbation α(x̑2 + ŷ2)2. The introduction of phase space deformation implies the appearance of a constant θ and Φ terms in the Hamiltonian and it is shown that the resulting shift in the eigenvalue of the Hamiltonian has an observational signature. We look for the effects that can cause noncommutativity in eigenvalues. We have already obtained a new representation for M and Ω. The energy eigenvalues are non-degenerate, which is unexpected and it could have an important impact on the quantum physical systems. Such a feature deserves further investigation to better understand the underlying physical mechanism.
It should be noted that the effect of θ is to increase the energy of the states, nevertheless, these effects are more notorious as the α value increases. Besides, Φ shows a similar behavior but with two order of magnitude smaller than the effect of θ. An important characteristic that arise is that the energy levels grows lineally with Φ for intermediates values of Φ. These levels are more sensitive to the noncommutative of coordinates than noncommutative momenta. Finally, if we take the limits θ → 0 and Φ → 0 in the noncommutative anharmonic oscillator we get (3) which is the usual anharmonic oscillator.











 text new page (beta)
text new page (beta)