1. Introduction
Convection flow process has fascinated researchers due to its frequent uses fields such as electronic component cooling, food processing and crystal growth. Nanotechnology has been selected as a helpful passive methods to augment the rate of heating when magnetic forces exist. Haq et al. [1] scrutinized mass transfer of cross flow in a duct. They presented stream wise patterns in their report. Nawaz and Zubair [2] demonstrated the Hall Effect due to magnetic induction on radiative heat transfer of nano-plasma. They simulated in 3-dimensional spaces via FEM. Qi et al. [3] examined the application of TiO2 nanoparticles for cooling of Central Processing Unit (CPU). They scrutinized impacts of spherical bulges on the behavior of nanoparticles. Sheikholeslami et al. [4] illustrated the magnetizable hybrid nanofluid motion through a circular enclosure. They employed a variable magnetic force on the domain. Nabil et al. [5] demonstrated the peristaltic MHD flow of nanoparticles inside a duct. They considered various boundary conditions. Soomro et al. [6] scrutinized cooper nanoparticles transportation inside a cylinder. They reported a dual solution for the behavior of water based nanofluid. Sheikholeslami and Shehzad [7] scrutinized the nanoparticle flow through a permeable space due to MHD impact. Daniel et al. [8] considered the magnetic dissipation effect on stratification of nanofluid. They employed the radiation effect and viscous dissipation in energy equations. Hassan et al. [9] demonstrated Casson fluid transportation through a permeable media due to an external filed considering pulsatile flow. Rehman et al. [10] examined the nano liquid stagnation-point flow under magnetic field. They studied the exponential stretching sheet. Sheikholeslami [11] inspected the new way for simulation of nanoparticle exergy analysis under the Lorentz forces. Shoib et al. [12] examined the oscillating flow of non-Newtonian fluid over a plate. This plate was under the influence of MHD. Lu et al. [13] established the radiation effect on Carreau fluid behavior along a sheet. They added MHD impact with special boundary condition. Gibanov et al. [14] illustrated the second law behavior of nanoparticles in a cavity with a moving wall. They modeled mixed convection with a heat source. Astanina et al. [15] scrutinized natural convection of ferrofluid in an open porous cavity. Recent decade, different means have been employed to enhance the thermal properties of common fluid [16-43].
In this research, the effects of magnetic forces on migration of a water based nanofluid are displayed including the Darcy number impact. The 3D-problem is modeled by LBM. Outputs for various amounts of buoyancy, Darcy and Hartmann numbers are demonstrated.
2. Current geometry
A three-dimensional porous space filled with alumina is depicted in Fig. 1. The lower surface is hot and other boundaries are clear form that figure. A constant magnetic field is applied in the y direction.
3. Boltzmann equations and mesoscopic scheme
3.1. Boltzmann equations
Here we present an application of LBM. To estimate the velocity and temperature, we should solve Boltzmann equations whose unknowns are the two distribution functions (g and f). According to Ref. [44], we used BGK model to simplify the equations as follows
In Eqs. (1) and (2), τν and τc are relaxation times for velocity and temperature. “i” represents each direction and in current mode this varies from 0 to 18 because we used the D3Q19 model (Fig. 2). In such model, Eq. (2) can be used to show the lattice velocity of each direction:
We need to know the functions gieq and fieq which are given in [44]
External Lorentz and buoyancy forces act according to
where B0 is magnitude of the magnetic field.
After solving the main equations, density, temperature and velocity can be calculated.
Temperature: T=∑igi[/p]
Momentum: ρu=∑icifi (8)
Flow density: ρ=∑ifi[/p]
3.2. Characteristics of working liquid
The properties of the nanofluid selected as working fluid of current paper can be calculated as [45]
“nf”, “s” and “f” represent “nanofluid”, “solid particle” and “base fluid”. “dp ” is the particle diameter.
We calculated three important variables namely, Kinetic energy, Nuave and Nuloc according to below formulas:
The required constraints are listed in Tables I and II.
Table I Details for water and nanoparticles.
| ρ(Kg/m3) | Cp(j/kgk) | k(W/mk) | dp(nm) | σ(Ω·m)-1 | |
| Pure water | 997.1 | 4179 | 0.613 | - | 0.05 |
| Al2O3 | 3970 | 765 | 25 | 47 | 10-12 |
4. Independency of grid and validation
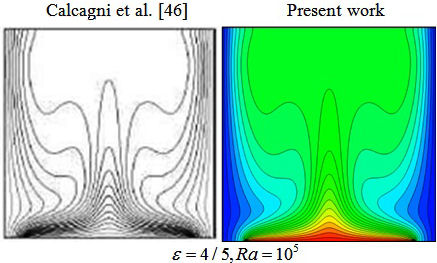
We should find unique solution which which are independent of the size. For this purpose, various grids have been used. As an example, Table III was reported. The code’s validation is visualized in Fig. 3 and Table IV [46-48]).
Table III Grid independency when Ra = 105, ϕ= 0:04 Da = 100 and Ha = 60.
| Mesh size | 51x51x51 | 61x61x61 | 71x71x71 | 81x81x81 | 91x91x91 |
| Nuave | 2.4167 | 2.4294 | 2.4371 | 2.4489 | 2.4499 |
Table IV Nusselt number for various Ha at Pr=0.733.
| Ha | Gr = 2 x104 | |
| Present | Rudraiah et al [48] | |
| 0 | 2.5665 | 2.566894 |
| 10 | 2.26626 | 2.261644 |
| 15 | 1.09954 | 1.083047 |
| 100 | 1.02218 | 1.008833 |
5. Results and discussion
In this report, we studied the behavior of a nanofluid in the presence of a uniform magnetic field inmersed in a 3D porous space. Using a homogenous model for the nanofluid, a nanoparticle concentration of 0.04 has been considered as working fluid. Outcomes are reported for various magnetic forces (Ha = 60, 0), buoyancy forces (Ra = 105, 104 and103) and Darcy number (Da = 100, to 0.001).
Figures 5, 6, 7, 8, 9 and 10 illustrate the impact of the significant variables on the hydrothermal behavior. The domain is affected by conduction when buoyancy force and permeability are low. A simple shape for temperature contours can be observed. As these factors grow, convective mode is gradually increased. The complex shape of the temperature profile is a result of the convective mechanism. Stronger rotating vortex and thermal plumes can be seen for the largest Ra and Da. In this situation, that includes the effects of the magnetic field, the velocity is reduced and the convection to decrease. So, the kinetic energy is reduced with the increase of Ha. Besides, the thermal plume vanishes as a result of the of strong Lorentz forces. Fig. 11 demonstrates the variation of the heat transfer rate with respect to the variables. Equation (16) has been obtained according to the outcomes of various cases
The thickness of the boundary layer along the bottom surface decreases with the increase of Da and Ra. Nu decreases with the increase of Hartmann number. Increasing Ha makes the isotherms becomes denser.
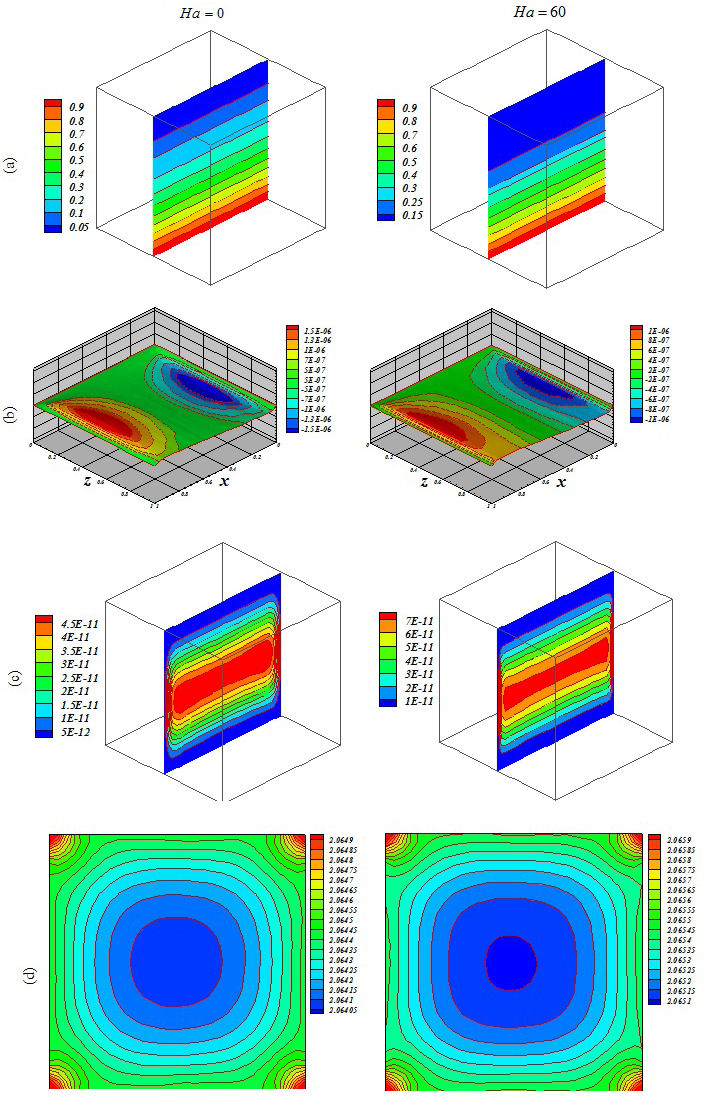
Figure 5 Influence of Lorentz forces on (a) isotherm, (b) streamlines, (c) isokinetic energy and (d) local Nusselt number at Y = y/L = 0:5 when Ra = 103, Da = 0:001, ϕ = 0:04 Ha = 0 and Ha = 60.
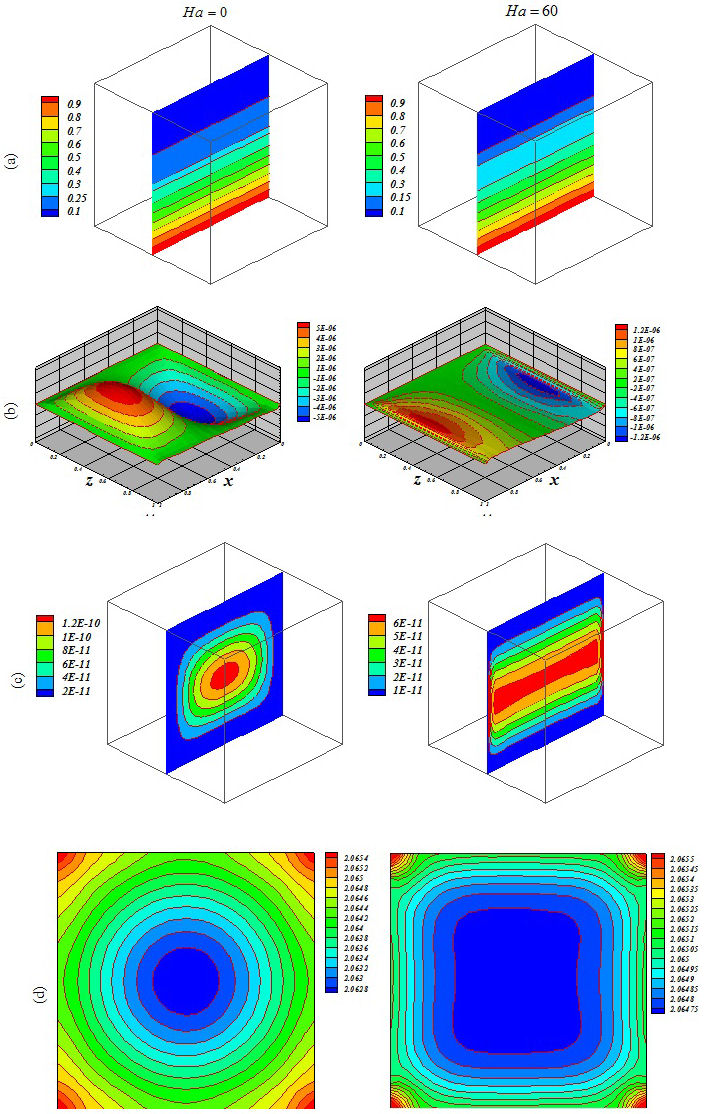
Figure 6 Influence of Lorentz forces on (a) isotherm, (b) streamlines, (c) isokinetic energy and (d) local Nusselt number at Y = y/L = 0:5 when Ra = 103, Da = 100, ϕ = 0:04 Ha = 0 and Ha = 60:
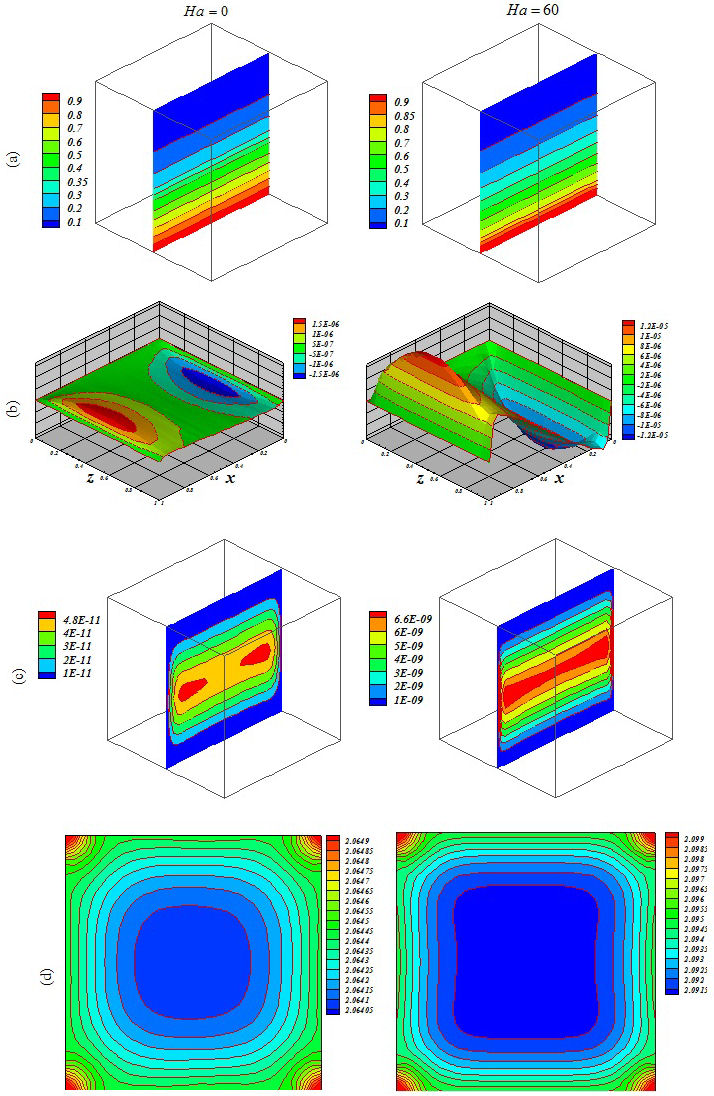
Figure 7 Influence of Lorentz forces on (a) isotherm, (b) streamlines, (c) isokinetic energy and (d) local Nusselt number at Y = y/L = 0:5 when Ra = 104, Da = 0:001, ϕ = 0:04, Ha = 0 and Ha = 60.
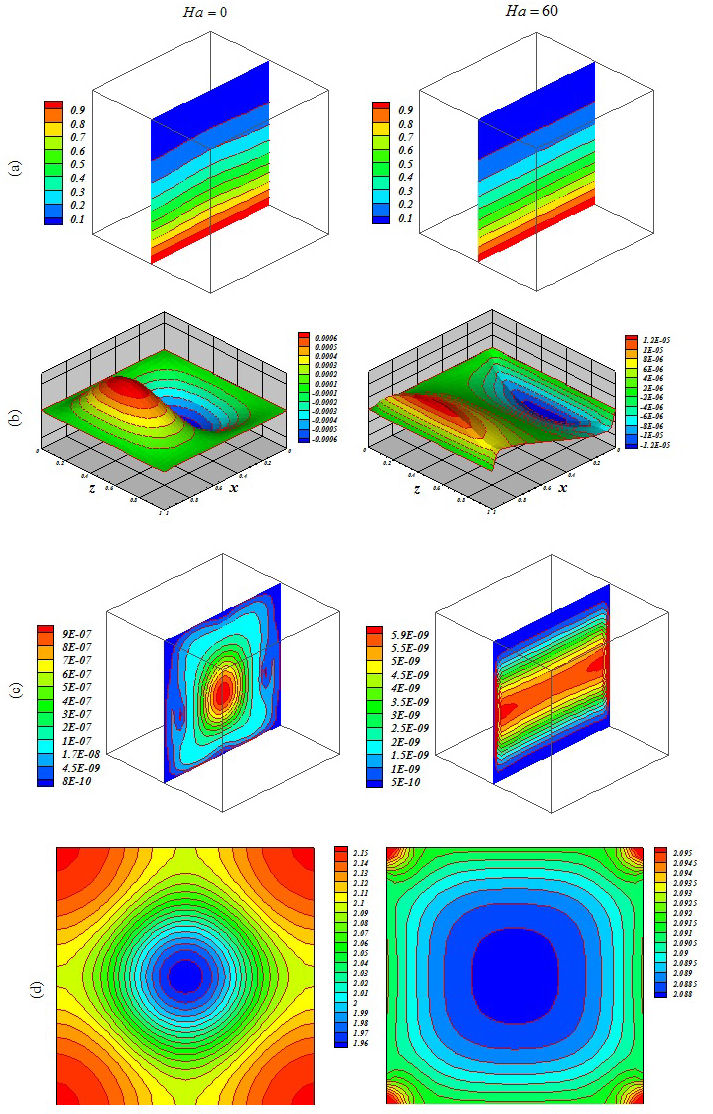
Figure 8 Influence of Lorentz forces on (a) isotherm, (b) streamlines, (c) isokinetic energy and (d) local Nusselt number at Y = y/L = 0:5 when Ra = 104, Da = 100, ϕ = 0:04, Ha = 0 and Ha = 60.
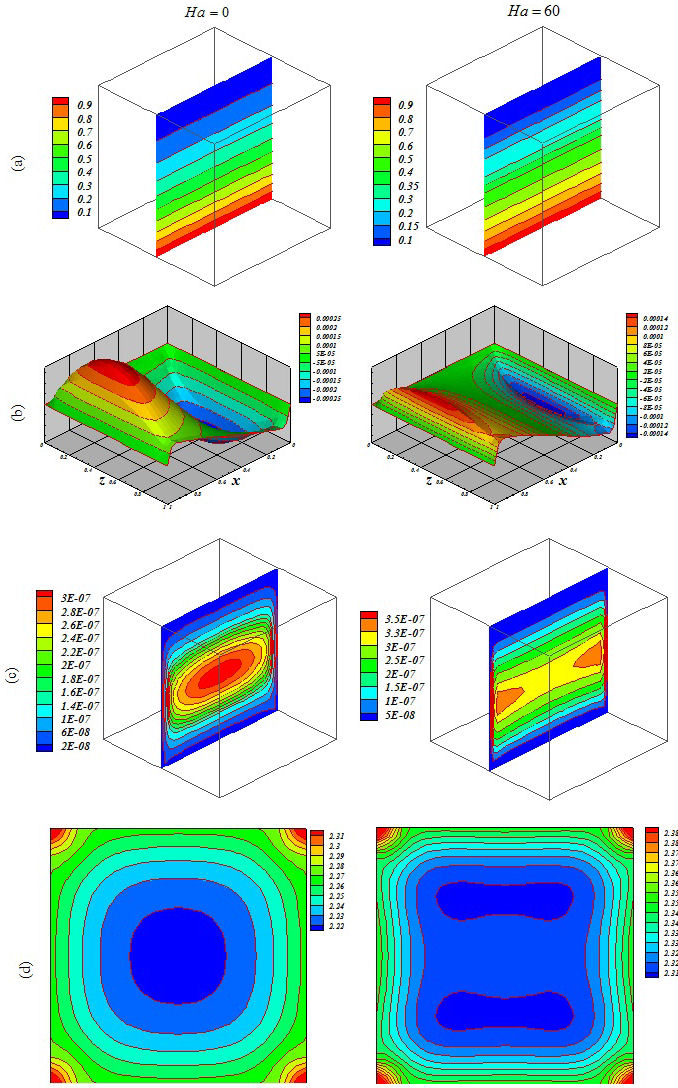
Figure 9 Influence of Lorentz forces on (a) isotherm, (b) streamlines, (c) isokinetic energy and (d) local Nusselt number at Y = y/L = 0:5 when Ra = 105, Da = 0:001, ϕ = 0:04, Ha = 0 and Ha = 60.
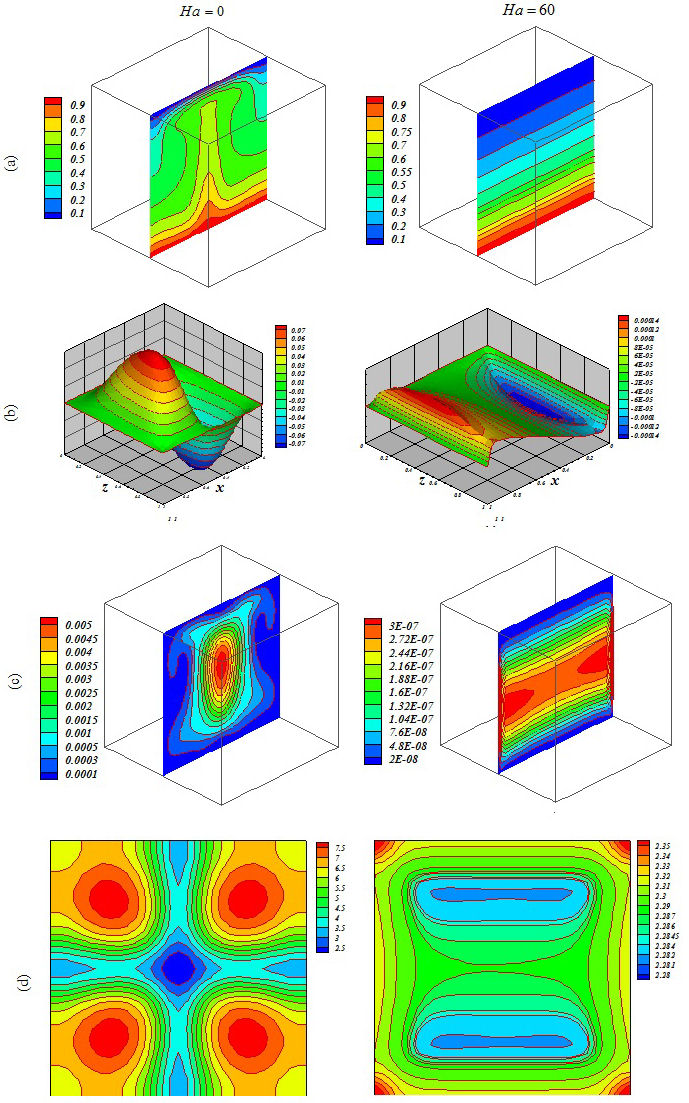
Figure 10 Influence of Lorentz forces on (a) isotherm, (b) streamlines, (c) isokinetic energy and (d) local Nusselt number at Y = y/L = 0:5 when Ra = 105, Da = 100, ϕ = 0:04, Ha = 0 and Ha = 60.
6. Conclusions
In this mesoscopic modeling, the impact of a uniform Lorentz force on the convective transportat of nanoparticles through a porous 3D cavity has been studied. Lattice Boltzmann method which is founded on molecular theory can show ferrofluid behavior in no-Darcy medium. Such method provides the impact of Hartmann, Darcy numbers and buoyancy forces on ferrofluid. Results illustrated that the velocity of the nanofluid decreases with a decrease of buoyancy forces and permeability of space. As Lorentz forces enhance dispersing, nanoparticles becomes more significant. As permeability of space increases, the convective flow of nanofluid enhances.
Future work: As a new idea, this problem can be extended for variable magnetic field with hybrid nanofluid. Also, a two phase model for nanofluid can be employed.
| Ha | Hartmann number |
| g, f | distribution functions |
| u, v, w | Velocity components |
| K | Permeability |
| Pr | Prandtl number |
| Eα | Discrete velocity |
| K | Thermal conductivity |
| cs | Sound velocity |
| feq, geq | Equilibrium distribution |
| Ec | Kinetic energy |
| Grek symbols | |
| ψ | stream function |
| ρ | Fluid density |
| Φ | Nanoparticles concentration |
| ν | Kinematic viscosity |
| σ | Electrical conductivity |
| τ | Lattice relaxation time |
| β | Thermal expansion coefficient |
| α | Thermal diffusivity |
| Subscripts | |
| ave | Average |
| f | Pure fluid |
| loc | Local |











 text new page (beta)
text new page (beta)