1. Introduction
Recent studies in science and engineering demonstrated that the dynamics of many systems may be described more accurately by means of differential equations of non-integer order. The diffusion equation is a partial differential equation that portrays density dynamics in a material subject to diffusion [1,2]. The convection-diffusion equation explains the flow of heat, particles, oil reservoir simulations, transport of mass and energy, global weather production, or other physical quantities in conditions where there are both diffusion and convection or advection [3-5]. Fractional diffusion equations are largely used in describing abnormal slowlydiffusion phenomenon, and fractional diffusion equations are always used in describing abnormal convection phenomenon. Time-fractional diffusion is derived by considering continuous time random walk problems, which are in general nonMarkovian processes.
Several definitions, related to fractional order-derivatives have been used in the literature. These definitions include, Riemann-Liouville, Liouville-Caputo, conformable derivatives, Caputo-Fabrizio, Atangana-Baleanu and AtanganaKoca, to mention a few [6]. The choice of fractional differentiation is motivated by the fact that the interaction with the medium is not local but global. The fractional operators can be a useful way to include memory in a dynamical process. A dynamical process that is modelled through fractional order derivatives carries information about its present as well as past states.
In this paper, we consider the time-fractional diffusion and convection-diffusion equations, obtained from the standard equations by replacing the time derivative with fractional derivatives of type Liouville-Caputo, Atangana-Baleanu-Caputo, fractional conformable derivative in Liouville-Caputo sense and Atangana-Koca-Caputo of order α, with 0 < α ≤ 1.
The following fractional diffusion equation is considered
where µ is the diffusion coefficient.
The fractional convection-diffusion equation considered is [4]
where µ = λ/cρ is the diffusion coefficient, 𝜖 is the porosity, η is the velocity, λ is the thermal conductivity, c is the specific heat, ρ is the mass density, and Q(x,t) is the source term.
2. Basic Tools
The Liouville-Caputo (C) fractional operator of order α is defined as [7]
Where
Atangana and Baleanu considered the generalized Mittag-Leffer function as the kernel of differentiation. This kernel is non-singular and nonlocal and preserves the benefits of the above fractional operators. Replaced the exponential kernel with the generalized Mittag-Leffler function, we obtain the fractional operator of type Atangana-Baleanu in Liouville-Caputo sense (ABC) of order α defined as follows [8]
where n∈ℕ and g(α) is a normalization function that depends of α, which satisfies that, g(0) = g(1) = 1.
Let 0 < α ≤ 1 and n ∈ ℕ, the Laplace transforms of the Liouville-Caputo and Atangana-Baleanu-Caputo fractional operators are given by
Khalil in [9] gives a new definition of derivative called “conformable derivative”. Let f : [a,∞) −→ ℝ. The conformable derivative of f(t) is given by
for all t > 0, α ∈ (0,1). If f(t) is α-differentiable in some (0,α), α > 0, and
The left conformable integral is given by
Iterating n-times the integral (10) and replacing the integer n, for β ∈C, with Re(β) > 0, we define the following fractional conformable integral
Considering the definition given by Eq. (11) we get the left fractional conformable derivative in the Liouville-Caputo sense. Let Re(β) ≥ 0, n = [Re(β)] + 1,
The Atangana-Koca fractional derivative in LiouvilleCaputo sense (AKC) is given by [11,12]
where g(α) is a normalization function as in the previous cases.
Let 0 < α ≤ 1, the Laplace transform of the AtanganaKoca fractional-order derivative is given as
Given a function u(x) ∈ L 1(ℝ), the Fourier transform is given by
and the inverse Fourier transform of u(x) is given by
3. Fractional diffusion equations
In this paper, we solved the diffusion and convectiondiffusion equation considering fractional operators of type Liouville-Caputo, Atangana-Baleanu-Caputo, fractional conformable derivative in Liouville-Caputo sense and AtanganaKoca-Caputo.
Diffusion Equation.
In the Liouville-Caputo sense we have the following diffusion equation
where µ is the diffusion coefficient.
Solution. Applying the Laplace transform to Eq. (17) and taking the condition (18) we get
Applying the Fourier transform in the left hand of the Eq. (19) we have
and for the right hand of the Eq. (19) we have
Equating Eqs. (20) and (21) the following explicit relation is deduced for
Now, applying the inverse Laplace and inverse Fourier transforms to Eq. (22) we have
In the Atangana-Baleanu-Caputo sense we have the following diffusion equation
where µ is the diffusion coefficient.
Solution. Applying the Laplace transform to Eq. (24) and taking the condition (25) we get
Applying the Fourier transform to Eq. (26) and simplifying, we have the following relation for
and applying the inverse Fourier transform to Eq. (27) we have
Finally, applying the inverse Laplace transform to the above equation we get
Considering the fractional conformable derivative in the Liouville-Caputo sense we have the following diffusion equation
where µ is the diffusion coefficient.
Solution. Applying the Laplace transform to Eq. (30) and taking the condition (31) we get
Applying the Fourier transform to Eq. (32) and simplifying, we have
Now applying the inverse Laplace and inverse Fourier transforms to Eq. (33) we have
In the case when α = 1 the expression (34) matches the solution obtained in the Eq. (23) in the Liouville-Caputo sense.
Considering the Atangana-Koca fractional-order derivative in the Liouville-Caputo sense we have the following diffusion equation
where µ is the diffusion coefficient.
Solution. Applying the Laplace transform to Eq. (35) and taking the condition (36) we get
Where α=g(α)(1-g(α))α
Applying the Fourier transform to Eq. (37) and simplifying, we have
Now applying the inverse Laplace and inverse Fourier transforms to Eq. (38) we have
Convection-Diffusion Equation
In the Liouville-Caputo sense we have the following convection-diffusion equation
where µ = λ/cρ is the diffusion equation.
Solution. Applying the Laplace transform to Eq. (40) and taking the condition (41) we get
Applying the Fourier transform to Eq. (42) and simplifying, we have the following relation for û(k,s)
Applying the inverse Laplace transform and the inverse Fourier transforms to Eq. (43) we get
In the Atangana-Baleanu-Caputo sense we have the following convection-diffusion equation
where µ = λ/cρ is the diffusion equation.
Solution. Applying the Laplace transform to Eq. (45) and taking the condition (46) we get
Applying the Fourier transform to Eq. (47) and simplifying, we have the following relation for û(k,s)
Finally, applying the inverse Fourier transform and the inverse Laplace transform to Eq. (48) we get
Considering the fractional conformable derivative in the Liouville-Caputo sense we have the following convectiondiffusion equation
where µ is the diffusion coefficient.
Solution. Applying the Laplace transform to Eq. (50) and taking the condition (51) we get
Applying the Fourier transform to Eq. (42) and simplifying, we have
Finally, applying the inverse Laplace transform and the inverse Fourier transform to Eq. (53), we get
In the case when α = 1 the expression (54) matches the solution obtained in the Eq. (44) in the Liouville-Caputo sense.
Considering the Atangana-Koca fractional-order derivative in the Liouville-Caputo sense we have the following convection-diffusion equation
where µ is the diffusion coefficient.
Solution. Applying the Laplace transform to Eq. (55) and taking the condition (56) we get
where b=g(α)(1-g(α))α.
Applying the Fourier transform to Eq. (57) and simplifying, we have
Applying the inverse Laplace transform and the inverse
Fourier transform to Eq. (58) we get
4. Illustrative examples
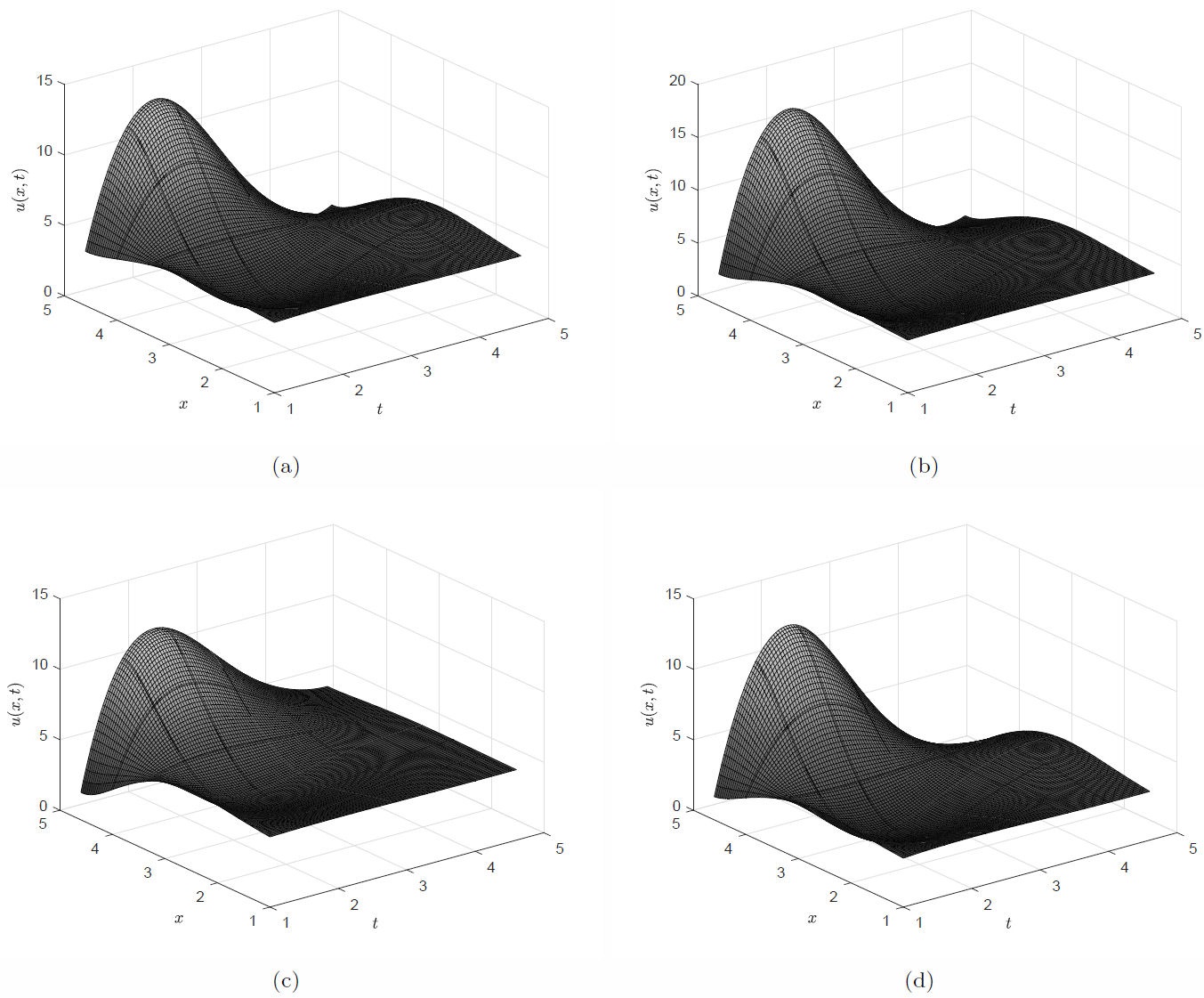
Figures 1(a-d) show numerical simulations of the Eqs. (44), (49), (54) and (59) for α = 0.85 and α = 0.92-β = 0.83 for the fractional conformable derivative in the Liouville-Caputo sense, these values were chosen arbitrarily.
5. Conclusion
In this work we applied fractional-order derivatives of type Liouville-Caputo, Atangana-Baleanu, fractional conformable derivative and Atangana-Koca to obtain analytical solutions for the diffusion and convection-diffusion equation. The fractional equations were solved using the Laplace and Fourier transform. The anomalous diffusion concept is naturally obtained from diffusion equations using the fractional calculus approach. Our results indicate that the kernel involved in the fractional derivative and the fractional-order α has an important influence on the concentration. When memory effects described by the fractional order α are incorporated using fractional time derivatives, the crossover dynamics is richer. The alternative solutions obtained in this paper provide a new theoretical perspective of the diffusion and convection-diffusion phenomena.











 text new page (beta)
text new page (beta)