1.Introduction
The characterization of non-Newtonian fluids plays an important role in the fields of Science and Engineering. Especially for the Chemical Engineering industry the most important property of fluids is the non-Newtonian viscosity. The generalized Newtonian fluids are those in which the viscosity of the fluid depends on the shear rate. The change in the viscosity by two or three orders of magnitude is feasible for some fluids, and this cannot be ignored when the lubrication problems and polymer processing is considered. Therefore, one of the basic empirically obtained modifications of the Newton’s law of viscosity is to allow the viscosity to change with the shear rate. Such variety of fluids is commonly referred to as generalized Newtonian fluids and explained by Bird 1. The simplest generalized Newtonian fluid is the power-law constitutive relation. The power-law viscosity model has the limitation that it cannot adequately predict the viscosity for very small or very large shear rates. In view of such limitation of the power law model, generally for very large and very small shear rates, we use another viscosity model from the class of generalized Newtonian fluids, namely Carreau rheological model. This model overcomes the limitations of the power-law model identified above, and appears to be gaining wider acceptance in Chemical Engineering and technological processes. The rheology of various polymeric solutions can be explored by the Carreau liquid. In view of this, Akbar and Nadeem 2 analyzed the blood as Carreau fluid in tapered artery. Khan et al. 3 applied the Runge-Kutta Fehlberg method to solve momentum and temperature equations assuming MHD stagnant Carreau fluid over moving surface with convective boundary condition. Khan et al. 4 investigated the heat transfer characteristics of squeezed Carreau fluid flow over a sensor surface in the presence of variable thermal conductivity. The stretching phenomenon of Carreau polymer liquid with Robin’s conditions has been identified by Hayat et al. 5.
At present, the phenomenon of heat transport has vital importance in several branches of technology, engineering and science like nuclear reactor cooling, microelectronics etc. The applications of such phenomenon in bio-medical applications include: heat conduction in tissues, magnetic drug targeting and many others. The Fourier heat conduction law explores the heat transfer mechanism since two centuries in appropriate situations. The main drawback of this law is that any disturbance created at the initial state affects the whole system. To overcome this drawback, Cattaneo 6 modified Fourier law and obtained hyperbolic energy equation by incorporating thermal relaxation time. This is later developed by Christov 7 to obtain material invariant formulation by adopting Oldroyd’s derivatives. Hayat et al. 8 analyzed the Impact of Cattaneo-Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Li et al. 9 examined the features of Cattaneo-Christov model of heat diffusion in vertical stretched flow of non-Newtonian liquid. Flow between two rotating disks in the presence of theory of Cattaneo-Christov for heat diffusion has been discussed by Hayat et al. 10. The fractional model of Cattaneo-Christov heat diffusion formula is developed by Liu et al. 11. Abbasi et al. 12 considered the two-type non-Newtonian liquids to describe the behavior of Cattaneo-Christov heat flux formula. Darcy-Forchheimer porosity flow of Jeffrey liquid with non-uniform conductivity and theory of Cattaneo-Christov for heat flux has been elaborated by Meraj et al. 13.
Magnetic fields are copiously used in various manufacturing industries include MHD power generators, flow meters, pumps, in the design of cooling system, purification of molten metal’s from metallic inclusions with liquid metals, etc. Recently the analysis of MHD flow and heat transfer gained significance due to its applications. For example, several metallurgical processes involve cooling of continuous filaments or strips. During this process these strips are stretched through a fluid, the quality of the end product depends on the rate of cooling, and the rate of cooling of these final products with desired quality is accomplished by using electrically conducting fluids with applications of magnetic fields. The electrically conducting flow with microorganisms has much more importance in various processes of industry and engineering. According to such strong importance of this phenomenon, Mehryan et al. 14 inserted the motile gyrotactic micro-organisms and nanoparticles to discuss the heat transport in viscous liquid flow. Devi and Prakash 15 elaborated the results of non-uniform viscosity and conductivity flow of MHD viscous liquid induced by slendering surface. Sekhar et al. 16 imposed different slip condition on flow of MHD liquid flow. Palani and Kim 17 described the nature of thermal radiation in convective viscous liquid flow generated by the rotation of cone. Kuznetsov 18 demonstrated a boundary layer flow of bio convection suspension of gyrotactic-microorganisms with finite depth heated from below. Many authors analyzed MHD with different flow characterizes have been modulated by 19-27. Zhang and Zheng 28 demonstrated that the analysis of magnetohydrodynamic thermos-solutal convection with the heat generation and first order chemical reaction can be computed by double-parameter transformation perturbation expansion method and Pade’s approximant technique. They found the wall velocity is non-zero due to the Marangoni or surface tension effect which causes to decrease with increase in magnetic field parameter. The magnetohydrodynamic flow and radiation heat transfer of nanofluids in porous media with variable surface heat flux in the presence of chemical reaction was studied by Zheng et al. 29. They observed that the solutal boundary layer thickness increased by increase in chemical reaction parameter.
To author knowledge, there exists no such analysis that simultaneously described the impacts of chemical reaction and heat sink/source on the fluid flow suspending microorganisms. The further novelty of this work is the utilization of Cattaneo-Christov model of heat diffusion. In this paper the steady laminar mixed convection three dimensional heat and mass transfer flow of electrically conducting Carreau fluid over a stretching sheet in a suspension of microorganisms in the presence of multiple slips. The influences of the Weissenberg number, thermal relaxation parameter, magnetic parameter, Prandtl number, heat generation/absorption parameter, Peclet number, Lewis number, and chemical reaction parameter on various quantities are discussed.
2.Mathematical Formulation
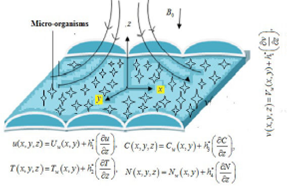
In the present investigation, we considered the Cattaneo-Christov heat flux on MHD three-dimensional flow over a variable thickness sheet. To emerge the temperature and concentration fields, gyro-tactic microorganisms and non-uniform heat source or sink are considered. The x-axis is considered along the sheet motion and y-axis is perpendicular to it as depicted in Fig. 1. Assuming
With these suppositions, the governing equations of continuity, momentum, thermal and mass species equations are8:
The corresponding boundary conditions are
where
The irregular heat source/sink parameter
From the equation above,
with the help of (11), (12) and (13), Eqs. (2)-(4) converted as the below differential equations:
With the corresponding boundary conditions are
The dimensional parameters M, Pr, Le, Nt, Nb, Kr, h1, h2, γ, h3, h4, δ Pe and
The skin-friction coefficient Cf, local Nusselt Nux and Sherwood number Shx are defined as
Where
3. Results and Discussion
The set of ordinary differential Eqs. (15)-(19) are solved numerically by applying Runge-Kutta fourth order method with shooting technique. The numerical values of non-dimensional parameters such as M, We, kr, γ, Pe, A*, B*, β1, and β1, on local skin friction coefficient, local Nusselt number and Sherwood numbers are demonstrated in the Tables I and II. In the present investigation, we examine two cases such as Newtonian and non-Newtonian, and obtained dual solutions by keeping n= 0.5 and n= 1 for Newtonian and non-Newtonian fluids.
TABLE I Values of local friction factor for different physical governing parameters for n = 1 and n = 0:5 cases.
| M | We | Kr | γ | Pe | A* | B* | β1 | -f’’(0) | -g’’(0) | ||
| n =1 | n =0.5 | n =1 | n =0.5 | ||||||||
| 0.5 | 1.198579 | 1.204921 | 1.213151 | 1.219822 | |||||||
| 1.0 | 1.276179 | 1.284636 | 1.314271 | 1.323920 | |||||||
| 1.5 | 1.345101 | 1.355883 | 1.400997 | 1.413920 | |||||||
| 1 | 1.108638 | 1.210664 | 1.119063 | 1.224781 | |||||||
| 3 | 0.915229 | 1.226421 | 0.921319 | 1.238011 | |||||||
| 5 | 0.808500 | 1.236994 | 0.813276 | 1.246745 | |||||||
| 0.1 | 1.198579 | 1.204921 | 1.213151 | 1.219822 | |||||||
| 0.3 | 1.198579 | 1.204921 | 1.213151 | 1.219822 | |||||||
| 0.5 | 1.198579 | 1.204921 | 1.213151 | 1.219822 | |||||||
| 0.1 | 1.198583 | 1.204917 | 1.213148 | 1.219819 | |||||||
| 0.3 | 1.198579 | 1.204921 | 1.213152 | 1.219822 | |||||||
| 0.5 | 1.198579 | 1.204921 | 1.213152 | 1.219822 | |||||||
| 0.1 | 1.198585 | 1.204921 | 1.213151 | 1.219822 | |||||||
| 0.4 | 1.198579 | 1.204921 | 1.213151 | 1.219822 | |||||||
| 0.7 | 1.198573 | 1.204921 | 1.213151 | 1.219822 | |||||||
| 0.1 | 1.198579 | 1.204921 | 1.213150 | 1.219821 | |||||||
| 0.4 | 1.198578 | 1.204921 | 1.213150 | 1.219821 | |||||||
| 0.7 | 1.198578 | 1.204921 | 1.213144 | 1.219820 | |||||||
| 0.1 | 1.198579 | 1.204921 | 1.213150 | 1.219821 | |||||||
| 0.15 | 1.198579 | 1.204921 | 1.213151 | 1.219822 | |||||||
| 0.2 | 1.198579 | 1.204921 | 1.213152 | 1.219822 | |||||||
| 0.1 | 1.198579 | 1.204921 | 1.213151 | 1.219822 | |||||||
| 0.3 | 1.198579 | 1.204921 | 1.213151 | 1.219822 | |||||||
| 0.5 | 1.198579 | 1.204921 | 1.213151 | 1.219822 | |||||||
TABLE II Values of local Nusselt, Sherwood number and motile Sherwood numbers for different physical governing parameters for n = 1 and n = 0:5 cases.
| M | We | Kr | γ | Pe | A* | B* | Β1 | ( Nux) | Shx | MShx | |||
| n =1 | n =0.5 | n =1 | n=0.5 | n =1 | n =0.5 | ||||||||
| 0.5 | 0.280175 | 0.333139 | 0.582159 | 0.670933 | 0.128627 | 0.197692 | |||||||
| 1.0 | 0.249072 | 0.289382 | 0.569954 | 0.650575 | 0.112324 | 0.171775 | |||||||
| 1.5 | 0.221223 | 0.248416 | 0.559690 | 0.633886 | 0.099315 | 0.151585 | |||||||
| 1 | 0.285105 | 0.339112 | 0.585471 | 0.675937 | 0.131859 | 0.202557 | |||||||
| 3 | 0.300297 | 0.355684 | 0.595672 | 0.690700 | 0.143005 | 0.218644 | |||||||
| 5 | 0.311365 | 0.366383 | 0.603558 | 0.701693 | 0.152836 | 0.232245 | |||||||
| 0.1 | 0.280175 | 0.333139 | 0.509237 | 0.606086 | 0.163399 | 0.227578 | |||||||
| 0.3 | 0.280175 | 0.333139 | 0.642994 | 0.725634 | 0.100818 | 0.173453 | |||||||
| 0.5 | 0.280175 | 0.333139 | 0.742534 | 0.816177 | 0.057197 | 0.134867 | |||||||
| 0.1 | 0.263228 | 0.336052 | 0.582158 | 0.670931 | 0.128630 | 0.197698 | |||||||
| 0.3 | 0.270681 | 0.334158 | 0.582159 | 0.670933 | 0.128627 | 0.197692 | |||||||
| 0.5 | 0.280175 | 0.333139 | 0.582159 | 0.670933 | 0.128627 | 0.197692 | |||||||
| 0.1 | 0.280176 | 0.333139 | 0.582158 | 0.670933 | 0.357354 | 0.458658 | |||||||
| 0.4 | 0.280175 | 0.333139 | 0.582159 | 0.670933 | 0.184660 | 0.262361 | |||||||
| 0.7 | 0.280175 | 0.333139 | 0.582159 | 0.670933 | 0.019269 | 0.069907 | |||||||
| 0.1 | 0.323435 | 0.385548 | 0.582159 | 0.128627 | 0.670933 | 0.197692 | |||||||
| 0.4 | 0.193656 | 0.228322 | 0.582159 | 0.128627 | 0.670933 | 0.197692 | |||||||
| 0.7 | 0.063877 | 0.071093 | 0.582159 | 0.128627 | 0.670933 | 0.197692 | |||||||
| 0.1 | 0.280175 | 0.333139 | 0.582159 | 0.670933 | 0.128627 | 0.197692 | |||||||
| 0.15 | 0.197842 | 0.218259 | 0.582159 | 0.670933 | 0.128627 | 0.197692 | |||||||
| 0.2 | 0.083141 | 0.009758 | 0.582159 | 0.670933 | 0.128627 | 0.197692 | |||||||
| 0.1 | 0.280175 | 0.333139 | 0.582159 | 0.670933 | 0.174098 | 0.258137 | |||||||
| 0.3 | 0.280175 | 0.333139 | 0.582159 | 0.670933 | 0.151362 | 0.227915 | |||||||
| 0.5 | 0.280175 | 0.333139 | 0.582159 | 0.670933 | 0.128627 | 0.197692 | |||||||
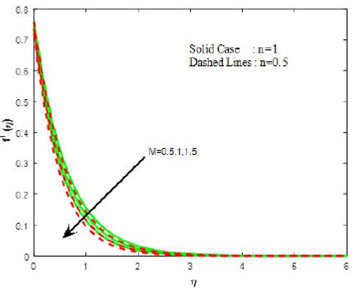
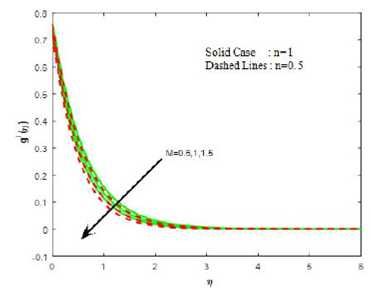
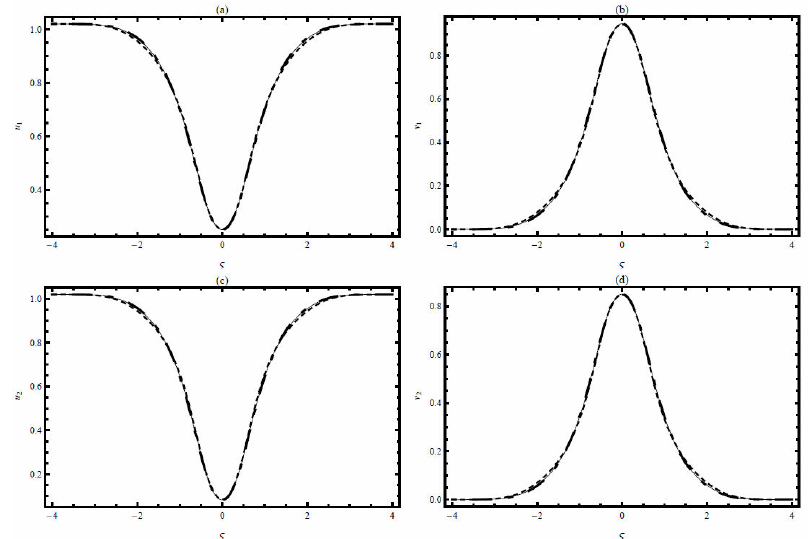
Figures 2-6 show the effect of the magnetic parameter on velocities, temperature, concentration and density of motile organism for both Newtonian (n= 1) and non-Newtonian (n= 0.5) liquids. From Figs. 2 and 3, it is evident that the strength of magnetic field is to diminish the velocities. This reduction can be attributed to the fact that the magnetic field provides a resisting type force known as the Lorentz force. This force tends to lessen the motion of liquid and as a consequence, the velocity depreciates. From Fig. 4, temperature is found to be enhancing with the magnetic field. Here the frictional resistance on account of the magnetic field resulting in the reduction of velocity, and there by, enhances the temperature. The effect of magnetic field performs an increasing effect on concentration and density of motile organism (see Figs. 5 and 6).
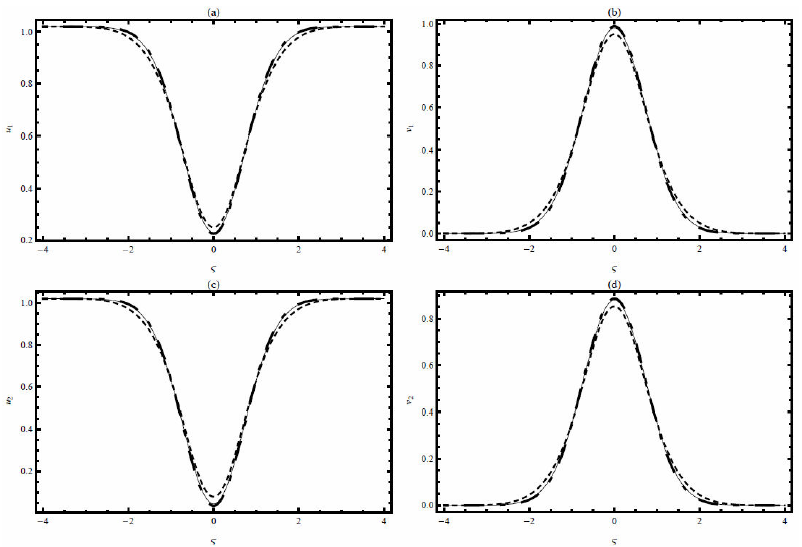
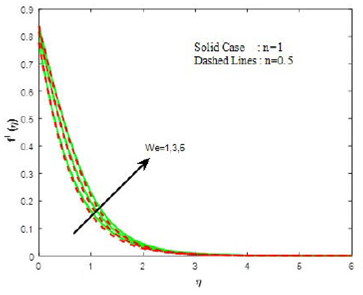
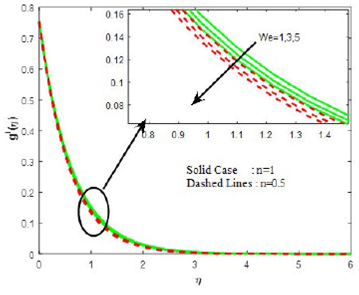
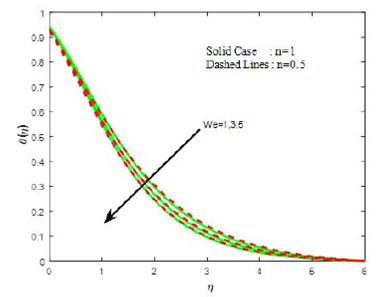
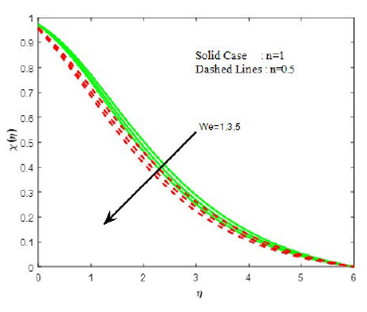
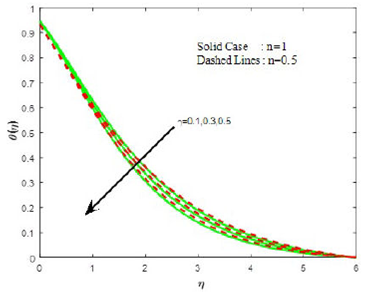
Figures 7 and 8 are plotted to demonstrate the influence of the Weissenberg number (We) on the velocities.Figure 7 investigates that the primary velocity increases with the increasing values of Weissenberg number, whereas the secondary velocity shows the opposite behavior (see Fig. 8). In Figs. 9-11, the physical behavior of the boundary layer near to the surface can be seen by observing the temperature, concentration and density of motile organism profiles respectively for various values of Weissenberg number. The profiles of temperature (Fig. 9), concentration (Fig. 10) and density of motile organism (Fig. 11) clearly depict the decreasing phenomenon with the increasing Weissenberg number.
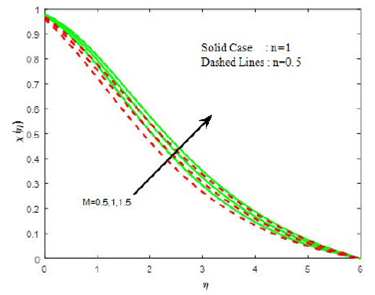
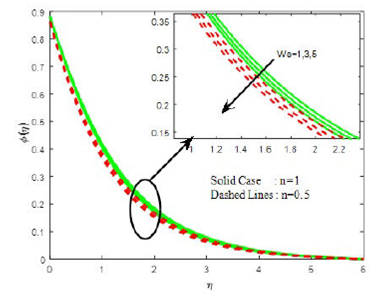
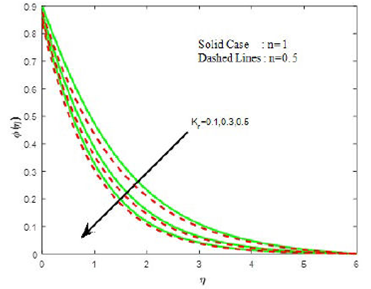
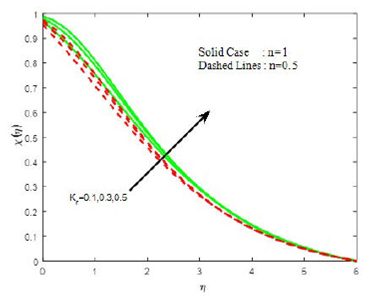
The impact of chemical reaction parameter kr on species concentration profile is depicted in Fig. 12. It is observed that an increase in the value of chemical reaction parameter reduces the concentration of species in the boundary layer owing to the fact that destructive chemical reaction reduces the solutal boundary layer and enhances the mass transfer while it shows opposite trend on density of motile organism (see Fig. 13).
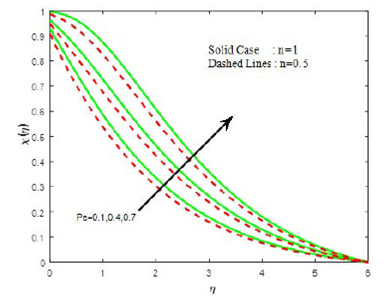
Figure 14 depicts the temperature profile for various values of thermal relaxation parameter γ. From this Fig. 14, it is evident that the temperature as well as thermal boundary layer thickness retard, with the presence of thermal relaxation parameter. This is due to the fact, that for enhancing values of thermal relaxation, time the fluid particles steadily transfer heat to its surrounding particles. Figure 15 elucidates that density of motile organism increases with increasing values of Peclet number Pe.
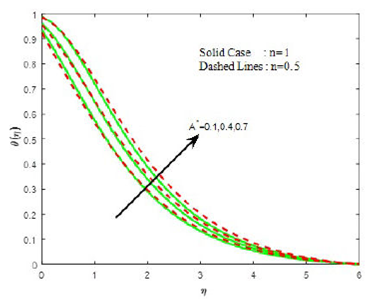
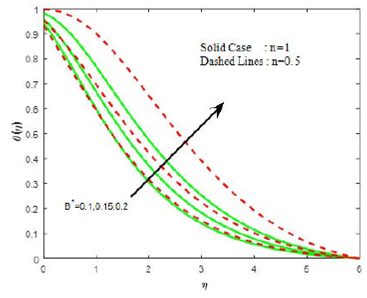
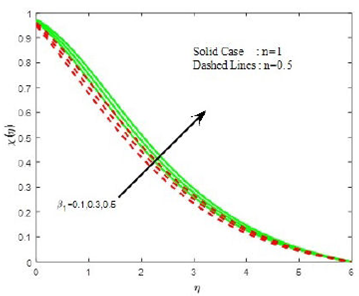
Figures 16 and 17 represent the plots of temperature with variation in A* and B*. The temperature increases rapidly throughout the boundary layer due to the release of energyin thermal boundary layer for increasing values of temperature dependent heat source/sink parameter. The density of motile organism increases with the increasing values of liquid parameter β1 (see Fig. 18).
The numerical values of dimensionless friction factor for various values of physical parameters are displayed in Table I. It is observed that the skin friction coefficient increased for magnetic parameter M and thermal relaxation parameter γ for both n = 1 and n = 0.5. The local Nusselt number, local Sherwood number and motile microorganisms are studied for different physical parameters like Magnetic parameter, Weissenberg number, chemical reaction parameter, thermal relaxation parameter, Peclet number, time and space dependent parameters, and liquid parameter are investigated in Table II. From this Table, we found that the magnetic parameter decreases the local Nusselt number and local Sherwood numbers for both n = 1 and n = 0.5. An opposite phenomena can be observed for increasing values of Weissenberg number. The chemical reaction parameter enhances the mass transfer rate and decelerates the density of motile mass transfer rate. The space dependent and temperature dependent heat source/sink suppress the local Nusselt number.
4. Conclusions
The present study addresses the 3D flow of Carreau fluid over variable thickness sheet in suspension of microorganisms with Cattaneo-Christov heat diffusion formula. The key observations of this investigation can be described as:
The temperature increases rapidly throughout the boundary layer owing to the release of energy in thermal boundary layer for increasing values of temperature dependent heat source/sink parameter.
The profiles of temperature, concentration and density of motile organism phenomenon reduced with an increment in Weissenberg number.
Non-Newtonian liquid showed better heat transfer performance compare with Newtonian liquid.
The magnetic parameter decreases the local Nusselt and local Sherwood numbers for both n = 1 and n = 0.5.
The chemical reaction parameter enhances the mass transfer rate and decelerates the density of motile mass transfer rate. The space dependent and temperature dependent heat source/sink suppress the local Nusselt number.











 text new page (beta)
text new page (beta)