1. Introduction

In physics exist many pulsed signals which have a brief oscillation in time and carry a finite amount of energy. The analysis and characterization of these transient oscillations are essential for the fundamental and applied science¹. The propagation of pulses is a complex phenomenon, especially if the signals are traveling through dispersive media where each frequency propagates with different phase velocity. In these systems, the pulse waveform undergoes a distortion related to the various reshaping delays as well as to the broadening and absorption.

In traditional textbooks, the transit time (τ) of a pulse is defined as the time to travel between two points². However, when multiple pulses travel simultaneously, they interfere and produce a complicate waveform where becomes challenging to determine the transit times. One area of research where pulses are actively investigated is the transmission through waveguides. In these structures exist a discrete number of allowed frequencies. If only a mode is excited, it is relatively easy to detect the transit time by measuring between peaks. This strategy was explored experimentally by Wang et al. many years ago is the case of an elastic waveguide³. They reported the characterization of the transit time of a single pulse traveling in a thin fluid layer embedded between two elastic solids. However, some years later, Thomas et al.⁴. demonstrated that if multiple pulses are excited in a thicker Solid-Liquid-Solid (SLS) waveguide, the interference between them causes an undesirable deformation that makes difficult to identify the transit time by comparing the waveforms.

Recently, we have revisited this problem investigating the transit times of high-order modes on SLS waveguides by using the Short-Time Fourier Transform (STFT)⁵. During this study, some of us that did not know the STFT technique were surprised by all the information that could be extracted of a pulse that at a first view looks only like a noisy signal⁵. In this work, we present a way to understand how the STFT allows determining the transit times of multiple pulses traveling simultaneously.

The STFT is a mathematical tool derived from the Fourier Transform. In the traditional background of Mathematical Methods in Physics, the analysis of transient signals is not a usual theme⁶. Some books have recently been devoted to the STFT and other related techniques as the wavelets, Gabor or Wigner-Ville. These methods are widely used by the engineering community in areas such as the digital analysis, spectral analysis, speech recognition, and radars^7,8. Usually in these books are studied changes of a continues signal^7-11. In contrast, here we introduce the study of the STFT considering the case of transient signals.

The main idea of the STFT is to produce a spectrogram where the transit time is on one axis and the frequency on the other⁹. In 1998, W. C. Lang and K. Forinash published a work on spectrograms where in their abstract presented an valuable observation:¹² “While this technique is commonly used in the engineering community for signal analysis, the physics community has, in our opinion, remained relatively unaware of this development. Indeed, some find the very notion of frequency as a function of time troublesome.” After 20 years, the situation is different. Nowadays exist a broad applicability of spectrograms to analyze signals that change in time. For example, in areas such as gravitational waves¹³, radio astronomy^14,15, nuclear dynamics^16,17, or sensing of cancerous cells¹⁸.

Nonetheless, while these techniques are widely used in various areas of physics research, they are not so widely taught. In the context of the literature of physics, we have found only a few papers presenting an introductory analysis of the use of spectrograms^12,19. In this work, we propose a theoretical treatment of the STFT where it is possible to obtain an analytical formula for the case of a Gaussian function. We demonstrate that this technique allows the characterization of a complex signal composed by the superposition of five pulses strongly overlapping in time. To test in the laboratory our analysis, we present an experiment where the transit time and frequency of each one of the components of a complex signal can be identified in a spectrogram.

The rest of the paper is organized as follows. In Sec. 2, we propose a succinct introduction to the STFT. In Sec. 3, we present a theoretical analysis for Gaussian pulses. In Sec. 4, is shown an experiment that demonstrates the utility of spectrograms. Finally, in Sec. 5 we have the conclusions.

2. What is the Short-Time Fourier Transform?

An example that illustrates the importance of the analysis of transient signals is the detection of the Gravitational Waves that recently proved the existence of a Binary Black Hole¹⁴. In Fig. 1 (a) we present a transient signal s(t) that is similar to the waveform received at the Laser Interferometer Gravitational-Wave Observatory (LIGO)^14,15 . It is observed that in the interval Δτa there are fewer oscillations than in the interval Δτb, which means that the frequencies in these ranges are different. How can these frequencies be measured?

Figure 1 In panel (a) is presented a chirped signal s(t). Panel (b) illustrates a window function h(t - τ) centered at τ_a [τ_b ] using a dashed [dotted] line. In panel (c) we present the signal s(t) viewed through the temporal window h(t - τ_a) [h(t - τ_b)] using a dashed [dotted] line. 

The analysis of frequencies based on the Fourier Transform defined by the relation

is beyond reproach. However, it is not appropriate to characterize the transient signal s(t). The Fourier Transform is designed to detect the frequency components of the signal s(t) for an infinite temporal domain but does not allow to identify the localfrequencies. Additionally, the Fourier Transform cannot to determine the time-of-flight. As consequence, it is convenient to introduce a variation of the Fourier Transform to analyze transient signals.

The basic idea of the STFT is to slice the signal through a temporal window and then to determine the frequencies contained in each segment. For this reason, we introduce a window that glides performing time-localized Fourier Transforms. To illustrate how the spectrum changes over time, we introduce a function h(t-τ) that defines a temporal window centered around the time τ and zero-valued elsewhere. It is convenient to introduce the normalization of this equation as

In Fig. 1 (b) we present two examples of the window function h(t-τ). Using a dashed [dotted] line, we present the window functions h(t-τa) [h(t-τb)] centered at τa [tb]. In Fig. 1 (c) are presented two transient signals that represent the function s(t) viewed through each window. The role of the window function is to isolate a temporal segment where it is possible to identify the local frequencies. To obtain a time-frequency spectrogram, we multiply the Eqs. (1) and (2) to obtain

where is defined the STFT as the function

This integral can be understood as follows. The function h(t-τ) is a sliding window centered at τ which glides along the time to define local Fourier Transforms. In this manner, the STFT decomposes a time domain signal into a two-dimensional representation, where the frequency content of the transient signal is revealed inside the temporal window. Usually this integral is solved numerically, in some cases using sophisticated numerical algorithms¹¹. To have an intuitive insight of the STFT, in the next section we present an analytical solution for a Gaussian pulse.

3. Theory

We consider an acoustic pulse in the form

The subscript i allows identifying the pulse and its components. The pulse is a solution of the acoustical wave equation, and it is composed of two functions, a Gaussian and other sinusoidal. The width of the Gaussian component is defined by σi and xi is a spatial displacement. The wave vector (ki) and the angular frequency (ωi) are related by ki=ωi/c, where c=343 m/s is the speed of sound.

3.1. A single pulse

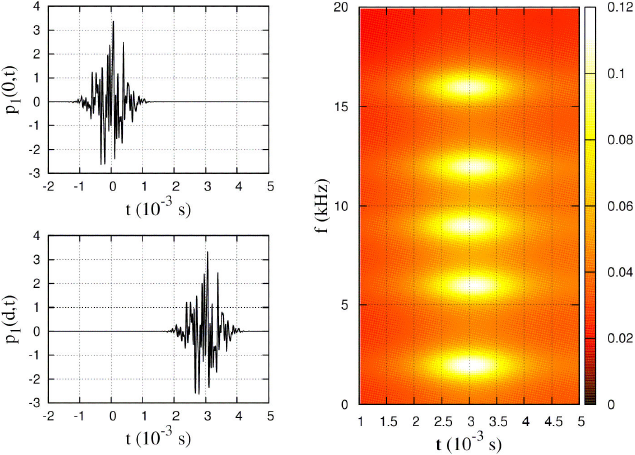
In Figs. 2(a) and 2(b) we present the acoustic pulse for the time-dependent amplitude at the spatial points x = 0 and x = d, respectively. The parameters for the case i = 1 are σ1=0.1 m, x1=0 and f1=2 kHz. We observe that for a single pulse, it is possible to determine the transit time τ as the interval between peaks. Alternatively, the transit time can be found using the relation

Pi(x,f,τ)=∫-∞∞pi(x,t)h(t-τ)ei2πftdt. (6)

Figure 2 In panels (a) and (b) are presented the time-dependent amplitude of the pulse p₁(x, t) detected at the positions x = 0 and x = d, respectively. The transit time τ is measured between peaks. Panel (c) shows the spectrogram defined by the function |P₁(d, f, τ)|². 

The choice of the function h(t-τ) is an important decision because this window affects the spectral estimation of frequencies. There are different choices of windows functions as the triangular, Hann, Hamming or Gaussian.^20,21 In this work, we choose a Gaussian window in the form

h(t-τ)=1τh2πexp-12τh2(t-τ)2, (7)

where τh defines a temporal width. The integral defined by Eq. (6) can be solved analytically and the procedure is described in Appendix A. The solution of the integral is

Pix,f,τ=12βiτh exp⁡{+ikix-xi-δi2

+12βi2γi+i2πf-fi]2

+12βiτh exp⁡{-ikix-xi-δi2

+12βi2γi+i2πf+fi]2. (8)

The functions βi2, γi and δi are defined in Appendix A. In Fig. 3 (c) we show the absolute value |P1(d,f,τ)|2 considering τh=4x10-4 s. The spectrogram in the plane (f,τ) determine the transit times and frequencies at the position x = d.

Figure 3 In panels (a) and (b) are presented the time-dependent amplitude of the pulse p_t (x, t) detected at the positions x = 0 and x = d, respectively. Panel (c) shows the spectrogram defined by the function |P_t(d, f, τ)|². 

4. Experiment

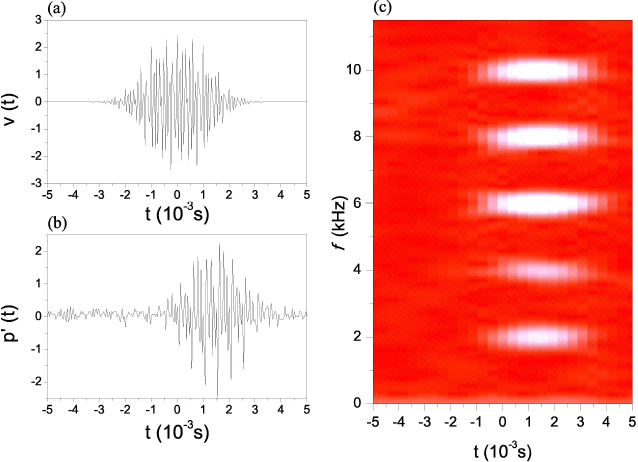
The acoustic transmitting and receiving experimental setup is presented in Fig. 4. We used a Tektronix AFG3021B function generator to produce a customized time-dependent voltage signal v(t) using a software provided by the manufacturer. The signal v(t) is sent simultaneously to the oscilloscope (d) and the speaker (b). The speaker emits an acoustic pulse p(t). A Shure-SM57 unidirectional dynamic microphone placed at a distance d=0.40 m from the speaker receives an acoustical signal p'(t). The microphone produces an electrical signal that is sent to a Tektronik TDS2012 oscilloscope (d) that digitize the signal and send the information to a personal computer (e).

Figure 4 Schematic of the experimental setup. A function generator (a) sends simultaneously a voltage v(t) to the the osciloscope (d) and the speaker (b) which generates a time-dependent sound pulse p(t). The acoustic signal p^'(t) is received by the microphone (c) which sends a signal to the osciloscope (d) that digitize and sends the information to the personal computer (e) 

The transient voltage signal is defined as follows

The parameters are as follows, σ'1=σ'2=σ'3=σ'4=σ'5=0.343 m. We also define x1=0, x2=-0.0175 m, x3=+0.0175 m, x4=-0.0175 m and x5=+0.0175 m. The frequencies are f1=2 kHz, f2=4 kHz, f3=6 kHz, f4=8 kHz and f5=10 kHz. The wave vectors are defined by the relation kj=ωj/c.

Figure 5 (a) presents the voltage pulse v(t) that is submitted from the signal generator (a) into the speaker (b). In Fig. 5 (b) we present the acoustical signal p'(t) measured by the microphone (d). We observe that it exist a complicate interference pattern that is result of the speaker signal but also exist an additional noisy contribution from the environment. In panel 5(c) we present the short time-Fourier transform of the signal p'(t) which is obtained by using the Origin software. We observe that the STFT is able to identify the transit time and frequencies of the five pulses components.

Figure 5 In panel (a) is presented the transient voltage signal v(t) received by the speaker. In panel (b) is presented the time-dependent amplitude p^'(t). Panel (c) shows the experimental STFT of the p'(t) signal. 

5. Conclusions

In this work, we demonstrate that the transit times and frequencies of a transient signal with a complex waveform can be recovered by using the STFT. The characterization is made using a spectrogram where the transit time is on one axis and the frequency on the other. This method of analysis has been applied to study Gaussian pulses with a sinusoidal component. For the case of a single pulse, we have found closed formulas for the STFT that allow understanding how this technique works. In the case of a pulsed signal formed by the superposition of multiple pulses, we have demonstrated theoretically and experimentally that it is possible to identify the transit times and frequencies for each pulse component.

The analysis of transient signals permits the study of many physical phenomena that can not be understood using the traditional Fourier theory. In our mathematical methods for physics, most of the work is devoted to the stationary case and the case of transient signals is rarely considered. However, as the measurement techniques have been improved, nowadays are explored a vast number of ultrafast phenomena. These signals are very important in various branches of physics, as for example the interaction of waves with nano-structures, nonequilibrium process , transient process in networks, seismological vibrations or the finding of black holes.