PACS: 11.10.St; 03.65.Ge; 02.60.Nm; 31.15.-p
1. Introduction
The Bethe-Salpeter equation 1 is based on the relativistic field theory and is an appropriate tool to deal with bound states. In comparison with the four-dimensional Bethe-Salpeter equation 2,3,4,5, the three-dimensional reductions of it are relatively easy to be handled . In Ref. 12, it was shown that there exist infinite versions of the reduced Bethe-Salpeter equation. One of them is the Maung-Norbury-Kahana (MNK) equation 8.
The MNK equation is covariant, obeys the unitarity relation and possesses a one-body limit. It is a proportionally off-mass-shell equation and is a relativistic, three-dimensional equation for bound states with two constituents. Moreover, the MNK equation gives a physically meaningful prescription of how the constituents go off-mass-shell in the intermediate states. The MNK equation allows the components of bound states to go off-mass-shell proportionally to their masses. In this paper, the MNK equation is solved numerically and is applied to discuss the equal-mass systems (positronium and true muonium) and the unequal-mass system (muonium).
The paper is organized as follows. In Sec. 2, the MNK equation is reviewed and the spinless MNK equation is derived. In Sec. 3, the spinless MNK equation is solved numerically and the discussions are presented. The conclusion is in Sec. 4.
2. Maung-Norbury-Kahana equation
In this section, the MNK equation is reviewed and the spinless MNK equation is derived. To discuss the bound states,
2.1. Reduction of the Bethe-Salpeter equation
The Bethe-Salpeter equation in momentum space reads 1,6
where
In order to have a correct one-body limit in three-dimensional reduced equations, the Wrightmann-Gordon choice 13 of
where s = P
2. In Eq.(1),
where m1 and m2 are interpreted as effective masses for the fermion and antifermion.
We introduce components of the relative momentum
where
with the properties
In this paper the covariant instantaneous approximation is employed 14, in which the approximated kernel is independent of the change of the longitudinal component of the relative momentum,
It is a good approximation for a system composed of heavy and light constituents or of two heavy constituents which can move relativistically as a whole. It will reduce to the instantaneous approximation in the rest frame of the bound state.
Introduce the notation for later convenience
where
where
and
In Refs. 7 and 8,
where
In the above equation,
Eq. (13) can be simplified as
where
and
If constituent 1 takes positive energy as
After integrating over
From Eqs. (11), (16) and (20), we have
Using Eqs. (9), (19) and (21), Eq. (10) reduces to the MNK equation
The MNK equation has been understood physically meaningful: when masses of constituents are not equal but comparable, this kind of choice of
Assuming
we have from Eq. (22)
Neglecting any reference to the spin degrees of freedom of the involved bound-state constituents, we have the spinless MNK equation from Eq. (24)
where
2.2. Landé subtraction method
In this paper, the Coulomb potential is considered. The Coulomb potential reads in the momentum space
where
where n is the principal quantum number, l is the orbital angular quantum number. f (M, p) reads
where Q l (z) is the Legendre polynomial of the second kind,
The Coulomb potential has the logarithmic singularity at point p' = p, and the singularity comes from Q 0(z).
Applying the Landé subtraction method 17,18,19,20,21 to cancel out the singularity, the singular equation (27) becomes
where z' = 1, Pl (1) = 1,. In the above calculation, we have used the identity
3. Numerical results and discussions
In this section, the spinless MNK equation with the Coulomb potential is solved numerically by employing the Gauss-Legendre quadrature rule. The positronium, muonium and true muonium are discussed.
3.1. Eigenvalue integral equation
The eigenvalue integral equation (31) can be written formally as
Due to the complicated form of
where
3.2. Gauss-Legendre quadrature rule
Rewrite the subtracted integral equation (31) in the form of Eq. (34), then apply the Gauss-Legendre quadrature rule to the regular integral 21. Finally, a matrix equation can be obtained from Eq. (31) by employing the Nyström method and it can be solved easily.
At first, we map the semi-infinite interval
where
The Gauss-Legendre quadrature formula for regular integral reads
where
In Eq. (38), prime stands for the derivative.
3.3. Numerical results and discussions
By employing the methods discussed above, the spinless MNK equation [Eq. (25)] with the
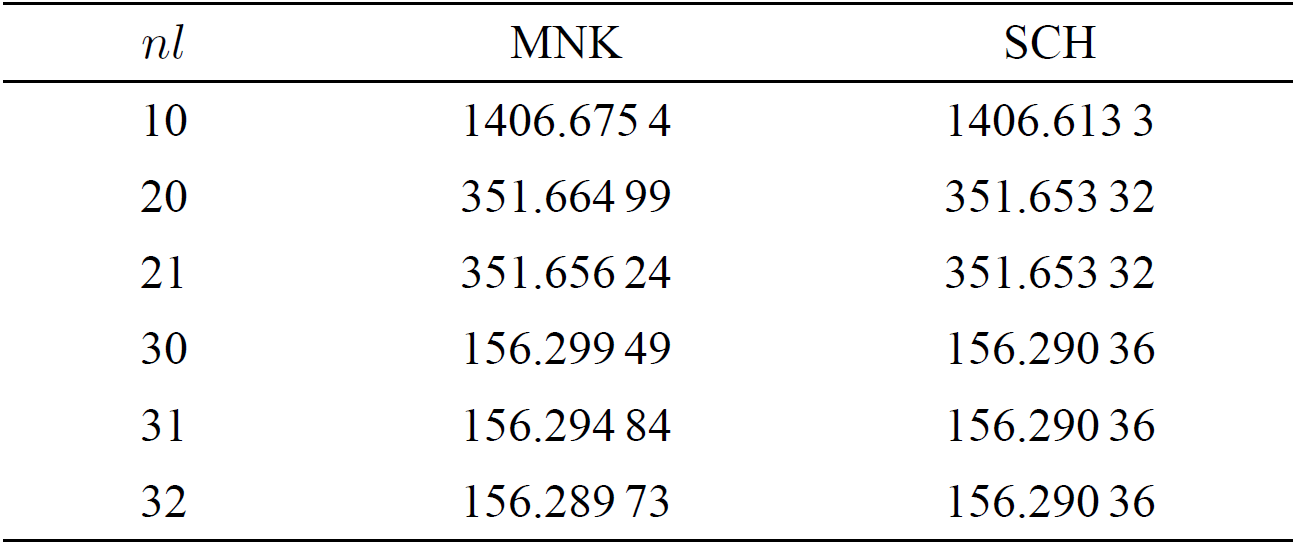
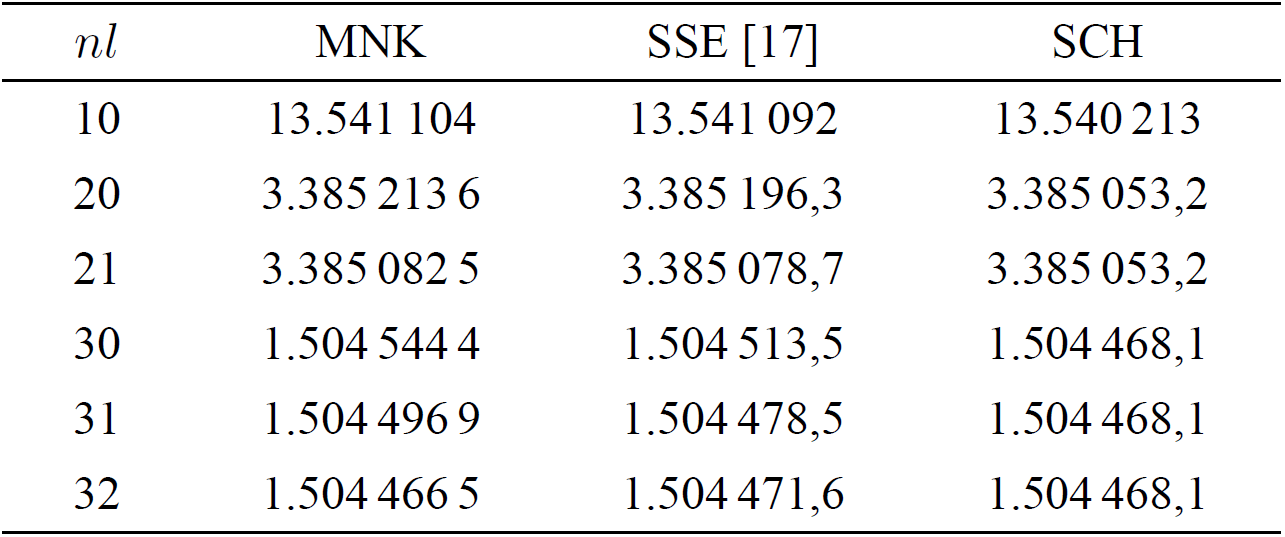
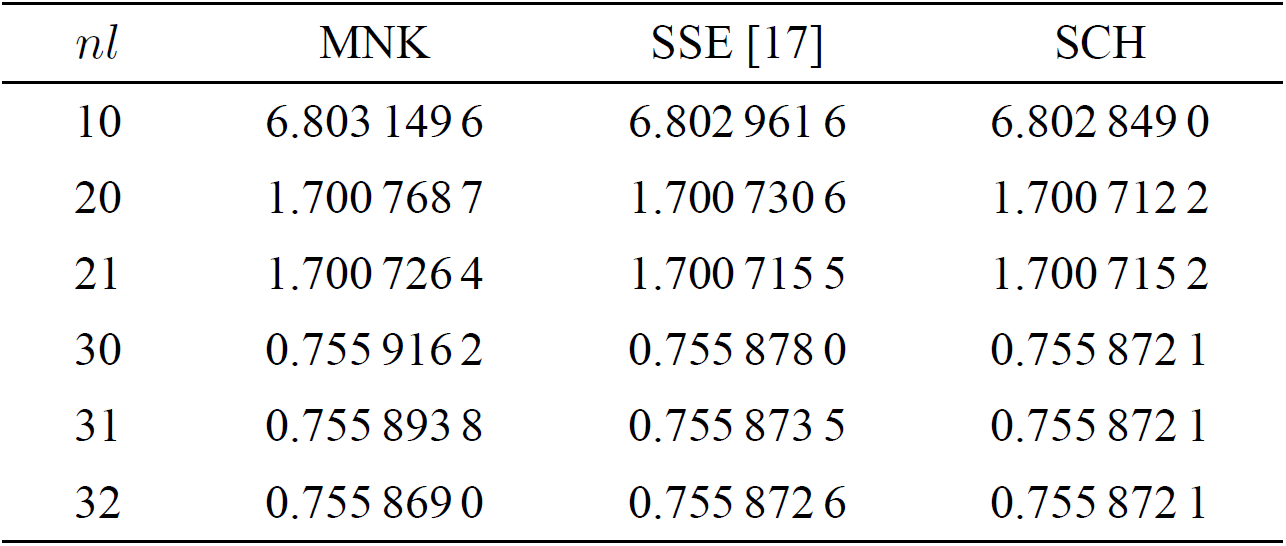
Coulomb potential is solved numerically and the numerical results are listed in
Tables I, II and III. The input
parameters are N = 180,
Table I. Binding energies
In the spinless MNK equation (25), the virtuality parameter
The spinless MNK equation includes not only the relativistic effects but also the virtuality effects. By comparing the eigenvalues of the spinless MNK equation and that of the spinless Salpeter equation, we can obtain the virtuality effects. The eigenvalues of the spinless MNK equation are smaller than that of the spinless Salpeter equation and the Schrödinger equation, see Tables I, II and III. It means that the virtuality effect of constituents results in stronger binding. For the positronium, the virtuality effect is about of the same order as the relativistic effects. For the muonium, the virtuality effect is smaller than the relativistic effect. The data show that the virtuality effect varies with the virtuality parameter
The spinless MNK equation (25) describes the bound states composed of the spinless virtual constituents. By employing the approaches applied in Refs. 6 and 24, the spin-independent terms and spin-dependent terms can be obtained from Eq. (24). Then spin effects can be included according to the discussed problems.
4. Conclusion
In this paper, the spinless Maung-Norbury-Kahana equation is derived and is solved
numerically. Taken as examples, the positronium, muonium and true muonium are
studied by employing the spinless MNK equation with the Coulomb potential. The MNK
equation allows the constituents of bound states to go off-mass-shell proportionally
to their masses. The numerical results show that the binding of virtual constituents
will be stronger than that of the on-mass-shell constituents and the virtuality
effect varies with different virtuality parameter











 nueva página del texto (beta)
nueva página del texto (beta)