PACS: 75.50.Pp; 75.50.Ee; 75.60.Ej
1. Introduction
The orthorhombic semiconductor Ag2FeGeSe4 which crystallizes with the wurtz-stannite structure 1,2 belongs to family of the I2-II-IV-VI4 compounds where I = Cu or Ag;II = Zn, Cd, Hg, Mn, Fe or Co; IV = Si, Ge, Sn or Pb; and VI = S, Se or Te. These materials are of great interest because of both their applications in the fabrication of low cost solar cells 3 and their large magneto-optical effects which are observed when II atoms are paramagnetic ions 4,5. The study of the magnetization of Ag2FeGeSe4 over the temperature range from 2 to 300 K shows that this material has an antiferromagnetic behavior 6. The large numbers of known antiferromagnetic substances exhibit a rich variety of magnetic phase transitions. These transitions are described with particular emphasis in uniaxial antiferromagnets of the easy -axis type. Susceptibility measurements made at high magnetic field (5 T) showed a magnetic moment of 4.4
The present paper describes the behavior of the critical-fields and the thermal broadening for Ag2FeGeSe4 at various temperatures obtained in a previous work 6. To our knowledge, there are no previous reports on thermal broadening in Ag2FeGeSe4 compound, and the literature information on it is very scarce.
2. Theoretical details
Theoretical and experimental analysis e.g.4,7,8,9 for an antiferromagnetic material show that three phases can occur in the magnetic field-temperature (B - T) plane of the magnetic phase diagram. These are the paramagnetic (P), the antiferromagnetic (AF) and the spin-flop (SF). At the AF to SF first-order phase transition the magnetization increases linearly with applied field and show a discontinuity, whereas the SF to P phase transition is of second-order type and the magnetization breaks off from this line 10. These analyzes have been concerned mainly with uniaxial materials with an easy-axis z. It is seen in such a case that the details of the diagram depend on the orientation of the applied magnetic field with the z direction. Critical fields for these transitions are obtained as a function of temperature and the phase diagram in the B - T plane can thus be determined.
According to the scheme proposed by Ehrenberg et al.7, for sufficiently low-fields in the AF region, the magnetization is proportional to the applied magnetic field as given by the expression,
where
On the other hand, for sufficiently high fields, the magnetic moments are forced into a ferromagnetic-like arrangement, which belongs to the P region in the phase diagram, where all the magnetic moments are aligned with the magnetic field. In this paramagnetic region, the expressions usually applied to single crystals for describing the field and temperature dependence of the magnetization, based on a quantum mechanical description of the phenomena through the function of Brillouin are expected to be inappropriate for polycrystalline samples. This is because polycrystals are macroscopic objects that combine thousands of spins at random. The simplest approximation in such a case is an isotropic distribution of easy axes at angle
where M S is the saturation magnetization and L(x) is the Langevin function which is given by
with
Finally, in the SF phase, the magnetization is proportional to the applied field strength corrected in real systems by an offset M 0:
For all magnetizations curves below of the Néel temperature the field dependence of the magnetization, assuming the existence of an SF phase, can be described by the following expression:
Here B
SF
and B
P
are the critical field strengths for the transitions AF
3. Results and Discussion
The magnetization of Ag2FeGeSe4 at 2 K as a function of the applied magnetic field is shown in Fig. 1a). Only the up-stroke cycle is presented in this figure. The application of the external field induces the two successive AF
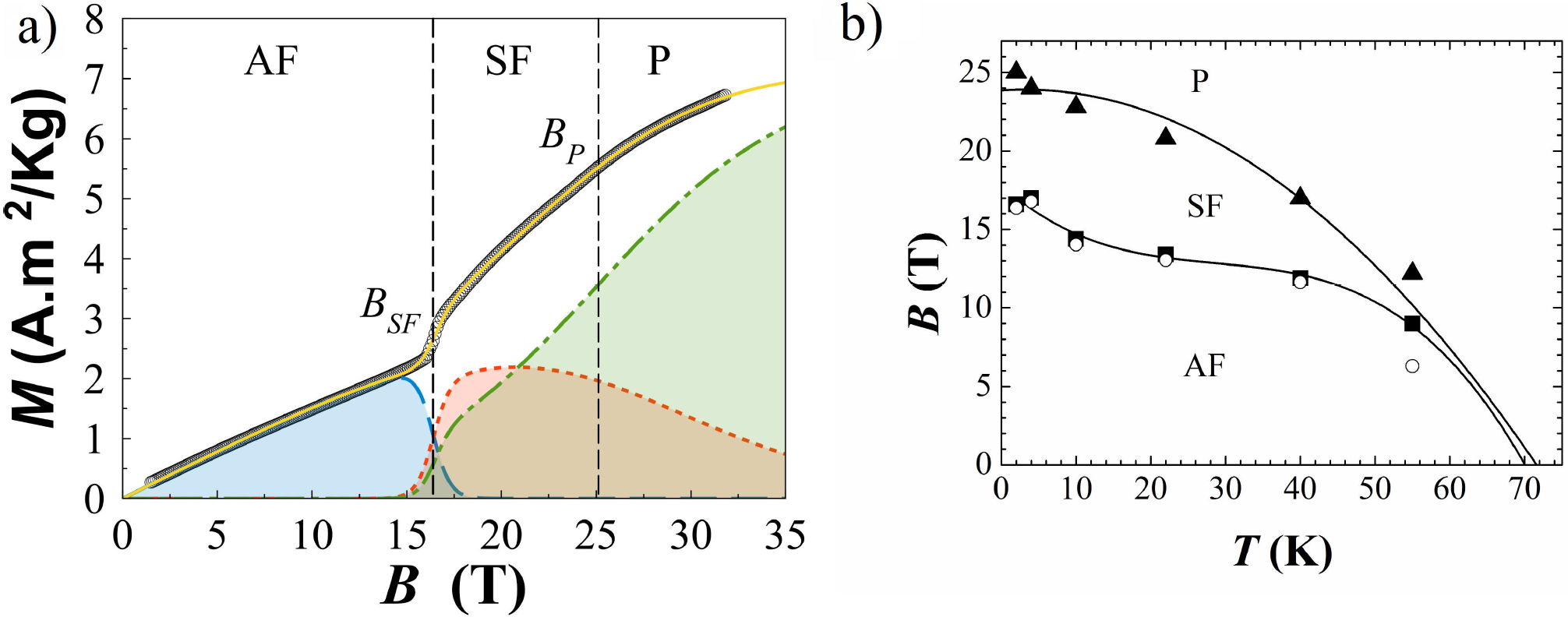
Figure 1. (a) Magnetization M against external applied magnetic field B at 2 K from pulsed field measurements for upstroke cycle. The dashed vertical lines show the positions of the B SF and B P points (see Table I). The solid yellow line is a fit of the data (open circles) by using Eq. (5) extrapolated until 35 T. The contributions from the three terms: M AF (dash blue line), MSF (dot red line) and MP (dash-dot green line) are also shown. (b) The magnetic phase diagram for the Ag2FeGeSe4 compound showing the experimental values for field-up (full points) and the calculated values (open circles) for up-stroke cycle from Table I. The solid lines are guides for eyes extrapolated until the Néel point. Adapted from Ref. 6.
The solid yellow line in Fig. 1a) represents a fit of Eq. (5) to the experimental M (B) data. It is clear from this figure that the saturation magnetization was not reached in the range of magnetic field values achieved in this work. Also, an appreciable hysteresis effect was observed for all curves (see Fig. 2 in Ref. 6). For this reason, the M S values were fixed during the fitting for all the curves in the down-stroke cycle, not shown here, at the values obtained in the up-stroke cycle.
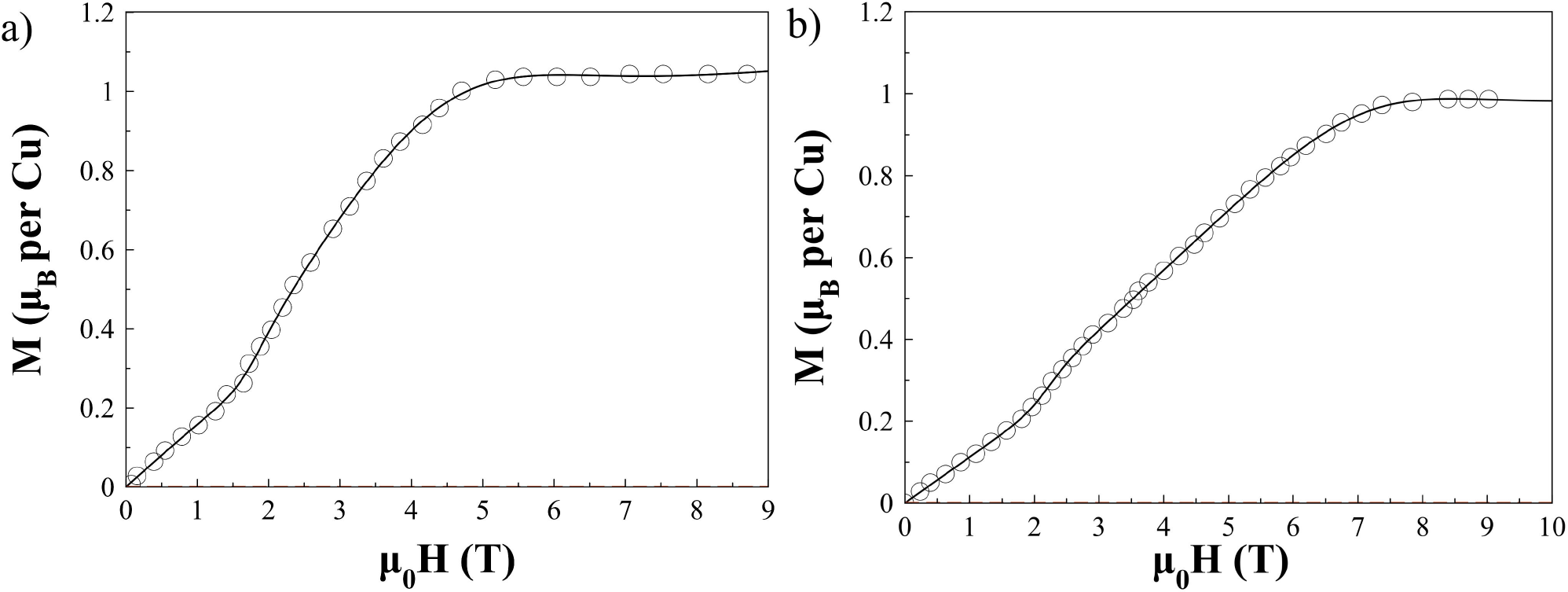
Figure 2. The solid line represents the best fits with Eq. (5). The open circles are 2 K data on polycrystalline a) Ba3Cu3In4O12 and b) Ba3Cu3Sc4O12 taken from Ref. 14.
Table I summarizes the results obtained by fitting with Eq. (5) the curves of magnetization at various temperatures for up-stroke cycles. The susceptibilities calculated and the critical field strength B SF agree with the experimental values previous report in Ref. 6. It is worth mentioning that attempt was also made to adjust the magnetizations curves by using the Brillouin function. However, no fit was obtained. This is probably due to the polycrystalline nature of the present sample as was explained above.
Table I. Parameters obtained from fitting Eq. (5) to curves M vs. B at various temperatures. The BP parameter was taken from the Ref. 6 and the μ parameter was fixed at μexp. = 4.90 (Fe+2). Numbers in parentheses are statistical errors. For B P values was estimated an error of ±2 T.
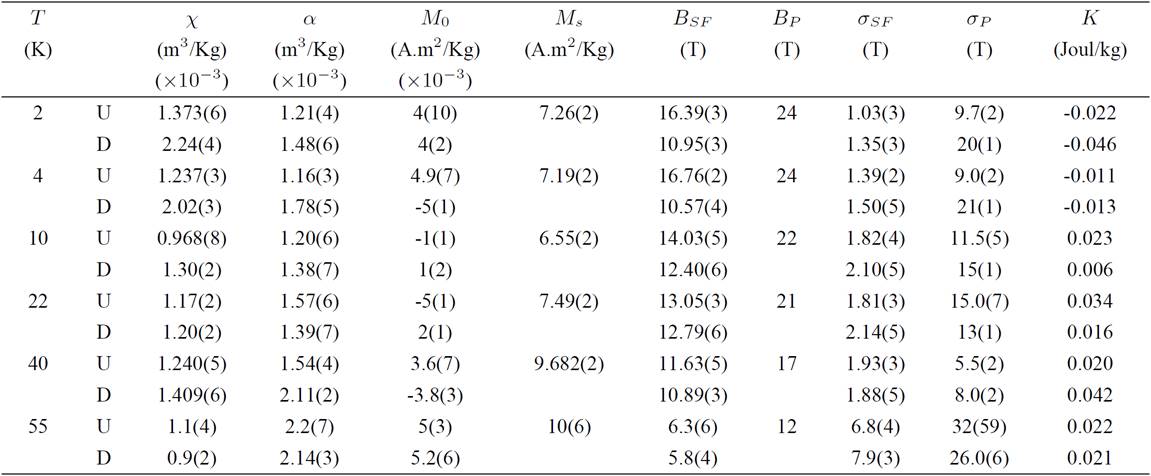
Note. The labels U and D mean up-stroke and down-stroke cycles, respectively.
For a uniaxial antiferromagnet of the easy-axis type, at temperatures below the Neel temperature T
N
, the orientation of M
l
and M
2 relative to the crystallographic axes is determined by the anisotropy energy. As indicated by Shapira 11, The AF
where K is the effective anisotropy energy per unit mass,
Thus, the values for K at various temperatures were calculated from Eq. (7) (see Table I). For above of 10 K, the values for susceptibility
Since for Ag2FeGeSe4 the saturation of the magnetization was not reached experimentally, in order to test the present model in the region of high fields where the magnetization saturates, M(B) curves for Ba3Cu3In4O12 and Ba3Cu3Sc4O12 compounds recently reported 14 were fitted using Eq. (5). The obtained parameters are summarized in Table II. It can be seen that the values for B
P
and B
SF
obtained for these compounds agree quite well with those reported. Also, their widths
Table II. Parameters obtained for Ba3Cu3In4O12 and Ba3Cu3Sc4O12 compounds with Eq. (5). Numbers in parentheses are statistical errors. The μ parameters for Cu2+ were taken from Ref. 14.
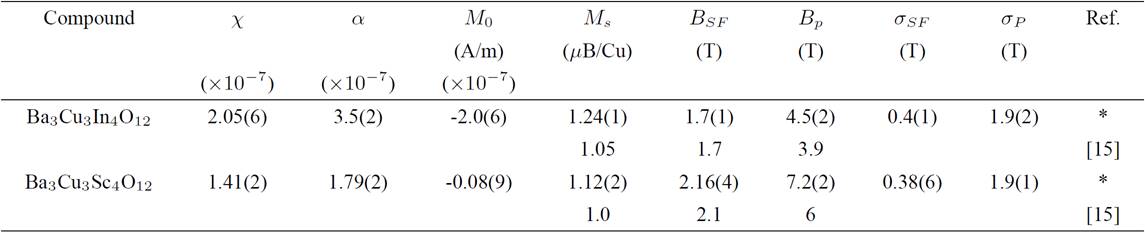
*This work.
In summary, we have shown that the scheme proposed by Ehrenberg et al.7 to study the temperature and magnetic field dependence of magnetization in the AF, SF and P phases of the low anisotropy antiferromagnetic materials, success describe all magnetization curves below Néel temperature for the Ag2FeGeSe4 compound. In the present case, for the analysis of the paramagnetic region, the model was adapted for polycrystalline samples by using the classical Langevin function instead of the Brillouin one normally used for single crystals. Transitions given by B
SF
and B
P
, lead to the magnitudes











 text new page (beta)
text new page (beta)


