PACS: 77.80.B; 75.50Cc.
1. Introduction
In the last few years, the study of magnetic-field induced phenomena across the first-order martensitic transformation (MT) in ferromagnetic shape memory alloys of the ternary alloy systems Ni-Mn-X (X= Sn, In, Sb) has been a subject of considerable attention. Among them, the most studied are giant inverse magnetocaloric effect 1,2,3.4, magnetic shape memory effect 5.6, and magnetoresistance 7. Another field-induced effect, less common, sometimes observed in various alloys is the kinetic arrest (KA) of martensitic transformation. It was first detected by Sharma et al. in a bulk Ni50Mn34In16 alloy 8, but later it has been also observed in other Ni-rich 8,9,10.11,12,13,14.15,16,17,18.19 and Mn-rich 20,21,22 Heusler-type Ni-Mn-X (X= Sn, In, Sb) alloys. In addition, it also appears in a variety of other materials exhibiting first-order phase transitions, either alloys or oxides, such as the Laves phases Ce(Fe,X)2 (X = Al, Ru) 23,24,25,26 and HfFe227, Gd5Ge428, MnSi 29, NiCoMnAl 30, Mn2PtGa 31, Mn3GaC0.932 and phase-separated manganites 26,33,34,35. An overview about the manifestation of this phenomenon in different magnetic materials is found in Ref. 36.
In the case of Ni-rich and Mn-rich Heusler-type alloys, a volume fraction of the parent austenite phase remains frozen into the equilibrium martensitic matrix under the application of a static magnetic field of strength beyond a certain critical value when the material is cooled down below the martensitic finishing structural transition temperature M
f
. This mixed, or two-phase, state is metastable in nature and is commonly characterized by means of magnetization 8,9,11,25, resistivity 9, and neutron diffraction measurements 22. The relevant information provided by these experiments is found when the information obtained from the zero-field-cooled and field-cooled states in the phase coexistence region is compared. As expected, due to the higher saturation magnetization of austenite with respect to martensite (MST), the zero-field cooling (ZFC) and field-cooling (FC) (and field-heating, FH) pathways of the temperature dependence of magnetization
Most of the studies carried out on the observation and characterization of KA phenomenon in Ni-rich and Mn-rich Heusler-type alloys have been performed in bulk alloys. In the case of melt-spun ribbons, the field-induced arrest of MT has been only reported in a few alloys such as Mn50Ni40In1020, Ni45Co5Mn38Sn1217, Ni38Co12Mn41Sn918, and Ni47Mn35Fe5In1319. However, most of these studies are limited to report its existence based on the above mentioned splitting between ZFC and FC
2. Experimental
A bulk alloy of nominal composition Mn50Ni36In14 was prepared by arc melting in argon atmosphere from highly pure elements (Ni 99.98%, Mn 99.98%, and In 99.999%). The sample was remelted three times to ensure good starting homogeneity. Additional amount of Mn was added to compensate the loss of this element during the arc melting process in order to preserve the starting 50:36:14 composition in the resulting pellet. From this as-cast alloy, melt spun ribbons were obtained in a highly pure argon environment (99.999%) at a high tangential speed of the copper wheel of 48 ms-1 (wheel diameter: 20 cm); the process was carried out by using a homemade single-roller melt spinner apparatus. The as-cast pellet was melted by radio frequency induction heating in a quartz crucible with an orifice of 0.5 mm; the molten alloy was ejected with an Ar overpressure of 20 bar onto the polished surface of the copper wheel.
X-ray powder diffraction, differential scanning calorimetry (DSC), scanning electron microscopy (SEM), energy dispersive spectroscopy (EDS) and magnetization measurements were used to study ribbon samples. The DSC measurements were performed in a TA Instruments model Q200 under a high purity Ar flow at a heating/cooling rate of 10 Kmin-1. X-ray diffraction patterns of finely powdered ribbon samples were recorded in a Bruker D8 Advance powder diffractometer (
3. Results and discussions
The room temperature XRD pattern of powdered as-solidified ribbons is shown in Fig. 1(a). All the diffraction peaks were satisfactorily indexed on the basis of a B2-type crystal structure with a lattice parameter of 0.299(3) nm. The crystallization of AST in this crystal structure, instead of the highly ordered L21-type structure, has been frequently reported in as-solidified Ni-Mn-In alloy ribbons with similar composition and results from the high cooling rate during solidification 41,42. The inset in Fig. 1(a) shows the typical cross sectional microstructure of ribbons. Their average thickness is ~ 9 - 12
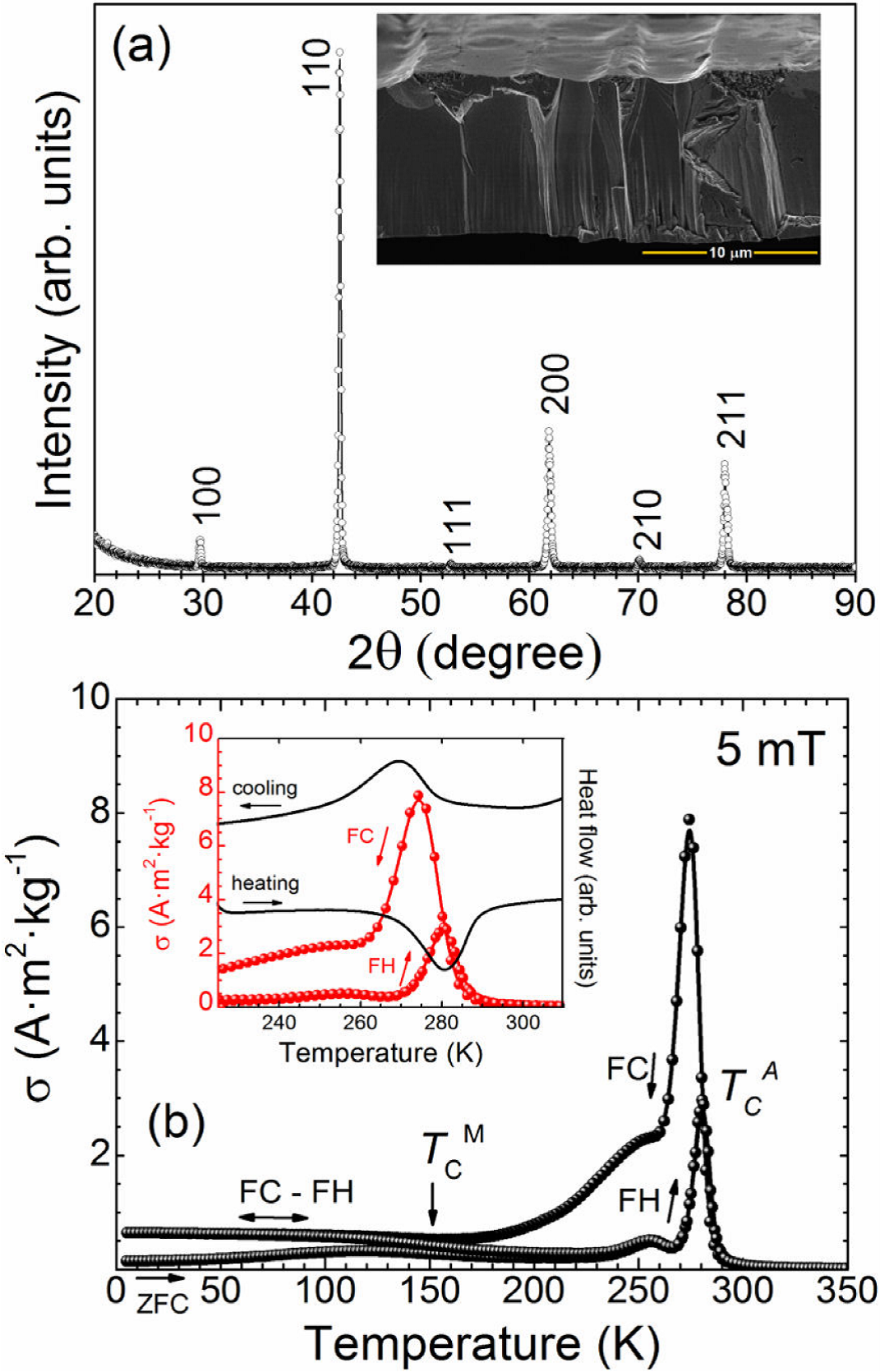
Figure 1 Room temperature XRD pattern (a) and ZFC, FC and FH σ(T) curves at 5 mT (b) for as-solidified ribbon samples. The insets in (a) and (b) show the typical cross section microstructure and the σ(T) curves (red dots) and DSC scans (black line) in the structural transition region.
The temperature dependencies of the magnetization
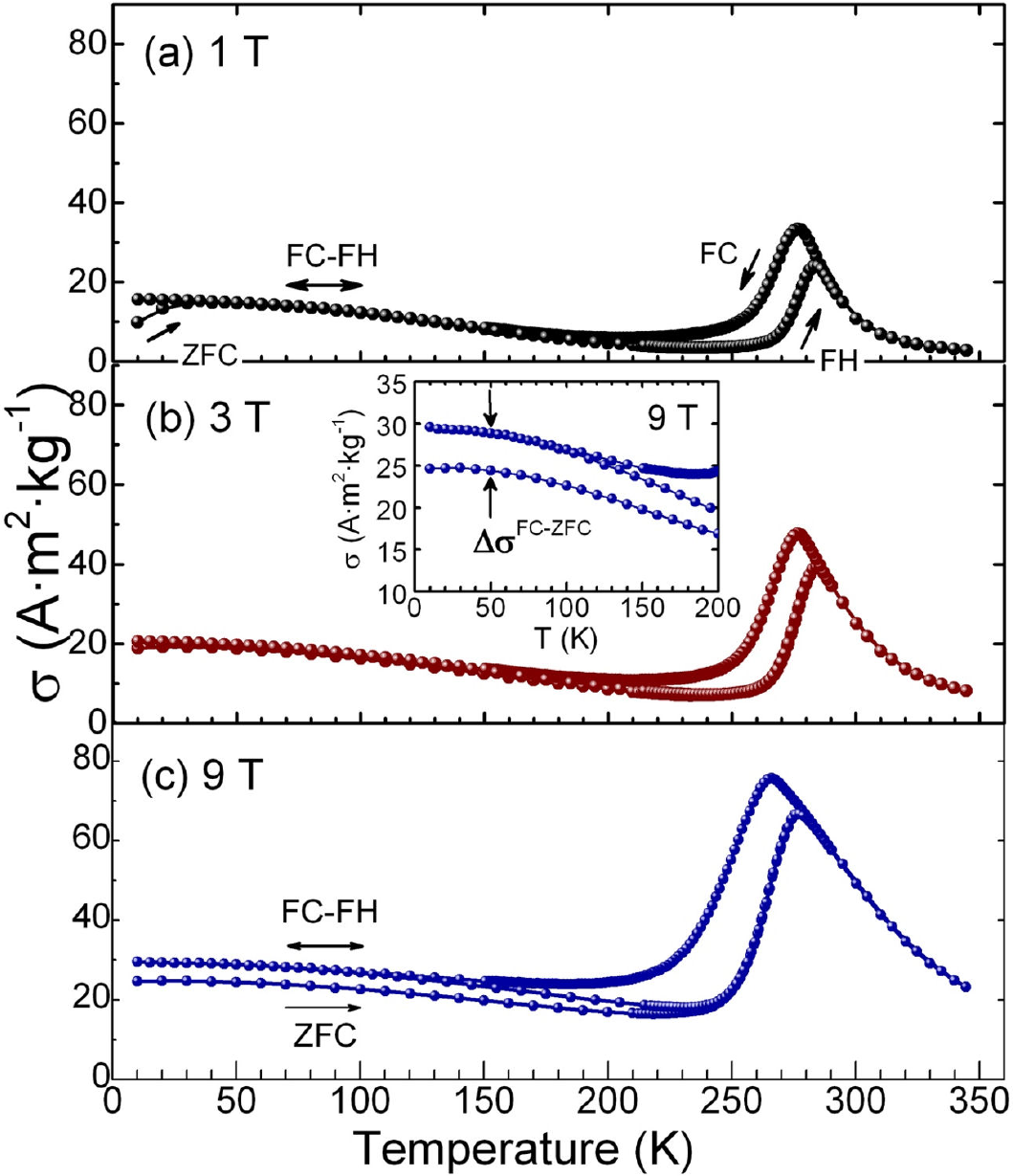
Figure 2. σ(T) curves measured in FH, FC and ZFC regimes under static magnetics fields of: 1 T (a), 3 T (b), and 9 T (c). Inset in (c): zoom into the σ(T) curve at 9 T in the martensitic region to show the magnetization difference
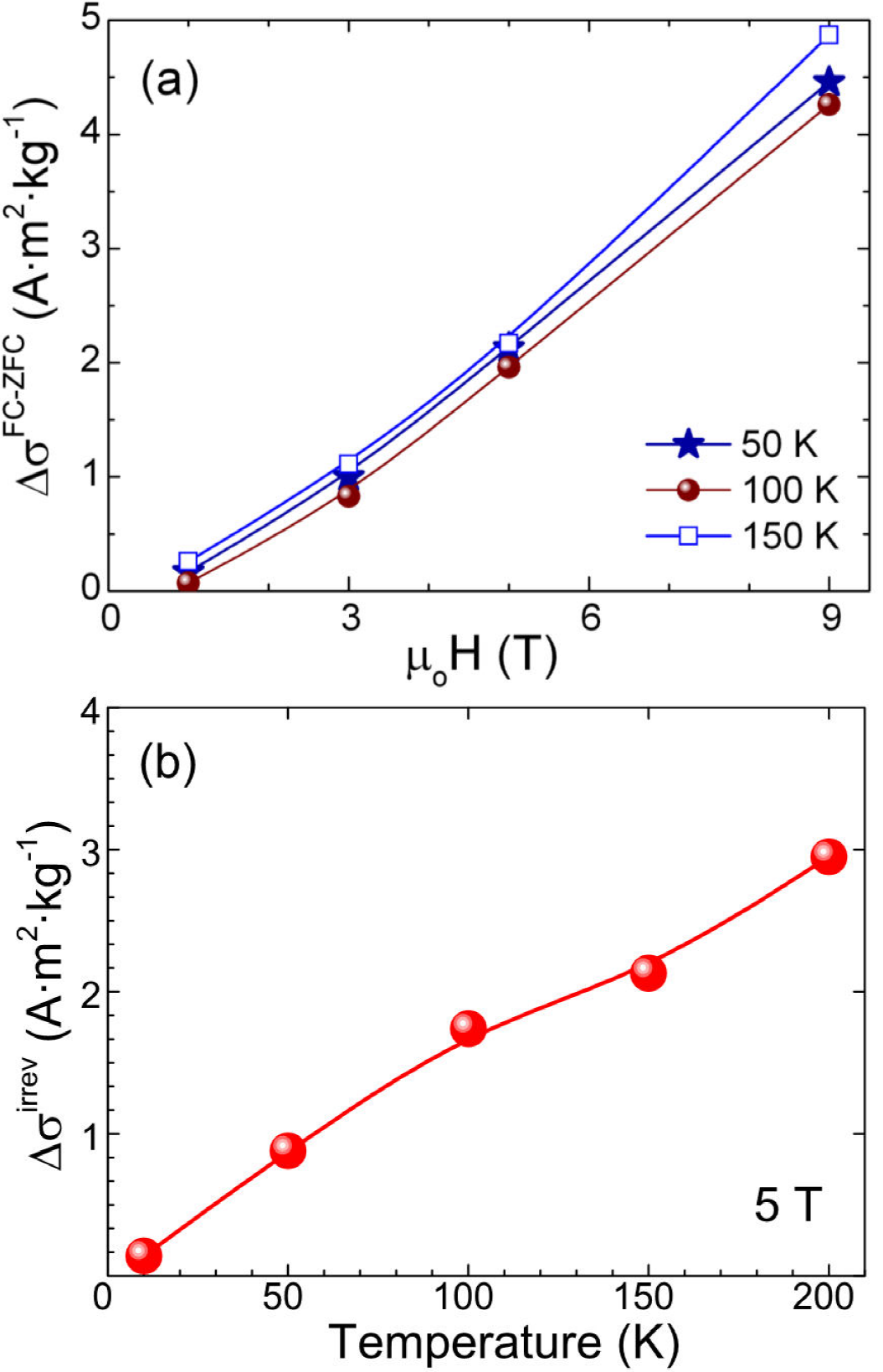
Figure 3.
To characterize the metastable nature of the FC inhomogeneous state, different magnetization experiments were performed in the martensitic existence region under an applied magnetic field of 5 T. In the first one, thermal energy fluctuations were introduced through successive thermal cycling. From 350 to 10 K the sample follows the FC regimen under a large magnetic field of 5 T. Then, the temperature was increased from 10 K to successively increasing maximum temperatures T
max of 50 K, 100 K, and 150 K, after the sample reaches the respective T
max, temperature is decreased to 10 K (the magnetic moment as a function of T is continuously measured along all these increasing and decreasing pathways). The measured
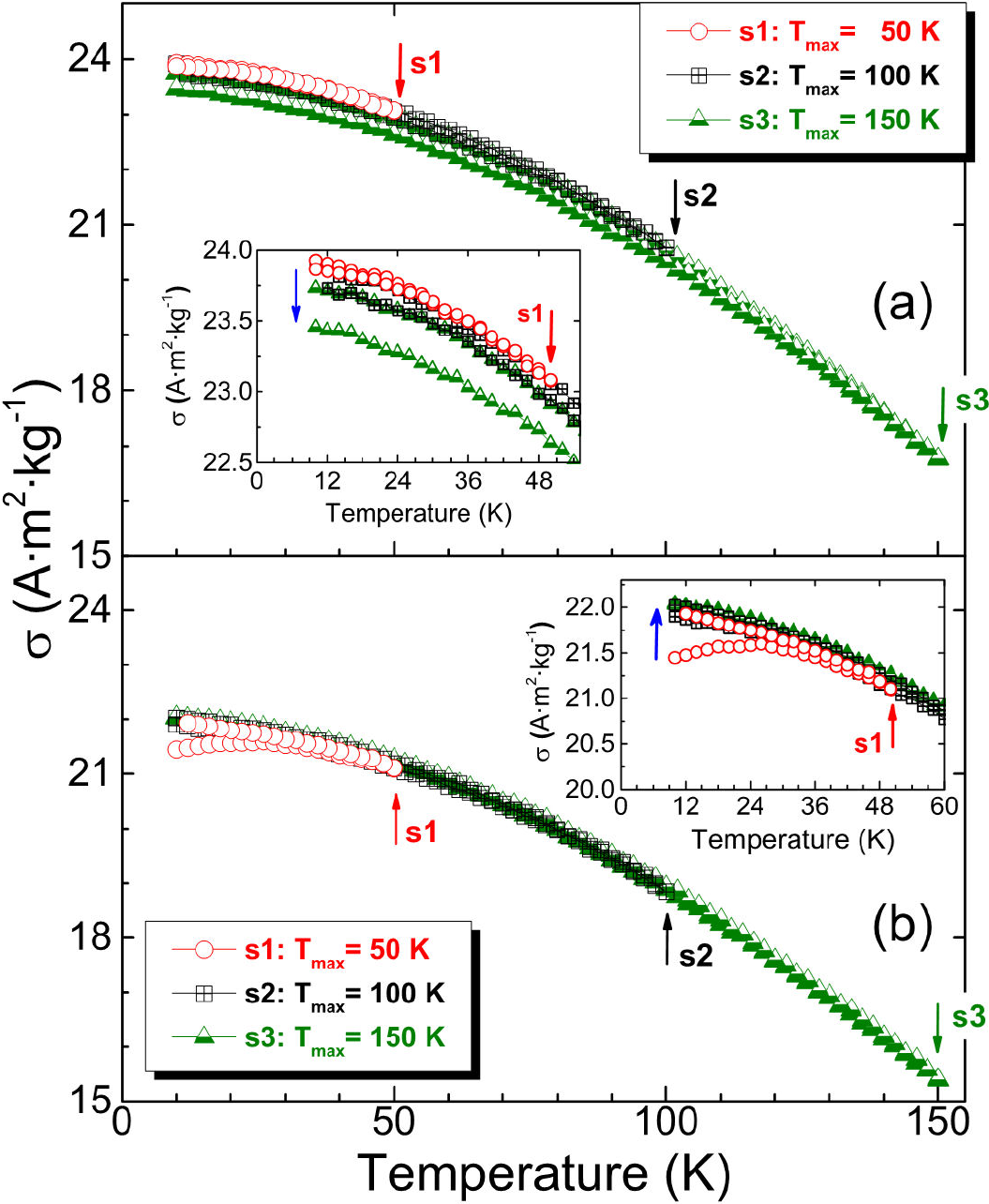
Figure 4. (a) Effect of the successive thermal cycling between 10 K and T
max (for T
max = 50 K, 100 K, and 150 K) on the σ(T) curve at
In a second experiment, the temperature was fixed at five selected values (referred to as T
meas), namely 10 K, 50 K, 100 K, 150 K and 200 K, and two different thermal protocols, FC and ZFC, were followed to reach these temperatures; then, the
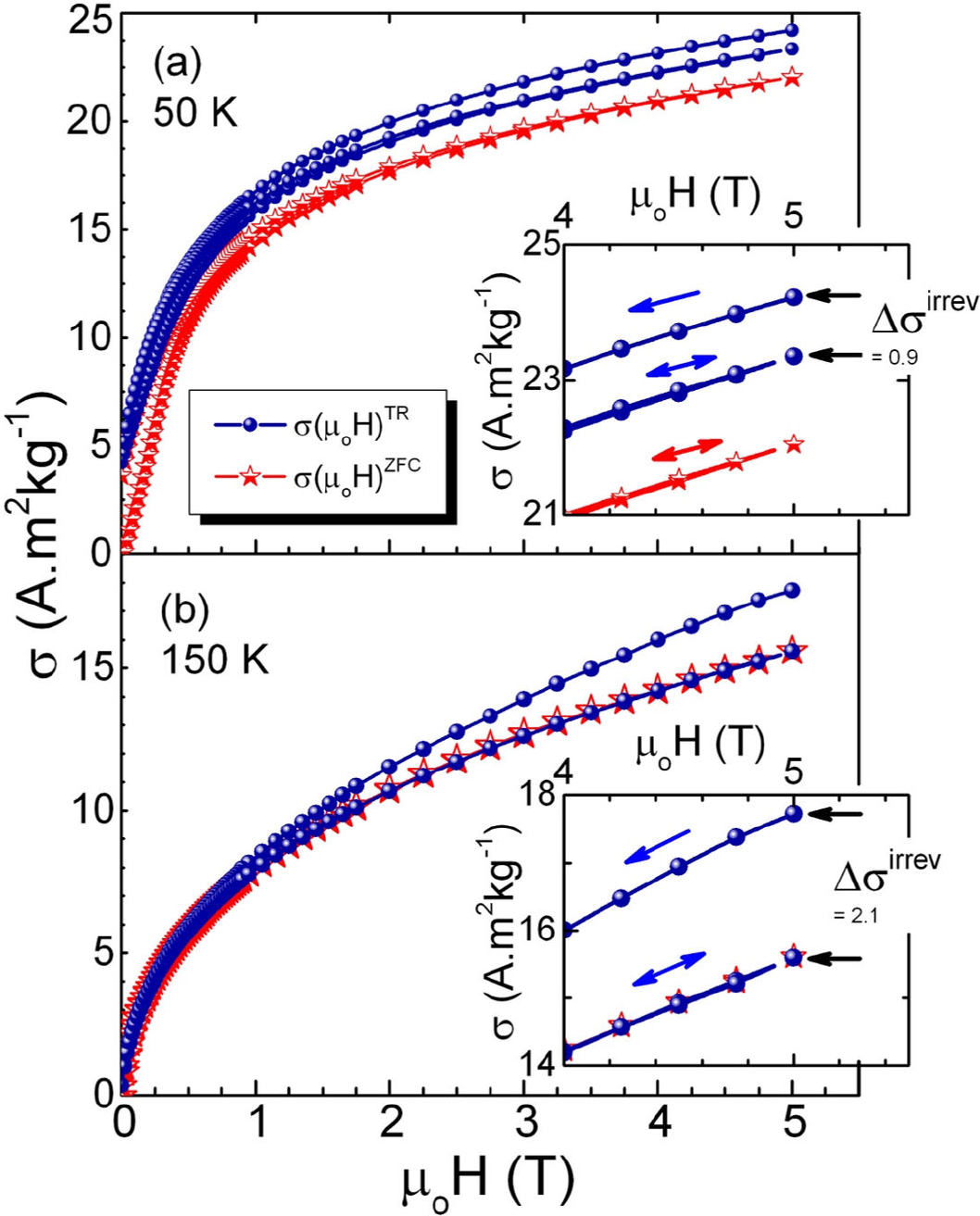
Figure 5 Demagnetization thermo-remanent curve
The dynamical behavior of this non-equilibrium magnetic state, or magnetic glassy state, is very similar to that of a structural glass 44. The relaxation of magnetization in the FC kinetically arrested state is another phenomenon that characterizes the metastable nature of the magnetic glassy state 45. For this state, the normalized magnetization as a function of time
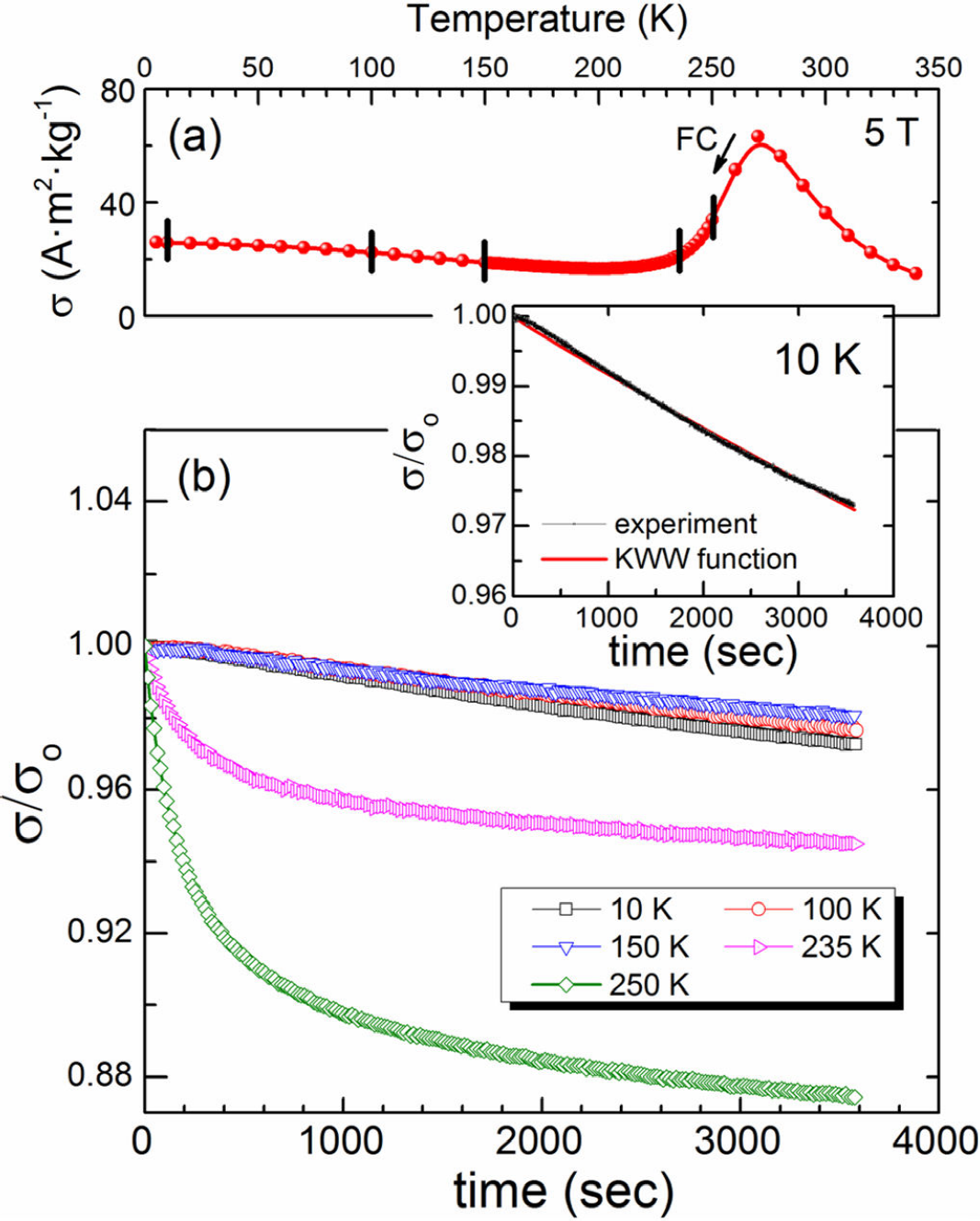
Figure 6. (a) FC pathway of the σ(T) curve measured at 5 T; the vertical bars indicate the temperatures at which the relaxation curves shown in (b) were measured. (b) Normalized magnetization σ/σ 0 versus time plots measured at 5 T and temperatures of 250, 235, 150, 100 and 10 K. Inset: experimental σ/σ 0(t) curve measured at 10 K and its fitting (solid red line) to a KWW stretched exponential function with a β value of 0.95.
The as-solidified ribbon samples were thermally annealed in vacuum at 1073 K during a short time interval of 10 min. For melt-spun ribbons obtained at high quenghing rates, this process is usually addressed to modify the structural disorder induced by the fast extraction of thermal energy during rapid solidification that in crystalline materials leads to structural deviations from equilibrium 41,42. However, it is unable to change the relevant microstructural features, such as grain morphology, grain orientation and average grain size owing to the short annealing time and the relatively low diffusion rate. In (Ni,Mn)-based Heusler type melt-spun ribbons the annealing improves the chemical and crystallographic order resulting in: (a) an increased saturation magnetization of both AST and MST phases; (b) a shift of the structural and magnetic phase transition temperatures, and; (c) a more abrupt magnetization change across the structural and magnetic transitions and a change in the crystal structure of AST 41,42. The room temperature XRD pattern measured on powdered annealed ribbons is presented in Fig. 7(a). The diffraction peaks were satisfactorily indexed on the basis of a highly ordered L21-type crystal structure with a lattice parameter of 0.599(6) nm. The crystallization of AST in this crystal structure is observed in bulk and melt-spun ribbons after a long annealing time 41,42,47. The inset in Fig. 7(a) shows that the typical cross sectional microstructure remains unchanged. The average elemental chemical composition determined by EDS slightly shifts to Ni51.5Mn33.5In15. Figure 7(b) shows both the DSC scans and the ZFC and FC
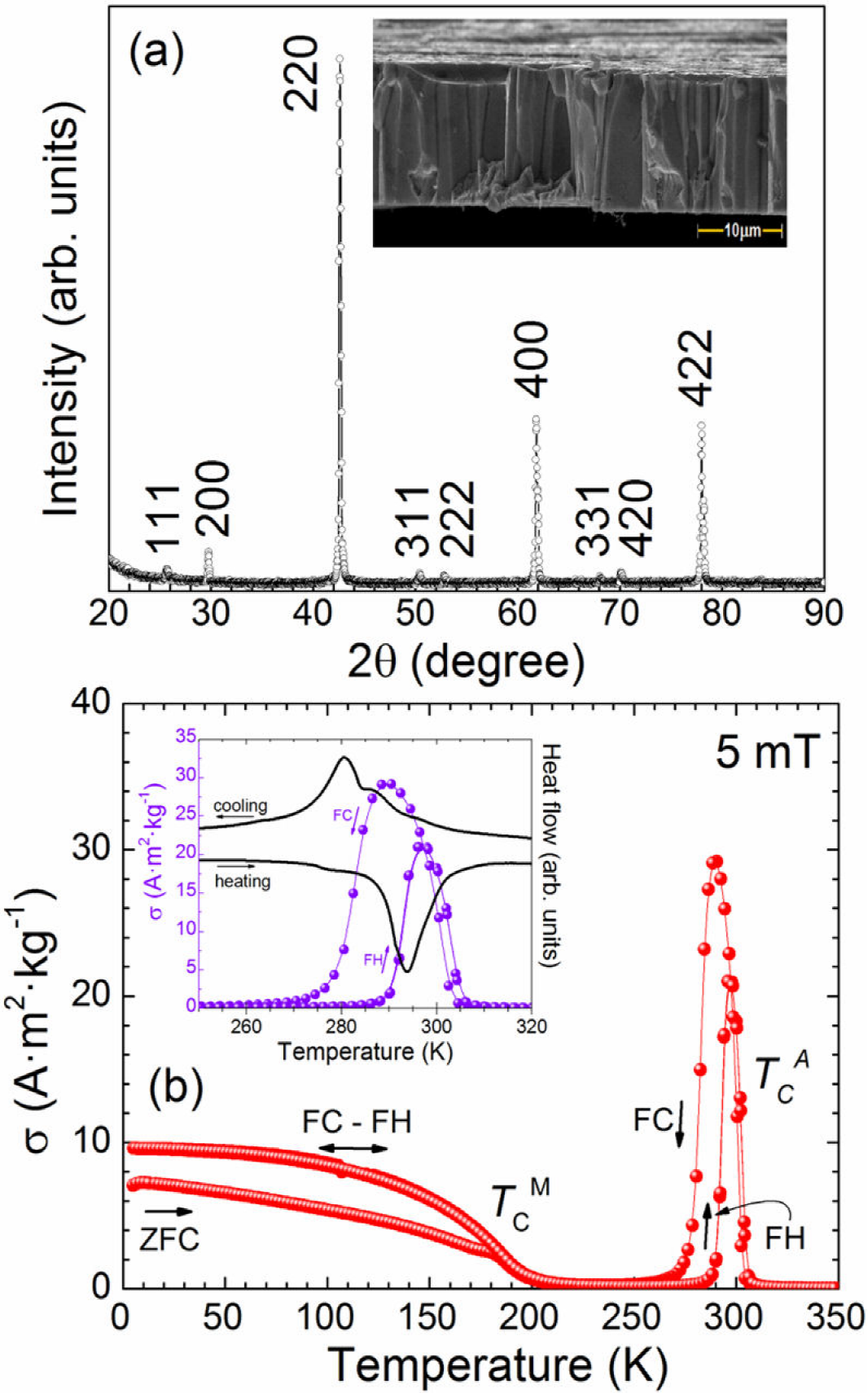
Figure 7. Room temperature XRD pattern (a) and heating and cooling σ(T)5mT curves (red dots) and DSC scans (black line) (b) for annealed ribbon samples. Inset in (a): typical cross section microstructure.
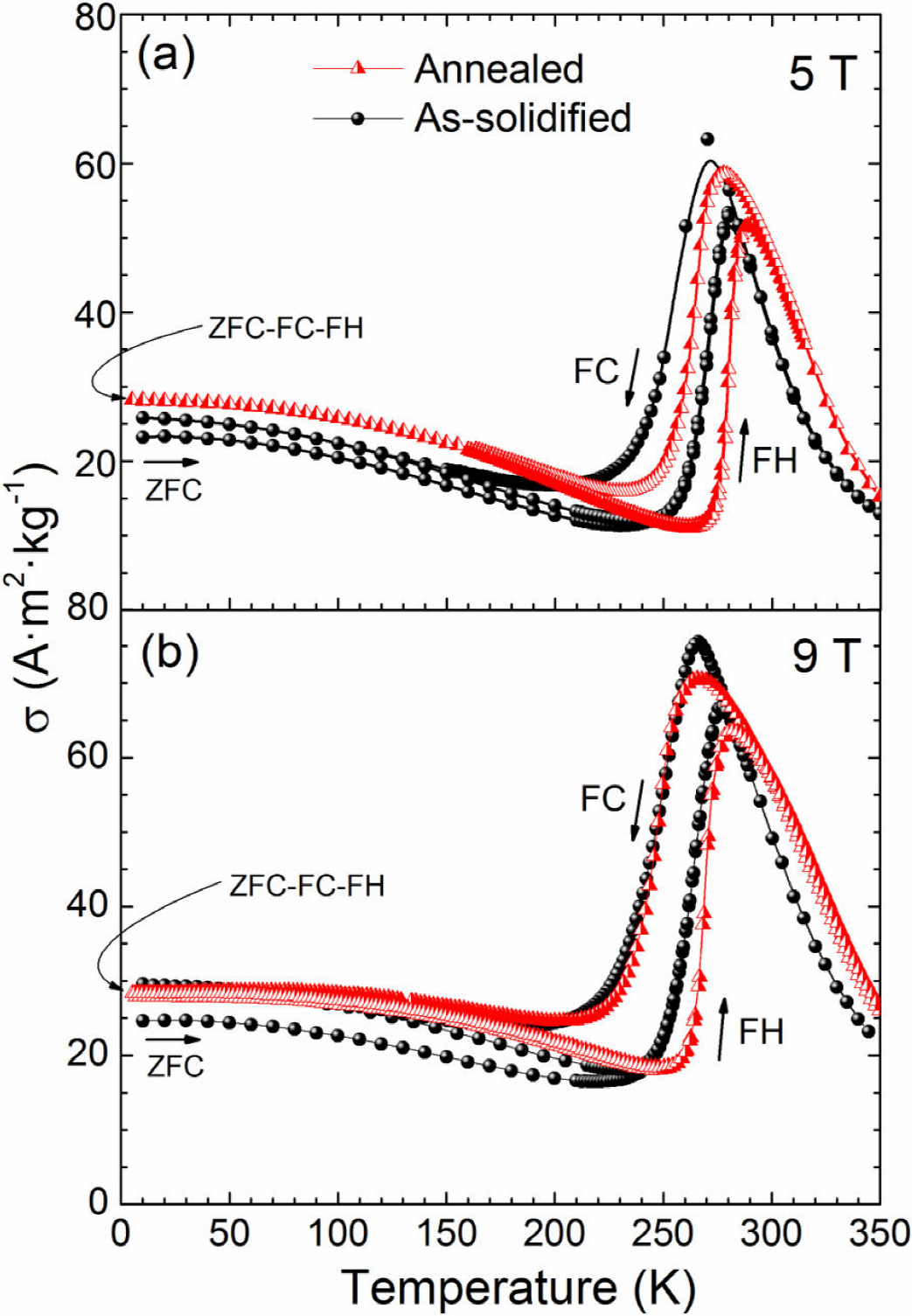
Figure 8. Comparison of the ZFC, FC, and FH σ(T) curves measured under static magnetic field of 5 T (b) and 9 T (b) for assolidified (black circles) and annealed (red triangles) ribbon samples.
The observed increase in the structural phase transition temperatures for annealed ribbons caused by the crystal and chemical change suggests that martensite is more stable than in as-solidified samples. Comparing the low-field thermomagnetic curves of Figs. 1(b) and 7(b), one can notice that, in contrast with the observed for the as-solidified sample, no delay in temperature for the MT. Besides, the increased thermal hysteresis of the transformation (determined as
At last, the possible formation mechanism of the retained AST into the martensitic matrix in Ni-Mn-In and Ni-Mn-Co-In melt-spun ribbons alloys has been recently explored by in-situ observations using optical microscopy and EBDS orientation maps of the microstructure 49; the author found that large lattice discontinuities between AST and MST (which are indirectly related to the lattice parameters of both phases), play an important role in the occurrence of this phenomenon. The difference is larger for Co-doped quaternary alloys than in Ni-Mn-In; this could explain why larger, or total, KA at a lower applied magnetic field has been reported for the former 9,14,48. Our results suggest a reduction of lattice discontinuity between both phases when the parent phase shows the L21-type crystal structure.
4. Conclusions
We have performed a dc magnetization study of the partial kinetic arrest of martensitic transformation found in as-solidified Ni52.2Mn34.3In13.5 melt-spun ribbons. The effect is observed for a magnetic field above 1 T and the volume fraction of B2 austenite frozen into the martensitic matrix is proportional to the applied magnetic field strength.
The metastable character of the non-equilibrium field-cooled magnetic glassy state was revealed by the decreasing behavior of magnetization over temperature cycling and time dependence. The magnetization change determined from the thermo-remnant and zero-field cooled magnetization isotherm measured at a given temperature shows irreversible and reversible components; the former decreases as the temperature decreases. This is in contrast with that observed in other alloys that exhibit this abnormal phenomenon such as Ni50Mn34In16 and Mn50Ni40In10 for which the fraction of AST frozen into the MST matrix is entirely metastable. This arrested metastable state was no longer observed in the thermally annealed samples because of an increase in the stability of martensite in the new L21 austenitic matrix.











 text new page (beta)
text new page (beta)


