Stable bound states of N’s, 						Λ					’s and 						Ξ					’s

Garcilazo, H.; Valcarce, A.; Vijande, J.; Garcilazo, H.; Valcarce, A.; Vijande, J.

Services on Demand

Journal

Article

Indicators

Cited by SciELO
Access statistics

Revista mexicana de física

Print version ISSN 0035-001X

Rev. mex. fis. vol.63 n.5 México Sep./Oct. 2017

Research

Stable bound states of N’s, Λ’s and Ξ’s

H. Garcilazo^a

A. Valcarce^b

J. Vijande^c

^{^a}Escuela Superior de Física y Matemáticas, Instituto Politécnico Nacional, Edificio 9, 07738 México D.F., México. e-mail: humberto@esfm.ipn.mx

^{^b}Departamento de Física Fundamental and IUFFyM, Universidad de Salamanca, E-37008 Salamanca, Spain. e-mail: valcarce@usal.es

^{^c}Unidad Mixta de Investigación en Radiofísica e Instrumentación Nuclear en Medicina, Instituto de Investigación Sanitaria La Fe (IIS-La Fe)-Universitat de Valencia (UV) and IFIC (UV-CSIC), Valencia, Spain. e-mail: javier.vijande@uv.es

Abstract

We review our recent work about the stability of strange few-body systems containing N’s, Λ’s, and Ξ’s. We make use of local central Yukawa-type Malfliet-Tjon interactions reproducing the low-energy parameters and phase shifts of the nucleon-nucleon system and the latest updates of the hyperon-nucleon and hyperon-hyperon ESC08c Nijmegen potentials. We solve the three- and four-body bound-state problems by means of Faddeev equations and a generalized Gaussian variational method, respectively. The hypertriton, Λnp (I)JP=(1/2)1/2+, is bound by 144 keV; the recently discussed Λnn (I)JP=(1/2)1/2+ system is unbound, as well as the ΛΛnn (I)JP=(1)0+ system, being just above threshold. Our results indicate that the ΞNN, ΞΞN and ΞΞNN systems with maximal isospin might be bound.

Keywords: Baryon-Baryon interactions; Faddeev equations; variational approaches

PACS: 21.45.-v; 25.10.+s; 11.80.Jy

1. Introduction

Strange nuclear physics is a very topical subject. The hyperon-nucleon (YN) and hyperon-hyperon (YY) interactions constitute the input for microscopic calculations of few- and many-body systems involving strangeness, such as exotic neutron star matter ¹^,²^,³^,⁴^,⁵ or hypernuclei ⁶^,⁷^,⁸. There are theoretical debates ⁹^,¹⁰^,¹¹^,¹²^,¹³^,¹⁴ on the possible existence of a neutral bound state of two neutrons and a Λ hyperon, nΛ3, suggested by recent data of the HypHI Collaboration ¹⁵. There have been also recent proposals regarding the stability of nΛΛ4 ¹⁴, the existence of Ξ hypernuclei ⁶^,⁷^,⁸, or the existence of a strangeness -2 hypertriton ¹⁶^,¹⁷. Obviously, all these predictions are subject to the uncertainties of our knowledge of the baryon-baryon interaction, in particular in the strangeness -2 sector. Experimentally, it has been recently reported an emulsion event, the so-called KISO event, providing evidence of a possible deeply bound state of Ξ--14N ¹⁸. Although microscopic calculations are impossible in this case and, consequently, their interpretation will be always affected by uncertainties, the ESC08c Nijmegen potential has been recently updated ¹⁹^,²⁰^,²¹ to give account for the most recent experimental information of the strangeness -2 sector, the KISO ¹⁸ and the NAGARA²² events. A thorough discussion of the present status of the experimental and theoretical progress in hypernuclear physics can be found in Refs. ²³ and ²⁴.

When a two-baryon interaction is attractive, if the system is merged with nuclear matter and the Pauli principle does not impose severe restrictions, the attraction may be reinforced. Simple examples of the effect of a third or a fourth baryon in two-baryon systems could be given. The deuteron, (I)J ^P = (0) 1⁺, is bound by 2.225 MeV, while the triton, (I)J ^P = (1/2)1/2⁺, is bound by 8.480 MeV, and the α particle, (I)J ^P = (0)0⁺, is bound by 28.295 MeV. The binding per nucleon B/A increases as 1: 3: 7. A similar argument could be employed for strangeness -1 systems. Whereas the existence of dibaryon states is still under discussion^ⁱ, the hypertriton HΛ3, (I)J ^P = (0)1/2⁺, is bound with a separation energy of 130 ± 50keV keV, and the HΛ4 , (I)J ^P = (0)0⁺, is bound with a separation energy of 2.12 ± 0.01 (stat) ± 0.09 (syst) MeV ²⁶. This cooperative effect of the attraction in the two-body subsystems when merged in few-baryon states was also made evident in the prediction of a ΣNN quasibound state in the (I)J ^P = (1)1/2⁺ channel very near threshold ²⁷^,²⁸. Such ΣNN quasibound state has been recently suggested in 3He(K-,π∓) reactions at 600 MeV/c ²⁹.

In this paper, we review our recent studies of the three-body systems: ΛNN, ΞNN, ΛΛN, and ΞΞN, as well as the four-body systems ΞΞNN and ΛΛNN. We make use of the most recent updates of the ESC08c Nijmegen potentials in the strangeness -1, -2, -3 and -4, sector ¹⁹^,²⁰^,³⁰ accounting for the recent KISO ¹⁸ and NAGARA ²² events in the strangeness -2 sector. As discussed above, the existence of two-body attractive interactions or bound states could give rise to other stable few-body systems when merged with other nucleons or hyperons. For example, the overall attractive character of the ΞN interaction comes suggested by recent preliminary results from lattice QCD ³¹ together with other indications of certain emulsion data ²⁰^,²¹^,³⁰. Besides the recent update of ESC08c Nijmegen model, Ξ- hypernuclear calculations ³² and chiral quark models ³³ found a ΞN attractive interaction before the KISO event. Furthermore, the possible existence of stable strange few-body states comes reinforced by the attractive character of the ΞΞ interaction for some partial waves ¹⁹^,³⁰^,³⁴^,³⁵^,³⁶^,³⁷^,³⁸. It is worth to mention that preliminary studies of the ΞΞN system ³⁹ indicate that lattice QCD calculations of multibaryon systems are now within sight. Analogously, if a second Λ would be added to the uncertain Λnn state, the weakly attractive ΛΛ interaction ²² and the reinforcement of the ΛN potential without paying a price for antisymmetry requirements, may give rise to a stable bound state ¹⁴.

One should bear in mind how delicate is the few-body problem in the regime of weak binding, as demonstrated in Ref. ⁴⁰ for the HΛΛ4 system. Besides, there are models for the YN interaction, like the hybrid quark-model based analysis of Ref. ⁴¹, the effective field theory approach of Ref.⁴², or even some of the earlier models of the Nijmegen group ³⁴ that, in general, predict interactions weakly attractive or repulsive. One does not expect that these models will give rise to stable three- or four-body states. However, it is worth to emphasize that current hypernuclei studies ⁶^,⁷^,⁸^,³²^,⁴⁰ have been performed by means of interactions derived from the Nijmegen models and, thus, the present review complements such previous work for the simplest systems that can be studied exactly. To advance in the knowledge of the details of the YN interaction, high-resolution spectroscopy of Ξ hypernuclei using ¹²C targets in (K^-, K⁺) reactions has been awaited ⁴³^,⁴⁴ and it is now planned at J-PARC ⁴⁵. The new hybrid experiment E07 recently approved at J-PARC is expected to record of the order of 10⁴Ξ- stopping events ⁴⁶, one order of magnitude larger than the previous E373 experiment, and will hopefully clarify the phenomenology of some of the systems studied in the present work.

The review is organized as follows. In Sec. 2 we describe the technical details to solve the three-body bound state Faddeev equations as well as the generalized Gaussian variational method used to look for bound states of the four-body problem. In Sec. 3 we construct the two-body amplitudes needed for the solution of the bound state three- and four-body problems. The results are presented and discussed in Sec. 4. Finally, in Sec. 5 we summarize our main conclusions.

2. The three- and four-body bound-state problems

In this section we outline the solution of the three- and four-body bound-state problems. We will restrict ourselves to configurations where all particles are in S-wave states. The three-body problem has been widely discussed in the literature and we refer the reader to Refs. ⁴⁷^,⁴⁸^,⁴⁹ for a more detailed discussion. The Faddeev equations for a system with total isospin I and total spin J are,

Ti;IJiiji(piqi)=∑j≠i∑ijjjhij;IJiiji;ijjj12∫0∞qj2dqj×∫-11dcosθti;iiji(pi,pi';E-qi2/2νi)×1E-pj2/2μj-qj2/2νjTj;IJijjj(pjqj), (1)

where ti;iiji stands for the two-body amplitudes with isospin i _i and spin j _i p _i is the momentum of the pair jk (with ijk an even permutation of 123) and q _i the momentum of particle i with respect to the pair jk. μi and v _i are the corresponding reduced masses, and hij;IJiiji;ijjj are spin-isospin coefficients.

Expanding the amplitude ti;iiji(xi,xi';e) in terms of Legendre polynomials, Eq. (1) can be written as,

Ti;IJiiji(xiqi)=∑nPn(xi)Ti;IJniiji(qi) , (2)

where Ti;IJniiji(qi) satisfies the one-dimensional integral equation,

Ti;IJniiji(qi)=∑j≠i∑mijjj∫0∞dqjAij;IJniiji;mijjj×(qi,qj;E)Tj;IJmijjj(qj), (3)

with

Aij;IJniiji;mijjj(qi,qj;E)=hij;IJiiji;ijjj∑rτi;iijinr(E-qi2/2νi)qj22×∫-11dcosθPr(xi')Pm(xj)E-pj2/2μj-qj2/2νj. (4)

The four-body problem has been addressed by means of the variational method, specially suited for studying low-lying states. The nonrelativistic hamiltonian is be given by,

H=∑i=14mi+p⃗i 22mi+∑i<j=14V(r⃗ij) , (5)

where the potential V(r⃗ij) corresponds to an arbitrary two-body interaction.

The variational wave function must include all possible spin-isospin channels contributing to a given configuration. For each channel s, the wave function will be the tensor product of a spin (|Ss1⟩), isospin (|Is2⟩), and radial (|Rs3⟩) component,

|ϕs⟩=|Ss1⟩⊗|Is2⟩⊗|Rs3⟩, (6)

where s≡{s1,s2,s3}. Once the spin and isospin parts are integrated out, the coefficients of the radial wave function are obtained by solving the system of linear equations,

∑sˊ s∑iβs3iRsˊ3j H Rsˊ3i-E Rsˊ3jRs3i δs, sˊ =0 ∀j, (7)

where the eigenvalues are obtained by a minimization procedure.

For the description of the four-body wave function we consider the Jacobi coordinates:

r→NN=x→=r→1-r→2,r→YY=y→=r→3-r→4,r→NN-YY=z→=12(r→1+r→2)-12(r→3+r→4),R→CM=R→=∑mir→i∑mi, (8)

The total wave function should have well-defined permutation properties under the exchange of identical particles. The spin part can be written as,

(s1s2)S12(s3s4)S34S≡|S12S34⟩S , (9)

where the spin of the two N’s (Y’s) is coupled to S ₁₂ (S ₃₄). Two identical spin-1/2 fermions in a S = 0 state are antisymmetric (A) under permutations while those coupled to S = 1 are symmetric (S). We summarize in Table I the corresponding vectors for each total spin together with their symmetry properties^ⁱⁱ

Table I. Spin basis vectors for all possible total spin states (S). The ’Symmetry’ column stands for the symmetry properties of the pair of identical particles.

The most general radial wave function with total orbital angular momentum L = 0 may depend on the six scalar quantities that can be constructed with the Jacobi coordinates of the system, they are: x⃗ 2, y⃗ 2, z⃗ 2, x⃗⋅y⃗, x⃗⋅z⃗ and y⃗⋅z⃗. We define the variational spatial wave function as a linear combination of generalized Gaussians,

|Rs3⟩=∑i=1nβs3iRs3i(x→,y→,z→)=∑i=1nβs3iRs3i, (10)

where n is the number of Gaussians used for each spin-isospin component. Rs3i depends on six variational parameters: asi, bsi, csi, dsi, esi, and fsi, one for each scalar quantity. Therefore, the four-body system will depend on 6 × n × n _s variational parameters, where n _s is the number of different channels allowed by the Pauli principle. Eq. (10) should have well-defined permutation symmetry under the exchange of both N’s and Y’s,

P12(x⃗→-x⃗)Rs3i=PxRs3iP34(y⃗→-y⃗)Rs3i=PyRs3i, (11)

where P _x and P _y are -1 for antisymmetric states, (A), and +1 for symmetric ones, (S). Thus, one can build the following radial combinations, (P _x P _y ) = (SS), (SA), (AS), and (AA):

(SS)⇒R1i=Exp(-asix→2-bsiy→2-csiz→2-dsix→⋅y→-esix→⋅z→-fsiy→⋅z→)+Exp(-asix→2-bsiy→2-csiz→2+dsix→⋅y→-esix→⋅z→+fsiy→⋅z→)+Exp(-asix→2-bsiy→2-csiz→2+dsix→⋅y→+esix→⋅z→-fsiy→⋅z→)+Exp(-asix→2-bsiy→2-csiz→2-dsix→⋅y→+esix→⋅z→+fsiy→⋅z→), (12)

(SA)⇒R2i=Exp(-asix→2-bsiy→2-csiz→2-dsix→⋅y→-esix→⋅z→-fsiy→⋅z→)-Exp(-asix→2-bsiy→2-csiz→2+dsix→⋅y→-esix→⋅z→+fsiy→⋅z→)+Exp(-asix→2-bsiy→2-csiz→2+dsix→⋅y→+esix→⋅z→-fsiy→⋅z→)-Exp(-asix→2-bsiy→2-csiz→2-dsix→⋅y→+esix→⋅z→+fsiy→⋅z→), (13)

(AS)⇒R3i=Exp(-asix→2-bsiy→2-csiz→2-dsix→⋅y→-esix→⋅z→-fsiy→⋅z→)+Exp(-asix→2-bsiy→2-csiz→2+dsix→⋅y→-esix→⋅z→+fsiy→⋅z→)-Exp(-asix→2-bsiy→2-csiz→2+dsix→⋅y→+esix→⋅z→-fsiy→⋅z→)-Exp(-asix→2-bsiy→2-csiz→2-dsix→⋅y→+esix→⋅z→+fsiy→⋅z→), (14)

(AA)⇒R4i=Exp(-asix→2-bsiy→2-csiz→2-dsix→⋅y→-esix→⋅z→-fsiy→⋅z→)-Exp(-asix→2-bsiy→2-csiz→2+dsix→⋅y→-esix→⋅z→+fsiy→⋅z→)-Exp(-asix→2-bsiy→2-csiz→2+dsix→⋅y→+esix→⋅z→-fsiy→⋅z→)+Exp(-asix→2-bsiy→2-csiz→2-dsix→⋅y→+esix→⋅z→+fsiy→⋅z→). (15)

The last equations can be expressed in a compact manner by defining the following function,

gs1, s2,s3 =Exp-asix→2-bsiy→2-csiz→2-s1dsix→∙y→-s2esix→∙z→-s3fsiy→∙z→ , (16)

and the vectors

G⃗si=g(+,+,+)g(-,+,-)g(-,-,+)g(+,-,-) , (17)

and

α⃗SS=(+,+,+,+)α⃗SA=(+,-,+,-)α⃗AS=(+,+,-,-)α⃗AA=(+,-,-,+), (18)

which allows to write Eqs. (13)-(15) as,

(SS)⇒R1i=α⃗SS⋅G⃗si(SA)⇒R2i=α⃗SA⋅G⃗si(AS)⇒R3i=α⃗AS⋅G⃗si(AA)⇒R4i=α⃗AA⋅G⃗si . (19)

The radial wave function includes all possible internal relative orbital angular momenta coupled to L = 0. It has also well-defined symmetry properties on the z⃗ coordinate. Being P(12)(34)(z⃗→-z⃗)Rs4i=PzRs4i one obtains,

P(12)(34)R1i=+R1iP(12)(34)R2i=-R2iP(12)(34)R3i=-R3iP(12)(34)R4i=+R4i . (20)

To evaluate radial matrix elements we use the notation introduced in Eq. (19):

Rγifx, y, zRβj=∫Vα→sγ∙G→sifx, y, zα→sβ∙G→sj,dV= α→sγ∙Fij∙α→sβ (21)

where γ and β stand for the symmetry of the radial wave function and F ^ij is a matrix whose element (a,b) is defined through,

Fabij=∫V(G⃗si)a(G⃗s'j)bf(x,y,z)dV , (22)

being (G⃗si)a the component a of the vector G⃗si. From Eq. (16) one obtains,

gs1, s2, s3gs1ˊ, s2ˊ, s3ˊ=Exp -aijx→2-bijy→2-cijz→2-s-ijx→∙y→-e-ijx→∙z→-f-ijy→∙z→ , (23)

where we have shortened the previous notation according to asi→ai, aij=ai+aj and d¯ij=(s1di+s1'dj). Therefore, all radial matrix elements will contain integrals of the form,

I = ∫VExp-aijx→2-bijy→2-cijz→2-s-ijx→∙y→-e-ijx→∙z→-f-ijy→∙z→fx, y, zdx→dy→dz→ , (24)

where the functions f (x, y, z) are the potentials. Being all of them radial functions (not depending on angular variables) one can solve the previous integral by noting:

∫Exp-∑i, j=1nAijx→i∙x→jf∑αkx→kdx→1…dx→n = πndet⁡A324πΩijπ32 FΩij, f , (25)

where

1Ωij=α¯⋅A-1⋅αFA,f=∫e-Au2fuu2dudetA>01Ωij>0. (26)

One can extract some useful relations for the radial matrix elements using simple symmetry properties. Let us rewrite Eq. (21)

Rγifx, y, zRβj = RPxPyPzifx, y, zRPxˊPyˊPzˊj = ∫x∫y∫zRPxPyPzifx, y, zRPxˊPyˊPzˊjdx→dy→dz→ . (27)

If f (x, y, z) depends only in one coordinate, for example x⃗, the integrals over the other coordinates will be zero if one of them has different symmetry properties, Py≠Py' or Pz≠Pz' in our example. Therefore

RγifxRβj ∝δγβ

RγifyRβj ∝δγβ

RγifzRβj ∝δγβ (28)

RγiConstantRβj ∝δγβ

The radial wave function described in this section is adequate to describe not only bound states, but also it is flexible enough to describe states of the continuum within a reasonable accuracy ⁵⁰^,⁵¹^,⁵².

3. Two-body amplitudes

We have constructed the two-body amplitudes for all subsystems entering the three- and four-body problems studied by solving the Lippmann-Schwinger equation of each (i, j) channel,

tijp, pˊ;e=Vijp, pˊ+∫0∞pˊˊ2dpˊˊVijp, pˊˊ×1e-pˊˊ2∕2μtijpˊˊ, pˊ;e (29)

where

Vij(p,p')=2π∫0∞r2dr j0(pr)Vij(r)j0(p'r) , (30)

and the two-body potentials consist of an attractive and a repulsive Yukawa term, i.e.,

Vij(r)=-Ae-μArr+Be-μBrr . (31)

The parameters of the ΛN, ΞN, ΛΛ and ΞΞ channels were obtained by fitting the low-energy data and the phase shifts of each channel as given by the most recent update of the strangeness -1 ¹⁹, -2 ²⁰ and -3 and -4 ³⁰ ESC08c Nijmegen potentials. In the case of the NN interaction we use the Malfliet-Tjon models ⁵³ with the parameters given in Ref. ⁵⁴. The low-energy data and the parameters of these models are given in Table II. It is worth to note that the scattering length and effective range of the most recent update of the ΛΛ interaction derived from chiral effective field theories are very much like those of the ESC08c Nijmegen potential (see Table II of Ref. ⁴²) unlike the earlier version used in Ref. ¹⁴ (see Table IV of Ref. ⁵⁵) reporting remarkably small effective ranges.

Table II. Low-energy data and parameters of the local central Yukawa-type potentials given by Eq. (31) for the NN potential ⁵⁴, and the most recent updates of the ESC08c Nijmegen interactions for the ΛN ¹⁹, ΞN ²⁰, ΞΞ ³⁰, and ΛΛ ²⁰ systems.

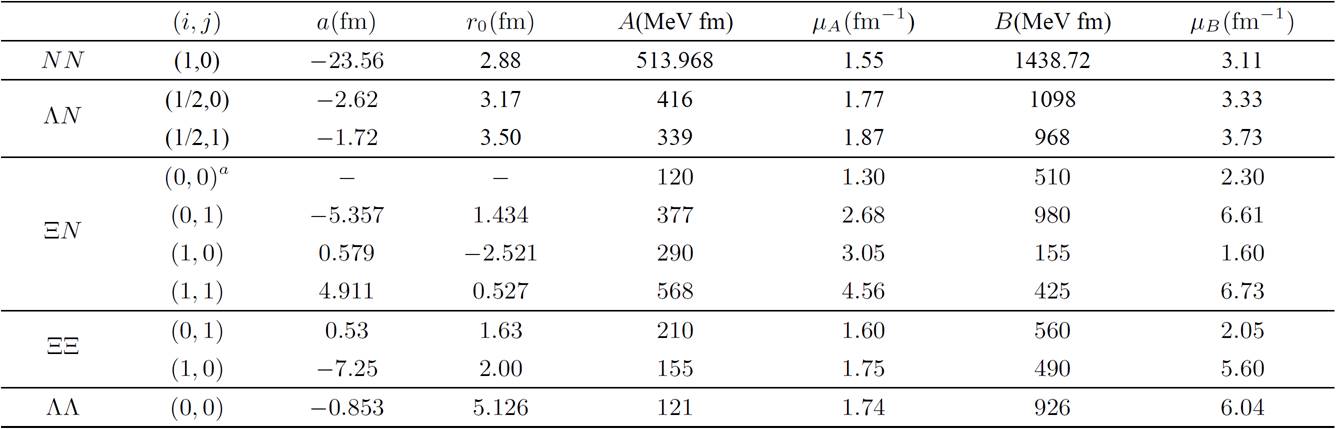
^aThis channel is discussed on Sec. III.

The ΞN¹ S ₀ (I = 0) potential was fitted to the ΞN phase shifts given in Fig. 14 of Ref. ²⁰ without taking into account the inelasticity, i.e., assuming ρ=0 (this two-body channel does not contribute to the three- and four-body bound states found in this work). Regarding the two-body interactions containing a single Λ, they are constrained by a simultaneous fit to the combined NN and YN scattering data, supplied with constraints on the YN and YY interaction originating from the G-matrix information on hypernuclei ¹⁹.

The potentials obtained are shown in Fig. 1. In Fig. 1(a) we show the VΛN(r) potential that it is tightly constrained by the existing experimental data. The interaction is attractive at intermediate range and strongly repulsive at short range, but without having bound states. In Fig. 1(b) we show the VΞN(r) potential, where one notes the attractive character of the ³ S ₁ (I = 1) ΞN partial wave, giving rise to the D^* bound state ¹⁸ with a binding energy of 1.6 MeV. We also confirm how all the J = 1 and I = 1 ΞN interactions are attractive^ⁱⁱⁱ ³⁰. Regarding the ΞΞ interaction, Fig. 1(c), we observe the attractive character of the ¹ S ₀ (I = 1) potential, that although having bound states in earlier versions of the ESC08c Nijmegen potential ³⁴, in the most recent update of the strangeness -4 sector it does not present a bound state ³⁰. The existence of bound states in the ΞΞ system has been predicted by different calculations in the literature ³⁵^,³⁶^,³⁷. It can be definitively stated that all models agree on the fairly important attractive character of this channel, either with or without a bound state ³⁸. Finally, in Fig. 1(d) we show the VΛΛ(r) potential, mainly determined by the NN and YN data, and SU(3) symmetry ²⁰^,²¹. It gives account of the pivotal results of strangeness -2 physics, the NAGARA ²² and the KISO ¹⁸ events. Although other double-Λ hypernuclei events, like the DEMACHIYANAGI and HIDA events ⁴³, are not explicitly taken into account, the G-matrix nuclear matter study of Ξ- capture both in ¹²C and ¹⁴N (see section VII of Ref. ²⁰), concludes that the ΞN attraction in the ESC08c potential is consistent with the Ξ-nucleus binding energies given by the emulsion data of the twin Λ-hypernuclei.

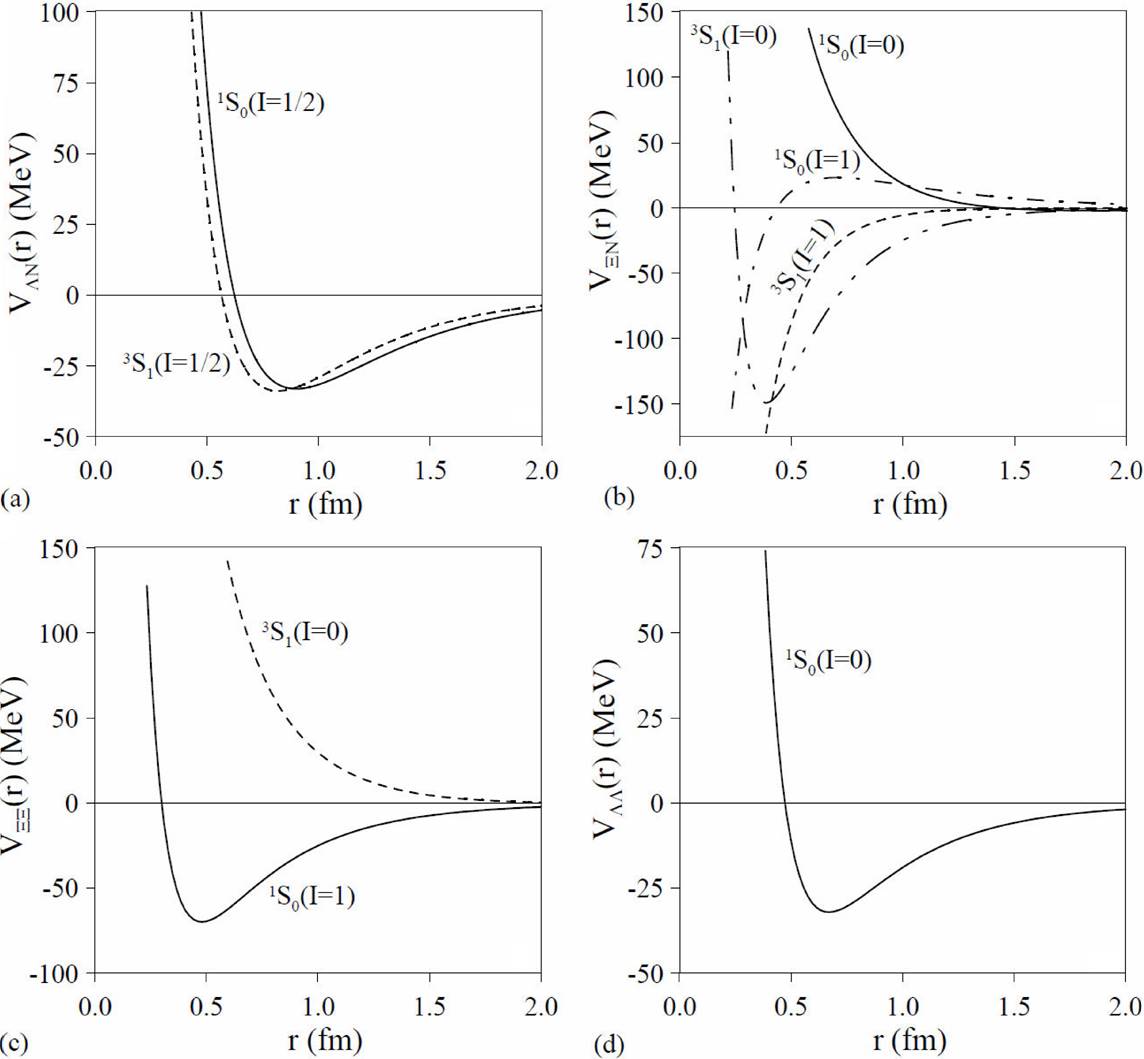
Figure 1. (a) VΛN(r) potential as given by Eq. (31) with the parameters of Table II. (b) Same as (a) for the VΞN(r) potential. (c) Same as (a) for the VΞΞ(r) potential. (d) Same as (a) for the VΛΛ(r) potential.

4. Results and discussion

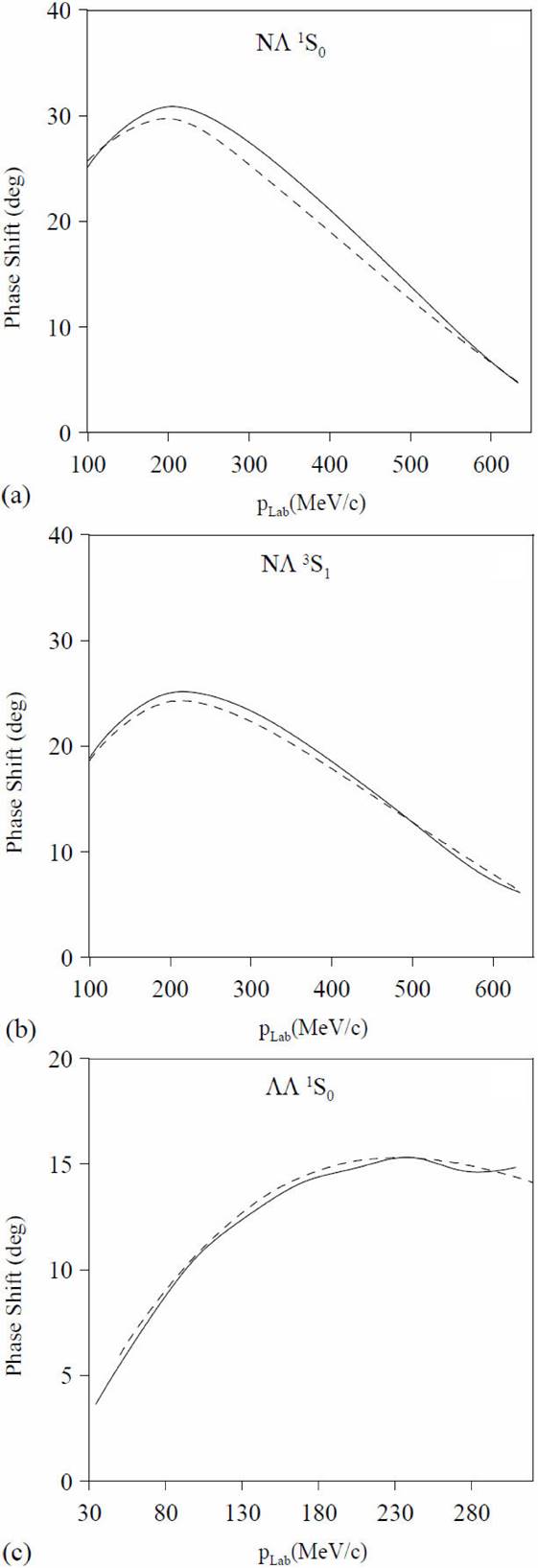
Let us first of all show the reliability of the input potentials. We compare in Fig. 2 the ΛN and ΛΛ phase shifts reported by the ESC08c Nijmegen potential and those obtained by our fits with the two-body potentials of Eq. (31) and the parameters given in Table II. As can be seen the agreement is good. As stated above, the ΞN¹ S ₀ (I = 0) potential was fitted to the ΞN phase shifts given in Fig. 14 of Ref. ²⁰. Once we have described the phase shifts, the ΛN and ΛΛ potentials include in an effective manner the coupling to other two-body channels as it may be the ΣN or ΞN two-body systems^{^iv}. We have also tested the two-body interactions in the three-body problem of systems made of N’s and Λ’s. The hypertriton is bound by 144 keV, and the Λnn system is unbound.

Figure 2. (a) ΛN¹ S ₀ phase shifts. The solid line stands for the results of the ESC08c Nijmegen potential and the dashed line for the results of the two-body potential of Eq. (31) with the parameters given in Table II. (b) Same as (a) for the ΛN³ S ₁ phase shifts. (c) Same as (a) for the ΛΛ¹ S ₀ phase shifts.

The reasonable description of the known two- and three-body problems gives confidence to address the study of other three- and four-body systems. We show in Table III the channels of the different two-body subsystems contributing to each (I, J) three- and four-body state that we will study. For the ΞΞNN system we only consider the I = 2 channels, because the I = 0 and 1 states would decay strongly to ΛΛNN states. The three- and four-body problems are studied by means of the ESC08c Nijmegen interactions described in Sec. 3 and given in Table II. The binding energies are measured with respect to the lowest threshold, indicated in Table III for each particular state.

Table III. Two-body NN, YN and YY isospin-spin (i, j) channels that contribute to a given three- or four-body state with total isospin I and total spin J. The last column indicates the corresponding threshold for each state, that would come given by ∑i=134M _i - E where M _i are the masses of the baryons of each channel, B ₁ stands for the binding energy of the deuteron and B ₂ for the binding energy of the D^*ΞN state.

4.1. Three-body systems

We show in Fig. 3 the Fredholm determinant of all ΞNN channels ⁵⁹^,⁶⁰. As we can see in Fig. 3(b), a bound state is found for the (I)J ^P = (3/2)1⁺/2 ΞNN state, 1.3 MeV below the corresponding threshold, 2mN+mΞ-B2, where B ₂ is the binding energy of the D^*ΞN state. However, the most interesting result of the ΞNN system is shown in Fig. 3(a), the very large binding energy of the (1/2/3)⁺/2 state, which would make it easy to identify experimentally as a sharp resonance lying some 17.2 MeV below the ΞNN threshold. The ΛΛ-ΞN (i, j) = (0,0) transition channel, which is responsible for the decay ΞNN→ΛΛN, does not contribute to the (I)J ^P = (1/2)3⁺/2 state in a pure S-wave configuration ⁶⁰. One would need at least the spectator nucleon to be in a D -wave or that the ΛΛ-ΞN transition channel be in one of the negative parity P-wave channels, with the nucleon spectator also in a P-wave. Thus, due to the angular momentum barriers the resulting decay width of the (1/2)3⁺/2 state is expected to be very small.

Figure 3. (a) Fredholm determinant for the J = 1/2 and J = 3/2 I = 1/2 ΞNN channels. (b) Fredholm determinant for the J = 1/2 I = 3/2 ΞNN channel.

For the ΞNN three-baryon system with (I, J) = (3/2,3/2), only the (i, j) = (1, 1) ΞN channel contributes (see Table III), and the corresponding Faddeev equations with two identical fermions can be written as ²⁷,

T=- tNNΞ G0 T . (32)

Thus, due to the negative sign in the r.h.s. the ΞN interaction is effectively repulsive and, therefore, no bound state is possible in spite of the attraction of the ΞN subsystem. The minus sign in Eq. (32) is a consequence of the identity of the two nucleons since the first term of the r.h.s. of Eq. (32) proceeds through Ξ exchange and it corresponds to a diagram where the initial and final states differ only in that the two identical fermions have been interchanged which brings the minus sign. This effect has been pointed out before ⁶¹. This is the reason why the Fredholm determinant for the (I, J) = (3/2, 3/2) ΞNN channel is not shown in Fig. 3(b).

Finally, we show in Fig. 4 the Fredholm determinant of all ΞΞN channels. The Fredholm determinant for the (I)J ^P = (3/2)3/2⁺ channel is not shown in Fig. 4(b) for the same reason explained above for the ΞNN system, it is strongly repulsive. In the ΞΞN system there appears a bound state with quantum numbers (I)J ^P = (3/2)1⁺/2, 2.9 MeV below the lowest threshold, 2mΞ+mN-B2, where B ₂ stands for the binding energy of the D^*ΞN subsystem. Since this ΞΞN state has isospin 3/2 it can not decay into ΞΛΛ due to isospin conservation so that it would be stable. This stable state appears in spite of the fact that the last update of the ESC08c Nijmegen ΞΞ¹ S ₀(I = 1) potential has not bound states, as it is however predicted by several models in the literature. If bound states would exist for the ΞΞ system the three-body state would become deeply bound as it happens for the ΞNN system. The I = 1/2 channels are also attractive but they are not bound.

Figure 4. (a) Fredholm determinant for the J = 1/2 and J = 3/2 I = 1/2 ΞΞN channels. (b) Fredholm determinant for the J = 1/2 I = 3/2 ΞΞN channel.

Let us finally mention that our results for three-body systems containing a ΞN subsystem has been recently reproduced by means of the configuration-space Faddeev equations ⁶².

4.2. Four-body systems

In the previous section we have seen that all three-body systems made of N’s and Ξ’s in the maximal isospin channel, i.e., systems consisting only of neutrons and negative Ξ’s or protons and neutral Ξ’s, are bound. As mentioned above, the uniqueness of these systems is a consequence of the two-body interactions between NN, ΞN and ΞΞ pairs being all in the isospin 1 channel. Thus, the strong decay ΞN→ΛΛ is forbidden. Therefore, such states, if bound, would be stable under the strong interaction. This is why we now proceed to study four-body systems made of N’s and Ξ’s in the maximal isospin channel, I = 2. The most favorable configuration to minimize the effect of the Pauli principle is the ΞΞNN system, that due to identity of two N’s and two Ξ’s can only exist with J = 0 ⁶³.

The binding energy of the ΞΞNN state has been calculated by means of the variational method with generalized Gaussians described in Sec. 2. The method has been used in the four-body sector to study the possible existence of tetraquarks ⁶⁴^,⁶⁵^,⁶⁶ and tested against the hyperspherical harmonic formalism with comparable results ⁵¹^,⁵². We show in Fig. 5 the binding energy of the (I)J ^P = (2)0⁺ΞΞNN state as a function of the number of Gaussians in the variational calculation. As we can see the result is almost stable considering 12 Gaussians, although we have pushed further our calculation with a negligible gain of binding in the second decimal digit. The lowest threshold for this state is 2B ₂ = 3.2 MeV, where B ₂ is the binding energy of the D^*ΞN state (see Table III). Thus, the state lies 7.4 MeV below the ΞΞNN mass, with a separation energy of 4.2 MeV with respect to an asymptotic state made of two D^*ΞN dibaryons.

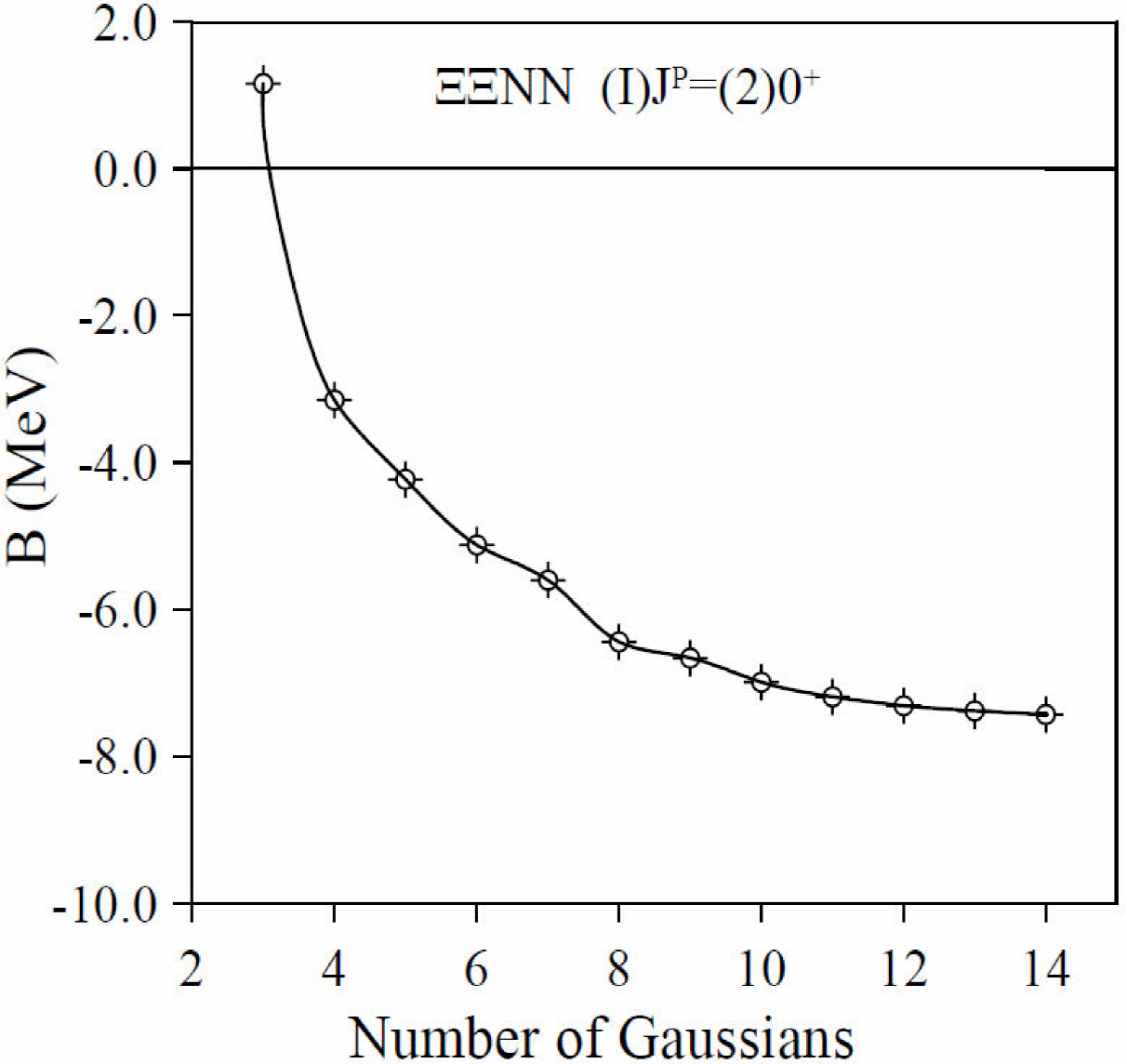
Figure 5. Binding energy of the (I)J ^P = (2)0⁺ΞΞNN state as a function of the number of Gaussians in the variational calculation.

One can also study the behavior of the root mean square radius (RMS) of the four-body system, defined in the usual way,

RMS=∑i=14mir→i-R→CM2∑i=14mi1/2=12rNN21+mΞ/mN+rΞΞ2mΞ/mN1+mΞ/mN+rNN-ΞΞ2mΞ/mN1+mΞ/mN21/2 (33)

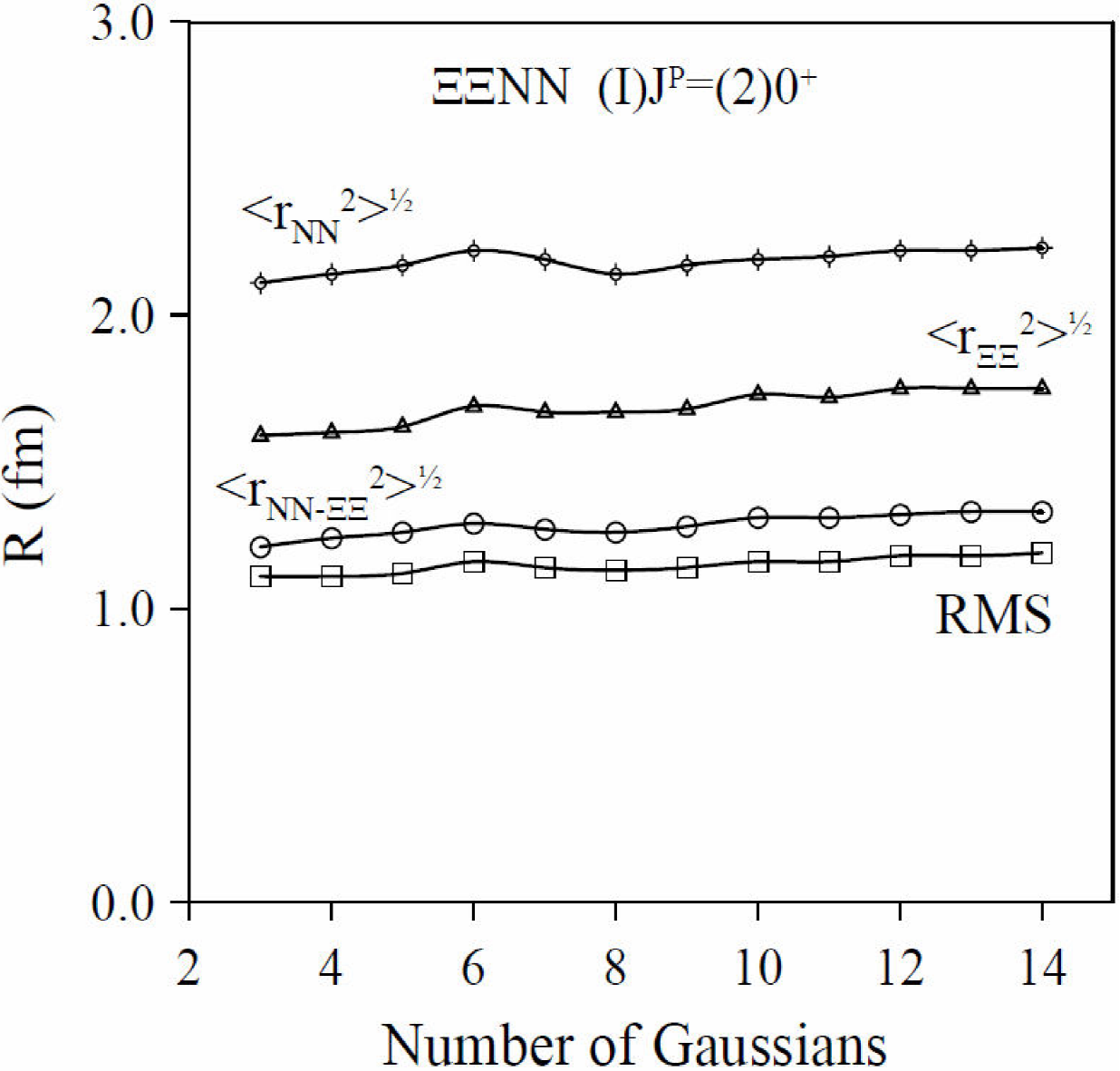
The results are shown in Fig. 6, where besides the RMS radius we have also calculated the root mean square radii of the different Jacobi coordinates. As seen in Table III, only the ¹S₀(I = 1) NN and ΞΞ channels contribute to the (I)J ^P = (2)0⁺ΞΞNN state. As discussed in Sec. 3, although they are attractive, the ¹S₀(I = 1) NN and ΞΞ channels do not present a bound state, giving the largest internal radii. In the ΞN subsystem one finds contributions from the ¹S₀(I = 1) and ³S₁(I = 1) channels, the last one presenting the D ^* bound state, which is the responsible of the smallest radius in the Ξ-N relative coordinate. The RMS gets fully stabilized with 14 Gaussians with a value of 1.18 fm.

Figure 6. Root mean square radii of the (I)J ^P = (2)0⁺ΞΞNN state as a function of the number of Gaussians in the variational calculation. See text for details.

We have finally evaluated the binding energy of the ΛΛNN system with quantum numbers (I)J ^P = (1)0⁺⁶⁷. The system is unbound appearing just above threshold and thus it does not seem to be Borromean, a four-body bound state without two- or three-body stable subsystems. An unbound result was also reported in Ref. ⁶⁸, although in this case the authors made use of repulsive gaussian-type potentials for any of the two-body subsystems (see the figure on pag. 475) what does not allow for the existence of any bound state.

We have studied the dependence of the binding on the strength of the attractive part of the different two-body interactions entering the four-body problem. For this purpose we have used the following interactions,

VB1B2(r)=-gB1B2 A e-μArr+B e-μBrr (34)

with the same parameters given in Table II. The system hardly gets bound for a reasonable increase of the strength of the the ΛΛ, gΛΛ, interaction. Although one cannot exclude that the genuine ΛΛ interaction in dilute states as the one studied here could be slightly stronger that the one reported in Ref.²⁰, however, one needs gΛΛ≥1.8 to get a bound state, what would destroy the agreement with the ESC08c Nijmegen ΛΛ phase shifts. Note also that this is a very sensitive parameter for the study of double - Λ hypernuclei ⁴⁰ and this modification would produce an almost ΛΛ bound state in free space, in particular it would give rise to a1S0ΛΛ=-29.15 fm and r01S0ΛΛ=1.90 fm. The four-body system would also become bound taking a factor 1.2 in the NN interaction. However, such modification would make the ¹ S ₀ NN potential as strong as the ³ S ₁⁵³ and thus the singlet S-wave would develop a dineutron bound state, a1S0NN=6.07 fm and r01S0NN=1.96 fm. The situation is slightly different when dealing with the ΛN interaction. We have used a common factor gNΛ for attractive part of the two ΛN partial waves, ¹ S ₀ and ³ S ₁. We show in Fig. 7 the binding energy of the (I)J ^P = (1)0⁺ΛΛNN state as a function of the multiplicative factor gNΛ, for gNN=gΛΛ=1. As one can see the four-body system develops a bound state for gNΛ=1.1, giving rise to the ΛN low-energy parameters: a1S0ΛN=-5.60 fm, r01S0ΛN=2.88 fm, a3S1ΛN=-2.91 fm, and r03S1ΛN=2.99 fm, far from the values constrained by the existing experimental data.

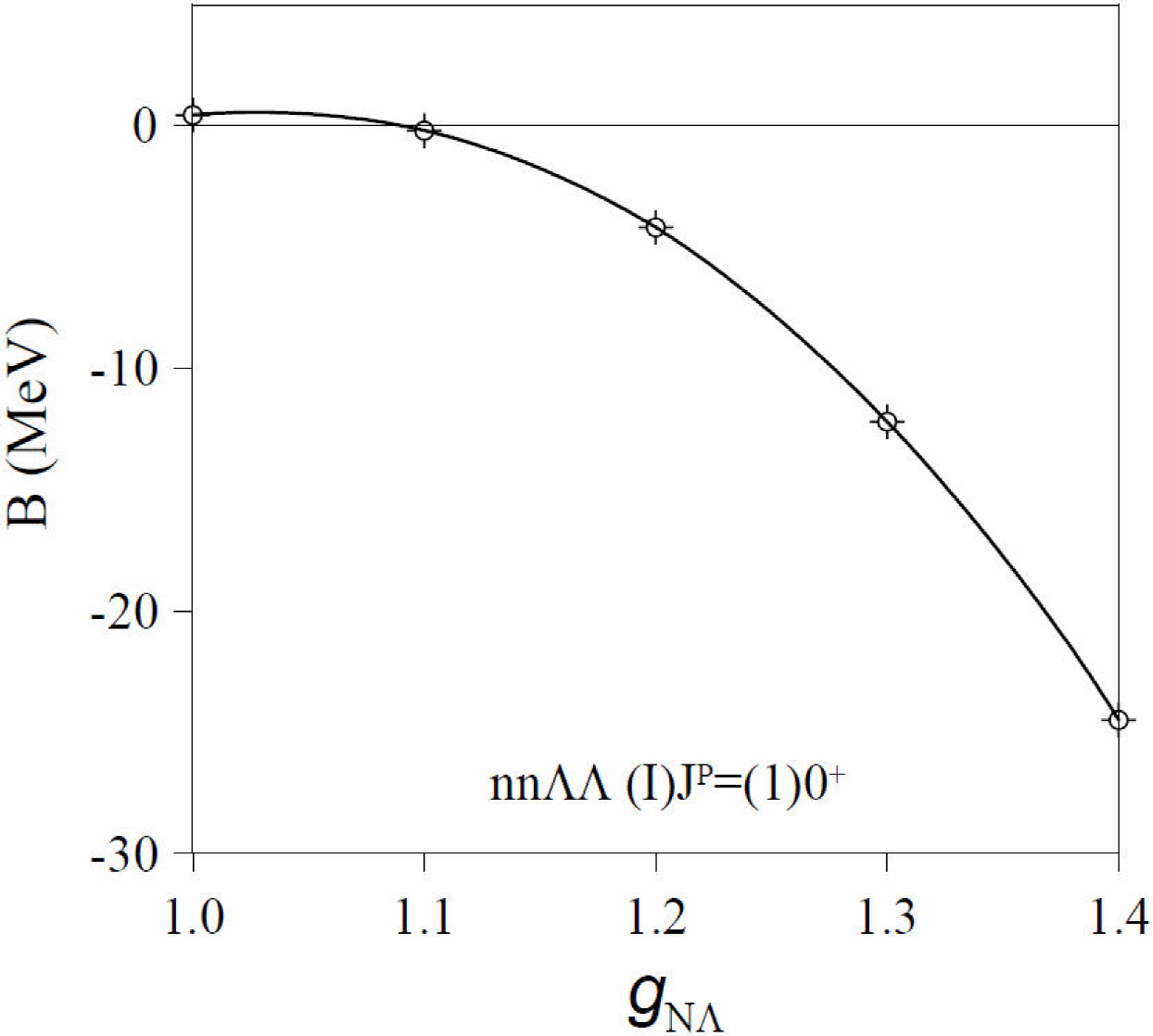
Figure 7. Binding energy of the (I)J ^P = (1)0⁺ nn ΛΛ state as a function of the multiplicative factor, gNΛ, in the attractive part of VNΛr interaction for gNN=gΛΛ=1.

Reference ¹⁴ tackled the same problem by fitting low-energy parameters of older versions of the Nijmegen-RIKEN potential ³⁰^,⁶⁹ or chiral effective field theory ⁵⁵^,⁷⁰, by means of a single Yukawa attractive term or a Morse parametrization. The method used to solve the four-body problem is similar to the one we have used in our calculation, thus the results might be directly comparable. Our improved description of the two- and three-body subsystems and the introduction of the repulsive barrier for the ¹ S ₀ NN partial wave, relevant for the study of the triton binding energy (see Table II of Ref. ⁷¹), leads to a four-body state just above threshold, that cannot get bound by a reliable modification in the two-body subsystems. As clearly explained in Ref. ¹⁴, the window of Borromean binding is more an more reduced for potentials with harder inner cores.

5. Summary

This manuscript intends to summarize our recent work on few-body systems made of N’s, Λ’s and Ξ’s based on the most recent updates of the ESC08c Nijmegen potential in the different strangeness sectors, accounting for the recent experimental information. We have solved the three- and four-body bound state problems by means of Faddeev equations and a generalized Gaussian variational method, respectively.The hypertriton, npΛ (I)J ^P = (1/2)1/2⁺, is bound by 144 keV, and the recently discussed nnΛ (I)J ^P = (1/2)1/2⁺ system is unbound. We have found that the ΞNN system presents bound states with quantum numbers (I)J ^P = (3/2)1/2⁺ and (1/2)3/2⁺, the last one being a deeply bound state lying 15 MeV below the Ξd threshold. The ΞΞN system presents a bound state with quantum numbers (I)J ^P = (3/2)1/2⁺, in spite of having used the most recent update of the ESC08c Nijmegen potential that does not predict ΞΞ bound states. In the case of the three-body systems we note that there appear bound states in all systems made of N’s and Ξ’s with maximal isospin. The same conclusion has been obtained in the four-body system, concluding a ΞΞNN bound state with quantum numbers (I)J ^P = (2)0⁺, lying 7.4 MeV below the ΞΞNN threshold with a root mean square radius of 1.18 fm. We have also studied the (I)J ^P = (1)0⁺ΛΛNN state, it does not present a bound state. Thus, the ΛΛ 4n four-body system does not seem to be Borromean.

Acknowledgments

This work has been partially funded by COFAA-IPN (México), by Ministerio de Economía, Industria y Competitividad and EU FEDER under Contracts No. FPA2016-77177 and FPA2015-69714-REDT, by Junta de Castilla y León under Contract No. SA041U16, by Generalitat Valenciana PrometeoII/2014/066, and by USAL-FAPESP grant 2015/50326-5.

References

1. P. Demorest, T. Pennucci, S. Ransom, M. Roberts, and J. Hessels, Nature 467 (2010) 1081. [ Links ]

2. J. Antoniadis et al., Science 340 (2013) 1233232. [ Links ]

3. S. Weissenborn, D. Chatterjee, and J. Schaffner-Bielich, Phys. Rev. C 85 (2012) 065802 [Erratum Phys. Rev. C 90 (2014) 019904(E)]. [ Links ]

4. D. Lonardoni, F. Pederiva, and S. Gandolfi, Phys. Rev. C 89 (2014) 014314. [ Links ]

5. K. A. Maslov, E. E. Kolomeitsev, and D. N. Voskresensky, Phys. Lett. B 748 (2015) 369. [ Links ]

6. Y. Yamamoto, E. Hiyama, and Th. A. Rijken, EPJ Web of Conferences 3 (2010) 07007. [ Links ]

7. E. Hiyama , Y. Yamamoto , T. Motoba, Th. A. Rijken , and M. Kamimura, Phys. Rev. C 78 (2008) 054316. [ Links ]

8. M. Yamaguchi, K. Tominaga, Y. Yamamoto , and T. Ueda, Prog. Theor. Phys. 105 (2001) 627. [ Links ]

9. H. Garcilazo and A. Valcarce, Phys. Rev. C 89 (2014) 057001. [ Links ]

10. E. Hiyama , S. Ohnishi, B.F. Gibson, and Th. A. Rijken , Phys. Rev. C 89 (2014) 061302(R). [ Links ]

11. A. Gal and H. Garcilazo , Phys. Lett. B 736 (2014) 93. [ Links ]

12. S.-I. Ando, U. Raha, and Y. Oh, Phys. Rev. C 92 (2015) 024325. [ Links ]

13. I. R. Afnan and B. F. Gibson, Phys. Rev. C 92 (2015) 054608. [ Links ]

14. J. -M. Richard, Q. Wang, and Q. Zhao, Phys. Rev. C 91 (2015) 014003. [ Links ]

15. C. Rappold et al., Phys. Rev. C 88 (2013) 041001(R). [ Links ]

16. H. Garcilazo and A. Valcarce , Phys. Rev. Lett. 110 (2013) 012503. [ Links ]

17. H. Garcilazo , Phys. Rev. C 93 (2016) 024001. [ Links ]

18. K. Nakazawa et al., Prog. Theor. Exp. Phys. (2015) 033D02. [ Links ]

19. M.M. Nagels, Th. A. Rijken, and Y. Yamamoto, arXiv:1501.06636. [ Links ]

20. M.M. Nagels , Th. A. Rijken, and Y. Yamamoto, arXiv:1504.02634. [ Links ]

21. Th.A. Rijken and H.-F. Schulze, Eur. Phys. J. A 52 (2016) 21. [ Links ]

22. H. Takahashi et al., Phys. Rev. Lett. 87 (2001) 212502. [ Links ]

23. T. Nagae, Prog. Theor. Phys. Supp. 185 (2010) 299. [ Links ]

24. A. Gal , E.V. Hungerford, and D.J. Millener, Rev. Mod. Phys. 88 (2016) 035004. [ Links ]

25. H. Machner et al., Nucl. Phys. A 901 (2013) 65. [ Links ]

26. A. Esser et al., Phys. Rev. Lett. 114 (2015) 232501. [ Links ]

27. H. Garcilazo , T. Fernández-Caramés, and A. Valcarce , Phys. Rev. C 75 (2007) 034002. [ Links ]

28. H Garcilazo, A. Valcarce , and T. Fernández-Caramés , Phys. Rev. C 76 (2007) 034001. [ Links ]

29. T. Harada and Y. Hirabayashi, Phys. Rev. C 89 (2014) 054603. [ Links ]

30. Th.A. Rijken , M.M. Nagels, and Y. Yamamoto , Few-Body Syst. 54 (2013) 801. [ Links ]

31. K. Sasaki et al., Prog. Theor. Exp. Phys. (2015) 113B01. [ Links ]

32. E. Hiyama , M. Kamimura, Y. Yamamoto , T. Motoba, and Th.A. Rijken, Prog. Theor. Phys. Supp. 185 (2010) 152. [ Links ]

33. T.F. Caramés and A. Valcarce , Phys. Rev. C 85 (2012) 045202. [ Links ]

34. V.G.J. Stoks and T.A. Rijken, Phys. Rev. C 59 (1999) 3009. [ Links ]

35. J. Haidenbauer and U. -G. Meissner, Phys. Lett. B 684 (2010) 275. [ Links ]

36. S.R. Beane et al., Phys. Rev. D 85 (2012) 054511. [ Links ]

37. G.A. Miller, Chin. J. Phys. 51 (2013) 466. [ Links ]

38. J. Haidenbauer , Ulf.-G. Meissner, and S. Petschauer, Eur. Phys. J. A 51 (2015) 17. [ Links ]

39. S. R. Beane et al., Phys. Rev. D 80 (2009) 074501. [ Links ]

40. H. Nemura, Y. Akaishi, and K.S. Myint, Phys. Rev. C 67 (2003) 051001(R). [ Links ]

41. Y. Fujiwara, Y. Suzuki, and C. Nakamoto, Prog. Part. Nucl. Phys. 58 (2007) 439. [ Links ]

42. J. Haidenbauer , Ulf.-G. Meissner, and S. Petschauer , Nucl. Phys. A 954 (2016) 273. [ Links ]

43. K. Nakazawa (KEK-E176, E373 and J-PARC-E07 Collaborations), Nucl. Phys. A 835 (2010) 207. [ Links ]

44. K. Nakazawa and H. Takahashi, Prog. Theor. Phys. Supp. 185 (2010) 335. [ Links ]

45. T. Nagae et al., J-PARC E05 experiment. Proposal for J-PARC 50 GeV Proton Synchrotron: Spectroscopic Study of Ξ-Hypernucleus, ¹² _Ξ Be, via the ¹² C(K ^- , K ⁺ ) Reaction; available at: http://j-parc.jp/researcher/Hadron/en/pac 0606/pdf/p05-Nagae.pdf, (2015). [ Links ]

46. K. Nakazawa et al., Phys. Proc. 80 (2015) 69. [ Links ]

47. H. Garcilazo and A. Valcarce , Phys. Rev. C 93 (2016) 064003. [ Links ]

48. I.R. Afnan and A.W. Thomas, Phys. Rev. C 10 (1974) 109. [ Links ]

49. H. Garcilazo and T. Mizutani, in πNN Systems (World Scientific, Singapore, 1990). [ Links ]

50. Y. Suzuki and K. Varga, Lect. Not. Phys. M 54 (1998) 1. [ Links ]

51. J. Vijande and A. Valcarce , Symmetry 1 (2009) 155. [ Links ]

52. J. Vijande and A. Valcarce , Phys. Rev. C 80 (2009) 035204. [ Links ]

53. R.A. Malfliet and J.A. Tjon, Nucl. Phys. A 127 (1969) 161. [ Links ]

54. J.L. Friar et al., Phys. Rev. C 42 (1990) 1838. [ Links ]

55. H. Polinder, J. Haidenbauer , and U.-G. Meissner, Phys. Lett. B 653 (2007) 29. [ Links ]

56. K. Miyagawa, H. Kamada, W. Glöckle, and V. Stoks, Phys. Rev. C 51 (1995) 2905. [ Links ]

57. B. F. Gibson and D. R. Lehman, Phys. Rev. C 16 (1977) 1679. [ Links ]

58. B.F. Gibson and D.R. Lehman, Nucl. Phys. A 329 (1979) 308. [ Links ]

59. H. Garcilazo and A. Valcarce , Phys. Rev. C 92 (2015) 014004. [ Links ]

60. H. Garcilazo and A. Valcarce , Phys. Rev. C 93 (2016) 034001. [ Links ]

61. H. Garcilazo , J. Phys. G 13 L63. (1987). [ Links ]

62. I. Filikhin, V.M. Suslov, and B. Vlahovic, Math. Mod. Geom. 2 (2017) 1. [ Links ]

63. H. Garcilazo, A. Valcarce, and J. Vijande , Phys. Rev. C 94 (2016) 024002. [ Links ]

64. J. Vijande , A. Valcarce , and J.-M. Richard, Phys. Rev. D 76 (2007) 114013. [ Links ]

65. J. Vijande , A. Valcarce , and N. Barnea, Phys. Rev. D 79 (2009) 074010. [ Links ]

66. T.F. Caramés , A. Valcarce , and J. Vijande , Phys. Lett. B 699 (2011) 291. [ Links ]

67. H. Garcilazo, A. Valcarce, and J. Vijande , Chin. Phys. C 41 (2017) 074102. [ Links ]

68. M.L. Lekala, G.J. Rampho, R.M. Adam, S.A. Sofianos, and V.B. Belyaev, Phys. of Atom. Nucl. 77 (2014) 472. [ Links ]

69. Th.A. Rijken , M.M. Nagels , and Y. Yamamoto, Prog. Theor. Phys. Supp. 185 (2010) 14. [ Links ]

70. J. Haidenbauer et al., Nucl. Phys. A 915 (2013) 24. [ Links ]

71. R.A. Malfliet and J.A. Tjon, Ann. of Phys. 61 (1970) 425. [ Links ]

i. Note that the pronounced cusp-like structure seen in many ΛN related observables near the ΣN threshold could be very well a signature of a dibaryon ²⁵.

ii. Being the N and Ξ I = 1/2 particles, an analogous table serves for the symmetry properties of the wave function in isospin space. In the case of the Λ’s the isospin wave function is symmetric.

iii. There are also models for the strangeness -2 baryon-baryon interaction based on EFT calculations ⁵⁵ showing I = 1 ΞN attraction, although one cannot conclude the strength of the interaction due to the huge effective ranges reported.

iv. Although by fitting the ΛN phase shifts, the coupling to the ΣN system has been included in an effective manner, it would also be interesting to unfold the effective ΛN interaction, separating the contribution from ΛN↔ΣN. As it has been discussed in the literature ⁹^,¹⁰^,²⁷^,⁵⁶^,⁵⁷^,⁵⁸ the hypertriton does not get bound by considering only ΛNN channels, but it is necessary to include also ΣNN channels. Similar considerations hold for the ΛΛ↔ΞN coupling.

Received: April 21, 2017; Accepted: June 09, 2017

This is an open-access article distributed under the terms of the Creative Commons Attribution License