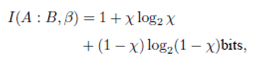1. Introduction

Telecommunication systems play a very important role in the connectivity of many devices, applications, and services in society; hence, the developments of security schemes for these systems are a high priority. The research community and technologists from around the world continue investing great amounts of time and effort to develop strategies that can improve and guarantee the security of the information carried in the telecommunication systems. Among these strategies, the most important alternative is the Quantum Key Distribution (QKD) system, which according to the foundations of quantum mechanics may provide a “true” unconditional security^1,2. The implementation of QKD systems has been previously addressed using Discrete Variables (DV), Continuous Variables (CV) and Differential-Phase Reference protocol known as DV-QKD, CV-QKD and DPR-QKD systems, respectively^3-5. Usually, the QKD systems are based on a generic scheme consisting of an optical private quantum channel (fiber or free space) and a public classical channel; the quantum signal (raw key) is sent through the private channel in a unidirectional manner and, the distillation protocol is performed using the public channel (e.g., Radio Frequency links (RF), copper cables and optical channel with many photons per observation time) in a bidirectional way in order to obtain the final quantum cryptographic key^6,7. The performance of a QKD system depends not only on the noise in the quantum channel (a crucial parameter), but also on the efficiency of the public channel⁸. This channel is susceptible to bit errors, hence it is convenient to utilize different encoders (according to the characteristics of each particular channel) in order to mitigate the erroneous bits that affect the process and performance of the distillation protocol. On the other hand, the errors in the private channel are characterized a priori and an excess of errors means the lack of information due to a spy system (Eve)⁹. Usually, the simulations and experiments of QKD systems only focus on the quantum channel and do not consider the classical channel performance. However, the public channel performance is also important for the performance of the final secret key rate, particularly when the atmospheric turbulence affects the classical RF and Free Space Optics (FSO) channels used in a QKD system, such is the case of the QKD systems that use satellite-ground station links^10,11. There exist many kind of coding schemes (e.g., Turbo, Reed-Solomon, Convolutional, etc.) that allow to mitigate individual and burst errors in the classical channel; nevertheless, the important issue with such encoders is that the transmission rate of the final quantum key is reduced drastically because these encoders need more processing time according to the processor unit used (Central Processing Unit or Graphics Processing Unit). However, some optimized methods using Turbo codes for QKD systems have been researched^12,13. In fact, to the best of our knowledge, currently there are not commercially available QKD systems using the encoders mentioned earlier. Hence, the LDPC (Low- Density Parity-Check Codes) is the encoder most widely used in QKD systems due to its simplicity and processing speed. Nonetheless, the conventional LDPC is not suitable for classical channels with variable conditions (i.e. the code rate is fixed without considering the channel conditions) such as the atmospheric turbulence¹⁴. Thus, different techniques to mitigate the effect of the atmospheric turbulence in the classical channel for QKD systems have been proposed, such as the LDPC codes adapted in the Slepian-Wolf coding system¹⁵ and a hybrid RF-FSO system with adaptive modulation and coding (i.e. with adaptive powers and rates) in order to maximize the channel capacity¹⁶. However, in the context of FSO-QKD systems, mainly on the private channel, the power modification may not be an adequate technique, because it reduces the performance of the overall system and increases the risk for information losses due to Eve. Although¹³ presented a theoretical model of a QKD system using Turbo coding with better performance that a LDPC coding, the theoretical model does not consider the adaptability for different transmission conditions. On the other hand, there also exist other dynamical techniques based on the selection of the intervals with higher channel transmissivity in order to mitigate the effects of the atmospheric turbulence¹⁷. However, the main disadvantage is that this system uses only the interval with best performance of the raw key; therefore, the useful raw key rate is reduced. A general scheme of a complete FSO-QKD system using the adaptive code rate in the classical channel in order to mitigate the effect of the atmospheric turbulence over the final secret key rate from weak to moderate turbulence regimes is proposed in this paper. We consider that, our technique is different than other approaches because is based on the constant raw secret key rate allowing higher transmission rate. Also, our work considers the full FSO-QKD systems that permit the enhanced performance using optics link in the classical channel for particular application (e.g. FSO-QKD systems for deep space missions without uses RF link in the classical channel). The organization of this paper is as follows: Section 2 describes the mathematical framework necessary to calculate the final secret key rate in a QKD systems, Sec. 3 describes the mathematical framework concerning the effect of the atmospheric turbulence in the QKD systems and, finally, Secs. 4 and 5 show the scheme simulation proposed and the numerical results of the final secret key rate using a LDPC with adaptive code rate for different atmospheric turbulence levels.

2. Mutual information in real QKD systems

In general, the final secret key rate may be defined as the mutual information shared between the Alice (A) and Bob (B) systems in the presence of a spy system called Eve (E) using the expression shown in Eq. (1) (the final secret key rate considering the transmission rate will be considered after)¹⁸:

Here, Δ 𝐼 real is the real secret key rate of the QKD system after the distillation protocol without considering the kind of variables (CV-QKD and DV-QKD), 𝐼(𝐴:𝐵) represents the mutual information that Alice and Bob shared and 𝑆(𝐴:𝐸) is the maximum mutual information shared between Alice and Eve. Thus, 𝐼(𝐴:𝐵)−𝑆(𝐴:𝐸) represents the ideal secret key rate of any QKD system. However, the distillation protocol performed for generate the quantum key is imperfect (due to multiple variables in the channels and systems used), thus, the shared information between Alice and Bob is decreased by a factor of 𝛽. Therefore, the secret key is 𝛽𝐼(𝐴:𝐵)−𝑆(𝐴:𝐸), where 𝛽 is the reconciliation efficiency. In order to obtain a better approximation of the final secret key rate, the efficiency of the classical channel (𝛼) must be considered. The channel efficiency may be calculated as the ratio of the amount of bits without errors at the receiver and the amount of bits transmitted. In addition, this efficiency is related to the concept of code rate, i.e., different code rates provide different channel efficiency, where lower code rates produce greater efficiency, and higher code rates produce lower efficiency. In specific way, the code rate (𝑘/𝑛) is a value that relates the original information bits (𝑘) and the redundant bits (𝑛−𝑘) necessaries for the detection and correction of the erroneous bits, given that the encoder generates n bits of data. Therefore, an adequate encoder used in the classical channel must produce a value of 𝛼≈ (i.e. an adequate code rate will improve the channel efficiency), which means that a lot of errors are corrected. Finally, if a spy does not exist in the private channel (an FSO link in this case), it is possible to assume that 𝑆(𝐴:𝐸)=0, and therefore 𝛥 𝐼 real =𝛼(𝛽𝐼(𝐴:𝐵)). In other words, 𝛥 𝐼 real only depends of the efficiencies values (𝛽 and 𝛼). In a traditional and complete QKD system, the raw key is directly affected by 𝛽, while 𝛼 affects the sifted key. In this study, the parameter 𝛼 𝑓 was used to indicate that the value of 𝛼 is a fixed efficiency of the classical channel for a specific encoder with fixed code rate [19]. Thus, considering different technical parameters (i.e., the values of 𝛽 and 𝛼 depends of the overall efficiencies of the optical and electronical schemes), the efficiency of classical public communication channel has the mathematical limit shown in Eq. (2) to assure a secure communication link:

Therefore, the parameter 𝛥𝛽𝐼(𝐴:𝐵) may be calculated considering that the quantum channel of a QKD system can use different protocols or modulation schemes in order to transmit the raw key. For example, [20] shows a QPSK modulation scheme that transmits symbols and bases through the quantum channel based on a BB84 protocol and a Differential Phase Shift Keying (DPSK) protocol in [21]. However, the focus of the present work is related to the classical channel, which in general, it may use a variety of modulation schemes. Since the QPSK modulation scheme is utilized here for the communication through the classical channel, it is possible to represent the mathematical functions for the probability error (in the quantum limit) of the classical ( 𝑃 𝑒 (𝛼)) and quantum ( 𝑃 𝑒 (𝛽)) channels using the Eqs. (3) and (4) without considering the values of 𝛼 and 𝛽 (the efficiencies are not considered in many cases).

It is important to clarify that, a code rate variation affects in a direct way to the coding gain (related to 𝜂 𝑁 𝑐 ) and finally, also to the channel efficiency. However, in this paper the linear effect of the channel efficiency is taken into consideration caused by the variation of the code rate when coherent detection is used in the receiver stage. This kind of detection was selected due to its inherent spectral filtering and the coherent amplification that may be obtained on the received signal. Therefore, in this case, the error functions must consider the channel efficiency value as shown in Eqs. (3) and (4) where 𝑁 𝑐 and 𝑁 𝑞 represent the photons number of the classical and quantum channel respectively, 𝜃 𝑒 is the phase error signal using coherent detection and the phase synchronization schemes, and 𝜂 is the overall efficiency of the overall system.

An important assumption is that the error phase signal is minimized for the phase synchronization scheme in different time windows. For such reason, the performance done in this works takes into consideration the efficiency 𝛼 and that the value of 𝛽 is fixed; nevertheless, the improvement in the performance of both channels is possible. As mentioned above, in the case of the absence of the Eve system, the following expression is valid: 𝑆(𝐴:𝐸)=0⇔ 𝑁 𝐴𝐸 =0⇔ 𝑁 𝑞 = 𝑁 𝐴𝐵 . However, if an Eve system performs a Photon Number Splitting (PNS) attack, the expression will be 𝑆(𝐴:𝐸)≠0⇔ 𝑁 𝐴𝐸 ≠0⇔ 𝑁 𝑞 = 𝑁 𝐴𝐵 − 𝑁 𝐴𝐸 , where 𝑁 𝐴𝐸 is the amount of photons (stolen photons) received in Eve from Alice²². Thus, the Eq. (4) can be modified according to 𝑆(𝐴:𝐸). Finally, the parameter 𝐼(𝐴:𝐵,𝛽) can be expressed as^3,18:

(5)

where 𝜒= 𝑃 𝑒 (𝛽). Finally, considering the efficiency of the classical channel, the result of 𝛥 𝐼 real may be described in a more detailed way using (5) as 𝛥 𝐼 real (𝛼,𝛽)=𝛼𝐼(𝐴:𝐵,𝛽).

3. Atmospheric turbulence in FSO-QKD systems

In the FSO links used in communications, the atmospheric channel may be extremely aggressive with the performance of the complete system. Therefore, considering the performance parameters of the FSO-QKD systems, the adequate analysis and detailed design of the FSO links is essential. In order to reach the best performance, it is required the use of probabilistic models to describe the effect of the atmospheric turbulence in the free space links, in our case, for the QKD application. A common parameter used for characterizing the atmospheric conditions is the Rytov variance ( 𝜎 𝑅 2 ), which describes the variability of the optical intensity (i.e. irradiance fluctuations) under different weather conditions or regimes; for a regime of weak turbulence 𝜎 𝑅 2 ≪1, 𝜎 𝑅 2 ≈1 for moderate turbulence and 𝜎 𝑅 2 >1 for strong turbulence. The Rytov variance is defined in Eq. (8)²³:

where 𝐿 is the distance of the communications link, 𝐶 𝑛 2 is the refractive index structure parameter and 𝑘=2𝜋/𝜆 is the optical wave number for a specific wavelength 𝜆. Although there exist different probability functions for the analysis of optical turbulence in FSO systems, it is well known that the Gamma-Gamma function allows a good characterization of the channel (due to the fact that it considers the effects of both the small and large scale particles)²³. Therefore, the Gamma-Gamma function was chosen for the analysis of FSO-QKD system. At the same time, an analysis of the optical channel using the Rayleigh distribution was included because previous works have made use of it to describe the effects of the optical turbulence from the weak to moderate turbulence regimes; also, this function is useful for modeling the pointing losses in FSO systems^24,25. In addition, the results obtained in this way are straightforward and easier to interpret in comparison with the more general results obtained with the Gamma-Gamma function. Hence, in this case, the Rayleigh distribution function that describes the variation of the optical intensity may be written as shown in Eq. (9).

In particular, the Rayleigh function is dependent of the optical intensity ( 𝑁 𝑐 ℎ𝑣/𝑇 𝑚 2 ), where besides the Planck constant (ℎ), the frequency (𝑣), observation time (𝑇), and the area of the photo receiver ( 𝑚 2 ) remain also constant. Thus, Eq. (9) has a most appropriate representation in the QKD context. The function 𝑓( 𝑁 𝐶 , 𝜎 𝑅 2 ) describes the variation of the optical intensity of the classical signal received in a FSO-QKD system in a time window analysis. It is possible to relate it to the error probability of the overall system considering the effect of the channel efficiency and the atmospheric turbulence as shown in Eq. (10):

(8)

where 𝐸[ 𝑁 𝐶 ] is the expected value of the photons number using (9) in the time window used for the analysis; on the other hand, when the Gamma-Gamma function is used, Eq. (10) is modified so that 𝐸[ 𝑁 𝐶 ] is calculated based on the Gamma-Gamma function, where 𝛼 𝑔𝑔 and 𝛽 𝑔𝑔 are the effective numbers of large-scale and small-scale, respectively^23-25.

4. Simulation scheme

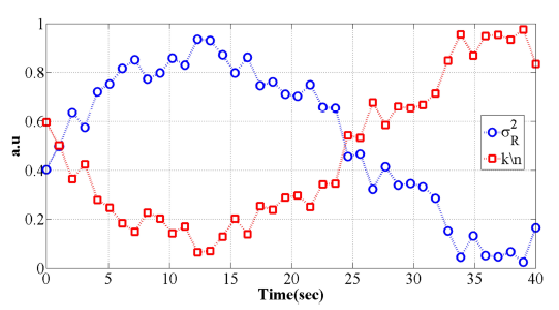
The simulation scheme shown in Fig. 1 was implemented to evaluate the proposed method. In this simulation, the Alice system has a quantum subsystem (unidirectional) and a classic transmitter / receiver subsystem (bidirectional). In the private channel segment, the parameters (𝛽𝐼(𝐴:𝐵),𝑆(𝐴:𝐸)) mentioned previously are calculated. The setup also has a dynamical and adaptive encoder able to modify the code rate considering the turbulence levels in the classical channel. Thus, the final secret key rate is also dynamical according to the value of 𝜎 𝑅 2 .

Figure 2 shows the dynamical iterative process for estimate parameters in the classical channel. In particular, the iterative procedure in the Bob system is as follows: First, the communication in the classical channel uses an initial code rate ((𝑘/𝑛 ) 𝑡 1 ) at time 𝑡 1 ; next, Bob calculates the classical channel efficiency using the Bit Error Rate (BER) measurement (the BER has a relationship with the theoretical value of error probability, 𝑃 𝑒 (𝛼, 𝜎 𝑅 2 ) 𝐶 and 𝑃 𝑒 (𝛼, 𝛼 𝑔𝑔 , 𝛽 𝑔𝑔 ) 𝐶 ). Once that Bob determinates the channel efficiency using the error probability calculated using the BER measurement, Bob informs to Alice using the same code rate (𝑘/𝑛 ) 𝑡 2 the future modification of the code rate (𝑘/𝑛 ) 𝑡 2 to be used in the next communication according to the atmospheric turbulence detected. The atmospheric turbulence characterization depends on the environmental conditions which may vary with time, but usually the atmospheric conditions has a relatively slow modification rate compared to the data signal processing speed currently available. Based on this fact, the value of the turbulence is assumed to be constant in the temporal processing interval ( 𝑡 2 − 𝑡 1 ), hence that the code rate is able to minimize the effect of the turbulence in the communication link.

As mentioned previously, both quantum and classical channels are FSO links; therefore, an important assumption is that the atmospheric turbulence level is considered the same (or very similar) in both channels in a time window analysis. In fact, both channels do not transmit at the same time, i.e., the raw key is transmitted in a non-continuous way in order to calculate a new quantum final key for each time window analysis. In addition, althoug turbulence in the quantum

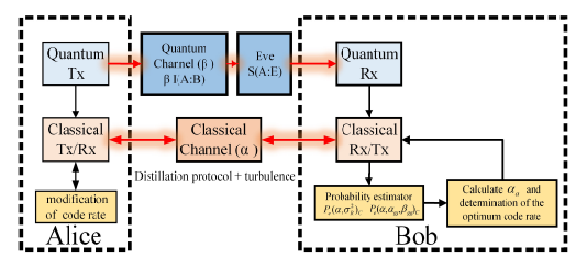
Figura 1 Block diagram of the simulation-experimental setup of the QKD system proposed with dynamical encoder for different atmospheric turbulence levels. 

Figura 2 Dynamical process of negotiation of the code rate considering the turbulence in the classical channel 

channel exists, the simulation does not take into consideration the modified characteristics of the raw key (i.e. the variation of the encoder in the quantum channel is not considered) in order to maintain the capability of detecting the excess of noise in the quantum channel due to future implementation of Eve.

Considering the classical theory of LDPC coding, the LDPC design parameters were modified in this work with respect to the turbulence regimes (Rytov variances); therefore, different generator matrices (𝐺) are established. Thus, the codeword (𝑐) transmitted through the classical channel using the binary message (u) is given in Eq. (11) where the index (i) represents the analysis iteration in the time ( 𝑡 𝑖+1 − 𝑡 𝑖 ).

Next, the codeword transmitted is affected by the channel noise ( 𝑛 𝑖 ) and turbulence ( 𝜎 𝑅 2 ), and this manner, the decoder uses the received signal ( 𝑟 𝑖 =𝑐( 𝑛 𝑖 , 𝜎 𝑅 2 )) in order to determine the syndrome (𝑠) considering the corresponding Parity-check matrix ( 𝐻 𝑖 ) as described in Eq. (12) (note that 𝐺 𝑖 𝐻 𝑖 𝑇 =0) .

The value of 𝑠 𝑖 allows the detection and correction of the errors in the communication link. An important parameter is n, that define the dimension of 𝐺 𝑖 and 𝐻 𝑖 and depends of the turbulence in the classical channel. At same time, the error probability is calculated in order to modify the parameters (𝑘/𝑛 ) 𝑖 , 𝐺 𝑖 and 𝐻 𝑖 to be used in the next analysis (for more details of LPDC coding consult¹⁹. Figure 3 shows the detailed block diagram of the LPDC encoder proposed where Bob determines the efficiency of the classical channel using the bit error rate measurement (the figure shows the error probability in order to maintain the style of the equations used). Given the fixed amount of information bits (𝑢), Bob modifies the code rate according to the turbulence regime calculated.

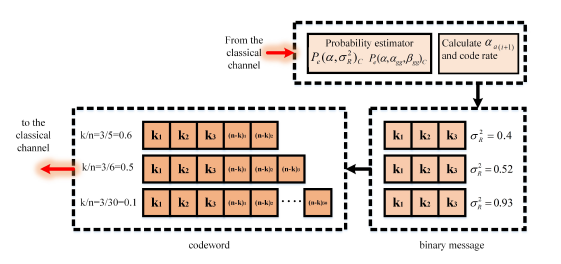
Figura 3 Block diagram of the LDPC coding with adaptive code rate considering the value of the Rytov variance. 

Figura 4 Numerical results of the code rate using different values of Rytov variance in order to obtain a ® = 0:55; The computation time required for the calculation of the code rate is 1 second (a.u.: arbitrary units). 

5. Numerical results and analysis

In the simulation, a bit stream of 10× 10 6 bit/sec (without encoding) was used for the transmission in the classical channel. In order to clarify this issue, the transmission rate is not possible to ensure in the simulation considering the hypothetical classical channel due to the different variations of processing time of the computer used; therefore, the stream length per second is used as assumption for the proof of concept of the scheme proposed. The bit error rate is measured in order to determine the value of the 𝜎 𝑅 2 using the Eq. (10) after the bit stream has been affected by the turbulence simulated. Thus, the values of 𝛼 𝑖 were calculated considering different 𝜎 𝑅 2 in order to modify the value of (𝑘/𝑛) and inherently the channel efficiency ( 𝛼 𝑖+1 ). Figure 4 shows the calculated numerical values of the code rate for the Bob system considering the variation of 𝜎 𝑅 2 calculated according to the Gamma-Gamma function in order to maintain a 𝛼=0.55. The calculation of the code rates was chosen each 1 second in a complete time analysis of 40 seconds, however the analysis time can be decreased or increased. In this way, for greater values of 𝜎 𝑅 2 the bit error rate measured ( ?? 𝑒 (𝛼, 𝜎 𝑅 2 ) 𝐶 and 𝑃 𝑒 (𝛼, 𝛼 𝑔𝑔 , 𝛽 𝑔𝑔 ) 𝐶 ) are significantly increased. Therefore, the code rate (𝑘/𝑛) is reduced because the Alice system has to add more redundant bits in order to maintain a constant channel efficiency.

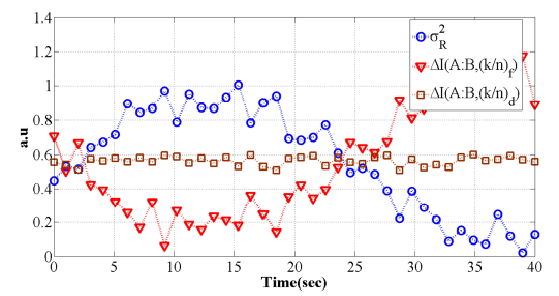
Figura 5 Performance of the mutual information considering different values of Rytov variance according to the Gamma-Gamma function using a fixed and variable code rates (a.u.: arbitrary units). 

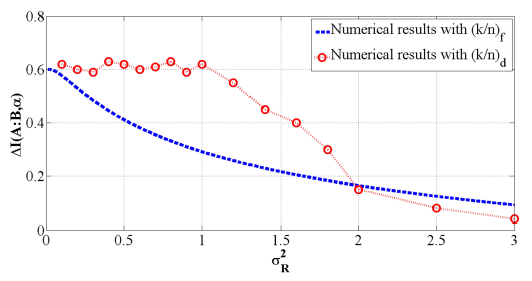
Figura 6 Numerical results for the mutual information using adaptive coding for different turbulence regimes. 

Figure 5 shows the mutual information results using a fixed code rate (𝑘/𝑑) 𝑓 (𝑖.𝑒., a 𝐺 𝑖 and 𝐻 𝑖 fixed).In this scenario, higher values of will result in a decreased in the mutual information; otherwise, when using a dynamical code rate (𝑘/𝑑) 𝑑 (𝑖.𝑒., dynamical 𝐺 𝑖 and 𝐻 𝑖 ), the mutual information is maintained constant. Based on the Fig. 5, it is possible to observe that for small values of with (𝑘/𝑑) 𝑓 , the mutual information is increased, while the mutual information is still constant when (𝑘/𝑑) 𝑑 is used. The reason of this performance is that the proposed system was designed in order to maintain a specific mutual information value between the Alice and Bob systems, regardless of the channel conditions. However, it is possible to modify the mathematical model of the encoder in order to improve the performance.

Figure 6 shows the numerical values for the mutual information considering a fixed and adaptive coding gain. In particular, the performance of the mutual information using the adaptive coding gain is constant from weak to moderate turbulence regimes; however, the mutual information decreased drastically in the strong turbulence regime. The latter can be explained due to the fact that for strong turbulence regime the coding scheme proposed has to add too much redundant bits in order to detect and correct the errors causing a final secret key rate reduction.

Finally, Fig. 7 shows the mutual information and channel efficiency performance when the code rate is modifiedwith respect to the error probability 𝑃 𝑒 (𝛼, 𝛼 𝑔𝑔 , 𝛽 𝑔𝑔 ) 𝐶 with

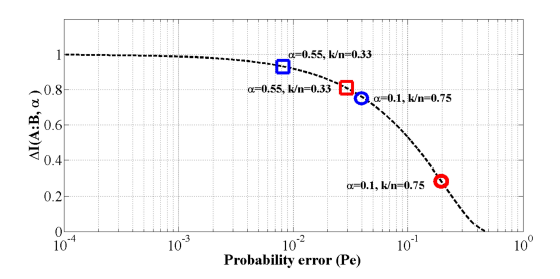
Figura 7 Mutual information between Alice and Bob with Rytov variance of 0.53 according to the Gamma-Gamma function. Circle: ® without using the adaptive coding. Square: ® using the adaptive coding. 

The results shown in the Figs. 6 and 7 contributed to determine the final secret key rate in a QKD system considering the raw and sifted key rates (bit/sec) without using the privacy amplification in the protocol. In particular, the final secret key rate is defined as 𝑅 secret = 𝑅 sift 𝛥𝐼(𝐴:𝐵,𝛼); thus, using a raw key rate of 350 Kbps that our work team reported in²⁶, the calculated ideal sifted key rate ( 𝑅 sift ) was 175 Kbps without considering turbulence in the quantum and classical channels. Consequently, the proposed scheme in this paper improves the performance of 𝑅 secret modifying the code rate considering the atmospheric turbulence. In particular, the final secret key rate was 52.5 Kbps without using the adaptive code rate, while that using of the adaptive code rate allowes reach up to 140 Kbps in our simulation analysis.

6. Conclusions

A dynamical and adaptive coding scheme is reported for improve the performance of the cryptographic key distillation protocol considering the atmospheric turbulence levels (it were modeled by Gamma-Gamma and Rayleigh functions) that may be present in the classic channel. Specifically, the main objective of this work was to enhance the performance of FSO/CV-QKD systems using a technique that does not require the change of the devices already installed; such technique is based in the knowledge of the dynamic parameters of the overall system, in this case, the classical channel and the modification of the code rate used. Besides, the technique proposed is suitable also for general FSO quantum communications systems due to that dynamical atmospheric turbulence levels are present also. However, on these terms, the modification of the performance theoretical expressions considering the particular technical specifications of such communication system (i.e., the Eve system does not exist and obviously, the distillation protocol is not required) will be necessary. In general, the proposed method showed to be feasible based on the numerical results by incrementing the final secret key rate by 87.5 Kbps (from 52.5 Kbps to 140 Kbps) when the code rate is modified with respect to the atmospheric turbulence. This means that the transmission of a longer final quantum key and higher secret key rate are possible (i.e., double length/rate or more). While it is true that the parameter 𝛥 𝐼 real (𝛼,𝛽)=𝛼𝐼(𝐴:𝐵,𝛽) is an adequate general approximation for the final secret key rate, more information regarding the raw key rate and the classical subsystems that will perform the distillation protocol is needed. Thus, the mathematical framework and results obtained in this work shows the potential to optimize the design of FSO/CV-QKD systems. In addition, the variation of the atmospheric turbulence is slow in general, hence, the processing time require for the parameters do not appear to be critical aspect for future physical implementations. In order to be able to mitigate the effects of the optical turbulence over the communications link, it is required that the physical implementation of our adaptive encoder works on real time, i.e., the total processing time must be faster than the cutoff frequency of the optical turbulence. With the high-speed FPGAs and DSPs commercially available, this requirement could be easily met. Finally, the technique proposed requires a complete quantum security analysis considering different attacks against QKD systems for a practical security performance, but due to the particular conditions of the FSO/CV-QKD systems, many considerations are necessary as mentioned previously, e.g., some kinds of attacks are nearly impossible to implement in the quantum channel (i.e. in the FSO link) and additional losses and noises should be considered^27,28. In fact, some parameters that are related in an inherently way with the losses were used in (1)-(4). On the other hand, a man-in-the-middle attack has to be prevented using authenticated classical systems²⁹. However, these attack conditions are not the essence of the paper.