PACS: 42.65.Tg; 42.79.Nv
1. Introduction
The Soliton self-frequency shift (SSFS)1,2 has been demonstrated as an important mechanism for the supercontinuum (SC) generation with femtosecond pulses in optical fibers 3,4. Specifically, many effects implied in SC generation would not be possible without the SSFS 5,6,7,8,9,10,11. Its characteristic large frequency shift has been exploited for the fabrication of infrared (IR) sources 12,13,14, even its optimization has been reported 15,16,17.
In previous works, we have shown that a fs-pulse can simultaneously generates several pre-defined spectral peaks by means of dispersive waves in the normal GVD18 or by soliton self-frequency shift in the anomalous GVD19. It is useful for potential applications of optical coherence tomography (OCT). Now, regarding the same kind of applications, we present a computational optimization with the use of a genetic algorithm (GA) to obtain not only a tunable frequency convertor (see, e.g., Refs. 20,21), but also achieving the maximum spectral conversion possible in the fixed channel regarding the scope of the initial set of input pulse parameters. This frequency convertor is useful for applications where high power is demanded.
We simulate pulses propagation in a commercial highly nonlinear photonic crystal fiber, NL-2.4-800 PCF (see Ref. 19 for details of cross sectional geometry), exhibiting SC generation at the Ti:Sapphire laser wavelengths. This method finds the optimal input pulse parameters, namely central wavelength,
2. Pulse propagation and genetic algorithms
Using a Fourier split-step method, we simulate the propagation of optical pulses with complex amplitude A(z, t) by integrating numerically the GNLSE 3,
where z is the axis coordinate along the fiber propagation, the dispersion coefficients
The input pulse used in this work belong to a realistic laser source, the form is
Optimization algorithms have been developed in order to solve problems involving multiple variables in which solution seems to be non trivial (see Refs. 37,38,39 for reviews on the topic). A GA is a evolutionary computational algorithm for optimization which makes evolve an initial population of individuals in order to find global minima when a number of generations is generated 40,41. Each individual is the result of the evaluation of a set of parameters (
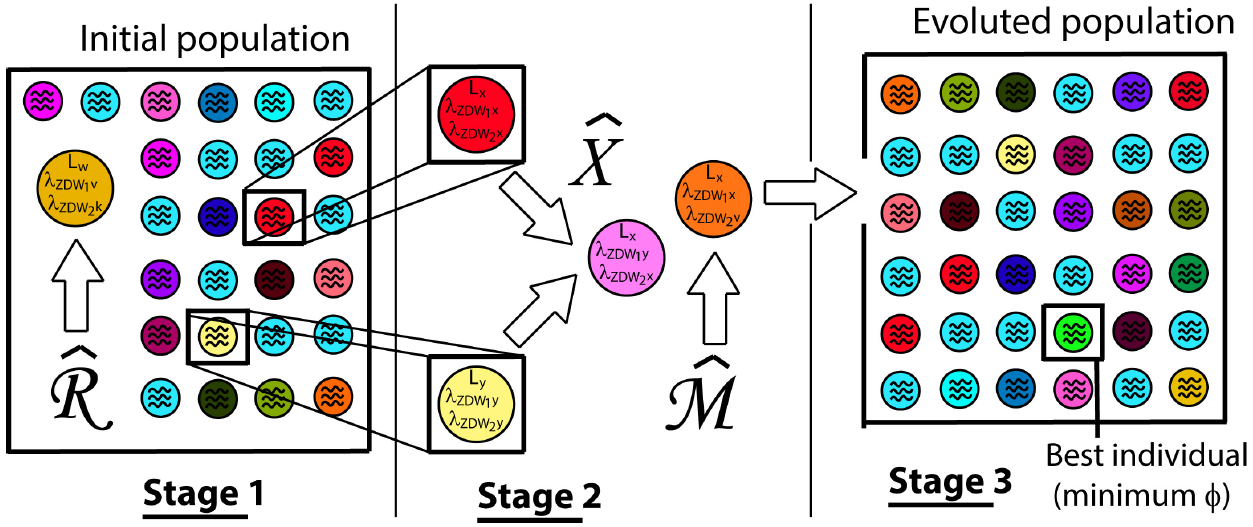
Figure 1. Diagram of the operation of the GA. In first stage a population of possible solutions is generated randomly. In the second stage, new individuals are created by
3. Raman frequency conversion
It has been proved that high axial resolution in OCT systems is aimed in the spectral region of 800 nm to 1400 nm 43,44. Aditionally, the NIR II light decrease in scattering and increase in transparency of the biological tissues over the NIR range 45. Moreover Gaussian spectral shapes avoid spurious structures in OCT images 46. For these reasons, IR-Raman soliton can be considered a very good option to OCT applications.
In Sec. 3.1, we search the optimal parameters,
where
In order to prove the convenience of our method, it is made an exhaustive search of the best fitness value by scanning the entire ranges of parameters. It is shown in Sec. 3.2
3.1. Optimal solution using genetic algorithms
The optimization consisted in the search of parameters that originate the maximum output power in each selected spectral channel on the NIR II using the GA to vary the pulse parameters P [1, 15] kW,
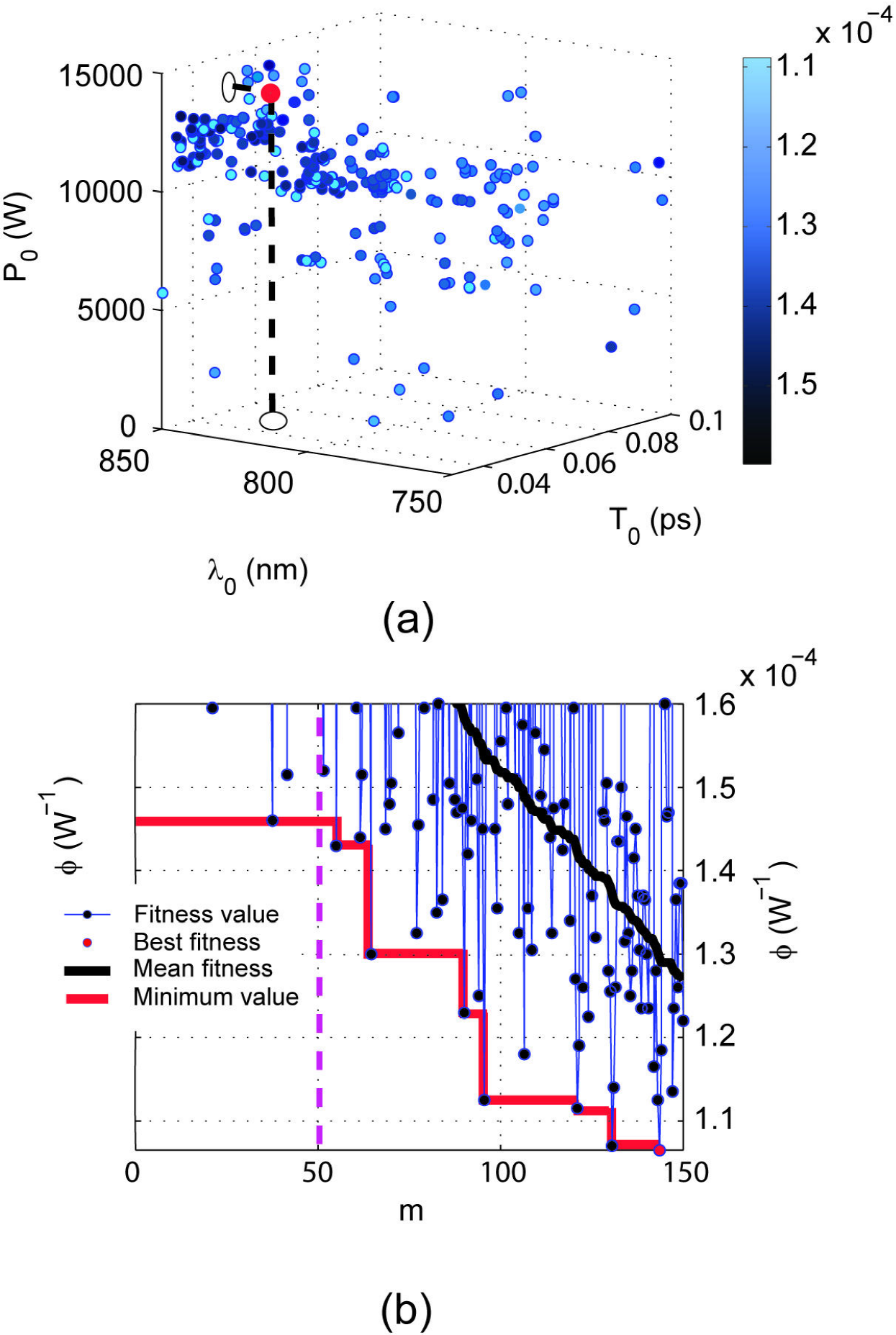
Figure 2. (a) Cloud of m = 150 individuals generated by the GA for a channel of
This “cloud" of individuals corresponds to all solutions generated by the GA, their fitness function being represented by the color code bar. Lighter points have smaller fitness values (thus, better) than darker ones. We observe that there exists a zone where the GA tends to accumulate points. It is precisely in this region where the best fitness value (red point) is found. It is worth mentioning that in general these regions could contain more candidates to optimal solutions than those eventually selected by the GA. Thus, keeping track of these “quasi-optimal" individuals can also be of great interest from the physical point of view since they can provide extra-local minima of the fitness function not considered in a preliminary physical analysis of the optimization scenario. Once the local minima have been detected, a more accurate search around them combining GA strategies and other optimization techniques can be performed in order to find a better minimum of the fitness function.
Figure 2(b) shows clearly the “dynamical" improvement in the fitness value as the GA evolves [referred to in Fig. 1]. The initial “optimized" value is obtained in the stage 1, when the initial population of 50 individuals is randomly generated (delimited by the vertical dashed line). After the 50th evaluation, the stage 2 of our algorithm initiates, when genetic operators start to act on the previous population. A significant improvement in the fitness of the population is apparent, the mean fitness value of the population is monotonically decreasing as new individuals are generated, as the black continuous curve. The red line shows the minimum global value until the instant of the last individual is generated in the process. Our GA has not a tendency to converge towards local optima or arbitrary points rather than the global optimum of the problem, this is caused because the operator
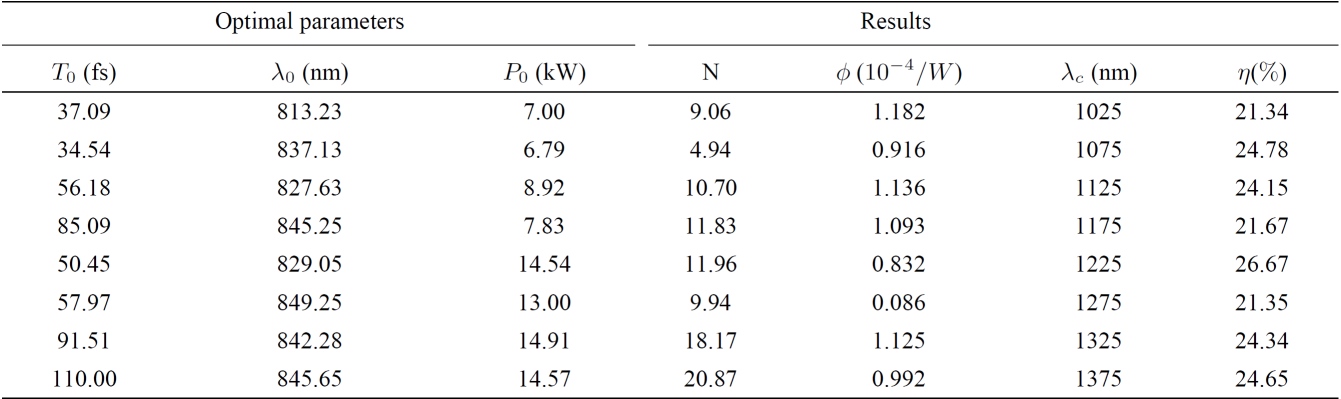
Table I. Optimal parameters,
The spectral and temporal evolutions of the best individual found in the optimization process (see Fig. 1) are shown in Figs. 3(a)-(b) respectively. It clearly demonstrates the optimality of the result provided by the GA: the spectrum of the first Raman soliton (the reddest one) is accurately centered in the targeted channel (delimited by the dashed lines).
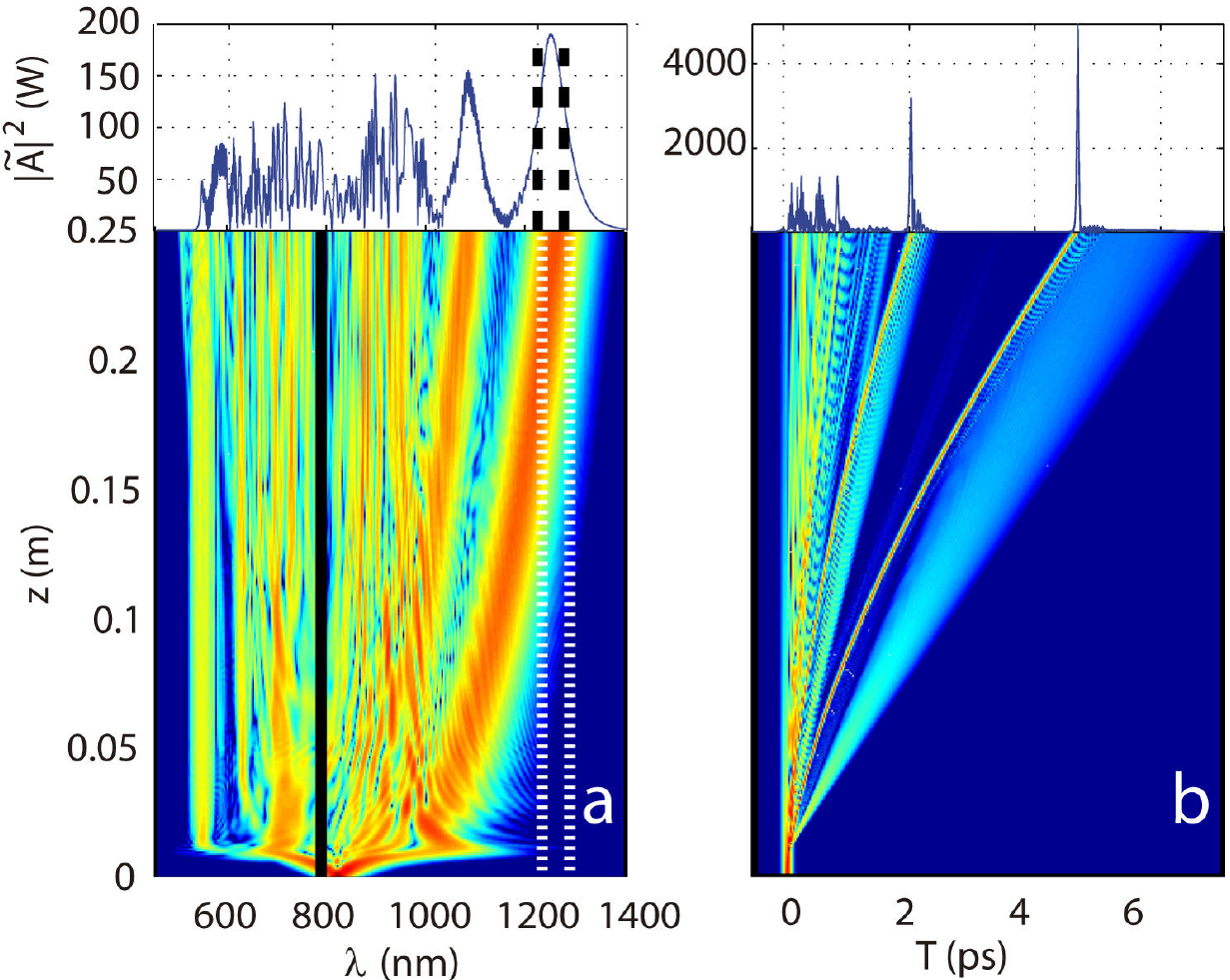
Figure 3. Spectral (a) and temporal (b) evolutions on distance z corresponding to optimized parameters T
0
= 50.45 fs,
The maximum spectral power found for each channel results very approximate to the Kodama and Hasegawa predictions for the soliton amplitude22.
It is known that SSFS can be made large by propagating shorter pulses with high peak powers inside highly nonlinear fibers and that the fission of higher-order solitons generates frequency-shifted pulses in form of Raman solitons 1,35.
In order to validate of our method, it is made an exhaustive search of the best fitness value by scanning the entire ranges of parameters. It is shown in Sec. 3.2.
3.2. Optimal solution using exhaustive search
Now, a searching method is implemented to check the reliability of our results. It consists of picking the individual with the best fitness value from a systematic evaluation of all possible combinations of parameters (m = 675) within the defined ranges with defined steps. It is worth mentioning that this process requires larger capabilities of time-machine (
Table II. Best parameters,
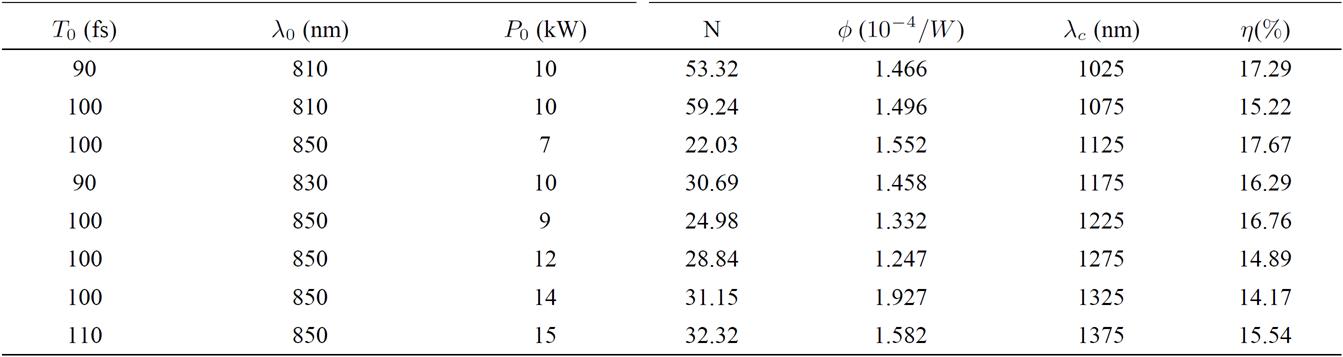
The chart of different values for the
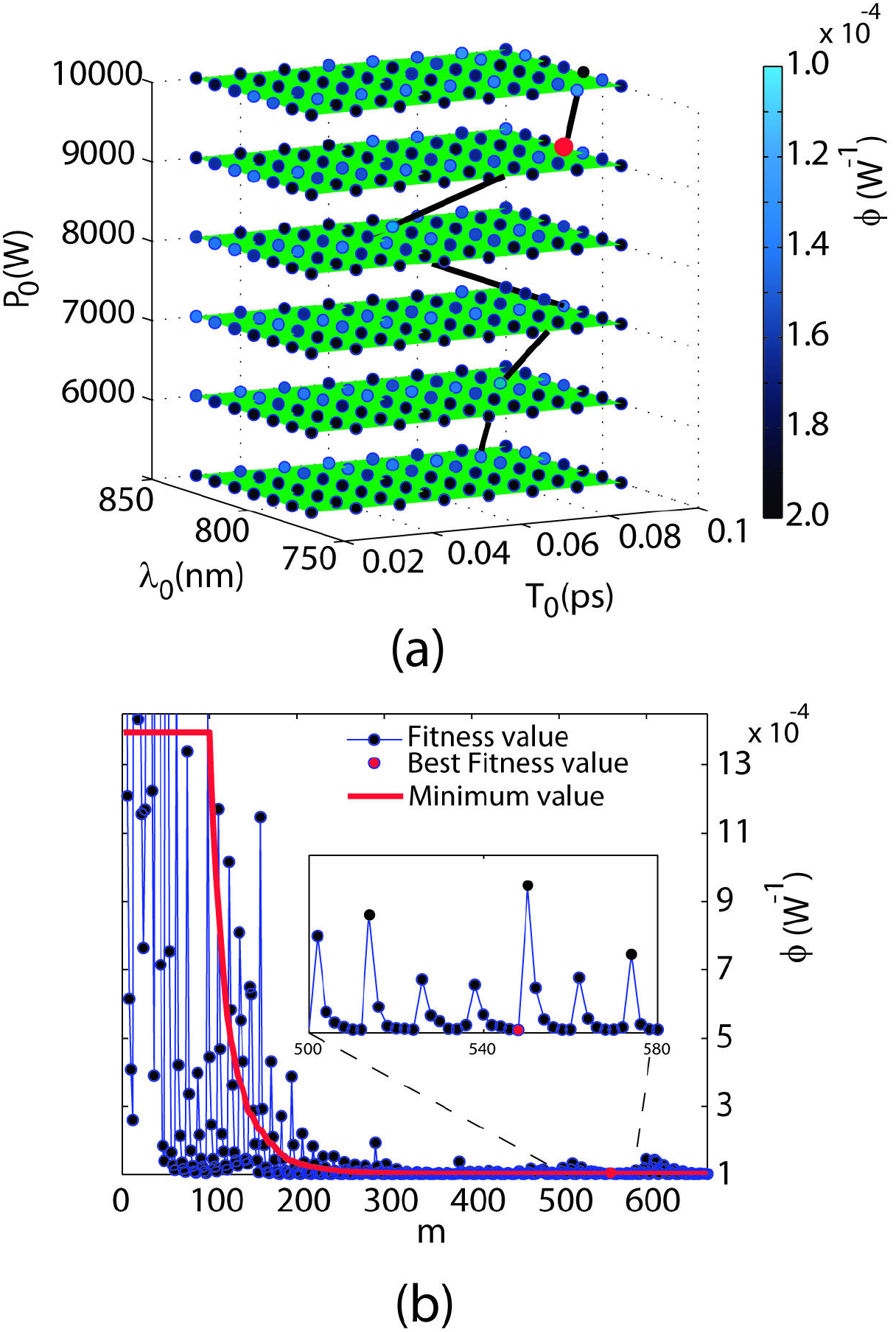
Figure 4. (a) Fitness value charts for different P
0
values with m = 675 generated for
By comparing Tables and , we can see that the efficiency obtained in the optimization using the GA is better than the search made without using the GA, even using more executions in the exhaustive search. We perform a new search level by focusing on a smaller region around the neighbourhood of the previously optimized results in Table . The new conditions are:
4. Conclusions
We have presented a well defined and efficient optimization procedure of a Ti:Saphire laser pulse parameters to obtain the maximum frequency conversion using a simple device by means of solitonic red-shift in the anomalous region. This optimization is achieved with the use of GAs. Therefore, it has been shown that efficient spectral conversion based on SSFS can be achieved using a simple PCF as a medium of generating spectral broadening pumped by a Ti:Sapphire laser just by properly controlling the input parameters of the input pulses. This scenario typically involves soliton fission and emission of dispersive waves into the normal GVD regime, situation in which precise analytical estimates are not available and therefore the use of numerical simulations in combination with GA is of great usefulness. In summary, this work results in a tool with great potential for optimization of the output of SC spectra for practical OCT applications in the NIR II region.











 text new page (beta)
text new page (beta)



