PACS: 75.50.Pp; 78.55.Et; 78.30.Fs; 81.05.Dz
1. Introduction
Zinc oxide (ZnO) is a direct wide band gap (
A ferromagnetic ordering with Curie temperatures above 425 K in Mn-doped ZnO bulk ceramic and thin films was reported9,10. It was also observed that, for temperature above 600°C, some Mn start to cluster into the Mn2O3 form, whereas the best ferromagnetic behavior was found for the samples prepared at 500°C. Other groups have reported higher Curie temperatures for ferromagnetic ordering in Mn-doped ZnO thin film11,12,13. More recently, Chang et al. have demonstrated ferromagnetism in samples of Mn-doped ZnO nanowire5. The capacity to produce powder, pellets, transparent thin films, as well as nanowires of Mn-doped ZnO open up a variety of possibilities to fabricate a lot of components for spintronic devices with ferromagnetic behavior at room temperature, and components for novel magneto-optic components.
In this paper, we report detailed Photoluminescent (PL) spectra of Mn-doped ZnO ceramic pellets in the excitonic region. An important issue to take into account is whether the resulting materials are indeed alloys of transition metal elements within the host material instead of remains as the host material with clusters, precipitates, or secondary phases aggregations. Rietveld refinement of the X-ray diffraction patterns, Energy-dispersive X-ray spectroscopy (EDS) technique, and Raman spectroscopies were performed to study these effects. For Mn-doped ZnO polycrystalline pellets, it was found that the better crystallinity takes place at temperatures below 550°C 9,10 as well as the highest 3d metals solubility of 3d metals in ZnO15. The Mn-doped ZnO pellets were prepared at two different synthetizing temperatures (500°C and 900°C) and the samples structure and propriety’s were compared. Our interest in optical properties study of bulk samples was motivated by a study recently that show that the optical properties in the DMS ZnO:Co2+ are independent of the structural conformation of the host and the cobalt concentration (for concentration less than 5% of Co2+)14.
2. Experimental details
2.1. Preparation of ZnO pure and Mn-doped ZnO
The ceramic pellets of polycrystalline Mn-doped ZnO were prepared following a similar procedure as given by Sharma et al.10. An Ar flow was used, at the beginning, to clean the system as de-scribed below. To prepare the samples in Oxygen atmosphere, a long quartz tube of length 1.20 metre (23.80 mm outer diameter) was kept coaxially inside a horizontal tubular furnace. Samples with 2 at.% Mn-ZnO were prepared through the solid-state reaction route using high-purity ZnO (2.9269 g) and MnO2 (0.0705 g) powder (at least 99.9 %), which were mixed together and ground during at least 15 min. Then, it was axially pressed into disks at
2.2. Instrumental analysis
The Raman spectra were taken at various temperatures under atmospheric pressure in backscattering geometry, with a confocal microscope and a 100X objective, with a Horiba T64000 triple spectrometer using the 514.5 nm line of a Coherent Innova Spectrum 70C Ar+-Kr+ laser. The Raman signal was detected using a nitrogen cooled CCD (Jobin-Yvon Symphony). The integration time was 40 s and the laser power was kept below 5 mW to avoid laser-heating effects on the tested material and the concomitant softening of the observed Raman peaks.
Photoluminescence (PL) measurements were carried out with a double excitation and emission monochromator Edinburg Instruments FSLP 920 fluorimeter with a spectral resolution in both emission and excitation of 0.1 nm. A Xe ozone free quartz 450 W lamp was used for excitation. The absorption spectra, at room temperature, of the Mn-doped ZnO pellets were measured using an Acton SpectraPro-500 spectrometer from 350 nm to 800 nm. For these measurements, the powdered ZnO samples were mixed with KBr powder in a ratio of 1:2 parts by weight and pressed into pellets.
X-ray powder diffraction (XRD) data were collected on a Bruker D8 automatic diffractometer in Bragg-Brentano geometry. The Cu-K
3. Results and discussions
3.1. EDS studies
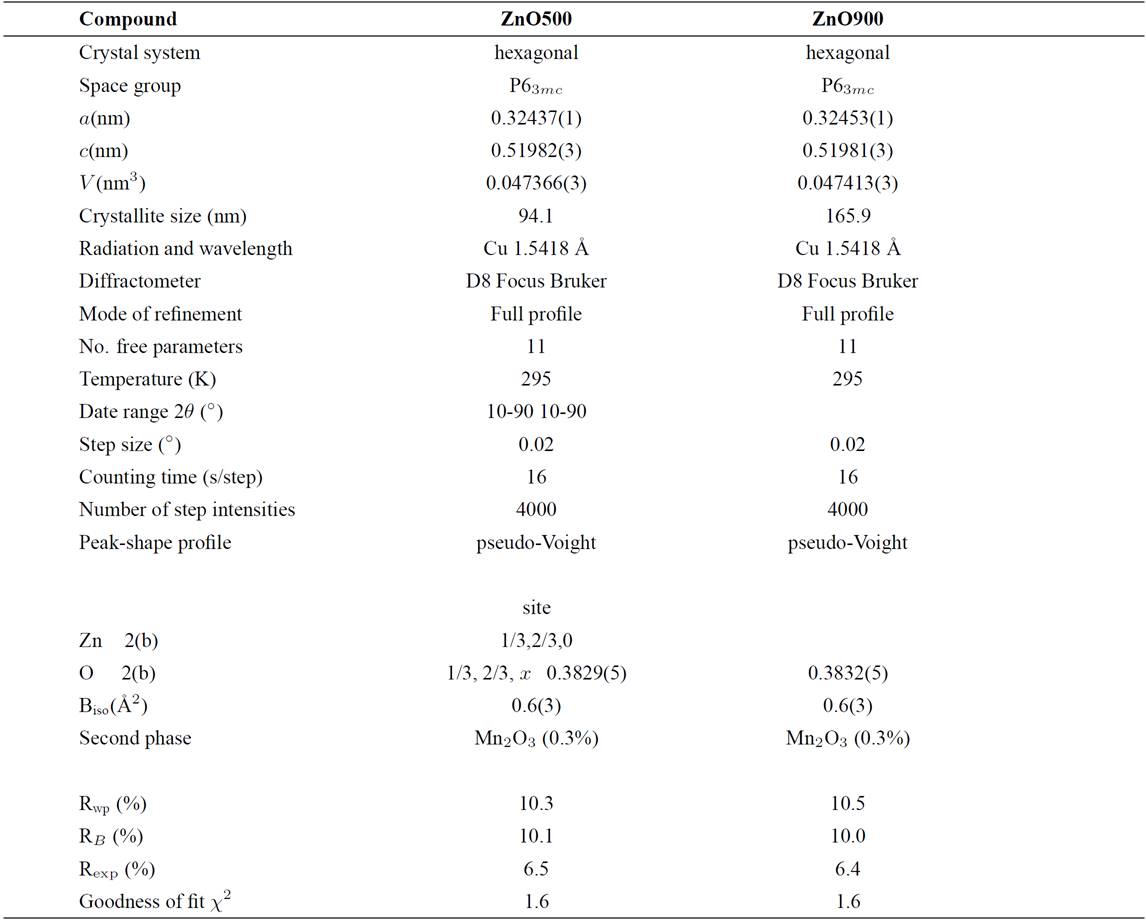
Figure 1 shows an elemental mapping for the samples ZnO500 and ZnO900 showing a uniform distribution of Mn atoms in the sample. However the average local Mn concentration, determined by the EDS technique was found to be very low (
3.2. XRD studies
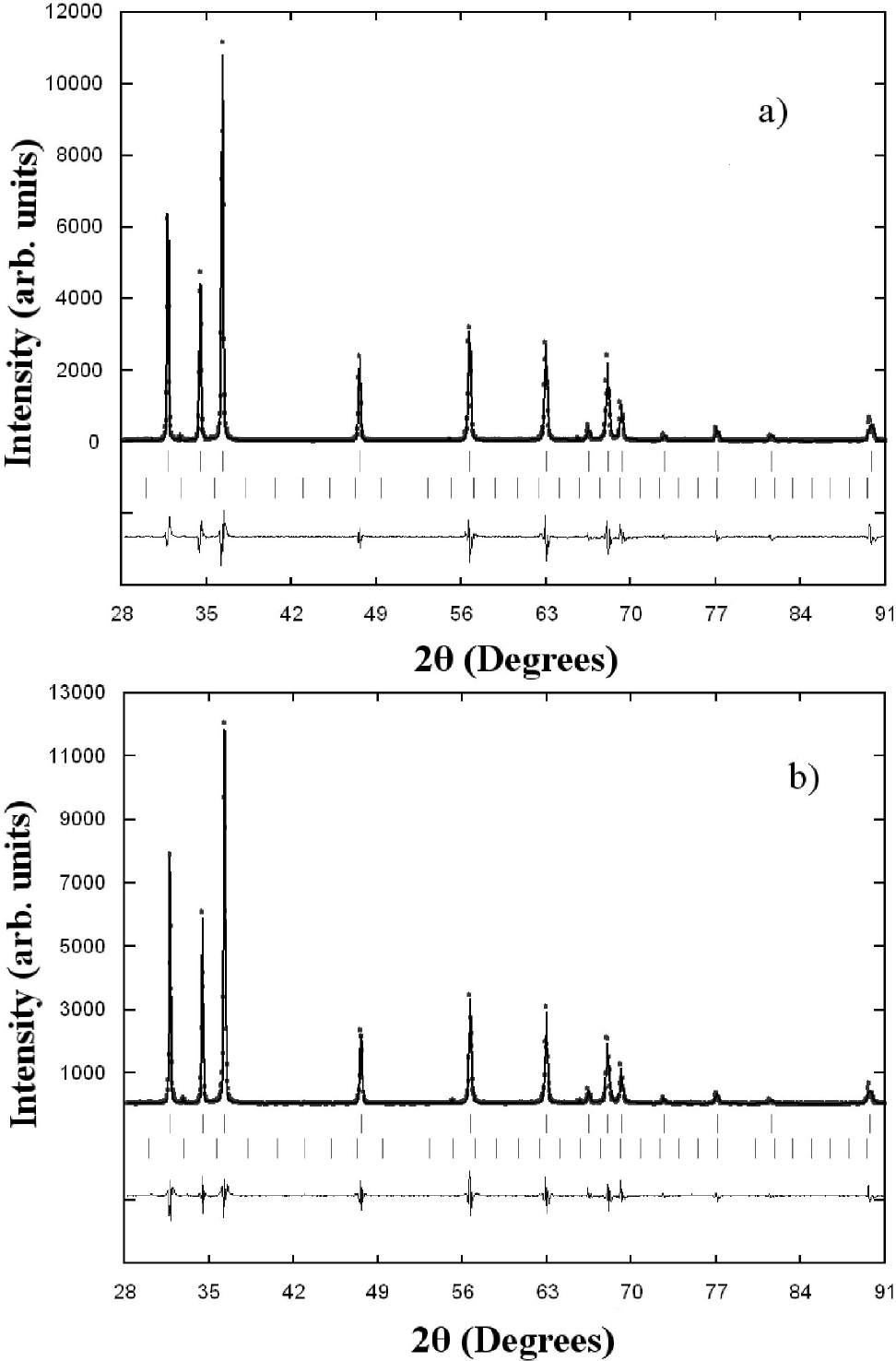
The Zn0.98Mn0.02O pellets were characterized by X-ray diffraction at room temperature, and the results are shown in Fig. 2. A search in the ICDD-PDF database16 using the software available with the diffractometer was performed, and one known phase present in small quantities were readily identified: Mn2O3 (PDF N° 76-015) for the samples doped with Mn. The crystal structure refinement was performed by Rietveld technique17,18, using the Fullprof program19,20. Details of the Rietveld refinement results for each compound are given in Table II. The initial positional parameters used were the ZnO bulk values taken from literature21. Atomic positions of the binary Mn2O3 compound were included as a secondary phase in the refinement. Since the amount of Mn2O3 phase (cluster) present in the samples is small (0.3%), and no other phase are seen, this seems to indicate that some Mn atoms might have been substitutionally incorporated in ZnO lattice. These Mn2O3 clusters are too small to be seen by conventional X-ray techniques, however from the Rietveld refinement results the formation of cluster, in both samples, seem to be independent of temperature sintering process. The chemical kinetic reaction deal in inhomogeneous samples of Mn-doped ZnO sintered at high temperature is difficult from the present experimental data, and requires further investigations.
3.3. Raman studies
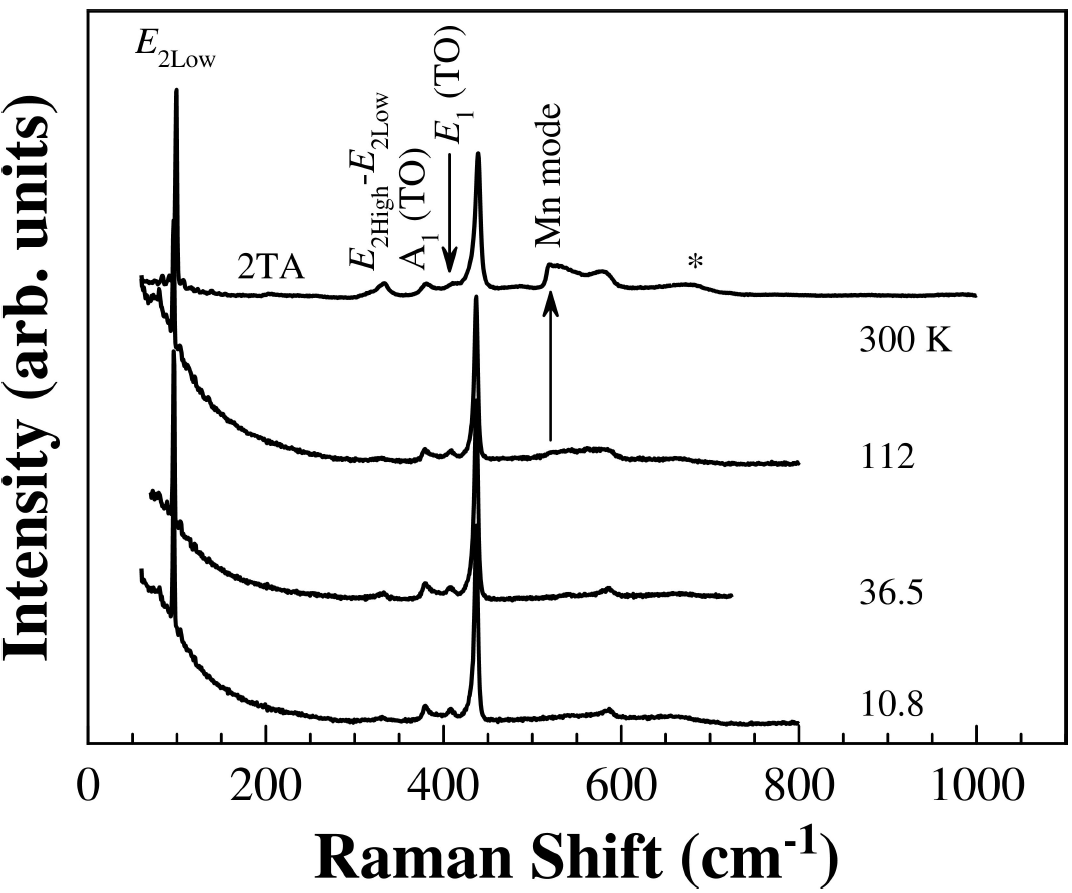
In order to check the tetrahedral coordinated Mn+2 ions into the ZnO host lattice and due to the limited sensitivity of the X-ray powder diffraction technique, Raman spectroscopy was carried out. The room temperature Raman spectrum of Zn0.98Mn0.02O pellets sintered at 500°C is shown in Fig. 3. The strongest peaks at 99 and 438 cm+1 belong to the low- and high-frequency branches of the E
2 mode of ZnO, which dominates the spectra. The 410 cm-1 peak is typically ascribed to E
1-TO phonon. The Raman peak at 382 cm-1 is assigned to A1 transverse optical (TO) mode. A peak at 538 cm-1 had been previously assigned to 2
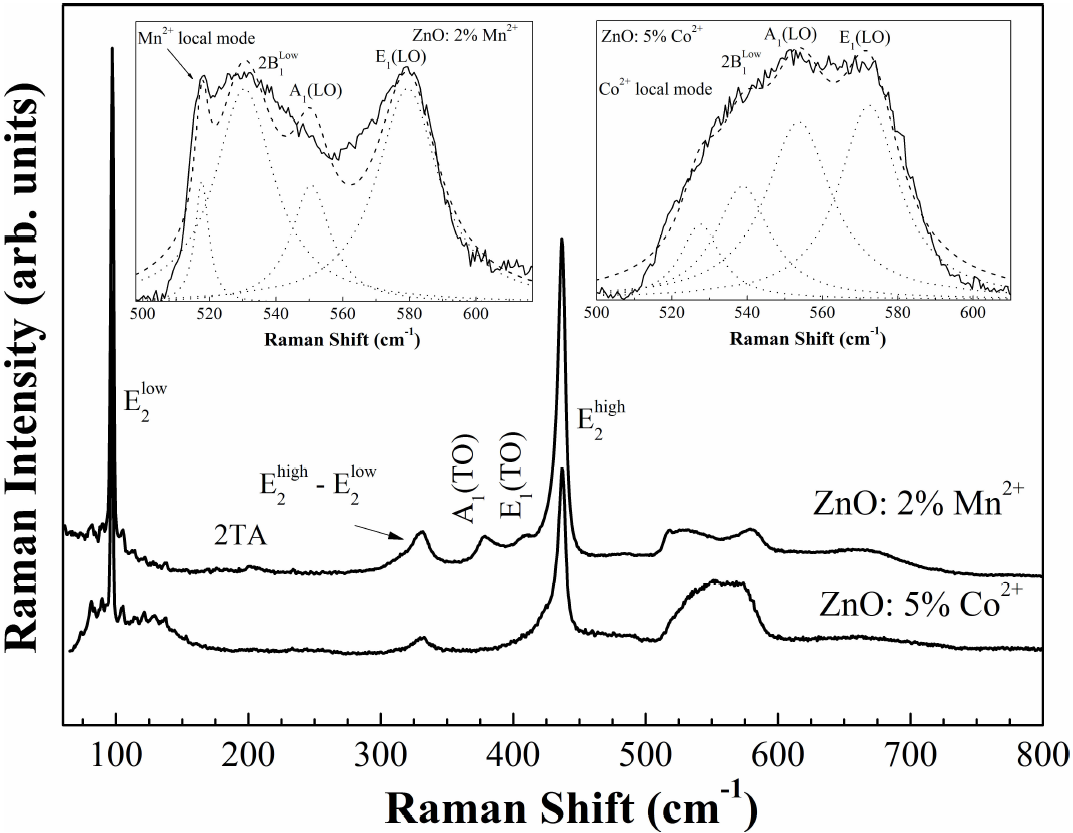
Figure 3. Raman spectra of ZnO500 pellets and Co-doped ZnO from Ref.33. The total fitting (dashed line) with four Lorentzian functions (dot lines) are shown in the inset figures.
Table III. Room temperature frequencies (v) and symmetry of the first- and second-order Raman spectra observed in the ZnO500 sample. Our results are compared with previous data in Ref.22.
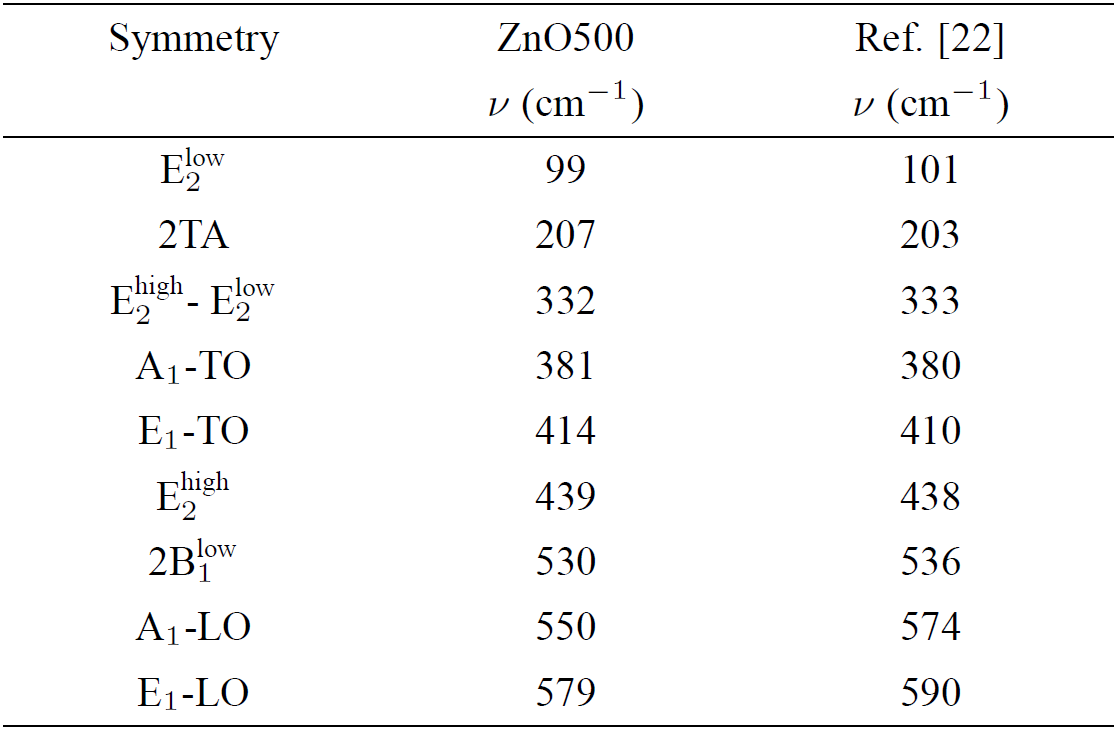
Doping ZnO with Mn2+ ions introduces an extra mode at
The scattering of the electrons and holes on the impurities can relax the selection rule of the dipole-allowed Raman scattering. Therefore, one can expect that phonons participating in the scattering will be a mixture of
3.4 Optical properties studies
The band gap energy of samples were determined by taking the intersection of the vertical dashed line near the band edge, as shown in Fig. 5. Thus, the band gap of both samples of Zn0.98Mn0.02O is
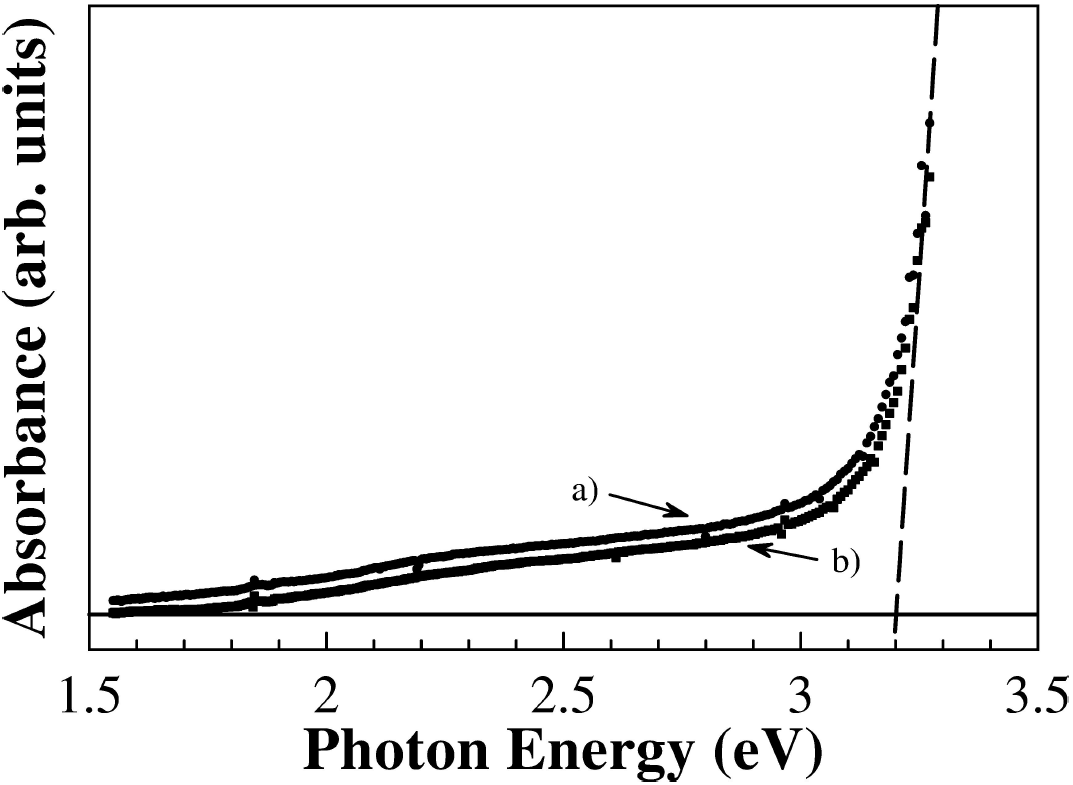
Figure 5. UV-Vis absorbance spectra at room temperature of Zn0.98Mn0.02O pellets (ZnO500, full circles a) and ZnO900, full squares b)). The horizontal line is the baseline and the vertical dashed line is a guide to eyes. The interception point is
The PL spectrum, at 10 K, of ZnO500 sample is shown in Fig. 6a, in which two emission bands at 3.309 and 3.365 eV are clearly seen. Although, the presence of only two bands, the assignments of these emissions are not obvious. Indeed, concerning the energy range of our 3.365 eV band, a recent PL study37 performed on high-pure ZnO bulk samples show that the near-band-edge emission is dominated by several bound excitons. Namely, in the energy region of 3.356 to 3.369 eV has been observed up to seven excitons bound to neutral (D0X) or ionized (D+X) donors, and up to four lines more on the high-energy side attributed to the excited states or excited rotator states of the neutral-donor-bound excitons38,39,40,41,42. Moreover, on the low-energy side, other two weak emissions have been observed and attributed to neutral acceptor bound excitons. Thus, the emission peak centered at 3.365 eV (labeled as DX in Fig. 6a) can be attributed to a process that involves both the recombination of excitons bound to neutral and/or ionized donor. It should be noted that this emission peak is broad and has an asymmetric shape on the lower energy side.
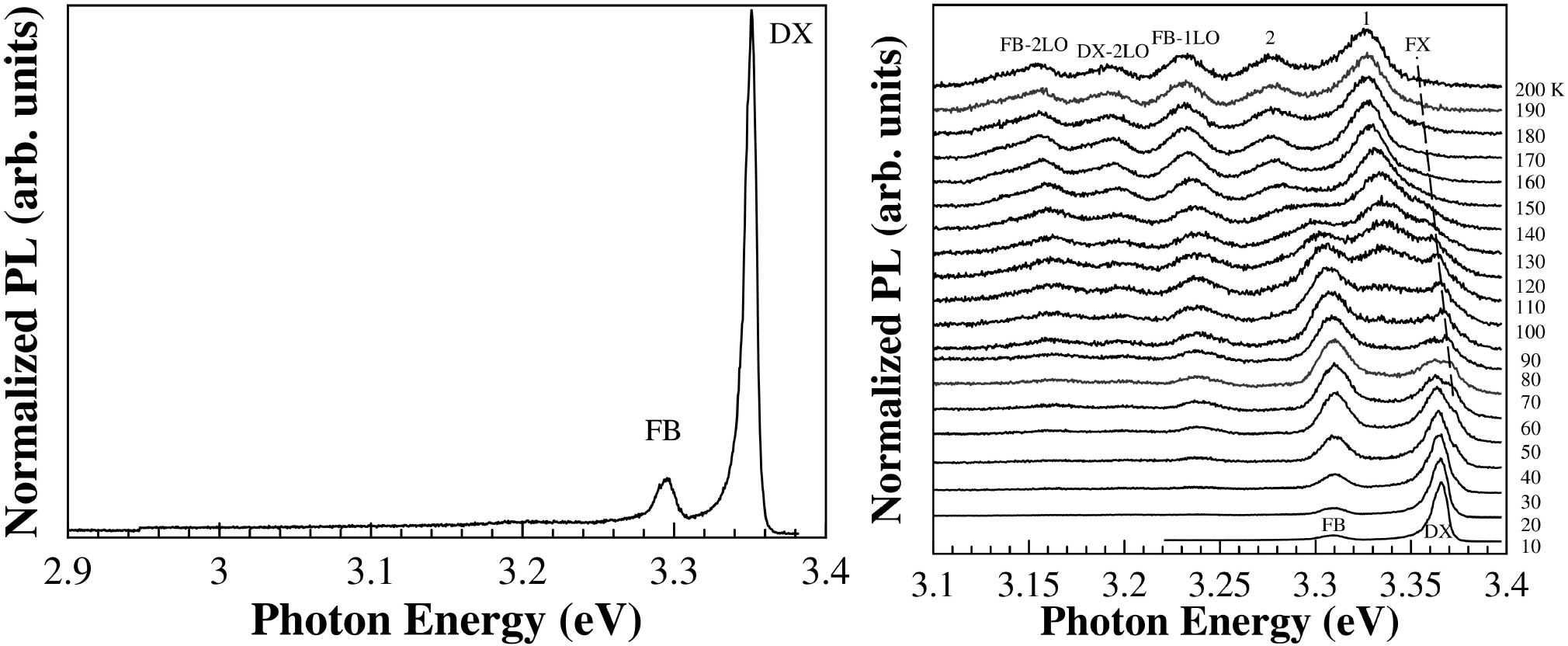
Figure 6. a) PL spectra of ZnO500 sample with the excitation 345 nm at 10 K. Temperature-dependence photoluminescence spectra of b) ZnO500 sample. The spectrum for each temperature is displaced vertically for clarity.
Concerning the low energy band (3.309 eV) seen in our samples (Fig. 6a), although commonly observed in high-pure ZnO bulk samples, the origin is not completely understood. Different mechanisms have been considered and are summarized in Ref.37. The energy distance between the FX line and this emission line, although almost constant (61-62 meV) is smaller than the energy of an LO phonon (71 meV). Based on (i) the temperature behavior of this band, namely the asymmetric lineshape on the high energy side at a higher temperature (see Fig. 6b) and (ii) on the PL results obtained in ZnO nanowires 37, we proposed that this emission may come from a free-to-bond (FB) recombination.
Figure 6b) show the PL spectra of ZnO500 sample as a function of temperature. It is clearly seen the decrease in intensity and a shift to lower energies of the main bands as also the presence of new PL features in the lower energy side of DX with the increase of the temperature. Figure 7a) shows the peak position of all the bands as a function of the temperature. It is seen that the energy separation between these new features is constant with temperature and can be attributed to optical phonon replicas, indicated as FB-1LO and FB-2LO emissions (see Fig. 7a) have an energy separation between 70 to 75 meV in good agreement with the energy value (574 cm-1 = 71 meV) for A 1 - LO phonon. The emission labeled as FB-2TO has an energy separation between 101-109 eV consistent with twice the energy value (410 cm-1 = 51 meV) for E 1 - LO phonon.
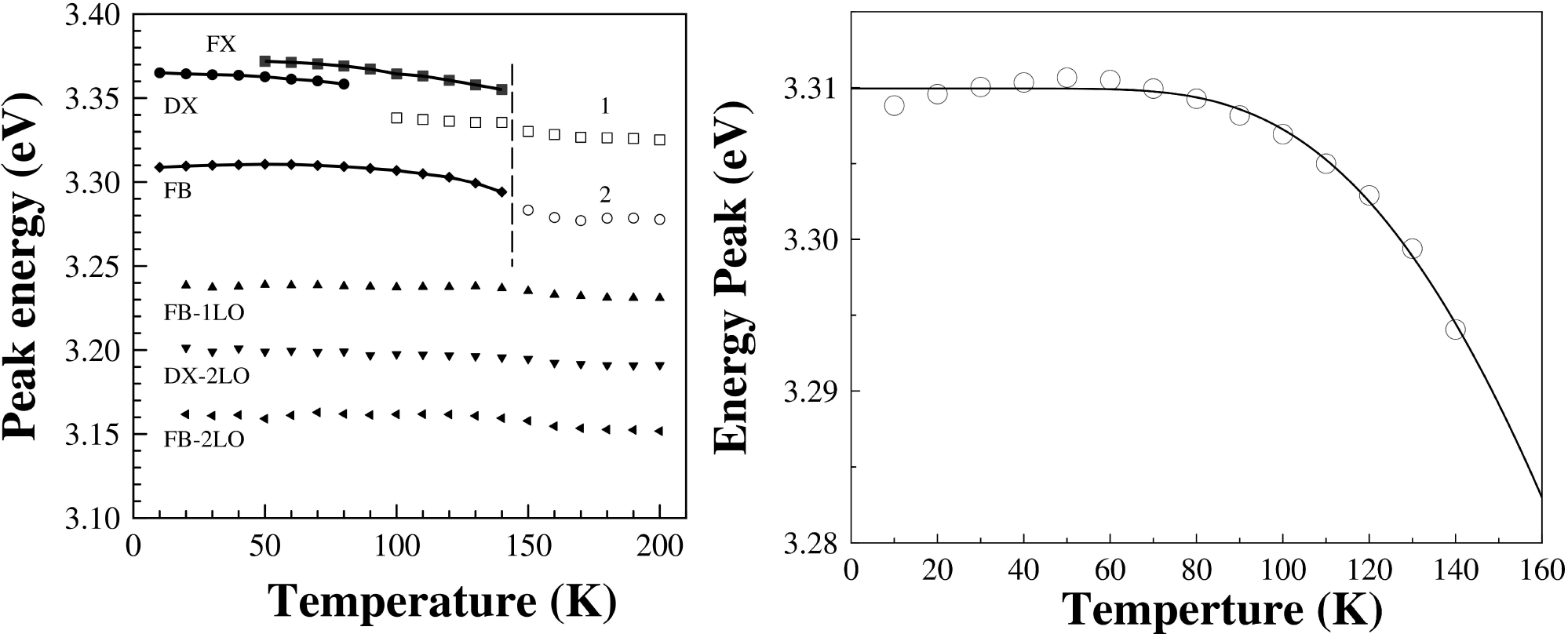
Figure 7. a) The peak energy is plotted against the temperature. The solid lines represent fits with Eq. (2). The dashed vertical line at 150 K is a guide for eyes. b) FB emission peak against the temperature, the solid line represent fits with Eq. (2).
The temperature dependence of the exciton energies was analyzed by fitting a single Bose-Einstein frequency according to43
where A 1 is a parameter that describes the variation of the energy with the temperature and n BE is the Bose-Einstein factor:
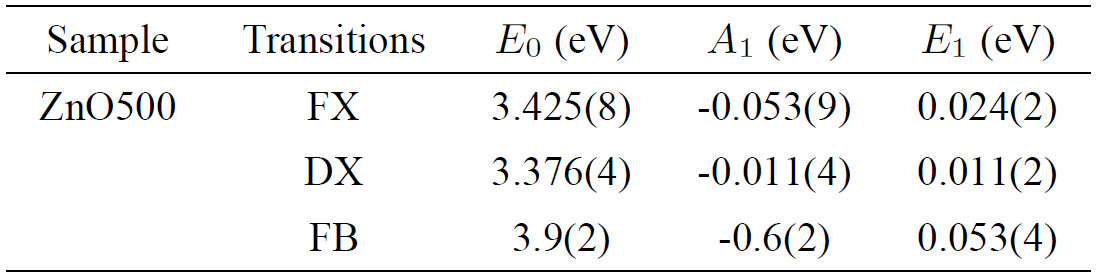
The fitted values E 0, E 1 and the weight A 1 are summarized in Table IV. The fitted values of A 1 and E 1 were found to be similar to the previous report for exciton energies of CuGaS2, CuGaSe2 and CuGaTe243. The choice of the Bose-Einstein model was motivated by the reported limitations44 of the well-known Varshni equation45.
Table IV. Parameters obtained from a fit of a single Bose-Einstein frequency, according to Eq. (1), to the experimental data of Zn0.98Mn0.02O pellets displayed in Fig. 7b).
The FX and FB emissions disappear at 150 K (see Fig. 7a). For above of 100 K appears a peak starting from 3.3382 eV (open squares) labeled as 1 and at 150 K appears to emerge another peak labeled as 2 that starting 3.2833 (open circle) and the signal intensity of it peaks goes up as the temperature is raised from 100 K to room temperature. We think that emission peaks involving phonon replicas of FX dominate the high-temperature spectra. On the other hand, the FB emission shows a slight anomalous temperature behavior with a maximum at
4. Conclusions
This paper reports the structural, electronic and vibrational properties of hexagonal ZnO doped with Mn2+ by means of SEM, XRD, UV-Vis absorption, PL spectroscopy and Raman spectroscopy. An extra mode at











 text new page (beta)
text new page (beta)