Research
A nonextensive wavelet (q,q´)-entropy for 1/𝑓α signals
J. Ramírez-Pachecoa
*
L. Rizo-Domínguezb
J.A. Trejo-Sáncheza
J. Cortez-Gonzálezc
aDepartamento de Ciencias Básicas e Ingeniería, Universidad del Caribe, Lote 1, Mza 1, Esq. Fracc. Tabachines, 77528, Cancún, Q. Roo, México.
bDepartamento de Electrónica, Sistemas e Informática, Instituto Tecnológico y de Estudios Superiores de Occidente, ITESO, 45604, San Pedro Tlaquepaque, Jalisco, México.
cDepartamento de Ingeniería y Tecnología, Instituto Tecnológico de Sonora, 85000, Ciudad Obregón, Sonora, México.
Abstract
This paper proposes a nonextensive wavelet (q,q')-entropy computed as a wavelet-domain generalization of the time-domain (q,q') entropy of Borges and obtains a closed-form expression of this measure for the class of 1/fα signals. Theoretical wavelet (q,q')-entropy planes are obtained for these signals and the effect of parameters q and q' on the shape and behaviour of these wavelet entropies are discussed with sufficient detail. The relationship of this entropy with Shannon and Tsallis entropies is studied and some applications of the proposed two-parameter wavelet entropy for the analysis/estimation of 1/f signals are outlined.
Keywords: Nonextensive entropies; wavelet information tools; 1=f α signals
PACS: 89.75.Da; 89.75.Cf; 61.43.-j; 05.20.-y; 05.10.Gg
1.Introduction
In statistical mechanics, the concept of entropy has traditionally been employed to measure the information content or uncertainty of a random signal or system 1,2. In the current literature, entropic functionals, such as the Shannon, Rényi and Tsallis entropies, have been used to quantify the complexities associated to random and nonlinear phenomena 3,4. Moreover, more elaborate information functionals, such as the so-called information planes 5, which consist of the product of entropy functionals and the Fisher information (and also of entropy and dissequilibrium), are currently being applied in numerous fields, for instance, in analyzing two-electron systems 6, many particle systems 7, randomness and localization of molecules 8 and x-ray astrophysical sources 9. In order to obtain an estimate of such an information functional within a signal or system, a probability density function (pdf) for continuous signals or probability mass function (pmf) for sampled data is required. Traditionally, pmfs in time and frequency domain are used, however, in recent years, with the advent of multiscale analysis and time-frequency distributions, wavelet-domain pmfs are utilized giving rise to the so-called wavelet entropies 10, generalized wavelet Fisher informations 11, among others. The advantages of extending spectral and time entropies to the wavelet domain are numerous including the possibility to analyze nonstationary signals or time-varying behaviour. Wavelets, also permit to compute entropies for specific details or resolutions of the signal in order to capture particular behaviour. Applications of such wavelet entropy functionals are diverse, from electroencephalogram (EEG) and electrocardiogram (ECG) signal analysis 12,13 to laser propagation 14 and characterization of complexity within random signals 15. Scale-invariant or 1/f signals, on the other hand, have been used to model a variety of phenomena in Physics and many other areas of science 16. For instance, Gilmore and co-workers 17 found evidence of scaling behaviour in plasma turbulence. Moreover, 1/fα noise behaviour was found in carbon nanotubes in 18 and this behaviour seems to be ubiquitous since it has been found in disciplines as diverse as Chemistry 19, Physiology 20, Psychology 21, Biomedical Engineering 22 among others. Within scale-invariant signal analysis, the estimation of the scaling parameter, α, plays a role of relevant importance since it determines the form of autocorrelation functions23 , the shape and behaviour of sample paths, the stationarity and nonstationarity of realizations24 , among other properties25 . Many techniques for estimating α have been proposed, however, nowadays, no single technique is able to accurately estimate α under the variety of complexities found in real measured data23,24,25 . Recently, wavelet-based information tools have found application in the analysis of 1/f signals 10,15,23,26. Wavelet information tools characterize adequately the theoretical complexities of these signals and as a consequence may help the signal analyst to propose tools or methodologies for their analysis/estimation. For instance, in 11, a novel technique based on generalized wavelet Fisher information allowed to detect level-shifts in fractional Gaussian noise (fGn) signals of parameter H. Generalized wavelet Fisher information not only detected and located level-shifts accurately but also permitted to enhance the time required to obtain an estimate than by using a standard tool of level-shift detection/location . Wavelet information tools, therefore offer many advantages and are becoming the tool of choice for analyzing the information content of a signal. In this contribution, a two parameter, nonextensive wavelet (q,q')-entropy for 1/fα signal analysis is proposed. This two-parameter entropy not only generalizes Shannon and Tsallis entropy but also provides more analysis flexibility due to its two-parameter nature and nonextensivity. This means that the Shannon and the Tsallis entropies can be obtained as special cases of their parameter values and moreover, due to its additional parameter q', increased sensitivity in the analyses may be obtained. In addition, its nonextensive nature makes it suitable for analysing 1/fα signals 27. The entropy planes for this two-parameter entropy are obtained for a variety of values of the parameter α and their relationship with the standard Shannon and Tsallis entropies is also found. The motivation behind the wavelet (q,q')-entropy is that it provides alternative configurations of parameters values for q and q' to analyze the same phenomena and the possibility to increase sensitivity in the analyses. The rest of the article is structured as follows. In Sec. 2, the concept of 1/f signals, wavelets and the wavelet analysis of 1/f signals is briefly revisited. Section 3 presents the wavelet (q,q')-entropy and computes the wavelet (q,q')-entropy of 1/fα signals. It also presents the wavelet (q,q')-entropy planes for 1/fα signals, obtained for a variety of values of the nonextensivity parameters q and q'. Section 4 outlines some applications of the wavelet (q,q')-entropy for the analysis of 1/f signals and presents some simple example applications on synthesized 1/f signals. Finally, Sec. 5 draws the conclusions of the article.
2. Wavelet analysis of 1/𝑓α signals
1/fα signals are ubiquitous in many fields of science and engineering and model phenomena as diverse as deoxyribonucleic acid (DNA) sequences 28, heart-beat time series 29, mood and self-steem 30. 1/fα signals are traditionally defined in terms of their power spectral density (PSD) which behaves as a power-law in a range of frequencies, i.e., as,
S(f)∼cf|f|-α, f∈(fa,fb),
1
where cf is a constant, α∈R is the scaling parameter and fa,fb represent the lower and upper bounds upon which holds 31. Depending upon α,fa and fb, several well-known random processes are obtained, e.g., when fb>fa, fa→0 and 0<α<1, long-memory signals result. Moreover, for all α∈R, 1/f signals are self-similar in the sense that their distributional properties are invariant under dilations in time and space. 1/f signals are stationary if α<1 and nonstationary if α>1
24. The well-known fractional Brownian motion (fBm), a Gaussian, nonstationary and self-similar signal with parameter H whose autocovariance is given by,
EBH(t)BH(s)=σ22|t|2H+|s|2H-|t-s|2H,
2
with H∈(0,1), has a spectral density given by
SfBm(f)∼c|f|-(2H+1), f→0,
3
and thus is a 1/fα signal with α
=2H+1
24,25. Fractional Gaussian noise (fGn), which is obtained from a fBm process via a differencing operation, is stationary, self-similar, Gaussian and has a PSD of the form 16,24,25:
SfGn=4σX2cHsin2(πf)∑j=-∞∞1|f+j|2H+1,|f|<12,
4
for H ϵ (0, 1). In the limit of 𝑓→0, the PSD of fGn behaves as SfGn∼c|f|-2H+1 and therefore is a 1/f signal with α=2H-1.
Wavelet analysis permits to represent a signal as a sum of small waves called wavelets. It has been employed for the analysis of complex time series 32 and 1/fα signal analysis/estimation 10,15,31. Wavelet analysis can be computed in two different ways allowing to capture different behaviour within a signal. The discrete wavelet transform (DWT) is primarily used for computing wavelet variance, entropy, etc. The continuous wavelet transform (CWT), on the other hand, is more convenient for quantifying the cycles, synchronization as well as the correlation within one or more time series via the wavelet cross-correlation and wavelet coherence . In this article, the DWT is employed and the wavelet spectrum is computed. The wavelet spectrum obtains the variances of DWT coefficients at each wavelet scale j and allows not only to estimate the scaling parameter α but also to obtain a pmf which in turn can be used to compute entropic functionals. In the work of Abry 31, the wavelet spectrum was studied and a formula for computing the wavelet spectrum of random signals was given by,
EdX2(j,k)=∫-∞∞SX(2-jf)|Ψ(f)|2 df,
5
where Ψ(f)=∫ψ(t)e-j2πft dt is the Fourier integral of the mother wavelet ψ(t), SX(.) is the PSD of the process Xt, E the expectation operator and dX(j,k) is the DWT of the process Xt at time k and wavelet scale j 31. Using the well-known PSD of 1/fα signals as given by Eq. (1) and substituting it into Eq. (5), the wavelet spectrum of 1/f signals results in:
EdX2(j,k)=C2jα,
6
where C is a constant. The wavelet spectrum obtained in Eq.(6) has been used to esitmate α 31 and also for computing wavelet-based information tools10,11 . For further information on wavelets, either continuous or discrete and in the wavelet analysis of 1/f signals please refer to 31,32 and references therein.
3. Wavelet (q,q') entropy of 1/fα signals
In this article, a two parameter wavelet (q,q')-entropy for 1/fα signal analysis is proposed. To obtain an expression for succh a wavelet entropy, a pmf in the DWT domain is required. As a matter of fact, by the use of Eq.(6) , the wavelet spectrum of 1/fα signals, the DWT pmf of these signals is given by:
pj=E^j∑i=1NE^i,
7
where E^j=Nj-1EdX2(j,k) and Nj represents the number of DWT coefficients at scale j. Equation (7) is indeed a pmf since 0<pj<1, ∑jpj=1 and ∑j1pj<∑j2pj for j1<j2. Equation (7), also called the relative wavelet energy (RWE) 10, quantifies the energy of a random signal per resolution level j. The RWE for the class of 1/ f α signals is therefore given by substituting(6) into (7) 10,11,15i.e.,
pj,1/f=2(j-1)α1-2α1-2αN,
8
where N and j represent the (logarithmic) length of the signal and the wavelet scale respectively. Many wavelet-based information tools have been obtained using Eq.(8) , the wavelet Fisher informations of 11 and 26, the wavelet Tsallis q-entropy of 15, among others. The article proposes a novel wavelet (q,q')-entropy which is computed using (8). As mentioned earlier, the concept of entropy is used to quantify the information content of a signal and when computed in the wavelet-domain it allows to quantify the information content at different resolution levels, thus adjusting the analyses to the nature of the data. An important requirement of any information functional is its ability to analyze linear, nonlinear and phenomena exhibiting long-range interactions. Tsallis entropy allows these type of analyses, however, it is limited to a single configuration of its parameter q. This means that Tsallis q-entropies can, for example, classify signals using a specific value of q but no other value of q can perform the same classification. There is, thus, a need for an information functional to provide alternative configurational parameters to analyze the same problem. The (q,q)'-entropy provides additional flexibility in the sense that it has an additional nonextensivity parameter q´ and the question is if it is able to provide alternative configurations of their parameter values to analyze a given problem. In this article, this (q,q')-entropy, originally proposed by Borges 34 is generalized to the wavelet domain and closed-form formulas of this entropy for 1/f signals are obtained. The (q,q')-entropy generalizes the Bolzmann-Gibbs statistic and the Tsallis q-entropy as well and is defined by the following equation 34,
H(q,q')T(πj)=∑j=1Nπjq-πjq'N1-q-N1-q' .
9
where q,q'∈R are the nonextensivity parameters. When q'→1, the usual normalized Tsallis q-entropy results and when q→1 and q'→1, the normalized Shannon entropy is obtained. (q,q')-entropy, therefore, increases not only parameter flexibility but also the possibility to obtain the same type of results as Shannon or Tsallis by adjusting q and q′ properly. As a matter of fact, Eq.(9) can be rewritten in terms of the Tsallis q-entropy (and Tsallis q'-entropy) as follows,
H(q,q')T(πj)=HqT(πj)1-N1-qN1-q-N1-q'-Hq'T(πj)1-N1-q'N1-q-N1-q'.
10
where HqT(πj) and Hq'T(πj) represent the normalized Tsallis q-entropy and Tsallis q'-entropy for distribution πj.
Substituting Eq.(8) into (10) and using the results 23 of the wavelet (q,q') entropy of 1/fα signals is given by:
H(q,q')T(πj)={PN-1(2cosh(αq'ln22))(PN-1(2cosh(αln22)))q'-PN-1(2cosh(αqln22))(PN-1(2cosh(αln22)))q}×(N1-q-N1-q')-1
11
where PN-1(2coshu) is a polynomial of order N-1, i.e.,
PN-1(.)=(2coshu)N-1-(N-2)1!(2coshu)N-3+(N-3)(N-4)2!(2coshu)N-5-…
12
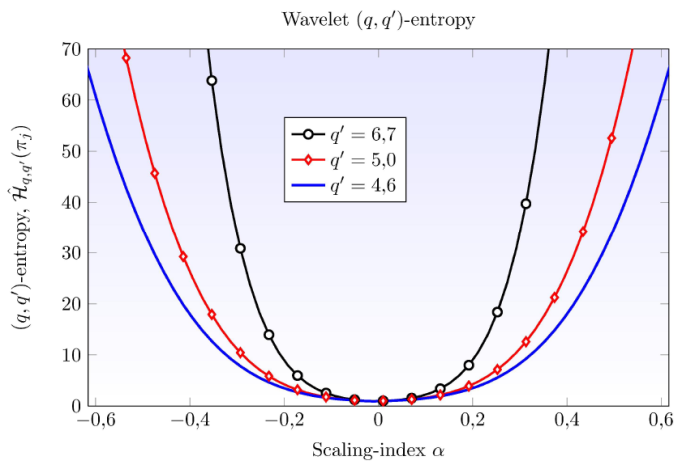
At this point and based on the results of Eqs.(11) and (12), an interesting question is how the wavelet (q,q')-entropy behaves according to the different values of q and a q´ and to investigate if different sets of values of q and q´ may permit to analyze the same problem, say detecting specific behaviour within a signal. The first question is answered if the wavelet (q,q')-entropy planes for different q and q´ are obtained and the second by identifying planes which in principle may be different but provide a similar description of a given phenomena. In the following, the entropy planes obtained for particular values of the nonextensivity parameters q and q´ are studied. Wavelet entropy planes can also be used for identifying potential applications of this entropy for the analysis/estimation of 1/f signals. Figure 1, shows the wavelet entropy plane for the nonextensivity parameters q =7 and q´ = 4 and which is a typical behaviour of wavelet (q,q')-entropies when q>1 and q'∈R-{1}. For these cases, the observed wavelet entropies are monotonically increasing and are not normalized to 1. Interestingly, wavelet (q,q')-entropies have even symmetry and for a range of the form (-αa,αa), zero entropies are observed. This symmetric range of zero entropies can be stretched depending upon the values of the nonextensivity parameters q and q´. The length of the signal N and the nonextensivity parameter q´ have the effect of increasing the rate at which entropies increase and in the same way of reducing the range of zero entropies as shown in Fig. 1. Increasing N, increases the rate at which entropies increase. Parameter q´ also increases this rate, however follows an interesting behaviour which depends upon the positivity or negativity of q´. To investigate further the effect of q´ on the shape of wavelet (q, q´) entropy planes, Fig. 2 displays a particular example when q = 13, N = 10 and negative q´. Note that as q´ decreases, the entropies increase more rapidly and the range of constant entropies decreases. Figure 3 displays another example when N =12, q = 7but using positive values of the nonextensivity parameter q´. Note that for this case, entropies increase more rapidly with higher values of q′ and the range of zero entropies decreases. From this, it is concluded that the rate at which entropies increase is boosted whenever q´ becomes more negative or q´ becomes more positive (mantaining N and q fixed). Figure 4 displays another wavelet entropy plane obtained when q=9 and q′→1. Note that in this case, wavelet entropies are monotonically decreasing and normalized to 1. This behaviour is similar to the one observed for the wavelet Tsallis q-entropy and the parameter q, in this case, permits to stretch the range over which constant entropies are observed. In contrast to Fig. 1, the wavelet (q, q´)-entropy plane of Fig. 4 is not sensitive to the length of the signal. Note that Fig. 1 and Fig. 4 provide alternative ways of characterizing complexity. The configuration of Fig. 1 treats purely random 1/f signals ( α=0) with zero entropies while the configuration of q and q´ values of Fig. 4 assigns unity entropies to these random signals.
4. Applications
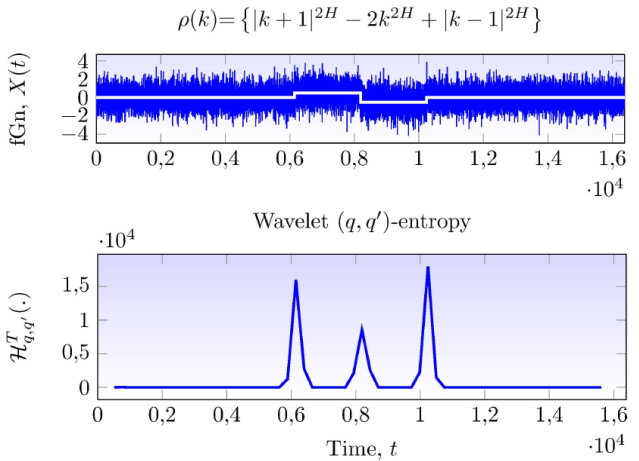
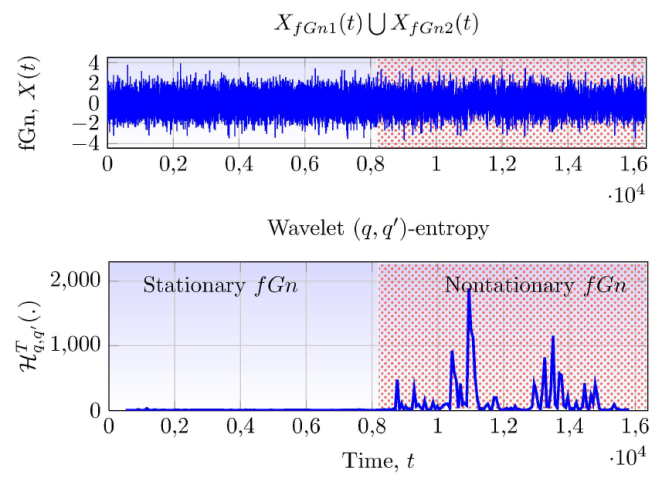
Wavelet (q, q´)-entropy may have several applications not only for the analysis/estimation of 1/ f α signals but also for the characterization of the complexities of any random signal. For 1/fα signal analysis and estimation, wavelet (q, q´)-entropy may help increase the accuracy of estimating algorithms by identifying and eliminating level-shifts that bias the estimations. Moreover, based on the results of Sec. 3, wavelet (q, q´)-entropy can also be used for classifying 1/f signals as stationary/nonstationary, extended fBms from fBms, among others. The 1/f signal classification problem as stationary or nonstationary is fundamental for 1/f signal estimation since the selection of the estimators of the parameter α is based on the stationarity nature of the signal. Some estimators work only in stationary signals while others are more suitable under nonstationary ones . Classification of 1/fα signals as stationary or nonstationary can be performed with wavelet (q, q´)-entropy in two different ways using different configuration of values for the nonextensivity parameters q and q′. First, by adjusting the range of zero frequencies in Fig. 1 to α∈(-1,1), an efficient way to classify 1/f signals reduces to the problem of identifying signals with zero entropies from varying ones. Therefore, a methodology for discriminating stationary signals from nonstationary ones is to compute entropies in sliding windows and to detect regions of zero entropies (which correspond to stationary signals) from regions of entropies that present variable behaviour (nonstationary signals). A second approach which is similar to the above one is based on the behaviour of entropies of Fig. 4. In this case, stationary behaviour is distinguished from nonstationary one based on the fact that stationary signals experiment constant unity entropies while entropies for nonstationary signals vary. Figure 5 provides a simple demonstration of the stationarity/nonstationarity classification capabilities of wavelet (q, q´)-entropy. Top plot represents a concatenated time series in which the first time points up to the middle of the duration are from a stationary signal and the rest come from a nonstationary signal. Bottom plot of Fig. 5 display the wavelet (q, q´)-entropy from the concatenated signal using sliding windows of length W=1024, q = 8 and q´= 6. Note that the entropies for the first part of the signal (stationary) are zero while entropies corresponding to the second half part vary. This simple example demonstrates that a robust and powerful technique for discriminating 1/fα signals based on wavelet (q, q´)-entropy can be obtained. Another interesting application of wavelet (q, q´)-entropy is in the field of level-shift detection and location. It has been shown in the work of Stoev that a single level-shift has the effect of overestimating H yielding H > 1, thus, wavelet (q, q´)-entropy applied to a segment with a single level-shift will result in an entropy value suddently decaying to zero (or sudently increasing above zero) resembling an impulse shaped form. Therefore, the wavelet (q, q´)-entropy of signal with level-shifts will result in a signal composed of impulses. The location and strength of the impulse is related to the location and amplitude of the level-shift. With the use of wavelet (q, q´)-entropy, a level-shift detection/location problem becomes in a peak detection and location problem. Figure 6 displays an example in which a signal with 3 level-shifts is detected by the use of wavelet (q, q´)-entropy. Therefore, with the use of wavelet (q, q´)-entropy, an efficient and fast methodology for detecting and locating weak level-shifts can be designed. Many other applications can be perfomed with the use of wavelet (q, q´)-entropy, the purpose of this article, however is not to investigate applications but to present the wavelet (q, q´)-entropy, their theoretical properties on 1/fα signals and highlight some potential applications.
5. Conclusions
In this article, a novel wavelet (q, q´)-entropy for the analysis of 1/fα signals was proposed. The entropy was obtained as a waveler-domain extension of the (q, q´) entropy of Borges and permits to quantify the complexities and information content of random signals and systems using the DWT. Closed-form expressions for this entropy are found for the class of 1/fα signals and based on this, wavelet (q, q´)-entropy planes are obtained. Wavelet (q, q´)-entropy planes, as demonstrated, are not only useful for explaining the complexities of 1/f signals but also for identifying potential applications for their analysis/estimation. A detail study of the behaviour of wavelet (q, q´)-entropy planes was presented for a variety of values of parameters q and q´. Finally, two possible application areas of the wavelet (q, q´)-entropy, specifically for classifying 1/fα signals and for detecting level-shifts within fGn signals were outlined. It was shown that wavelet (q, q´)-entropy may provide promising and robust techniques for signal classification and level-shift detection/location.
Acknowledgements
Julio C. Ramírez-Pacheco thanks the support of CONACYT grant for project infrastructure and PROMEP grant. J. Cortez-González thanks the support of PROFOCIE 2014.
References
1. J. Bonachela, H. Hinrichsen and M.A. Muñoz, J. Phys. A: Math. Theor. 41 (2008) 202001.
[ Links ]
2. U. Kumar, V. Kumar and J.N. Kapur, Int. J. Gen. Syst. 12 (1986) 55.
[ Links ]
3. M. Martin, A.R. Plastino and A. Plastino, Phys. A 275 (2000) 262.
[ Links ]
4. M. Rajković, Phys. A 340 (2004) 327.
[ Links ]
5. C. Vignat and J.-F. Bercher, Phys. Lett. A 312 (2003) 27.
[ Links ]
6. E. Romera and J.S. Dehesa, J. Chem. Phys. 120 (2004) 8906.
[ Links ]
7. E. Romera, and Á. Nagy, Phys. Lett. A 372 (2008) 6823.
[ Links ]
8. R. O. Esquivel, J. C. Angulo, J. Antolín, J. S. Dehesa, S. López-Rosa and N. Flores-Gallegos, Phys. Chem. Chem. Phys. 12 (2010) 7108.
[ Links ]
9. M. Lovallo and L. Telesca, J. Stat. Mech-Theory E., 2011 (2011) P03029.
[ Links ]
10. L. Zunino, D.G. Pérez, M. Garavaglia and O.A. Rosso Phys. A 379 (2007) 503.
[ Links ]
11. J. Ramirez-Pacheco, H. Toral-Cruz, L. Rizo-Dominguez and J. Cortez-Gonzalez, Adv. Math. Phys. 2015 (2015) 1.
[ Links ]
12. P.A. Ritto, Rev. Mex. Fis. 57 (2011) 362.
[ Links ]
13. O. A. Rosso and A. Figliola, Rev. Mex. Fis. 50 (2004) 149.
[ Links ]
14. L. Zunino, D.G. Pérez, M. Garavaglia and O.A. Rosso Fractals 12 (2004) 223.
[ Links ]
15. D.G. Pérez Zunino, M.T. Martin, M. Garavaglia, A. Plastino and O.A. Rosso Phys. Lett. A 364 (2007) 259.
[ Links ]
16. B. Pilgram and D. T. Kaplan, Physica D 114 (1998) 108.
[ Links ]
17. M. Gilmore, C.X. Yu, T.L. Rhodes and W.A. Peebles, Phys. Plasmas 9 (2002) 1312.
[ Links ]
18. P. G. Collins, M.S. Fuhrer and A. Zettl, Appl. Phys. Lett. 76 (2000) 894.
[ Links ]
19. A. Bancaud, C. Lavelle, S. Huet and J. Ellenberg, Nucleic Acids Res. 40 (2012) 8785.
[ Links ]
20. T. Stadnitski, Front. Physiol. 3 (2012) 127.
[ Links ]
21. G.C. Van Orden, J.G. Holden and M.T. Turney, J. Exp. Psychol. Gen. 134 (2005) 117.
[ Links ]
22. A. Schaefer, J. Brach, S. Perera and E. Sejdic, J. Neurosci. Meth. 222 (2014) 118.
[ Links ]
23. J. Ramirez-Pacheco, D. Torres-Román and H. Toral-Cruz, Math. Probl. Eng. 2012 (2012) 1.
[ Links ]
24. F. Serinaldi, Phys. A. 389 (2010) 2770.
[ Links ]
25. J. C. Gallant, I. D. Moore, M. F. Hutchinson and P. Gessler, Math. Geol. 26 (1994) 455.
[ Links ]
26. J. Ramirez-Pacheco et al., Entropy. 14 (2012) 1478.
[ Links ]
27. C. Tsallis, J. stat. phys. 52 (1998) 479.
[ Links ]
28. R. F. Voss, Phys. Rev. Lett. 68 (1992) 3805.
[ Links ]
29. A. De Felice G. D’Addio, M. Cesarelli, G. Balzano and A. Accardo, Eur. Respir. J. 42 (2013) P2560.
[ Links ]
30. D. Deligneres, S. Ramdani, L. Lemoine, K. Torre, M. Fortes and G. Ninot, J. Math. Psychol. 50 (2006) 525.
[ Links ]
31. P. Abry and D. Veitch, IEEE T. Inform. Theory. 44 (1998) 2.
[ Links ]
32. J. S. Murguía and E. Campos-Cantón, Rev. Mex. Fis. 52 (2006) 155.
[ Links ]
33. L. Aguiar-Conraria, N. Azevedo and M.J. Soares, Phys. A 387 (2008) 2863.
[ Links ]
34. E.P. Borges, Phys. Lett. A 246 (1998) 399.
[ Links ]
35. S. Stoev, M. Taqqu, C. Park and J. S. Marron, Comput. Netw. 48 (2005) 423.
[ Links ]













 text new page (beta)
text new page (beta)