Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista mexicana de física
Print version ISSN 0035-001X
Rev. mex. fis. vol.53 suppl.2 México Feb. 2007
From conformal Killing vector fields to boost–rotational symmetry
J. Estevez–Delgado* and T. Zannias**
* Facultad de Ciencias Físico–Matemáticas, Universidad Michoacana de San Nicolás de Hidalgo, Morelia, Mich, MÉXICO, e–mail: joaquin@fismat.umich.mx
** Instituto de Física y Matemáticas, Universidad Michoacana de San Nicolás de Hidalgo, Apartado Postal 82, 58040 Morelia, Mich, MÉXICO, e–mail: zannias@ginette.ifm.umich.mx
Recibido el 18 de julio de 2005
Aceptado el 14 de marzo de 2005
Abstract
We discuss a connection between three–dimensional Riemannian manifolds (Σ,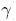 ) admitting a special conformal Killing vector field ξ and static vacuum or non–vacuum spacetimes. Any such (Σ,
) admitting a special conformal Killing vector field ξ and static vacuum or non–vacuum spacetimes. Any such (Σ,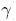 ) generates a vacuum spacetime (M,g) but it also generates a spacetime (M, g, Φ), where (g, Φ) satisfies the Einstein–Klein–Gordon massless minimally coupled gravity equations, or the Einstein–Conformal scalar field equations. The resulting spacetimes either admit four Killing vector fields or possess boost and rotational symmetry. We argue that this connection goes beyond the vacuum or Einstein–scalar field system and it should be viewed as a mechanism of generating solutions for the Einstein equations, admitting a hypersurface orthogonal Killing vector field.
) generates a vacuum spacetime (M,g) but it also generates a spacetime (M, g, Φ), where (g, Φ) satisfies the Einstein–Klein–Gordon massless minimally coupled gravity equations, or the Einstein–Conformal scalar field equations. The resulting spacetimes either admit four Killing vector fields or possess boost and rotational symmetry. We argue that this connection goes beyond the vacuum or Einstein–scalar field system and it should be viewed as a mechanism of generating solutions for the Einstein equations, admitting a hypersurface orthogonal Killing vector field.
Keywords: General relativity; conformal Killing vector field; Einstein equations.
Resumen
Se discute la conexión entre variedades Riemannianas (Σ,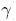 ) de dimension tres que admiten un campo vectorial de Killing conforme ξ y espacios– tiempo estáticos asociados a sistemas en el vacío o no–vacío. Cualquiera de estas variedades (Σ,
) de dimension tres que admiten un campo vectorial de Killing conforme ξ y espacios– tiempo estáticos asociados a sistemas en el vacío o no–vacío. Cualquiera de estas variedades (Σ,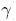 ) generan un espacio–tiempo (M, g) e igual generan un espacio–tiempo (M, g,Φ), donde (g, Φ) satisfacen las ecuaciones para el campo escalar asociadas a los sistemas de Einstein–Klein–Gordon con acoplamiento mínimo o conforme. Los espacios–tiempo asociados resultantes admiten cuatro campos vectoriales de Killing o una simetría de "boost" y rotacional. Se argumenta como esta conexión va mas allá de los sistemas en el vacío o de los sistemas de campos escalares y esto puede ser visto como un mecanismo para generar soluciones de las ecuaciones de Einstein, que admitan un campo vectorial de Killing ortogonal a una hipersuperficie.
) generan un espacio–tiempo (M, g) e igual generan un espacio–tiempo (M, g,Φ), donde (g, Φ) satisfacen las ecuaciones para el campo escalar asociadas a los sistemas de Einstein–Klein–Gordon con acoplamiento mínimo o conforme. Los espacios–tiempo asociados resultantes admiten cuatro campos vectoriales de Killing o una simetría de "boost" y rotacional. Se argumenta como esta conexión va mas allá de los sistemas en el vacío o de los sistemas de campos escalares y esto puede ser visto como un mecanismo para generar soluciones de las ecuaciones de Einstein, que admitan un campo vectorial de Killing ortogonal a una hipersuperficie.
Descriptores: Relatividad general; campo vectorial de Killing conforme; ecuaciones de Einstein.
PACS: 04.20.jb; 04.20.–q
DESCARGAR ARTÍCULO EN FORMATO PDF
Acknowledgments
The present work was sparked after Prof. Alberto Garcia pointed out to us the relevance of Ref. 13 to a generalized family of C–metrics constructed in Ref. 3. Our thanks to him and also to U.Nucamendi for discussions regarding the issues raised in this work. The research of TZ was partially supported by grant of Coordinación Científica – UMSNH while JED would like to acknowledge financial support through PROMEP via a grant: PTC–74.
References
1. R.M. Wald, General Relativity, (Chicago. Univ. Press. 1984). [ Links ]
2. Müller zum Hagen, D.C. Robinson, and H. J. Seifert, Gen. Rel. Grav. 4 53 (1973); [ Links ] D.C. Robinson, Gen. Rel. Grav. 8 (1977) 695. [ Links ]
3. J. Estevez Delgado and T. Zannias, J. Math. Phys. 43 (2002) 519. [ Links ]
4. J. Estevez–Delgado and T. Zannias: On Riemannian manifolds admitting a conformal Killing vector and static spacetimes. (submitted). [ Links ]
5. J. Estevez–Delgado and T. Zannias, Class. Quant. Grav. 24 (2004) 5147. [ Links ]
6. J. Estevez–Delgado and T. Zannias, (IFM report Unpublished, 2002). [ Links ]
7. In this work our sign convection for signature, Riemann, Ricci and components of extrinsic curvature are identical to those of Ref. 1.
8. J. Ehlers and W. Kundt in: Relativity, Introduction to current Research (Ed. L. Witten, Acad. Press, 1962). [ Links ]
9. H. Bondi, Rev. Mod. Phys. 29 (1957) 423. [ Links ]
10. J. Bicak and B. Schmidt, Phys. Rev. D. 40 (1989) 1627. [ Links ]
11. W.B. Bonnor, Gen. Rel. and Grav. 15 (1983) 535. [ Links ]
12. F.H.J. Cornish and W.J. Uttley, Gen. Rel. and Gravit 27 (1995) 439; [ Links ]Gen. Rel. and Gravit 27 (1995) 735. [ Links ]
13. W. Kinersley and M. Walker, Phys. Rev. D. 2 (1970) 1359. [ Links ]
14. A. Ashtekar and T. Dray, Commun. Math. Phys. 79 (1981) 581. [ Links ]
15. J. Estevez–Delgado: On three Lorentzian manifolds admitting a conformal Killing vector field and vacuum spacetimes. (in preparation). [ Links ]














